江苏省南通中学高二数学上学期期末考试试题苏教版

江苏省南通市第一初级中学高二数学理上学期期末试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 一炮弹在某处爆炸，在A处听到爆炸声的时间比在B处晚2s，则爆炸点所在曲线为( ) A．椭圆的一部分B．双曲线的一支C．.线段D．圆参考答案：B【考点】双曲线的定义；双曲线的标准方程．【专题】对应思想；数学模型法；圆锥曲线的定义、性质与方程．【分析】根据题意，结合双曲线的定义，即可得出爆炸点的轨迹为双曲线的一支．【解答】解：∵声速为340 m/s，以直线AB为x轴，线段BA的中点为坐标原点，建立直角坐标系；设炮弹爆炸点的轨迹上的点P（x，y），由题意可得|PA|﹣|PB|=680＜|AB|，∴点P（x，y）所在的轨迹为双曲线的一支．故选：B．【点评】本题考查了双曲线的定义与应用问题，是基础题目．2. 为了考察两个变量x和y之间的线性相关性，甲、乙两个同学各自独立做了15次和20次试验，并且利用线性回归方法，求得回归直线为l1和l2，已知在两人的试验中发现对变量x的观测数据的平均值恰好相等，都为s，对变量y的观测数据的平均值也恰好相等，都为t，那么下列说法正确的是()A. 直线l1和直线l2有交点(s，t)B. 直线l1和直线l2相交，但交点未必是点(s，t)C. 直线l1和直线l2必定重合D. 直线l1和直线l2由于斜率相等，所以必定平行参考答案：A【分析】根据回归直线过样本数据中心点，并结合回归直线的斜率来进行判断。

【详解】由于回归直线必过样本的数据中心点，则回归直线和回归直线都过点，做了两次试验，两条回归直线的斜率没有必然的联系，若斜率不相等，则两回归直线必交于点，若斜率相等，则两回归直线重合，所以，A选项正确，B、C、D选项错误，故选：A.【点睛】本题考查回归直线的性质，考查“回归直线过样本数据的中心点”这个结论，同时也要抓住回归直线的斜率来理解，考查分析理解能力，属于基础题。

2021年江苏省南通中学高二年级期末考试数学注意事项：1. 本试卷分选择题与非选择题两部分。

2. 答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置。

3. 全部答案在答题卡上完成，答在本试题上无效。

4. 考试结束后，将本试题和答题卡一并交回。

一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.数列{a n}是等比数列，公比为q，且a1>0.则“q<−1”是“∀n∈N∗，2a2n−1+a2n<a2n+1”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件2.已知等差数列{a n}的前n项和为S n，且S n=n2.定义数列{b m}如下：m+1mb m(m∈N∗)是使不等式a n≥m(m∈N∗)成立的所有n中的最小值，则b1+b3+b5+⋯+b19=()A. 25B. 50C. 75D. 1003.电影《夺冠》讲述中国女排姑娘们顽强奋斗、为国争光的励志故事，打造一部见证新中国体育改革40年的力作，该影片于2020年09月25日正式上映．在《夺冠》，上映当天，一对夫妇带着他们的两个小孩一起去观看该影片，订购的4张电影票恰好在同一排且连在一起．为安全起见，影院要求每个小孩子要有家长相邻陪坐，则不同的坐法种数是()A. 8B. 12C. 16D. 204.小李年初向银行贷款M万元用于购房，购房贷款的年利率为P，按复利计算，并从借款后次年年初开始归还，分10次等额还清，每年1次，问每年应还()万元．()A. M10B. MP(1+P)10(1+P)10−1C. M(1+P)1010D. MP(1+P)9(1+P)9−15.已知抛物线y2=2px(p>0)的焦点为F，准线l与x轴交于点H，过焦点F的直线交抛物线于A，B两点，分别过点A，B作准线l的垂线，垂足分别为A1，B1，如图所示，则：①以线段AB为直径的圆与准线l相切；②以A1B1为直径的圆经过焦点F；③A，O，B1(其中点O为坐标原点)三点共线；★绝密启用前④若已知点A 的横坐标为x 0，且已知点T(−x 0,0)，则直线TA 与该抛物线相切． 则以上说法中正确的个数为( )A. 1B. 2C. 3D. 46. 《九章算术》与《几何原本》并称现代数学的两大源泉．在《九章算术》卷五商功篇中介绍了羡除(此处是指三面为等腰梯形，其他两侧面为直角三角形的五面体)体积的求法．在如图所示的羡除中，平面ABDA′是铅垂面，下宽AA′=3m ，上宽BD =4m ，深3m ，平面BDEC 是水平面，末端宽CE =5m ，无深，长6m(直线CE 到BD 的距离)，则该羡除的体积为( )A. 24m 3B. 30m 3C. 36m 3D. 42m 37. 如图，某伞厂生产的“太阳”牌太阳伞的伞蓬是由太阳光的七种颜色组成，七种颜色分别涂在伞蓬的八个区域内，且恰有一种颜色涂在相对区域内，则不同的颜色图案的此类太阳伞至多有( ) A. 40320种 B. 5040种C. 20160种D. 2520种8. 已知点P 是椭圆x 216+y 212=1(xy ≠0)上的动点，F 1、F 2为椭圆的左、右焦点，O 为坐标原点，若M 是∠F 1PF 2的角平分线上的一点，且F 1M ⃗⃗⃗⃗⃗⃗⃗⃗ ⋅MP ⃗⃗⃗⃗⃗⃗ =0，则|OM ⃗⃗⃗⃗⃗⃗⃗ |的取值范围是( ) A. (0,2)B. (0,√3)C. (0,4)D. (2,2√3)二、选择题：本题共4小题，每小题5分，共20分。

高二上学期期末数学试题一、单选题1．在等比数列中，，公比，则（ ） {}n a 13a =2q =4a =A ．24 B ．48 C ．54 D ．66【答案】A【分析】根据等比数列通项公式基本量计算出答案.【详解】．33413224a a q ==⨯=故选：A2．曲线处的切线与直线平行，则实数（ ） y =()1,1y kx =k =A ． B ．C ．D ．12-12-12【答案】C【分析】根据导数的几何意义求解．【详解】时，，所以． y '=1x =12y ¢=12k =故选：C ．3．已知平面的一个法向量，平面的一个法向量，若，则α()13,0,n λ= β()22,1,6n =αβ⊥λ=（ ）A ．B ．4C ．D ．1921-【答案】C【分析】根据题意，由面面垂直可得法向量也相互垂直，结合空间向量的坐标运算，代入计算即可得到结果.【详解】因为，则可得，αβ⊥12n n ⊥且，， ()13,0,n λ= ()22,1,6n =则可得，解得 660λ+=1λ=-故选:C4．若直线与圆相切，则实数取值的集合为（ ）340x y m ++=2220x y y +-=mA ．B ．C ．D ．{}1,1-{}9,1-{}1{}8,2-【答案】B【分析】根据题意，由直线与圆相切可得，结合点到直线的距离公式，代入计算，即可得到d r =结果.【详解】由圆可得，表示圆心为，半径为的圆，2220x y y +-=()2211x y +-=()0,11则圆心到直线的距离340x y m ++=d 因为直线与圆相切，340x y m ++=2220x y y +-=所以，解得或，d r =11m =9m =-即实数取值的集合为 m {}9,1-故选:B5．已知，则n ＝（ ）22A C 30n n +=A ．3B ．4C ．5D ．6【答案】C【分析】利用排列数、组合数公式得到，解方程即得解. ()31302n n -=【详解】解：，整理得， ()()()22131A C 13022n nn n n n n n --+=-+==2200n n --=解得（舍），． n =-45n =故选：C ．6．函数的图象如图所示，则函数的图象可能是y ()y ()f x f x ==，的导函数y ()f x =A ．B ．C ．D ．【答案】D【详解】原函数先减再增，再减再增，且位于增区间内，因此选D ．0x =【名师点睛】本题主要考查导数图象与原函数图象的关系：若导函数图象与轴的交点为，且图x 0x 象在两侧附近连续分布于轴上下方，则为原函数单调性的拐点，运用导数知识来讨论函数单0x x 0x 调性时，由导函数的正负，得出原函数的单调区间．'()f x ()f x 7．安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有 ()A ．12种 B ．18种 C ．24种 D ．36种【答案】D【详解】4项工作分成3组,可得：=6，24C 安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成， 可得：种． 36363A ⨯=故选D.8．已知数列首项为2，且，则（ ）{}n a 112n n n a a ++-=n a =A ． B ． C ． D ．2n 121n -+22n -122n +-【答案】D【分析】由已知的递推公式，利用累加法可求数列通项.【详解】由已知得，，则当时，有112n n n a a ++-=12a =2n ≥ ，12111221()()(222)n n n n n n n a a a a a a a a -----=-+-++-=+++()12121121222222222212n n n n n n n a a --+-=++++=++++==-- 经检验当时也符合该式．∴.1n =122n n a +=-故选：D二、多选题9．下列四个选项中，不正确的是（ ） A ．数列，的一个通项公式是 2345,,,3456⋯1n n a n =+B ．数列的图象是一群孤立的点C ．数列1，，1，，与数列，1，，1，是同一数列1-1-⋯1-1-⋯D ．数列，，是递增数列11,24⋯12n 【答案】ACD【分析】由可判断A ；由数列的通项公式以及可判断B ；由数列定义可判断C ； 11223a =≠N*n ∈由递减数列定义可判断D ． 【详解】对于A ，当通项公式为时，，不符合题意，故选项A 错误；1n n a n =+11223a =≠对于B ，由数列的通项公式以及可知，数列的图象是一群孤立的点，故选项B 正确； N*n ∈对于C ，由于两个数列中的数排列的次序不同，因此不是同一数列，故选项C 错误；对于D ，数列，，是递减数列，故选项D 错误．11,24⋯12n 故选：ACD ．10．下列结论中正确的有（ ） A ．若，则B ．若，则 sin3y π=0y '=2()3(1)f x x f x =-'(1)3f '=C ．若，则D ．若，则y x =1y ='+sin cos y x x =+cos sin y x x +'=【答案】ABC【解析】根据常见的基本初等函数的导数公式和常用的导数运算法则求解即可.【详解】选项A 中，若，故A 正确； sin3y π==0y '=选项B 中，若，则， 2()3(1)f x x f x =-⋅'()6(1)f x x f '-'=令，则，解得，故B 正确； 1x =(1)6(1)f f ''=-(1)3f '=选项C 中，若，则，故C 正确；y x =+1y ='+选项D 中，若，则x ，故D 错误． sin cos y x x =+cos sin y x x '=-故选:ABC【点睛】1.常见的基本初等函数的导数公式 (1) (C 为常数); ()0C '＝(2)； ()1()nn x nx n '∈N －＋＝(3); ； ()sinx cosx '＝()cosx sinx '＝-(4);，且)； ()xx e e '＝()(0x x a a lna a '>＝1a ≠(5)； ，且)． 1(ln )'=x x a a 1 (log )'=log e(a>0x x1a ≠2.常用的导数运算法则法则1： ． ()()()()[]u x v x u x v x ±''±'＝法则2：． ()()()()()()[]u x v x u x v x u x v x '''＝＋法则3： ()()()()()()()()22[](0)u x u x v x u x v x v x v x v x '''≠-＝11．已知名同学排成一排，下列说法正确的是（ ） 7A ．甲不站两端，共有种排法 1656A A B ．甲、乙必须相邻，共有种排法 5252A A C ．甲、乙不相邻，共有种排法2555A A D ．甲不排左端，乙不排右端，共有种排法7657652A A A -+【答案】AD【分析】A 选项通过特殊元素法判断；B 选项利用捆绑法判断；C 选项利用插空法判断；D 选项用总情况减去不满足的情况即可.【详解】A 选项：甲不站两端，甲有种，剩余6人全排，共有种排法，正确；15A 1656A A B 选项：甲、乙必须相邻，甲、乙捆绑有种，作为整体和剩余5人全排，共有种排法，错22A 2626A A 误；C 选项：甲、乙不相邻，先排其他5人有种，再把甲、乙插入6个空中，共有种排法，错55A 5256A A 误；D 选项：甲不排左端，乙不排右端，用7人全排减去甲在左端的和乙在右端的，再加上甲在左端同时乙在右端的，共有种排法，正确.7657652A A A -+故选：AD.12．如图，在四面体中，点在棱上，且满足，点，分别是线段，OABC M OA 2OM MA =N G BC的中点，则用向量，，表示向量中正确的为（ ）MN OA OB OCA ．B ．111344GN OA OB OC =-++111344OG OA OB OC =-+C ． D ．113232GM OA OB OC =++111344GM OA OB OC =--【答案】AD【分析】连接，利用空间向量基本定理以及空间向量的线性运算进行求解即可. ON 【详解】连接，ON因为点，分别是线段，的中点，N G BC MN 所以，111211()222322OG OM ON OA OB OC =+=⨯+⨯+ 化简可得，故B 错误；111344OG OA OB OC =++所以，故A 正确 1111111()()2344344GN ON OG OB OC OA OB OC OA OB OC =-=+-++=-++ ，故C 错误，D 正确；11121113443344GM GO OM OA OB OC OA OA OB OC =+=---+=--故选：.AD三、填空题13．已知，1，、，2，、，，，若向量与垂直为坐标原(2A 3)(4B -)x (1C x -2)OA OB + OC(O点），则等于__． x 【答案】4【分析】由向量垂直的坐标表示求解.【详解】，()()()2,1,3,4,2,,1,,2OA OB x OC x ==-=-，∴()2,3,3OA OB x +=-+向量与垂直，OA OB + OC，∴()·23260OA OB OC x x +=--++=．4x ∴=故答案为：4．四、双空题14．已知函数，则函数的单调递增区间是______，值域为______．()()212log 43f x x x =-+-【答案】[2,3)[0,)+∞【解析】令，求得函数的定义域，根据在其定义域内为单调减函2430t x x =-+->()12log f x t =数，求函数的单调递增区间转化为求函数在定义域内的减区间，再利用()()212log 43f x x x =-+-t 二次函数的值域求整个函数的值域.【详解】解：令，可得，故函数的定义域为. 2430t x x =-+->13x <<()1,3因为在其定义域内为单调减函数，()12log f x t =故求在定义域内的减区间，又函数在定义域内的减区间为，243t x x =-+-t [2,3)所以函数的单调递增区间为，()()212log 43f x x x =-+-[2,3)当时，，则，()1,3x ∈243(0,1]t x x =-+-∈()12log [0,)f x t =∈+∞即函数的值域为. ()()212log 43f x x x =-+-[0,)+∞故答案为：；.[2,3)[0,)+∞【点睛】本题主要考查复合函数的单调性，对数函数、二次函数的性质，体现了转化的数学思想，属于基本知识的考查.五、填空题15．求和：Sn ＝1＋＋＋1＋＋＋＋…＋＝________.1(12+11(1)24++1214181111(1)242n -+++⋯+【答案】2n ＋－2 112n -【分析】先化简数列，结合分组求和法即可求解． 1212k ka ⎛⎫=- ⎪⎝⎭【详解】被求和式的第k 项为：111111121211242212kk k k a -⎛⎫- ⎪⎛⎫⎝⎭=++++==- ⎪⎝⎭-所以Sn ＝2＝22111(1)(1(1)222n -+-+⋯+-231111(2222n n ⎡⎤-+++⋯+⎢⎥⎣⎦ 111111222212212212n n n n n n -⎡⎤⎛⎫- ⎪⎢⎥⎡⎤⎛⎫⎝⎭⎢⎥=-=--=+- ⎪⎢⎥⎝⎭⎢⎥⎣⎦-⎢⎥⎣⎦故答案为：2n ＋－2． 112n -16．如图，圆形花坛分为部分，现在这部分种植花卉，要求每部分种植种，且相邻部分不能441种植同一种花卉，现有种不同的花卉供选择，则不同的种植方案共有______种（用数字作答）5【答案】260【分析】先分1，3相同与1，3不相同两类，每类中按分步计数原理，分2，4相同或不同两类求解，然后再分类计数原理求和.【详解】根据题意：当1，3相同时，2，4相同或不同两类，有：种， ()5411380⨯⨯⨯+=当1，3不相同时，2，4相同或不同两类，有：种， ()54312180⨯⨯⨯+=所以不同的种植方案共有种， 80180260+=故答案为：260【点睛】本题主要考查计数原理的应用问题，还考查了分析求解问题的能力，所以中档题.六、解答题17．已知等比数列的首项为2，前项和为，且. {}n a n n S 234230S S S -+=(1)求；n a(2)已知数列满足：，求数列的前项和. {}n b n n b na ={}n b n n T 【答案】(1)2n n a =(2)()1122n n T n +=-⋅+【分析】（1）根据题意，由可得公比，再由等比数列的通项公式即可得到结234230S S S -+=q 果；（2）根据题意，由错位相减法即可求得结果. 【详解】（1）设等比数列的公比为，{}n a q 因为，所以，234230S S S -+=()234320S S S S -+-=所以，所以，所以.342a a =2q =112n n n a a q -==（2）由（1）得，，所以，……①2nn b n =⨯212222n n T n =⨯+⨯++⨯ 所以，……②()23121222122n n n T n n +=⨯+⨯++-⨯+⨯ ①-②，得，()()21112122222212212n nn n n n T n n n +++⨯--=+++-⨯=-⨯=-⨯-- 所以.()1122n n T n +=-⋅+18．已知双曲线的实轴长为，一个焦点的坐标为-.2222:1x y C a b-=()0,0a b >>4()-（1）求双曲线的标准方程;（2）已知斜率为的直线与双曲线交于，两点，且的方程.1l C A B AB =l 【答案】（1）；（2）22148x y -=1y x =±【分析】（1）由双曲线的实轴长及焦点坐标，再由，，之间的关系求出，进而求出双曲线a b c b 的方程；（2）由题意设直线的方程，与双曲线联立求出两根之和及两根之积，进而求出弦长的AB ||AB 值，再由题意可得参数的值，即求出直线的方程．AB【详解】（1）由得，又，24a =2a =c =2228b c a =-=故双曲线的方程为．22148x y -=（2）设直线的方程为，代入双曲线方程可得，l y x m =+22280x mx m ---=设，，，，则，．1(A x 1)y 2(B x 2)y 122x x m +=2128x x m =--因为||AB ==， ==1m =±所以直线的方程为．l 1y x =±19．从4面不同颜色（红、黄、蓝、绿）的旗子中，选出3面排成一排作为一种信号，共能组成多少种信号？ 【答案】24【分析】分步完成：第一步选3面旗帜，第二步3面旗帜全排列，由此可得．【详解】从4面不同颜色旗子中，选出3面排成一排能组成种信号．3343C A 24=20．为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用（单位：万元）与隔热层厚度（单位：cm ）满足关系：，设为C x ()()4011035C x x x =≤≤+()f x 隔热层建造费用与20年的能源消耗费用之和． (1)求的表达式；()f x (2)隔热层修建多厚时，总费用达到最小，并求最小值． ()f x 【答案】(1) 800()635f x x x =++()110x ≤≤(2)当隔热层修建5cm 厚时，总费用最小，最小值为70万元．【分析】（1）根据已给模型确定函数解析式； （2）利用导数求得最小值．【详解】（1）每年能源消耗费用为，建造费用为， 40()35C x x =+6x ．． ()()800206635f x C x x x x ∴=+=++()110x ≤≤（2），令得或（舍． ()()22400'635f x x =-+()0f x '=5x =253x =-)当时，，当时，．∴15x ≤<()0f x '<510x <≤()0f x '>在，上单调递减，在，上单调递增．()f x ∴[15)[510]当时，取得最小值（5）．∴5x =()f x f 70=当隔热层修建厚时，总费用最小，最小值为70万元．∴5cm21．三棱柱中，，，线段的中点为，且111ABC A B C -112AB AB AA AC ====120BAC ∠= 11A B M .BC AM⊥(1)求证：平面；AM ⊥ABC (2)点在线段上，且，求二面角的余弦值. P 11B C 11123B P B C =11P B A A --【答案】(1)证明见解析【分析】（1）由、根据线面垂直的判定定理可得平面；AB AM ⊥BC AM ⊥AM ⊥ABC （2）以为原点，以所在的直线为建立空间直角坐标系，求出平面、A 、、AN AC AM x y z 、、11B AA 平面的一个法向量由二面角的向量求法可得答案.1PB A 【详解】（1）三棱柱中，，111ABC A B C -11//AB A B 在中，，线段的中点为，所以，所以；11AB A △11AB AA =11A B M 11A B AM ⊥AB AM ⊥因为，平面，平面，，平面，所以BC AM ⊥BC ⊂ABC AB ⊂ABC AB BC B ⋂=AB BC ⊂、ABC 平面； AM ⊥ABC （2）做交于点，AN AC ⊥BC N 以为原点，以所在的直线为建立空间直角坐标系，A 、、AN AC AM x y z 、、则，，， ()0,0,0A )1,0B-112B -，.()0,2,0C (M 所以，，，112AB =-()BC =(AM = 因为，所以，111222,033B P B C BC ⎛⎫=== ⎪ ⎪⎝⎭32P ⎛ ⎝所以，32AP ⎛= ⎝ 设平面的一个法向量，则， 11B AA ()1111,,n x y z =11111111020n AB y n AM ⎧⋅=-+=⎪⎨⎪⋅==⎩ 解得，令，所以， 10z=1y 11x =()1n = 设平面的一个法向量，则， 1PB A ()2222,,n x y z =222221222302102n AP y n AB x y ⎧⋅=+=⎪⎪⎨⎪⋅=-=⎪⎩令，，所以， 2y =23x =21z =-()21n =- 设二面角的平面角为，则11P B A A --()0180θθ≤≤ ，121212cos cos ,n n n n n n θ⋅==== 由图知二面角的平面角为锐角，11P B A A --所以二面角11P B A A --22．已知函数，．()()2e x f x x ax a =--R a ∈(1)讨论函数的单调性；()f x (2)当时，证明：．0a =()2(ln 2)f x x x >+【答案】(1)答案见解析；(2)证明见解析.【分析】（1）求出函数的导数，再分类讨论求出不等式，的解集作()f x ()f x '()0f x '<()0f x ¢>答.（2）将不等式等价变形，再分别证明和即可作答.e 1x x >+ln 1x x ≥+【详解】（1）依题意，，令，则或()()()()222e 2e x x f x x a x a x x a '⎡⎤=+--=+-⎣⎦()0f x '=2x =-.x a =当时，，则函数在上单调递增； 2a =-()()22e 0x f x x '+≥=()f x R 当时，当时，，当时，，2a >-()2,x a ∈-()0f x '<()(),2,x a ∈-∞-∞+ ()0f x ¢>于是得在，上单调递增，在上单调递减；()f x (),2-∞-(),a +∞()2,a -当时，当时，，当时，，2a <-(),2x a ∈-()0f x '<()(),2,x a ∞∞-∈-+ ()0f x ¢>因此函数在、上单调递增，在上单调递减，()f x (),a -∞()2,-+∞(),2a -所以当时，的单调递增区间为，，单调递减区间为；2a >-()f x (),2-∞-(),a +∞()2,a -当时，在上单调递增；2a =-()f x R 当时，函数的单调递增区间为，，单调递减区间为.2a <-()f x (),a -∞()2,-+∞(),2a -（2）当时，，，，0a =()2e x f x x =0x >()222(ln 2)e (ln 2)e ln 2x x f x x x x x x x >+⇔>+⇔>+令，则，函数在上单调递增，()e 1,0x g x x x =-->()e 10x g x '=->()g x (0,)+∞，，即，(0,)∀∈+∞x ()(0)0g x g >=e 1x x >+令，，当时，，当时，， ()ln 1,0h x x x x =-->1()1h x x'=-01x <<()0h x '<1x >()0h x '>即函数在上单调递减，在上单调递增，，，即()h x (0,1)(1,)+∞(0,)∀∈+∞x ()(1)0h x h ≥=，ln 1x x ≥+于是得，而，因此，，e 1ln 2x x x >+≥+20x >22e (ln 2)x x x x >+所以成立.()2(ln 2)f x x x >+【点睛】关键点睛：利用导数探讨含参函数的单调性，求出导数后分类讨论解不等式是解决问题的关键.。

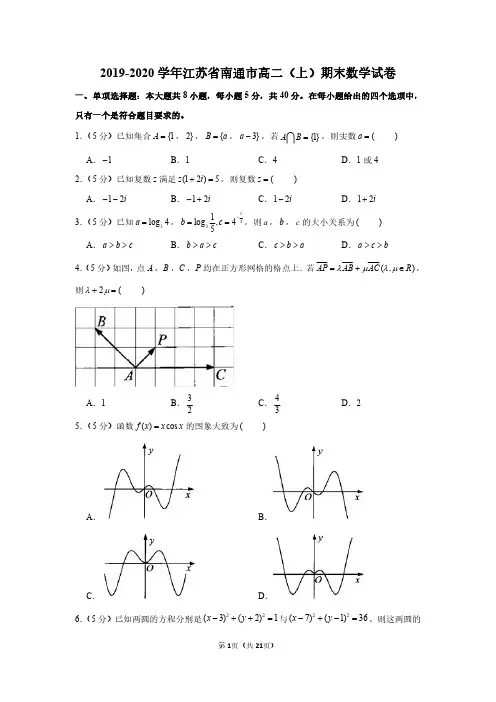
2019-2020学年江苏省南通市高二（上）期末数学试卷一、单项选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一个是符合题目要求的。

1．（5分）已知集合{1A =，2}，{B a =，3}a -，若{1}A B = ，则实数(a =)A ．1-B ．1C ．4D ．1或42．（5分）已知复数z 满足(12)5z i +=，则复数(z =)A ．12i--B ．12i-+C ．12i-D ．12i+3．（5分）已知3log 4a =，1331log ,45b c -==，则a ，b ，c 的大小关系为()A ．a b c >>B ．b a c >>C ．c b a >>D ．a c b>>4．（5分）如图，点A ，B ，C ，P 均在正方形网格的格点上．若(,)AP AB AC R λμλμ=+∈，则2(λμ+=)A ．1B ．32C ．43D ．25．（5分）函数()cos f x x x =的图象大致为()A ．B ．C ．D ．6．（5分）已知两圆的方程分别是22(3)(2)1x y -++=与22(7)(1)36x y -+-=，则这两圆的位置关系是()A ．内含B ．内切C ．相交D ．外切7．（5分）八音是中国古代对乐器的统称，包含“金、石、土、革、丝、木、匏(páo )、竹”八类，每类又包括若干种乐器．现有“土、丝、竹“三类乐器，其中“土”包括“缶(fǒu )、埙(x ūn )“2种乐器：“丝”包括“琴、瑟、筝、琵琶”4种乐器：“竹”，包括“箫、笛、笋“3种乐器．现从这三类乐器中各选1种乐器分配给甲、乙、丙三位同学演奏，则不同的分配方案有()A ．24种B ．72种C ．144种D ．288种8．（5分）已知22221(0)x y a b a b+=>>的左、右顶点分别为1A ，2A ，上、下顶点分别为1B ，2B ，右焦点为F ，直线11A B 与直线2B F 相交于点T ．若2A T 垂直于x 轴，则椭圆的离心率(e =)A ．13B C ．12D 二、多项选择题：本大题共4小题，每小题5分，共20分。

江苏省南通市数学高二上学期理数期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2016高二下·金沙期中) 已知i是虚数单位，则复数z=（1+2i）（2﹣i）的虚部为（）A . ﹣3B . ﹣3iC . 3D . 3i2. （2分） (2017高二下·三台期中) 设x∈R，则“x3=x“是“x=1“的（）A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件3. （2分） (2018高二下·衡阳期末) 抛物线的准线方程是（）A .B .C .D .4. （2分）给定下列三个命题：p1：若p∧q为假命题，则p，q均为假命题p2：∃a，b∈R，a2﹣ab+b2＜0；p3：在三角形ABC中，A＞B，则sinA＞sinB．则下列命题中的真命题为（）A . p1∨p2B . p2∧p3C . p1∨（￢p3）D . （￢p2）∧p35. （2分） (2017高一下·包头期末) 已知椭圆的左焦点为F，C与过原点的直线相交与A,B两点，连接若，则C的离心率为（）A .B .C .D .6. （2分）双曲线x2-2y2=1的右焦点的坐标为（）A .B .C .D .7. （2分）(2013·江西理) 等比数列x，3x+3，6x+6，…的第四项等于（）A . ﹣24B . 0C . 12D . 248. （2分） (2017高二上·太原期末) 抛物线y2=8x的准线方程是（）A . x=2B . y=2C . x=﹣2D . y=﹣29. （2分）(2020·阿拉善盟模拟) 如图，在三棱柱中，底面为正三角形，侧棱垂直底面，, .若，分别是棱，上的点，且，，则异面直线与所成角的余弦值为（）A .B .C .D .10. （2分） (2017高三下·深圳月考) 若双曲线的焦点到渐近线的距离是焦距的，则该双曲线的离心率为（）A .B .C . 2D .11. （2分）设数列的前n项和为Sn ，令，称Tn为数列a1 ， a2 ，，an的“理想数”，已知数列a1 ， a2 ，，a500的“理想数”为2004，那么数列12， a1 ， a2 ，，a500的“理想数”为（）A . 2002B . 2004C . 2008D . 201212. （2分）将进货单价为80元的商品按90元一个售出时，能卖出400个，已知该商品每个涨价1元，其销售量就减少20个，为了赚得最大利润，售价应定为（）A . 每个95元B . 每个100元C . 每个105元D . 每个110元二、填空题 (共4题；共4分)13. （1分） (2020高二上·黄陵期末) 如图，在正三棱柱ABC﹣A1B1C1中，所有棱长均为1，则点B1到平面ABC1的距离为________．14. （1分） (2016高二下·静海开学考) 已知双曲线的顶点到渐近线的距离为2，焦点到渐近线的距离为6，则该双曲线的离心率为________．15. （1分） (2020高二上·青铜峡期末) 已知过抛物线的焦点的直线交该抛物线于、两点，，则坐标原点到直线的距离等于________ .16. （1分） (2015高二下·遵义期中) 在数列{an}中，a1=1，an+1= （n∈N*）猜想这个数列的通项公式为________．三、解答题 (共6题；共50分)17. （10分） (2017高一下·瓦房店期末) 已知等差数列的前项和为，， .（1）求数列的通项公式；（2）若，求数列的前项和 .18. （10分） (2017高二上·安阳开学考) P（x0 ， y0）（x0≠±a）是双曲线E：上一点，M，N分别是双曲线E的左右顶点，直线PM，PN的斜率之积为．（1）求双曲线的离心率；（2）过双曲线E的右焦点且斜率为1的直线交双曲线于A，B两点，O为坐标原点，C为双曲线上一点，满足，求λ的值．19. （5分） (2015高三上·日喀则期末) 在△ABC中，a，b，c分别为内角A，B，C的对边，且asinB=﹣bsin （A+ ）．（1）求A；（2）若△ABC的面积S= c2，求sinC的值．20. （10分）(2017·孝义模拟) 在正三角形ABC中，E、F、P分别是﹣AB、AC、BC边上的点，满足AE：EB=CF：FA=CP：PB=1：2（如图1）．将△AEF沿EF折起到△A1EF的位置，使二面角A1﹣EF﹣B成直二面角，连结A1B、A1P （如图2）．（1）求证：A1E⊥平面BEP；（2）求二面角B一A1P一F的余弦值的大小．21. （10分）(2017·丰台模拟) 如图所示的几何体中，四边形ABCD为等腰梯形，AB∥CD，AB=2AD=2，∠DAB=60°，四边形CDEF为正方形，平面CDEF⊥平面ABCD．（Ⅰ）若点G是棱AB的中点，求证：EG∥平面BDF；（Ⅱ）求直线AE与平面BDF所成角的正弦值；（Ⅲ）在线段FC上是否存在点H，使平面BDF⊥平面HAD？若存在，求的值；若不存在，说明理由．22. （5分）(2018·朝阳模拟) 如图，椭圆经过点，且点到椭圆的两焦点的距离之和为 .（1）求椭圆的标准方程；（2）若是椭圆上的两个点，线段的中垂线的斜率为且直线与交于点，为坐标原点，求证：三点共线.参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共50分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、22-1、22-2、。

江苏省南通中学2014—2015学年度上学期期末考试高二数学试题一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．． 1．计算： ▲ ．2．函数f (x )＝ln x x的单调增区间是 ▲ ． 3．已知复数z=(2－i) i ，则z 的模为 ▲ ．4．曲线在点处的切线方程为 ▲ ．5．如图所示四个图形中，着色三角形的个数依次构成一个数列的前4项，则这个数列的一个通项公式为 ▲ ．6．已知函数的导函数为，且满足，则 ▲ ．7．已知复数2sin i z θθ=+⋅，则的取值范围是 ▲ ．8．若函数是R 上的单调函数，则实数m 的取值范围为 ▲ ．9．如图为函数32()f x ax bx cx d =+++的图象，为函数的导函数，则不等式的解集为 ▲ ．10．设P 是函数y ＝x (x ＋1)图象上异于原点的动点，且该图象在点P 处的切线的倾斜角为θ，则θ的取值范围是 ▲ ．11．已知定义域为的函数对于任意的x 都满足．若0<a < b ，则bf (a ) ▲ af (b )（请从“>”，“<”，“=”中选择正确的一个填写）．12．设直线y ＝a 分别与曲线y 2＝x 和y ＝e x 交于点M ，N ，则当线段MN 取得最小值时实数a 的值为▲ ．13．已知点，是函数的图象上任意不同的两点，依据图象可知，线段总是位于，两点之间函数图象的上方，因此有结论成立.运用类比思想方法可知若点，是函数的图象上的不同两点，则类似地有 ▲ 成立．14．若不等式|ax 3－ln x |≥1对任意x (0，1]都成立，则实数a 的取值范围是 ▲ ．二、解答题：本大题共6小题，共计90分．请注意文理科类，并在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤．15．（本小题共14分） 已知复数2276(56)i 1a a z a a a -+=+--+（）． （1）求实数为何值时，z 为实数；（2）求实数为何值时，z 为虚数；（3）求实数为何值时，z 为纯虚数．16．（本小题共14分）已知曲线C ： 与直线相切，其中e 为自然对数的底数．（1）求实数a 的值；（2）求曲线C 上的点P 到直线的距离的最小值，并求出取得最小值时点P 的坐标．17．（本小题共14分）某集团为了获得更大的收益，每年要投入一定的资金用于广告促销．经调查投入广告费t (百万元)，可增加销售额约为－t 2＋5t (百万元)(0≤t ≤5) (注：收益＝销售额－投放)．（1）若该公司将当年的广告费控制在3百万元之内，则应投入多少广告费，才能使该公司由此获得的收益最大？（2）现该公司准备共投入3百万元，分别用于广告促销和技术改造．经预测，每投入技术改造费x (百万元)，可增加的销售额约为－13x 3＋x 2＋3x (百万元)．请设计一个资金分配方案，使该公司由此获得的收益最大．18．（本小题共16分）（理）已知数列的前n 项和．（1）计算数列的前4项；（2）猜想数列的通项公式，并用数学归纳法证明．（文）求证：1，，3不可能是一个等差数列中的三项．19．（本小题共16分）已知函数322()4361f x x tx t x t =+-+-，其中，．（1）当时，求的单调区间；（2）证明：对任意的，函数在区间内均存在零点．20. （本小题共16分）已知，函数，e 为自然对数的底数．（1）若，求函数取得极值时所对应的x 的值；（2）若不等式22(12e )()e ea a x ax f x +--+≤恒成立，求的取值范围．江苏省南通中学2014—2015学年度第一学期期末考试高二数学答案9． 10．⎣⎡⎭⎫π3，π2 11．12．22 13． 14．a ≥e 23二、解答题：15．解：（1）当z 为实数时，则解得.所以，当时，z 为实数．（2）当z 为虚数时，则解得．所以，当且时，z 为虚数．（3）当z 为纯虚数时，则22560,760,10,a a a a a ⎧--≠⎪-+=⎨⎪+≠⎩解得．所以，当时，z 为纯虚数．16．解：（1）设曲线C ： 与直线相切的切点的横坐标为，由得切线的斜率=，所以，所以切点坐标为，代入直线得.（2）由（1）得曲线C 的方程为：，当过点P 的切线与直线平行时，点P 到直线的距离最小，设点P 的横坐标为，由得切线的斜率=1，所以，所以所求点P 的坐标为，所求距离的最小值为．17．解：(1)设投入t (t 百万元)的广告费后增加的收益为f (t )(百万元)，则有f (t )＝(－t 2＋5t )－t ＝－t 2＋4t ＝－(t －2) 2＋4(0＜t ≤3)，所以当t ＝2百万元时，f (t )取得最大值4百万元．即投入2百万元时的广告费时，该公司由此获得的收益最大．(2)设用技术改造的资金为x (百万元)，则用于广告促销的资金为(3－x )(百万元)，则有g (x )＝⎝⎛⎭⎫－13x 3＋x 2＋3x ＋[－(3－x )2＋5(3－x )]－3＝－13x 3＋4x ＋3(0≤x ≤3) 所以g ′(x )＝－x 2＋4.令g ′(x )＝0，解得x ＝2，或x ＝－2(舍去)．又当0≤x ＜2时，g ′ (x )＞0，当2＜x ≤3时，g ′(x )＜0．故g (x )在[0,2]上是增函数，在[2,3]上是减函数．所以当x ＝2时，g (x )取最大值，即将2百万元用于技术改造， 1百万元用于广告促销，该公司由此获得的收益最大．18．（理）解：（1）由，得．由，得．由，得．由1234424a a a a a +++=⨯-，得．（2）猜想．下面用数学归纳法证明：①时，左边，右边，猜想成立．②假设当时，猜想成立，即，此时121222k k k k S k a k --=-=-． 则当时，由，得1112(1)2k k k S a k a +++-=+-， 所以111(1)1112121[2(1)]122222k k k k k k a k S k k ++-+-⎛⎫--=+-=+--= ⎪⎝⎭． 因此，当时，等式也成立．由①②可知，对均成立．（文）证明：假设1，，3为同一等差数列中的三项，则存在两个不相等的整数，以及实数，使得，．所以．因为上式左边为无理数，右边为有理数，所以等式不成立，所以假设不成立，即1，，3不可能是同一等差数列中的三项．19．（1）解：，令，解得或．因为，以下分两种情况讨论：①若，则，列表如下：②若，则，列表如下：（2）证明：由（1）可知，当时，在上单调递减，在上单调递增，以下分两种情况讨论：①当即时，在内单调递减，，2(1)643644230f t t =-++-⨯+⨯+<≤，所以对任意，在区间内均存在零点．②当即时，在上单调递减，在上单调递增， 若，()337710244t f t t t =-+--<≤， 2(1)643643230f t t t t t =-++-++=-+>≥．所以在上存在零点．若，()()3377110244t f t t t =-+-<-+<，． 所以在上存在零点．所以，对任意，在区间内均存在零点．综上所述，对任意，在区间内均存在零点．说明：（2）中()371,(0,2),24t f t t t =-+-∈也可通过求导证明其恒小于0． 20．解：（1）若，则，．当时，，单调递增；当时，，单调递减．又因为，，当时，；当时，；当时，；当时，．故取得极值时所对应的x 值为1，和．（2）不等式22(12e )()e e a a x ax f x +--+≤，整理为22(12)ln 0e e a x ax x a ++-+≤． 设22(12)()ln e ea x ax g x x a +=+-+， 则21212()ee ax a g x x +'=+-（其中）． ①当时，，，当时，，为单调增函数；当时，，为单调减函数．所以，．。

一、单选题1．若直线经过，两点，则直线的倾斜角为（ ） (1,0)A B AB A ． B ． C ． D ．30︒45︒60︒135︒【答案】A【分析】利用两点坐标求出直线的斜率，再求对应的倾斜角即可． AB【详解】由直线经过，， (1,0)A B设直线的倾斜角为，则有， θtan θ=又，所以. 0180θ︒≤<︒30θ=︒故选：A.2．若直线与直线互相平行，则实数（ ） 1:20l x y +=2:10l mx y ++=m =A ． B ．C ．D ．2122-12-【答案】A【分析】判断不合题意，再根据直线的平行列出相应的比例式，即可求得答案. 0m =【详解】当时，直线，直线与不平行， 0m =2:10l y +=1l 2l 当时，，0m ≠12//l l ，解得， ∴21011m =≠2m =故选：A.3．若等差数列的前项和为，且，则的值为（ ） {}n a n n S 21012a a +=11S A ． B ． C ． D ．334466132【答案】C【分析】根据结合即可求解. 110211a a a a +=+1111111()2a a S +=【详解】等差数列的前项和为，且， {}n a n n S 21012a a +=由等差数列的基本性质，得，21101112a a a a +=+=. ∴1111111()11126622a a S +⨯===故选：C.4．若直线与圆交于，两点，且，关于直线对1y kx =+2240x y kx my +++-=M N M N 20x y +=称，则实数的值为（ ）k m -A ．3B ．2C ．1D ．0【答案】A【分析】先对圆的方程配方，求出圆心，再根据两直线以及圆之间的关系求解. 【详解】由圆的方程： 得： ， 2240x y kx my +++-=222242244k m k m x y ⎛⎫⎛⎫+++=++⎪ ⎪⎝⎭⎝⎭圆心坐标为 ，,22k m ⎛⎫-- ⎪⎝⎭直线与圆交于，两点，且，关于直线对称， 1y kx =+2240x y kx my +++-=M N M N 20x y +=则直线必定经过圆心，，，20x y +=(2k -2m -20k m --=又根据垂径定理：直线与直线垂直，可得，即，1y kx =+20x y +=1()12k ⋅-=-2k =所以，故； 1m =-213k m -=+=故选：A.5．数列满足，，，则数列的前10项和为（ ）{}n a 10a =21a =222,3,2,3,n n n a n n a a n n --+≥⎧=⎨≥⎩为奇数为偶数{}n a A ．51 B ．56C ．83D ．88【答案】A【分析】按照已知条件可以发现奇、偶项分别成等差和等比数列，一一列举前10项求和即可.【详解】数列满足，，，{}n a 10a =21a =222,3,2,3,n n n a n n a a n n --+≥⎧=⎨≥⎩为奇数为偶数不难发现，奇数项是等差数列，公差为2，偶数项是等比数列，公比为2， 所以数列的前10项和为：. {}n a (02468)(124816)51+++++++++=故选：.A 6．已知为双曲线的右焦点，为的左顶点，过点且斜率为的直线F 2222:1(0,0)x y C a b a b-=>>A C A 1l与交于另一点，且垂直于轴．则的离心率为（ ） C B BF x C AB ．2C D ．3【答案】B【分析】根据题意先求出，，再根据可得到关于，的关系式，进而即可得到|BF |AF 1BF AF=a c 双曲线的离心率．C【详解】联立，解得，所以， 22222221x cx y a b c b a=⎧⎪⎪-=⎨⎪=+⎪⎩2x c b y a =⎧⎪⎨=±⎪⎩2||b BF a =依题可得，，即， 1BFAF=AF c a =+()2221b c a a c a a c a -==++整理得，所以双曲线的离心率为． 2c a =C 2ce a==故选：B ．7．已知等差数列前项和为，公差是与的等比中项，则下列选项不正确{}n a n n S 670,90,d S a ≠=3a 9a 的是（ ） A ．B ．120a =2d =-C ．当，时，取得最大值 D ．当时，的最大值为2110n =11n S 0n S >n 【答案】D【分析】根据等差数列的通项公式，结合等比中项的定义、等差数列的前项进行求解即可. n 【详解】因为是与的等比中项，7a 3a 9a 所以，()()()22739111162810a a a a d a d a d a d =⋅⇒+=++⇒=-由，有，611906659060159022S a d d d d =⇒+⨯⨯=⇒-+=⇒=-120a =，()221121441121224n S na n n d n n n ⎛⎫=+⋅-=-+=--+ ⎪⎝⎭当，时，取得最大值，10n =11n S ，的最大值为，2210021n S n n n =-+>⇒<<n 20故选：D8．已知函数满足：，，则不等式的解集为()f x ()01f =()()'f x f x <()x f x e <A ． B ． C ．D ．()0,∞+(),0∞-()1,+∞(),1∞-【答案】A【详解】是减函数，由得： ()()()0,x xf x f x f x e e ''-⎛⎫=< ⎪⎝⎭()x f x e ()x f x e <0()(0)1,0x f x f x e e <=∴>故选A.点睛：用导数解抽象函数不等式，实质是利用导数研究对应函数单调性，而对应函数需要构造.构造辅助函数常根据导数法则进行：如构造；如()()f x f x '<()()x f x g x e=构造；如构造；如构()()0f x f x '+<()()x g x e f x =()()xf x f x '<()()f xg x x=()()0xf x f x '+<造等.()()g x xf x =二、多选题9．下列求导运算正确的是（ ） A ． 211()1x xx +'=-B ．(cos )sin x x x ⋅'=-C ．222(e )e x xx x x -'=D ．，则 ()sin(21)f x x =-)cos ()221(f x x '=-【答案】ACD【分析】利用导数计算公式分析各选项可得答案.【详解】A 选项，，故A 正确；()2111()1x x x x x ⎛⎫ ⎪⎝⎭''+'=+=-B 选项，，故B 错误；()()(cos )cos cos cos sin x x x x x x x x x ''⋅'=+=-C 选项，，故C 正确； ()()()2222222e e 2e e 2(ee e e xx x x xx xx x x xx x x x ''---'===D 选项，，则，D 正确. ()sin(21)f x x =-)cos ()221(f x x '=-故选：.ACD 10．在平面直角坐标系中，已知双曲线，则（ ）xOy 221412x y -=A ．离心率为2B ．渐近线方程为 y =C ．实轴长为2D ．右焦点到渐近线的距离为【答案】ABD【分析】根据双曲线方程确定的值，即可一一判断各选项，即得答案. ,,a b c 【详解】由双曲线的方程可得，，，，24a =212b =22216c a b =+=所以，，实轴长，离心率，所以A 正确，C 不正确， 2a =b =4c =24a =2ca=所以，渐近线方程为，所以B 正确， by x a=±=因为右焦点为，不妨取渐近线， (4,0)y =0y -=则到渐近线距离为D 正确.(4,0)y =d =故选：ABD.11．设数列的前项和为，且，则（ ） {}n a n n S 2121,log +=-=n n n n S a b a A ．数列是等比数列B ．{}n a 1(2)n n a -=-C ．D ．的前项和为22221232213n n a a a a -++++= {}n n a b +n 2n212n n n T +=-+【答案】ACD【分析】由已知可得数列是，2为公比的等比数列，从而可得通项公式，可判断A 、B ，{}n a 11a =进而可以求的值判断C ，也易求得的前项和判断D.2222123n a a a a ++++ {}n n a b +n 【详解】由已知，当时，可得21n n S a =-1n =11a =选项A ，，可得数列是，2为公比的等比数列，故A 正11122,2-----===n n n n n n n S S a a a a a {}n a 11a =确；选项B ，由选项A 可得解得，故B 错误；1121-==，n n a a a 1n 2n a -=选项 C ，数列是以1为首项，4为公比的等比数列，所以2{}n a ，故C 正确； 222212321441211433n n n n a a a a ---++++===- 选项D ，因为，故D 正确.212n+1n (12)(1)log ,2211222n n nn n n n n n n b a n a b n T --++==+=+=+=-+-，故选：ACD.12．已知函数的图象在处切线的斜率为9，则下列说法正确的是（ ） 3()1f x x ax =-+2x =A ．3a =B ．在上单调递减 ()f x [1,1]-C ．(1)(1)lim0x f x f x∆→+∆-=∆D ．的图象关于原点中心对称 ()f x 【答案】ABC【分析】根据导数的几何意义求得的值，即可判断A ；根据函数单调性与导数的关系，即可判断aB ；由导数的定义可判断C ；由函数的对称性即可判断D. 【详解】，则， 3()1f x x ax =-+2()3f x x a '=-因为函数的图象在处切线的斜率为9， ()f x 2x =所以，解得，故A 正确；()2129f a ='-=3a =，则，3()31,R f x x x x =-+∈2()333(1)(1)f x x x x '=-=-+令，可得，所以在上单调递减，故B 正确； ()0f x '≤11x -≤≤[1,1]-由于，故C 正确；20(1)(1)lim(1)3130x f x f f x'∆→+∆-==⨯-=∆函数，则，3()31,R f x x x x =-+∈3()31f x x x -=-++所以，则的图象关于点中心对称，故D 不正确. ()()2f x f x +-=()f x ()0,1故选：ABC.三、填空题13．等比数列中，则__. {}n a 59740,a a a -=7a =【答案】4【分析】利用等比数列性质可得，结合条件即可得答案.2597a a a =【详解】由题可得，， 259774a a a a ==70a ≠所以. 74a =故答案为：4.14．已知，则__.()2()e 0xf x xf '=-()1f '=【答案】22e 1-【分析】根据导数运算求得正确答案.【详解】，则，()2()e 0xf x xf '=-2()2e (0)x f x f ''=-将代入可得，，解得，0x =()()()002e 020f f f '''=-=-()01f '=故，，2()e x f x x =-()22e 1xf x '=-所以.()2122e 12e 11f ⨯=-=-'故答案为：.22e 1-15．已知为坐标原点，抛物线的焦点为，为上一点，与轴垂直，O ()2:20C y px p =>F P C PF x 为轴上一点，且，若，则的准线方程为______．Q x PQ OP ⊥4FQ =C 【答案】=1x -【分析】设点，求得点，由已知条件得出，求出正数的值，即,2p P p ⎛⎫⎪⎝⎭4,02p Q ⎛⎫+ ⎪⎝⎭0PQ OP ⋅= p 可得出抛物线的准线方程.C 【详解】抛物线的焦点，()2:20C y px p =>,02p F ⎛⎫ ⎪⎝⎭为上一点，轴，所以，将代入抛物线的方程可得，P C PF x ⊥2P p x =2P px =P y p =±不妨设，因为为轴上一点，且，所以在的右侧．,2p P p ⎛⎫⎪⎝⎭Q x PQ OP ⊥Q F 又，得，即点，所以，， 42Qp FQ x =-= 42Q p x =+4,02p Q ⎛⎫+ ⎪⎝⎭()4,PQ p =- 因为，所以，，，PQ OP ⊥2402p PQ OP p ⋅=⨯-= 0p > 2p ∴=所以抛物线的准线方程为． C =1x -故答案为：． =1x -16．函数有两个零点，则的取值范围是 __. ln ()2x kf x x =-k 【答案】20,e ⎛⎫⎪⎝⎭【分析】函数有两个零点，即方程有两个根，构造函数，利ln ()2x kf x x =-ln 2x k x =ln ()(0)x g x x x=>用导数求出函数的单调区间，从而可画出函数的大致图像，根据图象即可得解. ()g x 【详解】函数有两个零点，方程有两个根， ln ()2x k f x x =-∴ln 02x kx -=即方程有两个根， ln 2x kx =设，则函数与的图像有两个交点， ln ()(0)xg x x x =>()g x 2k y =， 21ln ()xg x x -'=当时，，单调递增； (0,e)x ∈()0g x '>()g x 当时，，单调递减，(e,)x ∈+∞()0g x '<()g x 函数在时，取得最大值，∴()g x e x =()1e eg =又当时，；当时，且，0x →()g x →-∞x →+∞()0g x >()0g x →函数的大致图像，如图所示，∴()g x由图像可知，，102ek <<的取值范围是.k ∴20,e⎛⎫⎪⎝⎭故答案为：.20,e ⎛⎫⎪⎝⎭四、解答题17．已知圆圆心为原点，且与直线相切，直线l 过点． 1C 34100x y +-=(1,2)M (1)求圆的标准方程；1C(2)若直线l 被圆所截得的弦长为l 的方程． 1C 【答案】(1)； 224x y +=(2)或 1x =3450x y -+=【分析】（1）直接由圆心到直线的距离求出半径，即可求出圆的方程；（2）先由弦长公式求出，斜率不存在时符合题意，斜率存在时，设出直线方程，由解出1d =1d =直线斜率，即可求解.【详解】（1）设圆的半径为，则，故圆的标准方程为；r 2r ==1C 224x y +=（2）设圆心到直线到的距离为，则；当直线l 斜率不存在时，易得l d =1d =，此时圆心到的距离，符合题意；:1l x =l 1d =当直线l 斜率存在时，设，即，则，解得，即:2(1)l y k x -=-20kx y k -+-=1d 34k =，:3450l x y -+=故直线l 的方程为或.1x =3450x y -+=18．已知等差数列满足. {}n a 13424,2a a a a +=-=(1)求数列的通项公式及前项和； {}n a n n S (2)记数列的前项和为，若,求的最小值. 1{}n S n n T 9950n T >n 【答案】(1) ()1,2n n n n a n S +==(2) 100【分析】（1）利用等差数列的通项公式及前项和公式即可求解；n （2）利用（1）的结论及裂项相消法求数列的前项和，结合不等式的解法即可求解. n 【详解】（1）设等差数列的公差为，则 {}n a d 因为，13424,2a a a a +=-=所以，即，解得. ()11112432a a d a d a d ++=⎧⎨+-+=⎩1222a d d +=⎧⎨=⎩111a d =⎧⎨=⎩所以数列的通项公式为， {}n a ()111n a n n =+-⨯=所以数列的通项公式及前项和为.{}n a n ()()1122n S n n n n ++==（2）由（1）知，， ()12n n n S +=所以， ()1211211n S n n n n ⎛⎫==- ⎪++⎝⎭所以数列的前项和为 1{}n S n 1231111n nT S S S S =++++ 111111224122223113n n ⎛⎫⎛⎫⎛⎫=+-+⎪⎛⎫- ⎪-++- ⎪ ⎪ +⎝⎭⎝⎝⎝⎭⎭⎭ 111111*********n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ . 1211n ⎛⎫=- ⎪+⎝⎭因为， 9950n T >所以，即，于是有，解得， 19921150n ⎛⎫->⎪+⎝⎭19911100n ->+111100n <+99n >因为， *N n ∈所以的最小值为.n 10019．已知：函数. 32()3f x x ax x =--(1)若，求的单调性；(3)0f '=()f x(2)若在上是增函数，求实数的取值范围. ()f x [)1x ∈+∞，a 【答案】(1)答案见解析；(2). (]0-∞，【分析】（1）求出导函数，利用，求出的值，解不等式，即可求出(3)0f '=a ()()''>0<0，f x f x ()f x 的单调性；（2）利用函数在区间上是单调增函数，导数大于等于0恒成立，推出关系式，求出实数的取值范围.a 【详解】（1），，32()3f x x ax x =-- 2()323'∴=--f x x ax ，，.(3)0'= f 27630∴--=a 4a ∴=将代入得，令得或. 4a =()2383'=--f x x x ()0f x '=13x =-3x =x1()3-∞-，13-1(3)3-， 3(3)+∞， ()f x ' +0 -0 +()f x↑↓↑在上单调递减，在上单调递增. ()f x ∴1(3)3∈-，x 1()(3)3∈-∞-+∞，，，x （2）方法1：在上是增函数， ()f x [)1x ∈+∞，在上恒成立， 2()3230f x x ax ∴--'=≥[)1+∞，， 31()2a x x∴≤-当时，是增函数，其最小值为，1x ≥31(2x x-3(11)02-=.实数的取值范围是. 0a ∴≤a (]0-∞，方法2：在上是增函数， ()f x [)1x ∈+∞，在上恒成立， 2()3230f x x ax ∴--'=≥[)1+∞，，. (1)2013f a a=-≥⎧⎪⎨≤'⎪⎩0a ∴≤实数的取值范围是. a (]0-∞，20．已知数列是公比为2的等比数列，，，成等差数列．{}n a 2a 3a 44a -(1)求数列的通项公式；{}n a (2)若，设数列的前n 项和，求证：． 21log n n na b a +={}n b n T 13n T ≤<【答案】(1)2n n a =(2)证明见解析【分析】(1)根据等差中项的性质和等比数列定义求解；(2)利用错位相减法求和即可证明.【详解】（1）因为，，成等差数列，所以，2a 3a 44a -32442a a a =+-又因为数列的公比为2，所以，{}n a 2311122242a a a ⨯=+⨯-即，解得，所以．1118284a a a =+-12a =1222n n n a -=⨯=（2）由（1）知，则， 2nn a =221log 1log 2122n n n n n n a n b a +++===所以， ① 2323412222n n n T +=++++L ， ② 231123122222n n n n n T ++=++++ ①②得 -23111111122222n n n n T ++⎛⎫=++++- ⎪⎝⎭L 212111111111122221111221122n n n n n n -+++⎛⎫-- ⎪++⎝⎭=+-=+---． 11112133122222n n n n n +++++=+--=-所以． 3332n n n T +=-<又因为， 102n nn b +=>所以是递增数列，所以，所以．{}n T 11n T T =≥13n T ≤<21．已知函数，其中. 211()()ln 2=-++f x x a x x a0a >(1)当时，求曲线在点处切线的方程；1a =()y f x =()()1,1f (2)试讨论函数的单调区间.()f x 【答案】(1)； 32y =-(2)答案见解析.【分析】（1）利用导数几何意义结合条件即得；（2）求函数的导函数,得到导函数的零点,讨论的范围，由导函数的零点对函数定义域分段,利()f x a 用导函数在各区间段内的符号判断原函数的单调性.【详解】（1）当时，,则， 1a =21()2ln 2f x x x x =-+1()2f x x x'=-+，又， ()10f '∴=()312f =-在点处切线的方程为； ∴()y f x =()()1,1f 32y =-（2）由题可得， 1()()11()(0)x a x a f x x a x a x x --⎛⎫'=-++=> ⎪⎝⎭令，解得或， ()0f x '=x a =1x a =若，，当变化时，，的变化情况如表： 01a <<1a a <x ()f x '()f x x (0,)a a 1(,)a a 1a ,1(a )∞+ ()f x ' +0-0 + ()f x 增函数减函数增函数的单调增区间为和,，单调减区间为； ()f x ∴(0,)a 1(a )∞+1(,)a a②若，，当变化时，，的变化情况如表： 1a >1a a <x ()f x '()f x x1(0,)a 1a , 1(a )a a (,)a +∞ ()f x ' +0-0 + ()f x 增函数减函数增函数的单调增区间为和，单调减区间为； ()f x ∴1(0,)a(,)a +∞1(,)a a③若，则，函数的单调增区间为；1a =()0f x '≥()f x ()0,∞+综上，当时，的单调增区间为和,，单调减区间为；当时，01a <<()f x (0,)a 1(a )∞+1(,a a1a >()f x 的单调增区间为和，单调减区间为；当时，函数的单调增区间为1(0,a(,)a +∞1(,)a a 1a =()f x .()0,∞+22．已知椭圆过点，且焦距为2222:1(0)x y C a b a b+=>>(2,1)P --(1)求椭圆的方程；C (2)过直线（不经过点交椭圆于点，，试问直线与直线的斜率之和为，求证：l )P C A B PA PB 1-l 过定点.【答案】(1) 22182x y +=(2)证明见解析【分析】（1）根据已知条件求得，从而求得椭圆的方程.,,a b c C （2）根据直线的斜率是否存在进行分类讨论，根据化简求得定点坐标.AB 1PA PB k k +=-【详解】（1）由题意可得，解得，22222411c aba b c ⎧=⎪⎪+=⎨⎪=+⎪⎩a b c ⎧=⎪⎪=⎨⎪=⎪⎩椭圆的方程：.∴C 22182x y +=（2）当直线的斜率不存在时，设其方程为，AB,x t x =-<<2x ≠-则， ,,A t Bt ⎛⎛⎝⎝所以， 212PA PB k k t +===-+解得（舍去），4t =-所以直线的斜率存在.AB 设直线的方程为，其中，AB y kx m =+21m k ≠-联立方程，消去得：， 22182y kx m x y =+⎧⎪⎨+=⎪⎩y 22(4)8801k x kmx -+=+设，()()1122,,,A x y B x y 则，， 122841km x x k -+=+21224841m x x k -⋅=+所以 12121122PA PB m kx m k k x k x x +++++=+++ 1212(2)21(2)2122k x m k k x m k x x ++-+++-+=+++ 122121()22m k m k k k x x -+-+=+++++ 12112(21)()22k m k x x =+-++++ 12121242(21)2()4x x k m k x x x x ++=+-++++ 2222841842(21)482()44141k m k m km k k k m k +-+-+=+-+-+++ 222221684412(21)16441641k km k k m k k m kmk -++=+-+⋅+--+ 224212(21)(2)1k km k m k k m -+=+-+⋅--， 24212121k km k k m -+-=+=--+整理得，直线的方程为，4m k =AB ()4y k x =+所以直线恒过定点.l ()4,0-【点睛】根据已知条件求解椭圆的方程，关键点在于列方程组来求得，要注意“隐藏条件”,,a b c .求解直线过定点问题，可先设出直线方程，然后根据已知条件列方程，求得直线方程中222a b c =+参数的关系，从而求得定点的坐标.。

★绝密启用前2021年江苏省南通中学高二年级期末考试数学注意事项：1. 本试卷分选择题与非选择题两部分。

2. 答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置。

3. 全部答案在答题卡上完成，答在本试题上无效。

4. 考试结束后，将本试题和答题卡一并交回。

一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.数列是等比数列，公比为q ，且则“”是“，”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件2.已知等差数列的前n 项和为，且定义数列如下：是使不等式成立的所有n 中的最小值，则A. 25B. 50C. 75D. 1003.电影夺冠讲述中国女排姑娘们顽强奋斗、为国争光的励志故事，打造一部见证新中国体育改革40年的力作，该影片于2020年09月25日正式上映．在夺冠，上映当天，一对夫妇带着他们的两个小孩一起去观看该影片，订购的4张电影票恰好在同一排且连在一起．为安全起见，影院要求每个小孩子要有家长相邻陪坐，则不同的坐法种数是A. 8B. 12C. 16D. 204.小李年初向银行贷款M万元用于购房，购房贷款的年利率为P，按复利计算，并从借款后次年年初开始归还，分10次等额还清，每年1次，问每年应还万元．A. B. C. D.5.已知抛物线的焦点为F，准线l与x轴交于点H，过焦点F的直线交抛物线于A，B两点，分别过点A，B作准线l 的垂线，垂足分别为，，如图所示，则：以线段AB为直径的圆与准线l相切；以为直径的圆经过焦点F；，O，其中点O为坐标原点三点共线；若已知点A的横坐标为，且已知点，则直线TA与该抛物线相切．则以上说法中正确的个数为A. 1B. 2C. 3D. 46.九章算术与几何原本并称现代数学的两大源泉．在九章算术卷五商功篇中介绍了羡除此处是指三面为等腰梯形，其他两侧面为直角三角形的五面体体积的求法．在如图所示的羡除中，平面是铅垂面，下宽，上宽，深3m，平面BDEC是水平面，末端宽，无深，长直线CE到BD的距离，则该羡除的体积为A. B. C. D.7.如图，某伞厂生产的“太阳”牌太阳伞的伞蓬是由太阳光的七种颜色组成，七种颜色分别涂在伞蓬的八个区域内，且恰有一种颜色涂在相对区域内，则不同的颜色图案的此类太阳伞至多有A. 40320种B. 5040种C. 20160种D. 2520种8.已知点P是椭圆上的动点，、为椭圆的左、右焦点，O为坐标原点，若M是的角平分线上的一点，且，则的取值范围是A. B. C. D.二、选择题：本题共4小题，每小题5分，共20分。

2023-2024学年江苏省南通市高二（上）期末数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.数列1,53,52，…的通项公式可能是a n =( )A. n 2+1n +1B. n +1n 2+1C. n 22n−1D. n 2+12n−12.圆(x +1)2+y 2=1和圆(x−2)2+(y−4)2=16的位置关系为( )A. 相离B. 相交C. 外切D. 内切3.某校文艺部有7名同学，其中高一年级3名，高二年级4名.从这7名同学中随机选3名组织校文艺汇演，则两个年级都至少有1名同学入选的选法种数为( )A. 12B. 30C. 34D. 604.已知F 是抛物线C ：x 2=2py(p >0)的焦点，点A(1,14)在C 上，则|AF|=( )A. 38B. 58C. 54D. 945.设S n 是等比数列{a n }的前n 项和，若S 4=6，S 8=18，则S 16=( )A. 48B. 90C. 96D. 1626.已知椭圆C ：x 24+y 23=1，直线l 经过点T(1,12)与C 交于A ，B 两点.若T 是线段AB 的中点，则l 的方程为( )A. 4x−6y−1=0 B. 3x−2y−1=0 C. 4x +6y−7=0 D. 3x +2y−4=07.已知平行六面体ABCD−A 1B 1C 1D 1中，AA 1=3，BD =4，AD 1⋅DC−AB 1⋅BC =5，则cos <AA 1，BD >=( )A. 512B. −512C. 415D. −4158.已知F 是双曲线C ：x 2a 2−y 2b 2=1(a >0,b >0)的右焦点，直线y = 52b 与C 交于A ，B 两点.若△ABF 的周长为7a ，则C 的离心率为( )A. 43 B. 65 C. 2 105二、多选题：本题共4小题，共20分。

江苏省南通中学2016～2017学年度第一学期期末考试高二数学一、填空题：本大题共14小题，每小题5分，共70分．请把答案直接填写在答题卡相应位．．．．．．置上．．. 1． 若直线经过(1,0)A 、(0,1)B -两点, 则直线AB 的倾斜角为 ▲ ．答案：45︒2． 已知平面//α平面β，若直线l ⊥平面α，则直线l 与平面β的位置关系为 ▲ ．答案：垂直3． 函数()e x f x x =⋅，则(1)f '= ▲ ．答案：2e4． 圆心在y 轴上，半径为1，且过点(1,2)的圆的方程为 ▲ ．答案：x 2＋(y －2)2＝15． 准线方程为2x =-的抛物线的标准方程是 ▲ ．答案：28y x =6． 棱长为1cm 的正方体的外接球表面积为 ▲ 2cm ．答案:3π7． 已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程为2y x =，则该双曲线的离心率为▲ ．答案8． 已知函数()ln f x x x =+，若函数()f x 在点00(,())P x f x 处切线与直线310x y -+=平行，则0x = ▲ ． 答案：129． 如果平面直角坐标系中的两点(1,1)A a a -+，(,)B a a 关于直线l 对称，那么直线l 的方程为 ▲ ． 答案：10x y -+=10．若椭圆22221(0)x y a b a b +=>>和圆2222b x y c ⎛⎫+=+ ⎪⎝⎭（其中c 为椭圆的半焦距）， 有四个不同的交点，则该椭圆离心率的取值范围为 ▲ ．答案：35⎫⎪⎪⎝⎭11．若函数32()1f x x ax =-+在[0,2]上单调递减，则实数a 的取值范围为 ▲ ．答案：[3,)+∞12．若直线10ax by -+=平分圆C ：222410x y x y ++-+=的周长,则ab 的取值范围是 ▲ ．答案：1,8⎛⎤-∞ ⎥⎝⎦13．定义在(0+)∞，上的单调函数()f x ，对任意(0+)x ∈∞，，2[()log ]3f f x x -=成立，若方程()()2f x f x '-=的解在区间(,1)()k k k +∈Z 内，则k = ▲ ．答案：114．过点(1,3)P 的动直线与抛物线2y x =交于A ，B 两点，在A ，B 两点处的切线分别为1l 、2l ，若1l 和2l 交于点Q ，则圆22(2)4x y +-=上的点与动点Q 距离的最小值为 ▲ ．答案：min 2d =二、解答题：本大题共6小题，共90分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说 明、证明过程或演算步骤．15．已知函数()321()33f x x x x a a =-+++∈R ．（1）求函数()f x 的单调增区间；（2）若函数()f x 在区间[]4,4-上的最大值为26，求a 的值．解：（1）因为321()33f x x x x a =-+++，所以2()23f x x x '=-++，令()0f x '>，即2230x x -++>，解得13x -<<， 所以函数()f x 的单调减区间为(1,3)-. （2）由函数在区间[]4,4-内的列表可知：函数()f x 在(4,1)--和(3,4)上分别是减函数，在(1,3)-上是增函数. 又因为76(4),(3)93f a f a -=+=+，所以(4)(3)f f ->，所以(4)f -是()f x 在[4,4]-上的最大值， 所以76263a +=，即23a =．16．如图，在三棱锥P ABC -中，90ABC ∠=︒，PA ⊥平面ABC ，E ，F 分别为PB ，PC 的中点．（1）求证：//EF 平面ABC ； （2）求证：平面AEF ⊥平面PAB ．FE CBAP17．已知圆M 的方程为22(2)1x y +-=，直线l 的方程为20x y -=，点P 在直线l 上，过P 点作圆M 的切线PA 、PB ，切点为A 、B ． （1）若点P 的坐标为(0,0)，求APB ∠；（2）若点P 的坐标为(2,1)，过P 作直线与圆M 交于C 、D两点，当CD 时，求直线CD 的方程；（3）经过A 、P 、M 三点的圆是否经过异于点M 的定点，若经过，请求出此定点的坐标；若不经过，请说明理由．解：（1）因为点P 坐标为(0,0) ，所以2M P =，又因为1MA MB ==，所以30MPA MPA ∠=∠=︒，故60APB ∠=︒． （2）当直线斜率不存在时，不合题意；当直线斜率存在时，设直线CD 方程为1(2)y k x -=-因为CD ，所以圆心M 到直线CD，=，解得1k =-或17k =-， 故直线CD 的方程为30x y +-=或790x y +-=． （3）设(2,)P m m ，MP 的中点(,1)2mQ m +， 因为PA 为圆M 的切线，所以经过A 、P 、M 三点的圆是以Q 为圆心，MQ 为半径的圆，故其方程为2222()(1)(1)22m mx m y m -+--=+- 化简得222(22)0x y y m x y +--+-= 由2220220x y y x y ⎧+-=⎨+-=⎩，解得02x y =⎧⎨=⎩或4525x y ⎧=⎪⎪⎨⎪=⎪⎩所以经过A 、P 、M 三点的圆经过异于点M 的定点42,55⎛⎫⎪⎝⎭．18．请你设计一个仓库．它的上部是底面圆半径为5m 的圆锥，下部是底面圆半径为5m 的圆柱，且该仓库的总高度为5m ．经过预算，制造该仓库的圆锥侧面、圆柱侧面用料的单价 分别为4百元/2m ，1百元/2m ，设圆锥母线与底面所成角为θ，且0π 4θ⎛⎫∈ ⎪⎝⎭，． （1）设该仓库的侧面总造价为y ，写出y 关于θ的函数关系式；（2）问θ为多少时，该仓库的侧面总造价（单位：百元）最少？并求出此时圆锥的高度． 解：（1）[]15255(1tan )12542cos y θθ⎡⎤=π⨯⨯-⨯+⨯π⨯⨯⨯⎢⎥⎣⎦2sin 501cos +θθ-⎛⎫=π ⎪⎝⎭，0π 4θ⎛⎫∈ ⎪⎝⎭，； （2）由22sin 1cos 500y θθ-⎛⎫'=π= ⎪⎝⎭得1sin 2θ=，04 θπ⎛⎫∈ ⎪⎝⎭，， 所以6θπ=，列表：所以当6θπ=时，侧面总造价ym ． 19.已知椭圆2222:1(0)x y C a b a b +=>>，一条准线方程为x =（1）求椭圆C 的标准方程；（2）设直线:l y kx m =+与椭圆交于P ,Q 两点.①若2m =-，当OPQ ∆面积最大时，求直线l 的方程；②当0k ≠时，若以PQ 为直径的圆经过椭圆的右顶点，求证：直线l 过定点.解：（1）2214x y +=.（第18题）（2）由2214x y y kx m ⎧+=⎪⎨⎪=+⎩ 得222(14)8440k x kmx m +++-=222(8)4(14)(44)0km k m ∆=-+->，整理得22410k m -+>（*）设11(,)P x y ，22(,)Q x y ，则122814km x x k +=-+，21224414m x x k -⋅=+（**）①当2m =-时，代入（*）和（**）式得：234k >，1221614k x x k +=+，1221214x x k ⋅=+.所以12PQ x =-=， 又O 到直线l的距离d =，所以12OPQS PQ d ∆=⋅=.令t =，则0t >，则244144OPQ t S t t t∆==≤++ 当且仅当2t =，即k =时等号成立，且227344k ⎛==> ⎝⎭因此OPQ ∆面积最大时，直线l的方程为：2y =-. ②由已知，AP AQ ⊥，且椭圆右顶点为(2,0)A所以12121212(2)(2)(2)(2)()()0x x y y x x kx m kx m --+=--+++=即22222121222448(1)(2)()4(1)(2)401414m kmk x x km x x m k km m k k--++-+++=+⋅+-⋅++=++ 整理得：22516120m km k ++= 解得2m k =-或65km =-，均满足（*）式， 所以当2m k =-时，直线l 的方程为:2l y kx k =-，过定点(2,0)与题意矛盾；当65k m =-时，直线l 的方程为6:5k l y kx =-，过定点6,05⎛⎫ ⎪⎝⎭，得证. 20. 已知函数ln ()a xf x x+=，曲线()f x 在点(e,(e))f 处的切线与直线2e e y x =+垂直. （1）求a 的值及()f x 的极值；（2）是否存在区间2,(0)3t t t ⎛⎫+> ⎪⎝⎭，使函数()f x 在此区间上存在极值和零点？若存在，求实数t 的取值范围，若不存在，请说明理由；（3）若不等式2()(1)x f x k x >-对任意(1,)x ∈+∞恒成立，求整数．．k 的最大值. 解：（1）由ln ()a x f x x +=，得21ln ()a xf x x --'=． 因为()f x 在点(e,(e))f 处的切线与直线2e e y x =+垂直， 所以2221lne 1(e)e e e a a f ---'===-，解得1a =， 所以1ln ()(0)x f x x x +=>，令2ln ()0xf x x'=-=，得1x =． 因为当()0,1x ∈时，()0f x '>，当()1,x ∈+∞时，()0f x '< 所以()f x 在()0,1上单调递增，在()1,+∞上单调递减， 故()f x 在1x =处取得极大值1，无极小值； （2）因为()f x 在()1,+∞上单调递减，且()0f x >又由（1）知()f x 在(0,1)上单调递增，且22221ln e (e )e 0ef ---+==-<，(1)10f => 所以由零点存在原理得()f x 在区间(0,1)存在唯一零点，函数()f x 的图象如图所示： 因为函数()f x 在区间2,(0)3t t t ⎛⎫+> ⎪⎝⎭上存在极值和零点，所以由20131ln ()0t t t f t t ⎧<<<+⎪⎪⎨+⎪=<⎪⎩，解得113e t <<．所以存在符合条件的区间，实数t 的取值范围为11,3e ⎛⎫⎪⎝⎭；（3）当(1,)x ∈+∞时，不等式2()(1)x f x k x >-可变形为(1ln )1x x k x +<-设(1ln )()1x x h x x +=-，(1)x >，则2ln 2()(1)x x h x x --'=-设()ln 2x x x ϕ=--，(1)x >，则1()1x xϕ'=- 因为1x >时，1()0x x xϕ-'=>，所以()ln 2x x x ϕ=--在(1,)+∞上单调递增， 又因为(3)1ln30ϕ=-<，(4)2ln 40ϕ=->所以存在唯一的0(3,4)x ∈，使得0()0x ϕ=，即00ln 2x x =-，当()01,x x ∈时，()0x ϕ<，即0()0h x '<，当()0,x x ∈+∞时，()0x ϕ>，即0()0h x '>， 所以()h x 在()01,x 上单调递减，在()1,+∞上单调递增，故000000min 00000(1ln )(12)(1)()()111x x x x x x h x h x x x x x ++--=====---，因为0min(1ln )1x x k x x +⎡⎤<=⎢⎥-⎣⎦，且0(3,4)x ∈，所以整数k 的最大值为3.。

江苏省南通市高二上学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2016高一下·九江期中) 设m，n是两条不同的直线，α，β是两个不同的平面，则下列叙述正确的是（）A . 若α∥β，m∥α，n∥β，则m∥nB . 若α⊥β，m⊥α，n∥β，则m⊥nC . 若m∥α，n∥α，m∥β，n∥β，m⊥n，则α∥βD . 若m⊥α，n⊂β，m⊥n，则α⊥β2. （2分）已知公差不为零的等差数列的第k、n、p项构成等比数列的连续三项，则等比数列的公比为（）A .B .C .D .3. （2分）过点作圆的两条切线，切点分别为A，B，则直线AB的方程为（）A . 2x+y-3=0B . 2x-y-3=0C . 4x-y-3=0D . 4x+y-3=04. （2分）(2012·全国卷理) 正方形ABCD的边长为1，点E在边AB上，点F在边BC上，，动点P从E出发沿直线向F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角，当点P第一次碰到E时，P与正方形的边碰撞的次数为（）A . 16B . 14C . 12D . 105. （2分）设是等差数列.下列结论中正确的是（）A . 若,则B . 若,则C . 若,则D . 若，则（）（）6. （2分）下列命题中正确的是（）A . 经过点P0(x0 ， y0)的直线都可以用方程y－y0＝k(x－x0)表示B . 经过定点A(0，b)的直线都可以用方程y＝kx＋b表示C . 经过任意两个不同点P1(x1 ， y1)，P2(x2 ， y2)的直线都可用方程(x2－x1)(y－y1)＝(y2－y1)(x－x1)表示D . 不经过原点的直线都可以用方程表示7. （2分） (2018高二上·长治期中) 若直线过点，，则此直线的倾斜角是（）A .B .C .D .8. （2分） (2016高二下·咸阳期末) 设已知椭圆的一个焦点是圆x2＋y2－6x＋8＝0的圆心，且短轴长为8，则椭圆的左顶点为（）A . (－3，0)B . (－4，0)C . (－10，0)D . (－5，0)9. （2分）已知等差数列中，则n=（）A . 4B . 5C . 6D . 710. （2分）已知点Q(-2,0)及抛物线x2=﹣4y上一动点P（x，y），则|y|+|PQ|的最小值是（）A .B . 1C . 2D . 311. （2分） (2019高三上·广东月考) 若函数的部分图象如图所示，将图象上所有点的横坐标缩短为原来的得到函数的图象，则在上的最小值是（）A . -1B .C .D .12. （2分） (2019高一下·佛山月考) 已知等比数列中，有，数列是等差数列，其前项和为，且，则（）A . 26B . 52C . 78D . 104二、填空题 (共4题；共4分)13. （1分） (2017高二上·日喀则期中) 在等比数列{an}中，a1=3，a4=24，则a3+a4+a5=________．14. （1分） (2019高一下·双鸭山期中) 设等差数列满足，则的前项和最大时的序号的值为________．15. （1分）(2017·南海模拟) 已知F1 ， F2分别为椭圆的左、右焦点，O为坐标原点，P （位于第一象限）为椭圆上一点，且PF1⊥PF2 ，若⊙O与PF1相切，则⊙O的方程为________．16. （1分） (2019高二下·深圳期末) 设是公差不为零的等差数列，为其前项和.已知成等比数列，且，则数列的通项公式为________.三、解答题 (共6题；共50分)17. （5分）(2017·吴江模拟) 如图，在四棱锥P﹣ABCD中，PA=PB，PA⊥PB，AB⊥BC，且平面PAB⊥平面ABCD，若AB=2，BC=1，．（1）求证：PA⊥平面PBC；（2）若点M在棱PB上，且PM：MB=3，求证CM∥平面PAD．18. （10分）(2020·兴平模拟) 在中，角，，的对边分别为，，，且.（1）求角的值；（2）若，且的面积为，求边上的中线的大小.19. （10分）设三个数， 2，成等差数列，其中（x，y）对应点的曲线方程是C．（1）求C的标准方程；（2）直线l1：x﹣y+m=0与曲线C相交于不同两点M，N，且满足∠MON为钝角，其中O为直角坐标原点，求出m的取值范围．20. （5分）已知椭圆的右焦点F2与抛物线的焦点重合，左端点为（1）求椭圆的方程；（2）过椭圆C1的右焦点且斜率为的直线l2被椭圆C1截得的弦AB，试求它的长度．21. （15分） (2019高二上·涡阳月考) 如图，是棱形，与相交于点，平面平面，且是直角梯形， .（1）求证：；（2）求二面角的余弦值.22. （5分） (2018高二上·长安期末) 一张坐标纸上涂着圆E：及点P（1，0），折叠此纸片，使P与圆周上某点P'重合，每次折叠都会留下折痕，设折痕与直线EP'交于点M ．（1）求的轨迹的方程；（2）直线与C的两个不同交点为A ， B ，且l与以EP为直径的圆相切，若，求△ABO的面积的取值范围．参考答案一、单选题 (共12题；共24分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：答案：8-1、考点：解析：答案：9-1、考点：解析：答案：10-1、考点：解析：答案：11-1、考点：解析：答案：12-1、考点：解析：二、填空题 (共4题；共4分)答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：答案：16-1、考点：解析：三、解答题 (共6题；共50分)答案：17-1、答案：17-2、考点：解析：答案：18-1、答案：18-2、考点：解析：答案：19-1、考点：解析：答案：20-1、答案：20-2、考点：解析：答案：21-1、答案：21-2、考点：解析：答案：22-1、答案：22-2、考点：解析：。

A BCD第一学期期末考试高二数学试卷(理)（考试时间为120分钟；总分为160分） 一、选择题（每题5分；共计50分） 1．已知()ln f x x =；则()f e '的值为A ．1B ．-1C ．eD ．1e2．设(,4,3)a x =；(3,2,)b z =；且//a b ；则xz 等于 A ．4-B ．9-C ．9D ．6493．函数()y f x =的图象如图所示；则导函数()y f x '=的图象大致是4．双曲线221169x y -=上的点P 到点(5； 0)的距离是15； 则点P 到点(－5； 0)的距离是 A ．7 B ．23 C ．11或19 D ．7或235．已知实数x ；y 满足条件⎪⎩⎪⎨⎧≥++≥≤0420y x x y y ；则z = x + 3y 的最小值是A ．316 B ．316-C ．12D ．－126．曲线221(6)106x y m m m +=<--与曲线221(59)59x y m m m+=<<--的 A ．焦距相等 B ．离心率相等 C ．焦点相同 D ．准线相同7．“a ＞b ＞0”是“ab ＜222b a +”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不允分也不必要条件8．设P 是ABC ∆所在平面外一点；若PA PB PB PC PC PA ⋅=⋅=⋅；则点P 在这 个平面上的射影是ABC ∆的A ．重心B ．垂心C ．外心D ．内心9．删除正整数数列1；2；3；……中的所有完全平方数；得到一个新数列．这个新数列 的第2007项是A ．2050B ．2051C ．2052D ．2053 10．已知不等式1()()9ax y x y++≥对任意正实数,x y 恒成立；则正实数a 的最小值为 A ．8 B ．6 C ．4 D ．2二、填空题（每题5分；共计30分）11．双曲线14322=-x y 的渐近线方程是 ▲ ． 12．命题：“若0xy =；则0x =或0y =”的否命题是 ▲ ．13．等差数列的第2；3；6项顺次成等比数列；该等差数列不是常数列；则这个等比数列的公比为 ▲ ．14．设点P 在抛物线212x y =上；且点P 到此抛物线的焦点的距离为6；则点P 的坐标 为 ▲ ．15．在曲线sin y x =(0)x π<<上取一点M ；使过M 点的切线方程与直线y =23x 平行；则M 点的坐标是点 ▲ ．16．以下四个关于圆锥曲线的命题中：①设A 、B 为两个定点；k 为正常数；||||PA PB k +=；则动点P 的轨迹为椭圆；②双曲线221259x y -=与椭圆22135x y +=有相同的焦点； ③方程02522=+-x x 的两根可分别作为椭圆和双曲线的离心率；④和定点)0,5(A 及定直线25:4l x =的距离之比为54的点的轨迹方程为221169x y -=． 其中真命题的序号为 ▲ ．三、解答题（共计80分）17．（本题满分14分）已知抛物线1C 的顶点在坐标原点；它的准线经过双曲线2C ：22221x y a b -=的一个焦点1F 且垂直于2C 的两个焦点所在的轴；若抛物线1C 与双曲线2C 的一个交点是2(,33M ． （1）求抛物线1C 的方程及其焦点F 的坐标；（2）求双曲线2C 的方程及其离心率e ．18．（本题满分16分）如图；已知长方体1111ABCD A BC D -中；2AB =；11AA =；直 线BD 与平面11AA B B 所成的角为30；AE 垂直 BD 于点E ；F 是11A B 的中点．（1）求异面直线AE 与BF 所成角的余弦值； （2）求直线1AA 与平面BDF 所成角的正弦值；19．（本小题满分16分）已知数列1230,,,a a a ；其中1210,,,a a a 是首项为1；公差为1的等差数列；201110,,,a a a 是公差为d 的等差数列；302120,,,a a a 是公差为2d 的等差数列（0d ≠）．（Ⅰ）若20a = 30；求d ；（Ⅱ）试写出a 30关于d 的关系式；并求a 30的取值范围；（Ⅲ）续写已知数列；可以使得403130,,,a a a 是公差为d 3的等差数列；请你依次类推；把已知数列推广为无穷数列；试写出10n a 关于d 的关系式（n ∈N *）；（Ⅳ）在（Ⅲ）条件下；且1d ≠；试用d 表示此数列的前100项和10012100...S a a a =+++．20．（本小题满分16分）已知32()f x x ax bx c =+++在1x =与23x =-时；都取得极值． (1) 求,a b 的值；(2)若3(1)2f -=；求()f x 的单调区间和极值； (3)若对[1,2]x ∈-都有3()f x c< 恒成立；求c 的取值范围．21．（本小题满分18分）已知A 、B 、C 是长轴长为4的椭圆上的三点；点A 是长轴的一个顶点；BC 过椭圆中心O ；如图；且0AC BC ⋅=；||2||BC AC =． （1）求椭圆的方程；（2）如果椭圆上两点P 、Q 使∠PCQ 的平分线垂直AO ；则总存在实数λ；使AB PQ λ=；请给出证明．D 1C 1B 1A 1EFDCBA班级________________ 姓名________________ 学号_________________ ……………………………………装…………………………………………………………订…………………………线……………………第一学期期末考试高二数学试卷答卷（理）二、填空题（每题5分；共计30分）11． 12．13． 14． 15． 16．三、解答题（共计80分）17．（本题满分14分）18．（本题满分16分）D 1C 1B 1A 1EFDCB A21．（本题满分18分）…………………………装……………………………………………………订……………………………………………线…………………………………第一学期期末考试高二数学试卷参考答案（理）一、选择题（每题5分；共计50分）二、填空题（每题5分；共计30分）11．2y x =±； 12．若0xy ≠；则0x ≠且0y ≠； 13．3 14．(6,3)±； 15．1(,)62π； 16．②③三、解答题（共计80分）17．（本题满分14分）已知抛物线1C 的顶点在坐标原点；它的准线经过双曲线2C ：22221x y a b -=的一个焦点1F 且垂直于2C 的两个焦点所在的轴；若抛物线1C 与双曲线2C 的一个交点是2(,33M ．（1）求抛物线1C 的方程及其焦点F 的坐标； （2）求双曲线2C 的方程及其离心率e ．解：（1）由题意可设抛物线1C 的方程为22y px =． (2分)把2(3M 代入方程为22y px =；得2p = (4分)因此；抛物线1C 的方程为24y x =． (5分) 于是焦点(1,0)F (7分)（2）抛物线1C 的准线方程为1y =-；所以；1(1,0)F - (8分) 而双曲线2C 的另一个焦点为(1,0)F ；于是17522333a MF MF =-=-= 因此；13a =(10分) 又因为1c =；所以22289b c a =-=． 于是；双曲线2C 的方程为2211899x y -=． (12分) 因此；双曲线2C 的离心率3e =． (14分)18．（本题满分16分）如图；已知长方体1111ABCD A BC D -中；2AB =；11AA =；直线BD 与平面11AA B B 所成的角为30；AE垂直BD 于点E ；F 是11A B 的中点． （1）求异面直线AE 与BF 所成角的余弦值； （2）求直线1AA 与平面BDF 所成角的正弦值；解：在长方体1111ABCD A BC D -中；以AB 所在的直线为x 轴；以AD 所在的直线为y 轴；以1AA 所在的直线为z 轴；建立如图 所示空间直角坐标系．由已知2AB =；11AA =；可得(0,0,0)A ；(2,0,0)B ；(1,0,1)F ．又AD ⊥平面11AA B B ；从而BD 与平面11AA B B 所成的角为30DBA ∠=；而2AB =； AE BD ⊥；1AE =；233AD =；因此易得13(,,0)22E ；23(0,,0)3D ． (4分)（1）因为1(2AE =；(1,0,1)BF =-；所以12cos ,42AE BF AE BF AE BF-⋅<>===-⋅．于是；异面直线AE 与BF 所成角的余弦值为4． (10分) （2）易知直线1AA 的一个方向向量为(0,0,1)m =；设(,,)n x y z =是平面BDF 的一个法向量；(2,3BD =-；由n BF n BD ⎧⊥⎪⎨⊥⎪⎩00n BF n BD ⎧⋅=⎪⇒⎨⋅=⎪⎩020x z x y -+=⎧⎪⇒⎨=⎪⎩x z y =⎧⎪⇒= 取1x =；得(1,3,1)n =；所以5cos ,5m n m n mn⋅<>==⋅；即直线1AA 与平面BDF 所成角的正弦值5． (16分)19．（本小题满分16分）已知数列1230,,,a a a ；其中1210,,,a a a 是首项为1；公差为1的等差数列；201110,,,a a a 是公差为d 的等差数列；302120,,,a a a 是公差为2d 的等差数列（0d ≠）． （Ⅰ）若20a = 30；求d ；（Ⅱ）试写出a 30关于d 的关系式；并求a 30的取值范围；（Ⅲ）续写已知数列；可以使得403130,,,a a a 是公差为d 3的等差数列；请你依次类推；把已知数列推广为无穷数列；试写出10n a 关于d 的关系式（n ∈N *）；（Ⅳ）在（Ⅲ）条件下；且1d ≠；试用d 表示此数列的前100项和10012100...S a a a =+++． 解：（Ⅰ）1010a =20101030a d =+=于是；2d = (4分)（Ⅱ）1010a =201010a d =+22302010101010a a d d d =+=++ 因此；230110()7.57.52a d =++≥ (8分) （Ⅲ）32340301010101010a a d d d d =+=+++ 11010,11010......1010(1),11n n n n d a d d d d d-=⎧⎪=+++=⎨-≠⎪-⎩ (12分) （Ⅳ）10012100......S a a a =+++12101112209192100(......)(......)......(......)a a a a a a a a a =++++++++++++29102090110110110110(10)(1010)(1010)...(1010)2222a d a d a d ++++=⨯++⨯++⨯+++⨯2910209010(......)55(1......)a a a d d d =++++++++29100(9......)1d d d d =-----+101551d d-⋅- 1110255451055955(1)d d d d +-+=- (16分)20．（本小题满分16分）已知32()f x x ax bx c =+++在1x =与23x =-时；都取得极值． (1) 求,a b 的值；(2)若3(1)2f -=；求()f x 的单调区间和极值； (3)若对[1,2]x ∈-都有3()f x c <恒成立；求c 的取值范围． 解：（1）f ′(x )＝3x 2＋2a x ＋b ＝0．由题设；x ＝1；x ＝－错误!为f ′(x )＝0的解．－错误!a ＝1－错误!；错误!＝1×(－错误!)．∴a ＝－错误!；b ＝－2． (4分)经检验得：这时1x =与23x =-都是极值点． (5分)（2）f (x )＝x 3－错误!x 2－2 x ＋c ；由f (－1)＝－1－错误!＋2＋c ＝错误!；c ＝1．∴f (x )＝x 3－错误!x 2－2 x ＋1．错误!；1）． 当x ＝－错误!时；f (x )有极大值；f (－错误!)＝错误!；当x ＝1时；f (x )有极小值；f (1)＝－错误!．(10分)（3）由（1）得；f ′(x )＝(x －1)(3x ＋2)；f (x )＝x 3－错误!x 2－2 x ＋c ；f (x )在[－1；－错误!)及（1；2]上递增；在（－错误!；1）递减．而f (－错误!)＝－错误!－错误!＋错误!＋c ＝c ＋错误!．f (2)＝8－2－4＋c ＝c ＋2． ∴ f (x )在[－1；2]上的最大值为c ＋2．∴ 32c c+< ∴ 2230c c c+-< ∴ 20230c c c >⎧⎨+-<⎩ 或20230c c c <⎧⎨+->⎩∴ 01c <<或3c <-． (16分)21．（本小题满分18分）已知A 、B 、C 是长轴长为4的椭圆上的三点；点A 是长轴的一个顶点；BC 过椭圆中心O ；如图；且0AC BC ⋅=；||2||BC AC =．（1）求椭圆的方程；（2）如果椭圆上两点P 、Q 使∠PCQ 的平分线垂直AO ；则总存在实数λ；使AB PQ λ=；请给出证明．解：（1）2a =；即2OA =；02AC BC ACB π⋅=⇒∠=． 12OC OB BC AC === ∴ 2OA OC ==∴ (1,1)C (4分)如图建立直角坐标系；设椭圆的方程为22221x y a b+=(0)a b >>． 则由(1,1)C 代入22221x y a b+=得22111a b +=； 把2a =代入22111a b +=得243b =． 所以椭圆的方程为223144x y += (8分) （2）设PCQ ∠的平分线CD 交OA 于点D ；则CD OA ⊥．由PCD QCD ∠=∠可知直线PC 与QC 的倾斜角互补． (10分) 于是直线PC 与QC 的斜率互为相反数；因此可设：直线PC 的方程为1(1)y k x -=-和直线QC 的方程为1(1)y k x -=--．由2231441(1)x y y k x ⎧+=⎪⎨⎪-=-⎩解得2222361321(,)3131k k k k P k k ----+++； (14分) 同理由2231441(1)x y y k x ⎧+=⎪⎨⎪-=--⎩解得2222361321(,)3131k k k k Q k k +--++++． ∴ 直线PQ 的斜率13PQ k =；而13AB k =（特例）． (16分) ∴ //PQ AB∴ 总存在实数λ；使AB PQ λ=． (18分)。

高二数学上学期期末考试试题注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，考试内容为必修3、选修2—1、选修2—2全部内容，共4页．考试时量120分钟，满分150分.2．答题前，考生务必将自己的姓名、准考证号填写在答题卡相应的位置. 3．全部答案在答题卡上完成，答在试题卷、草稿纸上无效.第I 卷一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知复数(12i)(1i)z =+-，则z 的虚部为A ．1-B ．3C ．1D ．i2．甲、乙两人下棋，甲获胜的概率为0.4，甲不输的概率为0.9，则甲、乙下成平局的 概率为A ．0.5B ．0.3C ．0.1D ．0.63．“11()()22b a >”是“77log log a b >”成立的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知直线l 的一个方向向量(213)=-，，m ，且直线l 过(03)A y ，，和(12)B z -，，两点，则y z -=A ．0B ．1C ．32D ．35．福利彩票“双色球”中红球的号码可以从01，02，03，…，32，33这33个二位号码中选取，小明利用如图所示的随机数表选取红色球的6个号码，选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字，则第四个被选中的红色球号码为81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 8506 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49A ．12 6．函数2()(31)e x f x x x =-+的极大值是A ．3e -B ．2e -C ．22eD ．5e7．洛书，古称龟书，是阴阳五行术数之源，在古代传说中有神龟出于 洛水，其甲壳上心有此图象，结构是戴九履一，左三右七，二四为肩，六八为足，以五居中，五方白圈皆阳数，四角黑点为阴数．如 图，若从四个阴数和五个阳数中分别随机选取1个数，则其和等于 11的概率是A ．15B ．25C ．310D ．148．已知抛物线2:8(0)C y px p =>的焦点为F ，C 与抛物线2x py =在第一象限的交点为M ，且4MF =，则p =A ．6B ．4C ．2D ．19．十七世纪，法国数学家费马提出猜想：“当整数2n >时，关于x 、y 、z 的方程 n n n x y z +=没有正整数解”，经历三百多年，1995年英国数学家安德鲁⋅怀尔斯给 出了证明，使它终成费马大定理，则下面命题正确的是① 对任意正整数n ，关于x 、y 、z 的方程n n n x y z +=都没有正整数解； ② 当整数2n >时，关于x 、y 、z 的方程n n n x y z +=至少存在一组正整数解； ③ 当正整数2n ≤时，关于x 、y 、z 的方程n n n x y z +=至少存在一组正整数解； ④ 若关于x 、y 、z 的方程n n n x y z +=至少存在一组正整数解，则正整数2n ≤．A ．①②B ．①③C ．②④D ．③④10．函数()ln sin f x x x =+（x ≤≤且0x ≠）的图象大致是A B C D11．已知12F F ，分别为双曲线22221(00)x y a b a b-=>>，的左、右焦点，以12F F 为直径的圆与双曲线在第一象限和第三象限的交点分别为M N ，，设四边形12F NF M 的周长为p ，面积为S ，且满足232S p =，则该双曲线的渐近线方程为A ．12y x =±B ．22y x =±C ．3y x =±D ．23y x =±12．若关于x 的方程1e 0e ex x xx m x +++=+有三个不相等的实根123x x x ，，，且1230x x x <<<，则3122312()()()e e ex x x x x x m m m +++的值为A ．eB ．2eC ．4(2)m m +D ．4(1)m m +第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分． 13．设1i2i 1iz --=+，则z =__________． 14．某班甲、乙两位同学在高二第一学期的5次物理考试成绩的茎叶图如图所示，则这两位同学中成绩比较稳定的同学的方差是__________．15．在区间[44]-，上任取一个实数a ，使得方程22123x ya a +=+-表示双曲线的概率为__________．16．已知M 是圆22:(1)(1)5C x y -+-=上一动点，A 为圆C 所在平面内一定点（C 为圆C 的圆心），线段MA 的垂直平分线与直线MC 交于点P ，则点P 的轨迹可能 是_______________．（写出所有正确结论的序号）① 圆； ② 椭圆； ③ 双曲线； ④ 抛物线； ⑤ 一个点； ⑥ 直线．三、解答题：本大题共6小题，满分70分．解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分10分）为推进农村经济结构调整，某乡村举办水果观光采摘节，并推出配套乡村游项目．现统计了4月份100名游客购买水果的情况，得到如图所示的频率分布直方图.（1）若将购买金额不低于80元的游客称为“优质客户”，现用分层抽样的方法从样本的“优质客户”中抽取5人，求这5人中购买金额不低于100元的人数；（2）从（1）中的5人中随机抽取2人作为幸运客户免费参加乡村游项目，请列出所有的基本事件，并求2人中至少有1人购买金额不低于100元的概率．18．（本小题满分12分）已知命题p ：复数5(2)(2)i ()z m m m =-++∈R 在复平面上对应的点位于第二象限，命题q ：椭圆22221(0)1x y m m m+=>+的离心率2(1)e ∈，．（1）若命题p 为真命题，求实数m 的取值范围； （2）若命题()p q ∧⌝为真命题，求实数m 的取值范围．19．（本小题满分12分）在统计学中，偏差是指个别测定值与测定的平均值之差，在成绩统计时，我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差．某高二班主任为了了解学生的偏科情况，对学生数学偏差x （单位：分）与历史偏差y （单位：分）之间的关系进行学科偏差分析，决定从全班52位同学中随机抽取一个容量为8的样本进行分析，得到他们的两科成绩偏差数据如下： （1）已知x 与y 之间具有线性相关关系，求y 关于x 的线性回归方程ˆˆˆybx a =+； （2）若这次考试该班数学平均分为118分，历史平均分为90.5，试预测数学成绩126分的同学的历史成绩． 附：参考公式与参考数据：1221ˆˆˆni ii nii x yn x y bay bx xn x ==-==--∑∑，，81324i ii x y==∑，8211256ii x==∑．20．（本小题满分12分）如图，在四棱锥P ABCD -中，ABCD 为矩形，PA PB =，PA PB ⊥，平面PAB ⊥平面ABCD ． （1）证明：平面PAD ⊥平面PBC ；（2）若M 为PC 的中点，直线PD 与平面PAB 所成的角为45︒，求二面角A MD B --的正弦值．学生序号 1 2 3 4 5 678数学偏差x 20 15 13 3 2 5- 10- 18- 历史偏差y6.53.53.51.50.50.5-2.5-3.5-21．（本小题满分12分）已知椭圆2222:1(0)x y C a b a b+=>>12F F ，分别为椭圆的左、右焦点，1B 为椭圆上顶点，112B F F △ （1）求椭圆C 的方程；（2）若直线(00)y kx m k m =+≠≠，与椭圆C 交于不同两点M N ，，已知1(0)2P ，，MP NP =，求实数m 的取值范围．22．（本小题满分12分）已知函数()ln f x x x =，2()()g x x ax a =+∈R ． （1）求函数()f x 的单调区间；（2）设()f x 图象在点(10)，处的切线与()g x 的图象相切，求a 的值； （3）若函数(()()2)x f F xx g x =+存在两个极值点12x x ，，且1232x x ≤，求12()()F x F x -的最大值．数学参考答案一、 选择题：本大题共12小题，每小题5分，共60分．二、填空题：本大题共4小题，每小题5分，共20分． 13．1 14．1015．5816．①②③⑤三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分10分）解：（1）如图易得，消费金额在[80100)，与[100120)，的人数比为0.00753:20.005=， ………………………2分∴ 这5人中消费金额不低于100元的人数为2； ………………………4分 （2）由（1）得，抽取的5人中购买金额低于100元的有3人，记为A B ，，C 购买金额不低于100元的有2人，记为a b ，， 所有基本事件如下：()A B ，，()A C ，，()A a ，，()A b ，，()B C ，，()B a ，，()B b ，，()C a ，，()C b ，，()a b ，，共有10种， …………………………………………………………8分 其中满足题意的有7种，所以710P =． ……………………………………10分18．（本小题满分12分） 解：（1）p ：2020m m -<⎧⎨+>⎩，22m -<<； ………………………………………………4分（2）q ：221a m =+，22b m =，222(1)1c m m =+-=， 则2211e m =+， 由题意，211112m <+<，解得01m <<，即m 的取值范围为(01)，………8分 ∴ q ⌝：0m ≤或1m ≥， ……………………………………………………9分由()p q ∧⌝为真命题，故q ⌝为真命题且p 为真命题， …………………10分 ∴ 20m ≤或12m ≤，故m 的取值范围为(20][12)-，，． ……12分19．（本小题满分12分） 解：（1）由题意，20151332(5)(10)(18)582x +++++-+-+-==，6.5 3.5 3.5 1.50.5(0.5)( 2.5)( 3.5)988y +++++-+-+-==， ……………3分25932481285412568()2ˆb-⨯⨯=-⨯=， ……………………………………………………6分 9151ˆˆ8422ay bx =-=-⨯=， ∴ 线性回归方程为1142ˆy x =+； ……………………………………………8分 （2）由题意，设该同学的历史成绩为w ，则历史偏差为90.5w -， 又该同学的数学偏差为1261188-=，由（1）得1890.5142w ⨯+-=，解得93w =，∴ 预测这位同学的历史成绩为93分． ……………………………………12分20．（本小题满分12分）证明：（1）∵ 平面PAB ⊥平面ABCD ，平面PAB 平面ABCD AB =矩形ABCD 中，DA AB ⊥ ∴ DA ⊥平面PAB ………………………2分 ∵ PB ⊂平面PAB ∴ DA PB ⊥ ……………………………………3分 又∵ PA PB ⊥，DA PA A = ∴ PB ⊥平面PAD …………………4分 ∵ PB ⊂平面PBC ∴ 平面PAD ⊥平面PBC ； ……………………5分解： （2）由（1）知DA ⊥平面PAB ，PA 为PD 在平面PAB 内的射影∴ DPA ∠即为直线PD 与平面PAB 所成的角，由题意，45DAP ∠=︒，DA PA = ………………………………………6分 取AB 中点O ，连结PA ，则PO AB ⊥，以O 为原点，建立如图所示的空间直角坐标系O xyz -，则(200)P ，，，(020)A -，，，(020)B ，，，(0222)D -，，，(112)M ，， 则(0022)DA =-，，，(132)DM =，(0422)DB =-，， …………8分设平面AMD 的一个法向量为()x y z =，，n ，则00DA DM ⎧⎪⎨⋅⎪⎩⋅==n n 即0320z x y z =+-=⎧⎪⎨⎪⎩， 令1y =-，则3x =，0z = ∴ 1()30-=，，n …9分同理易得：平面BMD 的一个法向量为(112)=-，，m 由10cos<>102⋅⋅===⋅，m n m n m n……11分 ∴ 二面角A MD B --15．…………12分 21．（本小题满分12分） 解：（1）由题意，1121232B F F S c b bc =⋅⋅==△， ……………………………………2分 又32c a =，222a b c =+，解得：2a =，1b =， …………………………4分 ∴ 椭圆C 的方程为2214x y +=； ……………………………………………5分（2）由2244y kx mx y =++=⎧⎨⎩，消去y 整理得：222(41)8440k x kmx m +++-=，设1122()()M x y N x y ，，，，则122841kmx x k -+=+， ……………………………7分 由222222644(41)(44)041k m k m k m ∆=-+->⇒>-， …………………8分 又设MN 中点D 的坐标为00()x y ，，∴ 12024241x x km x k +-=+=，2002244141k m m y kx m k m k -=+=+++= 即2244141()D km mk k -++， …………………………………………………………9分 ∵ MP NP =，∴ DP MN ⊥，即00112y x k+=-， ∴ 2461k m --= …10分 ∴ 2610611m m m -->-->-⎧⎨⎩，解得166m -<<-∴ m 的取值范围1(6)6--，．…………………………………………………12分22．（本小题满分12分）解：（1）()ln f x x x =的定义域为(0)+∞，，()ln 1f x x '=+， ………………………1分由()0f x '>，有1e x >，由()0f x '<，有10ex << ………………………2分 ∴ ()f x 的单调递减区间为1(0)e ，，单调递增区间为1()e+∞，； …………3分（2）由（1）及题意，易得()f x 图象在点(10)，处的切线斜率为(1)1f '=，则该切线方程为1y x =-， …………………………………………………4分联立21y x y x ax=-⎧⎨=+⎩，消去y 整理得：2(1)10x a x +-+=，由2(1)4031a a ∆=--=⇒=-或； ………………………………………6分（3）∵ 2()2ln F x x ax x =++，(0)x ∈+∞，，2222()2x ax F x x a x x++'=++=， 设2()22g x x ax =++，由（1）知函数()F x 的两个极值点12x x ，满足2220x ax ++=， 则122ax x +=-，121x x =， …………………………………………………7分 不妨设1210x x <<<，则()F x 在12()x x ，上是减函数，12()()F x F x >，∴ 221212111222()()()()2ln (2ln )F x F x F x F x x ax x x ax x -=-=++-++222211212222221()2ln2ln x x x a x x x x x x =-+-+=-- 22222212ln x x x =-- 令22t x =，则1t >，又1222132x x x x ≤，即2222320x x ≤，解得212x ≤ ∴ 2214x ≤ ∴ 14t ≤设1()2ln (14)h t tt t t≤，则22212(1)()10t h t t tt ≥∴ ()h t 在(14]，上为增函数 ∴ 1515()(4)2ln 44ln 244h t h ≤，即1215()()4ln 24F x F x ≤∴ 12()()F x F x -的最大值为154ln 24-． …………………………………12分。

2021-2022学年江苏省南通市高二上期末考试数学试卷一．选择题（共8小题，每小题5分，共40分）1．已知A ，B ，C 不共线，对空间任意一点O ，若OP →=12OA →+（14−λ）OB →+（λ+14）OC →成立，则“λ＝1”是“P ，A ，B ，C 四点共面”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既非充分也非必要条件2．若经过P （m ，﹣1）和Q （5，m ）的直线的斜率为2，则m 等于（ ） A ．1B ．3C ．1或3D ．43．已知平行四边形ABCD 内接于椭圆Ω：x 2a 2+y 2b 2=1（a ＞b ＞0），且AB ，AD 斜率之积的取值范围为(−45，−34)，则椭圆Ω的离心率的取值范围为（ ） A ．(√55，12)B ．(√55，√22) C ．(14，√55)D ．(15，14)4．在正四面体P ﹣ABC 中，棱长为2，且E 是棱AB 中点，则PE →⋅BC →的值为（ ） A ．﹣1B ．1C ．√3D ．735．若圆O 1：x 2+y 2＝5与圆O 2：（x ﹣m ）2+（y ﹣2m ）2＝20（m ＞0）相交，则实数m 的取值范围是（ ） A ．（1，3）B ．[1，3]C ．（3，+∞）D ．（0，1）6．已知F 1，F 2是椭圆C 的两个焦点，P 是C 上的一点，若以F 1F 2为直径的圆过点P ，且∠PF 2F 1＝2∠PF 1F 2，则C 的离心率为（ ） A ．1−√32B ．√3−1C ．√3−12D ．2−√37．圆C ：（x ﹣1）2+y 2＝4被直线y ＝kx ﹣1截得的最短弦长为（ ） A ．2√3 B ．2√2 C ．√3 D ．√28．已知双曲线C ：x 2a 2−y 2b 2=1（a ＞0，b ＞0）的右顶点为A ，左焦点为F ，动点B 在C 上．当AF ⊥BF 时，有AF ＝BF ，则C 的离心率是（ ） A ．√2B ．32C ．√3D ．2二．多选题（共4小题，每小题5分，共20分）9．已知点P 是平行四边形ABCD 所在的平面外一点，如果AB →=（2，﹣1，﹣4），AD →=（4，2，0），AP →=（﹣1，2，﹣1）．下列结论正确的有（ ） A ．AP ⊥AB B ．AP ⊥ADC ．AP →是平面ABCD 的一个法向量D ．AP →∥BD →10．已知点A （﹣5，0），B （﹣1，﹣3），点P 是圆C ：（x ﹣1）2+y 2＝1上任意一点，则△P AB 面积的可以等于（ ） A ．11B ．232C ．13D ．27211．已知椭圆E ：x 236+y 220=1的左、右焦点分别为F 1，F 2，定点A （1，4），若点P 是椭圆E 上的动点，则|P A |+|PF 1|的值可能为（ ） A ．7 B ．10 C ．17 D ．1912．已知椭圆C ：x 2a+y 2b=1（a ＞b ＞0）的左、右焦点分别为F 1，F 2且|F 1F 2|＝2，点P （1，1）在椭圆内部，点Q 在椭圆上，则以下说法正确的是（ ） A ．|QF 1|+|QP |的最小值为2√a −1 B ．椭圆C 的短轴长可能为2C ．椭圆C 的离心率的取值范围为（0，√5−12）D ．若PF 1→=F 1Q →，则椭圆C 的长轴长为√5+√17 三．填空题（共4小题，每小题5分，共20分）13．直线x +√3y +2021＝0的倾斜角为 .（用角度制表示）14．已知a →=（5，3，1），b →=（﹣2，t ，−25），若a →与b →的夹角为钝角，则实数t 的取值范围是 ． 15．已知椭圆标准方程为x 23+y 22=1，则该椭圆的长轴长是 ．16．过直线l ：y ＝2x 上一点P 向圆C ：（x +3）2+（y ﹣1）2＝8引切线，切线长为d 1，点P 到点M （﹣6，﹣2）的距离为d 2，则|d 1﹣d 2|的最大值为 ．四．解答题（共6小题，其中第17小题10分，第18-22小题各12分，共70分）17．已知两直线l1：ax+3y+4＝0和l2：x+（a﹣2）y+a2﹣5＝0．（1）若l1⊥l2，求实数a的值；（2）若l1∥l2，求实数a的值．18．在平面直角坐标系xOy中，A（﹣1，5），B（﹣2，﹣2），C（5，5），圆M为△ABC的外接圆．（1）求圆M的标准方程；（2）过点P（7，2）作圆M的切线，求切线方程．19．如图所示，菱形ABCD 的对角线AC 与BD 交于点O ，AB ＝AC ＝2，将△ABD 沿BD 翻折到△A 'BD 的位置，使得AA '=√2． （Ⅰ）求证：平面A 'BD ⊥平面ABCD ；（Ⅱ）当A′M →=2MD →时，求多面体MOCD 的体积．20．如图，一抛物线型拱桥的拱顶O离水面高4米，水面宽度AB＝10米．现有一船只运送一堆由小货箱码成的长方体形的货物欲从桥下中央经过，已知长方体形货物总宽6米，高1.5米，货箱最底面与水面持平．（1）问船只能否顺利通过该桥？（2）已知每加一层货箱，船只吃水深度增加1cm；每减一层货箱，船只吃水深度减少1cm．若每层小货箱高3cm，且货物与桥壁需上下留2cm间隙方可通过，问船只需增加或减少几层货箱可恰好能从桥下中央通过？21．已知点F(2√2，0)为中心在原点的椭圆C的右焦点，且P(2，2√63)在此椭圆上．（1）求椭圆C的方程；（2）若过点Q(−4√2，0)的直线交椭圆于A，B两点，点A关于x轴的对称点为点C，求证：直线BC经过定点，并求出定点的坐标．22．抛物线C的顶点为坐标原点O，焦点在x轴上，直线l：x＝1交C于P，Q两点，且OP⊥OQ．已知点M（2，0），且⊙M与l相切．（1）求C，⊙M的方程；（2）设A1，A2，A3是C上的三个点，直线A1A2，A1A3均与⊙M相切．判断直线A2A3与⊙M的位置关系，并说明理由．2021-2022学年江苏省南通市高二上期末考试数学试卷参考答案与试题解析一．选择题（共8小题，每小题5分，共40分）1．已知A ，B ，C 不共线，对空间任意一点O ，若OP →=12OA →+（14−λ）OB →+（λ+14）OC →成立，则“λ＝1”是“P ，A ，B ，C 四点共面”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既非充分也非必要条件【解答】解：知A ，B ，C 不共线，对空间任意一点O ，若OP →=12OA →+（14−λ）OB →+（λ+14）OC →成立，若“P ，A ，B ，C 四点共面，则12+14−λ+λ+14=1，恒成立，故λ＝1”是“P ，A ，B ，C 四点共面”的充分不必要条件， 故选：A ．2．若经过P （m ，﹣1）和Q （5，m ）的直线的斜率为2，则m 等于（ ） A ．1B ．3C ．1或3D ．4【解答】解：∵经过P （m ，﹣1）和Q （5，m ）的直线的斜率为2， ∴−1−m m−5=2，解得m ＝3，经过验证分母不等于0， ∴m ＝3， 故选：B ．3．已知平行四边形ABCD 内接于椭圆Ω：x 2a 2+y 2b 2=1（a ＞b ＞0），且AB ，AD 斜率之积的取值范围为(−45，−34)，则椭圆Ω的离心率的取值范围为（ ） A ．(√55，12)B ．(√55，√22) C ．(14，√55) D ．(15，14)【解答】解：设A （x 1，y 1），B （x 2，y 2），由平行四边形对角线互相平分可得A 与C ，B 与D 关于原点对称，所以可得D （﹣x 2，﹣y 2），所以k AB •k AD =y 2−y 1x 2−x 1•y 1+y 2x 1+x 2=y 12−y 22x 12−x 22，将A ，B 的坐标代入可得{x 12a 2+y 12b 2=1x 22a 2+y 22b 2=1相减可得x 12−x 22a 2+y 12−y 22b 2=0，可得y 12−y 22x 12−x 22=−b 2a 2，由题意可得：−45＜−b 2a 2＜−34，即34＜b 2a 2＜45，可得：34＜1−c 2a 2＜45，解得：e =c a ∈（√55，12），故选：A ．4．在正四面体P ﹣ABC 中，棱长为2，且E 是棱AB 中点，则PE →⋅BC →的值为（ ） A ．﹣1B ．1C ．√3D ．73【解答】解：如图，P ﹣ABC 为正四面体，则∠APC ＝∠BPC ＝∠APB ＝60°，E 是棱AB 中点，所以PE →=12(PA →+PB →)，BC →=PC →−PB →，所以PE →⋅BC →=12(PA →+PB →)•（PC →−PB →）=12PA →⋅PC →+12PB →⋅PC →−12PA →⋅PB →−12PB →2=12×2×2×cos60°−12×22=1﹣2＝﹣1， 故选：A ．5．若圆O 1：x 2+y 2＝5与圆O 2：（x ﹣m ）2+（y ﹣2m ）2＝20（m ＞0）相交，则实数m 的取值范围是（ ） A ．（1，3）B ．[1，3]C ．（3，+∞）D ．（0，1）【解答】解：O 1：x 2+y 2＝5的圆心是（0，0），半径是√5，O 2：（x ﹣m ）2+（y ﹣2m ）2＝20（m ＞0）的圆心是（m ，2m ），半径是2√5， 由题意得：√5＜√m 2+4m 2＜3√5，（m ＞0），解得：1＜m ＜3， 故选：A ．6．已知F 1，F 2是椭圆C 的两个焦点，P 是C 上的一点，若以F 1F 2为直径的圆过点P ，且∠PF 2F 1＝2∠PF 1F 2，则C 的离心率为（ ） A ．1−√32B ．√3−1C ．√3−12D ．2−√3【解答】解：如图，在焦点△PF 1F 2中，由题意知：|PF 1|+|PF 2|＝2a ⋯①，且△PF 1F 2为直角三角形，再由∠PF 2F 1＝2∠PF 1F 2＝2α，且∠PF 1F 2+∠PF 2F 1＝90°，故∠PF 1F 2＝30°， 所以|PF 1|＝|F 1F 2|cos 30°=√3c ，|PF 2|＝|F 1F 2|sin 30°＝c ，代入①式得(√3+1)c =2a ， 故e =c a =2√3+1=√3−1． 故选：B ．7．圆C ：（x ﹣1）2+y 2＝4被直线y ＝kx ﹣1截得的最短弦长为（ ） A ．2√3B ．2√2C ．√3D ．√2【解答】解：直线y ＝kx ﹣1过定点P （0，﹣1），圆心C （1，0）， 当直线CP 与弦垂直时，弦长最短， ∵|CP|=√12+12=√2，∴最短弦长为2√r 2−|CP|2=2√4−2=2√2， 故选：B ． 8．已知双曲线C ：x 2a 2−y 2b 2=1（a ＞0，b ＞0）的右顶点为A ，左焦点为F ，动点B 在C 上．当AF ⊥BF 时，有AF ＝BF ，则C 的离心率是（ ） A ．√2B ．32C ．√3D ．2【解答】解：由动点B 在C 上．当BF ⊥AF 时，|AF |＝|BF |， 可得B 在左支上，令x ＝﹣c ，可得c 2a 2−y 2b 2=1，解得y ＝±b √c 2a 2−1=±b 2a ， 即有|BF |=b2a，则a +c =b2a ，即a （a +c ）＝b 2＝c 2﹣a 2＝（c ﹣a ）（a +c ），可得a ＝c ﹣a ，即c ＝2a ， e =ca=2． 故选：D ．二．多选题（共4小题，每小题5分，共20分）9．已知点P 是平行四边形ABCD 所在的平面外一点，如果AB →=（2，﹣1，﹣4），AD →=（4，2，0），AP →=（﹣1，2，﹣1）．下列结论正确的有（ ） A ．AP ⊥AB B ．AP ⊥ADC ．AP →是平面ABCD 的一个法向量D ．AP →∥BD →【解答】解：对于A ，AB →•AP →=2×（﹣1）+（﹣1）×2+（﹣4）×（﹣1）＝0，∴AP →⊥AB →，即AP ⊥AB ，A 正确；对于B ，AP →•AD →=（﹣1）×4+2×2+（﹣1）×0＝0，∴AP →⊥AD →，即AP ⊥AD ，B 正确； 对于C ，由AP →⊥AB →，且AP →⊥AD →，得出AP →是平面ABCD 的一个法向量，C 正确； 对于D ，由AP →是平面ABCD 的法向量，得出AP →⊥BD →，则D 错误． 故选：ABC ．10．已知点A （﹣5，0），B （﹣1，﹣3），点P 是圆C ：（x ﹣1）2+y 2＝1上任意一点，则△P AB 面积的可以等于（ ） A ．11B ．232C ．13D ．272【解答】解：如图，圆C ：（x ﹣1）2+y 2＝1的圆心坐标为（1，0），半径为1， 过A ，B 的直线方程为y −3=x+5−1+5，即3x +4y +15＝0．|AB |=√(−5+1)2+32=5=5，所以圆C ：（x ﹣1）2+y 2＝1上的点P 到直线AB 距离的最大值为d +r =√3+4+1=235， 点P 到直线AB 的距离的最小值为d ﹣r ==√3+41=135， 因此△P AB 的面积的最大值为12|AB |•（d +r ）=12×5×235=232，△P AB 的面积的最小值为12|AB |•（d ﹣r ）=12×5×135=132， 所以△P AB 面积的可以是AB ， 故选：AB ．11．已知椭圆E ：x 236+y 220=1的左、右焦点分别为F 1，F 2，定点A （1，4），若点P 是椭圆E 上的动点，则|P A |+|PF 1|的值可能为（ ） A ．7B ．10C ．17D ．19【解答】解：由椭圆的定义可得|P A |+|PF 1|＝|P A |+2a ﹣|PF 2|＝2a +|P A |﹣|PF 2|， 由椭圆的方程可得：a ＝6，b ＝2√5，所以c =√36−20=4， 所以F 2（4，0），所以|AF 2|=√(1−4)2+42=5， 因为﹣5≤|P A |﹣|PF 2|≤5 所以7≤|P A |+|PF 1|≤17，故选：ABC ． 12．已知椭圆C ：x 2a+y 2b=1（a ＞b ＞0）的左、右焦点分别为F 1，F 2且|F 1F 2|＝2，点P （1，1）在椭圆内部，点Q 在椭圆上，则以下说法正确的是（ ） A ．|QF 1|+|QP |的最小值为2√a −1 B ．椭圆C 的短轴长可能为2C ．椭圆C 的离心率的取值范围为（0，√5−12）D ．若PF 1→=F 1Q →，则椭圆C 的长轴长为√5+√17【解答】解：由|F 1F 2|＝2可得2c ＝2，所以c ＝1，右焦点F 2（1，0）， 所以|PF 2|＝1，所以|QF 1|+|QP |＝|2√a |﹣|QF 2|+|QP |＝2√a −（|QF 2|﹣|QP ）≥2√a −|PF 2|＝2√a −1，所以A 正确； x ＝1与x 2a+y 2b=1的交点为（1，√a1）， 因为点P （1，1）在椭圆内部，所以√a1，所以b ＞√a ，b 2＞a ＝b +c 2＝b +1， 可得b ＞1+√52，有可能√b ＞1，即短轴长不可能为2，所以B 不正确； 或者a 2﹣c 2＞a ，即a 2﹣a ﹣1＞0，可得a ＞1+√52， 所以离心率e =√a 1+√52=√5−12，所以C 正确；若PF 1→=F 1Q →，可得F 1为PQ 的中点．所以可得Q （﹣3，﹣1），而Q 在椭圆上， 所以9a +1b=1，c 2＝a ﹣b ＝c 2＝1，解得a =11±√952（负号舍），所以长轴长2√a =√22−√95，所以D 不正确； 故选：AC ．三．填空题（共4小题，每小题5分，共20分）13．直线x +√3y +2021＝0的倾斜角为 150° .（用角度制表示） 【解答】解：根据题意，设直线x +√3y +2021＝0的倾斜角为α， 其斜率k ＝tan α=−√33，又由0°≤α＜180°， 则α＝150°，故答案为：150°．14．已知a →=（5，3，1），b →=（﹣2，t ，−25），若a →与b →的夹角为钝角，则实数t 的取值范围是 （﹣∞，−65）∪（−65，5215） ．【解答】解：∵a →=（5，3，1），b →=（﹣2，t ，−25），a →与b →的夹角为钝角， ∴a →⋅b →=5×（﹣2）+3t +1×（−25）＜0， 解得t ＜5215．又a →=（5，3，1）与b →=（﹣2，t ，−25）不共线， 由a →=（5，3，1）与b →=（﹣2，t ，−25）共线，可得−25=t 3=−25，解得t =−65，∴实数t 的取值范围是（﹣∞，−65）∪（−65，5215）．故答案为：（﹣∞，−65）∪（−65，5215）．15．已知椭圆标准方程为x 23+y 22=1，则该椭圆的长轴长是 2√3 ．【解答】解：椭圆标准方程为x 23+y 22=1，则该椭圆的长轴长是2a ＝2√3．故答案为：2√3．16．过直线l ：y ＝2x 上一点P 向圆C ：（x +3）2+（y ﹣1）2＝8引切线，切线长为d 1，点P 到点M （﹣6，﹣2）的距离为d 2，则|d 1﹣d 2|的最大值为 √26 ． 【解答】解：根据题意设P （x ，2x ），则d 1=√PC 2−r 2=√(x +3)2+(2x −1)2−8#/DEL/#=√5x 2+2x +2#/DEL/#=√5×√(x +15)2+925#/DEL/#=√5×√(x +15)2+(0−35)2#/DEL/#故d 1 的几何意义为：x 轴上一点与 (−15，35) 之间距离的√5倍， 又d 2＝MP =√(x +6)2+(2x +2)2−8=√5x 2+20x +40 =√5×√(x +2)2+(0−2)2，故d 2的几何意义为：x 轴上一点与（﹣2，2）之间的距离的√5倍，（﹣2，2）和 (−15，35) 位于x 轴的同侧，所以|d 1﹣d 2|的最大值即为这两点间距离的√5倍，即，|d 1−d 2|max =√5×√(−2+15)2+(2−35)2=√26． 故答案为：√26．四．解答题（共6小题，其中第17小题10分，第18-22小题各12分，共70分） 17．已知两直线l 1：ax +3y +4＝0和l 2：x +（a ﹣2）y +a 2﹣5＝0． （1）若l 1⊥l 2，求实数a 的值； （2）若l 1∥l 2，求实数a 的值．【解答】解：（1）若l 1⊥l 2，则a ×1+3×（a ﹣2）＝0， 解得a =32，故所求实数a 的值为32；（2）若l 1∥l 2，则{a(a −2)−3×1=0a(a 2−5)−1×4≠0，解得a ＝3，故所求实数a 的值为3．18．在平面直角坐标系xOy 中，A （﹣1，5），B （﹣2，﹣2），C （5，5），圆M 为△ABC 的外接圆．（1）求圆M 的标准方程；（2）过点P （7，2）作圆M 的切线，求切线方程． 【解答】解：（1）设圆M 的方程为x 2+y 2+Dx +Ey +F ＝0，A （﹣1，5），B （﹣2，﹣2），C （5，5），圆M 为△ABC 的外接圆 {26−D +5E +F =08−2D −2E +F =050+5D +5E +F =0，解得D ＝﹣4，E ＝﹣2，F ＝﹣20， 所以圆M 的方程为x 2+y 2﹣4x ﹣2y ﹣20＝0， 故圆M 的标准方程为（x ﹣2）2+（y ﹣1）2＝25． （2）当切线斜率不存在时，切线方程为x ＝7．当切线斜率存在时，设切线方程为y ﹣2＝k （x ﹣7），即kx ﹣y ﹣7k +2＝0． 由√1+k 2=5，解得k =−125所以切线方程为y −2=−125(x −7)，即12x +5y ﹣94＝0． 综上所述，所求切线方程为x ＝7或12x +5y ﹣94＝0．19．如图所示，菱形ABCD 的对角线AC 与BD 交于点O ，AB ＝AC ＝2，将△ABD 沿BD 翻折到△A 'BD 的位置，使得AA '=√2． （Ⅰ）求证：平面A 'BD ⊥平面ABCD ；（Ⅱ）当A′M →=2MD →时，求多面体MOCD 的体积．【解答】（Ⅰ）证明：∵四边形ABCD 为菱形，AB ＝AC ＝2 ∴AC ⊥BD ，∠ABC ＝60°，又∵AO ＝A ′O ＝1，AA '=√2，∴A ′O ⊥AO ，又∵AO ⊥BO ，A ′O ∩BO ＝O ，∴AO ⊥平面A ′OB ，即AC ⊥平面A ′BD ， 而AC ⊂平面ABCD ，∴平面A 'BD ⊥平面ABCD ； （Ⅱ）解：由（Ⅰ）可得A ′O ⊥平面ABCD ， 当A′M →=2MD →时，多面体MOCD 的体积V =13V A′−OCD =13×13S △OCD⋅A′O =19×12×OC ×OD =19×12×1×√3=√318．20．如图，一抛物线型拱桥的拱顶O 离水面高4米，水面宽度AB ＝10米．现有一船只运送一堆由小货箱码成的长方体形的货物欲从桥下中央经过，已知长方体形货物总宽6米，高1.5米，货箱最底面与水面持平． （1）问船只能否顺利通过该桥？（2）已知每加一层货箱，船只吃水深度增加1cm ；每减一层货箱，船只吃水深度减少1cm ．若每层小货箱高3cm ，且货物与桥壁需上下留2cm 间隙方可通过，问船只需增加或减少几层货箱可恰好能从桥下中央通过？【解答】解：（1）以O 为原点，过O 垂直于AB 的直线为y 轴，建立如图所示平面直角坐标系：设抛物线方程为x 2＝my ，根据题意知点B （5，﹣4）在抛物线上；.......................2分 ∴25＝﹣4m ；∴m =−254；∴x 2=−254y ；.......................5分 可设C （3，﹣4），过C 作AB 的垂线，交抛物线于D （3，y 0）， 则9=−254y 0；∴y 0=−3625；..................................8分 ∵|CD|=3625＜1.5；∴货箱不能顺利通过该桥．..................................10分 （2）由题（1）知，货物超出高度为（1.5﹣1.44）×100＝6cm ，..................................11分每减少一层，则船体连货物高度整体下降3﹣1＝2cm ，..................................13分 由货物与桥壁需留下2cm 间隙．则需要减少层数为62−1＝2，..................15分答：船只不能顺利通过该桥，需要减少2层可恰好能从中央通过．.....................16分 21．已知点F(2√2，0)为中心在原点的椭圆C 的右焦点，且P(2，2√63)在此椭圆上． （1）求椭圆C 的方程；（2）若过点Q(−4√2，0)的直线交椭圆于A ，B 两点，点A 关于x 轴的对称点为点C ，求证：直线BC 经过定点，并求出定点的坐标．【解答】解：（1）由已知：{a 2−b 2=8#/DEL/#4a2+83b2=1#/DEL/#⇒3a 4−44a 2+96=0，∴a 2＝12（a 2=83＜8，不合题意，舍去），∴b 2＝4，则椭圆C 的方程为x 212+y 24=1． （4分）（2）设直线BC 的方程为x ＝my +t ， 与椭圆方程联立得（my +t ）2+3y 2＝12， 即（m 2+3）y 2+2mty +t 2﹣12＝0， 设C （x 1，y 1），B （x 2，y 2），则y 1+y 2=−2mt m 2+3，y 1y 2=t 2−12m 2+3，（6分）由△＞0可得t 2＜4m 2+12． （7分） 又Q(−4√2，0)，A(x 1，−y 1)，B(x 2，y 2)三点共线， 故1x +4√2=2x +4√2⇒y 1(x 2+4√2)+y 2(x 1+4√2)=0，y 1(my 2+t +4√2)+y 2(my 1+t +4√2)=0，2my 1y 2+(t +4√2)(y 1+y 2)=0，（9分）∴2m ⋅t 2−12m 2+3−(t+4√2)⋅2mtm 2+3=0，∴√2mt +3m =0，又m ≠0，∴t =−32√2，即BC 恒过定点(−32√2，0)． （12分） 22．抛物线C 的顶点为坐标原点O ，焦点在x 轴上，直线l ：x ＝1交C 于P ，Q 两点，且OP ⊥OQ ．已知点M （2，0），且⊙M 与l 相切． （1）求C ，⊙M 的方程；（2）设A 1，A 2，A 3是C 上的三个点，直线A 1A 2，A 1A 3均与⊙M 相切．判断直线A 2A 3与⊙M 的位置关系，并说明理由．【解答】解：（1）因为x ＝1与抛物线有两个不同的交点，故可设抛物线C 的方程为：y 2＝2px （p ＞0）， 令x ＝1，则y =±√2p ，根据抛物线的对称性，不妨设P 在x 轴上方，Q 在X 轴下方，故P(1，√2p)，Q(1，−√2p)， 因为OP ⊥OQ ，故1+√2p ×(−√2p)=0⇒p =12，抛物线C的方程为：y2＝x，因为⊙M与l相切，故其半径为1，故⊙M：（x﹣2）2+y2＝1．另解：（1）根据抛物线的对称性，由题意可得∠POx＝∠QOx＝45°，因此点P，Q的坐标为（1，±1），由题意可设抛物线C的方程为：y2＝2px（p＞0），可得p=1 2，因此抛物线C的方程为y2＝x．而圆M的半径为圆心M到直线l的距离为1，可得⊙M的方程为（x﹣2）2+y2＝1．（2）很明显，对于A1A2或者A1A3斜率不存在的情况以及A2A3斜率为0的情况满足题意．否则：设A1（x1，y1），A2（x2，y2），A3（x3，y3）．当A1，A2，A3其中某一个为坐标原点时（假设A1为坐标原点时），设直线A1A2方程为kx﹣y＝0，根据点M（2，0）到直线距离为1可得√1+k2=1，解得k=±√33，联立直线A1A2与抛物线方程可得x＝3，此时直线A2A3与⊙M的位置关系为相切，当A1，A2，A3都不是坐标原点时，即x1≠x2≠x3，直线A1A2的方程为x﹣（y1+y2）y+y1y2＝0，此时有，12√1+(y1+y2)2=1，即(y12−1)y22+2y1y2+3−y12=0，同理，由对称性可得，(y12−1)y32+2y1y3+3−y12=0，所以y2，y3是方程(y12−1)t2+2y1t+3−y12=0的两根，则y2+y3=−2y1y12−1，y2y3=3−y12y12−1，依题意有，直线A2A3的方程为x﹣（y2+y3）y+y2y3＝0，令M到直线A2A3的距离为d，则有d2=(2+y2y3)21+(y2+y3)2=(2+3−y12y12−1)21+(−2y1y12−1)2=1，此时直线A2A3与⊙M的位置关系也为相切，综上，直线A2A3与⊙M相切．（2）另解：设A i（y i2，y i），i＝1，2，3，由直线的两点式可知，直线A1A2的方程为（y12−y22）（y﹣y2）＝（y1﹣y2）（x−y22），化简可得x﹣（y1+y2）y+y1y2＝0，因为直线A1A2与圆M相切，所以12√1+(y1+y2)2=1⇒（2+y1y2）2＝1+（y1+y2）2，整理得(y12−1)y22+2y1y2+3−y12=0，同理有(y12−1)y32+2y1y3+3−y12=0，所以y2，y3是关于y的方程(y12−1)y2+2y1y+3−y12=0的两个根，则y2+y3=−2y1y12−1，y2y3=3−y12y12−1，依题意有，直线A2A3的方程为x﹣（y2+y3）y+y2y3＝0，令M到直线A2A3的距离为d，则有d2=(2+y2y3)21+(y2+y3)2=(2+3−y12y12−1)21+(−2y1y12−1)2=1，此时直线A2A3与⊙M的位置关系也为相切，综上，直线A2A3与⊙M相切．。

加油！有志者事竟成答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好! 经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！一、选择题：本题共8小题，每小题5分，共40分。

二、选择题：本题共4小题，每小题5分，共20分。

三、填空题：本题共4小题，每小题5分，共20分。

13． (22) ， 14．221416y x或2214y x 15． 144 16． 12四、解答题：本题共6小题，共70分。

解答应写出文字说明、证明过程戓演算步骤。

17. （10分）【解】（1）设 n a 的公差为d ，由条件，得11154(4)8a d a d a d ，， …… 2分 解得183a d ，． …… 3分 由2(1)3198(3)0222m m m S m m m ， 解得0m 或193m ． 因为m N ，所以m 的最小值为7． …… 5分（2）设 n a 的公比为q ， 由条件，得64531226a a q a a ． 将2q 代入45123()6a a q q a ，得112a ． …… 7分所以11(12)122122n n n S ，22n n a ， 所以12=2n nS a ． ……10分 18. （12分）（1）【证】在正四棱柱1111ABCD A BC D 中，以1AD AB AA ，， 为正交基底建立如图所示的空间直角坐标系． 因为123AB AA ，，则(000)A ，，,(220)(103)(010)C E F ，，，，，，，，， …… 2分所以(220)(113)AC EF ，，，，，．…… 4分 因为2(1)210(3)0AC EF ， 所以AC EF ，即AC EF ． …… 6分（2）【解】由1(223)C ，，，得1(120)EC ，，． 设平面1C EF 的法向量()x y z ，，n ，由1EC EF ，，n n 即12030EC x y EF x y z，，n n 令1y ，得2x ，1z ，即(211) ，，n ． …… 9分 设直线AC 与平面1C EF 所成角的大小为 ，则sin cos AC ，n 即直线AC 与平面1C EF ． ……12分 19．（12分）【解】（1）因为抛物线C 的焦点为(20)F ，，所以22p ，即4p ， D 1 EC A 1F C 1 D A B B 1 yx z所以C 的方程为28y x ． …… 2分 设直线l 的方程为(2)y k x ，由2(2)8y k x y x ，，消y 得2222(48)40k x k x k ， 设 1122M x y N x y ，，，，则124x x ． …… 4分 又21212()88256y y x x ，120y y ，所以1216y y ，所以12124(16)12OM ON x x y y ． …… 6分（2）因为MF MP NF ，，成等差数列， 所以1202x x ，且1212(2)(2)(2)x x x ， 即1234x x ． …… 8分又124x x ，解得12263x x ，， ……10分 由212248203k x x k，解得23k ．所以2216NP ． ……12分20. （12分）【解】（1）以AB AD AP ，，为单位正交基底，建立如图所示的空间直角坐标系． 因为2BC ，1AP AB AD ， 所以(100)(001)(010)(120)B P D C ，，，，，，，，，，，，则(101)(011)(110)PB PD DC ，，，，，，，，． 设平面PBD 的法向量1111()x y z ，，n ， 由11PB PD ，，n n 即11111100PB x z PD y z ，，n n 取1(111) ，，n ． …… 2分 设平面PCD 的法向量2222()x y z ，，n ， E由22PD DC ，，n n 即22222200PD y z DC x y ，，n n 取1(111) ，，n ． …… 4分 设二面角B PD C 的大小为 ，则121cos cos 3 ，n n ，所以sin …… 6分 （2）设(2)PE PC ，，（01 ≤），则 (121)BE PE PB ，，． 因为异面直线PD 与BE 所成角的大小为60 ，所以1cos60cos 2PD BE ，， 解得23 ． …… 9分 此时242()333PE ，，，所以点E 到平面PBD的距离1143PE dn n……12分 21.（12分）【解】（1）由121n n a a ，得112(1)n n a a ． …… 1分 因为11a ，所以10n a ， 所以1121n n a a ，所以 1n a 是首项为2，公比为2的等比数列． 所以12n n a ，即21n n a ．…… 3分 由4(21)1n n S n b ，① 得114(21)1n n S n b ，② ①－②，得14(21)(21)n n n b n b n b （2n ≥），即1(23)(21)n n n b n b （2n ≥）， 即12123n n b b n n （2n ≥）． …… 5分 当1n 时，11b ，23b ，所以12121232n n b b b n n ，所以21n b n （2n ≥）， 因为11b 符合上式，所以21n b n （n N ）．…… 7分 （2）由（1）知，2(21)n n c n ． 所以123n n T c c c c 12332+52+72++(21)2n n ，③ …… 9分 所以234+1232+52+72++(21)2+(21)2n n n T n n ，④③－④，得234+162(2+2+2++2)(21)2n n n T n ，1+1+18(12)6(21)22(12)212n n n n n ，所以1(21)22n n T n ．……12分 22.（12分）（1）【证】由题意，12(10)(10)F F ，，，． 设直线l 的方程为(1)y k x ，由22(1)12y k x x y，，消y 得222(21)4220k k x k ． 设 1122A x y B x y ，，，， 则221212224222121k k x x x x k k ，．…… 2分 要证OMA OMB ． 即证直线MA MB ，的斜率之和0MA MB k k ． 因为2121222111(32()4222)(2)MA MB x x x y k x x x x k x y k kk，高二数学参考答案 第 6 页 （共 6 页） 而2313322144128423()4021k k k k k k k k k x x x x ， 所以0MA MB k k 得证，所以MA MB ，的倾斜角互补，即OMA OMB ． …… 4分（2）【解】由（1）及椭圆的对称性可知，直线AB 经过点(20)M ，． 设直线AB 的方程为(2)y m x ，由22(2)12y m x x y ，，消y 得222(21)8820m m x m ． 设 1133A x y B x y ，，，， 则213221328218221m x x m m x x m，，且422644(21)(82)0m m m ，即2102m ．所以13x x，所以AB …… 7分 又点1F 到直线AB，所以1F B A △的面积12S……10分 设221t m ，则(12)t ，，且S 当134t，即m 时，1F B A △……12分 注：过程中没有参数范围，扣1分．。

江苏省南通中学2016～2017学年度第一学期期末考试高二数学一、填空题：本大题共14小题，每小题5分，共70分．请把答案直接填写在答题卡相应位．．．．．．置上．．. 1． 若直线经过(1,0)A 、(0,1)B -两点, 则直线AB 的倾斜角为 ▲ ．答案：45︒2． 已知平面//α平面β，若直线l ⊥平面α，则直线l 与平面β的位置关系为 ▲ ．答案：垂直3． 函数()e x f x x =⋅，则(1)f '= ▲ ．答案：2e4． 圆心在y 轴上，半径为1，且过点(1,2)的圆的方程为 ▲ ．答案：x 2＋(y －2)2＝15． 准线方程为2x =-的抛物线的标准方程是 ▲ ．答案：28y x =6． 棱长为1cm 的正方体的外接球表面积为 ▲ 2cm ．答案:3π7． 已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程为2y x =，则该双曲线的离心率为▲ ．答案8． 已知函数()ln f x x x =+，若函数()f x 在点00(,())P x f x 处切线与直线310x y -+=平行，则0x = ▲ ． 答案：129． 如果平面直角坐标系中的两点(1,1)A a a -+，(,)B a a 关于直线l 对称，那么直线l 的方程为 ▲ ． 答案：10x y -+=10．若椭圆22221(0)x y a b a b +=>>和圆2222b x y c ⎛⎫+=+ ⎪⎝⎭（其中c 为椭圆的半焦距）， 有四个不同的交点，则该椭圆离心率的取值范围为 ▲ ．答案：35⎫⎪⎪⎝⎭11．若函数32()1f x x ax =-+在[0,2]上单调递减，则实数a 的取值范围为 ▲ ．答案：[3,)+∞12．若直线10ax by -+=平分圆C ：222410x y x y ++-+=的周长,则ab 的取值范围是 ▲ ．答案：1,8⎛⎤-∞ ⎥⎝⎦13．定义在(0+)∞，上的单调函数()f x ，对任意(0+)x ∈∞，，2[()log ]3f f x x -=成立，若方程()()2f x f x '-=的解在区间(,1)()k k k +∈Z 内，则k = ▲ ．答案：114．过点(1,3)P 的动直线与抛物线2y x =交于A ，B 两点，在A ，B 两点处的切线分别为1l 、2l ，若1l 和2l 交于点Q ，则圆22(2)4x y +-=上的点与动点Q 距离的最小值为 ▲ ．答案：min 2d =二、解答题：本大题共6小题，共90分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说 明、证明过程或演算步骤．15．已知函数()321()33f x x x x a a =-+++∈R ．（1）求函数()f x 的单调增区间；（2）若函数()f x 在区间[]4,4-上的最大值为26，求a 的值．解：（1）因为321()33f x x x x a =-+++，所以2()23f x x x '=-++，令()0f x '>，即2230x x -++>，解得13x -<<， 所以函数()f x 的单调减区间为(1,3)-. （2）由函数在区间[]4,4-内的列表可知：函数()f x 在(4,1)--和(3,4)上分别是减函数，在(1,3)-上是增函数. 又因为76(4),(3)93f a f a -=+=+，所以(4)(3)f f ->，所以(4)f -是()f x 在[4,4]-上的最大值， 所以76263a +=，即23a =．16．如图，在三棱锥P ABC -中，90ABC ∠=︒，PA ⊥平面ABC ，E ，F 分别为PB ，PC 的中点．（1）求证：//EF 平面ABC ； （2）求证：平面AEF ⊥平面PAB ．FE CBAP17．已知圆M 的方程为22(2)1x y +-=，直线l 的方程为20x y -=，点P 在直线l 上，过P 点作圆M 的切线PA 、PB ，切点为A 、B ． （1）若点P 的坐标为(0,0)，求APB ∠；（2）若点P 的坐标为(2,1)，过P 作直线与圆M 交于C 、D两点，当CD 时，求直线CD 的方程；（3）经过A 、P 、M 三点的圆是否经过异于点M 的定点，若经过，请求出此定点的坐标；若不经过，请说明理由．解：（1）因为点P 坐标为(0,0) ，所以2M P =，又因为1MA MB ==，所以30MPA MPA ∠=∠=︒，故60APB ∠=︒． （2）当直线斜率不存在时，不合题意；当直线斜率存在时，设直线CD 方程为1(2)y k x -=-因为CD ，所以圆心M 到直线CD，=，解得1k =-或17k =-， 故直线CD 的方程为30x y +-=或790x y +-=． （3）设(2,)P m m ，MP 的中点(,1)2mQ m +， 因为PA 为圆M 的切线，所以经过A 、P 、M 三点的圆是以Q 为圆心，MQ 为半径的圆，故其方程为2222()(1)(1)22m mx m y m -+--=+- 化简得222(22)0x y y m x y +--+-= 由2220220x y y x y ⎧+-=⎨+-=⎩，解得02x y =⎧⎨=⎩或4525x y ⎧=⎪⎪⎨⎪=⎪⎩所以经过A 、P 、M 三点的圆经过异于点M 的定点42,55⎛⎫⎪⎝⎭．18．请你设计一个仓库．它的上部是底面圆半径为5m 的圆锥，下部是底面圆半径为5m 的圆柱，且该仓库的总高度为5m ．经过预算，制造该仓库的圆锥侧面、圆柱侧面用料的单价 分别为4百元/2m ，1百元/2m ，设圆锥母线与底面所成角为θ，且0π 4θ⎛⎫∈ ⎪⎝⎭，． （1）设该仓库的侧面总造价为y ，写出y 关于θ的函数关系式；（2）问θ为多少时，该仓库的侧面总造价（单位：百元）最少？并求出此时圆锥的高度． 解：（1）[]15255(1tan )12542cos y θθ⎡⎤=π⨯⨯-⨯+⨯π⨯⨯⨯⎢⎥⎣⎦2sin 501cos +θθ-⎛⎫=π ⎪⎝⎭，0π 4θ⎛⎫∈ ⎪⎝⎭，； （2）由22sin 1cos 500y θθ-⎛⎫'=π= ⎪⎝⎭得1sin 2θ=，04 θπ⎛⎫∈ ⎪⎝⎭，， 所以6θπ=，列表：所以当6θπ=时，侧面总造价ym ． 19.已知椭圆2222:1(0)x y C a b a b +=>>，一条准线方程为x （1）求椭圆C 的标准方程；（2）设直线:l y kx m =+与椭圆交于P ,Q 两点.①若2m =-，当OPQ ∆面积最大时，求直线l 的方程；②当0k ≠时，若以PQ 为直径的圆经过椭圆的右顶点，求证：直线l 过定点.解：（1）2214x y +=.（第18题）（2）由2214x y y kx m ⎧+=⎪⎨⎪=+⎩ 得222(14)8440k x kmx m +++-=222(8)4(14)(44)0km k m ∆=-+->，整理得22410k m -+>（*）设11(,)P x y ，22(,)Q x y ，则122814km x x k +=-+，21224414m x x k -⋅=+（**）①当2m =-时，代入（*）和（**）式得：234k >，1221614k x x k +=+，1221214x x k ⋅=+.所以12PQ x =-=， 又O 到直线l的距离d =，所以12OPQS PQ d ∆=⋅=.令t =，则0t >，则244144OPQ t S t t t∆==≤++ 当且仅当2t =，即k =时等号成立，且227344k ⎛==> ⎝⎭因此OPQ ∆面积最大时，直线l的方程为：2y =-. ②由已知，AP AQ ⊥，且椭圆右顶点为(2,0)A所以12121212(2)(2)(2)(2)()()0x x y y x x kx m kx m --+=--+++=即22222121222448(1)(2)()4(1)(2)401414m kmk x x km x x m k km m k k--++-+++=+⋅+-⋅++=++ 整理得：22516120m km k ++= 解得2m k =-或65km =-，均满足（*）式， 所以当2m k =-时，直线l 的方程为:2l y kx k =-，过定点(2,0)与题意矛盾；当65k m =-时，直线l 的方程为6:5k l y kx =-，过定点6,05⎛⎫ ⎪⎝⎭，得证. 20. 已知函数ln ()a xf x x+=，曲线()f x 在点(e,(e))f 处的切线与直线2e e y x =+垂直. （1）求a 的值及()f x 的极值；（2）是否存在区间2,(0)3t t t ⎛⎫+> ⎪⎝⎭，使函数()f x 在此区间上存在极值和零点？若存在，求实数t 的取值范围，若不存在，请说明理由；（3）若不等式2()(1)x f x k x >-对任意(1,)x ∈+∞恒成立，求整数．．k 的最大值. 解：（1）由ln ()a x f x x +=，得21ln ()a xf x x --'=． 因为()f x 在点(e,(e))f 处的切线与直线2e e y x =+垂直， 所以2221lne 1(e)e e e a a f ---'===-，解得1a =， 所以1ln ()(0)x f x x x +=>，令2ln ()0xf x x'=-=，得1x =． 因为当()0,1x ∈时，()0f x '>，当()1,x ∈+∞时，()0f x '< 所以()f x 在()0,1上单调递增，在()1,+∞上单调递减， 故()f x 在1x =处取得极大值1，无极小值； （2）因为()f x 在()1,+∞上单调递减，且()0f x >又由（1）知()f x 在(0,1)上单调递增，且22221ln e (e )e 0ef ---+==-<，(1)10f => 所以由零点存在原理得()f x 在区间(0,1)存在唯一零点，函数()f x 的图象如图所示： 因为函数()f x 在区间2,(0)3t t t ⎛⎫+> ⎪⎝⎭上存在极值和零点，所以由20131ln ()0t t t f t t ⎧<<<+⎪⎪⎨+⎪=<⎪⎩，解得113e t <<．所以存在符合条件的区间，实数t 的取值范围为11,3e ⎛⎫⎪⎝⎭；（3）当(1,)x ∈+∞时，不等式2()(1)x f x k x >-可变形为(1ln )1x x k x +<-设(1ln )()1x x h x x +=-，(1)x >，则2ln 2()(1)x x h x x --'=-设()ln 2x x x ϕ=--，(1)x >，则1()1x xϕ'=- 因为1x >时，1()0x x xϕ-'=>，所以()ln 2x x x ϕ=--在(1,)+∞上单调递增， 又因为(3)1ln30ϕ=-<，(4)2ln 40ϕ=->所以存在唯一的0(3,4)x ∈，使得0()0x ϕ=，即00ln 2x x =-，当()01,x x ∈时，()0x ϕ<，即0()0h x '<，当()0,x x ∈+∞时，()0x ϕ>，即0()0h x '>， 所以()h x 在()01,x 上单调递减，在()1,+∞上单调递增，故000000min 00000(1ln )(12)(1)()()111x x x x x x h x h x x x x x ++--=====---，因为0min(1ln )1x x k x x +⎡⎤<=⎢⎥-⎣⎦，且0(3,4)x ∈，所以整数k 的最大值为3.。