热力学函数间关系及其相互变换

2.6 热力学函数间的关系及应用2.6.1. 定义式与热力学基本方程(公式)根据定义,在P,T,V,S,U,H,A,G 等热力学函数之间有如下关系:pV U H +=TS U A -=pV A TS pV U TS H G +=-+=-=上列均为定义式。

据热力学第一、第二定律,,有:pdV Q dU R -=δ和TdS Q R =δ,两式结合得:pdV TdS dU -= 根据pV U H +=,微分后代入上式可得:Vdp TdS dH +=pdV SdT dA --=Vdp SdT dG +-=上列四个公式称为热力学基本方程,其应用条件均相同。

pdV TdS dU -=是第一定律与第二定律的联合公式，是适用于组成不变且不做非体积功的封闭体系的热力学基本公式. 尽管在导出该式时,曾引用可逆条件的TdS Q R =δ,但该公式中各量均为状态函数,无论实际过程如何,上式的积分皆存在.但只有在可逆过程中,TdS 才代表体系所吸的热。

该式既适用于内部平衡的无相变化和化学变化的任意状态变化的单相封闭体系,也适用于已达相平衡和化学平衡的体系中同时发生pVT 变化及相变化和化学变化的可逆过程.从以四个热力学基本可导出一下微分关系式,如:p V SH S U T )()(∂∂=∂∂= ; T S V F V U p )()(∂∂-=∂∂-= T S pG T H V )()(∂∂=∂∂= ; p V T G T F S )()(∂∂-=∂∂-=2.6.2. 麦克斯韦(Maxwell )关系式若用z 代表体系的任一状态函数,且z 是两个变量x 和y 的函数.因其变化与过程无关,在数学上称z 具有全微分的性质.即若: ),(y x f z =则有: Ndy Mdx dy yz dx x z dz x y +=∂∂+∂∂=)()( M 对y 微分,N 对x 微分,得xy z y M x ∂∂∂=∂∂2)(及y x z x N y ∂∂∂=∂∂2)(显然: y x xN y M )()(∂∂=∂∂ 根据全微分函数性质，基于上述四个热力学基本方程可得到：S V TV p S )()(∂∂-=∂∂, S p T p V S )()(∂∂=∂∂,可以用容易从实验测定的偏微商代替那些不易直接测定的偏微商.2.6.3 .吉布斯-亥姆霍兹方程——温度对自由能变的影响在讨论化学反应问题时,常须自某一反应温度的)(0T G r ∆求另一个温度时的)(T G r ∆.因为: 2)(])([T G T G T T T G p p -∂∂=∂∂ 而: S T G p -=∂∂)( 故: 22)(](G/T)[T H T G S T T p -=--=∂∂ 由于体系的各个状态函数的绝对值均无法得到,故常将各状态函数写成相对值形式.因而,上式又可写成:2])([T H T T G p ∆-=∂∆∂ 上列二式均为吉布斯-亥姆霍兹方程式.因其推导过程中引入了等压的条件，故只能在等压下使用. 将其移项积分得:⎰∆-=∆-∆21)(21122T T dT TH T G T G 同理可得: 2])([T U T T A V -=∂∂ 及 2])([TU T T A V ∆-=∂∆∂ 上列均称吉布斯-亥姆霍兹方程或吉布斯-亥姆霍兹公式.2.6.4 克拉佩龙方程(1).克拉佩龙方程设在一定的压力和温度下,某物质的两个相呈平衡.若温度改变dT ,相应地压力也改变dp ,两相仍呈平衡.根据在等温等压下平衡的条件：0=∆G ,则有:p T, )()(βαB B −−→←平衡 )(αG )(βG)(αdG ↓ )(βdG ↓dp p ++dT,T )()(βαB B −−→←平衡)()(ααdG G + )()(ββdG G + 因)()(βG αG =,故)()(βdG αdG =,据Vdp SdT dG +-=得:dp V dT S dp V dT S ββαα+-=+-整理即得: VT H V S V V S S dT dp βαβαβαβααβαβ∆∆∆∆==--= 此式即称为克拉佩龙方程式.其对任何纯物质的两相平衡体系都可使用.(2)．克拉佩龙方程对于固-液、固-固平衡的应用如液-固两相平衡有: VT H dT dp fus fus ∆∆= 对凝聚体系的相变过程研究可知,其m fus V ∆和m fus H ∆与温度和压力的关系不大,可近似视为常数.因而有:12ln T T V H p fus fus ∆∆∆= 近似地有: 1111ln T T V H T T V H T T V H p fus fus fus fus fus fus ∆∆∆∆∆∆∆∆∆∆⨯≈⨯≈+==)( (3)．克拉佩龙方程对于液-气、固-气平衡的应用---克劳修斯-克拉佩龙方程 若为气-液两相平衡,则有: VT H dT dp vap vap ∆∆= 对于有气相参加的两相平衡,固体和液体的体积远较相同物质的量的的同类气体物质的气态要大,故常可忽略,并常令其气体符合理想气体状态方程.则:p/RT H p /nRT *T H TV H V T H dT dp m vapvap )g (vap vap vap 2∆∆∆∆∆==≈= 即: 2ln RTH dT p d m vap ∆= 该式称为克劳修斯-克拉佩龙方程式.若m vap H ∆与温度无关或在小的温度范围内可视为常数，则上式积分得:'ln C RT H p mvap +∆-= 或 C TB p +-=lg 上列二式最初是经验公式,在这里得到了热力学上的证明.若作定积分则:)11(ln 2112T T R H p p m vap -∆= 对于极性不太高,沸点在150K 以上,且分子没有缔合现象的液体,近似的有: 1188--⋅⋅≈=mol K J S T H m vap bmvap ∆∆ 该式称为楚顿(Trouton)规则.例: 已知θp 时水的沸点为100℃,蒸发热为42 kJ.mol -1.现将高压锅内的水加热,使其压力达到θp ⨯2.试求此时水的沸点.解: 由 )11(ln 2112T T R H p p m vap -∆= 得: 1212ln 11p p H R T T m vap ∆-= 代入已知数据得:)(10542722ln 1042314518153731ln 111331212--⨯=⨯⨯-=-=K .p p ..p p H R T T m vap θθ∆所以: C 120)(283931054272132︒≈≈⨯=-K ..T例 冰在273.15K 时的摩尔熔化热、水的摩尔体积和冰的摩尔体积分别为1mol kJ 025.6-⋅=∆f H132,mol dm 108018.1--⋅⨯=l m V 132,mol dm 109652.1--⋅⨯=s m V求在273.15K 时,使水的凝固点降低1K 需增加多大压强?解 由式(1)得1351molm 10)9652.1(1.8018K 15.273mol J 6025---⋅⨯-⨯⋅=∆∆=m f V T H dT dp 1K kPa 068.13499-⋅-=计算结果表明，使水的凝固点降低1K 需增加压强kPa 068.13499。

热力学函数的一些重要关系式(1) 基本公式在第一、二章中，一共出现了8个状态函数：p、V、T、U、H、S、A、G。

其中3 个是辅助函数，它们的定义是:H＝U＋pV；A＝U－TS；G＝H－TS。

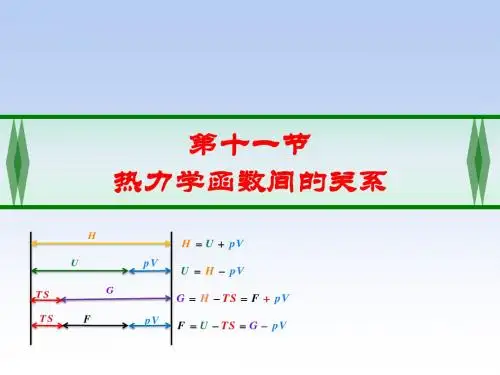
它们之间的定义和关系:H最大，H－pV＝U；U－TS＝A；H－TS＝G；G－pV＝A。

据第二定律，δQ r＝TdS，代入第一定律该式是封闭体系第一第二定律的联合公式。

在引出时用了可逆条件的限制（δQ r＝TdS），但是联合公式中出现的物理量均为状态函数，可以不考虑途径可逆与否。

再设体系不作非膨胀功，即δW f＝0，则得到热力学的4个基本公式：（2－21）注意，这一组公式的适用条件：1、仅适用于单组分单相或多组分但组成不变的单相封闭体系。

2、可以上述体系的任何过程。

（2）特性函数一个简单体系，当物质的量确定之后，只要两个状态函数就可以确定体系的全部状态。

那么，究竟选哪两个状态函数合适呢？从（2－21）可以看出(2-23)(2-23)与（2－22）比较，得到(2-24)这4式称为“对应系数关系式”，常常在推导公式时作等量代换用，可以第1项与第2项或第3项代换，也可以第2项与第3项互换。

（2）麦克斯韦关系式在数学上，二元函数Z=f(x,y)的全微分为M、N是偏微商，偏微商的微导数（二次微导数）有一个性质。

把这个性质应用到（2－21）的4个基本公式，有(2-25)此4式称为“麦克斯韦关系式”。

上面介绍了3类15个公式，是我们学习了第一、第二定律之后的一个总结和提高，它们在公式推导与证明以及用易测数据代替难测数据方面常用。

这里有一个图帮助同学记忆公式首先帮助记忆4个基本公式及UHAG 4个状态函数的特征函数。

其次帮助记忆“对应系数关系式”。

还可以帮助记忆Maxwell关系式。

不过从基本公式依次推导更有益。

书上3个例题和25～28四个习题是这方面的应用。

【例题】试证明：【证】首先要用到一个偏微商关系式：和一个等式：〖方法1〗等式两边都包含了T、p、S三个量，从循环关系式（P105，2－39）出发：〖方法2〗当dS=0时，〖方法3〗从Maxwell关系式出发：将右边拆成两项偏微商之积：【例题】（1）某实际气体的状态方程为，其中β为常数。

第一章 热力学函数及其相互关系（2）：热力学第零定律、第一定律热力学第零定律、状态函数、热、功、内能、热功当量、热力学第一定律、第一类永动机、焓、热容、过程热热力学的主要基础是热力学第一定律与第二定律，二者均为经验定律，或者说是人类长期宏观实践经验达到归纳与总结。

它们既不涉及物质的微观结构，也不能用数学来证明。

但实践业已证明，自然界还未发现有悖于这两大定律的现象。

两大定律的可靠性是无庸臵疑的。

第一定律的本质是能量守恒，因而是定量研究各种形式能量转化的基础，例如伴随着物质发生各种变化而产生的热、机械功、电功等。

在第一定律的基础上，还建立了内能U 及焓H 两个状态函数，因而本章的许多内容、结论是用热力学特有的状态函数法推演而得。

掌握热力学的状态函数与状态函数研究方法无疑是正确运用热力学解决实际问题之关键。

又因为热力学计算中还涉及诸如摩尔热容、汽化热、熔化热等基础数据，这类数据均由精确的实验所得。

实验数据的可靠性亦将直接影响到热力学计算的准确性，所以热力学研究非常重视基础数据的测定工作。

1.8 热力学第零定律(The zeroth law of thermodynamics)经验表明，如果一个“热”的系统与一个“冷”的系统相互接触、或者通过导热极好的介质相互作用，而发生热交换，并使其与环境隔离，则这两个系统的性质将发生变化。

经过相当长时间后，它们的各种性质都不再发生变化。

此时，我们就说这两个系统处于热平衡，或者说整个系统处于内部热平衡。

“当与环境隔离的两个系统分别与第三个系统处于热平衡时，这两个系统彼此间也处于热平衡。

”此即热力学第零定律。

1.9状态函数的数学本质如果积分⎰df 与路径无关，具有形如y)dy Q(x,y)dx P(x,dy yf dx x f df +=∂∂+∂∂=的微分就是恰当微分（exact differential ），又叫全微分(total differential)。

因为y)P(x,xf =∂∂，y)Q(x,yf =∂∂，而xy f yP 2∂∂∂=∂∂，xy f xQ 2∂∂∂=∂∂。

第一章热力学函数及其相互关系（1）：热力学状态与气体方程系统与环境、平衡状态、非平衡状态、稳定状态、可逆过程与不可逆过程、局部平衡、部分平衡与介稳平衡、温标的发展、热力学温标、理想气体定律、van der Waals状态方程、virial方程、Redlich-Kwong方程、实际气体的液化与临界现象、对应态理论1.1系统、环境、热力学状态1.1.1 系统与系统的环境热力学把相互联系的客观真实世界区分为系统与系统的环境两部分。

系统(system)是我们要研究的那部分真实世界，即我们要研究的那部分物质或空间。

假如要研究一台运行着的热机汽缸内气体性质的变化，或者要研究一反应器中的全部物质，就分别是两种不同情况下的系统。

又如一氧气缸瓶在不断地向外喷射氧气，我们要研究喷射过程到某阶段时钢瓶中剩余氧气的性质，则该瞬间瓶中残留的氧应当是系统。

以往的书刊中曾用过一些系统的同义词，例如“物系”、“体系”等等。

系统的环境(surroundings)是系统以外与之相联系的真实世界，可以简单称为环境或外界。

需要指出，系统与环境之间可以有实际存在的边界隔开，例如上述汽缸、反应器壁等；也可能在系统与环境间只有假象的边界隔开，例如上述氧气瓶中作为系统的残留氧气与喷射出去的那些氧气本来是存在于同一钢瓶中，它们之间没有任何间隔，而喷射出去的那些氧气实际是环境的一部分。

系统与环境之间的联系包括有能量交换与物质交换两类。

针对二者之间联系情况的差别，可以把系统分成以下三种：(1) 隔离系统（孤立系统, isolated system）隔离系统（孤立系统）与环境之间既无能量交换，又无物质交换，所以环境对隔离系统中发生的任何变化不会有任何影响。

在热力学中，有时我们把所研究的系统及该系统的环境作为一个整体来看待，这个整体就应当是隔离系统。

(2)封闭系统(closed system)封闭系统与环境之间只有能量交换而无物质交换。

在前面提到的几个系统中，物质均被封闭于实有的容器间壁内或假象的边界内，使系统仅能通过界面与环境有热、功等形式的能量交换，故应当属于封闭系统。

热力学知识：热力学相转化和热力学状态函数热力学是探讨热力现象及其发生规律的学科，有着广泛的应用基础。

本文将主要讨论热力学相转化和热力学状态函数两个方面。

热力学相转化相转化是物质从一个相到另一个相的过程，如气体转化成液体、液体转化成固体等。

热力学相转化是指物质在相变过程中吸收或放出的热量，并且在一定条件下发生的状态改变。

相转化是一种热力学过程，因为在相变中物质的温度不改变，只有物质内部的分子结构或排布发生改变。

在一个相转化过程中，热量的转移是一个非常重要的因素。

以融化过程为例，当我们给固体物质添加热量时，固体的温度不变，而是直到它融化为止。

在相变开始后，物质消耗了除了潜热以外的热量来完成相变，这是因为在相变时，物质转化为新的相，维持原来相的结构将消耗热量。

同样地，当物质从液态转变为气态时，这个过程也需要吸收热量。

需要注意的是，物质在相变时需要吸收或放出的热量与是否是样品同质性的影响有关系。

如果物质发生相变是由于样品同质性的改变，需要吸收或放出的热量就很小，相变温度也很容易察觉。

而如果相变是由于Physico-chemical factors的影响导致的，则需要吸收或放出大量的热量，相变温度就很容易被忽略。

热力学状态函数热力学状态函数是指在热力学系统中，只与它的初始和最终状态有关的量。

这些函数包括内能、熵、焓、自由能和吉布斯。

内能是指热力学系统中分子带有的总能量，其中注意只有温度相同的系统之间才能比较它们的内能。

熵是指系统的随机性和不可逆过程的度量。

随着时间的推移，熵会增加。

当一个物体热量释放时，总的熵始终增加，因为热量在自由流动时必然增加系统的随机性。

当系统从更高熵的状态向更低熵的状态转化时，它就会吸收能量，而当它向更高熵的状态转化时就会释放能量。

焓是指系统的热量和体积的和。

在一个恒容系统中发生的相变所需要的焓是0，以固态至液态为例，固态相的体积小于液态相，相变时体积会发生改变，因此如果我们保持温度不变，我们需要完全把焓送入固态相内来完成相变。

用特性函数G与特征变量p,T求所有热力学函数的表达式1.热力学函数间的关系(1) H=U+pV(2) A=U-TS(3) G=H-TS(4) G=A+pV根据定义，五个热力学函数有如下关系。

这些关系一方面反映了体系的热力学函数之间的联系，另一方面可以利用这种关系从已知函数值求未知函数值。

它们的关系用图示的方法可看得更清楚。

(1) 这是焓的定义式，因为在等压，不作非膨胀功的条件下，焓变等于等压热效应。

等压热效应容易测定，所以定义了焓。

(2) 这是亥姆霍兹自由能的定义式。

在等温可逆条件下，亥氏自由能的降低等于对外所作的最大功，可以衡量体系的作功能力，所以又称功函。

(3) 这是吉布斯自由能的定义式。

在等温等压可逆条件下，吉布斯自由能的下降等于对外所作的最大非膨胀功。

(4) 从上面三个公式可导出G与A之间的关系式，该式也可看作吉布斯自由能的定义式.2. 用特性函数G与特征变量p,T求所有热力学函数的表达式。

用特性函数及其特征变量可以求出所有热力学函数的表达式。

现以吉布斯自由能G为特性函数，其特征变量为T，p，从而求出热力学能，焓，熵，亥氏自由能和体积的表达式。

之所以可以这样做是因为U，H，S，A，G，T，p，V这8个量之间只有两个变量是独立的，其它都是这两个变量的函数。

所有根据两个变量热力学函数之间的关系可以写出其它热力学量的表达式。

画面中间是G与特征变量T，p之间的关系式。

(1) 保持p不变，对T求偏导，得到熵的表达式(2) 保持T不变，对p求偏导，得到体积V 的表达式(3) 根据焓的定义式代入熵的表达式，得到焓的表达式(4) 根据亥氏自由能的定义式，代入体积的表达式，得到亥氏自由能的表达式(5) 根据焓的定义式，代入焓和体积的表达式，就得到热力学能的表达式。