云南省昆明市高一上学期数学期中考试试卷

云南省昆明市高一上学期期中数学试卷（兴国班）姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）将角α的终边顺时针旋转，则它与单位圆的交点坐标是（）A . （cosα，sinα）B . （cosα，－sinα）C . （sinα，－cosα）D . （sinα，cosα)2. （2分）(2018·南充模拟) 已知函数在定义域上是单调函数，若对于任意，都有，则的值是（）A . 5B . 6C . 7D . 83. （2分）定义在R上的函数f（x）满足f（x）=f（x+2），当x∈[3，5]时，f（x）=2﹣|x﹣4|，则下列不等式一定成立的是（）A . f（ cos ）＞f（sin ）B . f（sin 1）＜f（cos 1）C . f（sin ）＜f（cos ）D . f（cos 2）＞f（sin 2）4. （2分）设，则（）A . a>b>cB . c>a>bC . b>a>cD . b>c>a5. （2分）已知扇形的面积为2 cm2 ，扇形圆心角的弧度数是4，则扇形的周长为（）A . 2B . 4C . 6D . 86. （2分）某公司在甲、乙两地同时销售一种品牌车，利润（单位：万元）分别为和，其中为销售量（单位：辆）.若该公司在这两地共销售辆车，则能获得最大利润为（）A . 万元B . 万元C . 万元D . 万元7. （2分） (2018高一下·威远期中) 已知锐角α ，β满足sin α＝，cos β＝，则α＋β等于（）A .B .C . －D .8. （2分）已知命题p：函数y=2﹣ax+1的图象恒过定点（1，2）；命题q：若函数y=f（x﹣1）为偶函数，则函数y=f（x）的图象关于直线x=1对称，则下列命题为真命题的是（）A . p∨qB . p∧qC . ￢p∧qD . p∨￢q9. （2分）(2020·江西模拟) 已知函数在上单调递增，则的取值范围（）A .B .C .D .10. （2分）已知函数，则函数在上的所有零点之和为（）A .B .C .D .11. （2分）已知扇形的弧长为3，面积为6，则这个扇形的圆心角的弧度数为（）A .B .C . 2D . 412. （2分）已知函数则，，的大小关系为（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分）已知cos31°=a，则sin239°的值为________．14. （1分）若750°角的终边上有一点（4，a），则a=________．15. （1分） (2017高一上·珠海期末) 设y=f（x）是定义在R上的偶函数，且f（1+x）=f（1﹣x），当0≤x≤1时，f（x）=2﹣x ，则f（3）=________．16. （1分） (2019高三上·上海月考) 函数的反函数 ________.三、解答题 (共6题；共45分)17. （10分） (2019高一上·思南期中) 计算下列各式的值．（1）（2）18. （10分）计算题（1）已知tanα= ，求的值；（2）化简：．19. （10分） (2019高二上·成都期中) 在中，分别是内角的对边，且2cos A·cos C(tan Atan C－1)＝1.（1）求的大小；（2）若，，求的面积．20. （5分） (2017高二下·武汉期中) 已知函数f（x）= ，g（x）=af（x）﹣|x﹣1|．（Ⅰ）当a=0时，若g（x）≤|x﹣2|+b对任意x∈（0，+∞）恒成立，求实数b的取值范围；（Ⅱ）当a=1时，求g（x）的最大值．21. （5分） (2018高一上·沈阳月考) 己知函数 .（Ⅰ）当时，解关于x的不等式；（Ⅱ）若不等式的解集为D，且，求m的取值范围。

【高一】云南省昆明市第24中学高一上学期期中考试数学试题(含答案)试卷说明：昆明市第二十四中学高一一年级第一学期期中数学试题命题老师：云福泽考官：（考试时间：120分钟，满分：150分）第一卷多项选择题：这道大题有12道小题，每道小题5分，共60分。

在每个子问题中给出的四个选项中，只有一项是满足问题要求的集合，那么下面公式中正确的选项是a.b.c.d.2。

如果，那么=（）a.b.c.d.3。

以下四组函数代表同一个函数is（）A.B.，C.，D.>4。

在下列函数中，单调递增的是（）a.b.c.d.5的零点所在的区间。

是（）a.b.c.d.6。

这个函数是一个减法函数，然后实数M=（）a.2b。

-1C。

4D。

2或-17。

设置，则和的大小关系为（）a.b.c.d.8。

设置函数，则满足的值为（）a.2b。

16C。

2或16天。

-2或169。

图中显示了，，，的图像，然后是AB，c。

D的数量级是（）a.1<D<c<a<BB。

C<d<1<a<BC。

C<d<1<B<ad.d<C<1<a<B10。

如果它是区间上的单调递减函数，则它是（）a.b.c.d.11。

定义集合a和B的运算：if，，中所有元素的数量之和为（）a.9b。

14c。

18d。

2112.函数的大致情况是（）第二卷填空：这个大问题有4个小问题，每个小问题5分，总共20分。

13.不等式的解集是（结果必须用一个集合表示）14。

如果函数在间隔上减小，则实数的值范围为。

15.已知函数是一个奇数函数，当时定义在，。

16如果函数满足以下属性（），则定义字段为，值字段为；（2）图像对称性；（3）对于任何，和，请写一个函数的分析公式（只写一个）。

18.（这个问题的满分是12分）已知：函数，找到函数的零点，找到满足条件的集合；求区间[0,3]上函数的最大值和最小值。

，以及（I）定义的范围；（二）判断平等性并加以证明；（三）当时，需求的价值范围。

昆明第一中学 2012-2013 学年度上学期期中考试 高一数学 试题 命题：莫利琴 试卷总分：150 分 审题：鲁开红 考试时间：120 分钟 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分 150 分,考试时间 120 分钟. 第Ⅰ卷(选择题 满分 60 分) 一、选择题：本大题共 12 小题，每小题 5 分，满分 60 分．在每个小题给出的四个选项中，只有一项是 符合题目要求的． １．下列函数中哪个与函数 是同一个函数 （ ） Ａ． Ｂ． Ｃ． Ｄ． ２．下列从集合 到集合 的对应中为映射的是 （ ）Ａ． Ｂ． Ｃ． Ｄ． ,对应法则 对应法则 ,对应法则 ,对应法则 的定义域是 （ ） Ａ． Ｃ． Ｂ． Ｄ． ４．下列各组集合中的 Ａ． Ｃ． Ｄ． 表示同一集合的是（ ） Ｂ． 2012-2013 学年度上学期期中考试 高一数学 试题 共 6 页 第 1 页 5. 已知 ，则（ ） Ａ． Ｂ． Ｃ． Ｄ． 6．如果幂函数 的图象不过原点，则实数 的值是 ( ) Ｃ． 或 Ｄ．17．下列说法中正确的有（ ） ①若 函数；③函数 当 在定义域上是增函数；④函数 上是增函数；②函数 的单调区间是 在 上是增 Ａ．0 个 Ｂ． 1 个 Ｃ．2 个 Ｄ． 3 个 ８.若函数 ，则 的图象是 （ ） ９. 下列叙述①函数 的图象与直线 最多有一个交点； 在区间 的值域是 上单调递增，则 ； ； ④函数 则正确的叙述个数为（ ） 的值域为 R，则实数 的取值范围是 ．A. 1 10. 如图所示的曲线 B. 2 C. 3 分别是指数函数 、 D. 4 、 Ａ． Ｃ． 、 的图象，则 Ｂ． Ｄ． 与 1 的大小关系是 （ ） 2012-2013 学年度上学期期中考试 高一数学 试题 共 6 页 第 2 页 11．已知 则函数 的最值情况为（ ） ，但无最大值 Ｂ．有最小值 ，有最大值 1 Ｃ．有最小值 1，有最大值 Ｄ．无最小值，也无最大值 12．已知函数 不等式 Ａ． 是 的解集是 （ Ｂ． 上的偶函数，且在 ） Ｃ． 上递增， Ｄ． 是其图象上的点，则 第Ⅱ卷(非选择题 共 90 分)二、填空题：本大题共 4 个小题，每小题 5 分，满分 20 分，把答案填在答题卡中的横线上． 13．若 ，则 的取值范围是 ． 14．已知 ，则 的值为 ． 是定义在 R 上的奇函数，当 时， = ，则当 时，= ． 16．设函数 的定义域为 ，如果对于任意的 ，存在唯一的 ，使得 （ 为常数）成立，则称函数 在 上的均值为 ．给出四个函数：① ，② ， ③ ，④ ，则满足在定义域上均值为 2 的函数是 （填正确函数的序号）． 三、解答题：本大题共 6 小题，满分 70 分．解答应写出文字说明、证明过程或演算步骤． 17．(本小题满分 10 分) 计算： . 18．(本小题满分 12 分) 集合 ， ,满足 2012-2013 学年度上学期期中考试 高一数学 试题 ， 共 6 页 求实数 的值. 第 3 页 19．(本小题满分 12 分)已知定义在 上的函数 是偶函数，且 时， ， (1)当 时，求 解析式；(2)写出 的单调递增区间． 20．（本小题满分 12 分） 已知函数 （1）画出函数 （2）求 图像； ， 的值； （3）当 时，求 取值的集合. 21．(本小题满分 12 分)已知 ，求 的最大值与最小值； 的最大值与最小值． 22．(本小题满分 12 分) 设 （1）求 的值； 为奇函数， 为常数． （2）判断函数 在 时的单调性，并说明理由； （3）若对于区间 上的每一个 值，不等式 恒成立，求实数 的取值范围． 2012-2013 学年度上学期期中考试 高一数学 试题 共 6 页 第 4 页 昆明第一中学 2012-2013 学年度上学期期中考试 高一数学 参考答案 一、选择题：本大题共 12 小题，每小题 5 分，满分 60 分．在每个小题给出的四个选项中， 只有一项是符合题目要求的． 第Ⅱ卷(非选择题 共 90 分)二、填空题：本大题共 4 个小题，每小题 5 分，满分 20 分，把答案填在答题卡中的横线上． 13． ； 14． ； 15. 16. ①，③ 三、解答题：本大题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤． 17．解： ┉┉┉┉┉┉┉┉４ ┉┉┉┉┉┉┉┉１０ 18. 解： , ，┉┉┉┉┉┉┉┉４ 而 ，则-1,6 至少有一个元素在 中，又 ，∴ ， ，即得 或 ┉┉┉８而 ∴ ┉┉┉┉┉┉┉┉１２ 矛盾， 19．解：（1）设 ，则 又所以 时， ┉┉┉┉┉┉┉┉４ （2）当 时， 在 单调递增，当 时，在 单调递减，在 单调递增，而 在定义域上是单调递增的， 2012-2013 学年度上学期期中考试 高一数学 试题 共 6 页 第 5 页 所以 的单调递增区间为 和 ．┉┉┉┉┉┉┉┉１２ 20．解：（1） 图象如图所示 ┉┉┉┉４（2） = ＝11．┉┉┉┉８ ，(3)由图象知，当 值的集合为 21．解：（1） ， 在 时， ．┉┉┉１２ 是单调增函数 ┉┉┉４ 故 取 （2）令 原式变为： ， ， ， 当 时，此时 ， ， 当 时，此时 ， ．┉┉┉１２ 22．解：（1）由条件得： ， ∴ ，化简得 ， 因此 （2） 当 时， ，但 不合题意，因此 ， 单调递减，因此 ．┉┉┉４ 单调递减， 单调递减．┉┉┉８（3）不等式为 恒成立，所以 ∵ 在 上单调递增， 在 上单调递增， 所以 在 上单调递增， 当 时取得最小值为 10，所以 ．┉┉┉１２ 共 6 页 第 6 页 题号123456789101112答案CBCCDAADABCB。

2024-2025学年度云南省昆明市高一上学期期中测试数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

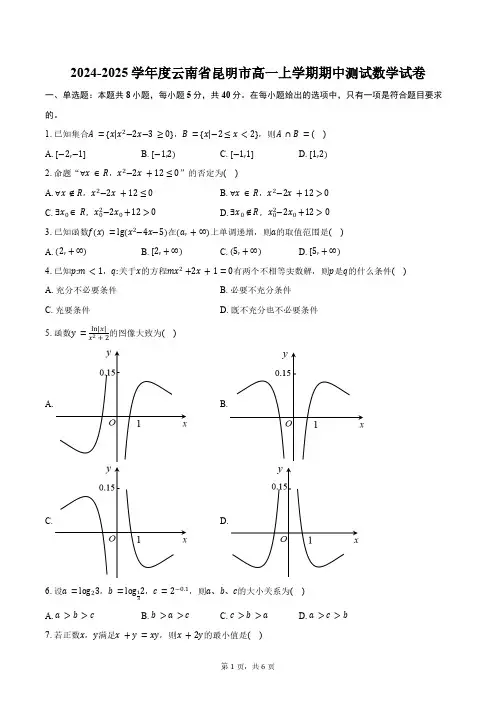
1.已知集合A={x|x2−2x−3≥0}，B={x|−2≤x<2}，则A∩B=( )A. [−2,−1]B. [−1,2)C. [−1,1]D. [1,2)2.命题“∀x∈R，x2−2x+12≤0”的否定为( )A. ∀x∉R，x2−2x+12≤0B. ∀x∈R，x2−2x+12>0C. ∃x0∈R，x20−2x0+12>0D. ∃x0∉R，x20−2x0+12>03.已知函数f(x)=lg(x2−4x−5)在(a,+∞)上单调递增，则a的取值范围是( )A. (2,+∞)B. [2,+∞)C. (5,+∞)D. [5,+∞)4.已知p:m<1，q:关于x的方程mx2+2x+1=0有两个不相等实数解，则p是q的什么条件( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5.函数y=ln|x|的图像大致为( )x2+2A. B.C. D.2，c=2−0.1，则a、b、c的大小关系为( )6.设a=log23，b=log13A. a>b>cB. b>a>cC. c>b>aD. a>c>b7.若正数x，y满足x+y=xy，则x+2y的最小值是( )A. 6B. 2+32C. 3+22D. 2+238.已知f(x)是定义在R上的奇函数，当x>0时，f(x)=x2−4x，则不等式xf(x)<0的解集为( )A. (−∞,−4)∪(4,+∞)B. (−4,0)∪(4,+∞)C. (−4,0)∪(0,4)D. (−4,4)二、多选题：本题共3小题，共18分。

在每小题给出的选项中，有多项符合题目要求。

9.对于任意的实数a，b，c，d下列命题错误的有( )A. 若a>b，则ac>bcB. 若a>b，c>d，则ac>bdC. 若ac2>bc2，则a>bD. 若a>b，则1a >1b10.下列说法正确的是( )A. a>b的一个必要条件是a−1>bB. 若集合A={x|ax2+x+1=0}中只有一个元素，则a=14C. “ac<0”是“一元二次方程ax2+bx+c=0有一正一负根”的充要条件D. 已知集合M={0,1}，则满足条件M∪N=M的集合N的个数为411.已知函数f(x)的定义域为R，f(x+1)为奇函数，f(x+2)为偶函数，且对任意的x1，x2∈(1,2)，x1≠x2，都有f(x1)−f(x2)x1−x2>0，则( )A. f(x)是奇函数B. f(2023)=0C. f(x)的图象关于(1,0)对称D. f(π)>f(e)三、填空题：本题共3小题，每小题5分，共15分。

云南省昆一中高一上学期期中考试（数学）试卷总分：150分 考试时间：1第Ⅰ卷（选择题，共60分）一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在答题卡上；每小题5分，共60分）1.设全集}7,6,5,4,3,2,1{=U ，集合}5,3,1{=A ，集合}5,3{=B ，则 （ ） A ．B A U ⋃= B ． B A C U U ⋃=)(C ．)(B C A U U ⋃=D ．)()(B C A C U U U ⋃=2．下列哪组中的两个函数是同一函数 （ ）（A）2y =与y x = （B）3y =与y x =（C）y =2y = （D）y =与2x y x=3.设 1.50.90.4812314,8,2y y y -⎛⎫=== ⎪⎝⎭，则 （ ）A.312y y y >>B.213y y y >>C.132y y y >>D.123y y y >>4.函数f(x)=x +2(x ≥0)的反函数f 1-(x)的图象是 （ ）5.若函数log ()b y x a =+（b >0且b 1≠）的图象过点（0，1）和（1-，0），则a b +=（ ）A ．4B ．2C ．3D ．6.函数0)(,)1,1(213)(00=--+=x f x k kx x f 使上存在在，则k 的取值范围是（ ）A ．)51,1(- B ．)1,(--∞C ．),51(+∞ D ．),51()1,(+∞--∞7.下列函数中，值域是（0，+∞）的是 （ ） （A ）y=132+-x x （B ）y=2x+3 x +∞∈,0()（C ）2y=x +x+1 （D ）y=8.某商品价格前两年每年递增20%，后两年每年递减20%，则四年后的价格与原来价格比较，变化的情况是 （ ）A.减少7.84%B.增加7.84%C.减少9.5%D.不增不减 9．函数xx x a y --=22(a ＞0)的定义域是（ ）A ．［－a ，a ］B ．［－a ，0)∪(0，a )C ．(0，a )D ．［－a ，0)10.函数R x x x y ∈=|,|，满足（ ）A ．既是奇函数又是减函数B ．既是偶函数又是增函数C ．既是奇函数又是增函数D ．既是偶函数又是减函数11.函数22)(23--+=x x x x f 的一个正数零点附近的函数值用二分法逐次计算，参考数据如下表：那么方程02223=--+x x x 的一个近似根（精确到0.1）为 （ ）A ．1.2B ．1.3C ．1.4D ．1.512.对于幂函数21)(x x f =，若210x x <<，则)2(21x x f +，2)()(21x f x f + 的大小关系是 （ ）A ．)2(21x x f +>2)()(21x f x f + B ． )2(21x x f +<2)()(21x f x f + C ．)2(21x x f +=2)()(21x f x f +D ．无法确定第∏卷二.填空题(请把答案填在答题卡中的横线上,每小题5分，共13.计算：214964-⎪⎭⎫⎝⎛+32827⎪⎭⎫ ⎝⎛=_______. 14.设函数22,(,1]()1,(1,)x x f x x x⎧∈-∞⎪=⎨∈+∞⎪⎩，则满足41)(=x f 的x 值为 .15.3436x y==，则21x y+=____________. 16.若)(x f 是一次函数且为减函数，14)]([-=x x f f ，则)(x f =________________.三．解答题：本大题共6个小题，共70分.解答应写出文字说明，证明过程或演算步骤． 17.(本小题满分10分)已知{}3|+≤≤=a x a x A ，{}51|>-<=x x x B 或. （1）若φ=B A ，求a 的取值范围； （2）若B B A = ，求a 的取值范围． 18. （本小题满分12分）已知21()log 1xf x x+=-（1）求()f x 的定义域； （2）求使()0f x >的x 的取值范围. 19.( 本小题满分12分)已知函数()3241+-=+x xx f .（1）当()11=x f 时，求x 的值；（2）当[]12，-∈x 时，求()x f 的最大值和最小值. (本小题满分12分) f (x )是定义在R 上的偶函数，在区间]0,(-∞上递增，且有)123()12(22+-<++a a f a a f ,求a 的取值范围.21. （本题满分12分）设f(x)为定义在R 上的偶函数，当20≤≤x 时，y ＝x ；当x>2时，y ＝f(x)的图像是顶点在P(3,4),且过点A(2,2)（1） 求函数f （x ）在)2,(--∞上的解析式；（2） 在下面的直角坐标系中直接画出函数f （3） 写出函数f(x)值域.22.（本题满分12分） 已知函数()2(0,)af x x x a R x=+≠∈ （1）讨论()f x 的奇偶性;（2）若()f x 在[)2,+∞是增函数，求实数a参考答案∴11,(1,1),10,1101xx x x x x x+>∈-∴->∴+>-⇒>- 又∵函数21()log 1xf x x+=-的定义域为(1,1)-，∴使()0f x >的x 的取值范围为(0,1)19.解：（1）当()1=x f ，即113241=+-+x x时，()()()022*******=+-=-⨯-x x x x02>x ， 42=∴x ，2=∴x —————5分（2）()()32222+⨯-=x xx f令02>=xt ，[]12，-∈x ，⎥⎦⎤⎢⎣⎡∈∴241，t ()⎥⎦⎤⎢⎣⎡∈+-=+-=∴241213222，，t t t t y322+-=t t y 在⎥⎦⎤⎢⎣⎡141，上单调递减，在[]21，上单调递增∴当1=t ，即0=x 时，()2min =x f当2=t ，即1=x 时，()3max =x f —— 12分21.解：（1）当)2,(--∞∈x 时，解析式为4)3(2)(2++-=x x f ； (2) 图像如右图所示。

云南省昆明市高一上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分） (2019高一上·淄博期中) 已知全集，且集合，集合，则（）A .B .C .D .2. （2分）已知f（tanx）=sin2x，则f（﹣1）的值是（）A . 1B . -1C .D . 03. （2分） (2017高一下·正定期中) 已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′（如图所示），其中A′D′=2，B′C′=4，A′B′=1，则直角梯形DC边的长度是（）A .B .C .D .4. （2分）给出下列函数①②③④，其中是奇函数的是（）A . ①②B . ①④C . ②④D . ③④5. （2分）函数f（x）=2x+x3的零点所在区间为（）A . （0，1）B . （﹣1，0）C . （1，2）D . （﹣2，﹣l）6. （2分）设，则（）A .B .C .D .7. （2分）根据表格中的数据，可以判定方程ex﹣x﹣2=0的一个根所在的区间为（）x﹣10123ex﹣x﹣2﹣0.63﹣1﹣0.28 3.3915.09A . （﹣1，0）B . （0，1）C . （1，2）D . （2，3）8. （2分） (2017高一下·鸡西期末) 已知一个四棱锥的正视图、侧视图如图所示，其底面梯形的斜二测画法直观图是一个如图所示的等腰梯形，且该等腰梯形的面积为，则该四棱锥的体积为（）A .B .C .D .9. （2分）定义在R上的函数f（x）满足f（x）=f（x﹣2），当x∈（1，3）时，f（x）=1+（x﹣2）2 ，则（）A . f（sin ）＞f（sin ）B . f（sin ）＜f（cos ）C . f（cos ）＞f（cos ）D . f（tan ）＜f（tan ）10. （2分）设偶函数满足,则不等式的解集为（）A . 或B . 或C . 或D . 或11. （2分）已知函数则下列关于函数y=f[f(x)]+1的零点个数的判断正确的是（）A . 当k>0时，有3个零点；当k<0时，有2个零点B . 当k>0时，有4个零点；当k<0时，有1个零点C . 无论k为何值，均有2个零点D . 无论k为何值，均有4个零点12. （2分）已知f(x)=2ax2-2(4-a)x+1,g(x)=ax，若对任意,f(x)与g(x)的值至少有一个为正数，则实数a的取值范围是（）A . (0,2)B . (0,8)C . (2,8)D .二、填空题 (共4题；共4分)13. （1分） (2017高一上·佛山月考) 已知，则求函数的解析式为________ .14. （1分） (2016高一上·杭州期末) 已知幂函数f（x）=k•xα的图象过点（，2），则k+α=________．15. （1分）的值域是________．16. （1分） (2016高一上·闵行期中) 设非空集合s={x|m≤x≤l}满足：当x∈S时，有y=x2∈S．给出如下三个命题：①若m=1，则S={1}；②若m=﹣，则≤l≤1；③若l= ，则﹣≤m≤0．④若l=1，则﹣1≤m≤0或m=1．其中正确命题的是________．三、解答题 (共6题；共65分)17. （10分） (2017高一上·宜昌期末) 计算下列各式：（1）；（2）．18. （5分） (2016高三上·浦东期中) 已知全集U=R，集合A={x|4x﹣9•2x+8＜0}，B={x| }，C={x||x ﹣2|＜4}，求A∪B，CUA∩C．19. （15分） (2019高一上·银川期中) 已知函数是定义在上的偶函数，已知时，.（1）画出偶函数的图像；（2）指出函数的单调递增区间及值域；（3）若直线与函数恰有个交点，求的取值范围.20. （10分） (2016高一上·武侯期中) 甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品x（百台），其总成本为G（x）（万元），其中固定成本为3万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本），销售收入R（x）= ，假定该产品产销平衡（即生产的产品都能卖掉），根据上述统计规律，请完成下列问题：（1）写出利润函数y=f（x）的解析式（利润=销售收入﹣总成本）；（2）甲厂生产多少台新产品时，可使盈利最多？21. （15分） (2016高一下·石门期末) 对于定义域为D的函数y=f（x），若同时满足下列条件：①f（x）在D内单调递增或单调递减；②存在区间[a，b]⊆D，使f（x）在[a，b]上的值域为[a，b]，则把y=f（x），x∈D叫闭函数．（1）求闭函数y=x3符合条件②的区间[a，b]；（2）判断函数f（x）= x+ ，（x＞0）是否为闭函数？并说明理由；（3）已知[a，b]是正整数，且定义在（1，m）的函数y=k﹣是闭函数，求正整数m的最小值，及此时实数k的取值范围．22. （10分）(2020·肥城模拟) 已知函数在处取得极小值.（1）求实数的值；（2）若函数存在极大值与极小值，且函数有两个零点，求实数的取值范围.（参考数据：，）参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共65分)17-1、17-2、18-1、19-1、19-2、19-3、20-1、20-2、21-1、21-2、21-3、22-1、22-2、第11 页共11 页。

2024-2025学年云南省昆明市五华区云南师范大学附属中学高一上学期10月期中数学试题一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.命题“∃x>2，4x2−x=0”的否定是( )A. ∀x>2，4x2−x=0B. ∃x>2，4x2−x≠0C. ∀x>2，4x2−x≠0D. ∀x≤2，4x2−x≠02.设集合A={x|2≤x<6}，B={x|y=x+1⋅5−x}，则A∩B=( )A. {x|2≤x<5}B. {x|2≤x≤5}C. {x|−1≤x<6}D. {x|−1≤x≤5}3.已知a为实数，则“a=1”是“f(x)=ax3+(a2−1)x2+x(x∈R)是奇函数”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.已知a=1π，b=2−π，c=eπ，d=π+1，则( )A. d>c>b>aB. d>c>a>bC. c>d>b>aD. c>d>a>b5.按复利计算利息的一种储蓄，本息和y(单位：万元)与储存时间x(单位：月)满足函数关系y=e kx+b(e为自然对数的底数，k，b为常数).若本金为6万元，在第26个月时本息和为24万元，则在第39个月时本息和是( )A. 30万元B. 36万元C. 48万元D. 60万元6.已知函数f(x)={4x−a⋅2x+2+a2,x≤1,x+4x+2a,x>1,若函数f(x)的最小值为f(1)，则实数a的取值范围是( )A. [1,10]B. [1,+∞)C. [0,10]D. (−∞,1]7.已知定义在R上的函数f(x)满足f(x)+f(−x)=0，∀x1,x2∈[0,+∞)，当x1≠x2时，都有f(x1)−f(x2)x2−x1<1，则不等式f(2x)−f(5−x)<5−3x的解集为( )A. (−53,0)B. (0,53)C. (−∞,53)D. (53,+∞)8.若实数x,y满足2x2−xy−y2=1，则3y8x2−4xy+5y2的最大值为( )A. 22B. 12C. 24D. 14二、多选题：本题共3小题，共18分。

云南省昆明市第一中学2020-2021学年高一上学期期中考试试题一､选择题1. 已知A ={-1，0，1}，B ={x |x 2<1}，则A ∩B 等于（ ） A. {-1，0，1}B. ∅C. {0}D. {0，1}『答案』C『解析』22110x x <⇔-<，解得：11x -<<，即{}11B x x =-<<，所以{}0A B ⋂=.故选：C2. 不等式x 2-3x +2≤0的解集是（ ） A. {x |x >2或<1}B. {x |x ≥2或x ≤1}C. {x |1≤x ≤2}D. D .{x |1<x <2}『答案』C 『解析』()()2320120x x x x -+≤⇔--≤，解得：12x ≤≤ ，所以不等式的解集为{}12x x ≤≤.故选：C3. 下列各组集合中，满足E =F 的是（ ）A. E =，F ={1.414}B. (){}(){}2,1,1,2E F ==C.{}{}22,E x y x F y y x ====D.{}{}2,1,1,2E F ==『答案』D『解析』对于A 1.414≠，所以{}1.414≠即E F≠，故A 错误；对于B ，因为()2,1与()1,2是不同的点，所以(){}(){}2,11,2≠即E F ≠，故B 错误；对于C ，{}2E x y x R===，{}{}20F y y x y ===≥，所以E F ≠，故C 错误；对于D ，由集合元素的无序性可得E F =，故D 正确. 故选：D.4. 设x ∈R ，则“x ≤2”是“|x -1|≤1”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件D. 既不充分也不必要条件『答案』B 『解析』11111x x -≤⇔-≤-≤，解得：02x ≤≤，所以不等式的解集{}02x x ≤≤，设{}2A x x =≤，{}02B x x =≤≤ B A ，所以2x ≤是11x -≤的必要不充分条件.故选：B5. 不等式111x ≥-的解集为（ ）A. (-∞，1)∪『2，+∞)B. (-∞，0』∪(1，+∞)C. (1，2』D. 『2，+∞)『答案』C『解析』不等式111x -等价于(1)(2)0x x --且10x -≠，解得12x <，∴不等式的解集为(1，2]． 故选：C ．6. 向高为H 的水瓶中注水，注满为止．如果注水量V 与水深h 的函数关系的图象如图所示，那么水瓶的形状是 （ ）A. B. C. D.『答案』B『解析』取2Hh =，由图象可知，此时注水量大于容器容积12，故选B.7. 已知{}|21,A x x k k ==+∈Z ，|2x B x ⎧⎫=∈⎨⎬⎩⎭Z ，C =Z ，下列关系判断正确的是（ ） A. C =A ∪B B. C =A ∩B C. A =C ∪B D. A =C ∩B『答案』A『解析』因为{}|21,A x x k k ==+∈Z ，为奇数集；|2x B x ⎧⎫=∈⎨⎬⎩⎭Z ，为偶数集； C =Z ，为整数解；所以C A B =.故选：A.8. 已知一元二次不等式ax 2+bx +c ≤0的解集为『1，2』，则cx 2+bx +a ≤0的解集为（ ）A. 1[,1]2B. 『1，2』C. 『-2，-1』D.[211,]-- 『答案』A『解析』20ax bx c ++≤的解集是[]1,2，可知0a >，并且方程20ax bx c ++=的两个实数根是11x =和22x =，所以32b a c a ⎧-=⎪⎪⎨⎪=⎪⎩，得32b a c a =-⎧⎨=⎩，代入20cx bx a ++≤， 得2230ax ax a -+≤，即22310x x -+≤，()()1210x x --≤，解得：112x ≤≤，所以不等式的解集是[]1,2.故选：A9. 已知集合A ={x |a ≤x <3)，B =『1，+∞)，若A 是B 的子集，则实数a 取值范围为（ ） A. 『0，3)B. 『1，3)C. 『0，+∞)D. 『1，+∞)『答案』D『解析』{|3}A x a x =<，[1B =，)+∞，且A B ⊆，∴①A =∅时，3a ；的②A ≠∅时，31a a <⎧⎨⎩，解得13a <， ∴综上，实数a 的取值范围为[1，)+∞．故选：D ．10. 已知集合A ={x |x ≥0}，集合B ={x |x >1}，则以下真命题的个数是（ ） ①0x ∃∈A，0x ∉B ；②0x ∃∈B ，0x ∉A ；③x ∀∈A ，x ∈B ；④x ∀∈B ，x ∈A .A. 4B. 3C. 2D. 1『答案』C『解析』B A ，0x A ∴∃∈，0x B∉，正确，故①正确；x B ∀∈，x A ∈,故②不正确，③不正确，④正确，所以正确的有2个. 故选：C11. 已知集合A ={1，a ，b }，B ={a 2，a ，ab }，若A =B ，则a 2021+b 2020=（ ） A -1B. 0C. 1D. 2『答案』A『解析』因为A =B ，若21a =，解得1a =±，当1a =时，不满足互异性，舍去，当1a =-时，A ={1，-1，b }，B ={1，-1，-b }， 因为A =B ，所以b b =-，解得0b =，所以202120201ab +=-；若ab =1，则1b a =，所以21{1,,},{,,1}A aB a a a ==，若2a a =，解得0a =或1，都不满足题意，舍去，若21a a =，解得1a =，不满足互异性，舍去，故选：A 12. 已知2()2af x x ax =-+在区间『0，1』上的最大值为g (a )，则g (a )的最小值为（ ）A. 0B. 12 C. 1 D. 2 『答案』B『解析』因为2()2af x x ax =-+的开口向上，对称轴2a x =， ①122a即1a 时，此时函数取得最大值()()112ag a f ==-，②当122a >即1a >时，此时函数取得最大值()()02a g a f ==， 故()1,12,12aa g a a a ⎧-⎪⎪=⎨⎪>⎪⎩，故当1a =时，()g a 取得最小值12．故选：B ． 二､填空题：13. 设命题p ：1x ∀≥，2430x x -+≥，则命题p 的否定形式为：________.『答案』01x ∃≥，200430x x -+<『解析』全称命题的否定为特称命题，故命题p 的否定形式为：01x ∃≥，200430x x -+<. 故答案为：01x ∃≥，200430x x -+<.14. 已知集合{0,1,2}A =，则A 的子集个数为__________．『答案』8『解析』由题意，集合A 中有三个元素，则集合A 的子集个数为328=.15. 已知m ∈R ，x 1，x 2是方程x 2-2mx +m =0的两个不等的正根，则12124x x x x ++的最小值为________.『答案』『解析』因为∈m R ，1x ，2x 是方程220x mx m -+=的两个不等的正根，所以21212440·020m m x x m x x m ⎧∆=->⎪=>⎨⎪+=>⎩，所以1m ．根据题意知，122x x m +=，12·x x m=，则121224224442x x m m x x m m++=+=（当且仅当42m m=即m =“=” )．故答案是：16. 若集合A 具有以下两条性质，则称集合A 为一个“好集合”.（1）0A ∈且1A ∈；（2）若x 、y A ，则x y A -∈，且当0x ≠时，有1Ax ∈.给出以下命题： ①集合{}2,1,0,1,2P =--是“好集合”；②Z 是“好集合”； ③Q 是“好集合”； ④R 是“好集合”；⑤设集合A 是“好集合”，若x 、y A ，则x y A +∈；其中真命题的序号是________.『答案』③④⑤『解析』对于命题①，2P ∈，2P -∈，但()224P--=∉，①错误；对于命题②，2Z ∈，但12Z ∉，②错误；对于命题③④，显然，集合Q 、R 均满足（1）（2），所以，Q 、R 都是“好集合”，③④正确；对于命题⑤，当y A 时，由于0A ∈，则0y y A -=-∈，当x A ∈，则()x y x y A+=--∈，⑤正确.故答案为：③④⑤. 三､解答题 17. 设集合{}2|230A x x x =+-<，集合{|||1}B x x a =+<.（1）若3a =，求AB ；（2）设命题 : p x A ∈，命题:q x B ∈，若p 是q 成立的必要不充分条件，求实数a 的取值范围. 『解』（1）{}{}2|230|31A x x x x x =+-<=-<<.因为3a =，所以{||3|1}{|42}B x x x x =+<=-<<-， 因此{|41}A B x x =-<<；（2）{}|31A x x =-<<，{|||1}{|11}B x x a x a x a =+<=--<<-，因为p 是q 成立的必要不充分条件，所以集合B 是集合A 的真子集，因此有1113a a -≤⎧⎨-->-⎩或1113a a -<⎧⎨--≥-⎩，解得02a ≤≤. 18. 已知正数a ，b 满足a +3b =4.（1）求ab 的最大值，且写出取得最大值时a ，b 的值；（2）求13a b +的最小值，且写出取得最小值时a ，b 的值. 『解』（1）由基本不等式可知：43a b =+≥=2即43ab ≤，当且仅当3a b =，即2a =，23b =时，等号成立，所以ab 最大值43，此时2a =，23b =； （2）由题意，13(3)131335104442a b b a a b a b a b +⎛⎫⎛⎫+=+=++≥ ⎪ ⎪⎝⎭⎝⎭， 当且仅当b a a b =，即1a b ==时，等号成立，所以13a b +的最小值为4，此时1a b ==.19. 关于x 的不等式ax 2-(a +2)x +2<0. （1）当a =-1时，求不等式的解集； （2）当a >0时，求不等式的解集.『解』（1）当a =-1时，此不等式为-x 2-x +2<0，可化为x 2+x -2>0， 化简得(x +2)(x -1)>0，解得即{x |x <-2或x >1} （2）不等式ax 2-(a +2)x +2<0，化为(ax -2)(x -1)<0，当a >0时，不等式化为2()(1)0x x a --<，若21a <，即a >2，解不等式得21x a <<； 若21a，即a =2，解不等式得x ∈∅；若21>a ，即0<a <2，解不等式得21x a <<； 综上所述：当0<a <2时，不等式的解集为2{|1}x x a <<；当a =2时，不等式的解集为∅ 当a >2时，不等式的解集为2{|1}x x a <<.20. 某商品在近30天内每件的销售价格p （元）与时间t （天）的函数关系是20,025,100,2530,+<<∈⎧=⎨-+≤≤∈⎩t t t p t t t NN，该商品的日销售量Q （件）与时间t （天）的函数关系是()40030,=-+<≤∈Q t t t N ．求这种商品的日销售金额y 的最大值，并指出日销售金额最大的一天是30天中的第几天？（注：日销售金额=日销售价格×日销售量） 『解』∵日销售金额y p Q =⋅，∴()()2220800025,14040002530,⎧-++<<∈⎪=⎨-+≤≤∈⎪⎩t t t t y t t t t N N ()()()()2210900025,709002530,⎧--+<<∈⎪=⎨--≤≤∈⎪⎩t t t t t t N N . 当025t <<，∈t N ，10t =时，max 900y =（元）； 当2530t ≤≤，∈t N ，25t =时．max 1125y =（元）；∵1125900>，∴第25天日销售金额最大，max 1125y =（元）．21. 已知二次函数f (x )=ax 2+bx +2a -1的对称轴为x =-1.（1）设x 1，x 2为方程f (x )=0的两个实数根，且1232x x =，求f (x )的表达式；（2）若f (x )≥0对任意，x ∈『-3，0』恒成立，求实数a 的取值范围.『解』（1）因为12b x a =-=-，所以b =2a ，由根与系数的关系可得122132a x x a -==， 解得：a =2，则b =4，则f (x )=2x 2+4x +3； （2）因为f (x )=ax 2+2ax +2a -1的对称轴为x =-1，若a >0，y =f (x )开口向上，则f (x )在『-3，0』的最小值在x =-1处取得， 则f (-1)=a -1≥0，解得a ≥1；若a <0，y =f (x )开口向下，又因为|-3-(-1)|>|0-(-1)|， 则f (x )在『-3，0』的最小值在x =-3处取得，则f (-3)=5a -1≥0，解得15a ≥(舍)；综上所述，a ∈ 『1，+∞).22.设函数()f x =，b >0的定义域为A ，值域为B . （1）若1a =-，b =2，c =8，求A 和B ； （2）若A =B ，求满足条件的实数a 构成的集合. 『解』（1）由题意，()f x =令(2)(4)0x x +-≥，则[]2,4A =-,因为()f x又209(1)9x ≤--≤，所以[]()0,3f x ∈即[]0,3B =；（2）当0a =时，()f x =,c A b -⎡⎫=+∞⎪⎢⎣⎭，[)0,B =+∞，当c =0时满足A =B ； 当a ≠0时，设二次函数2()g x ax bx c =++的判别式为∆， 当0∆≥时，设方程()0g x =的两实数根为1212,()x x x x ≤，①若a >0，当0∆≥时，则{1|A x x x =≤或}2x x ≥，[)0,B =+∞，则A ≠B ，不合题意；当∆<0时，则A =R，B ⎫=∞⎪⎪⎭，则A ≠B ，不合题意；②若a <0，当∆<0时，则A =∅，B =∅，虽有A =B ，但不符合函数的定义，舍去；当0∆≥时，则}{12|A x x x x =≤≤，B ⎡=⎢⎢⎣，若要使A =B，则120,x x ==c =0， 又2()0g x =得2b x a -==2224b b a a -=，解得4a =-； 综上，满足条件的实数a 构成的集合为{}4,0-.。

云南省昆明市高一上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共12分)1. （1分） (2016高一上·安庆期中) 已知全集U={﹣2，﹣1，0，1，2}，集合A={x∈Z|x2+x﹣2＜0}，则∁UA=（）A . {﹣2，1，2}B . {﹣2，1}C . {1，2}D . {﹣1，0}2. （1分） (2017高一上·长春期中) 设集合A={x|0≤x≤2}，B={y|1≤y≤2}，若对于函数y=f（x），其定义域为A，值域为B，则这个函数的图象可能是（）A .B .C .D .3. （1分） (2016高一上·仁化期中) 下列函数中哪个与函数y=x相等（）A . y=B . y=C . y=D . y=4. （1分） (2019高一上·白城期中) 已知函数，，则f[g(2)]的值为（）A .B .C .D . 65. （1分）函数f(x)(x∈R)为偶函数，且f(x)在[0，＋∞)上是增函数，则f(－2)、f(－π)、f(3)的大小顺序是（）A . f(－π)＞f(3)＞f(－2)B . f(－π)＞f(－2)＞f(3)C . f(－π)＜f(3)＜f(－2)D . f(－π)＜f(－2)＜f(3)6. （1分）A . c<a<bB . c<b<aC . a<b<cD . b<c<a7. （1分） (2015高一上·深圳期末) 函数f（x）=lnx﹣的零点所在的区间为（）A . （0，1）B . （1，2）C . （2，3）D . （3，4）8. （1分）某车间分批生产某种产品，每批的生产准备费用为400元．若每批生产x件，则平均仓储时间为天，且每件产品每天的仓储费用为1元．为使平均到每件产品的生产准备费用与仓储费用之和最小，每批应生产产品（）A . 20件B . 30件C . 40件D . 50 件9. （1分）设,则的值是（）A . 128B . 16C . 8D . 25610. （1分） (2019高一上·衢州期末) 已知，，若对任意 ,或，则的取值范围是（）A .B .C .D .11. （1分）若直角坐标平面内A、B两点满足条件：①点A、B都在f（x）的图象上；②点A、B关于原点对称，则对称点对（A，B）是函数的一个“姊妹点对”（点对（A，B）与（B，A）可看作同一个“姊妹点对”）．已知函数 f（x）=，则f（x）的“姊妹点对”有（）个．A . 1B . 2C . 3D . 412. （1分） (2016高一上·淄博期中) 若函数f（x）是定义在R上的奇函数，且在（﹣∞，0]上满足＜0，且f（1）=0，则使得＜0的x的取值范围是（）A . （﹣∞，1）B . （﹣∞，﹣1）∪（1，+∞）C . （﹣1，0）∪（1，+∞）D . （﹣1，1）二、填空题 (共4题；共4分)13. （1分） (2016高一上·东海期中) 设集合A={3，m}，B={3m，3}，且A=B，则实数m的值是________．14. （1分） (2016高一上·温州期末) 若幂函数f（x）=xa的图象过点（2，），则a=________．15. （1分） (2017高一上·咸阳期末) 函数y=αx﹣2﹣1（α＞0且α≠1）的图象恒过的点的坐标是________．16. （1分）(2018·吉林模拟) 已知函数在上单调递减，则的取值范围是________.三、解答题 (共6题；共12分)17. （1分） (2017高一上·中山月考) 若集合．（1）若，全集，试求；（2）若，求实数的取值范围．18. （2分） (2018高一上·江津月考) 已知二次函数对都有成立，且．（1）求函数的解析式；（2）若函数在上的最小值为，求实数的值。

2020-2021学年云南省昆明一中高一（上）期中数学试卷一、选择题：（在每小题给出的四个选项中，选出符合题目要求的一项．）1．（3分）已知集合{1A =-，0，1}，2{|1}B x x =<，则(AB = ) A ．∅ B ．{0}C ．{1-，1}D ．{1-，0，1}2．（3分）不等式2320x x -+的解集是( )A ．{|1x x -或2}x -B ．{2x 或1}xC ．{|21}x x -- D ．{|12}x x 3．（3分）下列各组集合中，满足E F =的是( )A ．{2}E =，{1.414}F =B ．{(2,1)}E =，{(1,2)}F =C ．2{|}E x y x ==，2{|}F y y x ==D ．{2E =，1}，{1F =，2}4．（3分）已知x R ∈，“20x -”是“|1|1x -”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 5．（3分）不等式111x -的解集为( ) A ．(,1)[2-∞，)+∞ B ．(-∞，0](1,)+∞ C ．(1，2] D ．[2，)+∞6．（3分）向高为H 的水瓶中注水，注满为止．如果注水量V 与水深h 的函数关系如图，那么水瓶的形状是图中的( )A ．B ．C ．D ．7．（3分）已知{|21A x x k ==+，}k Z ∈，{|}2x B x Z =∈，C Z =，下列关系判断正确的是( )A ．C AB = B ．C A B = C ．A C B =D ．A C B =8．（3分）已知一元二次不等式20ax bx c ++的解集为[1，2]，则20cx bx a ++的解集为( )A ．1[,1]2B ．[1，2]C ．[2-，1]-D ．1[1,]2-- 9．（3分）已知集合{|3}A x a x =<，[1B =，)+∞，若A 是B 的子集，则实数a 取值范围为( )A ．[0，3)B ．[1，3)C ．[0，)+∞D ．[1，)+∞10．（3分）已知集合{|0}A x x =，集合{|1}B x x =>，则以下真命题的个数是( ) ①0x A ∃∈，0x B ∉；②0x B ∃∈，0x A ∉；③x A ∀∈，x B ∈；④x B ∀∈，x A ∈．A ．4B ．3C ．2D ．111．（3分）已知集合{1A =，a ，}b ，2{B a =，a ，}ab ，若A B =，则20212020(a b += )A ．1-B ．0C ．1D ．212．（3分）已知2()2a f x x ax =-+在区间[0，1]上的最大值为g （a ），则g （a ）的最小值为( ) A ．0B ．12C ．1D ．2二、填空题： 13．（3分）设命题:1p x ∀，2430x x -+，则命题p 的否定形式为： ．14．（3分）集合{0A =，1，2}的真子集的个数是 ．15．（3分）已知m R ∈，1x ，2x 是方程220x mx m -+=的两个不等实根，则12121x x x x ++的极大值为 ．16．（3分）若集合A 具有以下两条性质，则称集合A 为一个“好集合”．（1）0A ∈且1A ∈；（2）若x ，y A ∈，则x y A -∈；且当0x ≠时，有1A x∈． 给出以下命题：①集合{2P =-，1-，0，1，2}是“好集合”；②Z 是“好集合”；③Q 是“好集合”；④R 是“好集合”；⑤设集合A 是“好集合”，若x ，y A ∈，则x y A +∈；其中真命题的序号是 ．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．设集合2{|230}A x x x =+-<，集合{|||1}B x x a =+<．（1）若3a =，求A B ；（2）设命题:p x A ∈，命题:q x B ∈，若p 是q 成立的必要不充分条件，求实数a 的取值范围．18．已知正数a ，b 满足34a b +=．（1）求ab 的最大值，且写出取得最大值时a ，b 的值；（2）求13a b+的最小值，且写出取得最小值时a ，b 的值． 19．关于x 的不等式2(2)20ax a x -++<．（1）当1a =-时，求不等式的解集；（2）当0a >时，求不等式的解集．20．某商品在近30天内每件的销售价格p （元)与时间t （天)的函数关系是20,025,100,2530,t t t N p t t t N +<<∈⎧=⎨-∈⎩，该商品的日销售量Q （件)与时间t （天)的函数关系是40(030,)Q t t t N =-+<∈，求这种商品的日销售金额的最大值，并指出日销售金额最大的一天是30天中的第几天？21．已知二次函数2()21f x ax bx a =++-的对称轴为1x =-．（1）设1x ，2x 为方程()0f x =的两个实数根，且1232x x =，求()f x 的表达式；（2）若()0x∈-，0]恒成立，求实数a的取值范围．f x对任意[322．设函数()b>的定义域为A，值域为B．f x=，0（1）若1c=，求A和B；b=，8a=-，2=，求满足条件的实数a构成的集合．（2）若A B2020-2021学年云南省昆明一中高一（上）期中数学试卷参考答案与试题解析一、选择题：（在每小题给出的四个选项中，选出符合题目要求的一项．）1．（3分）已知集合{1A =-，0，1}，2{|1}B x x =<，则(AB = ) A ．∅ B ．{0}C ．{1-，1}D ．{1-，0，1}【分析】解不等式得集合B ，根据交集的定义写出A B ．【解答】解：集合{1A =-，0，1}，2{|1}{|11}B x x x x =<=-<<， 则{0}A B =．故选：B ．【点评】本题考查了解不等式与交集的运算问题，是基础题．2．（3分）不等式2320x x -+的解集是( )A ．{|1x x -或2}x -B ．{2x 或1}xC ．{|21}x x -- D ．{|12}x x 【分析】根据题意，将原不等式变形可得(1)(2)0x x --，解可得12x ，即可得答案．【解答】解：根据题意，2320(1)(2)0x x x x -+⇒--，解可得12x ，即不等式2320x x -+的解集{|12}x x ；故选：D ．【点评】本题考查一元二次不等式的解法，注意结合二次函数的性质进行分析．3．（3分）下列各组集合中，满足E F =的是( )A ．E =，{1.414}F =B ．{(2,1)}E =，{(1,2)}F =C ．2{|}E x y x ==，2{|}F y y x ==D ．{2E =，1}，{1F =，2}【分析】利用集合相等的概念直接求解．【解答】解：在A 中， 1.414，E F ∴≠，故A 错误； 在B 中，(2,1)和(1,2)表示两个不同的点，E F ∴≠，故B 错误；对于C ，2{|}{|}E x y x x x R ===∈，2{|}{|0}F y y x y y ===，E F ∴≠，故C 错误；对于D ，{2E =，1}，{1F =，2}，两个集合中含的元素都是1，2，E F ∴=，故D 正确． 故选：D ．【点评】本题考查两个集合是否相等的判断，集合的概念等基础知识，是基础题．4．（3分）已知x R ∈，“20x -”是“|1|1x -”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件【分析】求出不等式的解集，根据集合的包含关系判断即可．【解答】解：由20x -，解得：2x ，由|1|1x -，解得：02x ，故20x -”是“|1|1x - “的必要不充分条件，故选：B ．【点评】本题考查了集合的包含关系，考查不等式问题，是一道基础题．5．（3分）不等式111x -的解集为( ) A ．(,1)[2-∞，)+∞ B ．(-∞，0](1,)+∞ C ．(1，2] D ．[2，)+∞【分析】先移项，将不等号右边变为0，再转化为一元二次不等式求解即可，注意分母不能为0．【解答】解：不等式111x -等价于(1)(2)0x x --且10x -≠， 解得12x <，∴不等式的解集为(1，2]． 故选：C ．【点评】本题考查分式不等式的解法，考查学生的转化思想和运算求解能力，属于基础题．6．（3分）向高为H 的水瓶中注水，注满为止．如果注水量V 与水深h 的函数关系如图，那么水瓶的形状是图中的( )A ．B ．C ．D ．【分析】本题利用排除法解．从所给函数的图象看出，V 不是h 的正比例函数，由体积公式可排除一些选项；从函数图象的单调性及切线的斜率的变化情况看，又可排除一些选项，从而得出正确选项．【解答】解：如果水瓶形状是圆柱，2V r h π=，r 不变，V 是h 的正比例函数，其图象应该是过原点的直线，与已知图象不符．故D 错；由已知函数图可以看出，随着高度h 的增加V 也增加，但随h 变大，每单位高度的增加，体积V 的增加量变小，图象上升趋势变缓，其原因只能是瓶子平行底的截面的半径由底到顶逐渐变小．故A 、C 错．故选：B ．【点评】本题主要考查知识点：旋转体（圆柱、圆锥、圆台）等简单几何体和函数的图象，属于基础题．本题还可从注水一半时的状况进行分析求解．7．（3分）已知{|21A x x k ==+，}k Z ∈，{|}2x B x Z =∈，C Z =，下列关系判断正确的是( )A ．C AB = B ．C A B = C ．A C B =D ．A C B =【分析】可得出{|2B x x k ==，}k Z ∈，然后进行交集和并集的运算即可判断每个选项的正误．【解答】解：{|21A x x k ==+，}k Z ∈，{|2B x x k ==，}k Z ∈，C Z =，C A B ∴=，A B =∅，C C B =，B C B =．故选：A ．【点评】本题考查了描述法的定义，整数分奇数和偶数，交集和并集的运算，考查了计算能力，属于基础题．8．（3分）已知一元二次不等式20ax bx c ++的解集为[1，2]，则20cx bx a ++的解集为( )A ．1[,1]2B ．[1，2]C ．[2-，1]-D ．1[1,]2-- 【分析】由一元二次不等式20ax bx c ++的解集求出a 、b 、c 的关系，代入不等式20cx bx a ++中化简求解即可．【解答】解：一元二次不等式20ax bx c ++的解集为[1，2]，所以0a >，且1和2是方程20ax bx c ++=的两实数解； 由根与系数的关系知，1212b a c a ⎧+=-⎪⎪⎨⎪⨯=⎪⎩，3b a =-，2c a =； 所以不等式20cx bx a ++可化为2230ax ax a -+，即22310x x -+，解得112x ； 所以，所求不等式的解集为1[2，1]． 故选：A ．【点评】本题考查了一元二次不等式的解法与应用问题，也考查了运算求解能力，是基础题．9．（3分）已知集合{|3}A x a x =<，[1B =，)+∞，若A 是B 的子集，则实数a 取值范围为( )A ．[0，3)B ．[1，3)C ．[0，)+∞D ．[1，)+∞【分析】根据条件讨论A 是否为空集：A =∅时，3a ；A ≠∅时，31a a <⎧⎨⎩，解出a 的范围即可．【解答】解：{|3}A x a x =<，[1B =，)+∞，且A B ⊆，∴①A =∅时，3a ；②A ≠∅时，31a a <⎧⎨⎩，解得13a <， ∴综上，实数a 的取值范围为[1，)+∞．故选：D ．【点评】本题考查了子集的定义，描述法、区间的定义，分类讨论的思想，考查了计算能力，属于基础题．10．（3分）已知集合{|0}A x x =，集合{|1}B x x =>，则以下真命题的个数是( ) ①0x A ∃∈，0x B ∉；②0x B ∃∈，0x A ∉；③x A ∀∈，x B ∈；④x B ∀∈，x A ∈．A ．4B ．3C ．2D ．1【分析】直接利用恒成立问题和存在性问题的应用判定A 、B 、C 、D 的结论．【解答】解：对于①：0x A ∃∈，0x B ∉；当0x =时，成立，故①为真命题；对于②：0x B ∃∈，0x A ∉；无论0x 取何值，0x A ∈，故②为假命题；对于③：x A ∀∈，x B ∈；当0x =时，不成立，故③为假命题；对于④：x B ∀∈，x A ∈，由于B A ⊆，故④为真命题．故选：C ．【点评】本题考查的知识要点：存在性问题和恒成立问题，集合间的关系，主要考查学生的转换能力，属于基础题．11．（3分）已知集合{1A =，a ，}b ，2{B a =，a ，}ab ，若A B =，则20212020(a b += )A ．1-B ．0C ．1D ．2【分析】根据集合元素的互异性得到关于a 的方程组21ab b a =⎧⎨=⎩或21a b ab ⎧=⎨=⎩，通过解方程组求得a 、b 的值，则易求20212020a b +的值．【解答】解：由题意得①组21ab b a =⎧⎨=⎩或②21a b ab⎧=⎨=⎩， 由②得1a =±，当1a =时，{1A =，1，}b ，不符合，舍去；当1a =-时，0b =，{1A =，1-，0}，{1B =-，1，0}，符合题意．由①得1a =，舍去，所以1a =-，0b =．202120201a b ∴+=-．故选：A ．【点评】本题考查了集合相等的应用，注意要验证集合中元素的互异性，属于基础题．12．（3分）已知2()2a f x x ax =-+在区间[0，1]上的最大值为g （a ），则g （a ）的最小值为( ) A ．0 B ．12 C ．1 D ．2【分析】由已知结合对称轴与区间端点的远近可判断二次函数取得最值的位置，从而可求．【解答】解：因为2()2a f x x ax =-+的开口向上，对称轴2a x =， ①122a即1a 时，此时函数取得最大值g （a ）f =（1）12a =-， ②当122a >即1a >时，此时函数取得最大值g （a ）(0)2a f ==， 故g （a ）1,12,12a a a a ⎧-⎪⎪=⎨⎪>⎪⎩， 故当1a =时，g （a ）取得最小值12． 故选：B ． 【点评】本题主要考查了二次函数闭区间上最值的求解，体现了分类讨论思想的应用．二、填空题：13．（3分）设命题:1p x ∀，2430x x -+，则命题p 的否定形式为： 01x ∃，200430x x -+< ．【分析】利用全称命题与特称命题的否定关系，写出结果即可．【解答】解：因为全称命题的否定是特称命题，所以命题:1p x ∀，2430x x -+，则命题p 的否定形式是：0:1p x ⌝∃，200430x x -+<． 故答案为：01x ∃，200430x x -+<． 【点评】本题考查全称命题与特称命题的否定关系，是基础题．14．（3分）集合{0A =，1，2}的真子集的个数是 7 ．【分析】由真子集的概念一一列出即可．【解答】解：集合{0A =，1，2}的真子集有：∅，{0}，{1}，{2}，{0，1}，{0，2}，{1，2}，共7个故答案为：7【点评】本题考查集合的真子集个数问题，属基础知识的考查．15．（3分）已知m R ∈，1x ，2x 是方程220x mx m -+=的两个不等实根，则12121x x x x ++的极大值为-【分析】由根与系数的关系得到122x x m +=，12x x m =，将其代入所求的代数式，然后求出极大值．【解答】解：因为m R ∈，1x ，2x 是方程220x mx m -+=的两个不等实根， 所以△2440m m =->，所以1m >或0m <． 根据题意知，122x x m +=，12x x m =，则1212112x x m x x m++=+， 由1m >或0m <， 易知函数12y m m=+在(,-∞和(1,)+∞上单调递增，在(上单调递减，所以当m =12y m m=+的极大值为- 即12121x x xx ++的极大值为- 故答案是：-【点评】本题主要考查了根与系数的关系，属于基础计算题，考查学生的计算能力． 16．（3分）若集合A 具有以下两条性质，则称集合A 为一个“好集合”． （1）0A ∈且1A ∈；（2）若x ，y A ∈，则x y A -∈；且当0x ≠时，有1A x ∈．给出以下命题：①集合{2P =-，1-，0，1，2}是“好集合”； ②Z 是“好集合”； ③Q 是“好集合”； ④R 是“好集合”；⑤设集合A 是“好集合”，若x ，y A ∈，则x y A +∈； 其中真命题的序号是 ③④⑤ ．【分析】直接利用“好集合”的两个条件的应用和相关的运算判断①②③④⑤的结论． 【解答】解：集合A 具有以下两条性质，则称集合A 为一个“好集合”． （1）0A ∈且1A ∈；（2）若x ，y A ∈，则x y A -∈；且当0x ≠时，有1A x∈．对于①：集合{2P =-，1-，0，1，2}是“好集合”．由于2P -∈，2P ∈，所以224P --=-∉，故①为假命题；对于②：Z 是“好集合”．由于当2x =时，1Z x∉，故②为假命题；对于③④：Q 、R 都是“好集合”．由于都满足“好集合”的两个条件，故③④为真命题； 对于⑤：集合A 是“好集合”，所以0A ∈，若x ，y A ∈，则0y A -∈，所以()x y x y A --=+∈，即x y A +∈，故⑤为真命题． 故答案为：③④⑤．【点评】本题考查的知识要点：定义性问题，“好集合”的两个条件的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题．三、解答题：解答应写出文字说明，证明过程或演算步骤． 17．设集合2{|230}A x x x =+-<，集合{|||1}B x x a =+<． （1）若3a =，求AB ；（2）设命题:p x A ∈，命题:q x B ∈，若p 是q 成立的必要不充分条件，求实数a 的取值范围．【分析】（1）通过解不等式，求出集合A 、B ，从而求出其并集即可；（2）问题转化为集合B 是集合A 的真子集，得到关于a 的不等式组，解出即可．【解答】解：（1）解不等式2230x x +-<， 得31x -<<，即(3,1)A =-，⋯（2分） 当3a =时，由|3|1x +<，解得42x -<<-，即集合(4,2)B =--，⋯（4分） 所以(4,1)AB =-；⋯（6分）（2）因为p 是q 成立的必要不充分条件， 所以集合B 是集合A 的真子集⋯（8分）又集合(3,1)A =-，(1,1)B a a =---+，⋯（10分）所以1311a a ---⎧⎨-+<⎩或1311a a -->-⎧⎨-+⎩，⋯（12分）解得02a ，即实数a 的取值范围是02a ⋯（14分）【点评】本题考查了解不等式问题，考查充分必要条件，考查集合的包含关系，是一道基础题．18．已知正数a ，b 满足34a b +=．（1）求ab 的最大值，且写出取得最大值时a ，b 的值； （2）求13a b+的最小值，且写出取得最小值时a ，b 的值． 【分析】（1）由基本不等式可知，4323a b a b =+，得解； （2）利用“乘1法”，13313()4a b a b a b++=+，展开后，由基本不等式即可得解． 【解答】解：（1）由基本不等式可知，4323a b a b =+，即43ab ， 当且仅当3a b =，即2a =，23b =时，ab 取得最大值为43． （2）1331313313()(10)(10)4444a b a b a ba b a b b a a++=+=⨯++⨯+=， 当且仅当b aa b=，即1a b ==时，13a b +取得最小值为4．【点评】本题考查基本不等式的应用，熟练掌握“乘1法”是解题的关键，考查学生的逻辑推理能力和运算能力，属于基础题． 19．关于x 的不等式2(2)20ax a x -++<． （1）当1a =-时，求不等式的解集； （2）当0a >时，求不等式的解集．【分析】（1）1a =-时不等式为220x x --+<，求出解集即可；（2）不等式化为(2)(1)0ax x --<，讨论a 的取值，从而求出不等式的解集． 【解答】解：（1）当1a =-时，此不等式为220x x --+<，可化为220x x +->， 化简得(2)(1)0x x +->，解得2x <-或1x >， 所以不等式的解集为{|2x x <-或1}x >；（2）不等式2(2)20ax a x -++<，化为(2)(1)0ax x --<，当0a >时，不等式化为2()(1)0x x a --<，若21a<，则2a >，解不等式得21x a <<；若21a=，则2a =，解不等式得x ∈∅； 若21a>，则02a <<，解不等式得21x a <<；综上所述：当02a <<时，不等式的解集为2{|1}x x a <<；当2a =时，不等式的解集为∅； 当2a >时，不等式的解集为2{|1}x x a<<． 【点评】本题考查了含有字母系数的一元二次不等式解法与应用问题，也考查了分类讨论思想，是中档题．20．某商品在近30天内每件的销售价格p （元)与时间t （天)的函数关系是20,025,100,2530,t t t N p t t t N +<<∈⎧=⎨-∈⎩，该商品的日销售量Q （件)与时间t （天)的函数关系是40(030,)Q t t t N =-+<∈，求这种商品的日销售金额的最大值，并指出日销售金额最大的一天是30天中的第几天？【分析】设日销售金额为y （元)，则y p Q =，对每段化简和配方，根据二次函数的性质，分别求解每段函数的最大值，由此能求出商品的日销售额y 的最大值． 【解答】解：设日销售金额为y （元)，则y p Q =， (20)(40),025,(100)(40),2530,t t t t N y t t t t N +-<<∈⎧=⎨--∈⎩2220800,025,1404000,2530,t t t t Nt t t t N ⎧-++<<∈=⎨-+∈⎩ 22(10)900,025,(70)900,2530,t t t Nt t t N ⎧--+<<∈=⎨--∈⎩， 当025t <<，t N ∈，10t =时，900max y =（元)； 当2530t ，t N ∈，25t =时，1125max y =（元)．由1125900>，知1125max y =（元)，且第25天，日销售额最大．【点评】本题考查分段函数在生产实际中的应用，考查二次函数的最值问题和运算求解能力，属于中档题．21．已知二次函数2()21f x ax bx a =++-的对称轴为1x =-． （1）设1x ，2x 为方程()0f x =的两个实数根，且1232x x =，求()f x 的表达式； （2）若()0f x 对任意[3x ∈-，0]恒成立，求实数a 的取值范围．【分析】（1）由已知结合方程的根与系数关系即可求解a ，b ，进而可求函数解析式， （2）由已知不等式恒成立转化为求解函数在闭区间上的最值，对a 的范围分类讨论可求． 【解答】解：（1）因为12b x a =-=-，所以2b a =，由根与系数的关系可得122132a x x a -==，解得：2a =，则4b =，则2()243f x x x =++； （2）因为2()221f x ax ax a =++-的对称轴为1x =-，若0a >，()y f x =开口向上，则()f x 在[3-，0]的最小值在1x =-处取得， 则(1)10f a -=-，解得1a ；若0a <，()y f x =开口向下，又因为|3(1)||0(1)|--->--， 则()f x 在[3-，0]的最小值在3x =-处取得， 则(3)510f a -=-，解得15a （舍)； 综上所述，[1a ∈，)+∞．【点评】本题主要考查了二次函数闭区间上最值的求解及不等式的恒成立与最值关系的相互转化，体现了分类讨论思想的应用．22．设函数()f x =，0b >的定义域为A ，值域为B ． （1）若1a =-，2b =，8c =，求A 和B ； （2）若A B =，求满足条件的实数a 构成的集合．【分析】（1）由()f x =利用函数的定义域求出集合A ，再根据函数()f x 的值域，得到集合B ． （2）当0a =时，[,)cA b-=+∞，[0B =，)+∞，由A B =，知0c =满足题意；当0a ≠时，当△0时，设方程()0g x =的两实数根为1x ，212()x x x ，推导出12{|}A x x x x =，B =，由此能求出满足A B =的实数a 构成的集合．【解答】解：（1）()f x 因为(2)(4)0x x +-，所以[2A =-，4]，因为()f x ， 又209(1)9x --，所以[0B =，3]；（2）当0a =时，()f x [,)cA b-=+∞，[0B =，)+∞，又A B =，故0c =满足题意；当0a ≠时，设二次函数2()g x ax bx c =++的判别式为△， 当△0时，设方程()0g x =的两实数根为1x ，212()x x x假设0a >，当△0时，则1{|A x x x =或2}x x ，[0B =，)+∞，则A B ≠，矛盾；当△0<时，则A R =，)B =∞，则A B ≠，矛盾； 当0a <时，假设△0<，则A =∅，B =∅，虽有A B =，但不符合函数的定义，舍去；当△0，则12{|}A x x x x =，B =，要使A B =，则10x =，且2x =即0c =，又2()0g x =得2b x a -==2224b b a a-=，解得4a =-； 综上，满足条件的实数a 构成的集合为{4-，0}．【点评】本题考查集合的求法，考查函数的定义域、值域等基础知识，考查分类讨论思想，是中档题．。