2.用等式性质(1)解方程

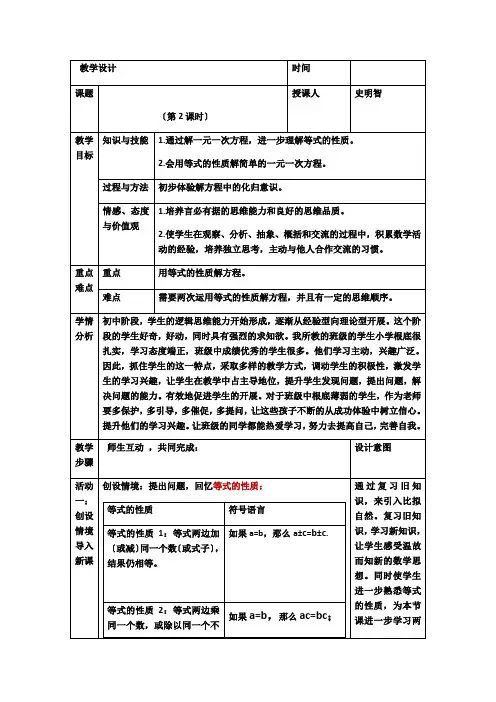
一元一次方程利用等式的性质解方程一元一次方程是代数中的基础内容，是我们学习数学的第一步。

解一元一次方程的过程中，我们可以利用等式的性质来简化计算，帮助我们更快地找到方程的解。

下面我将详细介绍一元一次方程的解法以及利用等式性质解方程的方法。

解一元一次方程的基本步骤如下：步骤一：将方程化为标准形式首先，我们需要将方程转化为标准形式，即将未知数x的系数设为1、做法是将方程两边同时除以a，得到：x+b/a=0。

步骤二：消去常数项由于方程等号右边是0，我们可以通过消去常数项来简化方程。

具体做法是将方程两边同时减去b/a，得到：x=-b/a。

步骤三：求解未知数现在，我们已经得到了未知数x的解。

根据一元一次方程的解的定义，x的解即为方程的解。

所以，方程ax + b = 0的解是x = -b/a。

这是解一元一次方程的基本步骤，但在实际问题中，我们可能会遇到一些复杂的情况。

这时，我们就需要利用等式性质来简化解方程的过程。

下面我将介绍一些常用的等式性质。

性质一：等式两边同时加上（或减去）一个相同的数，等式仍然成立。

利用这个性质，我们可以在解一元一次方程的过程中，将常数项移到方程的另一边，使得方程形式更简单。

例如，对于方程2x+3=7，我们可以通过减去3来简化方程，得到2x=4性质二：等式两边同时乘以（或除以）一个相同的非零数，等式仍然成立。

利用这个性质，我们可以在解一元一次方程的过程中，通过乘以或除以一个非零数，使方程的系数变为1例如，对于方程3x=6，我们可以通过除以3来简化方程，得到x=2性质三：平方等式两边，等式仍然成立。

利用这个性质，我们可以在解一元一次方程的过程中，将含有未知数的平方项消去。

例如，对于方程x^2-5x+6=0，我们可以通过平方来简化方程，得到(x-2)(x-3)=0。

这样，我们可以得到方程的两个解x=2和x=3利用这些等式性质，我们可以在解一元一次方程的过程中，将方程变得更简单，从而更容易找到方程的解。

五年级数学上册
《解方程》6大基本类型
①未知数是加数，比如，x+3＝6，6+x＝8
方法：用等式的性质等1等式两边同时减去另一个加数。

x+3=6 6+x=8
解：x+3-3=6-3 解：6+x-6=8-6
x=3 x=2
②未知数是被减数，比如，x-3＝6
方法：用等式的性质1，等式两边同时加上减数。

x-3=6
解：x-3+3=6+3
x=9
③未知数是因数，比如，5x＝10
方法：用等式的性质2，等式两边同时除以另一个因数。

5x=10
解：5x÷5=10÷5
x=2
④未知数是被除数，比如，x÷3＝6
方法：用等式的性质2，等式两边同时乘除数。

x÷3=6
解：x÷3×3=6×3
x=18
⑤未知数是减数，比如，20-x＝9
方法：用的等式的性质1，等式两边同时加上x，把未知数转化到右边，再把左右交换位置，变成未知数是加数的类型进行求求解。

20-x=9
解：20-x+x=9+x
20=9+x
9+x=20
9+x-9=20-9
x=11
⑥未知数是除数，比如：21÷x＝3
方法：用的等式的性质2，等式两边同时乘x，把未知数转化到右边，再把左右交换位置，变成未知数是因数的类型进行求解。

21÷x=3
解：21÷x×x=3×x
21=3x
3x=21
3x÷3=21÷3
x=7。

初中数学等式的性质如何应用于解一元一次方程等式的性质是解决一元一次方程的重要工具。

在解题过程中，我们可以利用等式的性质来简化计算和转化等式，从而更加轻松地解决方程问题。

下面将介绍等式的性质在解一元一次方程中的应用。

一、等式的加法性质和减法性质一元一次方程的一般形式为ax + b = c，其中a，b，c 是已知数，x 是未知数。

我们可以利用等式的加法性质和减法性质来解决方程问题。

具体方法如下：1. 如果方程中有多项式，可以将其中的同类项合并，然后利用等式的加法性质和减法性质化简方程。

例如，对于方程2x + 3x + 4 = 7x + 2，我们可以将方程中的同类项合并：5x + 4 = 7x + 2，然后用等式的减法性质将5x 移到方程的一边，将常数项移到另一边：5x - 7x = 2 - 4，即-2x = -2。

最后，用等式的乘法性质将x 的系数消去，解得x = 1。

2. 如果方程中有分式，可以通过通分来化简方程。

例如，对于方程2/x + 1/(x+1) = 3/2，我们可以通过通分将方程化简为(4(x+1) + 2x) / (2x(x+1)) = 3/2，即6x + 6 = 3x^2 + 3x，然后移项得到3x^2 - 3x - 6 = 0。

最后，用一元二次方程的求解公式解得x = 2 或x = -1。

二、等式的乘法性质和除法性质一元一次方程的另一种解法是利用等式的乘法性质和除法性质。

具体方法如下：1. 如果方程中有一个未知数的系数为1，可以利用等式的乘法性质将系数移动到未知数的一边。

例如，对于方程x/3 + 2 = 5，我们可以通过等式的乘法性质将1/3 移到未知数x 的一边，得到x = 9。

2. 如果方程中有一个未知数的系数不为1，也可以利用等式的乘法性质来解决方程。

例如，对于方程2x/3 + 4 = 8，我们可以将方程两边都乘以3，得到2x + 12 = 24，然后移项得到2x = 12，最后解得x = 6。

讲解等式性质法解方程的基本思路并通过例题演示等式性质法的具体步骤等式性质法是解方程的一种常用方法，通过观察等式的特点，运用等式性质进行变形和化简，从而得到方程的解。

本文将介绍等式性质法解方程的基本思路，并通过例题演示具体的步骤。

1. 基本思路等式性质法的基本思路是通过等式的相等性质，将复杂的方程逐步简化为易于求解的形式。

具体步骤如下：(1) 观察等式，分析方程的结构，判断可利用的等式性质；(2) 运用等式性质进行变形，将方程化简为新的形式；(3) 若方程未求解出，则重复步骤1和步骤2，直至方程求解完成。

2. 具体步骤接下来通过几个例题，演示等式性质法的具体步骤。

例题1：解方程3(x+1) = 7解：根据等式性质，可以利用乘法逆性进行变形。

将3(x+1)展开后，得到3x+3=7。

再利用减法逆性，将等式两边都减去3，得到3x=4。

最后，再利用乘法逆性，将等式两边都除以3，得到x=4/3。

所以，方程的解为x=4/3。

例题2：解方程2x+3=5x-1解：根据等式性质，可以利用加法逆性和乘法逆性进行变形。

将2x+3与5x-1的变量项分别移到等式的两边，得到2x-5x=-1-3。

利用减法逆性进行合并，得到-3x=-4。

最后，再利用乘法逆性，将等式两边都除以-3，得到x=4/3。

所以，方程的解为x=4/3。

例题3：解方程2(x-1) + 3x = 4(1-x)解：根据等式性质，可以利用分配律、加法逆性和乘法逆性进行变形。

首先，利用分配律将等式两边的括号展开，得到2x-2+3x=4-4x。

然后，将变量项移到等式的一边，常数项移到另一边，得到2x+3x+4x=4+2。

利用合并同类项，得到9x=6。

最后，再利用乘法逆性，将等式两边都除以9，得到x=6/9=2/3。

所以，方程的解为x=2/3。

通过以上例题，我们可以清晰地看到等式性质法解方程的基本思路和具体步骤。

在实际解题过程中，我们只需仔细观察方程的特点，灵活运用等式性质法，就能够有效解决各类方程。