小学六年级数学能力提高题_3

六年级数学应用题能力测试卷（1）（含详细解答）1.某圆锥体的高和底面半径都等于一个正方体的棱长．已知正方体的体积是9立方分米，圆锥的体积是多少分米？2．（8分）探索规律．有若干长5厘米，宽3厘米的长方形纸片（如图）．（1）如果将这些长方形纸片按照如上图所示的方法，由上至下一层层摆下去．想一想，随着摆的层数的增加，图形的周长有怎样的变化规律？请边计算填表，边3．我市的出租车收费标准是：起步3千米5元，白天每多行1千米加1元．晚上10时以后，每多行1千米加1.2元，不足1千米的按1千米算．一次张小磊同学22：10坐出租车到火车站接爸爸，共行了7.8千米．小磊应付多少车费？4.甲、乙两校参加数学竞赛的共有22人，甲校参加人数的20%比乙校参加人数的25%少1人．求两校参加的人数各是多少．5.某服装商店出售服装，去年按定价的85%出售，能获得25%的盈利，由于今年买入价降低，按同样定价的75%出售，却能获得30%的盈利，求今年买入价与去年买入价的比.6．一批零件，王师傅单独做需要9小时完成，李师傅每小时做20个．现在两人合作，完成时王师傅做了这批零件的，李师傅做了多少个零件？7.有一个分数，如果分母加上6,分子不变，约分后为61；如果分子加上4，原分母不变，约分后为41。

问原分数是多少？8.有三堆围棋子，每堆40枚．第一堆黑子与第二堆白子同样多，第三堆有是白子．这三堆棋子一共有白子多少枚？9.梨子、苹果、桔子、柿子共有100个。

如果梨子个数加4，苹果个数减4，桔子个数乘4，柿子个数除以4，所得的个数相等。

问四种水果各有多少个？10.现在弟弟的年龄恰好是哥哥年龄的21，而九年前弟弟年龄是哥哥的51，则哥哥现在的年龄是多少？答案解析1.解：设正方体的棱长为x分米，x×x×x=1.5（立方分米）圆锥的体积=3.14×x2×x÷3=3.14×9÷3=9.42（立方分米）答：圆锥的体积是9.42立方分米．2.解：通过观察得出规律：周长是层数的16倍．（1）摆2层周长是：16×2=32（厘米）摆3层周长是：16×3=48（厘米）摆4层周长是：16×4=64（厘米）摆10层，得到的图形的周长是160厘米．故答案为：32；48；64；16n．3.解：7.8﹣3=4.8≈5（千米）5×1.2+5=6+5=11（元）答：小磊应付11元．4.解：设甲校参加的有x人，则乙校参加的就有22﹣x人（22﹣x）×25%﹣1=20%x5.5﹣25%x﹣1=20%x4.5=20%x+25%x4.5÷0.45=0.45x÷0.45x=1022﹣x=22﹣10=12（人）答：甲校参加的有10人，乙校有12人．5.解：解：[0.75÷（1+30%）]÷[85%÷（1+25%）]=÷==375：442．答：今年买入价与去年买入价的比为375：442．6.解：×20=5×20=100（个）答：李师傅做了100个零件．7.解设分母加6后，分子为x, 分母为6x则由题意知：（6x-6）:(x+4)=4：16x+6=4x+16x =1111所以原分数为608.解：40+40×=40+10=50（枚）答：这三堆棋子中共有白子50枚．9.解：设四种水果个数变化后相等为x个，则变化前的水果个数分别是：梨子x ﹣4个、苹果x+4个、桔子x÷4个、柿子4x个，根据题意可得方程：x﹣4+x+4+x÷4+4x=100，x=100，x=16，16﹣4=12（个），16+4=20（个），16÷4=4（个），16×4=64（个），答：梨子有12个、苹果有20个、桔子有4个、柿子有64个．10.解：设弟弟现在的年龄是x岁，那么哥哥现在的年龄是2x岁；x﹣9=（2x﹣9），5x﹣45=2x﹣9，3x=36，x=12；哥哥现在的年龄是：2x=2×12=24（岁）．答：哥哥现在的年龄是24岁．。

六年级分数百分数应用题集中训练（提升篇）1.商店同时卖出两台洗衣机，每台售价均为2400元，其中一台比进价高20%，另一台比进价低20％，商店卖出这两台洗衣机是赚了还是亏了？赚了（亏了）多少元？2.张叔叔家买了一套新房，准备买一些家电，他带了10000万来到家电超市，看见一1。

款家电组合：电脑4000元，彩电的价钱是电脑的80％，冰箱的价钱比彩电便宜16请你帮张叔叔算一算，他带的钱够不够买这一款家电组合？3.王叔叔新购进200件西服，每件的成本为300元，准备按每件500元上柜销售。

由于市场因素，他决定打八折出售。

全部售出后，要向税务部门按销售款的5%纳税。

税后他盈利多少元？4.甲仓库有粮食80吨，乙仓库有粮食120吨，如果把乙仓库的一部分粮食调到甲仓库，使得乙仓库的粮食是甲仓库的60%，那么需从乙仓库调入甲仓库多少吨粮食？2桶油，用去桶中油的40%，桶中还有油24千克。

整个最多能5.有一个油桶，现装有3装油多少千克？6.甲、乙两个仓库共存粮食1360吨，已知甲仓库的存粮是乙仓库存粮的60%，甲、乙两个仓库各存量多少吨？1。

每只大桶和每7.4只大桶和16只小桶共装油80升，已知每只小桶的容量是大桶的4只小桶各装油多少升？8.妈妈买回5千克苹果和3千克香蕉，一共用去45元。

已知每千克苹果的价格是香蕉的120%，苹果和香蕉的单价各是多少元？2，如果再运50吨，那么剩下的煤比已经运的少30吨。

这堆煤9.运一堆煤，已经运了5原来有多少吨？10.六年级二班体育达标的人数是39，未达标的人数是11,半年后体育未达标的人数是1。

在这半年中又有多少人体育达标？达标人数的911.甲、乙两车在上午8时分别从两个车站相对开出，中午12时在途中相遇。

已知甲4。

两个车站相距多少千米？车每小时行驶75千米，乙车的速度是甲车的57。

现两车同时从甲、乙两地出发，12.一辆货车每小时行70千米，相当于客车速度的8相对开出，结果在距中点50千米处相遇。

六年级数学下册专项练习：提高类型题1.甲、乙、丙、丁四人用600元合买了一台潜水本泵，付款办法是，甲付的钱是其他三人应付总数的一半，乙付的钱是其他三人应付总数的1/3，丙付的钱是其他三人应付总数的1/4，丁应付款多少元？2.一个圆柱形木料高9分米，沿底面直径切成两个半圆柱，表面积增加36平方分米，这根木料的体积是多少立方分米？3.一种冰箱，元月份按成本价提高20%出售，九月份又打九折出售，降价后每台卖2700元，这种冰箱卖出一台是赔还是赚，如果是赚，那么赚多少钱？如果是赔，赔多少钱？4.一个圆柱形木料高9分米，切成两个小圆柱后，表面积增加36平方分米，这根木料的体积是多少立方分米？5.一个圆柱的侧面积是37.68平方厘米，底面半径是2厘米，它的体积是多少立方厘米？6.某厂向银行申请甲乙两种贷款共40万元，每年需要付利息5万元，甲种贷款年利率12%，乙种贷款年利率14%，该厂申请甲乙两种贷款的金额各是多少？7.把一个高4分米的圆柱体底面平均分成若干个扇形，然后切开拼成一个等底等高的近似长方体，长方体的表面积比圆柱增加16平方分米，原来圆柱体的体积是多少？8.一根铁丝第一次用去全长的1/5，第二次用去15米，这时用去的与剩下的长度正好是4:1，这根铁丝原来长多少米？9.将一个长8厘米，高4厘米的长方体削成圆柱，圆柱的体积最大是多少立方厘米？10.将一个长方体的高减少2厘米，就得到一个正方体，表面积就少了48平方厘米，求原来长方体的体积？11.将一个长8厘米，宽6厘米，高4厘米的长方体削成一个圆柱，圆柱的体积最大是多少立方厘米？12.一个蛋糕盒（如图）①蛋糕盒的体积是多少立方厘米？②用彩带包扎至少需要彩带多少厘米？(打结处大约用20厘米)13.一个圆柱与一个圆锥等底等高他们体积相差0.8立方米，这个圆锥的体积是多少？14.一段圆柱形木材，如果截成两个圆柱，它的表面积增加6.28平方分米，如果沿着直径劈开，它的表面积增加80平方分米，求原来圆柱体的表面积？15.将一个援助沿底面直径分成完全相同的两部分，表面积比原来多了60平方厘米，圆锥高是5厘米，圆锥体积是多少？16.客车从甲站开往乙站，火车同时从乙站开往甲站，客车开到全程的9/16的地方与火车相遇，如果客车每小时行驶45千米，火车8小时行完全程，求甲乙两站的距离?17.一段圆柱体材料如果截成两个圆柱它的表面积增加6.28平方分米，如果沿着直径劈开，它的表面积就增加了80平方米，求原来圆柱体的表面积？18.一个长方体总和是220厘米，长与宽的比是2：1，宽与高的比例是3：2，这个长方体体积是多少立方厘米？19.一根电线第一次用去与剩下的比是2：3，第二次用去28米，这是剩下与用去的比是1：3，这根电线全长多少米?20.一种商品随季节变化降价出售，如果按现价降低10%，那么可盈利180元，如果降价20%，那么亏损240元，这种商品进价多少元？21.把含盐率为5%的400克盐水稀释成含盐率为4%的盐水应加水多少克？22.一种电线第一次用去的与剩下的比是2:3，第二次用去28米，这时剩下的与用去的比是1:3，着根电线全长多少米？23.一个长方体棱长总和是220厘米，长和宽的比是2:1，宽与高的比是3:2，这个长方体的体积是多少立方厘米？24.在一棱长为20厘米的正方体容器里注入深10厘米的水，再沉入6千克的石头后，水深为17.5厘米，这块石头每立方厘米重多少克？25.把一个直径是10厘米的圆柱体沿直径纵向切开后，它的表面积增加了200平方厘米，原来这个圆柱的体积是多少？26.一种商品的原价是100元，商场把价格提高到140元出售，发现销售有些困难，只得将提高的价格降低40%，这种商品的售价比原来便宜多少钱？27.商店运来橘子、苹果和梨一共360千克，橘子和苹果的重量比是5:6，梨的重量是苹果的1/6，运来橘子是多少千克？28.有底面积相等的两个圆柱，高的比是7:5，第一个圆柱的体积是175立方厘米，则第二个圆柱的体积是多少立方厘米？29.甲，乙两个车间共有162个人，甲车间人数的1/4与乙车间人数的1/5相等，甲乙两个车间各有多少人？。

六年级数学上册典型例题系列之第三单元分数除法应用题提高部分（解析版）编者的话：本试题是在《分数除法应用题基础部分》上进行编辑总结的，分数除法应用题提高部分，难度较大，题型主要分为两个大类，即量率对应类型题和单位“1”转化类型题，共计十五个考点，其中十五个考点全部是考试试卷出现过的类型考题，值得注意的是，解析版本编者全部采用算术方法解决问题，除此以外方程法亦可采用，根据学生掌握情况而定，欢迎使用。

【考点一】稍复杂的量率对应问题。

【方法点拨】“量率对应”是使用算术方法解决分数除法应用题的核心思路，稍复杂的量率对应问题，关键在于明确分量和分率表示的意义是否一样，即是否一一对应。

【典型例题1】量率直接对应型小华的妈妈开车到姥姥家，已经行驶了80km ，正好是剩下路程的54。

小华家到姥姥家的距离是多少千米？ 解析：已行驶的路程正好是剩下路程的54，即80km 与54是直接对应的。

剩下路程：80÷54=100（km ） 全部路程：80+100=180（km ）答：略。

【典型例题2】量率间接对应型 一辆汽车从甲地开往乙地先行全程的81，然后又行400千米正好到达，甲乙两地相距多少千米？解析：400km 表示的是后段路程，81表示的是前端路程的分率，所以用（1-81）表示后段路程分率。

400÷（1-81）=73200（km ） 答：略。

【对应练习1】修路队要修一条公路，已经修了3600米，还剩下83没有修，这段公路全长有多少米？解析：3600÷（1-83）=5760（米） 答：略。

【对应练习2】 一本书，小丽上午看了全书的51，下午看了30页，一天正好看了这本书的一半，这本书有多少页？解析：30÷（21-51）=100（页） 答：略。

【对应练习3】一筐苹果连筐重49kg ，卖出这筐苹果的32后，连筐重17kg 。

这筐苹果原来有多少千克？解析：（49-17）÷32=18（千克） 答：略。

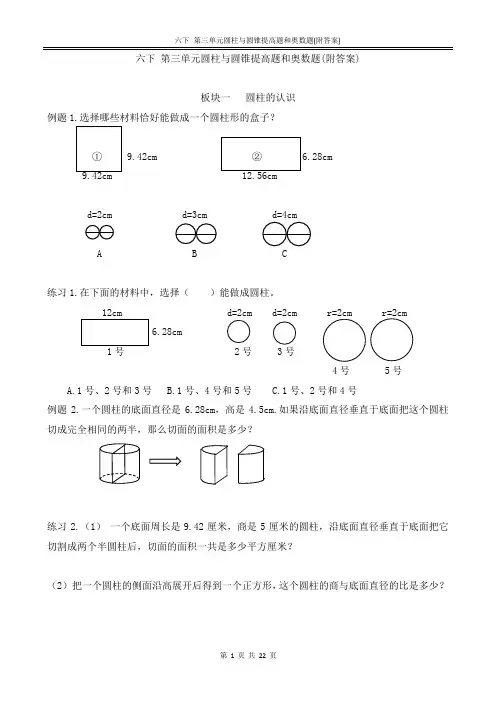
六下第三单元圆柱与圆锥提高题和奥数题(附答案)板块一圆柱的认识例题1.选择哪些材料恰好能做成一个圆柱形的盒子？d=2cm d=3cm d=4cmA B C练习1.在下面的材料中，选择（）能做成圆柱。

3号4号 5号A.1号、2号和3号B.1号、4号和5号C.1号、2号和4号例题2.一个圆柱的底面直径是6.28cm，高是4.5cm.如果沿底面直径垂直于底面把这个圆柱切成完全相同的两半，那么切面的面积是多少？练习2.（1）一个底面周长是9.42厘米，商是5厘米的圆柱，沿底面直径垂直于底面把它切割成两个半圆柱后，切面的面积一共是多少平方厘米？（2）把一个圆柱的侧面沿高展开后得到一个正方形，这个圆柱的商与底面直径的比是多少？例题3.一个圆柱形蛋糕盒的底面直径是20厘米，高是15厘米，用彩绳将它捆扎（如右图），打结处在圆心，打结部分长30厘米。

求所用彩绳的全长是多少厘米？练习3.一个圆柱形蛋糕用彩绳捆扎，如果打结部分用了35厘米，打结处在圆心，一共用了多长彩绳？板块二圆柱的表面积例题1.一块长方形的钢板，利用图中阴影部分刚好能做成一个圆柱形的带盖水桶（接头处忽略不计），求这个水桶的表面积。

练习 1.（1）如下图，有一张长方形铁皮，剪下两个圆及一个长方形，正好可以做成一个圆柱，这个圆柱的底面半径为10厘米，原来这张长方形铁皮的面积是多少平方厘米？（2）有一张长方形铁皮（尺寸如图所示），剪下阴影部分正好能围成一个圆柱，求圆柱的表面积是多少。

例题2.工人师傅要在一个零件（如右图）的表面涂一层防锈材料。

这个零件是由两个圆柱构成的，小圆柱的直径是4厘米，高是2厘米；大圆柱的直径是6厘米，高是5厘米。

这个零件涂防锈材料的面积是多少？练习2.用3个高都是2分米，底面半径分别为2分米、1分米和0.5分米的圆柱组成一个物体（如图），求该物体的表面积。

例题3.如图，是长为8，宽为4的长方形，以长方形的长为轴旋转一周。

求所形成的立体图形的表面积。

1阶段提升演练一、我会填。

1.512( )( )( )2.已知35÷▲=35×▲,则▲所代表的数是( )。

3.在○里填上“>”“<”或“=”。

6×512○6 15×14○15 6÷512○6 15÷14○1559×32○59 56×65○56 59÷32○59 56÷65○56二、我会选。

1.28除以1415的商( )28乘1415的积。

A.大于B.小于C.等于2.已知小红的邮票数量除以45与小明的邮票数量相等,则小红的邮票数()小明的邮票数。

A.多于 B.少于 C.等于三、我会解方程。

x÷56=25 23x=415 x+23x=154113x-12x=5 7x÷110=35 (23-12)x =132四、我会算。

12÷89÷34 56÷2536×16 815÷(89+23)215÷25+14 49÷83+38÷59 35×18+25÷8五、我会解答。

1.买一支铅笔花35元,24元钱可以买几支铅笔?2.3台碾米机32小时碾米95 t,每台碾米机平均每小时碾米多少吨?3.这壶油可以用多少天?★4.王老师12小时能批改20本作业,照这样计算,批改50本作业需要多少小时?910小时能批改多少本作业?3 阶段提升演练一、1.5 5 5 2.13.< < > > > > < < 二、1.A 2.B三、x=13 x=25 x=94 x=6 x=3350 x=2 四、34 15 1235 712 101120 18 五、1.24÷35=40(支) 2.95÷32÷3=25(t)3.方法一:3÷(340×2)=3÷320=20(天)方法二:3÷340÷2=40÷2=20(天)4.50÷(20÷12)=54(小时)20÷12×910=40×910=36(本)。

专项知识集中训练（三）统计与概率一、填空题。

（24分）1.常用的统计图有（）统计图，（）统计图，（）统计图。

2.如果要反映小亮6～11岁的身高变体情况，选（）统计图比较合适；如果要反映小红、小强等6名同学11岁时的体重情况，选用（）统计图比较合适。

3.小玲和小红做摸球游戏．口袋里有白球、红球各1个．(球的大小相同)（1）小玲前3次都是摸到红球、第4次一定摸到红球吗？（）(填一定或不一定)（2）小红连摸10次，一定是5次红球、5次白球吗？（）(填一定或不一定)4.有一列数：142，143，140，154，145，144，168，这列数的平均数（）。

5.苹苹期末测试语文和数学的平均成绩是96分，英语99分，她三科成绩的平均分是（）。

6.小李的年龄与身高的关系如下图。

有一段时间，小李在2年内长高了15厘米，这两年小李的年龄最有可能在（）岁至（）岁之间。

二、选择题。

（6分）1.反映各种蔬菜种植面积与总面积的关系，应选用（）。

A.条形统计图B.折线统计图C.扇形统计图2.在一个正方体的六个面上分别标有4个“1”，1个“2”，1个“3”，抛起正方体，落下后，朝上的面上的数（）。

A.一定是奇数B.可能是偶数C.一定大于33.为了表示某地上半年每月的平均气温变化情况，应绘制（）。

A.统计表B.条形统计图C.折线统计图D.扇形统计图4.李红向下面第一个靶掷一块石头(四个靶大小相等，均为等分)，她最有可能击中（）靶的阴影部分。

A. B. C. D.5.口袋里放着大小、材质都相同的3个白球和3个黑球，每次摸出一个，记录下来，然后放回袋里。

第1次摸出的是白球，第2次摸球的结果是（）。

A.一定还是白球B.一定是黑球C.摸出白球的可能性大D.有可能摸出白球，也有可能摸出黑球6.学校教学楼有四层．六（1）班的同学第一节课到三楼上数学课，第二节课到二楼上美术课，第三节课到四楼上音乐课，第四节课回到三楼上语文课，中午到一楼食堂吃饭．下面哪一幅图比较准确地描述了这一过程？（）。

苏教版小学六年级数学上册第1--3单元（月考）能力拓展培优提升试卷（附答案）时间：90分钟 满分：100分学校: __________姓名：__________班级：__________考号：__________一、选择题（每题2分，共14分）3．用边长1分米的小正方体搭成一个模型，从正面看是，从上面看是，从侧面看是，这个模型的体积是（ ）立方分米。

A ．4B ． 5C ．6D ．10A ．甲大B ．乙大C ．丙大D ．同样大二、填空题（每空1分，共14分）22÷5 ×÷8 ÷÷×．59三、判断题（每题1分，共7分） 18．÷5和 × 的结果相同，但意义不同．( )19．把两个相同的正方体拼成一个长方体后，表面积不变。

( )20．“白粉笔盒数的等于红粉笔的盒数”，这里是把红粉笔的盒数看作单位“1”。

…………………………………………………………………( )四、计算(共16分) 22．口算．（每题1分，共8分）五、解答题（29题9分，其余每题8分，共49分）28．某批发商店进了 吨白糖，第一周卖出这些白糖的，第二周卖出吨．还剩下多少吨?29．有一个花坛，高0.4米，底面是边长1.2米的正方形。

四周用砖砌成，砖墙的厚度是0.2米，中间填满泥土。

（1）花坛所占的空间有多大？（2）如果在花坛的侧面贴瓷砖，需要瓷砖多少平方米？ （3）花坛里大约有泥土多少立方米？如图所示，搭成这个模型需要6个小正方体，所以这个模型的体积是6立方分米。

【分析】根据正方体的展开图的特征，是正方体展开图的“1－4－1”型，a 对应是2，b 对应的是23，根据题意，正方体相对两个面上的数字互为倒数，求出a和b的值，再求出a×b的值，据此解答。

【详解】a×2＝1解：（1）÷5=×，（2）÷8＜，（3）÷＞，（4）÷＞×，故答案依次为：=，＜，＞，＞．故÷5和× 的结果相同，【详解】【分析】考点：分数四则复合应用题．＝1.44×0.4＝0.576（立方米）答：花坛所占空间有0.576立方米。

特殊工程问题一、知识要点有些工程题中，工作效率、工作时间和工作总量三者之间的数量关系很不明显，这时我们就可以考虑运用一些特殊的思路，如综合转化、整体思考等方法来解题。

二、精讲精练【例题1】修一条路，甲队每天修8小时，5天完成；乙队每天修10小时，6天完成。

两队合作，每天工作6小时，几天可以完成？把前两个条件综合为“甲队40小时完成”，后两个条件综合为“乙队60小时完成”。

则1÷[15×8+110×6]÷6=4（天）或1÷[（15×8+110×6）×6]=4（天）答：4天可以完成。

练习1：1.修一条路，甲队每天修6小时，4天可以完成；乙队每天修8小时，5天可以完成。

现在让甲、乙两队合修，要求2天完成，每天应修几小时？2.一项工作，甲组3人8天能完成，乙组4人7天也能完成。

现在由甲组2人和乙组7人合作，多少天可以完成？3.货场上有一堆沙子，如果用3辆卡车4天可以完成，用4辆马车5天可以运完，用20辆小板车6天可以运完。

现在用2辆卡车、3辆马车和7辆小板车共同运两天后，全改用小板车运，必须在两天内运完。

问：后两天需要多少辆小板车？【例题2】有两个同样的仓库A和B，搬运一个仓库里的货物，甲需要10小时，乙需要12小时，丙需要15小时。

甲和丙在A仓库，乙在B仓库，同时开始搬运。

中途丙转向帮助乙搬运。

最后，两个仓库同时搬完，丙帮助甲、乙各多少时间？设搬运一个仓库的货物的工作量为“1”。

总整体上看，相当于三人共同完成工作量“2”①三人同时搬运了2÷（110+112+115）=8（小时）②丙帮甲搬了（1-110×8）÷115=3（小时）③丙帮乙搬了8-3=5（小时）答：丙帮甲搬了3小时，帮乙搬了5小时。

练习2：1.师、徒两人加工相同数量的零件，师傅每小时加工自己任务的110，徒弟每小时加工自己任务的115。

小学六年级上册 数学《能力强化训练+答案》秋季第3讲 万变不离其宗例题练习题例1 河马的平均寿命是大象的38，长颈鹿的平均寿命是河马的23，那么长颈鹿的平均寿命是大象的几分之几？ 【答案】14【解析】设大象的平均寿命是“1”，则河马的平均寿命是38，所以长颈鹿的平均寿命是大象的321834⨯=.练1 乙数是甲数的67，丙数是乙数的56，丙数是甲数的几分之几？ 【答案】57【解析】设甲数是“1”，则乙数是67，所以丙数是甲数的655767⨯=.例2 有三个桶里面装满了酸奶，乙桶中的酸奶比甲桶中的少16，丙桶中的酸奶比甲桶中的多16。

请问：如果把三桶酸奶倒入一个大缸里，甲桶中的酸奶占其中的几分之几？【答案】13【解析】设甲桶中的酸奶有“6”，则乙桶中有“5”，丙桶中有“7”，所以甲桶中的酸奶占其中的615673=++.练2 甲桶中的水比乙桶中的少15，丙桶中的水比乙桶中的多15.如果把三桶水倒入一个大缸里，甲桶中的水占其中的几分之几？ 【答案】415【解析】设乙桶中的水有“5”，则甲桶中的水有“4”，丙桶中的水有“6”，所以甲桶中的水占其中的4454615=++.例3 某人从甲城去乙城，第一天走了全程的14，第二天走了剩下的23，这时距乙城还有40千米.问甲、乙两城相距多少千米？ 【答案】160千米【解析】第二天走了全程的1211432⎛⎫-⨯= ⎪⎝⎭，所以甲、乙两城相距1140116042⎛⎫÷--= ⎪⎝⎭（千米）.练3 小明看一本书，第一天看了全书的13，第二天看了剩下的25，还剩下144页没有看.问这本书共有多少页？ 【答案】360页【解析】第二天看了全书的12413515⎛⎫-⨯= ⎪⎝⎭，所以这本书共有141441360315⎛⎫÷--= ⎪⎝⎭（页）.例4 现有苹果、桔子、梨三种水果各若干个，苹果的数量是其它两种水果总数的16。

桔子的数量是其它两种水果总数的516，梨有26个.这些水果一共有多少个？ 【答案】42个【解析】先把每种水果“占其它”的几分之几转化成“占总数”的几分之几.苹果的数量占全部水果的11167=+，桔子的数量占全部水果的5551621=+，那么梨的数量占全部水果1513172121--=；所以这些水果共有13264221÷=（个）.练4 现有包子、饺子、馒头各若干个，包子的数量是其它两种主食总数的15，饺子的数量是其它两种主食总数的57，馒头有15个.这些主食一共有多少个？ 【答案】36个【解析】先把每种主食“占其它”的几分之几转化成“占总数”的几分之几.包子的数量占总数的11156=+，饺子的数量占总数的555712=+，那么馒头的数量占总数的155161212--=.所以这些主食共有5153612÷=（个）挑战极限1 阿呆和阿瓜一起玩游戏牌.开始时阿呆手里的牌数是阿瓜手里牌数的35；玩了若干局后，阿呆赢了阿瓜的20张牌，此时阿呆手里的牌数反而是阿瓜手里牌数的75.请问：阿呆此时一共有多少张牌？ 【答案】56张【解析】两人的总牌数不变，所以将单位“1”统一为总牌数.开始时，阿呆手里的牌数占总数的33538=+，后来，阿呆手里的牌数占总数的775712=+，则共有732096128⎛⎫÷-= ⎪⎝⎭（张）牌，此时阿呆有7965612⨯=（张）牌.自我巩固1.把一批面粉分给三个工厂，甲厂先分得这批面粉的25，乙厂分得余下的25，最后丙厂分得14.45吨，这批面粉共重________吨. 【答案】40【解析】23214.4140555⎛⎫÷--⨯= ⎪⎝⎭（吨）.2.某校五年级人数是四年级的54，六年级人数是五年级的67，那么六年级人数是四年级的________. A.1514 B.528C.1114【答案】A【解析】设四年级人数是“1”，则五年级是54，所以六年级人数是四年级的56154714⨯=. 3.某年级分成三队，二队人数是一队人数的34，三队人数是一队人数的54，那么一队人数占全部的________. A.1516 B.35 C.13【答案】C【解析】设一队人数是“4”，则二队人数是“3”，三队人数是“5”，所以一队人数占全部的41 3453=++.4.甲数比乙数大18，丙数比乙数小18，那么丙数占三个数总和的________.A.124B.724C.78【答案】B【解析】设乙数是“8”，则甲数是“9”，丙数是“7”，所以丙数占三个数总和的77 98724=++.5.一瓶油第一次用去15，第二次用去余下的34，这时瓶内还有15千克，这瓶油原来有________千克.【答案】1【解析】1143115554⎛⎫÷--⨯=⎪⎝⎭（千克）.6.修一条公路，第一周修了全长的14，第二周修的长度只有第一周的45，比第一周少修了45米，第一周修了________米. 【答案】225【解析】公路全长：11445900445⎛⎫÷-⨯=⎪⎝⎭（米），那么第一周修了19002254⨯=（米）.7.在一个城市中，小学生人数是居民的15，大学生人数是小学生的14，那么大学生人数是居民的________.A.15B.14C.120【答案】C【解析】设居民人数是“1”，则小学生人数是15，所以大学生人数是居民的1115420⨯=.8.有一块披萨，阿瓜吃了其中的12，乐乐吃了剩下的45，最后还剩50克，那么这块披萨共_________克.【答案】500【解析】乐乐吃了全部的1421255⎛⎫-⨯=⎪⎝⎭，所以这块披萨共1250150025⎛⎫÷--=⎪⎝⎭（克）.9.兄弟三人合作修路，老大修了另外两人总数的一半，老二修了另外两人总数的14，老三修了91米，那么兄弟三人一共修了________米. 【答案】195【解析】1191119535⎛⎫÷--=⎪⎝⎭（米）.10.某煤矿去年第一季度采煤量是其它季度采煤量的523，第二季度采煤量是其它季度采煤量的311，第三季度采煤量是其它季度采煤量的25，第四季度采煤180吨，则该煤矿去年采煤________吨.【答案】560【解析】设该煤矿去年采煤量为单位“1”，则第一季度占总量的5235+，第二季度占总量的3113+，第三季度占总量的225+，那么第四季度占总量的532912814728---=，所以该煤矿去年采煤918056028÷=（吨）.课堂落实1.已知甲数是乙数的56，乙数是丙数的35，那么甲数是丙数的________.A.12B.13C.14【答案】A2.乙数比丙数多13，甲数比丙数少13，那么丙数占三个数之和的________.A.13B.14C.15【答案】A3.有一车西瓜，第一天卖掉全部的15，第二天卖掉剩下的34，此时还剩120千克，那么原来一共有________千克西瓜. 【答案】6004.兄弟三人合作修路，老大修了另外两人总数的14，老二修了另外两人总数的13，老三修了220米，那么这条路长________米. 【答案】4005.亮亮读一本科普读物，第一周读完了25，第二周读了剩下的12.最后还剩30页没有读，那么这本科普读物共________页. 【答案】100。

一、选择题1．一个围棋兴趣小组，有男生7人，女生5人，后来又有2个男生、1个女生加入．现在男生占全小组人数的（ ）A. 712B. 715C. 915D. 914C解析： C【解析】【解答】解：（7+2）÷（7+5+2+1）＝915， 所以现在男生占全小组人数的915。

故答案为：C 。

【分析】现在男生占全小组人数的几分之几=（原来男生的人数+加入男生的人数）÷加入男、女生之后的总人数。

2．一批汽车．第一次售出库存的 12，第二次售出剩下的 12，结果还剩下全部库存的（ ）A. 13B. 14C. 12D. 没有库存了B解析： B【解析】【解答】（1﹣ 12）×（1﹣ 12）＝ 12 × 12＝ 14故答案为：B 。

【分析】根据题意可知，把这批汽车的总量看作单位“1”，先求出剩下的量，单位“1”-第一次售出的占库存的分率=剩下的量，然后用剩下的量×（1-第二次售出的占剩下的分率）=剩下的占库存的分率，据此列式解答。

3．若a 是非零自然数，则下列算式中计算结果最大的是（ ） A. a× 37B. a÷ 37C. a+ 37D. a- 37B解析： B【解析】【解答】选项A ，因为37＜1，所以a×37＜a ；选项B ，因为37＜1，所以a÷37＞a ，大约是2.3a ；选项C ，a+37＜2.3a ； 选项D ，a-37＜a 。

故答案为：B 。

【分析】①在乘法里，一个非0数乘小于1的非0数，积小于这个数，一个非0数乘大于1的数，积大于这个数，据此比较大小；②在除法里，一个非0数除以小于1的非0数，商大于被除数，一个非0数除以大于1的数，商小于被除数，据此判断。

4．一个非零自然数与它的倒数和是20.05，这个自然数是（ ）A. 120B. 21C. 20D. 121C解析： C【解析】【解答】20.05=20120 ， 则这个自然数为20。