第三章 电阻电路的一般分析课本分部习题
- 格式:doc
- 大小:457.00 KB
- 文档页数:24

§3-1 叠加定理3-l 电路如题图3-l 所示。
(1)用叠加定理计算电流I 。
(2)欲使0=I,问S U 应改为何值。
题图3-1解:(1)画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得A3 A1633 A 263V 18"'"'=+==Ω+ΩΩ==Ω+Ω=I I I I I(2)由以上计算结果得到下式V 9A 1)9(0A 191 S S "'-=⨯Ω-==+⨯Ω=+=U U I I I3-2用叠加定理求题图3-2电路中电压U 。
题图3-2解:画出独立电流源和独立电压源分别单独作用的电路如图(a)和图(b)所示。
由此求得V8V 3V 5 V3V 9)363V 53A 3)31(55 "'"'=+=+==⨯Ω+ΩΩ==Ω⨯⨯Ω+Ω+ΩΩ=U U U U U3-3用叠加定理求题图4-3电路中电流i 和电压u 。
题图3-3解:画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得V )3cos 104( A )3cos 52( V3cos 10)2(A 3cos 53cos 1232332321554V V 8636326363 A 263632V8 "'"'"""''t u u u t i i i t i u t t i u i +=+=-=+==Ω-=-=⨯+-⨯+⨯++==⨯Ω+⨯+ΩΩ+⨯==Ω+⨯+Ω=3-4用叠加定理求题图3-4电路中的电流i 和电压u 。
题图3-4解:画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得V 3V 6V 3 A 3A 2A 1V 6)-A 4(3A 26V 12 1 0A)4(321 KVL )b (V33A 16V 6 1 0V 62)31( KVL )a ("'"'"""""1""1"'''''1'1'=+-=+==+=+==⨯Ω==Ω=⨯Ω==-⨯Ω++⨯Ω-=⨯Ω-==Ω=⨯Ω==-+Ω+Ωu u u i i i i ui i u i u i i u i i u u i 最后得到得到代入方程电路列出图得到代入方程电路列出图3-6用叠加定理求题图3-6电路中电流i 。



第3章电阻电路的一般分析3.1 复习笔记一、电路图论的基本概念1.图(G)图(G)是具有给定连接关系的结点和支路的集合,其中每条支路的两端都连到相应的结点上,允许孤立结点的存在,没有结点的支路不能称为图。
路径:从G的一个结点出发,依次通过图的支路和结点(每一支路和结点只通过一次),到达另一个结点(或回到原出发点),这种子图称为路径。
连通图:当G的任意两结点都是连通的,称G为连通图。
有向图:赋予支路方向的图称为有向图。
2.树(T)满足下列三个条件的子图,称为G的一棵树:①连通的;②包含G的全部结点;③本身没有回路。
树支与连支:属于树的支路称为树支;不属于树的支路称为连支。
基本回路:对于G的任意一个树,有且只有一条连支回路,这种回路称为单连支回路或基本回路。
树支数:对于有n个结点,b条支路的连通图,树支数=n-1。
推论:连枝数=b-n+1;基本回路数=连支数=b-n+1。
二、KCL和KVL的独立方程数KCL的独立方程数:对一个具有n个结点的电路而言,其中任意的(n-1)个结点的KCL方程是独立的。
KVL的独立方程数:对一个具有n个结点和b条支路的电路而言,其KVL的独立方程数为(b-n+1)。
三、电路的分析方法1.支路电流法(1)支路电流法是以b个支路电流为变量列写b个方程,并直接求解。
其方程的一般形式为(2)支路电流法解题步骤①标出各支路电流的方向;②依据KCL列写(n-1)个独立的结点方程;③选取(b-n+1)个独立回路,标出回路绕行方向,列写KVL方程。
注:①独立结点选择方法:n个结点中去掉一个,其余结点都是独立的;②独立回路选择方法:先确定一个树,再确定单连支回路(基本回路),仅含唯一的连支,其余为树支。
2.网孔电流法(1)网孔是最简单的回路,即不含任何支路的回路。
网孔数=独立回路数=b-n+1。
网孔电流法是以网孔电流为未知量,根据KVL对全部网孔列出方程求解。
(2)网孔电流法解题步骤①局部调整电路,当电路中含有电流源和电阻的并联组合时,可转化为电压源和电阻的串联组合;②选取网孔电流,指定网孔电流的参考方向;③依据KVL列写网孔电流方程,自阻总为正,互阻视流过的网孔电流方向而定,两电路同向取“+”,异向取“-”。

第一章 电路模型和电路定律1.1 图示元件当时间t <2s 时电流为2A ,从a 流向b ;当t >2s 时为3A ,从b 流向a 。
根据图示参考方向,写出电流i 的数学表达式。
1.2图示元件电压u =(5-9e -t /τ)V ,τ >0。
分别求出 t =0 和 t →∞ 时电压u 的代数值及其真实方向。
babu +-图 题1.21.3 图示电路。
设元件A 消耗功率为10W ,求A u ;设元件B 消耗功率为-10W,求B i ;设元件C 发出功率为-10W ,求C u 。
Au +-10V+-Cu +-(a)(b)(c)图 题1.31.4求图示电路电流4321i i i i 、、、。
若只求2i ,能否一步求得?图 题1.41i 4i 3i 图 题1.51.5 图示电路,已知部分电流值和部分电压值。
(1) 试求其余未知电流1234,,,i i i i 。
若少已知一个电流,能否求出全部未知电流?(2) 试求其余未知电压 u 14、u 15、u 52、u 53。
若少已知一个电压,能否求出全部未知电压?1.6 图示电路,已知A 21=i ,A 33-=i ,V 101=u ,V 54-=u 。
求各元件消耗的功率。
图 题1.61uSu (a)(b)图 题1.71.7 图示电路,已知10cos()V S u t ω=,8cos()A S i t ω=。
求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。
1.8 求图示电路电压12,u u 。
1u +-2u +-图 题1.830u-+图 题1.91.9 求图示电路两个独立电源各自发出的功率。
1.10 求网络N 吸收的功率和电流源发出的功率。
10V0.5A8V1.11 求图示电路两个独立电源各自发出的功率。
1.12 求图示电路两个受控源各自发出的功率。
1.13 图示电路,已知电流源发出的功率是12W ,求r 的值。
1V图 题1.13图 题1.141V2V1.14 求图示电路受控源和独立源各自发出的功率。
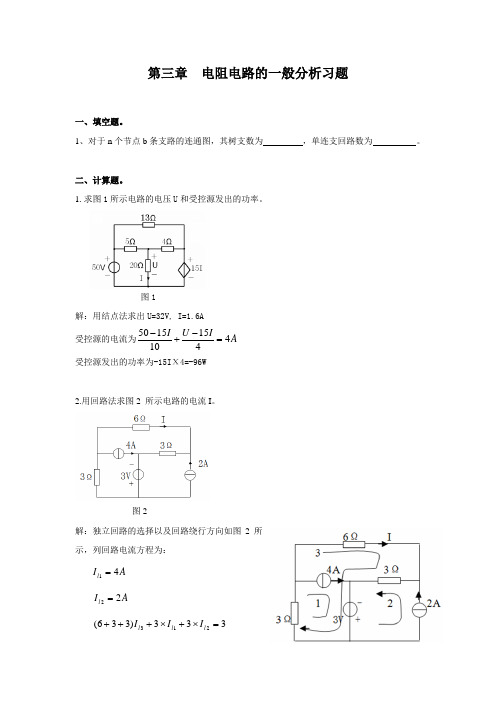
第三章 电阻电路的一般分析习题一、填空题。
1、对于n 个节点b 条支路的连通图,其树支数为 ,单连支回路数为 。
二、计算题。
1.求图1所示电路的电压U 和受控源发出的功率。
图1解:用结点法求出U=32V, I=1.6A 受控源的电流为A IU I 4415101550=-+- 受控源发出的功率为-15I Χ4=-96W2.用回路法求图2 所示电路的电流I 。
图2解:独立回路的选择以及回路绕行方向如图2所示,列回路电流方程为: A I l 41= A I l 22=333)336(213=⨯+⨯+++l l l I I I求得:A I l 25.112153-=-= 即有 A I I l 25.13-==3.图3所示电路,用回路法求I 。
图3解:由图列回路电流方程:⎩⎨⎧-⨯=-=⨯-⨯-++)5(24252)222(11I u u I解的 I=2A4.图4所示,以0为参考点,列出结点①②③的结点电压方程。
图4解:41231237377123334554123755676724411111()11111()011111()s S rI V V V I R R R R R R R V V V R R R R R U rI V V V R R R R R R R V I R ⎧++--=-⎪+⎪⎪-+++-=⎪⎪⎨⎪--+++=+⎪⎪⎪=⎪⎩5.分别列出如图5所示电路的网孔电流ia 、ib 、ic 的网孔电流方程和结点A 、B 、C 的结点电压方程。
图56.列写如图6所示电路的网孔方程(网孔方向为顺时针)和节点方程(以④为参考节点)。
+_1Ω1Ω1Ω10V 3U 1图6①②③1V _1Ω++_Ω+_U 1解:网孔方程: 12312311231303134103I I I I I I U I I I U --=-+-=---+=+ 补充方程:121U I =-+节点方程: 1231231123311332.55U U U U U U U U U U --=-+-=--+=-7.写出如图7所示电路的网孔方程(网孔电流I 1,I 2)。
第三章 电阻电路的一般分析一、是非题 (注:请在每小题后[ ]内用"√"表示对,用"×"表示错).1. 利用节点KCL方程求解某一支路电流时,若改变接在同一节点所有其它已知支路电流的参考方向,将使求得的结果有符号的差别。
[×] .2. 列写KVL方程时,每次一定要包含一条新支路才能保证方程的独立性。
[√] .3. 若电路有n个节点,按不同节点列写的n-1个KCL方程必然相互独立。
[√] .4. 如图所示电路中,节点A的方程为: (1/R 1 +1/ R 2 +1/ R 3)U =I S +US /R 3 [×]解:关键点:先等效,后列方程。
图A 的等效电路如图B :节点A的方程应为: 332)11(R U I U R R S S A +=+ .5. 在如图所示电路中, 有 12232/1/1/S S A I U R U R R +=+ [√]解:图A 的等效电路如图B :.6. 如图所示电路,节点方程为:12311()S S G G G U GU I ++-=; 3231S G U G U I -=; 13110GU GU -=. [×]解:图A 的等效电路如图B :S S U G I U G G 1121)(+=+.7. 如图所示电路中,有四个独立回路。
各回路电流的取向如图示, 则可解得各回路 电流为: I1=1A;I2=2A; I3=3A;I4=4A。
[×] 解:;11A I = ;22A I =;33A I = ;7344A I =+=二、选择题(注:在每小题的备选答案中选择适合的答案编号填入该题空白处,多选或不选按选错论).1.对如图所示电路,下列各式求支路电流正确的是 C_。
(A) 12112E E I R R -=+; (B) 222E I R =(C) AB L LUI R =.2. 若网络有b 条支路、n 个节点,其独立KCL方程有_C_个,独立KVL方程有_D__个,共计为_A_个方程。
第三章电阻电路的一般分析电路的一般分析是指方程分析法,它是以电路元件的约束特性(VCR)和电路的拓扑约束特性(KCL,KVL)为依据,建立以支路电流或回路电流,或结点电压为变量的回路方程组,从中解出所要求的电流、电压、功率等。
方程分析法的特点是:(1)具有普遍适用性,即无论线性和非线性电路都适用;(2)具有系统性,表现在不改变电路结构,应用KCL,KVL,元件的VCR建立电路变量方程,方程的建立有一套固定不变的步骤和格式,便于编程和用计算机计算。
本章的重点是会用观察电路的方法,熟练运用支路法、回路法和结点电压法的“方程通式”写出支路电流方程、回路方程和结点电压方程,并加以求解。
3-1 在一下两种情况下,画出图示电路的图,并说明其节点数和支路数(1)每个元件作为一条支路处理;(2)电压源(独立或受控)和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理。
解:(1)每个元件作为一条支路处理时,图(a)和(b)所示电路的图分别为题解3-1图(a1)和(b1)。
图(a1)中节点数6=n,支路数11=b图(b1)中节点数7=n,支路数12=b(2)电压源和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理时,图(a)和图(b)所示电路的图分别为题解图(a2)和(b2)。
图(a2)中节点数4=n,支路数8=b图(b2)中节点数15=n,支路数9=b3-2指出题3-1中两种情况下,KCL,KVL独立方程数各为多少?解:题3-1中的图(a)电路,在两种情况下,独立的KCL方程数分别为(1)5161=-=-n (2)3141=-=-n独立的KVL方程数分别为(1)616111=+-=+-nb (2)51481=+-=+-nb图(b)电路在两种情况下,独立的KCL方程数为(1)6171=-=-n (2)4151=-=-n独立的KVL方程数分别为(1)617121=+-=+-nb (2)51591=+-=+-nb3-3对题图(a)和(b)所示G,各画出4个不同的树,树支数各为多少?解:一个连通图G的树T是这样定义的:(1) T包含G的全部结点和部分支路;(2) T本身是连通的且又不包含回路。
根据定义,画出图(a)和(b)所示图G的4个树如题解3-3图(a)和(b)所示。
树支数为结点数减一。
故图(a)的数有树支,图(b)的树有树支1615n -=-=3-4 图示桥形电路共可画出16个不同的树,试一一列出(由于节点树为4,故树支为3,可按支路号递减的方法列出所有可能的组合,如123,124,…,126,134,135,…等,从中选出树)。
解:图示电路,16个不同的树的支路组合为:(123),(124),(125),(136),(145), (146),(156),(234),(235),(236),(246), (256),(345),(346),(456)3-5 对题图3-3所示的1G 和2G ,任选一树并确认其基本回路组,同时指出独立回路数和网孔数各为多少?解:在连通图G 中,由树支和一个连支组成的回路称为G 的基本回路(或单连支回路),基本回路是独立回路,网孔也是独立回路,因此,基本回路数=独立回路数+网孔数。
对一个节点数为n ,支路数为b 的连通网,其独立回路数)1(+-=n b l。
从题图3-3所示的1G 和2G 中任选一树,(见题解3-5图(a)和(b)中粗线所示),对应于这一树的基本回路分别为6,521==l l 。
3-6 对图示非平面图,设:(1)选择支路(1,2,3,4)为树;(2)选择支路(5,6,7,8)为树,问独立回路各有多少?求其基本回路组。
解:图中有结点数5=n,支路数10=b ,故独立回路树为615101=+-=+-n b(1)选择支路(1,2,3,4)为树,对应的基本回路组为:(1,2,3,4,5),(1,2,3,7),(1,2,6),(2,3,4,8),(2,3,9),(3,4,10)(2)选择支路(5,6,7,8)为树,对应的基本回路组为:(1,5,8),(2,5,6,8),(3,6,7),(4,5,7),(5,7,8,9),(5,6,10)3-7图示电路中Vu V u R R R R R R s s 40,20,2,8,4,1063654321==Ω=Ω==Ω=Ω==,用支路电流法求解电流5i 。
解:本题电路有4个节点,6条支路,独立回路数为6-4+1=3。
设各支路电流和独立回路绕行方向如图所示,由KCL 列方程,设流出节点的电流取正号。
节点①0621=++i i i节点② 0432=++-i i i 节点③0654=-+-i i i 由KVL 列方程回路Ⅰ 401082246-=--i i i 回路Ⅱ 2041010321-=++-i i i 回路Ⅲ20884543=++-i i i联立求解以上方程组,得电流A i 956.05-=注:由本题的求解过程可以归纳出用支路电流法分析电路的步骤如下: (1)选定各支路电流的参考方向;(2)任取(n-1)个结点,依 KCL 列独立结点电流方程;(3)选定(b-n+1)个独立回路(平面回路可选网孔),指定回路的绕行方向,根据KVL 列写独立回路电压方程;(4)求解联立方程组,得到个支路电流,需要明确:以上支路电流法求解电路的步骤只适用于电路中每一条支路电压都能用支路电流表示的情况,若电路中含有独立电流源或受控电流源,因其电压不能用支路电流表示,故不能直接使用上述步骤。
此外,若电路中含有受控源,还应将控制量用支路电流表示,即要多加一个辅助方程。
3-8 用网孔电流法求解题图3-7中电流5i 。
解:设网孔电流为1,23,l l l i i i ,其绕行方向如题图3-7中所标。
列写网孔方程⎪⎩⎪⎨⎧=+---=-+--=--20204820424104081020321321321l l l l l l l l l i i i i i i i i i应用行列式法解上面方程组48802048202410401020,5104204842410810203-=------=∆=------=∆所以A i i l 956.051044880335-=-=∆∆==注:网孔电流法是以假想的网孔电流作为求解量,它仅适用于平面电路。
从本题的求解可以归纳出用网孔电流法求解电路的步骤是: (1)选取网孔电流1,23,l l l i i i ,如网孔电流方向即认为是列网孔 KVL 方程的绕行方向。
(2)列网孔电流方程。
观察电路求自电阻1122,R R (一个网孔中所有电阻之和称该网孔的自电阻,如本题中11223320,24,20R R R =Ω=Ω=Ω,自电阻总为正值);互电阻121323,,R R R (两网孔公共支路上的电阻之和,如本题中12132310,8,4R R R =-=-=-,当流过互电阻的两网孔电流方向一致,互电阻为正值,否则为负值),等效电压源数值(方程右方为各回路中电压源的代数和,与网孔电流方向一致的电压源前取负号,否则取正号)。
3-9 用回路电流法求解题图3-7中电流3i 。
解法一:取回路电流为网孔电流,如题图3-7中所示。
回路方程同题3-8中方程。
故有488051043-=∆=∆128002020842010840203-=------=∆所以A i i i Ai A i l l l l 5517.19561.05078.29561.0510448805078.25104128003233322-=+-=-=-=-=∆∆=-=-=∆∆=解法二:取回路电流如题解3-9图所示。
仅让Ⅱ号回路电流流经3i 所在的支路。
列写回路方程。
⎪⎩⎪⎨⎧=++--=++--=--03620182020241040181020321321321l l l l l l l l l i i i i i i i i i用行列式法求上面方程组79203618202010184020,51043620182024101810202-=-----=∆=----=∆所以A i i l 5517.151047920223-=-=∆∆==显然解法二中回路电流的选取法使计算量减小。
注:回路电流法适用于平面或非平面电路,比网孔法更具灵活性。
回路法分析电路时,首先要确定一组基本回路,表定回路电流的绕行方向,其余步骤与网孔法类似。
需要指出的是回路电流法中两回路的共有支路有时会有多条,因而互有电阻的确定要特别细心。
否则会发生遗漏互有电阻的错误。
3-10 用回路电流法求解题图中Ω5电阻中的电流i 。
解:选取网孔为基本回路,回路电流的绕行方向如图中所示。
列回路方程⎪⎩⎪⎨⎧=+-=-+-=+-=-016848817601648326123232121l l l l l l l i i i i i i i应用行列式法460808481760612 ,19201680817606123=---=∆=----=∆所以 A i i l 4.21920460833==∆∆==3-11 用回路电流法求解图示电路中电压o U 。
解:回路电流如图中所标。
因A 3电流源仅与回路Ⅰ相关,即有,A i l 31=其余两回路的方程为865013620101813610508321321=-=++-=++-l l l l l l i i i i i i把A i l 31=带入两个方程中,加以整理得⎩⎨⎧=+=+140201016010503232l l l l i i i i解得 A i l 22=电压Vi U l o 80240402=⨯=⨯=3-12 用回路电流法求解图示电路中电压U 。
解:按图示设网孔电流为回路电流。
因受控电流源仅和Ⅲ号回路相关,故有1615n -=-=,对回路Ⅰ和Ⅱ列方程,并代入131.0l l i i -=有⎩⎨⎧-=⨯++-=⨯+-4201.0510401.010*********l l l l l l i i i i i i整理得⎩⎨⎧-=+-=-420105.304352121l l l l i i i i解得A i i A i i i l l l l l 5.0)5(1.01.053575.43435475.4313222=-⨯-=-=-=⨯-=⨯=-=选外层回路列KVL 方程 042012021=-+⨯+U i i l l从中解出 V U 25.276420)75.43(1)5(20=+-⨯+-⨯=3-13 用回路电流法求解题图(a),(b)两电路中每个元件的功率,并做功率平衡检验。
解(a):选取(a)图中网孔为基本回路,回路电流方向如图中所标,列回路方程⎪⎪⎩⎪⎪⎨⎧==++⨯-=ϕU i i i i i l l l l l 41102311533211 )3()2()1(式中ϕU 为受控电流源的控制量,需要用回路电流加以表示,所以增补一个方程3324)(2l l l i i i U =+⨯=ϕ )4(从中解得32l l i i =把方程)1(和)4(代入方程)2(中,有10231522=++-l l i i即 Ai i l l 552532===各元件的功率分别为V 10电压源发出的功率W i p l 505101021=⨯=⨯=A 15电流源发出功率[][]Wi i i i p l l l l 105010120315 )(1)(31521312=⨯+⨯⨯=-⨯++⨯⨯=受控电流源发出功率[][]W i i U i i U p l l l l 400)2060(54203 )(34133313=+⨯=⨯+⨯⨯=++⨯⨯=ϕϕ三个电阻消耗的功率Wi i i i i i p l l l l l l 1500203102101 )(3)(2)(12223132221=⨯+⨯+⨯=+⨯++⨯+-⨯=吸 电路共发出功率 Wp p p p1500400105050321=++=++=发满足 吸发p p=解(b):解法一:取网孔为基本回路,电路电流如图(b)中所标。