4-2简谐振动例题阻尼受迫振动
- 格式:pdf
- 大小:693.74 KB
- 文档页数:38

第4章 机械振动基本要求1.掌握描述简谐振动的振幅、周期、频率、相位和初相位的物理意义及之间的相互关系2.掌握描述简谐振动的解析法、旋转矢量法和图线表示法,并会用于简谐振动规律的讨论和分析3.掌握简谐振动的基本特征,能建立一维简谐振动的微分方程,能根据给定的初始条件写出一维简谐振动的运动方程,并理解其物理意义4.理解同方向、同频率简谐振动的合成规律,了解拍和相互垂直简谐振动合成的特点基本概念1.简谐振动 离开平衡位置的位移按余弦函数(或正弦函数)规律随时间变化的运动称为简谐振动。
简谐振动的运动方程 cos()x A t ωϕ=+2.振幅A 作简谐振动的物体的最大位置坐标的绝对值。
3.周期T 作简谐振动的物体完成一次全振动所需的时间。
4.频率ν 单位时间内完成的振动次数,周期与频率互为倒数,即1T ν=5.圆频率ω 作简谐振动的物体在2π秒内完成振动的次数,它与频率的关系为22Tπωπν== 6.相位和初相位 简谐振动的运动方程中t ωϕ+项称为相位,它决定着作简谐振动的物体状态;t=0时的相位称为初相位ϕ7.简谐振动的能量 作简谐振动的系统具有动能和势能。
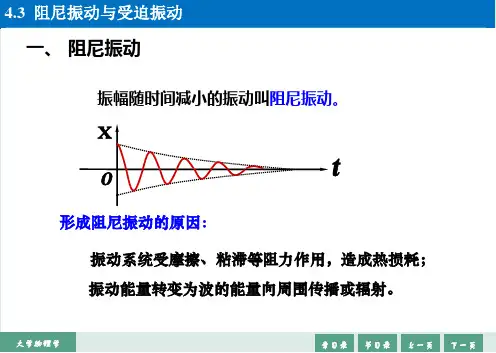
弹性势能222p 11cos ()22E kx kA t ωϕ==+动能[]22222k 111sin()sin ()222E m m A t m A t ωωϕωωϕ==-+=+v弹簧振子系统的机械能为222k p 1122E E E m A kA ω=+==8.阻尼振动 振动系统因受阻尼力作用,振幅不断减小。
9.受迫振动 系统在周期性外力作用下的振动。
周期性外力称为驱动力。
10.共振 驱动力的角频率为某一值时,受迫振动的振幅达到极大值的现象。
基本规律1.一个孤立的简谐振动系统的能量是守恒的物体做简谐振动时,其动能和势能都随时间做周期性变化,位移最大时,势能达到最大值,动能为零;物体通过平衡位置时,势能为零,动能达到最大值,但其总机械能却保持不变,且机械能与振幅的平方成正比。

【实验目的】1.观测阻尼振动,学习测量振动系统基本参数的方法。
2.研究受迫振动的幅频特性和相频特性,观察共振现象。
3.观察不同阻尼对受迫振动的影响。
【实验原理】当摆轮受到周期性强迫外力矩t M M ωcos 0=的作用,并在有空气阻尼的媒质中运动时(阻尼力矩为 ),其运动方程为t M dt d b k dtd J ωθθθcos 022+--= (1)其中,J 为摆轮的转动惯量,θk -为弹性力矩,0M 为强迫力矩的幅值,ω为强迫力的圆频率。
令J k =20ω,J b=β2,JM m 0=,则(1)式变为 t m dt d dtd ωθωθβθcos 22022=++ (2) 其中,β为阻尼系数,0ω为系统的固有频率,m 为强迫力矩。
当0cos =t m ω时,(2)式即为阻尼振动方程,当0=β,即在无阻尼情况时,(2)式变为简谐振动方程。
方程(2)的通解为()()0201cos cos ϕωθαωθθβ+++=-t t e t (3)由(3)式可见,受迫振动可分为两部分:第一部分,()αωθβ+-t e t 01cos 表示阻尼振动,经过一定时间后衰减消失。
第二部分,说明强迫力矩对摆轮作功,向振动体传递能量,最后达到一个稳定的振动状态,其振幅为()22222024ωβωωθ+-=m(4)它与强迫力矩之间的相位差ϕ为()2022022012T T T T tg -=-=-πβωωβωϕ (5) 由(4)式和(5)式可看出,振幅2θ与相位差ϕ的数值取决于强迫力矩m 、频率ω、固有频率0ω和阻尼系数β四个因素,而与振动起始状态无关。
由()[]04222220=+-∂∂ωβωωω极值条件可得出,当受迫力的圆频率2202βωω-= 时产生共振,θ有极大值。
若共振时的圆频率和振幅分别用r ω 、r θ表示,则dtd b θ-2202βωω-=r (6)2222βωβθ-=m r (7)(6)式和(7)式表示,阻尼系数β越小,共振时圆频率越接近于系统固有频率,振幅也越大。


阻尼振动与受迫振动教学设计一、引言振动是物理学中的一个重要概念,它广泛应用于工程、生物和环境等领域。
在振动的研究中,阻尼振动和受迫振动是两个重要的概念。
本文将从阻尼振动和受迫振动的基本概念入手,介绍它们的特点、公式及实验操作等内容。
二、阻尼振动1.基本概念阻尼振动指的是在有阻力存在时,弹簧质点做简谐运动时所产生的一种现象。
在阻尼振动中,弹簧质点会随着时间逐渐减小其幅度,并最后停止运动。
2.特点(1)幅度随时间逐渐减小;(2)周期不变;(3)频率不变;(4)相位不变。
3.公式阻尼振动可以用以下公式来描述:x(t) = A*e^(-γt)cos(ωt+φ)其中,x(t)表示弹簧质点的位移;A表示初始位移;γ表示阻力系数;ω表示角频率;φ表示相位差。
4.实验操作进行阻尼振动实验时需要使用弹簧、质点和振动台等设备。
具体实验步骤如下:(1)将弹簧固定在振动台上;(2)将质点挂在弹簧上方;(3)将质点向下拉,使其产生初始位移;(4)释放质点,观察并记录其运动过程;(5)通过数据处理得到阻尼系数γ。
三、受迫振动1.基本概念受迫振动是指在外力作用下,弹簧质点做简谐运动的一种现象。
在受迫振动中,外力的频率与系统的固有频率相同或接近。
2.特点(1)幅度随时间逐渐增大或减小;(2)周期不变;(3)频率不变;(4)相位差与外力有关。
3.公式受迫振动可以用以下公式来描述:x(t) = A*cos(ωt+φ)+B*cos(Ωt+θ)其中,x(t)表示弹簧质点的位移;A表示自由振幅;B表示强制振幅;ω表示自由角频率;Ω表示强制角频率;φ和θ分别表示自由振动和强制振动的相位差。
4.实验操作进行受迫振动实验时需要使用弹簧、质点、振动台和外力源等设备。
具体实验步骤如下:(1)将弹簧固定在振动台上;(2)将质点挂在弹簧上方;(3)将外力源连接到振动台上,并调节其频率和幅度;(4)观察并记录弹簧质点的运动过程;(5)通过数据处理得到自由角频率ω和强制角频率Ω。




153第4章 综合与提高实验思考与练习1.简述用共振干涉法、相位比较法测声速的原理、方法。
2.实验中信号发射器和示波器起到什么作用? 3.为什么换能器的发射面和接收面要保持平行? 4.用逐差法处理数据的优点是什么?4.2 受迫振动的研究振动科学是物理学的重要组成部分。
其中,受迫振动和共振问题的研究,不但在理论上涉及经典物理科学和现代物理科学的发展,而且在工程技术领域受到极大的重视并不断取得新的成果。
例如,在建筑、机械等工程问题中,经常须避免共振现象出现以保证工程质量。
但目前新研发的很多仪器和装置的工作原理又是基于各种共振现象的产生,在微观科学研究领域中,共振也已成为重要的研究手段,如利用核磁共振和顺磁共振研究物质结构等。
本实验以音叉振动系统为研究对象,用电磁激振线圈的电磁力作为驱动力使音叉起振,并以另一电磁线圈作为检测振幅传感器,观测受迫振动系统的振幅与驱动力频率之间的关系,以研究受迫振动与共振的现象及其规律。
【实验目的】1)研究音叉振动系统在周期性外力作用下振幅与驱动力频率的关系,测绘其关系曲线,并求出系统的共振频率和系统的振动锐度(和品质因数Q 值有关的参量)。
2)通过改变音叉双臂同一位置处所加金属块的质量,研究系统的共振频率与系统质量的关系。
3)通过测量音叉的共振频率,确定未知物体的质量,以了解音叉式传感器的工作原理。
【实验器材】THQGZ-2型智能受迫振动与共振实验仪、电子天平、十字螺钉旋具。
【实验原理】1.简谐振动与阻尼振动众所周知,弹簧振子、单摆、复摆、扭摆等振动系统做小幅度振动,在其所受各种阻尼力小到可以忽略的情况下,可视为简谐振动状态。
此类振动满足简谐振动方程2202d =0d x x tω+ (4-2-1)式(4-2-1)的解为00=cos(+)x A t ωϕ(4-2-2)以理想弹簧振子为例,其固有角频率0ω,其中,K 为弹簧的劲度系数,m 为振动系统的有效质量(本实验中01=+m m m ,0m 为双臂的质量,1m 为质量块的质量);振幅A 和初位相0ϕ与振动系统的初始状态有关;系统的振动周期02==2T ωπ,即振动周期仅与系统的质量及弹簧的劲度系数有关。


2、单自由度系统的有阻尼受迫振动单自由度系统的受迫振动理论单自由度系统的受迫振动理论(1)振动微分方程kOx②恢复力F e , 方向指向平衡位置O ,大小与偏离平衡位置的距离成正比。
kxF -=e ③黏性阻尼力F d , 方向与速度方向相反,大小与速度大小成正比。
d dd x xF cv ct=-=-物块的运动微分方程为:22d d sin()d d x x m kx c H t t tw =--+方程两边同除以m ,并令:(ω0, 固有角频率) , (δ, 阻尼系数),得到:mk =20w 2c md =2202d d 2sin()d d x x x h t t td w w ++=——有阻尼受迫振动微分方程的标准形式①激振力F , 简谐激振力。
sin()F H t w =H h m =解可以写成:12xx x =+x 1 对应齐次方程的通解; x 2 对应的是特解。
欠阻尼的情况下( δ<ω0),齐次方程的通解可写为:1e )t x A d q -=+特解可写为:)sin(2e w -=t b x ε表示受迫振动的相位角落后于激振力的相位角2、单自由度系统的有阻尼受迫振动单自由度系统的受迫振动理论将x 2 代入微分方程,得到:220sin()2cos()sin()sin()b t b t b t h t w w e d w w e w w e w --+-+-=将等式右边的h sin(ωt )做一个变换,得到:sin()sin[()]h t h t w w e e =-+cos sin()sin cos()h t h t e w e e w e =-+-代入微分方程,整理得到:)cos(]sin 2[)sin(]cos )([220=--+---e w e w d e w e w w t h b t h b 对任意瞬时t ,上式都必须是恒等式,所以有:cos )(220=--e w w h b 0sin 2=-e w d h b 2222204)(wd w w +-=hb 2202tan w w dwe -=于是,微分方程的通解为:e)sin()tx A b t d q w e -=++-式中,A 和θ为积分常数,由运动的初始条件确定。
机械振动中的简谐受迫振动机械振动是物体在受到外力作用下沿某一方向上周期性地来回振动。
其中一种重要的机械振动类型是简谐振动。
简谐振动是指物体在恢复力作用下以正弦或余弦函数的形式进行周期性振动的现象。
而受迫振动是指振动系统受到外部周期性作用力的影响而产生的振动。
一、简谐振动简谐振动是振动学的基本概念之一,广泛应用于物理学和工程学中。
在简谐振动中,物体的振动将以固定的频率和振幅进行周期性的往复运动。
简谐振动的特点有以下几点:1. 恢复力与位移成正比:在简谐振动中,恢复力与物体的位移成正比。
当物体偏离平衡位置时,恢复力将使物体向平衡位置回归。
恢复力的大小与物体的位移成正比,且方向与位移方向相反。
2. 反弹力恒定:简谐振动的恢复力是恒定的,即简谐振动系统的恢复力不随时间变化而改变。
3. 以正弦曲线进行描述:简谐振动的位移随时间变化的图像是正弦曲线或余弦曲线。
位移达到极大值或极小值时,速度和加速度都为零;位移过零点时,速度达到极大值或极小值,且方向相反。
二、受迫振动受迫振动是指振动系统受到外部周期性作用力的影响而产生的振动。
在受迫振动中,振动系统的固有频率与外力的频率相同或接近。
当外力频率接近振动系统的固有频率时,振动系统会出现共振现象。
受迫振动的特点如下:1. 振动系统受到周期性外力作用:受迫振动是振动系统受到外力作用下进行的振动。
外力可以是周期性变化的,可以是正弦函数或其他类型的周期性函数。
2. 外力频率与振动系统固有频率相近:受迫振动中,外力的频率与振动系统的固有频率相近,这将导致振动系统出现共振现象。
共振时,振幅会被进一步放大。
3. 外力对振动系统的影响:外力将改变振动系统的振幅和相位,振动系统的响应将随外力的变化而变化。
受迫振动在实际生活和工程中有着重要的应用。
例如,建筑结构在地震时的振动是一种受迫振动;无线电和电子设备中的电路振荡器也是受迫振动的例子。
结论机械振动中的简谐受迫振动是振动学中的重要概念。
阻尼振动与受迫振动●阻尼振动●受迫振动●共振1.阻尼振动实例a. 阻尼弹簧振子,阻力γγ其中。
实例b. RLC谐振电路或写作其中。
分析:引入阻尼将引起能量的减小,计算能量改变率,β(等于阻尼做功的功率)。
如果很小,基本上还是简谐振动,但由于能量消耗,振幅会逐渐减小,解的形式近似为:能量,β一个周期内能量的消耗率:其中称为品质因数(quality factor),简称值(Q factor)。
从数量级上讲,Q值就是把储存的能量衰减完,振子中能够振荡的次数。
(注:RLC谐振电路,)精确解:(a)弱阻尼()其中。
与近似分析的结果相比,只是频率有所减小。
(b)过阻尼()其中。
无振荡,呈指数衰减。
注意是的减函数,衰减速度随增大反而减慢。
(c)临界阻尼(),无振荡,但衰减最快。
2.受迫振动实例a. 驱动弹簧振子γ实例b. RLC串联电路非齐次线性方程解的一般形式:其中是原方程的一个解(称为特解),是齐次方程的任意解。
写成复数形式,令满足方程则满足方程令,其中所以可取称为稳态解,而把称为暂态解。
3.共振为简单起见,只讨论速度共振。
的振幅为性质:(1)驱动频率与固有频率相等()时,时速度振幅(或平均动能)最大,出现共振。
(2)共振时,速度与驱动力同相位,驱动一直做正功。
(3)驱动频率与固有频率相差越大,振幅(动能)越小,形成一个共振峰。
(4)Q值越大,共振峰越高,同时也越窄(对驱动频率的选择性越高)。
共振的应用:乐器、无线电接收、调Q激光、核磁共振与电子自旋共振等。
共振有时会造成破坏,需要避免。