线性系统理论作业

目录题目一 (2)（一）状态反馈加积分器校正的输出反馈系统设计 (2)(1)建立被控对象的状态空间模型，并判断系统性质 (2)(2)状态反馈增益矩阵和积分增益常数的设计 (4)(3)全维观测器设计 (6)(4)如何在闭环调速系统中增加限流环节 (8)（二）二次型最优全状态反馈控制和按负载扰动前馈补偿的复合控制系统设计 (8)(1)线性二次型最优全状态反馈设计 (8)(2)降维观测器设计 (13)题目二 (15)(1)判断系统是否存在最优控制律 (15)(2)非零给定点的最优控制设计和仿真分析 (16)(3)权矩阵的各权值对动态性能影响分析 (17)题目一（一）状态反馈加积分器校正的输出反馈系统设计 (1)建立被控对象的状态空间模型，并判断系统性质1)画出与题目对应的模拟结构图，如图1所示：图1原始系统结构图取状态变量为1x =n ，2x =d I ，3x =d u ，控制输入u=c u1222212333375375111T Le la la la s s s C x x T GD GD C x x x x RT T RT K xx u T T ⎧=-⎪⎪⎪=--+⎨⎪⎪=-+⎪⎩将已知参数代人并设输出y=n=1x ，得被控对象的状态空间表达式为L x Ax Bu ET y Cx=++=其中，237500039.768011=-3.696-17.85727.05600-588.235100T ela lala s C GD C A RT T RT T ⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦，000=023529.41s s B K T ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦，2375-30.4880=000GD E ⎡⎤-⎢⎥⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦，[]100C = 2)检查被控系统的结构性质判断系统能控性、能观性、稳定性 程序如下：A=[0 39.768 0;-3.696 -17.857 27.056;0 0 -588.235]; B=[0;0;23529.41];C=[1 0 0]; Qc=ctrb(A,B); Qo=obsv(A,C); L=length(A); if rank(Qc)==Ldisp('系统是状态完全能控'); elsedisp('系统是状态不完全能控'); endif rank(Qo)==Ldisp('系统是状态完全能观'); elsedisp('系统是状态不完全能观'); enddisp(eig(A))%利用A 的特征值判断系统稳定性 运行结果：系统是状态完全能控 系统是状态完全能观 1.0e+02 *-0.0893 + 0.0820i -0.0893 - 0.0820i -5.8823 + 0.0000i由于矩阵A 全部特征值均具有负实部，因此系统渐近稳定。

X 和模态矩阵 M。
4、求
2 0 A= 0 0
0 0 0 0
1 0 0 0
0 1 0 0
的特征值λ，特征向量 X 和模态矩阵 M。
5、将二次型 Q(Z)= 2 x1 x2 2 x1 x3 6 x2 x3 化为标准型。 6、将 Q= X
T
AX X 1
X2
2 5 X 1 8 X 3 2 11 2 X 2 5 2 8 X3
= 8 X 12 11X 22 8 X 32 4 X 1 X 2 10 X 1 X 3 4 X 2 X 3 化为标准型。 7、用求矩阵秩的程序，验证题 1、2
第 5 页 共 7 页
4、用叠加法对下图电路列状态方程。
第七、八章 习题 1、已知状态方程的系数矩阵 A(t)＝ 2、求离散系统状态方程齐次解
t 1 （级数取三项即可） ，求 (t ,0) 。 1 t
X 1 ( K 1) 1 5 1 X 1 ( K ) 2 , 其中X (0) 。 1 X 2 ( K 1) 12 1 5 X 2 ( K )
第九章 习题 1、一连续系统中 A= 和可观测性。 2、判断下图电路的能控性和能观性。
2 5 1 ，B= ，C= 1 4 0 1
1 ，试判断该系统的可控性
第 6 页 共 7 页
第十一章 习题 1、已知 X X ，用李氏第一方法和二次型法确定其稳定性。 1 1 2、用 LYAPUNOV 两种方法判断下面系统在原点的稳定性。已知系统方程 为：
4.求
2 X 1 X 2 3X 3 2
X1 2X 2 X 3 1

若 li 是 A 的特征值，试证 [1 li li 2 li n -1 ]T 是属于 li 的特征向量。 1—2 若 li 是 A 的一个特征值，试证 f (li ) 是矩阵函数 f (A) 的一个特征值。 1—3 试求下列矩阵的特征多项式和最小多项式
é l1 1 0 0 ù ê ú ê 0 l1 1 0 ú ê ú ê ú ê 0 0 l1 0 ú ê ú ê 0 0 0 l1 ú ë û é l1 1 0 0 ù ê ú ê 0 l1 0 0 ú ê ú ê ú ê 0 0 l1 0 ú ê ú ê 0 0 0 l1 ú ë û é l1 1 0 0 ù ê ú ê 0 l1 0 0 ú ê ú ê ú ê 0 0 l1 1 ú ê ú ê 0 0 0 l1 ú ë û
y =
t
ò0 g(t - t )u(t )d t
若脉冲响应 g 由图 1—12(a)给定。试问，由图 1—12(b)所示的输入而激励的输出为何？ g(t) 1 1 (a) 图 1—12 脉冲响应和输入作用 1—12 试求图 1—13 所示系统的动态方程式(略)
29
u(t) 1 2 t 1 2 (b) t
n >m
试证，给定初始状态 x(m ) = x0 下，时刻 n 的状态为 x(n )=F(n, m )x(0) 。若 A 与 n 无关，则
F(n, m ) 为何？
1—27 证明 x(n + 1) = A(n )x(n ) + B(n )u(n ) 的解为
n -1
x(n ) = F(n, m )x(m ) +
1 ù ú s+3ú 5s + 1 úú s + 2 úû
的实现，并画出其模拟图。 1—25 设{ A , B , C , D }和{ A , B , C , D }是两个线性时不变系统，其维数不一定相同。证明当 且仅当

2．(根据框图写出状态空间描述) 图2.2中描述了列车悬浮系统的工作原理，其中，1、2、3、 4为电磁装置，车辆通过电磁力的作用，悬浮于轨道上。磁悬浮控制系统的目的是通过调整 电磁作用力的输入，保证列车在运行过程中的平稳。这里我们考虑车辆运行过程中产在x和y 轴两个方向的位移，给出其线形化系统框图如图2.1所示
描述，其中g 是重力加速度常数，如图3所示，h 是自行车质心距地面高度，w 是两个轮子 与地面接触点的距离， b 是自行车质心投影与后轮和地面接触点的距离。 试给出该线性系统 的一个状态空间描述。
图3 参考文献： [3.1] Bicycles, motorcycles, and models-single-track vechicle modeling and control, IEEE Control Systems Magazine, October, 2006. 参考解答：
作业一
1．（线性化）已知倒立摆系统满足如下非线性状态方程
1 (t ) x2 (t ) x 2 (t ) ( g / l ) sin x1 (t ) u (t ) x
通过线性化给出系统在平衡解 [ x1 (), x2 ()] [0,0] ， u () 0 的邻域内的线性模型。 参考解答：
图 2.2
参考解答：
注意状态变量的维数. 3． （从传递函数得到状态方程描述）图3中给出了解释自行车姿态动态平衡的原理图示。在 前进速度保持为定常v 的假设下，车把转角 对车身姿态角 的作用在平衡点（ ＝0， ＝0）附近范围内可用微分方程

g v2 bv h hw wh
图2.1 这里A11=[100 0；0 200] B21=[10 -3；-5 16] C22=[1 1；1 -1]。 这里输入向量u是控制的作用力， 也就是车辆的加速度量， 输出向量y是车辆在两个轴方向的 位移量，通过间隙传感器测量。试列写出系统的状态空间模型。 参考文献： [2.1] H2 and H∞ control for MagLev vehicles，IEEE Control System Magazine, 1998 [2.2] Experimental comparison of linear and nonlinear controllers for a magnetic suspension, Proceedings of the 2000 IEEE International Conference on Control Applications，2000 [2.3] 广义线性磁悬浮对象的H∞控制问题，西安交通大学学报，Feb，2000

⎡ s +1 ⎢s2 + s +1 ⎢ −1 = [1 0 1]⎢ 2 ⎢s + s +1 ⎢ 0 ⎢ ⎣
9－7 设有三维状态方程
⎡0 ⎤ ⎢1 ⎥ ⎢ ⎥ ⎢ ⎣1 ⎥ ⎦
1 s + s +1 s 2 s + s +1
2
0
⎤ 0 ⎥ ⎥ ⎡0 ⎤ s 2 + 2 s 1⎥ = 3 0 ⎥ ⎢ ⎢ s −1 ⎥ ⎥ 1 ⎥ ⎢ ⎣1⎥ ⎦ s − 1⎥ ⎦
⎡ R M ⎤ ⎡ R −1 ∵⎢ ⎥×⎢ ⎣0 T ⎦ ⎣ 0
− R −1 MT −1 ⎤ ⎡ R −1 ⎥=⎢ T− ⎦ ⎣ 0
⎡R M ⎤ ∴⎢ ⎥ ⎣0 T ⎦
9－10 解
−1
⎡ R −1 =⎢ ⎣ 0
− R −1 MT −1 ⎤ ⎥ T −1 ⎦
−1
对可控标准形 A 和 b ，计算 ( sI − A) b
+
v2
& 2 = x1 + y = x1 − C 2 x
写成矩阵形式为
1 1 x2 + U R2 R2
图 9－1 RLC 网络
⎡ R1 − & x ⎡ 1 ⎤ ⎢ L1 ⎢x ⎥=⎢ ⎣ &2 ⎦ ⎢ 0 ⎢ ⎣
⎤ ⎡ 1 ⎤ 0 ⎥ x ⎡ ⎤ ⎢ L ⎥ ⎥ ⎢ 1 ⎥ + ⎢ 1 ⎥U − 1 ⎥ ⎣ x2 ⎦ ⎢ − 1 ⎥ ⎢ R2 C 2 ⎥ ⎦ ⎣ R2 C 2 ⎥ ⎦
x1 ， x 2 有下列关系存在 x1 = x1 + x 2 x 2 = − x1 − 2 x 2
试求系统在 x 坐标中的状态方程。 解 ①
&1 = x & = x2 x &2 = & & = −2 x1 − 3 x 2 + u x x

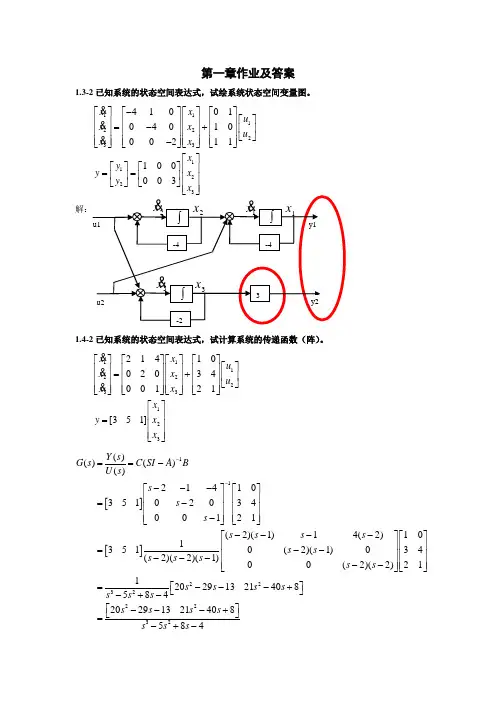
第一章作业及答案1.3-2已知系统的状态空间表达式，试绘系统状态空间变量图。

11122233112241001040100021110003xx u x x u x x x y y x y -⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦1.4-2已知系统的状态空间表达式，试计算系统的传递函数（阵）。

11122233123214100203400121[351]xx u x x u x x x y x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦[][]112232()()()()21410351020340121(2)(1)14(2)1013510(2)(1)034(2)(2)(1)00(2)(2)21120291321408584Y s G s C SI A B U s s s s s s s s s s s s s s s s s s s s s s --==----⎡⎤⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦----⎡⎤⎡⎤⎢⎥⎢⎥=--⎢⎥⎢⎥---⎢⎥⎢⎥--⎣⎦⎣⎦⎡⎤=---+⎣⎦-+-223220291321408584s s s s s s s ⎡⎤---+⎣⎦=-+-注意：也可写做[][][]23220212940138584s s s s s +--+--+-1.5-1已知系统传递函数，试用传递函数求出系统的状态空间模型。

2()35()()(3)(2)Y s s G s U s s s +==++解：通过赋予研究对象不同的内部结构可将传递函数转换成不同的状态空间模型。

（1）求出上述传递函数能控标准型表示由已知条件可知该传递函数为严格真分式，且该系统为单入单出（SISO ）三阶系统。

根据公式10111()...(),(1)()...mm mn n nY s b s b s b G s n m U s s a sa --+++===++++其中，可将传递函数写为223235035()(3)(2)82118s s s G s s s s s s +++==+++++其中，123012a 8,21,18,0,3,5a a b b b ======。

x 11 e t x 21 , 21 0 , x
x11 ( t 0 ) 1 x 21 ( t 0 ) 0
，
x 12 e t x 22 , 22 0 , x
x12 ( t 0 ) 0 x 22 ( t 0 ) 1
解得
x12 e t e t 0 x11 1 ， x 21 0 x 21 1 1 (t ) x 0 e
( sI A )
1
s ( s 1) 0 2 det( sI A ) s ( s 1) 0 adj ( sI A ) 1
s 1 ( s 1) 0
2
s ( s 1) 1 s ( s 1) 1 s 1 1
2
所以 e
。
可以看出， f ( i ) 是 f ( A ) 的一个特征值。
1-3 解：(1) 特征多项式为 1 ( ) ( 1 ) .
4
验证
A 1 I 0 , ( A 1 I ) 2 0 , ( A 1 I ) 3 0 , ( A 1 I ) 4 0
At
e t 1 1 L [( sI A ) ] 0 0
e 1 1 0
t
t t 1 e te t e 1 。 t e
1-5 证明：因为 D 1 存在，所以由 D R p p
A det C B IA det D 0 BD A I D C
c
k 0
k
A
k
设 x 是属于 i 的一个非零特征向量，故
A x i x
.
2 2 因此 A x A Ax A i x i Ax i i x i x .

三、求状态转移矩阵的几种方法
求的方法有时域的求解方法和频域的求解方法。 方法1：根据或者的定义直接计算：
=I+++…++…= 从公式可以看出，右边是一个无穷项的和，要精确计算出
结果是很困难的，所以无论是手工计算还是利用电脑计算，都 不可能取无穷项计算，通常是取有限项,得到一个近似的值， 以满足不同的精度要求即可.对于不同的精度要求，n的值会不 同。在工程上，只要取它的前几项就可以满足要求，本方法易 于理解，适合计算机编程。 方法2：利用拉氏反变换法求：
版本）正在进行着陆（速度V=16英里/小时）。描述飞机纵向 运动的状态空间方程
给出如下：
控制输入是升降舵角度和向量的状态变量分别是速度的变化， 迎角，俯仰速率和俯仰度。
该飞机的纵向模式称为短周期和长周期。在长周期特征 值，这也是一种复杂的共轭特征值接近虚轴，造成长周期运 动，在水平面缓慢地震荡。
二、状态转移矩阵的重要性与意义
线性系统理论大作业
专业：控制理论与控制工程 学号与姓名：
一、飞行器原理及结构和空间坐标系
为了进行控制系统设计的目的，飞机动力学经常称为飞行 姿态的一些操作状态进行线性化，它假设飞机的速度（马赫 数）和姿态是不变的。控制面（The control surfaces）和发动 机推力装置设置或修改，以达到这些状态，我们设计控制系统 就是为了维护这些条件，例如，强制将到这些状态的扰动（偏 差）变为零。
syms M s d1 t XT X0; A=[-0.0507 -3.861 0 -32.2;-0.00117 -0.5164 1 0;-0.000129 1.4168 -0.4932 0;0 0 1 0]; disp('矩阵A的行列式如下:'); d1=det(A); I=eye(4); disp('[sI-A]^(-1)为:'); B=(s*I-A); C=inv(B); digits(4) C=vpa(C) disp('状态转移阵为'); D=ilaplace(C); digits(4); M=vpa(D) X0=[0;0;0;0]; B=[0;-0.0717;-1.645;0]; XT=M*(X0+B) %求解系统的状态响应。 %画图 subplot(2,2,1) %画出x(t)d第一个分量X1(t),并把它显示在左上 角。 ezplot(XT(1,1),[0,2]) subplot(2,2,2) %画出x(t)d第二个分量X2(t),并把它显示在右上 角。 ezplot(XT(2,1),[0,2])

《线性系统理论》作业参考答案1-1 证明：由矩阵úúúúúúûùêêêêêêëé----=--121000001000010a a a a A n n nL M O M M M L L L则A 的特征多项式为nn n n n n n n n n n n n n n n n n na a a a a a a a a a a a a a a a a A I +++==+--++--=--++--=+--=--------+-----L L L M O MM ML LL L M O M M M L L L L M O MMM L L L112114322111321121)1()1(00001001)1()1(000010001000010001l l l l l l ll l l l l l l l l ll 若i l 是A 的特征值，则00001000010001)(1112121=úúúúúúûùêêêêêêëé+++=úúúúúúûùêêêêêêëéúúúúúúûùêêêêêêëé+--=-----n n i n i n i i i in n ni i i i i a a a a a a A I L M M L M O M M M L L L l l l l l l l l l u l 这表明[]Tn ii i121-l l l L 是i l 所对应的特征向量。

分数: ___________任课教师签字：___________ 华北电力大学研究生结课作业学年学期：2014-2015学年第一学期课程名称：线性系统理论学生姓名：学号：提交时间：2014年11月27日目录1.绪论 (1)2.球杆系统分析与建模 (1)2.1球杆模型简介 (1)2.2拉格朗日法建模 (1)2.3拉格朗日模型线性化及状态空间表达式求取 (4)3. 系统稳定性分析 (5)3.1有初始状态下求取系统响应曲线 (6)3.3稳定性判断并求取零极点分布图 (7)4.系统能控性判别 (8)4.1代数判据 (8)4.2模态判据 (8)4.3可控性与可稳定性 (10)5.系统极点配置 (10)5.1极点配置方法 (10)5.1.1状态反馈原理 (11)5.1.2输出反馈原理 (11)5.1.3PID配置极点原理 (12)5.1.4三种反馈对比 (12)5.2.用状态反馈进行极点配置 (12)6.可观性分析及带状态反馈的状态观测器的设计 (16)6.1能观性分析 (16)6.1.1代数判据 (16)6.1.2模态判据 (16)6.3全维观测器原理 (17)6.4全维状态观测器结构 (17)6.5全维状态观测器设计 (18)6.6全维状态观测器Simulink仿真 (18)6.7全维状态观测器在干扰下的性能研究 (20)7.总结 (22)1.绪论球杆系统是控制理论中很经典的一个模型，通常用来检验控制策略的效果，并且很多实际系统都可以近似抽象为球杆模型，因此，对球杆系统的研究很有意义，本文从球杆模型的拉格朗日法建模入手，对球杆系统稳定性，能控能观性等控制特性进行分析。

2.球杆系统分析与建模2.1球杆模型简介球杆系统由底座，直流伺服电机，光滑导轨，小球等组成，导轨在伺服电机的带动下转动，小球在自身重力的作用下沿着光滑的金属导轨自由滚动，球杆系统简图如下，其中x 是小球在导轨上相对于导轨中心的位移量，以导轨左侧为正，α是导轨相对于水平线的倾斜角。

xdot=zeros(2,1);
xdot(1)=-R/L*x(1)-1/L*x(2)+1/L*f(t);
xdot(2)=1/C*x(1);
function in=f(t)
in=(t>0)*2;
end
end
仿真求解状态方程代码如下：
L=1;
C=0.1;
R=1.5;
[t,x]=ode45('funcforex14',[-1,10],[0;1],[],R,L,C);
的根。方阵A有n个特征值；实际物理系统中，A为实数方阵，故特征值或为实数，或为成对共轭复数；如A为实数对称方阵，则其特征值都是实数。
4.2系统的不变量与特征值的不变性
同一系统，经非奇异变換后，得
公式(4.1)
其特征方程为
公式(4.2)
公式(4.1)与公式(4.2)形式虽然不同，但实际是相等的，即系统的非奇异变换，其特征值是不变的。可以证明如下：
xlabel('t/ms');ylabel('电压/V');title('系统响应');
[t,x]=ode45('funcforex13',[-1,10],[0;1],[],R,L,C);
figure(1);plot(t,x(:,1),'k');hold on;xlabel('time sec');
figure(1);plot(t,x(:,1),'r');hold on;xlabel('time sec');grid;
xlabel('t/ms');ylabel('电压/V');title('齐次性');

《线性系统理论》大作业报告引言：研究线性定常连续系统状态方程的解时，求解状态方程是进行动态系统分析与综合的基础，是进行定量分析的主要方法。

而线性定常连续系统状态方程的解由两个部分相加组成。

第一个部分是由初始状态所引起的自由运动，即状态的零输入响；第二个部分是由输入所引起的系统强迫运动,其值为输入函数与矩阵指数函数的卷积，即状态的零状态响应。

由于这两部分中都包含有状态转移矩阵，因此状态转移矩阵的计算是线性定常连续系统状态方程求解的关键。

本文先总结了的计算方法，并运用matlab命令求解证明各方法的正确性及给出相应的零输入响应仿真结果。

然后推导了脉冲响应的公式，希望通过飞机模型的例子来研究其系统的脉冲响应。

最后推广研究了任意输入的零状态响应。

第一部分的计算方法及零输入响应的仿真证明一．的计算方法1.根据的定义直接计算定义式是一个无穷级数，故在计算中必须考虑级数的收敛条件和计算收敛速度问题。

类似于标量指数函数，对所有有限的常数矩阵A和有限的时间t来说，矩阵指数函数这个无穷级数都是收敛的。

显然用此方法计算一般不能写成封闭的解析形式，只能得到数值计算的结果。

2.变换A为约旦标准型因为任何都可经线性变换成为对角矩阵或约旦矩阵，因此下面将利用对角矩阵和约旦矩阵的矩阵指数函数计算的简便性质，通过线性变换将一般形式的系统矩阵变换成对角矩阵或约旦矩阵计算其矩阵指数函数。

对于矩阵A，若经过非奇异变换（相似变换）矩阵Ｐ作变换后，有则3. 利用拉氏反变换求已知齐次方程两边取拉氏变换即对上式两边取拉氏反变换得齐次微分方程的解：而由定义法求得的齐次微分方程的解为比较两式得4. 应用凯莱—哈密顿定理求（1）由凯莱—哈密顿定理，方阵A 满足其自身的特征方程，即()1110 0n n n fA A a A a A a I--=++++=故121210...n n n n n A a A a A a A a I ----=-----它是的线性组合。

注：可能答案不唯一。 6*(选做)．试给出如图4系统的一个能控性的状态空间实现，并求其能控性指数。
图4
作业二
1．给定矩阵指数函数 e 如下，求出其系统矩阵A：
At
t 2 2 t e (cos 2t sin 2t ) e sin 2t 2 2 e At 3 2 t 2 t e sin 2t e (cos 2t sin 2t ) 2 2
图3 编队的控制可以分为内外两个控制回路， 外环回路通过编队的拓扑变化计算编队内各个飞机 的飞行轨迹， 内环回路则控制单架飞机按照外环控制回路给定的飞行轨迹飞行， 从而达到飞 行编队变换的目的。这里我们只考虑飞机横向飞行的姿态控制。取飞机的侧向飞行速度v， 飞机滚转速度p，和飞机的滚转角度 为状态变量，取飞机的副翼偏转控制量 a 和飞机的方 向舵偏转控制量 r 为输入。飞机的横向动力方程可以给出如下
[提示] 矩阵A可根据矩阵指数函数 e 的若干性质得到，参加教材相关章节；其中比较简洁 的方法是通过拉普拉斯变换。 参考解答：
At
2．对作业一中第2题中系统的状态空间模型（如图2）判断能控性和能观性。
C22
y,z
图2 这里A11=[100 0；0 200] B21=[10 -3；-5 16] C22=[1 1；1 -1]。[提示]在利用秩判据进行判断时， 有时候没有必要计算出Q矩阵的所有列或者行即可判断其是否满秩。 参考解答： 略 3．飞机自动编队飞行如图3所示。
1 0 1 1 0 0 1 0 x 0 1 u x 1 1 0 1 0
其中状态向量为 x v
p ，输入向量为 u a
T
r T 。试

分数: ___________任课教师签字：___________研究生结课作业学年学期：课程名称：线性系统理论学生姓名：学号：提交时间：目录1 前言 (1)2.1状态反馈控制 (1)2.2数学模型 (3)3 直流电动机调速系统的设计与仿真 (5)3.1系统的能控性能观性分析 (5)3.1.1能控性定义 (5)3.1.2能控性判据 (5)3.1.3能观性定义 (7)3.1.4能观性判据 (7)3.1.5判断系统的能观性能观性 (8)3.2系统的稳定性分析 (9)3.3 LQR最优调节器的设计与仿真 (10)3.4通过状态反馈实现系统的极点配置 (12)3.4.1状态反馈的基本原理 (12)3.4.2 状态反馈的matlab实现 (13)4 状态观测器的设计 (15)4.1状态观测器的基本原理 (15)4.2状态观测器的matlab实现 (16)5 利用离散化方法研究系统的特性 (20)5.1连续线性系统离散化的概念 (20)5.2采样周期和仿真时间的选择 (21)5.3控制系统的离散化 (21)5.3.1 零阶保持器 (22)5.3.2双线性变换法离散化 (25)5.3.3采用一阶保持器离散化 (28)参考文献 (32)直流电动机调速系统的建模与控制系统的设计1 前言直流电机，是指输出或输入为直流电能的旋转电机，它是能实现直流电能和机械能互相转换的电机。

当它作电动机运行时是直流电动机，将电能转换为机械能；作发电机运行时是直流发电机，将机械能转换为电能。

直流电机由定子（由机座、主磁极、换向磁极、前后端盖和刷架等部件组成）和转子（由电枢、换向器（又称整流子）和转轴等部件构成）两部分组成，其间有一定的气隙。

电能够实现直流电能这机械能相互转化的电机，当它作电动机运行时是直流电动机，将直流转换为机械能；作发电机运行时是直流发电机，将机械能转化为直流电能。

电动机作为最主要的机电能量转换装置，其应用范围已遍及国民经济的各个领域和人们的日常生活。

1、在造纸流程中，投料箱应该把纸浆流变成2cm 的射流，并均匀喷洒在网状传送带上。

为此，要精确控制喷射速度和传送速度之间的比例关系。

投料箱内的压力是需要控制的主要变量，它决定了纸浆的喷射速度。

投料箱内的总压力是纸浆液压和另外灌注的气压之和。

由压力控制的投料箱是个耦合系统，因此，我们很难用手工方法保证纸张的质量。

在特定的工作点上，将投料箱线性化，可以得到下面的状态空间模型：ẋ = [−0.8+0.02−0.020] x+[0.0510.0010] u y =[x 1 , x 2]其中，系统的状态变量x1=液面高度，x2=压力，系统的控制变量u1=纸浆流量u2=气压阀门的开启量。

在上述条件下，试设计合适的状态变量反馈控制器，使系统具有实特征根，且有一个根大于5解：下面是对此设计的MATLAB 程序实现：>> A=[-0.8 0.02;-0.02 0];>> B=[0.05 1;0.001,0];>> r=rank(ctrb(A,B))r =2>> C=[1 1];>> P=[1 6];>> K=place(A,B,P)K =1.0e+003 *-0.0200 -6.0000-0.0008 0.30002、描述恒速制导导弹的运动方程为：ẋ = [ 01000−0.1−0.50000.500000 010000.51000]x + [ 01000] uy =[ 0 0 0 1 0 ] x(a) 运用ctrb 函数计算系统的能控型矩阵，并验证系统是不可控的；(b) 计算从u 到Y 的传递函数，并消去传递函数中的分子和分母公因式，由此可以得到能控的状态空间模型。

在消去了公因子之后，请用tf2ss 函数确定新的状态变量模型；(c) 证明(b)中得到的状态变量模型是能控的；(d) 说明恒速制导导弹是否稳定？(e) 讨论状态变量模型的能控性和复杂性的关系（假设用状态变量的数目来度量复杂性）解程序如下:clearA=input('请输入系统矩阵:');B=input('请输入输入矩阵:');C=input('请输入输出矩阵:');Qc1=ctrb(A,B)N1=size(A);n1=N1(1) %判断状态方程维数rc1=rank(Qc1)if rc1==n1disp('系统可控')elseif rc1<n1disp('系统不可控')endsyms sI=eye(n1);Q=inv(s*I-A);sys=collect(C*Q*B) %求解原状态方程的频域传递函数并化简num=[500 250 50];den=[1 0 0];[A1 B1 C1 D1]=tf2ss(num,den)Qc2=ctrb(A1,B1)N2=size(A1);n2=N2(1) %判断状态方程维数rc2=rank(Qc2)if rc2==n2disp('系统可控')elseif rc2<n2disp('系统不可控')endd1=eig(A)'d2=eig(A1)'flag1=0;flag2=0;for i=1:n1if real(d1(i))>0flag1=1;endendif flag1==1disp('原系统不稳定')elsedisp('原系统稳定')endfor j=1:n2if real(d2(j))>0flag2=1;endendif flag2==1disp('新系统不稳定')elsedisp('新系统稳定')end运行结果：请输入系统矩阵:[0 1 0 0 0;-0.1 -0.5 0 0 0;0.5 0 0 0 0;0 0 10 0 0;0.5 1 0 0 0]请输入输入矩阵:[0;1;0;0;0]请输入输出矩阵:[0 0 0 1 0]Qc1 =0 1.0000 -0.5000 0.1500 -0.02501.0000 -0.5000 0.1500 -0.0250 -0.00250 0 0.5000 -0.2500 0.07500 0 0 5.0000 -2.50000 1.0000 0 -0.1000 0.0500n1 =5rc1 =4系统不可控sys =50/s^2/(10*s^2+5*s+1)A1 =0 01 0B1 =1C1 =250 50D1 =500Qc2 =1 00 1n2 =2rc2 =2系统可控d1 =0 0 0 -0.2500 - 0.1936i -0.2500 + 0.1936id2 =0 0原系统稳定新系统稳定分析：由上述分析结果可知原系统和新系统均稳定，而实际上由系统的极点可知，原系统是稳定的，新系统实际上处于临界稳定状态也可认为是不稳定的；若以状态变量的数目来度量复杂性，可知系统的完全可控性与复杂性存在类似反比的关系，及复杂性越高系统完全可控的难度越大，复杂性越低系统完全可控的难度越低。

第2章一、状态空间描述的建立1． (由系统机理建立状态空间描述) 如图电路，写出系统的状态方程和输出方程。

选择状态变量x =u c ，输入变量u = e (t )，输出变量y = u c 。

解：如图电路，写出系统的状态方程和输出方程。

选择状态变量x =u c ，输入变量u = e (t )，输出变量y = u c 。

解：11c c du e u R C ,x x u ,y xdt RC RC=+⋅=-+=2．(由输入输出描述建立状态空间描述)系统的传递函数如下，求系统的状态空间描述41265)(232+++++=s s s s s s G解：可控标准形， []x 115100x 6124100010x =⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎥⎦⎤⎢⎢⎣⎡---=y u ； ； 或可观标准形， []x 100115x 6101201400x =⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎥⎦⎤⎢⎢⎣⎡---=y u ； 3．例2.3 给定单输入单输出线性定常系统的输入输出描述为3324160720()16194640s s G s s s s ++=+++ 试求系统的状态空间表达式。

解：此例中3m n ==。

由长除法得3232324160720646161840()41619464016194640s s s s G s s s s s s s ++---==+++++++则系统的状态空间表达式为e(t)u c[][]112233123010000106401941611840616644x x x x u x x x y x u x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=---+⎢⎥⎢⎥⎣⎦4．例2.2：已知二阶系统的微分方程22yy y T u u ξωω++=+ 试求系统的状态空间表达式。

解：可控规范形实现为：[]1112222010121c c c c c c xx x u y T x x x ωξω⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦； 则可观测规范形实现为：[]2111222100112o o o o o o x x x u y x x x T ωξω⎡⎤⎡⎤-⎡⎤⎡⎤⎡⎤=+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ ；二、传递函数矩阵的计算1．系统的状态空间描述如下，求系统的传递函数矩阵G (s )，u 10x 5261x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--= ；x 0210⎥⎦⎤⎢⎣⎡=y 解：⎥⎦⎤⎢⎣⎡+-+=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+--+⎥⎦⎤⎢⎣⎡=-=--1217611052610210)I ()(211s s s s s B A s C s G 。

摘要：本文主要讨论线性系统解集的几何结构与系统能观性、能控性和稳定性之间的关系。

这一关系从两个方面来说明，第一部分讲述系统解集几何结构与特征值和特征向量之间的关系，通过Matlab 仿真例子说明这一关系；第二部分分别讲述特征值和特征向量与系统能观性、能控性和稳定性之间的关系，并讲述了能观性，能控性以及稳定性的定义和判据，通过以约旦标准型为例来讲述相同特征值和不同特征值情况下的能观性，能控性，最后在Simulink中仿真一定特征值条件下系统的稳定性。

从以上两个方面来说明解集的几何结构与系统能观性、能控性和稳定性之间的关系。

>1. 零输入响应解集与特征值和特征向量之间的关系线性定常系统状态方程x Ax Buy Cx Du=+⎧⎨=+⎩，0(0),0x x t =≥的解为()00()(),0t At A t x t e x e Bu d t τττ-=+≥⎰。

为了研究线性定常系统状态方程解集的几何结构与线性系统的特征之间的关系，将系统简化，只考虑系统为零输入的状态响应，即x Axy Cx=⎧⎨=⎩，0(0),0x x t =≥的解为0()At x t e x =。

所有的零输入状态响应组成了一个线性空间，且该线性空间中有n 个独立的元素，它们的线性组合决定了所有零输入响应。

所以可以通过选择一组线性独立的初始条件得到一组零输入响应集中的基底。

下面先考虑最简单的零输入状态响应集的基底。

若12,,...n λλλ是A 的两两互异的特征值，且12,,...n v v v 是相应的单位特征向量，即,1,2,...i i i Av v i n λ==。

选0,1,2,...i x v i n ==，则0()(...)......i At At i2233i 2233i i i i 2233i i i i i i i t i x t e x e v 11I +At +A t +A t +v 2!3!11v Av t A v t A v t 2!3!11v v t v t v t 2!3!e v λλλλ====++++=++++=-所以取01122...n n x v v v ααα=+++时，相应的零输入响应为121122()...n t t t n nx t e v e v e v λλλααα=+++由此可以看出线性定常系统的零输入响应解集的几何结构可以由系统矩阵A 的特征值和特征向量来表征。