7-2安培定律

1、安培定则，也叫右手螺旋定则，是表示电流和电流激发磁场的磁感线方向间
关系的定则。

（1）通电直导线中的安培定则（安培定则一）：用右手握住通电直导线，让大拇指指向电流的方向，那么四指的指向就是磁感线的环绕方向；
（2）通电螺线管中的安培定则（安培定则二）：用右手握住通电螺线管，使四指弯曲与电流方向一致，那么大拇指所指的那一端是通电螺线管的N极。

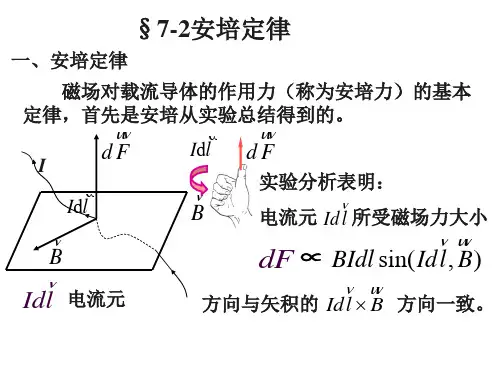
2、左手定则：通电导体放入磁场，
伸开左手，让磁场垂直穿过手掌，四指指向电流方向，则大拇指指的方向即为通电导体所受磁场力的方向。

左手定则可称“电动机定则”，是判断通电导线在磁场中的受力方向的法则，说的是磁场对电流的作用力，或者是磁场对运动电荷的作用力。

其内容是：将左手放入磁场中，使四个手指的方向与导线中的电流方向一致，那么大拇指所指的方向就是受力方向。

无论是直流发电机还是交流发电机，它们的工作原理都是相同的，区别是直流发电机有换向器，而交流发电机则没有换向器
3、右手定则
导体切割磁感线，产生感应电动势。

伸开右手，让磁场垂直穿过手掌，则大拇指指向运动方向，则四指指向即为电流方向。

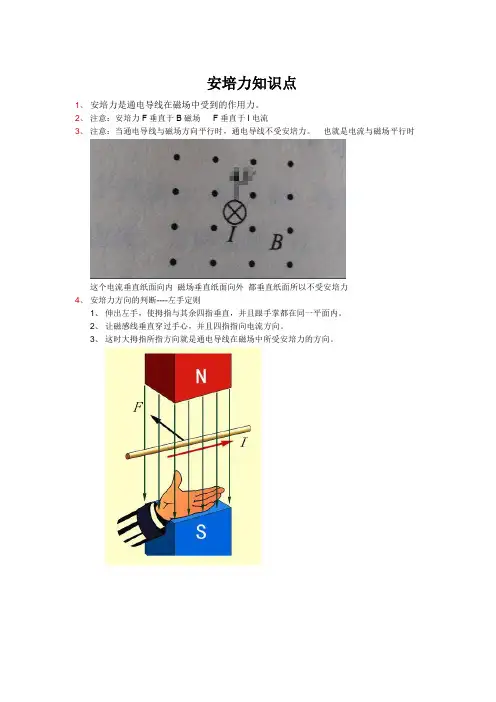
安培力知识点
1、安培力是通电导线在磁场中受到的作用力。

2、注意：安培力F垂直于B磁场F垂直于I电流
3、注意：当通电导线与磁场方向平行时，通电导线不受安培力。

也就是电流与磁场平行时
这个电流垂直纸面向内磁场垂直纸面向外都垂直纸面所以不受安培力
4、安培力方向的判断----左手定则
1、伸出左手，使拇指与其余四指垂直，并且跟手掌都在同一平面内。

2、让磁感线垂直穿过手心，并且四指指向电流方向。

3、这时大拇指所指方向就是通电导线在磁场中所受安培力的方向。

4、两条平行导线通上电流：同向电流相互吸引，反向电流相互排斥。

5、安培力的大小
F=BILsinθθ表示导线中电流方向与磁场方向之间的夹角。

班级组别姓名教师寄语：同学们，积极地思考和展示是一种对自我的挑战和锻炼，它能为你的成长积攒一缕光芒！让我们在今天的课堂上勇敢地挑战自我吧！§7--2欧姆定律及其应用郝戈庄初中冯守彬学习目标：1、理解欧姆定律，能运用欧姆定律进行简单的计算。

2、能根据欧姆定律以及电路的特点，得出串、并联电路中电阻的关系。

预习感知：一、请同学们根据“学习目标”，仔细阅读课本第4页－7页的相关内容，独立完成以下几个问题，请将你的答案写在题目下面的空白处。

（一）欧姆定律：公式：说明：（1）I、U、R三个物理量是针对同一段导体同一时刻的量。

（2）I、U、R计算过程中采用国际单位制。

（4）、阅读例题，归纳解题步骤并试做P29练习题1——3（二）理解：1、串联电路的总电阻与各分电阻的关系：2、并联电路的总电阻与各分电阻的关系：3、在此探究实验中是如何衡量总电阻是变大还是变小了？理解此种研究问题的方法。

4、结合P28图7.2-3如何理解串并联电路中总电阻与分电阻的关系。

（四）初步完成课本第29页练习题。

二、在你预习的过程中，你还有哪些自己不能解决的疑问，请记录下来。

合作达标：一、预习反馈，生成目标结合学习目标，组内交流“预习感知”中的问题：（将在预习过程中自己解决不了的疑问在组内交流，将本组解决不了的问题写到黑板上）二、组内交流，合作探究问题一：组内交流讨论利用欧姆定律公式及变式解题应注意的问题，交流练习题。

问题二：观看演示实验，根据观察到的现象思考并在小组内交流讨论串并联电路中总电阻与分电阻的关系。

三．展示质疑，释疑点拨四、巩固练习、拓展延伸（先独立完成，再在小组内交流，最后以小组为单位展示。

）1、导体的电阻与导体的、、有关。

材料、横截面积一定时，长度越长，电阻越；材料长度一定时，横截面积越大，电阻越。

2、P29练习题1-6五、梳理总结、构建网络（请同学们整理、反思刚才的学习内容，用简短的语言完成下列知识网络，然后小组内交流完善。

高中物理安培力的计算及方向的判断编稿老师 刘汝发 一校 杨雪 二校 黄楠 审核 王红仙知识点考纲要求题型 说明 安培力的计算及方向的判断 1. 熟悉安培力计算公式并能熟练计算安培力的大小； 2. 掌握左手定则并能熟练判断安培力的方向；3. 用左手定则分析解决通电导体在磁场中的受力及平衡类问题选择题、计算题 本知识点属于高频考点，是电磁学部分的重要内容，考查方向主要为安培力参与的平衡问题、能量问题等 二、重难点提示：重点：应用左手定则分析解决通电导体在磁场中的受力及平衡类问题。

难点：安培力方向的判断（左手定则）。

一、安培力1. 定义：通电导线在磁场中受的力称为安培力。

2. 安培力的大小（1）磁场和电流垂直时，F ＝BIL ；（2）磁场和电流平行时：F ＝0；（3）磁场和电流夹角为θ时：θsin BIL F =。

理解：（1）当B 和I 不垂直时，只保留B 的垂直分量即可；（2）当导线不规则时，取其两端连线为研究对象，电流由流入端指向流出端。

3. 安培力的方向（1）用左手定则判定：伸开左手，使拇指与其余四个手指垂直，并且都与手掌在同一个平面内，让磁感线从掌心进入，并使四指指向电流的方向，这时拇指所指的方向就是通电导线在磁场中所受安培力的方向。

（2）安培力的方向特点：F ⊥B ，F ⊥I ，即F 垂直于B 和I 所决定的平面。

二、安培力作用下导体运动情况的判定1. 判定通电导体在安培力作用下的运动或运动趋势，首先必须弄清楚导体所在位置的磁场分布情况（安培定则），然后利用左手定则准确判定导体的受力情况，进而确定导体的运动方向或运动趋势的方向。

2. 在应用左手定则判定安培力方向时，磁感线方向不一定垂直于电流方向，但安培力方向一定与磁场方向和电流方向垂直，即大拇指一定要垂直于磁场方向和电流方向所决定的平面。

电流元法分割为电流元安培力方向―→整段导体所受合力方向―→运动方向特殊位置法在特殊位置―→安培力方向―→运动方向等效法环形电流和通电螺线管都可以等效为条形磁铁，条形磁铁也可等效成环形电流或通电螺线管，通电螺线管也可以等效成很多匝的环形电流来分析。

安培定律和毕奥--萨伐尔定律1.物质的磁性与电流的磁效应从天然磁体到指南针的发明人类对磁现象的最初认识，是发现天然磁体之间存在互相吸引或排斥作用，以及天然磁体对诸如铁这类物体产生吸引力.人们观察到，任何磁性物体都有两个不同的“磁极”，同性磁极互相排斥，异性磁极互相吸引.后来又发现，如果将一根条形小磁体的中心支撑起来并让它可以自由转动,小磁体的某一极总是转向北方.人们由此认识到，原来我们所居住的地球就是一个巨大的天然磁体.磁性物体中指向北方的那个极被称为“北磁极”或N极，指向南方的另一极称为“南磁极”或S极.中国人对磁现象的发现和应用，比西方人要早得多.春秋战国时期（公元前770-221年）的文献已有“磁石吸铁”的记载，北宋时期已经利用磁针制造指南针并应用于航海.至公元1600年，英国人吉尔伯特（M.Gilbert）发表《论磁体》一书，这被认为是人类对磁现象系统而定性研究的最早著作.从库仑到奥斯特 From Coulomb To Oersted库仑（C.A.de Coulomb）大家已经知道，1785年,法国的库仑通过实验，总结出静电相互作用的规律.大约同期，库仑也通过实验对磁力进行了测量，并指出与电力一样，磁力“与磁分子之间的距离平方成反比”.库仑的“磁分子”包含有南、北两种磁荷，它们在磁体内首尾相吸形成“磁分子纤维”,使磁荷不能象电荷那样从一个物体转移到另一个物体.但是，电力与磁力有关吗？库仑和他同时代的许多物理学家都认为：虽然磁力与电力在距离关系上有相似性，但并无同一性.奥斯特（H.C.Oersted）然而，丹麦人奥斯特在德国哲学家康德（I.Kant）和谢林（W.J.Schelling）关于自然力转化与统一的思想影响下，经过20多年对电力、磁力及化学亲和力等的广泛研究，终于在1820年4月发现了电流的磁效应——通有电流的导线使其附近的磁针发生了偏转！奥斯特的伟大发现，轰动了当时欧洲的物理学界，由此开创了实验上与理论上研究电磁统一性的纪元.从奥斯特到安培、毕奥和萨伐尔安培（A.M.Ampere）法国物理学家安培获知奥斯特的发现之后，很快（1820年9月）就发现两根通电流的导线之间也存在相互作用力，并于同年12月发表了这种相互作用力的定量公式——现在我们称之为安培定律. (见教材P336)安培进而用“分子电流”假说解释磁体的磁性——磁性体内分子电流的有规排列，呈现出宏观磁化电流，正是宏观磁化电流使之产生宏观磁性（见教材P336）毕奥和萨伐尔（J.B.Biot and F.Savart）也是在1820年，法国物理学家毕奥和萨伐尔,通过实验测量了长直电流线附近小磁针的受力规律,发表了题为“运动中的电传递给金属的磁化力”的论文，后来人们称之为毕奥--萨伐尔定律.稍后，在数学家拉普拉斯的帮助下，以数学公式表示出这一定律.从奥斯特到安培，两个引人深思的问题一个引人深思的问题是：从奥斯特发现电流磁效应（1820年4月）到安培发现电流相互作用的规律（1820年9月），前后只是相差5个月，我们可以从中获得什么教益？另一个同样引人深思的问题是：安培提出磁性的“分子电流假说”，比1897年汤姆孙发现电子，以及后来发现物质的原子和分子电结构，早了70多年以上.我们又可以从中获得什么教益？安培的“分子电流圈”，按现在的理解，就是分子内的电荷运动形成的磁偶极矩m .由照经典模型，分子磁偶极矩矢量描述为其中，I 是分子电流强度，为电流圈的面积矢量，规定它的方向与电流流向成右手螺旋关系.今天，人们对磁现象的认识，已经比安培那个时代深刻得多：不仅原子和分子中的电子绕核运动形成一定的“轨道磁矩”，而且，电子、质子等“基本的”带电粒子，都有一定的自旋磁矩.分子的总磁矩是所有粒子轨道磁矩和自旋磁矩的矢量和.磁场读者知道，电荷之间的相互作用，通过电荷的电场传递.电流之间的相互作用，则是通过电流的磁场传递的.如果我们在一块水平放置的平板上，放上一块条形磁铁，再在其周围撒上小铁粉，我们将会看到，小铁粉会呈现很有规律性的排列，如图2-1.这是由于：磁铁内分子电流（磁矩）的有规排列所形成的宏观“磁化”电流产生了宏观磁场，在这磁场作用下，小铁粉（小磁矩）发生了朝着“磁力线”方向的偏转而呈现有规律的排列.同样的，两条电流线之所以存在互作用力，是一条电流线产生的磁场，作用于另一条电流线的结果.2.安培定律（Amperes’ Law）（教材P337）现在，让我们写出安培作用定律真空中，两个稳恒的电流回路L1和L2，电流元I1dl1对I2dl2的作用力为(2.2-1)其中，I1和I2 是两个回路的电流强度，r12是从I1dl1到I2dl2的距离，是这方向上的单位矢量.在MKSA单位制中，比例常数（2.2-2）其中，m0称为真空磁导率，它与真空介电常数ε0（真空电容率）共同构成作为基本物理常数的真空中光速C：（2.2-3）读者将会看到，电流强度I 的单位——“安培”，是由(2.2-1）来定义的.由于力的单位为牛顿，距离的单位为米，故从定义“安培”这一需要出发，真空磁导率取值为（2.2-4）这也是真空介电常数ε0为什么由下式表示（2.2-5）的原因.由于回路L1的每个电流元对另一回路L2每个电流元都将产生作用力，因此，回路L1对回路L2的合力应当是一个二重积分：（2.2-6)回路L2对回路L1的作用力则是（2.2-7)其中，r21 = r12,是电流元I2dl2到I1dl1的方向上的单位矢量.可以证明，两个稳恒电流回路之间的作用力与反作用力，大小相等方向相反：F21 = -F12（2.2-8)但是，对于两个“孤立的稳恒电流元”，一般地 dF21≠ - dF12这是因为：稳恒电流必定构成闭合回路，既孤立又“稳恒”的电流元实际上并不存在.3.磁感应强度 (magnetic induction) （P346）前面我们已指出，电流之间的相互作用是通过磁场来传递的.因此，安培定律（2.2-6)中，电流回路L2受到的合力，实质上是电流回路L1产生的磁场对它施加的总作用力，因此，安培定律实质上是：（2.2-9)B 是电流回路L1在L2各点上产生的磁感应强度（注：这一称胃是历史上形成的，现在，有些国外的教科书已把B 称为磁场强度——magnetic field strength）.对于任何一个稳恒的电流回路L ，其中一个电流元Idl 在任意点P产生的元磁感应强度为（2.2-10)其中，x是场点的位置矢量，r是电流元到场点的距离，是这方向的单位矢量.——图中，P点的dB 沿什么方向？类似于电场叠加原理 , 回路L的全部电流元在P点产生的总磁感应强度,也是一个矢量积分：（2.2-11)这称为毕奥—萨伐尔定律.应当注意，B是一个与场点P的坐标有关的矢量函数 .如果导线截面上的电流密度函数为J (x ’)，则一个电流元是J (x ’)dV ’(小电流管中很小一段)，（2.2-11)将写成（2.2-12)此处，r 是电流分布点到场点P的距离，是这方向的单位矢量.磁感应强度的物理意义(1) 像点电荷产生的电场强度与距离的平方成反比一样，电流元产生的磁感应强度，也与距离的平方成反比；(2）积分式（2.2-11)和（2.2-12)表示电流的磁场也遵从叠加原理(3) 电流的磁场分布于其周围空间.根据安培定律，一个电流元I dl 在磁场中受到的作用力为dF = I dl ×B (2.2-13)B是电流元所在点的磁感应强度.我们设想，在磁场中某一点有一个电流元，由上式，它受力的大小为dF =I dl B sinθ (2.2-14)θ是矢量B与电流元的夹角，显然，仅当θ =π/2，即电流元的方向与此处B 的方向垂直时，它受到的力才有最大值（dF ）max = I dl B ，我们就以比值(2.2-15)来定义该点的磁感应强度，表示单位电流元在磁场某点受到的最大作用力.（请将这个定义与由库仑定律定义的电场强度比较一下）于是B 的单位是：牛顿/安培·米（N/Am），通常把它称为特斯拉（tesla），即 1 特斯拉（T）=1牛顿/安培·米（N/Am）你们以后将看到，B2/2 μ0表示磁场能量密度(电场能量密度为ε0E2/2). 在有些文献中，仍然用“高斯”作为磁感应强度的单位，它与特斯拉的换算关系是 1高斯（gauss）= 10-4特斯拉习题P351：3题[例2-3] 直线电流的磁场(Magnetic Field of a Rectilinear Current)（P352）[解] 我们考虑某个稳恒电流回路的一段，电流是沿着直线流动的，电流强度为I ,设其流向沿坐标系的z轴正向，场点P到电流线的垂直距离为r0 , 我们就以o为坐标原点，如下图.任意一个电流元到原点o的距离为z ,到场点P的距离为r, 从毕奥—萨伐尔定律可知，电流元在场点P产生的元磁感应强度的方向，必定垂直于电流线和P点构成的平面，亦即图中的方向，这正是以r0为半径的圆周的切线方向. 因此我们有其中θ 是电流元与方向的夹角，从图中我们看到对上式两边取微分，便可实现积分变量从z 到θ的变换：于是我们有设这段直线电流的两个端点为a 和 b ,则θ将从θ1变到θ2，对上式积分，便得到这段直线电流在P点产生的磁感应强度(2.2-16)当直线电流的长度为“无限长”，即θ1→0，θ2→π时, （2.2-16）将给出离开电流线为r0的任一点处，磁感应强度为(2.2-17)这表明，“无限长”直线电流在其周围产生的磁感应强度，与距离的一次方成反比，它的场线——即B线按右手规则，相对于电流的流向形成一族与电流线为中心的同心圆.在实际问题中，只要电流线足够长，在它中部附近r0远小于电流线长度的范围内，就有近似于(2.2-17)的结果.请大家考虑下面两个问题：（1）对于通以稳恒电流的金属导线，通常我们只观测到它在外部产生的磁场，而没有观测到它在外部产生的电场.这是为什么？（2）但是对于离子束（无论是正离子束还是负离子束），我们会同时观测到它在外部的磁场和电场，这又是为什么？练习题：假定离子束沿着直线运动并且是稳定的，电流强度为I ，试找出离开离子束中心为 r 处的磁感应强度B和电场强度E .例2-4]平行电流线之间的互作用力.电流强度的单位“安培”的定义. （教材P344，及P387）[解] 我们在第一章的开头就指出，在MKSA单位制中，除了长度（单位：米）、质量（单位：千克）和时间（单位：秒）之外，电流强度（单位：安培）是第四个基本物理量.而电流强度的单位“安培”，正是以安培定律为依据来定义的.设两条很长且平行的线电流之间，相距为r0 ,电流强度分别为I1和I2 ,并且流向相同，如图. 由(2.2-17)，强度为I1的电流在另一电流线上产生的磁感应强度为于是据安培定律，电流I2中的一个电流元受到的作用力为：(2.2-18)负号表示此力是一个吸引力.显然，若两个电流的流向相反，则d F12将是排斥力.两电流线单位长度相互作用力的大小是(2.2-19)我们以前指出，m0的数值取为 4 ×10-7,现在令I1 = I2 =I , 上式便给出(2.2-20)于是，当 r0 = 1米，并且测得f = 2×10-7牛顿/米时，两导线中的电流强度I 就定义为“1安培”.下图就是用来测量平行电流线相互作用力的天平——“安培秤”.[例2-5]圆电流圈的磁场（Magnetic Field of a Circular Current）（P355）[解] 设电流圈的半径为a ，电流强度为I .我们以其中心O为坐标原点，对称轴为z轴，任一电流元到轴上P点的距离为r ,是这方向上的单位矢量.显然，由于，故∣Idl×∣= Id l,因此，一个电流元在轴上P点产生的磁感应强度dB 垂直于与构成的平面，其值则为由于电流分布存在着z轴对称性，我们注意到，与Idl 对称的另一个电流元 Idl ’在P点产生的dB’，与dB 叠加后，与z 轴垂直方向的分量为零，因而只剩下z方向的分量. 因此，仅需对dB 的z分量积分.记场点P到原点O的距离为z = R ，则于是，轴上P点的磁感应强度之值为(2.2-21)显然，在电流圈的中心O，即R = 0 处，有(2.2-22)但在远处，即R>>a 时，(2.2-23)上面我们只求出电流圈对称轴上的场强，但大家应当注意到，这圆形电流圈的电流分布，是存在着z轴对称性的，因此它的磁场必定也存在着同样的对称性.电流圈的磁偶极矩（magnetic dipole moment of a current loop）（P390）和它的磁场设小电流圈的电流强度为I，面积为S，我们定义这电流圈的磁偶极矩矢量为(2.2-24)IS是磁偶极矩的值.按规定，矢量m 的方向，亦即的方向，与电流的流向遵从右手螺旋规则，如图.对于上例的圆形电流圈，其磁偶极矩矢量为于是，据（2.2-23）这磁矩在其轴上而且很远的P点处，产生的磁感应强度就是(2.2-25)现在，让我们回过头去看看，一个位于坐标原点的电偶极矩在远处产生的电场强度为（2.2-26）它存在着z 轴的对称性. 在轴线上即 = 0的点，记r =R，我们看到，这电偶极子的电场强度同样只有z 分量：（2.2-27）它与上述磁偶极矩m在对称轴上的磁感应强度(2.2-25)十分相似——只需将p/ε0?与μ0m 代换，便可实现同一点上E与B的代换！事实上，由于这圆形电流圈的电流分布是存在着z 轴对称性的，因此它的磁场必定也存在着同样的对称性.更详细的理论计算表明：一个位于坐标原点、磁矩矢量为的磁偶极子，在远处，即当r>>a （磁矩的线度）时，它所产生的磁场为(2.2-28)这告诉我们，磁偶极子m 的磁场，与电偶极子p的电场存在着对称性.磁偶极子和它的磁场对于一般的闭合电流圈，其磁偶极矩由下式计算（2.2-29）其中，I d l 是电流圈中的电流元，x ’是电流元的位置矢量，积分遍及整个电流圈.在电流分布于一定体积V 的情形，电流密度为J，电流元I d l 是JdV ’,于是（2.2-30）积分遍及全部电流分布的区域.以后大家将会看到，带电粒子都有一定的自旋磁矩和轨道磁矩。