下载文档原格式
t检验使用条件及在SPSS中的应用t检验是对均值的检验，有三种用途，分别对应不同的应用场景：1)单样本t检验（One Sample T Test）：对一组样本，检验相应总体均值是否等于某个值；2)相互独立样本t检验（Independent-Sample T Test）：利用来自某两个总体的独立样本，推断两个总体的均值是否存在显著性差异；3)配对样本t检验：是采用配对设计方法观察以下几种情形，1，两个同质受试对象分别接受两种不同的处理；2,同一受试对象接受两种不同的处理；3，同一受试对象处理前后。
下文将分别介绍三种t检验的使用条件以及在SPSS中的实现。
一、单样本t检验1.1简介1)单样本t检验的目的利用来自某总体的样本数据，推断该总体的均值是否与指定的检验值之间存在显著性差异，它是对总体均值的检验。
2)单样本t检验的前提样本来自的总体应服从和近似服从正态分布，且只涉及一个总体。
如果样本不符合正态分布或不清楚总体分布的形状，就不能用单样本t检验，而要改用单样本的非参数检验。
3)单样本t检验的步骤a)提出假设单样本t检验需要检验总体的均值是否与指定的检验值之间存在显著性差异，为此，，提出假设：给定检验值μH0：μ = μ（原假设，null hypothesis）H1：μ≠μ（备择假设,alternative hypothesis，）b)选择检验统计量属于总体均值和方差都未知的检验采用t统计量：t =X ̅−μ0S ̂√n⁄，其中，X ̅和S ̂分别为样本均值和方差，t 的自由度为n-1SPSS 中还将显示均值标准误差，计算公式为S ̂√n ⁄，即t 统计量的分母部分。
c) 计算统计量的观测值和概率将样本均值、样本方差、μ0带入t 统计量，得到t 统计量的观测值，查t 分布界值表计算出概率P 值。
d) 给出显著性水平α，作出统计判断给出显著性水平α，与检验统计量的概率P 值作比较。
当检验统计量的概率值小于显著性水平时，则拒绝原假设，认为总体均值与检验值μ0之间有显著性差异；反之，如果检验统计量的概率值大于显著性水平，则接受原假设，认为总体均值与检验值μ0之间没有显著性差异。
S P S S中T检验的应用本文指在简述SPSS中的T检验，主要说明了T检验的原理和应用，及使用范围。
和SPSS中的基本操作。
T检验是检验样本的均值和给定的均值是否存在显著性差异。
T检验分为3类：单样本T检验、两独立样本T检验和两配对样本T检验。
关键词：T检验、SPSS、显著性水平、统计量、概率P-值、自由度、线性相关、置信区间、零假设。
目录一、单样本T检验 (3)1.单样本T检验的目的。
(3)2.单样本T检验的基本步骤。
(3)3.单样本T检验的应用举例 (4)三、两独立样本T检验 (5)1.两独立样本T检验的目的 (5)2．两独立样本T检验的基本步骤。
(5)3.两独立样本T检验的应用举例 (7)三．两配对样本T检验 (9)1.两配对样本T检验的目的 (9)2.两配对样本T检验的基本步骤。
(9)3.两配对样本T检验的应用举例。
(9)四、参考文献。
(12)一、单样本T 检验1.单样本T 检验的目的。
单样本t 检验的目的是利用来自某总体的样本数据，推断该总体的均值是否与制定的检验值之间存在显著性差异。
它是对总体均值的假设检验。
2.单样本T 检验的基本步骤。
⑴.提出原假设。
单样本T 检验的原假设0H 为：总体均值与检验值之间不存在显著差异，表述为0H ：0μμ=。
μ为总体均值，0μ为检验值。
⑵.选择检验统计量。
当总体分布为正态分布),(2σμN 时，样本均值的抽样分布仍为正态分布，该正态分布的均值为μ，方差为2σ/n ，即),(~2nN X σμ式中，μ为总体均值，当原假设成立时，0μμ=；2σ为总体方差；n 为样本数。
总体分布近似服从正态分布时。
通常总体方差是未知的，此时可以用样本方差2S 替代，得到的检验统计量为t 统计量，数学定义为:nS X t 2μ-=①式中，t 统计量服从n-1自由度为t 分布。
单样本t 检验的检验统计量即为t 统计量。
当认为原假设成立时μ用0μ代入。
⑶计算检验统计量观测值和概率P-值该步目的是甲酸检验统计量的观测值和相应的概率P-值。
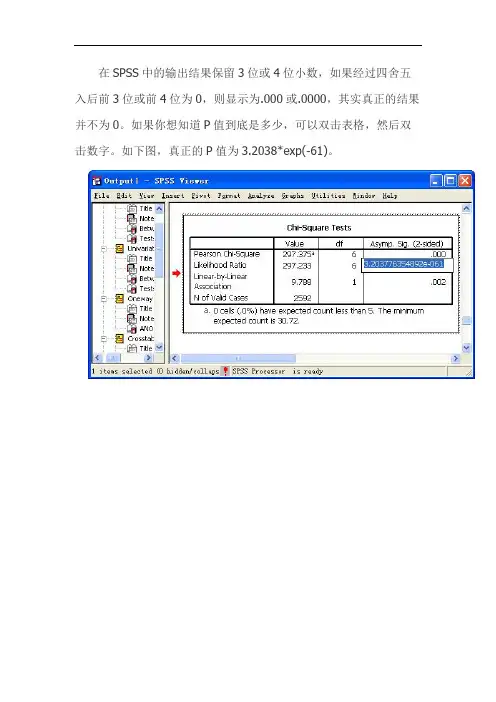
在SPSS中的输出结果保留3位或4位小数，如果经过四舍五入后前3位或前4位为0，则显示为.000或.0000，其实真正的结果并不为0。
如果你想知道P值到底是多少，可以双击表格，然后双击数字。
如下图，真正的P值为3.2038*exp(-61)。
目录一、单样本T检验 (4)1.单样本T检验的目的 (4)2.单样本T检验的基本步骤 (4)3.单样本T检验的应用举例 (5)三、两独立样本T检验 (6)1.两独立样本T检验的目的 (6)2．两独立样本T检验的基本步骤 (6)3.两独立样本T检验的应用举例 (8)三、两配对样本T检验 (10)1.两配对样本T检验的目的 (10)2.两配对样本T检验的基本步骤 (10)3.两配对样本T检验的应用举例 (10)四、参考文献 (12)一、单样本T 检验1.单样本T 检验的目的。
单样本检验的目的是利用来自某总体的样本数据，推断该总体的均值是否与制定的t 检验值之间存在显著性差异。
它是对总体均值的假设检验。
2.单样本T 检验的基本步骤。
⑴.提出原假设。
单样本T 检验的原假设为：总体均值与检验值之间不存在显著差异，表述为：0H 0H 。
为总体均值，为检验值。
0μμ=μ0μ⑵.选择检验统计量。
当总体分布为正态分布时，样本均值的抽样分布仍为正态分布，该正态分),(2σμN 布的均值为，方差为/，即μ2σn),(~2nN X σμ式中，为总体均值，当原假设成立时，；为总体方差；为样本数。
总μ0μμ=2σn 体分布近似服从正态分布时。
通常总体方差是未知的，此时可以用样本方差替代，得到2S 的检验统计量为统计量，数学定义为:t①nS X t 2μ-=式中，统计量服从n-1自由度为分布。
单样本检验的检验统计量即为统计量。
当t t t t 认为原假设成立时用代入。
μ0μ⑶计算检验统计量观测值和概率P-值该步目的是甲酸检验统计量的观测值和相应的概率P-值。
SPSS 将自动将样本均值、、样本方差、样本数代入式①中，计算出统计量的观测值和对应的概率P-值。
你的分析结果有T值，有sig值，说明你是在进行平均值的比较。
也就是你在比较两组数据之间的平均值有没有差异。
从具有t值来看，你是在进行T检验。
T检验是平均值的比较方法。
T检验分为三种方法：1. 单一样本t检验（One-sample t test）是用来比较一组数据的平均值和一个数值有无差异。
例如，你选取了5个人，测定了他们的身高，要看这五个人的身高平均值是否高于、低于还是等于1.70m，就需要用这个检验方法。
2. 配对样本t检验（paired-samples t test）是用来看一组样本在处理前后的平均值有无差异。
比如，你选取了5个人，分别在饭前和饭后测量了他们的体重，想检测吃饭对他们的体重有无影响，就需要用这个t检验。
注意，配对样本t检验要求严格配对，也就是说，每一个人的饭前体重和饭后体重构成一对。
3. 独立样本t检验（independent t test）是用来看两组数据的平均值有无差异。
比如，你选取了5男5女，想看男女之间身高有无差异，这样，男的一组，女的一组，这两个组之间的身高平均值的大小比较可用这种方法。
总之，选取哪种t检验方法是由你的数据特点和你的结果要求来决定的。
t检验会计算出一个统计量来，这个统计量就是t值，spss根据这个t值来计算sig值。
因此，你可以认为t值是一个中间过程产生的数据，不必理他，你只需要看sig值就可以了。
sig值是一个最终值，也是t检验的最重要的值。
sig值的意思就是显著性（significance），它的意思是说，平均值是在百分之几的几率上相等的。
一般将这个sig值与0.05相比较，如果它大于0.05，说明平均值在大于5%的几率上是相等的，而在小于95%的几率上不相等。
我们认为平均值相等的几率还是比较大的，说明差异是不显著的，从而认为两组数据之间平均值是相等的。
如果它小于0.05，说明平均值在小于5%的几率上是相等的，而在大于95%的几率上不相等。
我们认为平均值相等的几率还是比较小的，说明差异是显著的，从而认为两组数据之间平均值是不相等的。
配对样本T检验的SPSS应用前言：很多统计研究都发现，有大量的变量可以同时检验多种因素。
而 T检验是我们常用的方法之一。
配对样本 T检验就是在 T检验中较常用的一种检验方法。
目前，配对样本 T检验一般分为两种：一种是配对样本 T检验，另一种是配对样本 T检验。
配对样本 T检验主要应用于临床中，其检验结果具有较高的可靠性（图1)。
但这两种检验方法都有一个缺陷，那就是必须在非配对样本中进行检验。
因此配对样本 T检验在临床中的应用越来越受到重视。
一、引言随着科技的发展，医学领域中应用新方法越来越多，配对样本 T检验作为一种常用的检验方法已经得到了广泛应用。
配对样本 T检验方法的优点是：能够从一个不同性别的样本中同时检验多个变量以及多个因素。
配对样本 T检验是指在同一实验室内测定配对样本中某一个样本与另一个样本之间的 t检验结果与其样本上同性别群体的所有样本中对应的样本误差。
由于这两个样本量通常较大，检验结果较为可靠。
并且容易被人接受。
因此临床应用范围非常广泛，尤其是一些慢性病患者以及临床实验室研究人员都会使用配对样本 T检验来检查相关变量之间是否存在多个配对之间的差异情况。
通常会将相同因素和不同类别样本进行配对检验。
但是不同个体情况不同。
因此配对样本 T检验还可以将同一变量的多个组别相配而出现的相同结果通过对比，或者其他方法得出与之相类似的结果。
通过研究表明随着变量数目的增加，样本大小呈现出不同的趋势。
所以配对样本是一个很好的检验方法。
本文就配对样本 T检验的原理以及方法做一简要介绍。
具体做法如下：用 SPSS软件对配对样本 T检验的操作步骤进行了详细说明，本文主要是通过介绍 SPSS软件，来实现配对样本 T检验方法在临床中的应用。
1、操作流程首先，将各年龄段样本按照性别分别装入相应的试剂盒和测试卡内。
在实验室 SPSS软件中设置数据，并自动对样本数据提取。
然后，根据不同性别进行配对检测。
将不同性别样本依次用不同的试剂盒和测试卡进行配对检测。
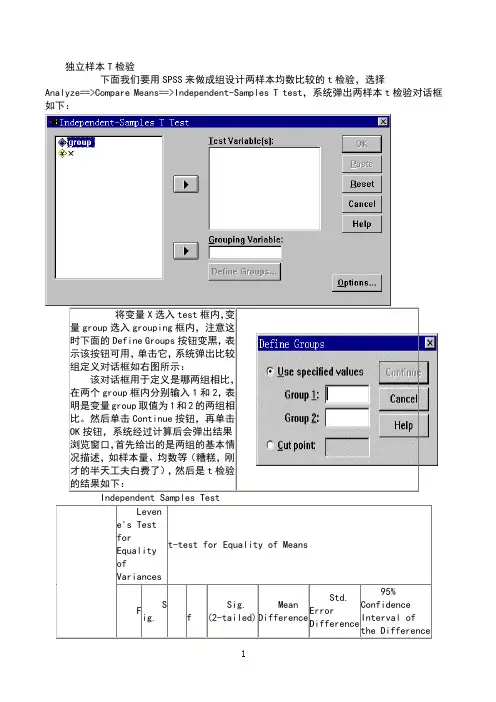
独立样本T检验下面我们要用SPSS来做成组设计两样本均数比较的t检验，选择Analyze==>Compare Means==>Independent-Samples T test，系统弹出两样本t检验对话框如下：将变量X选入test框内，变量group选入grouping框内，注意这时下面的Define Groups按钮变黑，表示该按钮可用，单击它，系统弹出比较组定义对话框如右图所示：该对话框用于定义是哪两组相比，在两个group框内分别输入1和2，表明是变量group取值为1和2的两组相比。
然后单击Continue按钮，再单击OK按钮，系统经过计算后会弹出结果浏览窗口，首先给出的是两组的基本情况描述，如样本量、均数等（糟糕，刚才的半天工夫白费了），然后是t检验的结果如下：Levene's TestforEqualityofVariancest-test for Equality of MeansFSig.tdfSig.(2-tailed)MeanDifferenceStd.ErrorDifference95%ConfidenceInterval ofthe Difference体方差是否齐，这里的戒严结果为F = ，p = ，可见在本例中方差是齐的；第二部分则分别给出两组所在总体方差齐和方差不齐时的t检验结果，由于前面的方差齐性检验结果为方差齐，第二部分就应选用方差齐时的t检验结果，即上面一行列出的t= ，ν=22，p=。
从而最终的统计结论为按α=水准，拒绝H0，认为克山病患者与健康人的血磷值不同，从样本均数来看，可认为克山病患者的血磷值较高。
SPSS软件在医学科研中的应用计算机实习（SPSS10.0）何平平北大医学部流行病与卫生统计学系实习三连续变量的假设检验（t检验、方差分析及协方差分析）一、t检验（一）样本均数与已知总体均数的比较（三）配对设计的两样本均数比较二、方差分析三、协方差分析t检验的目的一、t检验推断两个总体均数是否相等假设检验的结论具有概率性。
当Pδ0.05，拒绝H0 时，有可能犯第一类错误（〈）当P>0.05，不拒绝H0时，有可能犯第二类错误（®）〈为事先指定的检验水平（一般取0.05），®未知；增大样本量n，可以同时减小〈和®。
一、t检验（一）样本均数与已知总体均数的比较（单样本t检验）例1 通过大量调查，已知某地正常男婴出生体重为3.26kg。
某医生随机抽取20名难产男婴，测得出生体重如下（见数据文件p192.sav）。
问该地难产男婴出生体重均数是否与正常男婴不同？3.5 3.5 3.2 3.5 3.3 3.0 3.3 3.23.4 2.7 3.4 3.6 3.5 2.8 3.4 2.93.5 3.54.0 4.0SPSS 操作步骤： 变量说明：weight ：出生体重。
t 检 验已知的总体均数Sig：significance结论：因为t=1.330，P＝0.199>0.05，所以尚不能认为难产男婴出生体重均数与正常男婴不同。
一、t检验（二）完全随机设计（成组设计）的两样本均数比较（两独立样本t检验）例2 某医师测得12名正常人和13名病毒性肝炎患者血清转铁蛋白含量（g/L），结果如下（见数据文件p193.sav）。
问病毒性肝炎患者和正常人血清转铁蛋白含量有无差异？病毒性肝炎患者：2.34 2.47 2.22 2.31 2.36 2.38 2.15 2.572.19 2.25 2.28 2.31 2.42正常人：2.61 2.71 2.73 2.64 2.68 2.81 2.762.55 2.91 2.85 2.71 2.64SPSS操作步骤：变量说明：group：分组，1＝患者；2＝正常人。
S P S S中T检验的应用1本文指在简述SPSS中的T检验，主要说明了T检验的原理和应用，及使用范围。
和SPSS中的基本操作。
T检验是检验样本的均值和给定的均值是否存在显著性差异。
T检验分为3类：单样本T检验、两独立样本T检验和两配对样本T检验。
关键词：T检验、SPSS、显著性水平、统计量、概率P-值、自由度、线性相关、置信区间、零假设。
目录一、单样本T检验 (3)1.单样本T检验的目的。
(3)2.单样本T检验的基本步骤。
(3)3.单样本T检验的应用举例 (4)三、两独立样本T检验 (5)1.两独立样本T检验的目的 (5)2．两独立样本T检验的基本步骤。
(5)3.两独立样本T检验的应用举例 (7)三．两配对样本T检验 (9)1.两配对样本T检验的目的 (9)2.两配对样本T检验的基本步骤。
(9)3.两配对样本T检验的应用举例。
(9)四、参考文献。
(11)一、单样本T 检验1.单样本T 检验的目的。
单样本t 检验的目的是利用来自某总体的样本数据，推断该总体的均值是否与制定的检验值之间存在显著性差异。
它是对总体均值的假设检验。
2.单样本T 检验的基本步骤。
⑴.提出原假设。
单样本T 检验的原假设0H 为：总体均值与检验值之间不存在显著差异，表述为0H ：0μμ=。
μ为总体均值，0μ为检验值。
⑵.选择检验统计量。
当总体分布为正态分布),(2σμN 时，样本均值的抽样分布仍为正态分布，该正态分布的均值为μ，方差为2σ/n ，即),(~2nN X σμ式中，μ为总体均值，当原假设成立时，0μμ=；2σ为总体方差；n 为样本数。
总体分布近似服从正态分布时。
通常总体方差是未知的，此时可以用样本方差2S 替代，得到的检验统计量为t 统计量，数学定义为:nS X t 2μ-=①式中，t 统计量服从n-1自由度为t 分布。
单样本t 检验的检验统计量即为t 统计量。
当认为原假设成立时μ用0μ代入。
⑶计算检验统计量观测值和概率P-值该步目的是甲酸检验统计量的观测值和相应的概率P-值。
SPSS将自动将样μ、样本方差、样本数代入式①中，计算出t统计量的观测值和对应本均值、的概率P-值。
⑷给定显著性水平α，并作出决策。
如果概率P-值小于显著性水平α，则应拒绝原假设，认为总体均值与检验值之间存在显著差异；反之，如果概率P-值大于显著性水平α，则不应拒绝原假设，认为总体均值与检验值之间无显著差异。
3.单样本T检验的应用举例案例：利用住房状况问卷调查数据，推断家庭人均住房面积的平均值是否为20平方米。
数据名字为“住房状况调查.sav”推断家庭人均住房面积的平均值是否为20平方米。
由于该问题设计的是单个总体，且要进行总体均值比较，同时家庭人均住房面积的总体可近似认为服从正态分布，因此，可采用单样本T检验来进行分析。
SPSS单样本T检验的基本操作步骤是：⑴选择菜单：【Analyze】→【Compare Means】→【One- Samples T Test】出现如图所示的窗口。
图1⑵选择待检验的变量到【Test Variables】，在【Test Value】框中输入检验值。
⑶按Option按钮定义其他选项，出现图2所示的窗口。
Option选项用来指定缺失值的处理方法。
另外，还可以输出默认95%的置信区间。
图2至此，SPSS将自动计算t同嘉陵和对应的概率P-值。
分析结果如表3和表4所示。
人均住房面积的基本描述统计结果表3人均住房面积单样本T 检验结果表4由表3可知，2993个家庭的人均住房面积的平均值为22平方米，标准差为12.7平方米，均值标准误差为（nS）为0.23.表4中，第二列是t 统计量的观测值为8.64；第三列是自由度为2992；第四列是t 统计量观测值的双尾概率P-值；第五列是样本均值与检验值的差，即t 统计量的分子部分；第六列和第七列是总体均值与原假设值差的95%的置信区间，为（1.55,2.46），由此计算出总体均值的95%的置信区间为（21.55,22.46）平方米。
该问题应采用双尾检验，因此比较α和p 。
如果α给定为0.05，由于p 小于α，因此应拒绝原假设，认为家庭人均住房面积的平均值与20平方米由显著差异。
95%的置信区间告诉我们有95%的把握认为家庭人均诸方面均值在21.55~22.46平方米之间。
三、两独立样本T 检验1.两独立样本T 检验的目的两独立样本T 检验的目的是利用来自两个总体的独立样本，推断两个总体的均值是否存在显著差异。
2．两独立样本T 检验的基本步骤。
⑴提出零假设两独立样本T 检验的原假设0H 为：两总体均值无显著差异。
表述为： 0H ：021=-μμ1μ，2μ分别为第一个和第二个总体的均值。
⑵选择检验统计量对两总体均值差的推断是建立在来自两个总体样本均值差的基础之上的，也就是希望利用两组样本均值的差去估计量总体均值的差。
因此，应关注两样本均值的抽样分布。
当两总体分布分别为),(211σμN 和),(222σμN 时，两样本均值差的抽样分布仍为正态分布，该正态分布的均值为21μμ-，方差为212σ。
在不同的情况下，212σ有不同的计算方式。
第一种情况：当两总体方差未知且相等，即21σσ=时，采用合并的方差作为两个总体方差的估计，数学定义为2)1()1(212222112-+-+-=n n S n S n Sp式中，21S ，22S 分别为第一组和第二组样本的方差；1n ，2n 分别为第一组和第二组样本的样本数。
此时两样本均值差的抽样分布的方差212σ为2212212n Sp n Sp +=σ 第二种情况：当两总体方差未知且不相等，即21σσ≠时，分别采用各自的方差，此时两样本均值差的抽样分布的方差212σ为：2212212n S n S +=σ ② 于是，两总体均值差检验的检验统计量为t 统计量，数学定义为： 2122121)(σμμ---=X X t ③在第一种情况下，t 统计量服从221-+n n 个自由度的t 分布；在第二种情况下，服从修正自由度的t 分布，修正的自由度定义为2222121212222121)()()(n nS n n S n S n S f ++= ⑶计算检验统计量观测值和概率P-值。
该步的目的是计算F 统计量和t 统计量的观测值以及相应的概率P-值。
SPSS 将自动依据单因素方差分析的方法计算F 统计量和概率P-值，并自动将两组样本的均值、样本数、抽样分布方差等代入式③中，计算出t 统计量的观测值和对应的概率P-值。
⑷给定显著性水平α，并作出决策。
第一步，利用F 检验判断两总体的方差是否相等，并据此决定抽样分布方差和自语度的计算方法和计算结果。
如果F 检验统计量的概率P-值小于显著想水平α，则应拒绝原假设，认为两总体方差没有显著差异，应选择式②和式③计算出的结果：反之，若果概率P-值大于显著性水平α则不应拒绝原假设，认为两总体方差无显著差异。
第二步，体用t 检验判断两总体均值是否存在显著差异。
如果t 检验统计量的概率P-值小于显著性水平α，则应拒绝原假设，认为两总体均值有显著性差异；反之，如果概率P-值大于显著性水平α，则不应拒绝原假设，认为两总体均值无显著差异。
3.两独立样本T 检验的应用举例原假设是：本市户口和外地户口的家庭收入人均值无显著性差异，即0:210=-μμH⑴选择菜单【Analyze 】 → 【Compare Means 】 → 【Indendent- Samples T Test 】 于是出现如图所示的窗口。
图3⑵选择检验变量到【Test Variables （s ）】框中。
⑶选择总体标识变量到【Grouping Variables 】框中。
⑷按Define Groups按钮定义两总体的标识值，显示如图4所示的窗口。
其中【Use Specified Values】表示分别输入对应两个不同总体的标志值；【Cut Point】框中应输入一个数字，大于等于该值的对应另一个总体。
图4⑸两独立样本t检验的Option选项含义与单样本t检验的相同。
分析结果如图5所示本市户口和外地户口家庭人均住房面积的基本描述统计Group Statistics户口状况N MeanStd.DeviationStd. ErrorMean人均面积本市户口2825 21.725812.17539 .22907外地户口168 26.716518.96748 1.46337图5由图5可以看出，本市户口和外地户口的家庭人均住房面积的样本平均值有一定的差距。
通过检验应推断这种差异是抽样误差造成的还是系统性的。
本市户口和外地户口家庭人均住房面积两独立样本t检验结果图6图6是本市户口和外地户口家庭人均住房面积的均值检验结果。
分析结论应通过两步完成。
第一步，两总体方差是否相等的F 检验。
这里，该检验的F 统计量的观测值为65.469，对应的概率P-值为0.00.如果显著性水平α为0.05，由于概率P-值小于0.05，可以认为两总体的方差有显著差异。
第二步，两总体均值的检验。
在第一步中，由于两总体方差有显著差，因此应看第二行T 检验的结果。
其中T 统计量的观测值为-3.369，对应的双尾开率P-值为0.001.如果显著性水平为0.05，由于概率P-值小于0.05，因此认为两总体的均值有显著差异，即本市户口和外地户口的家庭人均住房面积的平均值存在显著差异。
图6中的第七列和第八列分别为T 统计量的分子和分母；第九列和第十列为两总体差的95%置信区间的上限和下限。
三．两配对样本T 检验1.两配对样本T 检验的目的两配对样本T 检验的目的是利用来自两个不同总体的配对样本，推断两个总体的均值是否存在显著差异。
配对样本通常有两个特征：第一，两组样本的样本数相同;第二，两组样本观测值的先后顺序是一一对应的，不能随意更改。
2.两配对样本T 检验的基本步骤。
⑴提出原假设两配对样本T 检验的原假设0H 为：两总体均值无显著差异，表述为0H ：021=-μμ。
1μ，2μ分别为第一个和第二个总体的均值。
⑵选择统计量。
两配对样本T检验采用T统计量。
其思路是：首先，对两组样本分别计算出每对观测值的差值得到差值样本；然后，体用差值样本，通过对其均值是否显著为0的检验来推断两总体均值的差是否显著为0.如果差值样本的均值与0有显著差异，则可以认为两总体的均值有显著差异；反之，如果差值系列的均值与0无显著差异。
则可以认为两总体均值不存在显著差异。
⑶计算检验统计量观测值和概率P-值SPSS将计算两组样本的差值，并将相应数据代入式①，计算出T统计量的观测值和对应的概率P-值。
⑷给定显著水平α，并作出决策。
给定显著水平α，与检验统计量的概率P-值作比较。
