下载文档原格式
《统计分析与SPSS的应用(第五版)》课后练习答案(第3章)第三章：统计分析与SPSS的应用(第五版) 课后练习答案第一节：描述性统计在本章的课后习题中，我们将通过SPSS软件进行一系列的统计分析。
本节将提供第三章的课后习题答案，通过展示实际的数据和分析结果，帮助读者更好地理解统计分析的应用和SPSS软件的操作。
1. 描述性统计分析题目：使用某城市2019年1月至12月的气温数据，计算月平均气温、最高气温和最低气温的描述性统计指标。
答案：通过SPSS导入数据，选择变量"月份"和"气温"，并进行描述性统计分析。
结果显示，2019年1月至12月的气温数据的月平均气温、最高气温和最低气温的描述性统计指标如下：月平均气温：- 平均值：20°C- 标准差：2°C- 最小值：15°C- 最大值：25°C最高气温：- 平均值：28°C- 标准差：3°C- 最小值：22°C- 最大值：35°C最低气温：- 平均值：12°C- 标准差：2°C- 最小值：8°C- 最大值：18°C根据以上结果，我们可以得出结论：2019年该城市的月平均气温在20°C左右，最高气温在28°C左右，最低气温在12°C左右。
气温的变化范围相对较小，波动性较小。
这些结果可以帮助我们对该城市的气候情况进行初步了解。
2. 相关性分析题目：使用某企业2018年1月至12月的销售额和广告投入数据，计算销售额和广告投入之间的相关性。
答案：通过SPSS导入数据，选择变量"销售额"和"广告投入"，并进行相关性分析。
结果显示，2018年1月至12月的销售额和广告投入之间的Pearson 相关系数为0.85，表明二者呈现强正相关关系。
统计分析与SPSS的应⽤统计分析与SPSS的应⽤第1章SPSS统计分析软件概述常⽤的统计软件：SAS、SPSS、TSP、STATISTICA、EViews、MINITAB、Excel等。
1.1 SPSS使⽤基础数据编辑窗⼝是SPSS的主程序窗⼝，在软件启动时⾃动打开，并⼀直保持打开状态直到退出SPSS。
在运⾏时只能打开⼀个数据编辑窗⼝，它是由数据视图和变量视图组成的。
主要功能是：定义数据结构、录⼊编辑和管理待分析的数据。
结果输出窗⼝，主要功能是显⽰管理SPSS统计分析结果、报表和图形，与数据编辑窗⼝不同的是：结果输出窗⼝允许同时创建和打开多个窗⼝，⽬的是将同⼀批数据的不同分析结果指定输出到不同的输出窗⼝。
1.2 SPSS的基本运⾏⽅式SPSS的三种基本运⾏⽅式是：完全窗⼝菜单运⾏⽅式、程序运⾏⽅式、混合运⾏⽅式。
完全窗⼝菜单运⾏⽅式：所有的分析操作通过菜单、按钮、输⼊对话框等⽅式完成。
适合⼀般的统计分析⼈员和SPSS初学者。
程序运⾏⽅式：⾸先根据分析需要，将数据分析的步骤⼿⼯编写成SPSS命令程序，然后将编写好的程序⼀次性提交给计算机执⾏。
适合⼤规模的统计分析⼯作。
混合运⾏⽅式：完全窗⼝菜单运⾏⽅式和程序运⾏⽅式的综合。
1.3 利⽤SPSS进⾏数据分析的基本步骤⼀、数据分析的基本步骤1、明确数据分析的⽬标2、正确收集数据3、加⼯整理数据4、选择恰当的统计分析⽅法进⾏探索分析5、读懂统计分析结果⼆、利⽤SPSS进⾏数据分析的⼀般步骤1、SPSS数据的准备阶段在数据编辑窗⼝中定义SPSS数据的结构，录⼊和修改SPSS数据等。
2、SPSS数据的加⼯整理阶段对数据编辑窗⼝中的数据进⾏必要的预处理。
3、SPSS数据的分析阶段选择正确的统计分析⽅法，对数据编辑窗⼝中的数据进⾏分析建模。
4、SPSS分析结果的阅读和解释阶段读懂SPSS结果输出窗⼝中的分析结果，明确其统计含义，并结合应⽤背景知识做出切合实际的合理解释。
T检验的应用和注意事项（附图SPSS操作）（1）是定性还是定量资料？上表目的是反映迷走神经刺激后LHA的反映，可见是定性分析，而不是考查精确的神经元个数（全部个数一定不是以上的数目）处理：兴奋性，抑制性，无反应，三个水平是有序的，应该用秩和检验若无有序性，可用卡方检验和FISHER精确切线法。
（2）正态性上表安慰组合健脾组可见均值与方差基本相等，考虑可能为偏态分布。
处理：转换后符合正态分布和方差齐性，可用T检验。
（3）方差齐性上表示两组间的方差差异大，考虑方差不齐。
处理：应用t’检验（4）样本量当样本量n<60(总样本),总体均数未知时用t检验。
SPSS操作（1）正态性检验：SPSS操作示例SPSS中有很多操作可以进行正态检验，在此只介绍最主要和最全面最方便的操作：1、工具栏--分析—描述性统计—探索性2、选择要分析的变量，选入因变量框内，然后点选图表，设置输出茎叶图和直方图，选择输出正态性检验图表，注意显示（Display）要选择双项（Both）。
3、Output结果（1）Descriptives：描述中有峰度系数和偏度系数，根据上述判断标准，数据不符合正态分布。
S k=0，K u=0时，分布呈正态，Sk>0时，分布呈正偏态，Sk<0时，分布呈负偏态，时，Ku>0曲线比较陡峭，Ku<0时曲线比较平坦。
由此可判断本数据分布为正偏态（朝左偏），较陡峭。
（2）Tests of Normality：D检验和W检验均显示数据不服从正态分布，当然在此，数据样本量为1000，应以W检验为准。
（3）直方图直方图验证了上述检验结果。
（4）此外还有茎叶图、P-P图、Q-Q图、箱式图等输出结果，不再赘述。
结果同样验证数据不符合正态分布。
（2）方差齐性在SPSS中，如果进行方差齐性检验呢？命令是什么？方差分析(Anaylsis of V ariance, ANOV A)要求各组方差整齐，不过一般认为，如果各组人数相若，就算未能通过方差整齐检验，问题也不大。
利用SPSS进行统计检验经常需要利用不同的教学媒体或教学资源对不同的对象进行教学改革试验，但教学试验的总体往往都有较大数量，限于人力、物力与时间，通常都采用抽取一定的样本作为研究对象，这样，就存在样本的特征数量能否反映总体特征的问题，也存在着两种不同的样本的数量标志的参数是否存在差异的问题，这就必需对样本量数进行定量分析与推断，在教育统计学中称为“统计检验”。
一、统计检验的基本原理统计检验是先对总体的分布规律作出某种假说，然后根据样本提供的数据，通过统计运算，根据运算结果，对假说作出肯定或否定的决策。
如果现要检验实验组和对照组的平均数（μ1和μ2）有没有差异，其步骤为：1．建立虚无假设，即先认为两者没有差异，用表示；2．通过统计运算，确定假设成立的概率P。
⒊根据P 的大小，判断假设是否成立。
如表6-12所示。
二、大样本平均数差异的显著性检验——Z检验Z检验法适用于大样本（样本容量小于30）的两平均数之间差异显著性检验的方法。
它是通过计算两个平均数之间差的Z分数来与规定的理论Z值相比较，看是否大于规定的理论Z值，从而判定两平均数的差异是否显著的一种差异显著性检验方法。
其一般步骤：第一步，建立虚无假设，即先假定两个平均数之间没有显著差异。
第二步，计算统计量Z值，对于不同类型的问题选用不同的统计量计算方法。
（1）如果检验一个样本平均数（）与一个已知的总体平均数()的差异是否显著。
其Z 值计算公式为：其中是检验样本的平均数；是已知总体的平均数；S是样本的方差；n是样本容量。
（2）如果检验来自两个的两组样本平均数的差异性，从而判断它们各自代表的总体的差异是否显著。
其Z值计算公式为：其中，1、2是样本1，样本2的平均数；是样本1，样本2的标准差；是样本1，样本2的容量。
第三步，比较计算所得Z值与理论Z值，推断发生的概率，依据Z值与差异显著性关系表作出判断。
如表6-13所示。
第四步，根据是以上分析，结合具体情况，作出结论。
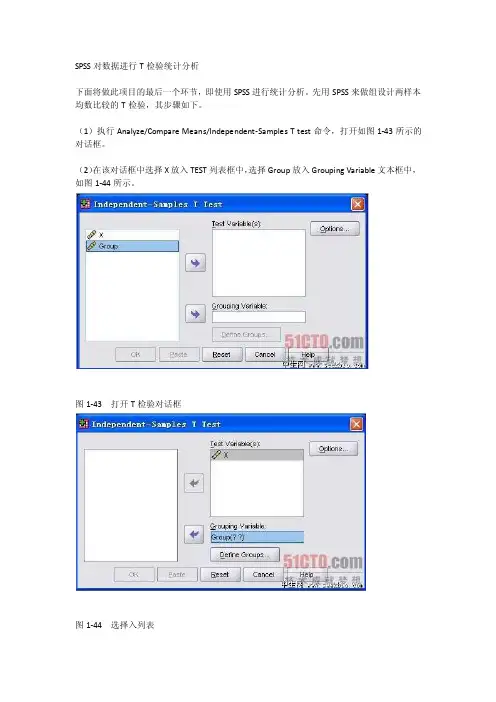
SPSS对数据进行T检验统计分析下面将做此项目的最后一个环节，即使用SPSS进行统计分析。
先用SPSS来做组设计两样本均数比较的T检验，其步骤如下。
（1）执行Analyze/Compare Means/Independent-Samples T test命令，打开如图1-43所示的对话框。
（2）在该对话框中选择X放入TEST列表框中，选择Group放入Grouping Variable文本框中，如图1-44所示。
图1-43 打开T检验对话框图1-44 选择入列表（3）单击Define Groups按钮，系统弹出比较组定义对话框，如图1-45所示。
（4）在该对话框中的两个值框中分别输入1和2，然后单击Continue按钮，如图1-46所示。
图1-45 比较组定义对话框图1-46 输入值（5）单击T检验对话框中的OK按钮，如图1-47所示。
图1-47 进行T检验（6）系统经过计算后，会弹出结果浏览窗口。
首先给出的是两组的基本情况描述，如样本量、均数等，然后是T检验的结果，如图1-48所示。
图1-48 T检验结果从上图中可见，结果分为两大部分：第一部分为Levene's方差检验，用于判断两体方差是否齐，这里的检验结果为F=0.032，p=0.860，可见在本例中方差齐；第二部分则分别给出两组所在部体方差齐和方差不齐时的T检验结果，即上面一行列出的T=2.542，V=22，p=0.019。
从而最终的统计结论为按=0.05水准，拒绝H0，认为克山病患者与健康人的血磷值是不同的。
从样本均数来看，可以确定克山病患者的血磷值较高。
《证券理论与实务》模块八考试精要（证券市场基础知识）模块八考试精要一、单项选择题1、涉及证券市场的法律、法规第一个层次是指（）。
A、法律B、行政法规C、厂纪厂规D、部门规章2、涉及证券市场的法律、法规第二个层次是指（）。
A、法律B、行政法规C、厂纪厂规D、部门规章3、涉及证券市场的法律、法规第三个层次是指（）。
SPSS数据分析3SPSS数据分析3SPSS（Statistical Package for the Social Sciences）是社会科学的一种数据分析软件，广泛应用在社会科学、心理学、教育学、经济学等领域。
在这篇文章中，我将介绍几种常用的SPSS数据分析方法。
首先是描述性统计分析。
描述性统计分析是用来总结和描述数据的基本统计特征的方法。
它可以帮助研究人员了解数据的分布情况、中心趋势和散布程度。
常见的描述性统计方法包括计算平均数、中位数、众数、标准差、方差和百分位数等。
通过这些统计指标，可以对数据集进行全面的分析和解读。
其次是t检验。
t检验是用来比较两组样本均值是否存在显著性差异的统计方法。
当我们想要比较两组样本的平均值时，可以使用t检验来检验差异是否达到了统计显著水平。
在SPSS中，可以通过选择“分析”-“比较均值”-“独立样本t检验”来进行t检验分析。
另外一种常用的数据分析方法是方差分析（ANOVA）。
方差分析用来比较三个或三个以上样本均值是否存在显著性差异。
它适用于研究因变量与多个自变量之间的关系。
在SPSS中，可以通过选择“分析”-“一元方差分析”来进行方差分析。
此外，相关分析是一种用于确定两个或多个变量之间关系强度和方向的统计方法。
在SPSS中，可以通过选择“分析”-“相关”来进行相关分析。
相关系数可以用来判断两个变量之间的相关程度，常见的相关系数包括Pearson相关系数和Spearman相关系数。
最后是回归分析。
回归分析是用来研究自变量与因变量之间关系的统计方法。
它可以确定自变量对因变量的影响程度，并建立回归方程来预测因变量的数值。
在SPSS中，可以选择“分析”-“回归”来进行回归分析。
常见的回归分析方法包括线性回归、多元回归和逐步回归等。
总之，SPSS是一种功能强大的数据分析软件，能够帮助研究人员对数据进行全面的分析和解读。
无论是描述性统计分析、t检验、方差分析、相关分析还是回归分析，SPSS都提供了简便易用的工具来进行数据分析。
spss t检验均数标准差SPSS t检验均数标准差。
SPSS（Statistical Product and Service Solutions）是一种统计分析软件，广泛应用于各个领域的数据分析和研究中。
在SPSS中，t检验是一种常用的假设检验方法，用于比较两组样本均数是否存在显著差异。
本文将介绍如何在SPSS中进行t 检验，并解释如何计算均数和标准差。
首先，我们需要明确t检验的基本概念。
t检验用于比较两组样本均数的差异是否显著。
在进行t检验之前，我们需要先对两组数据进行描述性统计分析，计算它们的均数和标准差。
均数是样本数据的平均值，用来衡量一组数据的集中趋势；标准差是样本数据的离散程度的度量，用来衡量数据的分散程度。
在SPSS中进行t检验，首先需要导入数据。
在“数据编辑器”中输入或导入两组数据，然后点击“分析”菜单中的“比较均数”选项。
在弹出的对话框中，选择“独立样本t检验”，将两组数据分别输入到“变量1”和“变量2”中，然后点击“确定”按钮进行分析。
SPSS将自动生成t检验的结果报告，其中包括了两组数据的均数、标准差、t 值、自由度和显著性水平等统计指标。
我们可以根据这些指标来判断两组数据的均数是否存在显著差异。
如果t值的绝对值较大，且显著性水平小于0.05，我们就可以拒绝原假设，认为两组数据的均数存在显著差异；反之，则接受原假设，认为两组数据的均数没有显著差异。
除了SPSS自动生成的结果报告，我们也可以手动计算两组数据的均数和标准差，然后利用t检验的公式来进行计算。
假设两组数据分别为X和Y，它们的均数分别为μ1和μ2，标准差分别为σ1和σ2，样本量分别为n1和n2，t值的计算公式为：t = (μ1 μ2) / √(σ1²/n1 + σ2²/n2)。
在计算t值之后，我们可以利用t分布表或SPSS软件来查找对应的显著性水平，从而判断两组数据的均数是否存在显著差异。
总之，t检验是一种常用的假设检验方法，用于比较两组样本均数的差异是否显著。
SPSS中t检验全都集中在分析—比较均值菜单中。
关于t检验再简单说一下，我们知道一个统计结果需要表达三部分内容，即集中性、变异性、显著性。
集中性的表现指标是均值变异的的表现指标是方差、标准差或标准误显著性的则是根据统计量判断是否达到显著性水平由于t分布样本均值的抽样分布，那么基于t分布的t检验就是样本均值的检验，是对均值差异的显著性检验。
t检验可以在以下三种分析中使用1.样本均数与总体均数的差异性分析（单样本t检验）2.配对设计样本均数或两非独立两样本均数差异性分析（配对t检验）3.两独立样本均数差异性分析（独立样本t检验）==============================================一、分析—比较均值—单样本T检验单样本T检验用来分析样本均值与总体均值的差异，以此来判断这个样本来自总体的均值是否等于（大于或小于）某个已知总体的均值，适用条件是样本数据分布呈正态分布，小样本情况下需要检验，大样本情况下近似正态，该方法比较稳健，只要不是严重偏态都可以使用。
二、分析—比较均值—配对样本T检验当配对设计的数据为连续变量时，可以使用配对T检验，配对T检验认为如果两种处理实际上没有差异，则每对数据的差值的总体均值应该为0，实际上就是已知均值为0的单样本T检验，因此适用条件也和单样本T检验一样。
三、分析—比较均值—独立样本T检验和配对设计相对应，独立样本t检验是针对成组设计，数据资料被分为两组，也就是两个样本，它们之间是相互独立的，检验的目的是判断这两个样本来自的总体均值是否存在差异。
由于涉及到两个总体，而每个总体的离散程度即方差也不一定相同，因此需要先对两样本的方差齐性做出检验，并且根据结果分为方差相同和方差不同两种算法。
独立样本t检验和配对样本t检验的区别：1.独立样本t检验用于检验两个独立样本是否来自具有相同均值的总体，也就是检验两个正态分布的总体均值是否相等。
配对样本t检验用于检验两个相关样本是否来自具有相同均值的正态总体，也就是检验两相关样本的差值的均值和零均值之间的差异显著性2.独立样本是指不同样本均值的比较，配对样本是相同样本均值的比较，例如同一个体的两次测量，如果分为实验组和对照组，那么就应该是独立样本。
