1线性规划及单纯形法
- 格式:ppt
- 大小:153.50 KB
- 文档页数:29


单纯形法与线性规划问题线性规划是一种优化问题,其基本形式是在给定的约束条件下,使目标函数最大或最小。
这种问题在工业、商业、农业和社会等领域有着广泛的应用。
在解决线性规划问题时,单纯形法是一种经典和常用的算法。
本文将介绍单纯形法和其在线性规划问题中的应用。
一、单纯形法概述单纯形法是一种基于向量空间的方法,其基本思想是沿着可行解空间中的边缘逐步搜索找到最优解。
单纯形法的运算是建立在基向量的概念上,基向量是指满足线性不可约条件的可行解基组成的向量。
单纯形法的步骤如下:1. 构造首行,确定初始基向量。
2. 选择离目标函数最远并且为正的变量,称为入基变量。
3. 选择离约束最近的基变量,称为出基变量。
4. 通过 Gauss-Jordan 消元法计算新的基向量组,确定更新后的基向量。
5. 重复步骤 2-4 直至无法选择入基变量为止。
6. 找到目标函数的最优解。
二、线性规划问题线性规划问题的一般形式如下:$$\max_{x_1,x_2,\dots,x_n\ge0}f(x_1,x_2,\dots,x_n)$$$$\text{s.t.}\begin{cases}\sum_{j=1}^na_{1j}x_j\le b_1\\\sum_{j=1}^na_{2j}x_j\le b_2\\\dots\dots\\\end{cases}$$其中,$f(x_1,x_2,\dots,x_n)$ 为线性目标函数,$a_{ij}$ 和$b_i$ 均为常数。
三、单纯形法解决线性规划问题1. 转化为标准型单纯形法只能用于标准型的线性规划问题,因此需要将原始问题转化为标准型。
标准型的形式如下:$$\max_{x_1,x_2,\dots,x_n\ge0}\sum_{j=1}^nc_jx_j$$$$\text{s.t.}\begin{cases}\sum_{j=1}^na_{1j}x_j\le b_1\\\sum_{j=1}^na_{2j}x_j\le b_2\\\dots\dots\\\end{cases}$$2. 添加松弛变量将约束条件转化为等式形式时需要添加松弛变量,松弛变量是一种关于决策变量的人工变量,其值可以取负数。



线性规划与单纯形法线性规划(Linear Programming)是一种在资源有限的情况下,通过最优化目标函数来确定最佳解决方案的数学优化方法。
而单纯形法(Simplex Method)则是一种常用的求解线性规划问题的算法。
本文将介绍线性规划与单纯形法的基本概念和运算步骤,以及实际应用中的一些注意事项。
一、线性规划的基本概念线性规划的基本思想是在一组线性不等式约束条件下,通过线性目标函数的最小化(或最大化)来求解最优解。
其中,线性不等式约束条件可表示为:```a1x1 + a2x2 + ... + anxn ≤ b```其中,x1、x2、...、xn为决策变量,a1、a2、...、an为系数,b为常数。
目标函数的最小化(或最大化)可表示为:```min(c1x1 + c2x2 + ... + cnxn)```或```max(c1x1 + c2x2 + ... + cnxn)```其中,c1、c2、...、cn为系数。
二、单纯形法的基本思想单纯形法是由乔治·丹尼尔·丹齐格尔(George Dantzig)于1947年提出的求解线性规划问题的算法。
其基本思想是通过逐步迭代改进当前解,直至达到最优解。
三、单纯形法的运算步骤1. 初等列变换:将线性规划问题转化为标准型,即将所有约束条件转化为等式形式,并引入松弛变量或人工变量。
2. 初始化:确定初始可行解。
通常使用人工变量法来获得一个初始可行解。
3. 检验最优性:计算当前基础解的目标函数值,若目标函数值小于等于零,则该基础解即为最优解。
否则,进入下一步。
4. 基本可行解的变换:选择一个入基变量和一个出基变量,并进行基本变换,得到新的基础解。
5. 迭代求解:根据目标函数值是否小于等于零,判断是否达到最优解。
若达到最优解,则算法终止;若未达到最优解,则返回步骤3进行下一轮迭代。
四、单纯形法的实际应用注意事项1. 线性规划问题的约束条件必须是线性的,且可行解集合必须是有界的。


第一章线性规划及单纯形法6.6单纯形法小结Drawingontheexampl,thetwoaxisinterceptsareplotted.2、求初始基可行解并进行最优性检验Cj比值CBXBb 检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000令非基变量x1=0,x2=0,找到一个初始基可行解:x1=0,x2=0,x3=8,x4=12,x5=36,σj>0,此解不是最优(因为z=3x1+5x2+0x3+0x4+0x5)即X0=(0,0,8,12,36)T,此时利润Z=03、寻找另一基可行解Cj比值CBXBb检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000-12/2=636/4=9主元首先确定入基变量再确定出基变量检验数?j81010060101/2012300-21x3x2x5050-30300-5/20Cj比值CBXBb检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000-12/2=636/4=9令x1=0,x4=0,得x2=6,x3=8,x5=12,即得基可行解X1=(0,6,8,0,12)T此时Z=30σ1=3>0,此解不是最优迭代4、寻找下一基可行解Cj比值CBXBb检验数?jx1x2x3x4x53500081010060101/2012300-21x3x2x5050-30300-5/208-4检验数?j40012/3-1/360101/204100-2/31/3x3x2x1053-42000-1/2-1令x4=0,x5=0,得x1=4,x2=6,x3=4,即X0=(4,6,4,0,0)T?j<0最优解:X=(4,6,4,0,0)T最优值:Z=42小结:单纯形表格法的计算步骤①将线性规划问题化成标准型。
②找出或构造一个m阶单位矩阵作为初始可行基,建立初始单纯形表。


第一章、 线性规划和单纯形法1.1 线性规划的概念一、线性规划问题的导出1.(引例) 配比问题——用浓度为45%和92%的硫酸配置100t 浓度为80%的硫酸。
取45%和92%的硫酸分别为x1和x2t,则有: 求解二元一次方程组得解。
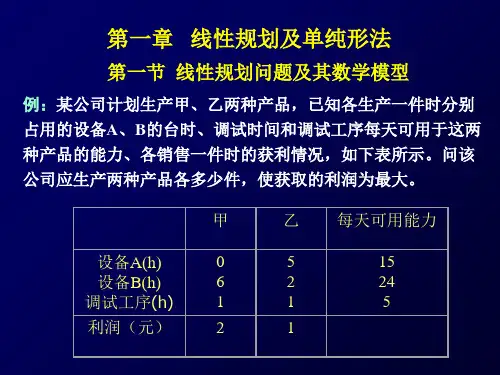
目的相同,但有5种不同浓度的硫酸可选(30%,45%,73%,85%,92%)会出现什么情况?设取这5种硫酸分别为 x1、x2、x3、x4、x5 t, 则有: ⎩⎨⎧⨯=++++=++++1008.092.085.073.045.03.01005432154321x x x x x x x x x x 请问有多少种配比方案?为什么?哪一种方案最好?假设5种硫酸价格分别为:400,700,1400,1900,2500元/t ,则有:2.生产计划问题如何制定生产计划,使三种产品总利润最大?考虑问题:⎩⎨⎧⨯=+=+1008.092.045.01002121x x x x ⎪⎩⎪⎨⎧=≥⨯=++++=++++++++=5,,2,1,01008.092.085.073.045.03.0100..250019001400700400543215432154321 j x x x x x x x x x x x t s x x x x x MinZ j(1)何为生产计划?(2)总利润如何描述?(3)还要考虑什么因素?(4)有什么需要注意的地方(技巧)?(5)最终得到的数学模型是什么?二、线性规划的定义和数学描述(模型)1.定义:对于求取一组变量xj (j =1,2,......,n),使之既满足线性约束条件,又使具有线性表达式的目标函数取得极大值或极小值的一类最优化问题称为线性规划问题,简称线性规划。
2.配比问题和生产计划问题的线性规划模型的特点:用一组未知变量表示要求的方案,这组未知变量称为决策变量;存在一定的限制条件,且为线性表达式;有一个目标要求(最大化,当然也可以是最小化),目标表示为未知变量的线性表达式,称之为目标函数; 对决策变量有非负要求。
线性规划单纯形法线性规划是一种优化问题求解方法,它通过建立数学模型,来寻找使目标函数达到最优的决策变量取值。
线性规划的主要特点是目标函数和约束条件都是线性的。
单纯形法是线性规划中最常用的求解方法之一,它是由美国数学家Dantzig在1947年提出的。
单纯形法通过迭代计算的方式,逐步优化目标函数的值,直到找到最优解为止。
单纯形法的步骤如下:1. 建立线性规划模型:确定决策变量、目标函数和约束条件,并确定它们的线性关系。
2. 初始可行解:选择一个初始可行解,使得所有的约束条件都得到满足。
一般来说,可以通过将约束条件全部转化为等式约束,从而求解出一个初始可行解。
3. 判断最优解:计算当前可行解对应的目标函数值,判断是否是最优解。
如果是最优解,则终止算法;如果不是最优解,则进入下一步。
4. 寻找进入变量:选择一个进入变量,即目标函数可以通过增加该变量的值而增大。
5. 寻找离开变量:选择一个离开变量,即通过增加进入变量来保持其他约束条件满足的同时,尽可能减小目标函数的值。
6. 更新可行解:根据进入变量和离开变量的取值更新可行解,并转化为下一个迭代的初始可行解。
7. 重复以上步骤,直到找到最优解为止。
单纯形法的优势在于它可以在有限的迭代次数内找到最优解。
然而,单纯形法的缺点也是显著的,它在处理大规模问题时计算复杂度很高,可能需要大量的计算时间。
总结来说,线性规划单纯形法是一种求解线性规划问题的有效方法。
通过迭代计算,单纯形法不断改进可行解,最终找到使目标函数达到最优的决策变量取值。
虽然单纯形法在处理大规模问题时存在一定的局限性,但在许多实际问题中仍然得到广泛应用。