当前位置：文档之家 › 第1章线性规划及单纯形法

第1章线性规划及单纯形法

  • 格式：doc
  • 大小：976.00 KB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

第一章线性规划问题及单纯形解法演示文稿

第一章线性规划问题及单纯形解法演示文稿
线性规划问题的可行解集S是凸集 设X属于S,若x=0,则一定为极点；若x 0，则为极点的充要条件是：x的正分量所 对应的系数列向量线性无关。
只要存在可行解，就一定存在极点
极点的个数是有限的
最优解只可能在凸集的极点上，而不可能发生 在凸集的内部
38
第38页，共65页。
关于标准型解的若干基本概念：
Z=15x11+21x12+18x13+
20x21+25x22+16x23, x11+x12+x13≤200, x21+x22+x23≤150, x11+ x21 ＝100, x12+x22＝80, x13+x23≥90, x13+x23≤120, xij≥0 ﹙i=1,2 j=1,2,3﹚.
10
第10页，共65页。
maxz( x) c x c x c x
11
22
nn
s.t.
a x a x a x b
11 1
12 2
1n n
1
ax 21 1
a x 22 2
a x 2n n
b 2
am1
x 1
a x m2 2
a x mn n
b m
x , x ,, x 0
1
2
n
12
第12页，共65页。
1、标准型的几种不同的表示方式
对有限个约束条件则其可行域的顶点也是有限的。
z=10000=50x1+100x
2
z=0=50x1+100x2
x2
x1+x2=300
AB C
E
z=27500=50x1+100x

第一章 线性规划及单纯形法

第一章 线性规划及单纯形法
37
线性规划问题的标准形式： 线性规划问题的标准形式：
max f = ∑ c j x
j =1 j n
n ∑ aij x j = bi , i = 1,2,L , m j =1 x j ≥ 0, j = 1,2,L , n
日产量（ 日产量（吨） 9 5 7 21
11
）（模型 例2（运输问题）（模型） （运输问题）（模型）
minf = 2 x11 + 9 x12 + 10 x13 + 7 x14 + x21 + 3 x22 + 4 x23 + 2 x24 + 8 x31 + 4 x32 + 2 x33 + 5 x34 x11 + x12 + x13 + x14 = 9 x +x +x +x =5 23 24 21 22 x31 + x32 + x33 + x34 = 7 x11 + x21 + x31 = 3 s.t. x12 + x22 + x32 = 8 x13 + x23 + x33 = 4 x14 + x24 + x34 = 6 xij ≥ 0(i = 1,2,3; j = 1,2,3,4)
18
3、（线性规划）数学模型的三要素 、（线性规划） 、（线性规划 变量/决策变量 决策变量； ①变量 决策变量； 目标函数（ ②目标函数（max/min）； ）； 约束条件。 ③约束条件。
19
决策变量： ①变量/决策变量：指决策者为实现规划目标采 变量 决策变量 取的方案、措施，是问题中要确定的未知量； 取的方案、措施，是问题中要确定的未知量；

运筹学

运筹学

11
目录
（三）LP问题的标准型
1.为了讨论LP问题解的概念和解的性质以及对LP问题求 解方便，必须把LP问题的一般形式化为统一的标准型：
minz=c1x1+c2x2+…+cnxn
j =1 a11 x2 + a12 x2 + + a1n xn = b1 a x + a x + + a x = b n 2n n 2 21 2 22 2 简 aij x j = bi (i = 1,2, L , m) s.t 化 j =1 x j ≥ 0( j = 1,2,L , n) am1 x2 + am 2 x2 + + amn xn = bm x1 , x2 , , xn ≥ 0
A ( 0 ,3 ) 10 15 , ) B( 7 7 5 C ( ,0 ) 2
max
Z = 5 x1 + 4 x 2
3 x 1 + 5 x 2 ≤ 15 2 x1 + x 2 ≤ 5 2 x 1 + 2 x 2 ≤ 11 x1 , x 2 ≥ 0
Z=
110 7
2x1+2x2=11
C 2.5
5x1+4x2=0 红线为目标函数的等值线 等值线. 红线为目标函数的等值线
j i= 1
j
(1.4) (1.5) (1.6)
ì n a ij x j = s .t . j = 1 í 1.从代数的角度看： x j 0 1.
b
i
可行解（Feasible Solution)： 满足约束条件(1.5)和(1.6)的 解X=(x1,x2,…,xn)T称为可行解。所有可行解构成可行解集， 即可行域。 最优解(Optimal Solution): 而使目标函数达到最大值的可 行解称为最优解，对应的目标函数值称为最优值。 求解LP问题就是求其最优解和最优值，但从代数的角 17 度去求是困难的。 目录

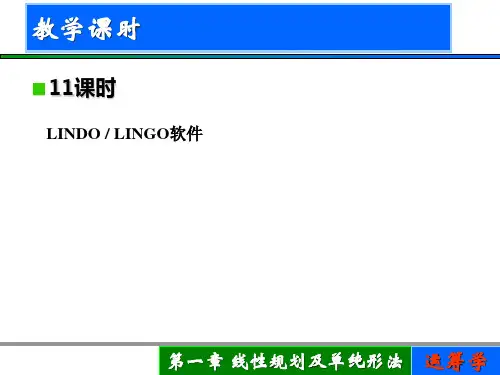
第1章-线性规划及单纯形法-课件(1)

第1章-线性规划及单纯形法-课件(1)

✓ x1、 x2 0
IБайду номын сангаас
设备
1
原材料 A 4
原材料 B 0
利润
2
II 资源限量
2 8 台时
0
16kg
4
12kg
3
第一章 线性规划及单纯形法 运筹学
该计划的数学模型
✓ 目标函数 ✓ 约束条件
Max Z = 2x1 + 3x2
x1 + 2x2 8 4x1 16 4x2 12 x1、 x2 0
x1
✓ 美国航空公司关于哪架飞机用于哪一航班和哪些 机组人员被安排于哪架飞机的决策。
✓ 美国国防部关于如何从现有的一些基地向海湾运 送海湾战争所需要的人员和物资的决策。
✓ ……
第一章 线性规划及单纯形法 运筹学
二、线性规划问题的数学模型
✓ 1、一般形式 ✓ 2、简写形式 ✓ 3、表格形式 ✓ 4、向量形式 ✓ 5、矩阵形式
1、唯一最优解
max Z 2 x 1 3 x 2
2 x 1 2 x 2 12 ⑴
x1 4 x1
2 x2
8 16
⑵ ⑶
4 x 2 12 ⑷
x 1 0 , x 2 0
1 234 56
x2
⑶ ⑷
(4，2)
0 1 234 5678
x1
⑵
⑴
✓最优解：x1 = 4,x2 = 2，有唯一最优解Z=14。
第一章 线性规划及单纯形法 运筹学
三、线性规划模型的标准形式
✓ 1、标准形式 ✓ 2、转换方式
第一章 线性规划及单纯形法 运筹学
1、标准形式
maZx cjxj
xj
aijxj 0
bi

运筹学第1章：线性规划问题及单纯型解法

运筹学第1章：线性规划问题及单纯型解法

原料甲 原料乙 最低含量 VA 0.5 0.5 2 VB1 1.0 0.3 3 VB2 0.2 0.6 1.2 VD 0.5 0.2 2 0.3 0.5 单价
分别代表每粒胶丸中甲, 设 x1, x2分别代表每粒胶丸中甲, 乙两种原料的用量
5
例3,合理下料问题 , 分别代表采用切割方案1~8的套数, 的套数, 设 xj 分别代表采用切割方案 的套数
19
( f(x
)= 3
6
1.2.2 单纯型法的基本思路
确定初试基础可行解
检查是否为 最优解? 最优解?
是
求最优解的目标函数值
否 确定改善方向
求新的基础可行解
20
1.2.3 单纯型表及其格式
IV CB III XB II x1 b c1 a11 a21 c1′′= cn+1 xn+1 b1 c2′′= cn+2 xn+2 b2 x2 … xn c2 … cn a12 … a1n a22 … a2n I xn+1 cn+1 1 0 0 zn+1 xn+2 cn+2 0 1 0 zn+2 … … … … … … xn+m cn+m 0 0 1 zn+m
OBJ : max f ( x) = 6x1 + 4x2 2x1 + x2 ≤ 10 铜资源约束 x1 + x2 ≤ 8 铅资源约束 s.t. x2 ≤ 7 产量约束 x1, x2 ≥ 0 产量不允许为负值 最优解: x1 = 2, x2 = 6, max f ( x) = 36.
4
例2,配料问题(min, ≥) ,配料问题(
2 max 1 O 1 2 3 4 D 5 6 7 H 8

运筹学第一章

运筹学第一章
OR1
30
1.1.3解的概念
概念： 1、可行解：满足所有约束条件的解。 2、可行域：即可行解的集合。所有约束条件的交 集，也就是各半平面的公共部分。满足所有约 束条件的解的集合，称为可行域。 3、凸集：集合内任意两点的连线上的点均属于这 个集合。如：实心球、三角形。线性规划的可 行域是凸集。
OR1
OR1
27
线性规划图解法例题
（无界解）
max z x 2 y x y 1 2 x 4 y 3 x 0, y 0
OR1
28
线性规划图解法例题
（无解）
min z x 2 y x y 2 2 x 4 y 3 x 0, y 0
请问该 医院至 少需要 多少名 护士？
5
例题2建模
目标函数：min Z=x1+x2+x3+x4+x5+x6 约束条件： x1+x2 ≥70
x2+x3 ≥60 x3+x4 ≥ 50 x4+x5 ≥20 x5+x6 ≥30 非负性约束：xj ≥0,j=1,2,…6
OR1
6
例题3：运输问题
三个加工棉花的加工厂，并且有三个仓库供应棉花，各 供应点到各工厂的单位运费以及各点的供应量与需求量 分别如下表所示：问如何运输才能使总的运费最小？
OR1
14
总
结
从以上 5 个例子可以看出，它们都属于优化问题，它们 的共同特征： 1 、每个问题都用一组决策变量表示某一方案；这组决 策变量的值就代表一个具体方案，一般这些变量取值是 非负的。 2 、存在一定的约束条件，这些约束条件可以用一组线 性等式或线性不等式来表示。 3 、都有一个要求达到的目标，它可用决策变量的线性 函数（称为目标函数）来表示。按问题的不同，要求目 标函数实现最大化或最小化。 满足以上三个条件的数学模型称为线性规划的数学模型。

第01次课--第一章 线性规划

（1-2） am1 x1 am 2 x2 amn xn (, )bm
(如果取≥0)
x1 , x2 , , xn (, )0
约束条件 （1-3）
决策变量
30
非负约束条件
国防科技大学
第一节 线性规划的问题及其数学模型
标准形式
max Z c1 x1 c2 x2
cn xn
顶点同时得到最优解，则它们连线上的任意一点都是最
优解，即有无穷最优解。
28
国防科技大学
第一节 线性规划的问题及其数学模型
图解法的优缺点分析
• 直观、简便 • 变量数多于三个以上时，无能为力
通用普遍的 求解方法 （代数方法）
？
单纯形法
模型的标准形式
？
29
国防科技大学
第一节 线性规划的问题及其数学模型 线性规划的数学模型的一般形式：
2
国防科技大学
第一章 线性规划与单纯形法
在军事活动，以及生产、管理、经营等社 会活动中经常提出一类问题，即如何合理地利用 有限的人力、物力、财力等资源，以得到最好的 效果。
3
国防科技大学
第一节 线性规划的问题及其数学模型
例 兵力运送问题 设有A、B两种型号的直升机，每次A能运 载35人，需驾驶员2人，B能运载20人，需驾
目标函数取 最大值
j 1 a11 x1 a12 x2 a1n xn b1 n a21 x1 a22 x2 a2 n xn b2 简记做 aij x j bi (i 1, 2, , m) j 1 x 0 ( j 1, 2, , m) a x a x a x b j mn n m m1 1 m 2 2 约束条件为等式， x , x , , x 0 且右端项为非负 1 2 n 值

第一章线性规划及单纯形法

第一章线性规划及单纯形法6.6单纯形法小结Drawingontheexampl,thetwoaxisinterceptsareplotted.2、求初始基可行解并进行最优性检验Cj比值CBXBb 检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000令非基变量x1=0，x2=0，找到一个初始基可行解：x1=0，x2=0，x3=8，x4=12，x5=36，σj＞0，此解不是最优（因为z=3x1+5x2+0x3+0x4+0x5)即X0=(0,0,8,12,36)T，此时利润Z=03、寻找另一基可行解Cj比值CBXBb检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000-12/2=636/4=9主元首先确定入基变量再确定出基变量检验数?j81010060101/2012300-21x3x2x5050-30300-5/20Cj比值CBXBb检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000-12/2=636/4=9令x1=0，x4=0，得x2=6，x3=8，x5=12，即得基可行解X1=(0,6,8,0,12)T此时Z＝30σ1=3＞0，此解不是最优迭代4、寻找下一基可行解Cj比值CBXBb检验数?jx1x2x3x4x53500081010060101/2012300-21x3x2x5050-30300-5/208-4检验数?j40012/3-1/360101/204100-2/31/3x3x2x1053-42000-1/2-1令x4=0，x5=0，得x1=4，x2=6，x3=4，即X0=(4,6,4,0,0)T?j＜0最优解:X=(4,6,4,0,0)T最优值:Z=42小结：单纯形表格法的计算步骤①将线性规划问题化成标准型。

②找出或构造一个m阶单位矩阵作为初始可行基，建立初始单纯形表。

第一章 线性规划及单纯形法1图解2006


简写为：
n
ma或 x(minz) cjxj
j1
jn1aijxj (,)bi (i 1,,m)
xj 0 (j 1,,n)
向量表达形式：
ma或 xm ( izn)CX
n
j 1
Pj
x
j
(, )b
X 0
C(c1,c2,,cn)
x 1
X
x2 xn
a 1 j
Pj
a2j
目标函数 mzi n 28(x1 0 1x 0 2 1x3 1x4)145(x1 02 0 x22 x3)260(x1 0 3x 0 2)373x10 4 0
约束条件
x11 x12 x13 x14 15
xx1132
x13 x14
x14 x22
x21 x23
x22 x31
x23 x32
第一章 线性规划及单纯形法
第一节 线性规划问题及其数学模型
例：某公司计划生产甲、乙两种产品，已知各生产一件时分别 占用的设备A、B的台时、调试时间和调试工序每天可用于这两 种产品的能力、各销售一件时的获利情况，如下表所示。问该 公司应生产两种产品各多少件，使获取的利润为最大。
甲
乙 每天可用能力
设备A(h)
可行域中使目标函数值达到最优的可行解称为最优解。
图解法的步骤：
（1）在平面上建立直角坐标系 （2）图示约束条件，找出可行域 （3）图示目标函数，寻求最优解
线性规划的图解
max z = x1+3x2 s.t. x1+ x2≤6
-x1+2x2≤8 x1 ≥0, x2≥0
x2 6
4
最优解 可行域
-8
0
目标函数等ห้องสมุดไป่ตู้线

运筹学基础及应用第五版胡运权第一章

问题的提出 某企业计划生产Ⅰ、Ⅱ两种产品。这两种产品都要分别在A、B、C、D四种不同设备上加工。生产每件产品Ⅰ需占用各设备分别为2、1、4、0h，生产每件产品Ⅱ，需占用各设备分别为2、2、0、4h。已知各设备计划期内用于生产这两种产品的能力分别为12、8、16、12h，又知每生产一件产品Ⅰ企业能获得2元利润，每生产一件产品Ⅱ企业能获得3元利润，问企业应安排生产两种产品各多少件，使总的利润收入为最大。
xi 0
aij
aLj
xL 0
i
∴ P1 , P2,······,PL-1, PL+1,······ Pm, Pj 线性无关。
∴ X1 也为基本可行解。
四、最优性检验和解的判别
令
，其中 随基的改变而改变
X1 = (x1 0- a1j ,x2 0- a2j ,···,xm 0- amj ,0,···,,···,0)T
必要性：X非基本可行解 X非凸集顶点 不失一般性，设X=(x1,x2,······,xm,0,0,······,0)T，为非基本可行解， ∵ X为可行解，
证：等价于 X非基本可行解X非凸集顶点
又 X是非基本可行解， ∴ P1,P2,······,Pm线性相关，即有 1P1+2P2+······+mPm=0， 其中1，2，······，m不全为0，两端同乘≠0，得 1P1+2P2+······+mPm=0，······（2）
∵ >0, 1->0 ，当xj=0， 必有yj=zj=0
∴
pjyj =
j=1
n
pjyj=b ······(1)
j=1
r
pjzj =
j=1
n
pjzj=b ······(2)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

线性规划及单纯形法 一．选择1. 运筹学应用分析、试验、（C ）的方法，对经济管理系统中人、财、物等有限资源进行统筹安排，为决策者提供有依据的最优方案，以实现最有效的管理。

A 统筹 B 量化 C 优化 D 决策2. 运筹学研究的基本手段是（A ）。

A 建立数学模型B 进行数学分析C 进行决策分析D 建立管理规范 3. 运筹学研究的基本特点是（ C ）。

A 进行系统局部独立分析B 考虑系统局部优化C 考虑系统的整体优化D 进行系统的整体决策4. 线性规划问题的数学模型包含三个组成要素：决策变量、目标函数、（B ） A 表达式 B 约束条件 C 方程变量 D 价值系数5. 线性规划问题的基可行解X 对应线性规划问题可行域（凸集）的（ C ） A 边 B 平面 C 顶点 D 内部6. 目标函数取极小化（Z min ）的线性规划问题可以转化为目标函数取极大化即（C ）的线性规划问题求解A Z minB )min(Z -C )max(Z -D Z max -7. 标准形式的线性规划问题，最优解（C ）是可行解A 一定B 一定不C 不一定D 无法确定8. 在线性规划问题中，称满足所有约束条件方程和非负限制的解为（ C ）。

A 最优解 B 基可行解 C 可行解 D 基解9. 生产和经营管理中经常提出任何合理安排，使人力、物力等各种资源得到充分利用，获得最大的效益，这就是所谓的（D ）A 管理问题B 规划问题C 决策问题D 优化问题10. 在线性规划问题中，图解法适合用于处理变量（ B ）个的线性规划问题 A 1 B 2 C 3 D 411. 求解线性规划问题时，解的情况有:唯一最优解、无穷多最优解、（ C ）、无可行解 A 无解B 无基解 C 无界解 D 无基可行解12. 在用图解法求解的时，找不到满足约束条件的公共范围，这时问题有（D ），其原因是模型本身有错误，约束条件之间相互矛盾，应检查修正。

A 唯一最优解 B 无穷多最优解 C 无界解D 无可行解13. 线性规划问题的基可行解()Tn X X X ,,1 =为基可行解的充要条件是X 的正分量所对应的系数列向量是（B ）A 线性相关B 线性独立C 非线性独立D 无法判断14. 线性规划问题进行最优性检验和解的判别时，如果当0≤j σ时，人工变量仍留在基本量中且不为零，（D ）A 唯一最优解B 无穷多最优解C 无界解D 无可行解15.如果集合C 中任意两个点21,X X 其连线上的所有点也都是集合C 中的点，称C 为（B ）A 集合B 凸集C 顶点D 子集16.线性规划问题求解的时候，目标函数与某一个约束条件平行，则解的情况为（ D ） A 无穷多最优解B 无可行解C 唯一最优解D 无法确定17.线性规划问题求解的时候,该线性规划问题有可行域，目标函数与某一个约束条件平行，则解的情况为（A ）A 无穷多最优解B 无可行解C 唯一最优解D 无法确定 18．运筹学涉及的主要领域是（C ）A 技术问题B 经济问题C 管理问题D 以上都不是 19.齐王赛马的故事运用运筹学的（C ）理论。

A 规划论B 存贮论C 博弈论D 排队论20.工业企业生产中多台设备的看管、机修服务等问题属于（ D ） A 规划论B 存贮论C 博弈论D 排队论21.单纯形法的迭代计算实际上是对约束方程的系数矩阵实施行的初等变换。

由线性代数知道，对矩阵]|||[I N B b 实施行的初等变换时，当B 变换为I ，由此上述矩阵将变换为]|||['''B N b I . 其中b '为（Ｂ ）A I b =' Bb B b1'-= C B bb 1'-= DB b ='22. 单纯形法的迭代计算实际上是对约束方程的系数矩阵实施行的初等变换。

由线性代数知道，对矩阵]|||[I N B b 实施行的初等变换时，当B 变换为I ，由此上述矩阵将变换为]|||['''B N b I .其中N '为（C ）A I N =' BBN N 1'-= CN BN 1'-= DB N ='23. 单纯形法的迭代计算实际上是对约束方程的系数矩阵实施行的初等变换。

由线性代数知道，对矩阵]|||[I N B b 实施行的初等变换时，当B 变换为I ，由此上述矩阵将变换为]|||['''B N b I .其中P j'为（B ）ＡI j P ='ＢPBP jj 1'-= ＣB P P j j 1'-= ＤB j P ='24. 单纯形法的迭代计算实际上是对约束方程的系数矩阵实施行的初等变换。

由线性代数知道，对矩阵]|||[I N B b 实施行的初等变换时，当B 变换为I ，由此上述矩阵将变换为]|||['''B N b I .其中Y -'为（D ）ＡI Y =-'ＢPB Y j1'-=- ＣBP Y j1'-=- ＤB C YB 1'--=-25. 单纯形法的迭代计算实际上是对约束方程的系数矩阵实施行的初等变换。

由线性代数知道，对矩阵]|||[I N B b 实施行的初等变换时，当B 变换为I ，由此上述矩阵将变换为]|||['''B N b I .其中σ'N为（A ）ＡN C C B N N ''-=σＢ σσNNB 1'-=ＣN C C N B N ''-=σＤ B C B N1'--=σ26. 单纯形法的迭代计算实际上是对约束方程的系数矩阵实施行的初等变换。

由线性代数知道，对矩阵]|||[I N B b 实施行的初等变换时，当B 变换为I ，由此上述矩阵将变换为]|||['''B N b I .其中σ'N为（A ）ＡN B C C B N N 1'--=σ ＢσσN N B N B C C 1'--=ＣN C C N B N -=σ' Ｄ B C C B N N1'--=σ27. 单纯形法的迭代计算实际上是对约束方程的系数矩阵实施行的初等变换。

由线性代数知道，对矩阵]|||[I N B b 实施行的初等变换时，当B 变换为I ，由此上述矩阵将变换为]|||['''B N b I .其中σ'N为（A ）ＡN Y C N N ''-=σ ＢσσN B N Y C -=' ＣY C C N B N -=σ' Ｄ Y C C B N N''-=σ28. 单纯形法的迭代计算实际上是对约束方程的系数矩阵实施行的初等变换。

由线性代数知道，对矩阵]|||[I N B b 实施行的初等变换时，当B 变换为I ，由此上述矩阵将变换为]|||['''B N b I .其中σ'N为（A ）ＡP C C j B j N ''-=σ ＢσσN j B N P C -=' ＣP C C j N B N -=σ' ＤP C C j B N N-=σ'29. 单纯形法的迭代计算实际上是对约束方程的系数矩阵实施行的初等变换。

由线性代数知道，对矩阵]|||[I N B b 实施行的初等变换时，当B 变换为I ，由此上述矩阵将变换为]|||['''B N b I .其中σ'N为（A ）ＡP B C C j B j N 1'--=σ ＢσσN j B N P C -=' ＣP C C j N B N -=σ' ＤP C C j B N N-=σ'30. 单纯形法的迭代计算实际上是对约束方程的系数矩阵实施行的初等变换。

由线性代数知道，对矩阵]|||[I N B b 实施行的初等变换时，当B 变换为I ，由此上述矩阵将变换为]|||['''B N b I .其中σ'N为（A ）ＡP Y C j j N ''-=σ ＢY P C j B N -=σ' ＣP C C j N B N -=σ' ＤP C C j B N N-=σ'二．填空1. 在线性规划问题中，称满足所有约束条件方程和非负限制的解为（可行解）。

2. 在线性规划问题中，图解法适合用于处理 （变量）为两个的线性规划问题。

3. 运筹学的英文缩写为（OR ）4. 运筹学按照所解决问题性质的差别，将实际问题归纳不同类型的数学模型，分别是（线性规划）（非线性规划）（动态规划）（图与网络分析）（存贮论）（排队论）（对策论）（决策论）。

5. 运筹学研究的基本特点是（考虑系统的整体优化）（多学科的配合）以及(模型方法的应用）6.（ 朴素）运筹学思想在我国古代最早诞生。

7. 线性规划问题求解的时候,该线性规划问题可行域是空集，则（ 无可行解）。

8. 单纯形法计算线性规划问题的时候，θ值在单纯形表的（右）侧。

9. 单纯形法计算线性规划问题的时候，是计算变量为（ｎ ）维的情况。

10. 由于计算机计算取值的时候的误差，可以对添加人工变量后的线性规划问题分为（两个阶段 ）来计算。

11. 在单纯形法计算的时候，一般要求（0≤j σ）的时候停止计算。

12. 线性规划问题化为标准形式的时候，松弛变量和剩余变量统称为（松弛变量） 13. 图解法是应用（平面作图）的方式进行求解。

14. 运筹学一词来源于《史记》中（运筹帷幄之中，决胜千里之外）。

15. 运筹学作为一门数学学科，是在（第二次世界大战期间）形成的 16. 生产计划制定是典型的（ 线性规划问题） 数学模型的应用。

17. 人事管理是典型的（ 线性规划问题） 数学模型的应用。

18. 线性规划问题在添加松弛变量之后，其在目标函数中的系数为（ 零） 19. 线性规划问题的可行解的集合称为（ 可行域）。

20. 在线性规划中，如果系数矩阵中存在（ 单位阵）,就可以直接写出初始可行基。

21.据《大英百科全书》释义：运筹学是一门应用于管理有组织系统的科学，为掌管这类系统的人提供（决策目标）和（数量分析）的工具。

22.我国《辞海》中关于运筹学的释义为：运筹学主要是研究经济活动与军事活动中能用（数量）来表达有关运用、筹划与管理方面的问题。

它根据问题的要求，通过（数学分析与运算），作出综合性的合理安排，以达到较经济较有效地使用人力物力。

23.运筹学一词的英文为Operations Research,可直译为（运用研究）或（作业研究）。