定性数据分析第二章课后答案资料
- 格式:doc
- 大小:390.50 KB
- 文档页数:10

统计学课后思考题答案统计学课后思考题答案统计学课后思考题答案~~ 来源: 张倩倩Orange的日志在百度文库上下载下来的,奉献给同胞们~统计课后思考题答案第一章思考题1.1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1.6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。

统计学(第五版)课后习题答案(完整版)第一章思考题1.1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1.6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1.7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
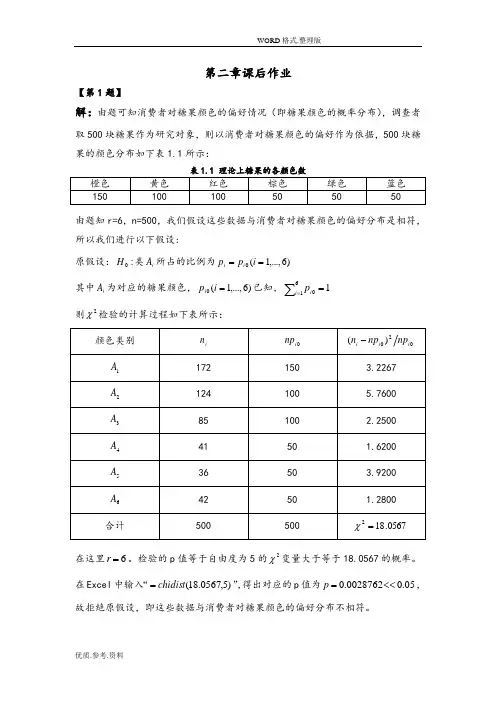
第二章课后作业【第1题】解:由题可知消费者对糖果颜色的偏好情况(即糖果颜色的概率分布),调查者取500块糖果作为研究对象,则以消费者对糖果颜色的偏好作为依据,500块糖果的颜色分布如下表1.1所示:表1.1 理论上糖果的各颜色数由题知r=6,n=500,我们假设这些数据与消费者对糖果颜色的偏好分布是相符,所以我们进行以下假设:原假设::0H 类i A 所占的比例为)6,...,1(0==i p p i i 其中i A 为对应的糖果颜色,)6,...,1(0=i p i 已知,1610=∑=i i p 则2χ检验的计算过程如下表所示:在这里6=r 。
检验的p 值等于自由度为5的2χ变量大于等于18.0567的概率。
在Excel 中输入“)5,0567.18(chidist =”,得出对应的p 值为05.00028762.0<<=p ,故拒绝原假设,即这些数据与消费者对糖果颜色的偏好分布不相符。
【第2题】解:由题可知 ,r=3,n=200,假设顾客对这三种肉食的喜好程度相同,即顾客选择这三种肉食的概率是相同的。
所以我们可以进行以下假设:原假设 )3,2,1(31:0==i p H i则2χ检验的计算过程如下表所示:在这里3=r 。
检验的p 值等于自由度为2的2χ变量大于等于15.72921的概率。
在Excel 中输入“)2,72921.15(chidist =”,得出对应的p 值为05.00003841.0<<=p ,故拒绝原假设,即认为顾客对这三种肉食的喜好程度是不相同的。
【第3题】解:由题可知 ,r=10,n=800,假设学生对这些课程的选择没有倾向性,即选各门课的人数的比例相同,则十门课程每门课程被选择的概率都相等。
所以我们可以进行以下假设:原假设)10,...,2,1(1.0:0==i p H i 则2χ检验的计算过程如下表所示:在这里10=r 。
检验的p 值等于自由度为9的2χ变量大于等于5.125的概率。

统计学(第五版)贾俊平课后习题答案(完整版)第一章思考题1.1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1.6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1.7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。

统计课后思考题答案第一章思考题1.1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1.6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1.7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。

第二章误差及分析数据的统计处理思考题1.正确理解准确度和精密度,误差和偏差的概念。
答:准确度是测定平均值与真值接近的程度,常用误差大小来表示,误差越小,准确度越高。
精密度是指在确定条件下,将测试方法实施多次,所得结果之间的一致程度。
精密度的大小常用偏差来表示。
误差是指测定值与真值之差,其大小可用绝对误差和相对误差来表示。
偏差是指个别测定结果与几次测定结果的平均值之间的差别,其大小可用绝对偏差和相对偏差表示,也可以用标准偏差表示。
2.下列情况分别引起什么误差?如果是系统误差,应如何消除?(1)砝码被腐蚀;(2)天平两臂不等长;(3)容量瓶和吸管不配套;(4)重量分析中杂质被共沉淀;(5)天平称量时最后一位读数估计不准;(6)以含量为99%的邻苯二甲酸氢钾作基准物标定碱溶液。
答:(1)引起系统误差,校正砝码;(2)引起系统误差,校正仪器;(3)引起系统误差,校正仪器;(4)引起系统误差,做对照试验;(5)引起偶然误差;(6)引起系统误差,做对照试验或提纯试剂。
3.用标准偏差和算术平均偏差表示结果,哪一种更合理?答:用标准偏差表示更合理。
因为将单次测定值的偏差平方后,能将较大的偏差显著地表现出来。
4.如何减少偶然误差?如何减少系统误差?答:在一定测定次数范围内,适当增加测定次数,可以减少偶然误差。
针对系统误差产生的原因不同,可采用选择标准方法、进行试剂的提纯和使用校正值等办法加以消除。
如选择一种标准方法与所采用的方法作对照试验或选择与试样组成接近的标准试样做对照试验,找出校正值加以校正。
对试剂或实验用水是否带入被测成分,或所含杂质是否有干扰,可通过空白试验扣除空白值加以校正。
5.某铁矿石中含铁39.16%,若甲分析得结果为39.12%,39.15%和39.18%,乙分析得39.19%,39.24%和39.28%。
试比较甲、乙两人分析结果的准确度和精密度。
解:计算结果如下表所示由绝对误差E 可以看出,甲的准确度高,由平均偏差d 和标准偏差s 可以看出,甲的精密度比乙高。

亲爱的,一章一章来,肯定能弄完的,你是最棒的!统计学(第五版)贾俊平课后习题答案(完整版)第一章思考题什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
解释分类数据,顺序数据和数值型数据答案同举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
第二章作业
2.4
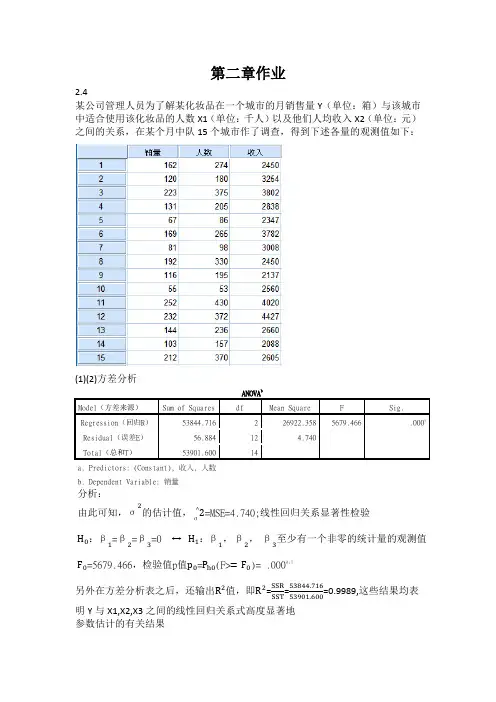
某公司管理人员为了解某化妆品在一个城市的月销售量Y(单位:箱)与该城市中适合使用该化妆品的人数X1(单位:千人)以及他们人均收入X2(单位:元)之间的关系,在某个月中队15个城市作了调查,得到下述各量的观测值如下:
另外在方差分析表之后,还输出R2值,即R2=SSR
SST =53844.716
53901.600
=0.9989,这些结果均表
明Y与X1,X2,X3之间的线性回归关系式高度显著地参数估计的有关结果
参数估计
(1)得到回归方程为
=Y ^
3.453+0.496X 1+0.009X 1
(3)
β1的置信区间为:(0.483,0.509) β2的置信区间为:(0.007,0.011) (4)
由上表可知对α=0.05时,上表第二行p 均小于α,则X 1,X 2对Y 的影响是显著地;
由SPSS的分析回归线性保存可得当()=(220,2500)是预测值为135.57141,预测区间为(134.08348,137.05934)。
(6)
由上Normal Q-Q Plot of m图知,该正态性近似符合。


统计课后思考题答案第一章思考题什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
解释分类数据,顺序数据和数值型数据答案同举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
统计应用实例人口普查,商场的名意调查等。
定性数据统计分析课后练习题含答案1. 问题描述一项研究调查了 100 名学生的职业意向,结果发现54人有医生的职业意向,23人希望成为工程师,11人希望成为演员,5人有投行的意向,7人希望成为教师。
请使用适当的统计方法回答以下问题。
2. 题目1.在这100个学生中,有多少人有IT行业的职业意向?2.有多少比例的学生有医生的职业意向?3.有多少比例的学生没有教师和医生的职业意向?4.哪个职业的意向最高?3. 答案1.IT行业的职业意向人数是5人。
解析:根据题目给出的数据,5人有投行的意向,而我们知道投行常常被归类为金融或者IT行业,所以可以推断出这5人中肯定包含有IT行业的职业意向。
2.有医生职业意向的学生比例是 $\\frac{54}{100} = 0.54$。
解析:根据题目给出的数据,有医生职业意向的学生人数为 54,而总样本数为100,所以比例为54/100=0.54。
3.没有教师和医生职业意向的学生比例是 $\\frac{23+11+5}{100} =0.39$,即 $39\\%$。
解析:根据题目给出的数据,有医生职业意向的有54人,有工程师职业意向的有23人,有演员职业意向的有11人,一共这三类职业意向的学生人数为54+23+11=88,而总样本数为100,所以没有这三类职业意向的学生人数为100−88=12,所以比例为12/100=0.12,即 $12\\%$,所以没有教师和医生职业意向的学生比例为1−0.54−0.12=0.34,即$34\\%$。
4.医生职业意向的比例最高,为 $54\\%$。
解析:根据题目给出的数据,有医生职业意向的学生人数为 54,有工程师职业意向的学生人数为 23,有演员职业意向的学生人数为 11,有投行的意向的学生人数为 5,有教师职业意向的学生人数为 7。
因此,医生职业意向的人数最多,比例为 $54\\%$。
定性数据分析第二章课后答案第二章课后作业【第1题】解:由题可知消费者对糖果颜色的偏好情况(即糖果颜色的概率分布),调查者取500块糖果作为研究对象,则以消费者对糖果颜色的偏好作为依据,500块糖果的颜色分布如下表1.1所示:表1.1 理论上糖果的各颜色数由题知r=6,n=500,我们假设这些数据与消费者对糖果颜色的偏好分布是相符,所以我们进行以下假设:原假设::0H 类i A 所占的比例为)6,...,1(0==i p p i i 其中i A 为对应的糖果颜色,)6,...,1(0=i p i 已知,1610=∑=i i p 则2χ检验的计算过程如下表所示:在这里6=r 。
检验的p 值等于自由度为5的2χ变量大于等于18.0567的概率。
在Excel 中输入“)5,0567.18(chidist =”,得出对应的p 值为05.00028762.0<<=p ,故拒绝原假设,即这些数据与消费者对糖果颜色的偏好分布不相符。
【第2题】解:由题可知 ,r=3,n=200,假设顾客对这三种肉食的喜好程度相同,即顾客选择这三种肉食的概率是相同的。
所以我们可以进行以下假设:原假设 )3,2,1(31:0==i p H i则2χ检验的计算过程如下表所示:在这里3=r 。
检验的p 值等于自由度为2的2χ变量大于等于15.72921的概率。
在Excel 中输入“)2,72921.15(chidist =”,得出对应的p 值为05.00003841.0<<=p ,故拒绝原假设,即认为顾客对这三种肉食的喜好程度是不相同的。
【第3题】解:由题可知 ,r=10,n=800,假设学生对这些课程的选择没有倾向性,即选各门课的人数的比例相同,则十门课程每门课程被选择的概率都相等。
所以我们可以进行以下假设:原假设)10,...,2,1(1.0:0==i p H i 则2χ检验的计算过程如下表所示:在这里10=r 。
检验的p 值等于自由度为9的2χ变量大于等于5.125的概率。
在Excel 中输入“)9,125.5(chidist =”,得出对应的p 值为05.0823278349.0>>=p ,故接受原假设,即学生对这些课程的选择没有倾向性,各门课选课人数的频率为0.1。
【第4题】解:(1)由题可知,r=3,n=5606,假设1997年8月中国股民投资状况的调查数据和比较流行的说法是相符合。
所以我们可以进行以下假设: 原假设::0H 类i A 所占的比例为)3,2,1(0==i p p i i其中)3,2,1(=i A i 为股票投资中对应的赢、持平和亏,)3,2,1(0=i p i 已知,1310=∑=i i p则2χ检验的计算过程如下表所示:在这里3=r 。
检验的p 值等于自由度为2的2χ变量大于等于3511.96137的概率。
在Excel 中输入“)2,72921.15(chidist =”,得出对应的p 值为05.00<<=p ,故拒绝原假设,即认为1997年8月中国股民投资状况的调查数据和比较流行的说法是不相符合的。
(2)解:由题知股票投资中,赢包括盈利10%及以上、盈利10%以下,符合条件的股民共有151+122=273人;持平可以指基本持平,符合条件的股民共有240人;亏包括亏损不足10%和亏损10%及以上,符合条件的股民共有517+240=757人。
由题可知,r=3,n=1270,假设2003年2月上海青年报上的调查数据和比较流行的说法是相符合。
所以我们可以进行以下假设:原假设::0H 类i A 所占的比例为)3,2,1(0==i p p i i其中)3,2,1(=i A i 为股票投资中对应的赢、持平和亏,)3,2,1(0=i p i 已知,1310=∑=i i p则2χ检验的计算过程如下表所示:在这里3=r 。
检验的p 值等于自由度为2的2χ变量大于等于188.21372的概率。
在Excel 中输入“)2,21372.188(chidist =”,得出对应的p 值为05.00<<=p ,故拒绝原假设,即认为2003年2月上海青年报上的调查数据和比较流行的说法是不相符合的。
【第5题】解:由题意,我们将“开红花”、“开白花”和“开粉红色花”分别记为321,,A A A ,并记i A 所占的比例为)3,2,1(=i p i ,本题所要检验的原假设为:pq p q p H 2 ,p ,p :322210===其中1=+q p ,这些i p 都依赖一个未知参数p 。
在原假设0H 成立时的似然函数为13210860362242)1()2()()()(p p pq q p p L -∝∝则对L(p)取对数得)1ln(132ln 108)(ln p p p L -+=从而有对数似然方程01132108)(ln =--=∂∂pp p p L 即p p 132)1(108=-。
据此求得p 的极大似然估计45.0ˆ=p,从而得到i p 的极大似然估计 3,2,1),ˆ(ˆ==i p p pi i 。
它们分别为0.2025、0.3025和0.495。
由此得各类的期望频数的估计值3,2,1,ˆ=i pn i 。
它们分别为24.3、36.3、132.20和59.4。
所以2χ统计量的值为0.012244.59)4.5960(3.36)3.3636(3.24)3.2424(2222=-+-+-=χ这里r=3,m=1,r-m-1=1。
检验的p 值等于自由度为1的2χ变量。
利用Excel 可以算出p 值05.0911893.0)1,01224.0(>>==chidist p ,故接受原假设,即我们认为以上数据在0.05的水平下与遗传学理论是相符的。
【第6题】解:由题意,我们可以得到以下信息:① 遗传因子的分布律为:(其中p+q+r=1)②血型的分布律为:将“O ”血型、“A ”血型、“B ”血型和“AB ”血型这四类血型分别记为41A ......, ,A ,并记i A 所占的比例为)4,......,1( =i p i ,本题所要检验的原假设为:pq p qr q p pr p r H 2 ,2 ,2p ,p :42322210=+=+==这些i p 都依赖两个未知参数q p ,。
在原假设0H 成立时的似然函数为5813213243643674858132243623742)2()22()22()1( )2()2()2()(),(pq p q qq p pq p pq qr q pr p r q p L ------∝++∝则对L(p,q)求对数得pqp q q q p p q p q p L 2ln 58)22ln(132ln 132)22ln(436ln 436)1ln(748),(ln +--++--++--=对),(ln q p L 求偏导数得⎪⎪⎩⎪⎪⎨⎧=+---+---+---=∂∂=+---+---+---=∂∂058221321322287201748ln 058222640224364361748ln q p q q q p q p qL p p q q p p q p p L利用Mathematica 软件求解(程序编码及运行结果见附录)解得p 和q 的极大似然估计为100.0ˆ89,2.0ˆ≈≈q p,从而得i p 的极大似然估计4,....,1 ),ˆ,ˆ(ˆ==i q p p pi i 。
它们分别为0.37332、0.43668、0.13220和0.05780。
由此得各类的期望频数的估计值1,....,4i ,ˆ=i pn 。
它们分别为373.32、436.68、132.20和57.80。
所以2χ统计量的值为003292.0 80.57)80.5758(20.132)20.132132(68.436)68.436436(32.373)32.373374(22222=-+-+-+-=χ 这里r=4,m=2,r-m-1=1。
检验的p 值等于自由度为1的2χ变量。
有Excel 可以算出p 值为05.0 954245.0)1 ,003292.0(>>==chidist p ,故接受0H ,我们认为以上数据与遗传学理论是相符的。
附录 ①程序代码:NSolve[{(-748)/(1-p-q)+436/p+(-436)/(2-p-2*q)+0+(-264)/(2-q-2*p)+58/p==0,(-748)/(1-p-q)+0+(-872)/(2-p-2*q)+132/q+(-132)/(2-q-2*p)+58/q==0},{p,q}]//MatrixForm②利用Mathematica 软件运行结果: Out[21] //MatrixForm⎪⎪⎪⎪⎪⎭⎫ ⎝⎛→→→→→→→→0.0999891 q 0.288632 p 0.473295q 0.722065 p 1.50996 q 0.209806 p 0.0900929 q 1.56083p 注:在上述结果中由于p + q = 1-r < 1,所以软件运行的结果中只有第四个解满足条件,即p 和q 的极大似然估计为100.0ˆ89,2.0ˆ≈≈q p。
【第7题】解:由题知,在豌豆实验中,子系从父系(或母系)接受显性因子“黄色”和“青色”的概率分别为p 和1-p ,而子系从父系(或母系)接受显性因子“圆”和“有角”的概率分别为q 和1-q 。
我们将豌豆实验中得到的“黄而圆的”、“青而圆的”、“黄而有角的”和“青而有角的”这四类豌豆分别记为1A ,2A ,3A ,4A ,则这四类豌豆的分布律如下表所示:将豌豆类型i A 所占的比例记为)4,......,1( =i p i ,则本题所要检验的原假设为:224232210)1()1( ,)1)(2( )1)(2(p ),2)(2(p :q p p q p p p p q q q p pq H --=--=--=--=这些i p 都依赖两个未知参数q p ,。
在原假设0H 成立时的似然函数为266280423416423416322210121082315)1()1()2()2( ])1()1[(])1)(2([])1)(2([)]2)(2([),(q p q p q p q p q p p p q q q p pq q p L ----∝--------∝则对L(p,q)求对数得)1ln(266)1ln(280)2ln(423)2ln(416ln 423ln 416),(ln q p q p q p q p L -+-+-+-++=对),(ln q p L 求偏导数得⎪⎪⎩⎪⎪⎨⎧=----=∂∂=----=∂∂012662423423ln 012802416416ln q q q qL p p p p L 即得出下列方程:⎪⎩⎪⎨⎧=+-=+-08322224111208462224111222q q p p 解得p 和q 的极大似然估计为498.0ˆ511,.0ˆ≈≈q p,从而得i p 的极大似然估计4,....,1 ),ˆ,ˆ(ˆ==i q p p pi i 。