数据分析(梅长林)第1章习 题答案

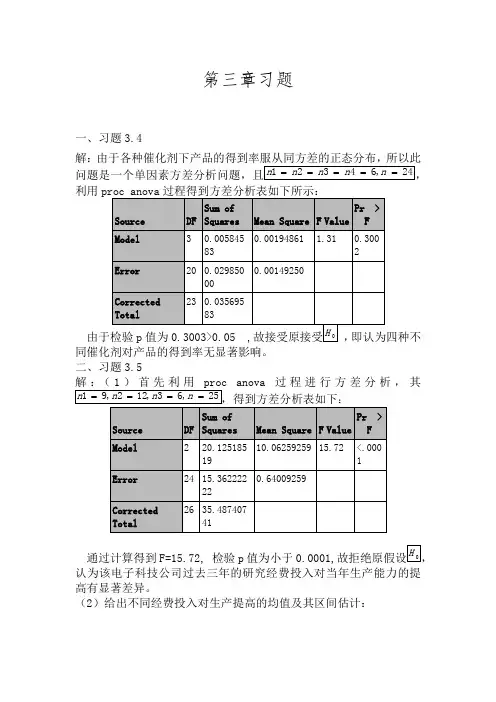
第三章习题一、习题3.4解：由于各种催化剂下产品的得到率服从同方差的正态分布，所以此利用proc anova过程得到方差分析表如下所示：同催化剂对产品的得到率无显著影响。

二、习题3.5anova过程进行方差分析，其通过计算得到F=15.72, 检验p值为小于0.0001,认为该电子科技公司过去三年的研究经费投入对当年生产能力的提高有显著差异。

（2）给出不同经费投入对生产提高的均值及其区间估计：为95%的置信区间为：95%的Bonferroni 同时置信区间为：Bonferroni 同时置信区间都位于负值区间可知随着三年科研经费的投入越高，当年生产能力的改善越显著。

三、习题3.6解：（1）首先利用SAS 的proc anova 过程的means 语句，求出各水平的均值和标准差：如下所示：由上表可知，（a1,b1）组合和（a1,b3）组合的标准差分别为2.030875、2.8067751与其他组合的标准差相差较大，所以我认为假定误差的等方差性不太合理。

故不能直接进行方差分析。

（2）由（1）可知直接进行方差分析是不合理的，所以对观测数据做对数变换，首先来分析个水平组合是否是方差齐性的。

由以上结果可以看出各组合水平上的标准差趋于一致，各组之间的标准差差异比较小。

说明各组合的离散程度比较接近。

故可以利用变换之后的数据在进行方差分析。

（3）由SAS系统的proc anova过程对进行自然对数变换后的数据进行方差分析，得到如下的误差分析表：x1*x2的影响是不显著的，检验P=0.3143>0.05，即两种铁离子残留量的百分比差异在不同剂量水平下可认为是相同的。

而由因素A和因素B对残留量的百分比的影响均显著,检验P值分别为0.0161和<.0001，所以两种铁离子残留量的百分比是有显著差异的，不同剂量水平下残留量的百分比也是有显著差异的。

（4）求出各因素在不同水平下的均值以及估计区间：SAS系统的proc anova过程对数据进行方差分析，得到各因素两两的Bonferroni同时置信区间为：均值之差的置信度为95%（注：可编辑下载，若有不当之处，请指正，谢谢!）。

习题4.5实验报告一、实验目的问题描述：在习题1.5表1.9中，列出了历年人口出生率、死亡率和自然增长率（单位：%）。

设对应于人口出生率、人口死亡率、自然增长率的数据变量分别为x1,x2,x3。

（1）分别从样本协方差矩阵S及样本相关矩阵R出发，求x1,x2,x3的样本主成分y1,y2，计算各样本主成分的贡献率。

（2）分别从样本协方差矩阵S及样本相关矩阵R出发，将第一样本主成分y1从小到大排序，并给与分析。

二、所用方法及工具（1）主成分分析法与贡献率：主成分分析法即构造原变量的一系列线性组合，使各线性组合在彼此不相关的前提下尽可能多地反映原变量的信息，即使其方差最大。

求的各主成分,等价于求它的协方差矩阵的各特征值及相应的正交单位化特征向量.按特征值由大到小所对应的正交单位化特征向量为组合系数的X,Xz ,…,X,的线性组合分别为X的第一,第二、直至第p个主成分,而各主成分的方差等于相应的特征值。

（2）SAS编程：SAS语言是一种专用的数据管理与分析语言，它提供了一种完善的编程语言。

类似于计算机的高级语言，SAS用户只需要熟悉其命令、语句及简单的语法规则就可以做数据管理和分析处理工作。

因此，掌握SAS编程技术是学习SAS的关键环节。

在SAS中，把大部分常用的复杂数据计算的算法作为标准过程调用，用户仅需要指出过程名及其必要的参数。

这一特点使得SAS编程十分简单。

三、实验内容本次实验采用SAS编程实现，代码如下：data a;set sjfx.rk1;run;proc princomp n=2 cov out=out1;var x1 x2 x3;run;proc sort data=out1 out=a1;by prin1;run;proc print data=a1;run;proc princomp n=2 out=out2;var x1 x2 x3;run;proc sort data=out2 out=a2;by prin1;run;proc print data=a2;run;实验结果：PRINCOMP 过程。

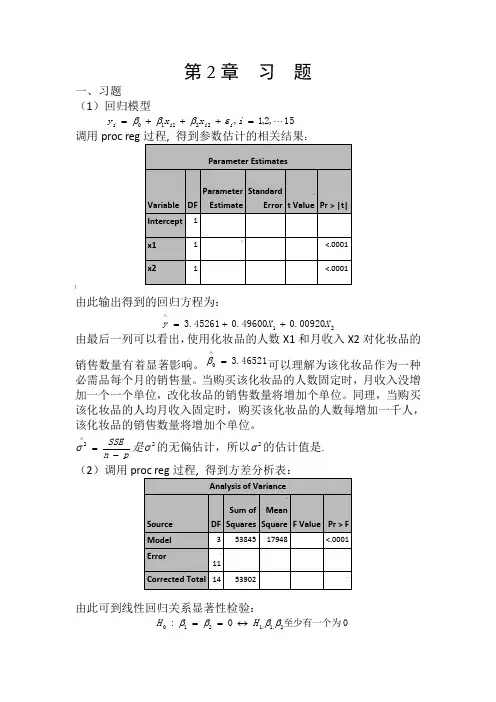
第2章 习 题一、习题（1）回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用proc reg：]由此输出得到的回归方程为：2100920.049600.045261.3X X y ++=∧由最后一列可以看出，使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显著影响。

46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。

当购买该化妆品的人数固定时，月收入没增加一个一个单位，改化妆品的销售数量将增加个单位。

同理，当购买该化妆品的人均月收入固定时，购买该化妆品的人数每增加一千人，该化妆品的销售数量将增加个单位。

pn SSE-=∧2σ是2σ的无偏估计，所以2σ的估计值是. （2）调用由此可到线性回归关系显著性检验：0至少有一个为0:2,1:1210ββββH H ↔==的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ，2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。

2R 越大，表明线性关系越明显。

这些结果均表明Y 与X1，X2之间的回归关系高度显著。

（3）若置信水平05.0=α，由17881.2)12(975.0=t ，利用参数估计值得到21,0,βββ的置信区间分别为：对,0β2942.54516.343065.21781.245216.3±=⨯±，即)7458.8,8426.1(-） 对1β：01318.049600.000605.01781.249600.0±=⨯±，即)50198.0,48282.0( ）2β：0021.000920.00009681.01781.200920.0±=⨯±，即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显著性影：假设其约简模型为：15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得：88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为：3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设，所以x2对Y 有显著影响。

数据分析方法课后答案【篇一：数据的分析练习题及答案】、选择题:(每题3分,共15分)1.小明家要买台电脑,下面是甲、乙、丙三种电脑近几年来的销量,如果小明想买一台近期比较流行的电脑,他应买()a.甲b.乙c.丙2.小李是个彩票迷,为了能得奖,他特意询问了前15天的中奖号码分别是:519、、706、328、556、768、215、435、741、624、307、821、696、741、471、285. 你认为这样的观点是否合理()a.不合理b.合理3.小靖想买双好的运动鞋,于是她上网查找有关资料,得到下表:她想买一双价格在300-600元之间,且她喜欢白色、红白相间、浅绿或淡黄色, 并且防水性能很好,那么她应选()a.甲b.乙c.丙d.丁4.为了计算植树节时本班同学所种植的30棵树苗的平均高度, 三位同学先将所有树苗的然后,他们分别这样计算这30棵树苗的平均高度:130130列式正确的是()a.(1)b.(1)和(2);c.(1)和(3)d.(2)和(3)5.某班在一次物理测试中的成绩为:100分7人,90分14人,80分17人,70分8人, 60分2人,50分2人.则该班此次测试的平均成绩为() a.82分b.62分c.64分d.75分二、填空题:(每题4分,共20分)6.一次知识竞赛中,36名参赛选手的得分情况为:5人得75分,8人得80分,6 人得85分,8人得90分,7人得95 分, 2 人得100 分, 要计算他们的平均得分, 可列算式:_____________.(1)7.某校九年级6个班级的学生的人数和平均体重如下表:要计算全校学生的平均体重,可列算式________,平均体重约为__________.8.某家庭搬进新居后,又添置了新的家用电器,为了了解用电量的大小, 该家庭在6月初连续几天观察电表的度数,如下表所示:9.为了解我国14岁男孩的平均身高,从北方抽取了300个男孩,平均身高1.60m; 从南方抽取了200个男孩,平均身高为1.50m;若北方14岁男孩数与南方14岁男孩数的比为3:2,由此可推断我国14岁男孩的平均身高约为______m.10.小明先用5千米/时的速度行驶3小时后,又用4千米/时的速度行驶5小时到达目的地,则小明的平均速度为________. 三、解答题:(每题9分,共54分)11.某同学对他在本学期的自我检测成绩进行了统计:95分的有12次,90 分的有10次,85分的有15次,80分的有3次,75分的有1次,65分的有3次.试计算该同学本学期自我检测的平均成绩..12.超市里要举行转盘摇奖活动,转盘如图所示,买满100元可摇奖一次,有人说:如果大家都摇到自行车,那么超市岂不是亏本了?如果你是超市决策者,会不会因此而改变有奖销售的方案呢?说说你的理由?自行车300元洗洁精2.80元酱油5.0元西红柿2.00元墨水3.50元13.请你根据上表比较这两个国家的数据,你能得出什么结论?14.由于水资源贫乏,节约用水非常重要,请你调查一下,本班每位学生所在家庭的月人均用水量,并据此制作频数分布图,同时估计一下当地家庭的月人均用水量.15.爸爸给小明一串钥匙,共有4把,小明决定先试试哪把是防盗门的钥匙. 请你用模拟实验方法估计一下,他第1次试开就成功的机会有多大?16.转动如图所示的转盘两次,每次指针都指向一个数字. 如果两次所指的数字之积是质数,游戏者a得10分;乘积不是质数,游戏者b得10分.你认为这个游戏公平吗?如果你认为这个游戏不公平,你愿意做游戏者a还是游戏者b?为什么?31246517.有人对记忆和遗忘的规律进行研究,人在记忆过某些知识后, 在不同时间段对其进行测试,结果如下表:分析测试结果,在图中绘制曲线图,并回答遗忘在数量上的变化规律.记忆效果1%记忆的保持曲线图答案:一、1.b 2.a 3.d 4.d 5.a148?50?49.8?46?50.2?55?49.5?48?51?52?50.3?547., 49.8kg50?46?55?48?52?54358.387.75 9.1.56 10.千米/时8三、144所以,美国的吸烟总人数和每天吸烟的总数都大于日本,但吸烟人口占总人口的比例小于日本.14.列出调查表,对本班学生实事求是地进行调查以获得真实的信息.15.可用4个相同的球,1个白的,3个黑的,每次抽1个,则第1次抽到白球的概率为所求概率,1为. 41516.不公平,愿做b 解:乘积是质数的概率是,乘积不是质数的概率是, 游戏不公平,故66愿做b.17.遗忘曲线表明了遗忘在数量上的变化规律,遗忘的数量随时间的前进而递增;这种递增先快后慢,在识记后的短时间内特别迅速,然后逐渐缓慢下来.二、6.记忆效果1%/d记忆的保持曲线图【篇二：定性数据分析第三章课后答案】9、对72个可疑患者用两种不同的方法进行检测，检测结果如下：问：检测方法1阳性和阴性的比例是否与检测方法2阳性和阴性的比例相同？解：（1）提出原假设根据题意，我们假设检测方法1阳性和阴性的比例与检测方法2阳性和阴性的比例是相同。

数据分析答案梅长林【篇一：1.1一维数据数字特征】013学年第一学期主讲教师李晓燕课程名称数据分析课程类别专业限选课学时及学分 68；4授课班级信息101 102使用教材《数据分析方法》系(院.部) 数理系教研室(实验室) 信息和计算科学教研室数据分析总学时：68 理论38.上机28 适用专业：信息和计算科学内容：? sas软件介绍 3学时 ? 数据的描述性分析10学时 ? 线性回归分析 13学时 ? 方差分析 10学时 ? 主成分分析和典型相关分析8学时? 判别分析 8学时 ? 聚类分析 8学时 ? 学生报告 8学时教材：《数据分析方法》，梅长林、范金城编，高等教育出版社.2006. 参考资料：《实用统计方法》，梅长林编，科学出版社；《使用多元统计分析》，高惠璇编，北京大学出版社，2005；《使用统计方法和sas系统》，高惠璇编，北京大学出版社，2001；《多元统计分析》(二版)，何晓群编，中国人民大学出版社，2008；《使用回归分析》(二版)，何晓群编，中国人民大学出版社，2007；《统计建模和r软件》，薛毅编著，清华大学出版社，2007. 考核：期末成绩（闭卷测试+上机测试）：70%。

平时成绩（平时作业+考勤+大报告）：30%。

课程作业（1）作业题目在网络教学平台公布，按格式要求，以电子版方式通过平台提交。

（2）大报告：2-3人一组，每组一个选题，成员按相同的成绩计分。

收集数据，撰写小论文，做ppt讲解。

每组讲10-20分钟，提问环节。

同学打分。

课时授课计划课次序号： 01一、课题：1.1 一维数据的数字特征及相关系数二、课型：新授课三、目的要求：1.掌握数据的数字特征（均值、方差等）；2.掌握几种描述性分析的sas过程和作图过程计算这些数字特征及进行描述性分析.四、教学重点：均值、方差等数字特征.教学难点：基本概念的理解.五、教学方法及手段：传统教学和上机实验相结合．六、参考资料：1.《实用统计方法》，梅长林，周家良编，科学出版社；2.《sas统计分析使用》，董大钧主编，电子工业出版社．七、作业：1.1八、授课记录：九、授课效果分析：0 绪论0.1 课程内涵数据分析(即多元统计学statistics）：是以数据为依据，以统计方法为理论、计算机及软为工具，研究多变量问题、挖掘数据的统计规律的学科. 通过收集数据、整理数据、分析数据和由数据得出结论的一组概念、原则和方法。

数据分析参考答案数据分析参考答案数据分析是一项重要的技能，它帮助我们从大量的数据中提取有用的信息和洞察力。

在当今信息爆炸的时代，数据分析已经成为了各行各业的必备技能。

无论是企业决策、市场营销还是科学研究，数据分析都扮演着重要的角色。

在本文中，我将提供一些数据分析的参考答案，帮助读者更好地理解和应用数据分析。

首先，数据分析的第一步是数据清洗和整理。

在进行数据分析之前，我们需要确保数据的质量和准确性。

这包括删除重复数据、处理缺失值、解决异常值等。

只有经过清洗和整理的数据才能真正反映出问题的本质和规律。

其次，数据分析需要选择合适的方法和工具。

根据问题的性质和数据的类型，我们可以选择不同的数据分析方法。

常见的数据分析方法包括描述性统计、推断统计、机器学习等。

同时，我们还需要选择适合的数据分析工具，如Excel、Python、R等。

选择合适的方法和工具可以提高数据分析的效率和准确性。

第三，数据可视化是数据分析的重要环节。

通过数据可视化，我们可以将抽象的数据转化为直观的图表和图形，更好地理解数据的分布和趋势。

数据可视化不仅可以提高数据分析的效果，还可以帮助我们向他人传达分析结果。

在进行数据可视化时，我们需要选择适当的图表类型，如柱状图、折线图、散点图等，以及合适的颜色和字体。

第四，数据分析需要进行合理的假设和推断。

在进行数据分析时，我们需要建立合理的假设，并通过数据进行验证。

通过统计方法和推断统计学，我们可以对数据进行推断和预测。

然而，我们需要注意的是，数据分析只能提供相关性而非因果性的结论。

因此，在进行数据分析时，我们需要谨慎解读结果，并避免错误的推断。

最后，数据分析需要不断的学习和实践。

数据分析是一个不断发展和演进的领域，新的方法和工具不断涌现。

为了保持竞争力，我们需要不断学习新的数据分析技术，并将其应用到实际问题中。

同时，我们还需要通过实践不断提高自己的数据分析能力，不断优化分析结果和方法。

综上所述，数据分析是一项重要的技能，它帮助我们从大量的数据中提取有用的信息和洞察力。

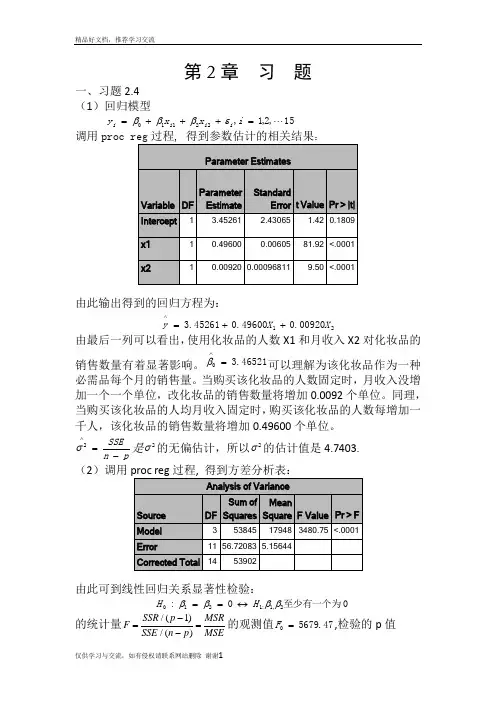
第2章 习 题一、习题2.4 （1）回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用：由此输出得到的回归方程为：2100920.049600.045261.3X X y ++=∧由最后一列可以看出，使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显著影响。

46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。

当购买该化妆品的人数固定时，月收入没增加一个一个单位，改化妆品的销售数量将增加0.0092个单位。

同理，当购买该化妆品的人均月收入固定时，购买该化妆品的人数每增加一千人，该化妆品的销售数量将增加0.49600个单位。

pn SSE-=∧2σ是2σ的无偏估计，所以2σ的估计值是4.7403. （2）调用由此可到线性回归关系显著性检验：0至少有一个为0:2,1:1210ββββH H ↔== 的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ，2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。

2R 越大，表明线性关系越明显。

这些结果均表明Y 与X1，X2之间的回归关系高度显著。

（3）若置信水平05.0=α，由17881.2)12(975.0=t ，利用参数估计值得到21,0,βββ的置信区间分别为：对,0β2942.54516.343065.21781.245216.3±=⨯±，即)7458.8,8426.1(-） 对1β：01318.049600.000605.01781.249600.0±=⨯±，即)50198.0,48282.0( 2β：0021.000920.00009681.01781.200920.0±=⨯±，即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显著性影：假设其约简模型为：15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得：88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为：3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设，所以x2对Y 有显著影响。

第一章测试1【单选题】(20分)在数值计算中因四舍五入产生的误差称为（）A.方法误差B.舍入误差C.模型误差D.观测误差2【多选题】(20分)当今科学活动的三大方法为（）。

A.理论B.科学计算C.实验D.数学建模3【判断题】(20分)计算过程中如果不注意误差分析，可能引起计算严重失真。

A.对B.错4【判断题】(20分)算法设计时应注意算法的稳定性分析。

A.错B.对5【判断题】(20分)在进行数值计算时，每一步计算所产生的误差都是可以准确追踪的。

A.对B.错第二章测试•第1部分•总题数:71【单选题】(14分)A.B.C.D.2【单选题】(14分)某函数过(0,1)，(1,2)两点，则其关于这两点的一阶差商为A.B.2C.3D.13【单选题】(14分)A.B.C.D.4【单选题】(14分)下列说法不正确的是A.分段线性插值的几何图形就是将插值点用折线段依次连接起来B.分段线性插值的导数一般不连续C.高次多项式插值不具有病态性质D.分段线性插值逼近效果依赖于小区间的长度5【多选题】(20分)下列关于分段线性插值函数的说法，正确的是A.对于光滑性不好的函数优先用分段线性插值B.一次函数的分段线性插值函数是该一次函数本身C.二次函数的分段线性插值函数是该二次函数本身D.对于光滑性较好的函数优先用分段线性插值6【多选题】(20分)A.B.C.D.7【判断题】(14分)同一个函数基于同一组插值节点的牛顿插值函数和拉格朗日插值函数等价。

A.对B.错第三章测试1【单选题】(15分)A.B.C.D.2【单选题】(15分)以下哪项是最佳平方逼近函数的平方误差A.B.C.D.3【单选题】(15分)当区间为[-1,1],Legendre多项式族带权()正交。

A.B.C.D.4【单选题】(15分)n次Chebyshev多项式在(-1,1)内互异实根的个数为A.n+1B.nC.n+2D.n-15【多选题】(10分)用正交函数族做最小二乘法有什么优点A.得到的法方程非病态B.不用解线性方程组，系数可简单算出C.每当逼近次数增加1时，之前得到的系数不需要重新计算D.每当逼近次数增加1时，系数需要重新计算6【判断题】(10分)用正交多项式作基求最佳平方逼近多项式，当n较大时，系数矩阵高度病态，舍入误差很大。

数值分析参考答案第一章数值分析与科学计算引论3、下列各数都是经过四舍五入得到的近似数，即，误差限不超过最后一位的半个单位，试指出它们是几位有效数字：* 11.1021x=，*20.031x=，*3385.6x=，*456.430x=，*57 1.0x=⨯解：法1：按p5的公式（2.1）展开法2：从左到右第一位非零开始数* 11.1021x=有5位有效数字，* 20.031x=有2位有效数字，* 3385.6x=有4位有效数字，* 456.430x=有5位有效数字，* 57 1.0x=⨯有1位有效数字（科学记数法）。

6 设028Y=，按递推公式11,2,n nY Y n-== ，计算到100Y。

若取27.982≈（5位有效数字），试问计算100Y将有多大误差？解：精确值Y=*27.983Y=从而，**30001102Y Yε-=-≤⨯第一次迭代：***111011282827.983100100Y Yεε⎛⎛⎫=-=--⨯≤⎪⎝⎝⎭第二次迭代：()()***22211*****1100000127.9831001112100100100100Y Y Y YY Y Y Yεεεε⎛⎛⎫=-=---⨯⎪⎝⎝⎭=---≤+=按规律递推得：***100n n nnY Yεε=-≤所以有：***310010010001001101002Y Yεε-=-≤=⨯因此，计算100Y 的误差限不超过31102-⨯7、求方程25610x x -+=的两个根，使它至少具有427.982）解：由求根公式得2828x ===±27.982≈具有5位有效数字，则有1282827.98255.982x =≈+=21280.0178655.982x ==≈=11、序列{}n y 满足递推关系：1101,1,2,n n y y n -=-= ，若0 1.41y =≈（3位有效数字），计算到10y 时误差有多大？这个计算过程稳定吗？解：0y =*0 1.41y =，则有**20001102y y ε-=-≤⨯ 按迭代公式有：()*****111000001011011010y y y y y y εε=-=---=-≤ ()****2*222111101011011010y y y y y y εε=-=---=-≤由递推式，可得()***10*10*101010990001011011010y y y y y y εε=-=---==-≤因此，此计算过程不稳定。

数据分析与统计智慧树知到课后章节答案2023年下山东工业职业学院山东工业职业学院第一章测试1.下面哪一个是数量标志( )。

答案:钢产量2.下列哪一个是品质标志( )。

答案:所有制3.构成统计总体的个别事物称为（）。

答案:总体单位4.下列变量中属于连续变量的有（）答案:身高;耕作深度;劳动生产率;平均工资5.总体的大量性是指总体的范围不能确定。

（）答案:错第二章测试1.在对总体现象进行分析的基础上，有意识地选择若干具有代表性的单位进行调查研究，这种调查方法是（）。

答案:典型调查2.有意识地选取几十块耕地来估算该地区的粮食产量，这种调查方式属于（）答案:典型调查3.在统计调查中，调查单位与填报单位之间（）答案:通常是有区别的，但有时也一致4.重点调查是（）答案:;非全面调查;可用于经常性调查5.各种调查方法的结合运用，会造成重复劳动，因此不应提倡。

（）答案:错第三章测试1.某连续型变量的组距数列，其末组为开口组，下限为600，其邻组的组中值为550，则末组的组中值为（）。

答案:6502.组数与组距的关系是（）。

答案:组数越多，组距越小3.有20 个工人看管机器台数资料如下: 2,5,4,4,3,4,3,4,4,2,2,4, 3,4,6,3,4,5,2,4。

如按以上资料编制分配数列,应采用（）答案:4.统计分组的作用在于（）答案:划分现象的类型;揭示现象的内部结构;保证统计分析结果的真实性5.对于连续型变量，其组限是按照“上限不包括在内”的原则进行汇总的。

（）答案:对第四章测试1.在相对指标中，可以用有名数表示的指标是（）。

答案:强度相对指标；2.人口出生率是（）。

答案:强度相对指标；3.下列指标中不是时期指标的是（）。

答案:商品库存额4.下列指标中，属于时点指标的有（）。

答案:期末职工数；;商品库存额；5.标准差大的平均数代表性小，标准差小的平均数代表性大( )答案:错第五章测试1.某银行1月1日存款余额为102万元，1月2日为108万元，1月3日为119万元，则三天平均存款余额为（）答案:（102+108+119）÷32.定基增长速度与环比增长速度的关系是（）。

1117.00、 习题1.3統計資料(1) .由表可知，全国居民的均值、方差、标准差、偏度、峰度分别为 1031680.286、1015.717、1.025、-0.457。

cv -100* S(%)变异系数有公式 x 计算得90.9325。

(2) 中位数为727.50，上四分位数304.35，下四分位数为1893.50 四分位极差由公式R1 =Q ^Q1得到1579.15A 1 ± 1 ± 1M = —Q 1 +—M +—Q 3三均值由公式 4 2 4得到913.1857。

(3) 直方图(4) 茎叶图全国居民Stem-and-Leaf Plot Freque ncy Stem & Leaf9.00 0 . 1222233445.00 0 . 567882.00 1 . 031.00 1 . 71.00 2 . 33.00 2 . 6891.00 3 . 1Stem width: 1000Each leaf: 1 case(s)4000-3000-1X0-o-(5)由箱图可以看出并不异常点統計資料(1).由图可知农村居民的平均数、方差、标准差、偏度、峰度分别为747.86、399673.838、632.198、1.013、-0.451。

由公式可以算得变异系数为84.5342。

(2)中位数530.50 ,上四分位数239.75 ,下四分位数1197.00。

由公式可得四分位极差为957.25，三均值为624.4375。

(3)茎叶图农村居民Stem-and-Leaf PlotFreque ncy Stem & Leaf10.00 0 . 11112223346.00 0 . 5556782.00 1 . 144.00 1 . 7889Stem width: 1000 Each leaf: 1 case(s)2000-1500- socrQ-农村展民箱图表明了并无异常点統計資料(1) 由表可知城镇居民均值、方差、标准差、偏度、峰度为2336.41、4536136.444、2129.821、0.970、-0.573。

第2章 习 题一、习题（1）回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用proc reg ：由此输出得到的回归方程为：2100920.049600.045261.3X X y ++=∧由最后一列可以看出，使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显着影响。

46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。

当购买该化妆品的人数固定时，月收入没增加一个一个单位，改化妆品的销售数量将增加个单位。

同理，当购买该化妆品的人均月收入固定时，购买该化妆品的人数每增加一千人，该化妆品的销售数量将增加个单位。

pn SSE-=∧2σ是2σ的无偏估计，所以2σ的估计值是. （2）调用由此可到线性回归关系显着性检验：0至少有一个为0:2,1:1210ββββH H ↔==的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ，2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。

2R 越大，表明线性关系越明显。

这些结果均表明Y 与X1，X2之间的回归关系高度显着。

（3）若置信水平05.0=α，由17881.2)12(975.0=t ，利用参数估计值得到21,0,βββ的置信区间分别为：对,0β2942.54516.343065.21781.245216.3±=⨯±，即)7458.8,8426.1(-） 对1β：01318.049600.000605.01781.249600.0±=⨯±，即)50198.0,48282.0( 2β：0021.000920.00009681.01781.200920.0±=⨯±，即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显着性影：假设其约简模型为：15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得：88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为：3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设，所以x2对Y 有显着影响。

2022年数据分析师题库及答案随着数据科学的快速发展，数据分析师的需求也越来越大。

作为一名数据分析师，掌握相关的知识和技能非常重要。

为了帮助广大数据分析师考生更好地备考，我们整理了2022年的数据分析师题库及答案。

第一部分：统计学基础统计学是数据分析的基础，掌握统计学的基本概念和方法对于数据分析师来说至关重要。

以下是一道关于假设检验的题目：题目：某公司声称其新推出的产品相比竞争对手的产品更受欢迎。

为了验证这一说法，我们进行了一项调查，随机选取了100位消费者，其中有75位表示喜欢该公司的产品。

在显著性水平为0.05的情况下，你能否证明该公司的说法？答案：对于这个问题，我们可以使用假设检验的方法。

首先，我们需要建立原假设（H0）和备择假设（H1）。

在这个问题中，原假设可以是“该公司的产品与竞争对手的产品一样受欢迎”，备择假设可以是“该公司的产品比竞争对手的产品更受欢迎”。

接下来，我们需要计算样本的均值和标准差，并使用正态分布的知识来计算临界值。

在显著性水平为0.05的情况下，临界值为1.96。

然后，我们计算统计量（Z 值）：(75-50)/√(0.5*0.5/100) = 5。

由于计算出的Z值大于临界值，我们可以拒绝原假设，即可以证明该公司的说法。

第二部分：数据清洗与预处理在进行数据分析之前，我们通常需要对原始数据进行清洗和预处理，以确保数据的质量和准确性。

以下是一道关于缺失值处理的题目：题目：某公司的销售数据中存在一些缺失值，你会如何处理这些缺失值？答案：处理缺失值的方法有多种。

一种常见的方法是删除包含缺失值的观察值。

然而，这种方法可能会导致数据的丢失，因此在删除之前需要仔细考虑。

另一种方法是使用均值、中位数或众数来填补缺失值。

这种方法可以保留更多的数据，但可能会引入一定的偏差。

还有一种方法是使用回归分析或插值方法来预测缺失值。

在选择处理方法时，需要根据具体情况来决定。

如果缺失值的比例很小，并且缺失值是随机的，那么删除观察值可能是一个合理的选择。

第1章 习 题一、习题1。

1解：（1）利用题目中的数据,通过SAS 系统proc univariate 过程计算得到：139.0=x 7.06387S =49.898312=S 0.142众数=51.0g 1-= 08192.5=CV126129.0g 2-=由得到的数据特征可知道，偏度为负，所以呈做偏态，峰度为负，所以均值两侧的极端值较少。

（2） 139.0=M31.0=R0.135Q 1= 5.144Q 3= 5.9R 131=-=Q Q375.139412141M 31=++=∧Q M Q （3） 通过SAS 系统proc capability 得到直方图，并拟合正态分布曲线:（4) 通过SAS 系统proc univariate 可以画出茎叶图,从茎叶图可以看出数据大致呈对称分布，由于所给数据都是整数,所以叶所代表的小位数都是０。

（5) 通过SAS 系统proc univariate 过程计算得到：0.971571W 0=00()H p P W W =≤= 0。

1741取0.05=α，因α>=0.1742p ，故不能拒绝0H ，认为样本来自正态总体分布。

通过画ＱＱ图和经验分布曲线和理论分布函数曲线，从图中可以看出ＱＱ图近似的在一条直线上，经验分布曲线的拟合程度也相当好，所以可以进一步说明此样本来自正态总体分布.Normal Line:Mu=139, Sigma=7.0639x 120125130135140145150155正态分位数-3-2-10123二、习题１.２7.8574027=x 1.62568785 S =2.642860982=S0.13721437g 1= 20.6898884=CV -1.4238025g 2=由得到的数据特征可知道，偏度为正，所以呈右偏态，峰度为负,所以均值两侧的极端值较少。

（2）7.636800=M 5.03650=R6.5859 Q 1= 9.3717Q 3= 2.78580R 131=-=Q Q809.7412141M 31=++=∧Q M Q （３）通过SAS 系统proc capability 得到直方图，SAS 系统自动将数据分为中值为4.5,5。

自学资料一、平均数【知识探索】1．一般地，如果一组数据：，，…，它们的平均数记作，这时．2．平均数反映了这组数据段平均水平．3．如果一组数据：，，…，它们的平均数为，则，，…，它们的平均数为．4．我们把样本中所有个体的平均数称为样本平均数（sample mean）．总体中所有个体的平均数称为总体平均数（population mean）．【说明】随机样本的容量越大，样本平均数就越接近于总体平均数．必要时，可以用样本平均数来估计总体平均数．5．①．这里的，，…，在不同的问题中有不同的意义；，，…，分别表示数据，，…，出现的次数．6．设，，…，，则公式①可以写为．其中，，…，叫做权，它们体现了，，…，对平均数所产生的影响．7．如果个数据，，…，，它们相应的权数为，，…，，那么由公式①或②给出的叫做这个数的加权平均数（weighted mean）．【说明】通常情况下，加权平均数中的权数的和为1．8．当各数据对平均数产生的影响不同时，可用加权平均数．当时，公式②就与公式①相同，因此公式①是公式②的特例．第1页共14页自学七招之日计划护体神功：每日计划安排好，自学规划效率高非学科培训9．用计算器计算一组数据的加权平均数：例如：用计算器计算下面这组数据的平均数，其操作步骤及按键过程如下：【错题精练】例1．烹饪大赛的菜品的评价按味道，外形，色泽三个方面进行评价（评价的满分均为100分），三个方面的重要性之比依次为7：2：1．某位厨师的菜所得的分数依次为92分、88分、80分，那么这位厨师的最后得分是（）A. 90分；B. 87分；C. 89分；D. 86分．【答案】A例2．已知一组数据a、b、c、d、e的平均数是m，则3a+1、3b+1、3c+1、3d+1、3e+1的平均数是．【答案】3m+1．【举一反三】1．有一组数据：2，5，5，6，7，关于这组数据的平均数为（）A. 3；B. 4；C. 5；D. 6．第2页共14页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训【答案】C2．某地连续9天的最高气温统计如下表，则这9天的平均气温为（∘C）．【答案】273．晨光中学规定学生的体育成绩满分为100分，其中早操及体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%，小惠的三项成绩依次是95分，90分，85分，小惠这学期的体育成绩为__________ 分．【解答】解：小惠这学期的体育成绩=（95×20%+90×30%+85×50%）=88.5（分）．故答案为88.5．【答案】88.5二、中位数【知识探索】1．将一组数据按由小到大（或由大到小）的顺序排列，如果数据的个数是奇数，则称处于中间位置的数为这组数据的中位数（median）；如果数据的个数是偶数，则称中间两个数的平均数为这组数据的中位数．【错题精练】例1．一组数据按从小到大排列为2，4，8，x，10，14．若这组数据的中位数为9，则x是（）A. 7；B. 8；C. 9；D. 10．【答案】D例2．某工厂第一车间有15个工人，每人日均加工螺杆数统计如图．该车间工人日均加工螺杆数的中位数是（）第3页共14页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训A. 4；B. 12；C. 13；D. 14．【答案】D【举一反三】1．下表是某校乐团的年龄分布，其中一个数据被遮盖了，下面对于中位数的说法正确的是（）A. 中位数是14；B. 中位数可能是14.5；C. 中位数是15或15.5；D. 中位数可能是16．【答案】D三、众数【知识探索】1．一组数据中出现次数最多的数据称为众数（mode）．【说明】当一组数据中出现较多的重复数据时，众数往往能更好地反映其集中趋势．【错题精练】例1．在开展“爱心捐助某灾区”的活动中，某支部8名团员捐款的数额（单位：元）分别为：3，5，6，5，5，6，5，10，这组数据的众数是（）A. 3元；B. 5元；C. 6元；D. 10元．第4页共14页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训例2．某景区在“五一”小长假期间，每天接待的旅客人数统计如下表.表中表示人数的一组数据中，众数和中位数分别为（）A. 2.5万，2万；B. 2.5万，2.5万；C. 2万，2.5万；D. 2万，2万．【答案】D例3．在乡村学校舞蹈比赛中，某校10名学生参赛成绩统计如图所示，对于这10名学生的参赛成绩，下列说法中错误的是（）A. 众数是90；B. 中位数是90；C. 平均数是90；D. 极差是15．【答案】C【举一反三】1．下表是某校乐团的年龄分布，期中一个数据被遮盖了，下面说法正确的是（）A. 中位数可能是14；B. 中位数可能是14．5；C. 平均数可能是14；D. 众数可能是16．【答案】D2．为了筹备班级元旦联欢晚会，班长对全班同学爱吃什么水果进行民意调查，再决定买哪种水果．下面的调查数据中，他最应该关注的是（）A. 众数；B. 中位数；C. 平均数；D. 加权平均数．第5页共14页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训3．右图是某市10月1日至7日一周内“日平均气温变化统计图”．在这组数据中，众数和中位数分别是（）A. 13，13；B. 14，14；C. 13，14；D. 14，13．【答案】D4．一组数据1,3,2,7,x,2,3的平均数是3，则该组数据的众数为________．【解答】【答案】3四、方差和标准差【知识探索】1．如果一组数据，，…，，它们的平均数为，那么这个数与平均数的差的平方分别为，，…，，它们的平均数叫做这个数的方差（variance），记做．即．【记忆方法】一均，二差，三方、四均．第一步：求数据平均数；第6页共14页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训第二步：求每个数据与平均数的差；第三步：求所求得的各个差的平方；第四步：求所得各个平方数的平均数．【说明】如未指明要写方差的单位，通常就将它省略．2．若一组数据，，…，的方差为，那么，，…，的方差为．3．方差的非负平方根叫做标准差（standard deviation），记做．即．4．若一组数据，，…，的标准差为，那么，，…，的标准差为．5．方差与标准差反应了一组数据波动的大小，即一组数据偏离平均数的程度．从计算公式可知，一组数据越接近于它们的平均数，则方差和标准差越小（波动程度越小），这时平均数就越具有代表性．只有一组数据中所有的数都相等时，方差与标准差才可能为零．【说明】（1）方差和标准差反映了一组数据波动的大小．即一组数据偏离平均数的程度；（2）方差和标准差均有单位，方差的单位为数据的单位的平方．但这样的单位有时没有明确的物理意义，而是在运算中形成的，有时计算结果省略了它的单位；标准差的单位与数据的单位相同；（3）一组数据越接近它们的平均数，方差和标准差就越小，这是平均数就越具有代表性；当一组数据中所有的数都相等时，方差和标准差才可能为零；（4）本章不引进样本的方差和标准差，总体的方差和标准差，也不要求由随机样本来估计总体的方差或标准差．用样本估计总体的方差和标准差时，所用的公式与本节中的公式有所不同，在本章不要涉及这类问题．（5）当两组数据平均数相等或较接近时，才能用方差来比较它们的波动程度．6．用计算器计算这组数据的标准差和方差【错题精练】例1．方差是刻画数据波动程度的量．对于一组数据x1，x2，…，x n，可用如下算式计算方差：s2=1[(x1−5)2+(x2−5)2+⋯+(x n−5)2]，其中“5”是这组数据的（）nA. 最小值；B. 平均数；C. 中位数；D. 众数．第7页共14页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训【答案】B例2．甲、乙、丙、丁四位选手各进行了10次射击，射击成绩的平均数和方差如下表：则这四人中成绩发挥最稳定的是（）A. 甲；B. 乙；C. 丙；D. 丁．【答案】B例3．若一组数据x1+1，x2+1，...，x n+1的平均数为17，方差为2，则另一组数据x1+2，x2+ 2，...，x n+2的平均数为和方差分别为（）A. 17，2；B. 18，2；C. 17，3；D. 18，3．【答案】B例4．市举行知识大赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．（1）根据图示填写下表：（2）结合两校成绩的平均数和中位数，分析哪个学校的决赛成绩较好；（3）计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．第8页共14页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训(75+80+85+85+100)=85（分），众数85（分）；【解答】（1）解：A校平均数为15B校中位数80（分）．填表如下：（2）解：A校成绩好些．因为两个队的平均数都相同，A校的中位数高，∴在平均数相同的情况下中位数高的A校成绩好些．（3）解：∵A校的方差s12=1×[(75−85)2+(80−85)2+(85−85)2+(85−85)2+(100−585)2]=70，×[(70−85)2+(100−85)2+(100−85)2+(75−85)2+(80−85)2]=160．B校的方差s22=15∴s12<s22，因此，A校代表队选手成绩较为稳定．【答案】（1）略；（2）位数高的A校成绩好些；（3）A校代表队选手成绩较为稳定．【举一反三】1．下面是甲、乙两人10次射击成绩（环数）的条形统计图，则下列说法正确的是（）A. 甲比乙的成绩稳定；B. 乙比甲的成绩稳定；C. 甲、乙两人的成绩一样稳定；D. 无法确定谁的成绩更稳定．【答案】B2．一组数据1，2，3，3，4，5．若添加一个数据3，则下列统计量中，发生变化的是（）A. 平均数；B. 众数；C. 中位数；D. 方差．【答案】D3．若一组数据x1+1，x2+1，x3+1…x n+1的平均数为18，方差为2，则数据x1+2，x2+2，x3+2……，x n+2的平均数和方差分别是（）第9页共14页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训第10页共14页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训1．下表是某校乐团的年龄分布，其中一个数据被遮盖了，下面对于中位数的说法正确的是（）A. 中位数是14；B. 中位数可能是14.5；C. 中位数是15或15.5；D. 中位数可能是16．【答案】D2．学校为了丰富学生课余活动开展了一次“校园歌手大奖赛”的歌咏比赛，共有18名同学入围，他们的决赛成绩如下表：成绩（分）9.409.509.609.709.809.90人数235431则入围同学决赛成绩的中位数和众数分别是（）A. 9.70，9.60；B. 9.60，9.60；C. 9.60，9.70；D. 9.65，9.60．【解答】根据中位数和众数的概念求解．解：∵共有18名同学，则中位数为第9名和第10名同学成绩的平均分，即中位数为：（9.60+9.60）=9.60，众数为：9.60．故选：B．【答案】B3．我区某中学举办了一次以“我的中国梦”为主题的演讲比赛，最后确定7名同学参加决赛，他们的决赛成绩各不相同，其中李华已经知道自己的成绩，但能否进前四名，他还必须清楚这名同学成绩的（）A. 众数；B. 中位数；C. 平均数；D. 方差．【答案】B4．如表记录了甲、乙、丙、丁四名学生最近几次数学综合测试成绩的平均数与方差：根据表中数据，要从中选择一名成好且发挥稳定的同学参加竟赛，应该选择（）A. 甲；B. 乙；C. 丙；D. 丁．【答案】A5．在“争创美丽校园，争做文明学生”示范校评比活动中，10位评委给某校的评分情况如下表所示：评分(分)80859095评委人数1252则这10位评委评分的平均数是__________ 分【解答】平均数的计算方法是求出所有数据的和，然后除以数据的总个数．这10位评委评分的平均数是：(80＋85×2＋90×5＋95×2)÷10＝89(分)【答案】896．教育局为了解我市八年级学生参加社会实践活动情况，随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数，并用得到的数据绘制了两幅统计图，下面给出了两幅不完整的统计图（如图）请根据图中提供的信息，回答下列问题：（1）a=（百分比），并写出该扇形所对圆心角的度数为，请补全条形图；（2）在这次抽样调查中，众数和中位数分别是多少？（3）如果该县共有八年级学生8000人，请你估计“活动时间不少于7天”的学生人数大约有多少人？【解答】（1）解：a=1−(40%+20%+25%+5%)=1−90%=10%，所对的圆心角度数=360°×10%＝36°，被抽查的学生人数：240÷40%＝600人，8天的人数：600×10%＝60人，补全统计图如图所示：（2）解：参加社会实践活动5天的人数最多，∴众数是5天，600人中，按照参加社会实践活动的天数从少到多排列，第300人和301人都是6天，∴中位数是6天；（3）解：8000×（25%+10%+5%）=8000×40%＝3200（人）．【答案】（1）10%，36°；（2）5，6；（3）3200．7．当今，青少年视力水平下降已引起全社会的关注，为了了解某市30000名学生的视力情况，从中抽取了一部分学生进行了一次抽样调查，利用所得数据绘制的频数分布直方图（长方形的高表示该组人数）如下：解解答下列问题：（1）本次抽样调查共抽测了名学生；（2）参加抽测的学生的视力的众数在范围内；（3）视力为4．9，5．0，5．1及以上为正常，试估计该市学生视力正常的人数约为多少？【解答】（1）解：30+50+40+20+10=150（人）；（2）解：根据总数定义，可知视力众数在4．25～4．55范围内；（3）解：∵150人中视力正常所占的百分比为20%，∴某市30000名学生的视力正常的人数为30000×20%=6000人．【答案】（1）150；（2）4．25～4．55；（3）6000．。

数据分析方法梅长林数据分析是指通过收集、整理、加工和解释数据，以提取有用信息、评估假设和支持决策的过程。

数据分析方法是指在数据分析过程中使用的各种技术和工具。

下面将介绍几种常见的数据分析方法。

1. 描述统计分析：描述统计分析是对数据进行总结和描述的方法。

常用的描述统计量包括平均值、中位数、众数、标准差等。

通过描述统计分析，可以对数据的集中趋势、离散程度和分布形态有一个直观的了解。

2. 相关分析：相关分析用于研究变量之间的相关关系。

常见的相关分析方法包括皮尔逊相关系数和斯皮尔曼相关系数。

通过相关分析，可以了解变量之间的线性相关程度和相关方向。

3. 回归分析：回归分析是一种用来研究自变量和因变量之间关系的方法。

回归分析可以分为线性回归分析和非线性回归分析。

通过回归分析，可以估计出自变量对因变量的影响程度，并进行预测和解释。

4. 时间序列分析：时间序列分析主要用于研究随时间变化的数据。

常见的时间序列分析方法包括趋势分析、季节性分析和周期性分析。

时间序列分析可以揭示数据的长期趋势、季节性变化和周期性波动。

5. 聚类分析：聚类分析是一种用于将数据按照某种相似性进行分组的方法。

聚类分析可以帮助我们发现数据中的模式和规律，并进行分类和预测。

6. 因子分析：因子分析是一种用于研究变量之间的潜在结构的方法。

因子分析可以将多个观测指标归纳为几个潜在因子，从而简化数据分析过程，并找出变量之间的内在关系。

7. 假设检验：假设检验是一种用来检验统计推断的方法。

通过对样本数据进行假设检验，可以判断样本数据与总体参数之间是否存在显著差异，以及差异的程度。

以上只是几种常见的数据分析方法，实际数据分析过程中还有其他各种方法和技术。

选择适合的数据分析方法需要根据具体的问题和数据情况进行判断。

同时，数据分析方法的选择也需要结合统计学原理和分析目的，确保结果具有可靠性和实用性。

数值分析引论课后习题与答案易大义版第一章绪论习题一1.设x>0,x*的相对误差为δ，求f(x)=ln x的误差限。

解：求lnx的误差极限就是求f(x)=lnx的误差限，由公式(1.2.4)有已知x*的相对误差满足，而，故即2.下列各数都是经过四舍五入得到的近似值，试指出它们有几位有效数字，并给出其误差限与相对误差限。

解：直接根据定义和式(1.2.2)(1.2.3)则得有5位有效数字，其误差限，相对误差限有2位有效数字，有5位有效数字，3.下列公式如何才比较准确？（1）（2）解：要使计算较准确，主要是避免两相近数相减，故应变换所给公式。

（1）（2）4.近似数x*=0.0310,是 3 位有数数字。

5.计算取，利用：式计算误差最小。

四个选项：第二、三章插值与函数逼近习题二、三1. 给定的数值表用线性插值与二次插值计算ln0.54的近似值并估计误差限.解：仍可使用n=1及n=2的Lagrange插值或Newton插值,并应用误差估计（5.8）。

线性插值时，用0.5及0.6两点，用Newton插值误差限，因，故二次插值时，用0.5，0.6，0.7三点，作二次Newton插值误差限，故2. 在-4≤x≤4上给出的等距节点函数表，若用二次插值法求的近似值，要使误差不超过，函数表的步长h应取多少?解：用误差估计式（5.8），令因得3. 若，求和.解：由均差与导数关系于是4. 若互异，求的值，这里p≤n+1.解：，由均差对称性可知当有而当P＝n＋1时于是得5. 求证.解：解：只要按差分定义直接展开得6. 已知的函数表求出三次Newton均差插值多项式，计算f(0.23)的近似值并用均差的余项表达式估计误差.解：根据给定函数表构造均差表由式(5.14)当n=3时得Newton均差插值多项式N3(x)=1.0067x+0.08367x(x-0.2)+0.17400x(x-0.2)(x-0.3)由此可得f(0.23) N3(0.23)=0.23203由余项表达式(5.15)可得由于7. 给定f(x)=cosx的函数表用Newton等距插值公式计算cos 0.048及cos 0.566的近似值并估计误差解：先构造差分表计算，用n=4得Newton前插公式误差估计由公式（5.17）得其中计算时用Newton后插公式（5.18)误差估计由公式（5.19）得这里仍为0.5658．求一个次数不高于四次的多项式p(x),使它满足解：这种题目可以有很多方法去做，但应以简单为宜。

第四章 习题一、习题解：（1）通过SAS 的proc princomp 过程对相关系数矩阵R 做主成分分析，得到个主成分的贡献率以及累计贡献率如表1所表 1从表中可以得到特征值向量为：]0.2429 0.4515 0.5396 0.8091 2.8567[=*λ第一主成分贡献率为： % 第二主成分贡献率为： % 第三主成分贡献率为： % 第四主成分贡献率为： % 第五主成分贡献率为： %进一步得到各主成分分析结果如表2所示：表 2（2）由（1）中得到的结果可知前两个主成分的累积贡献率为%，得到第一主成分、第二主成分为：54212.044215.034702.024571.014636.01x x x x x Y ++++=*55820.045257.032604.025093.012404.02x x x x x Y ++---=*由于1*Y 是五个标准化指标的加权和，由此第一主成分更能代表三种化工股票和两种石油股票周反弹率的综合作用效果，1*Y 越大表示各股票的综合周反弹率越大。

*2Y 中关于三种化工股票的周反弹率系数为负，而关于两种石油的系数为正，它放映了两种石油周反弹率和三种化工股票周反弹率的对比，*2Y 的绝对值越大，表明两种石油周反弹率和三种化工股票周反弹率的差距越大。

二、习题解：（1）利用SAS 的proc corr 过程求得相关系数矩阵如表3：表 3（2）从相关系数矩阵出发，通过proc princomp 过程对其进行主成分分析，表4给出了各主成分的贡献率以及累积贡献率：表4第一主成分贡献率为：% 第二主成分贡献率为：%第三主成分贡献率为：% 第四主成分贡献率为：%第五主成分贡献率为：% 第六主成分贡献率为：%其中前两个主成分的累计贡献率为%（3）通过上面的计算得到各主成分，见表5：表585093.73171.66927.502169.42541.30185.25192.12496.1xxxxxxxxY+++++-+ =0.0871x8-0.2607x7-0.1347x6+0.5754x5+0.5381x4+0.4754x3+0.0376x2--0.2413x12 Y由于是1Y 八个标准化标值的加权值，因此它反映了平均消费数据的综合指标。