2018年高三最新 福建省宁德市2018届高三教学质量检查(数学文) 精品

2018年福建省高三毕业班质量检查测试文科数学一、选择题：本大题共12个小题，每题5分，共60分.在每题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}2|230A x x x =--<，{}2,1,1,2B =--，则AB =〔 〕A ．{}1,2-B ．{}2,1-C ．{}1,2D ．{}1,2-- 2.已知向量()1,1AB =，()2,3AC =，则以下向量中与BC 垂直的是〔 〕 A ．()3,6a = B ．()8,6b =- C ．()6,8c = D ．()6,3d =-3.设等比数列{}n a 的前n 项和为n S ，假设12n n S λ+=+，则λ=〔 〕A ．-2B ．-1C ．1D ．2 4.如图，曲线sin32xy π=+把边长为4的正方形OABC 分成黑色部分和白色部分.在正方形内随机取一点，则此点取自黑色部分的概率是〔 〕A ．14 B ．13 C ．38 D ．345.假设α是第二象限角，且3sin 5α=，则12sin sin 22παπα+--=〔 〕A ．65-B ．45-C ．45D ．656.已知0.30.4a =，0.40.3b =，0.20.3c -=，则〔 〕A ．b a c <<B ．b c a <<C ．c b a <<D ．a b c <<7. 程大位是明代著名数学家，他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.它问世后不久便风行宇内，成为明清之际研习数学者必读的教材，而且传到朝鲜、日本及东南亚地区，对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是：“今有三角果一垛，底阔每面七个.问该假设干？”如图是解决该问题的程序框图.执行该程序框图，求得该垛果子的总数S 为〔 〕A ．120B ．84C ．56D ．288.某校有A ，B ，C ，D 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前，甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下： 甲说：“A 、B 同时获奖”； 乙说：“B 、D 不可能同时获奖”； 丙说：“C 获奖”；丁说：“A 、C 至少一件获奖”.如果以上四位同学中有且只有二位同学的预测是正确的，则获奖的作品是〔 〕 A ．作品A 与作品B B ．作品B 与作品C C ．作品C 与作品D D ．作品A 与作品D9.某几何体的三视图如下图，图中三个正方形的边长均为2，则该几何体的外表积为〔 〕A ．)2421π+B ．()24222π+-C ．)2451π+D ．()24232π+10.已知()f x 是定义在R 上的偶函数，且x R ∈时，均有()()32f x f x +=-，()28f x ≤≤，则满足条件的()f x 可以是〔 〕 A ．()263cos 5x f x π=+ B ．()53cos 5xf x π=+ C ．()2,8,R x Q f x x C Q ∈⎧=⎨∈⎩ D ．()2,08,0x f x x ≤⎧=⎨>⎩11.已知1F ，2F 为双曲线C ：221169x y -=的左、右焦点，P 为C 上异于顶点的点.直线l 分别与1PF ，2PF 为直径的圆相切于A ，B 两点，则AB =〔 〕A．3 C ．4 D ．512.已知数列{}n a 的前n 项和为n S ，2112n n n S a a ++=-，且29a a =，则所有满足条件的数列中，1a 的最大值为〔 〕A ．3B ．6C ．9D ．12二、填空题：此题共4小题，每题5分，共20分.13.已知复数z 满足()3443z i i +=+，则z = ．14.假设x ，y 满足约束条件2300260x y x y x y +-≥⎧⎪-≤⎨⎪+-≤⎩，则z x y =+的取值范围为 ．15.已知A ，B 分别为椭圆C 的长轴端点和短轴端点，F 是C 的焦点.假设ABF ∆为等腰三角形，则C 的离心率等于 ．16.已知底面边长为，侧棱长为S ABCD -内接于球1O .假设球2O 在球1O 内且与平面ABCD 相切，则球2O 的直径的最大值为 ．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答. 〔一〕必考题：共60分.17.ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c .cos sin C c B -=. 〔1〕求B ；〔2〕假设3a =，7b =，D 为AC边上一点，且sin BDC ∠=，求BD .18.如图，在直三棱柱111ABC A B C -中，AC BC ⊥，133CC =，3BC =，23AC =.〔1〕试在线段1B C 上找一个异于1B ，C 的点P ，使得1AP PC ⊥，并证明你的结论； 〔2〕在〔1〕的条件下，求多面体111A B C PA 的体积.19.某种常见疾病可分为Ⅰ、Ⅱ两种类型.为了解该疾病类型与地域、初次患该疾病的年龄〔以下简称初次患病年龄〕的关系，在甲、乙两个地区随机抽取100名患者调查其疾病类型及初次患病年龄，得到如下数据：初次患病年龄 〔单位：岁〕甲地Ⅰ型患者 〔单位：人〕甲地Ⅱ型患者 〔单位：人〕乙地Ⅰ型患者 〔单位：人〕乙地Ⅱ型患者 〔单位：人〕[)10,20 8 1 5 1 [)20,304 3 3 1 [)30,40 35 2 4 [)40,50 3 8 4 4 [)50,60 3 9 26 [)60,7021117〔1〕从Ⅰ型疾病患者中随机抽取1人，估计其初次患病年龄小于40岁的概率；〔2〕记“初次患病年龄在[)10,40的患者”为“低龄患者”，“初次患病年龄在[)40,70的患者”为“高龄患者”.根据表中数据，解决以下问题：〔i 〕将以下两个列联表补充完整，并判断“地域”“初次患病年龄”这两个变量中哪个变量与该疾病的类型有关联的可能性更大.〔直接写出结论，不必说明理由〕 表一：表二：〔ii 〕记〔i 〕中与该疾病的类型有关联的可能性更大的变量为X .问：是否有99.9%的把握认为“该疾病的类型与X 有关？”附：()()()()()22n ad bc K a b c d a c b d -=++++，20.在平面直角坐标系xOy 中，点F 的坐标为10,2⎛⎫ ⎪⎝⎭，以MF 为直径的圆与x 轴相切. 〔1〕求点M 的轨迹的方程；〔2〕设T 是E 上横坐标为2的点，OT 的平行线l 交E 于A ，B 两点，交E 在T 处的切线于点N .求证：252NT NA NB =⋅. 21.已知函数()12ln f x a x x x ⎛⎫=-- ⎪⎝⎭. 〔1〕讨论()f x 的单调区间； 〔2〕假设12a =，证明：()f x 恰有三个零点. 〔二〕选考题：共10分.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.[选修4-4：坐标系与参数方程]在直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴建立极坐标系.已知曲线M 的参数方程为1cos 1sin x y ϕϕ=+⎧⎨=+⎩〔ϕ为参数〕，1l ，2l 为过点O 的两条直线，1l 交M 于A ，B 两点，2l 交M 于C ，D 两点，且1l 的倾斜角为α，6AOC π∠=.〔1〕求1l 和M 的极坐标方程； 〔2〕当0,6πα⎛⎤∈ ⎥⎝⎦时，求点O 到A ，B ，C ，D 四点的距离之和的最大值.23.[选修4-5：不等式选讲]已知函数()2f x x =-，()1g x a x =-.〔1〕假设不等式()33g x -≥-的解集为[]2,4，求a 的值； 〔2〕假设当x R ∈时，()()f x g x ≥，求a 的取值范围.2018年福建省高三毕业班质量检查测试文科数学参考答案及评分细则一、选择题1-5:CDAAC 6-10:ABDBC 11、12：BB二、填空题13．1 14．[]24， 1516．8 三、解答题17．解：〔1cos sin C c B -=，得cos sin sin B C C B A -=，因为A B C π++=()cos sin sin B C C B B C -=+，cos sin sin cos sin B C C B B C B C -=+，即sin sin sin C B B C -=，因为sin 0C ≠，所以sin B B =，所以tan B =又()0,B π∈，解得23B π=. 〔2〕在ABC ∆中，由余弦定理2222cos b a c ac B =+-， 又3a =，7b =，所以222173232c c ⎛⎫=+-⨯⨯-⎪⎝⎭， 整理得()()850c c +-=，因为0c >，所以5c =，在ABC ∆中，由正弦定理sin sin b cB C =5sin 2C=，解得sin C =. 在BCD ∆中，由正弦定理sin sin BD aC BDC=∠，因为sin 3BDC ∠==4514BD =.18．解：〔1〕当P 满足11C P B C ⊥时，1AP PC ⊥.证明如下：在直三棱柱111ABC A B C -中，1C C ⊥平面ABC ，AC ⊂平面ABC ，所以1C C AC ⊥. 又因为AC BC ⊥，1C CBC C =，所以AC ⊥平面11BCC B .因为1PC ⊂平面11BCC B ，所以1AC PC ⊥. 又因为11C P B C ⊥，且1B C AC C =，所以1PC ⊥平面1AB C ，因为AP ⊂平面1AB C ，所以1AP PC ⊥.〔2〕因为1CC ⊥平面111A B C ，11B C ⊂平面111A B C ， 所以111CC B C ⊥.在11Rt B C C ∆中，113B C BC ==，133CC =，所以16B C =. 因为1111Rt Rt B PC B C C ∆∆，所以111111B P B C B C B C =，所以132B P =. 在11Rt BC C ∆中，11111tan 3CC CB C B C ∠==113CB C π∠=， 所以11111111sin 2B PC S B C B P CB C ∆=⋅⋅∠13393322=⨯⨯=. 因为AC ⊥平面11BCC B ，且23AC = 所以11111193923334A B C P B PC V S AC -∆=⋅==. 因为1AA ⊥平面111A B C ，且1133AA CC ==1123AC AC ==， 所以1111111111323339332A ABC A B C V S AA -∆=⋅=⨯⨯⨯=.所以多面体111A B C PA 的体积为11111945944A B C P A A B C V V --+=+=. 19．解：〔1〕依题意，从Ⅰ型疾病患者中随机抽取1人，其初次患病年龄小于40岁的概率估计值为15105408+=. 〔2〕〔i 〕填写结果如下： 表一：表二：由表中数据可以判断，“初次患病年龄”与该疾病类型有关联的可能性更大. 〔ii 〕根据表二的数据可得：25a =，15b =，15c =，45d =，100n =.则()221002545151514.06340604060K ⨯⨯-⨯=≈⨯⨯⨯.由于210.828K >，故有99.9%的把握认为该疾病类型与初次患病年龄有关. 20．解：〔1〕设点(),M x y ，因为10,2F ⎛⎫ ⎪⎝⎭，所以MF 的中点坐标为21,24x y +⎛⎫ ⎪⎝⎭. 因为以MF 为直径的圆与x 轴相切，所以2124MF y +=， 即212y MF +=，212y +=，化简得22x y =，所以M 的轨迹E 的方程为22x y =.〔2〕因为T 是E 上横坐标为2的点，由〔1〕得()2,2T ，所以直线OT 的斜率为1，因为l OT ∥，所以可设直线l 的方程为y x m =+，0m ≠. 由212y x =，得y x '=，则E 在T 处的切线斜率为22x y ='=，所以E 在T 处的切线方程为22y x =-.由,22y x m y x =+⎧⎨=-⎩得2,22,x m y m =+⎧⎨=+⎩所以()2,22N m m ++，所以()()2222222225NTm m m =+-++-=⎡⎤⎡⎤⎣⎦⎣⎦. 由2,2y x m x y=+⎧⎨=⎩消去y 得2220x x m --=， 由480m ∆=+>，解得12m >-. 设()11,A x y ，()22,B x y ，则122x x +=，122x x m =-. 因为,,N A B 在l 上，所以()122NA m =-+，()222NB m =-+，所以()()12222NA NB x m x m ⋅=-+⋅-+()()()21212222x x m x x m =-++++ ()()222222m m m =--+++22m =.所以252NTNA NB =⋅. 21．解：〔1〕()f x 的定义域为()0,+∞，()2221221ax x a f x a x x x -+⎛⎫'=+-= ⎪⎝⎭.①当0a ≤时，因为0x >，所以220ax x a -+<，所以()0f x '<， 所以()f x 的单调递减区间为()0,+∞.②当0a >时，令()0f x '=，得220ax x a -+=，当1a ≥时，2440a ∆=-≤，()0f x '≥， 所以()f x 的单调递增区间为()0,+∞，当01a <<时，2440a ∆=->，由220ax x a -+=得1x =，2x =因为01a <<，所以210x x >>，所以，当10,x a ⎛⎫-∈ ⎪ ⎪⎝⎭或1x a ⎛⎫+∈+∞ ⎪ ⎪⎝⎭时，()0f x '>；当11x a a ⎛∈ ⎪⎝⎭时，()0f x '<，所以()f x 的单调递增区间为⎛ ⎝⎭和⎫+∞⎪⎪⎝⎭，()f x 的单调递减区间为⎝⎭. 综上，当0a ≤时，()f x 的单调递减区间为()0,+∞；当1a ≥时，()f x 的单调递增区间为()0,+∞；当01a <<时，()f x 的单调递增区间为⎛ ⎝⎭和⎫+∞⎪⎪⎝⎭；()f x 的单调递减区间为⎝⎭. 〔2〕因为12a =，所以()112ln 2f x x x x ⎛⎫=-- ⎪⎝⎭.由〔1〕知，()f x 的单调递增区间为(0,2，()2+∞，()f x 的单调递减区间为()23,23-+. 又()10f =，()123,23∈-+，所以()f x 在()23,23-+有唯一零点，且()230f ->，()230f +<，因为30e 23-<<-，()333311e e 2ln e 2e f ----⎛⎫=-- ⎪⎝⎭3331e e 6702e 22=-+<-<， 所以()f x 在()0,23-有唯一零点.又()()33e e 0f f -=->，3e 23>+，所以()f x 在()23,++∞有唯一零点. 综上，当12a =时，()f x 恰有三个零点. 22．解：〔1〕依题意，直线1l 的极坐标方程为()θαρ=∈R ，由1cos ,1sin x y ϕϕ=+⎧⎨=+⎩消去ϕ，得()()22111x y -+-=， 将cos x ρθ=，sin y ρθ=，代入上式，得22cos 2sin 10ρρθρθ--+=，故M 的极坐标方程为22cos 2sin 10ρρθρθ--+=.〔2〕依题意可设()1,A ρα，()2,B ρα，3,6C πρα⎛⎫+⎪⎝⎭，4,6D πρα⎛⎫+ ⎪⎝⎭， 且1234,,,ρρρρ均为正数，将θα=代入22cos 2sin 10ρρθρθ--+=，得()22cos sin 10ρααρ-++=， 所以()122cos sin ρραα+=+，同理可得，342cos sin 66ππρραα⎡⎤⎛⎫⎛⎫+=+++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦， 所以点O 到,,,A B C D 四点的距离之和为()12342cos sin ρρρραα+++=+2cos sin 66ππαα⎡⎤⎛⎫⎛⎫++++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦((1sin 3cos αα=+(21sin 3πα⎛⎫=++ ⎪⎝⎭. 因为0,6πα⎛⎤∈ ⎥⎝⎦， 所以当sin 13πα⎛⎫+= ⎪⎝⎭，即6πα=时，1234ρρρρ+++取得最大值2+， 所以点O 到,,,A B C D四点距离之和的最大值为2+.23．解：〔1〕由()33g x -≥-，得32a x -≥-， 因为不等式()33g x -≥-的解集为[]2,4，所以0a <，故不等式可化为23x a -≤-， 解得2233x a a+≤≤-， 所以232,234,a a⎧+=⎪⎪⎨⎪-=⎪⎩解得2a =-. 〔2〕①当0x =时，21x a x -≥-恒成立，所以a ∈R . ②当0x ≠时，21x a x -≥-可化为21x a x-+≤， 设()()210x h x x x-+=≠，则()31,0,31,02,11, 2.x x h x x xx x ⎧-+<⎪⎪⎪=-<<⎨⎪⎪-+≥⎪⎩所以当2x =时，()min 12h x =，所以12a ≤. 综上，a 的取值范围是1,2⎛⎤-∞ ⎥⎝⎦.。

2018届宁德市普通高中毕业班第二次质量检查试卷文科数学本试卷分第I卷和第II卷两部分．第I卷1至3页，第II卷4至6页，满分150分．考生注意：1．答题前，考生务必将自己的准考证、姓名填写在答题卡上．考生要认真核对答题卡上粘贴的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致．2．第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．第II卷用0.5毫米的黑色墨水签字笔在答题卡上书写作答．若在试题卷上作答，答案无效．3．考试结束，监考员将试题卷和答题卡一并交回．第I卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．A B C D2．A BC D3．右图是具有相关关系的两个变量的一组数据的散点图和回归直线，若去掉一个点使最大，则应当去掉的点是ABCD4．A BCD5．ABCD6．ABCD7．几何体的三视图，则此几何体的表面积为ABCD 8．ABCD9．轴上方）A BCD 10．的值为ABCD11．四边形，则此空间四边形的外接球的半径为ABCD12．ABC D2018届宁德市普通高中毕业班第二次质量检查试卷文科数学第II卷注意事项：用0.5毫米黑色签字笔在答题卡上书写作答．在试题卷上作答，答案无效．本卷包括必考题和选考题两部分．第13～21题为必考题，每个试题考生都必须做答．第22、23题为选考题，考生根据要求做答．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．_______．14．______．15．我国南北朝时期的数学家张丘建是世界数学史上解决不定方程的第一人，他在《张丘建算经》中给出一个解不 定方程的百鸡问题，问题如下：鸡翁一，值钱五，鸡母 一，值钱三，鸡雏三，值钱一．百钱买百鸡，问鸡翁母 雏各几何？用代数方法表述为：设鸡翁、鸡母、鸡雏的______． 16．______．三、解答题：本大题共6小题，满分70分．解答须写出文字说明证明过程和演算步骤． 17．（12分）18．（12分）为响应绿色出行，某市在推出“共享单车”后，又推出“新能源租赁汽车”．每次租车收费的标准由两部分组成：①里程计费：1元//分．已知陈50次路上开车所用时间，在各时间段内频数分布情况如下表所示：将各时间段发生的频率视为概率，一次路上开车所用的时间视为用车时间，范围为，并说明理由.（同一时段，用该区间的中点值作代表）19．（12分）（i（ii20．（12分）21．（12分）请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题记分．做答时请写清题号．22．（10分）选修4—4：坐标系与参数方程数）．23．（10分）选修4—5：不等式选讲已知实数x, y（１）解关于x。

2018年福建省宁德市高三毕业班第三次质量检查数学（文）试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 复数2i(i 1i+为虚数单位）实部与虚部的和为（ ） A ．2 B ．1 C ．0 D ．2-2. 已知命题{}2:1|210∈-+≤p x x x ，命题[]2:0,1,10q x x ∀∈-≥，则下列命题是真命题的是（ ）A ．p q ∧B ．()p q ⌝∧⌝C ．p q ∨D ．p q ⌝∨ 3. 佳佳同学在8次测试中，数学成绩的茎叶图如图，则这8次成绩的中位数是（ ）A ．86B ．87C ．87.5D ．88.54. 已知直线:43200l x y +-=经过双曲线2222:1x y C a b-=的一个焦点，且与其一条渐近线平行，则双曲线C 的实轴长为（ ）A ．3B ．4 C.6 D ．8 5. 已知等差数列{}n a 的前n 项和为n S ，若35724a a a ++=，则9S =（ ） A ．16 B ．32 C.64 D ．72 6.将函数()sin 0,2y x πωϕωϕ⎛⎫=+><⎪⎝⎭的图象沿x 轴向左平移3π个单位长度，得到函数cos 24y x π⎛⎫=+ ⎪⎝⎭的图象，则ϕ= （ ）A ．12π B ．8π C. 6π D ．4π 7.如图是一个几何体的三视图，则该几何体的体积为 （ ）A ．2π+B ．32π+C.3π+ D ．43π+ 8. 已知函数()f x 是定义域为R 的奇函数，且当0≥x 时，()()2log 12x f x x a =++-，则满足()23190f x x --+<的实数x 的取值范围是（ ）A ．()2,1--B ．()1,0- C. ()0,1 D ．()1,29. 执行如图所示的程序框图，若输出的结果是99199，则判断框内应填的内容是（ ）A ．97n ≤B ．98n ≤ C.99n ≤ D ．100n ≤10.已知抛物线()2:20C y px p =>的焦点为F ，点P 是抛物线C 上一点，过P作PM l ⊥，垂足为M ，记7,0,2p N P F ⎛⎫⎪⎝⎭与MN 交于点T ，若2N F P F =，且P N T ∆的面积为则p = （ ）A ．211. 已知等边三角形ABC 三个顶点都在半径为2的球面上，球心O 到平面ABC 的距离为1，点E 是线段AB 的中点，过点E 作球O 的截面，则截面面积的最小值是（ ）A ．74π B ．2π C.94π D ．3π12.已知函数()f x 满足()()111f x f x +=+，当01x ≤≤时，()f x x =，若方程()(]()01,1f x mx m x --=∈-有两个不同实数根，则实数m 的最大值是 （ ）A ．12- B ．13-C.13 D ．12第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.若()2,,20a b a b a ==⋅-+=，则向量a 与b 的夹角为 ．14. 已知实数,x y 满足的约束条件220323010x y x y x y -+≥⎧⎪--≤⎨⎪+-≥⎩，表示的平面区域为D ，若存在点(),P x y D ∈，使22x y m +≥成立，则实数m 的最大值为 ．15.已知直线:0l kx y k -+=与圆2212x y +=交于,A B 两点，过,A B 分别作l 的垂线与x 轴交于,C D两点，若AB =，则CD = ．16.把正整数按一定的规律排成如图所示的三角形阵.设(,ij a i j ∈N *）是位于数阵中从上向下数第i 行，从左向右数第j 列的数，例如：4310a =，若173ij a =，则i j += ．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知在ABC ∆中，,,a b c 分别是角,,A B C 所对应的边，且20a b -=. （1）若6B π=，求C ；（2）若2,143C c π==，求ABC ∆的面积.18. 随着生活水平的提高，人们对空气质量的要求越来越高，某机构为了解公众对“车辆限行”的态度，随机抽查40人,并将调查情况进行整理后制成下表：（1）完成被调查人员年龄的频率分布直方图，并求被调査人员中持赞成态度人员的平均年龄约为多少岁？ （2）若从年龄在[)[)15,25,45,55的被调查人员中各随机选取1人进行调查.请写出所有的基本亊件,并求选取2人中恰有1人持不赞成态度的概率.19. 如图，在直三棱柱111ABC A B C -中，四边形11ABB A 3,BC D =为BC 上的一点，且平面1ADB ⊥平面11BCC B . （1）求证：AD ⊥平面11BCC B ；（2）若1B D 与平面ABC 所成角为60，求三棱锥11A CB D -的体积.20. 已知,A B 分别是椭圆 ()2222:10x y C a b a b+=>>的长轴与短轴的一个端点，12,F F 分别是椭圆C 的左、右焦点，D 椭圆上的一点，12,DF F ∆的周长为6,AB =（1）求椭圆C 的方程；（2）若P 是圆227x y +=上任一点，过点作P 椭圆C 的切线，切点分别为,M N ，求证：PM PN ⊥.21. 已知函数()ln 3mf x x x x=++. （1）求函数()f x 的单调区间；（2）若对任意的[]0,2m ∈，不等式()()1f x k x ≤+，对[]1,x e ∈恒成立，求实数k 的取值范围.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22. 选修4-4：坐标系与参数方程已知直线l的参数方程为12(x m t t y ⎧=+⎪⎪⎨⎪=⎪⎩为参数），以坐标原点为极点，以x 轴正半轴为极轴建立极坐标系，椭圆C 的极坐标方程为222455cos 9sin θθρ+=，且直线l 经过椭圆C 的右焦点F .（1）求椭圆C 的内接矩形PMNQ 面积的最大值； （2）若直线l 与椭圆C 交于,A B 两点，求FA FB ⋅的值.23.选修4-5：不等式选讲 已知()11f x x x =-++. （1）求()2f x x ≤+的解集； （2）若()33(22g x x x x =++-∈R ），求证：()121a a g x a+--≤对a ∀∈R ，且0a ≠成立.2018年福建省宁德市高三毕业班第三次质量检查数学（文）试题参考答案一、选择题1-5: ACACD 6-10:ADDBD 11-12：CD二、填空题13.3π 14. 1811615. 11 三、解答题17. 解：(1),20,sin 2sin 16B a b A B π=-=∴== ,又0,,23A A C AB ππππ<<∴=∴=--=.(2)由题意，得()222214222cos3b b b b π-+-⋅⋅⋅， 1sin 2ABC b a S ab C ∆∴==∴==18. 解：(1)被调查人员年龄的频率分布直方图如图所示：被调查人员持赞成态度人的平均年龄约为42063084045096042.646849x ⨯+⨯+⨯+⨯+⨯=≈++++（岁）.(2)设[)15,25中赞成的4人分别为1234,,,A A A A ，不赞成的1人为a ，[)45,55中赞成的4人分别为1234,,,B B B B ，不赞成的1人为b .基本事件为：()()()()()()()()()()111213141212223242,,,,,,,,,,,,,,,,,,,A B A B A B A B A b A B A B A B A B A b ，()()()()()()()()()()313233343414243444,,,,,,,,,,,,,,,,,,,A B A B A B A B A b A B A B A B A B A b ，()()()()()1234,,,,,,,,,a B a B a B a B a b 基本事件共有5525⨯=个，其中恰有1人持不赞成态度的基本事件为111148++++=个.据古典概型知：恰有1人持不赞成态度的概率825P =. 19. 解：(1)在四边形11BBCC 中，过B 点作1BE B D ⊥，垂足为E .因为平面1AB D ⊥平面11BCC B ，平面1AB D 平面11,BCC B B D BE =⊂平面11BCC B ，BE ∴⊥平面1AB D ，又AD ⊂ 平面1,AB D AD BE ∴⊥.因为直三棱柱111ABC A B C -中，1BB ⊥平面,ABC AD ⊂平面111,.,,ABC AD BB BB BE B BB BE ∴⊥=⊂ 平面11BCC B ，AD ∴⊥平面11BCC B .(2)1BB ⊥平面1,ABC B DB ∴∠是1B D 与平面ABC 所成的角，即160B DB ∠= .在1RtB BD中，11BB BD =∴=，又3,2BC CD =∴=.1111222CB D S CD BB ∆∴=⋅⋅=⨯=11//AA BB ，所以点1A 到平面1CB D 的距离等于点A 到平面1CB D 的距离.由（1）得AD ⊥平面11BCC B ，所以在Rt ADB ∆中，AD ==11111133A CB D A CB D CB D V V S AD --∆∴==⋅==.20. 解：(1)由12DF F ∆的周长为6，得226a c +=，由AB =227a b +=，又222,2,1b c a a b c +=∴==.故椭圆C 的方程为22143x y +=. (2) ① 当切线PM 的斜率不存在或为零时，此时取(P ，显然直线:PN y =:2PM x =恰是椭圆的两条切线.由圆及椭圆的对称性，可知PM PN ⊥.②点切线,PM PN 斜率存在且不为零时，设切线PM 的方程为1,y k x m PN =+的方程为()()2000,,2y k x t P x y x =+≠±，由122143y k x mx y =+⎧⎪⎨+=⎪⎩，消y ，得()()22211438430k x k mx m +++-=， PM 与椭圆C 相切，()()22222211164164330,43k m k m m k ∴∆=-+-=∴=+.()220100100101,,43y k x m m y k x y k x k =+∴=-∴-=+ .即()222010*******x k x y k y --+-=；同理：切线2:PN y k x t =+中，()2220200204230x k x y k y --+-=，12,k k ∴是方程()22200004230x k x y k y --+-=的两个根，又P 在圆上，2222220001222003737,7,1,44y x x y y x k k PM PN x x ---∴+=∴=-∴===-∴⊥--.综上所述：PM PN ⊥.21. 解：(1)()22213'3,0m x x mf x x x x x+-=-+=> ,所以①当0m -≥，即0m ≤时，()'0f x >在()0,+∞上恒成立，()f x ∴在()0,+∞上单调递增.②当0m >时，由()'0f x =，得10x =<（不符合题意，舍），20x =>，所以由()'0f x >得x >，由()'0f x <得106x -+<<，()f x ∴在10,6⎛- ⎝⎭上单调递减，在16⎛⎫-+∞ ⎪⎝⎭上单调递增.综上所述，当0m ≤时，()f x 的递增区间为()0,+∞，无递减区间；当0m >时，()f x 的递增区间为16⎛⎫-+∞ ⎪⎝⎭，递减区间为10,6⎛- ⎝⎭.(2) 对[]()()0,2,1m f x k x ∀∈≤+，即()ln 31mx x k xx++≤+，又()220,13ln x m k x x x x >∴≤+--恒成立，()2222ln 13ln 2,2x k x x x x k x x ∴+--≥∴≥++.令()2ln 22x g x x x=++，则()2231ln 4ln 4'x x x g x x x x ---=-=，又[]1,x e ∈时，ln 0,4,ln 40x x x x x x ≥<∴--<，()()'0,g x g x ∴<∴在[]1,e 上是减函数，()14k g ∴≥=，即[)4,k ∈+∞.22. 解：(1) 椭圆C 化为222222225cos 9sin 45,5945,195x y x y ρθρθ+=∴+=∴+=.设椭圆C 的内接矩形PMNQ 中，P的坐标为()3cos αα，43cos 12cos 2PMNQ S ααααα∴=⨯==≤.所以椭圆C 的内接矩形PMNQ面积最大值为(2)由椭圆C 的方程22195x y +=，得椭圆C 的右焦点()2,0F ，由直线l 经过右焦点()2,0F ，得2m =，易得直线l的参数方程可化为122(x t t y ⎧=+⎪⎪⎨⎪=⎪⎩为参数），代入到225945x y +=，整理得，21225810250,8t t t t +-=∴=-，即258FA FB ⋅=. 23. 解：（1）由()2f x x ≤+，得201112x x x x x +≥⎧⎪≤-⎨⎪---≤+⎩或2011112x x x x x +≥⎧⎪-<<⎨⎪-++≤+⎩或201112x x x x x +≥⎧⎪≥⎨⎪-++≤+⎩，解之得02x ≤≤，()2f x x ∴≤+的解集为{}|02x x ≤≤. （2）1211112a a a a a +--=+--，11111212a a a a+--≤++-，11111212a a a a+--≤++-，当且仅当11120a a ⎛⎫⎛⎫+-≤ ⎪⎪⎝⎭⎝⎭时，取等号.11123a a ∴+--≤，即1213a a a +--≤，又因为当x ∈R 时，()()min 1213,+--=∴≤a a g x g x a对a ∀∈R ，且0a ≠成立.。

2018届宁德市普通高中毕业班第二次质量检查试卷文科数学一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1.A. B. C. D.【答案】C【解析】分析：先化简集合B,.故答案为：C点睛：本题主要考查集合的化简和交集，意在考查学生对这些基础知识的掌握能力.2.B.【答案】A【解析】分析：利用复数的除法法则化简即得解.故答案为：A点睛：本题主要考查复数的除法运算，意在考查学生对这些知识的掌握能力.3. 下图是具有相关关系的两个变量的一组数据的散点图和回归直线，对应的数据的相关系数最大，则应当去掉的点是【答案】B【解析】分析：利用相关系数的定义性质分析得解.详解：因为相关系数的绝对值越大，越接近1，则说明两个变量的相关性越强.因为点E到直线的距离最远，所以去掉点E,.点睛：本题主要考查回归直线和相关系数，相关系数的绝对值越大，越接近1，则说明两个变量的相关性越强.4.【答案】D【解析】分析：先利用函数的奇偶性排除B,C，再求D选项的切线方程得解.详解：因为曲线关于原点对称，所以函数是奇函数.对于选项B,所以它是偶函数，不是奇函数，故排除B.对于选项C，由于函数的定义域为，定义域不关于原点对称，所以不是奇函数，故排除C.对于选项D,设切点为线方程为.故答案为：D点睛：(1)本题主要考查函数的奇偶性和求曲线的切线方程，意在考查学生对这些基础知识的掌握能力. (2)据切点在切线和曲线上，求出切点，最后写出切线的方程.5.D.【答案】B.详解：不等式组对应的平面区域如图所示：因为z=4x-y,所以y=-4x-z，直线的纵截距为-z,当直线经过点C时，纵截距-z最大值时，z最小.联立方程组故答案为：B点睛：(1)本题主要考查线性规划问题，意在考查学生对这些基础知识的掌握能力和数形结合的能力.(2) y=-4x-z，直线的纵截距为-z,当直线经过点C时，纵截距-z最大值时，z最小.不要理解为纵截距最小，则z 最小，一定看纵截距这个函数的单调性.对这一点，学生要理解掌握并灵活运用.6.【答案】C.，所以或,故答案为：C点睛：(1)本题主要考查等差数列的基本量的计算和通项公式，意在考查学生对这些基础知识的掌握能力和基本的运算能力.(2)等差数列,注意这个性质的灵活运用.7. 如下图所示，网格纸上小正方形的边长为粗线画出的是某几何体的三视图，则此几何体的表面积为【答案】B【解析】分析：首先通过三视图找到几何体原图，进一步求出几何体的表面积．详解：根据三视图，该几何体是边长为2的正方体，在右前方切去一个边长为1的正方体，则表面积没有变化．故S=6•2•2=24．故答案为：B点睛：（1）本题主要考查三视图和几何体的表面积的计算,意在考查学生对这些基础知识的掌握能力和空间想象能力. (2)得到几何体原图后，逐一计算出表面积也可以，但是观察到，虽然是正方体切去了一个小正方体，但是几何体的表面积没有变，提高了解题效率，意在考查学生的空间想象能力和观察能力.8. 的图象向右平移式为D.【答案】A【解析】分析：先化简f(x),再求出w的值，再求平移后的函数解析式得解.因为函数的周期是所以所以个单位后，所得的函数解析式为故答案为：A点睛：(1)本题主要考查三角函数解析式的求法，考查函数图像的变换，意在考查学生对这些基础知识的掌握能力.(2) 个单位，得到函数,个单位，得到函数,简记为“左加右减”.9.【答案】C.由题得，所以故答案为：C点睛：（1）本题主要考查抛物线的定义和简单几何性质，考查直线与抛物线的位置关系及推理分析能力.(2)本题的解法比较多，利用上面的方法比较简洁，关键是灵活运用抛物线的定义和解直角三角形.10.B. C. D.【答案】B【解析】分析:先求出分段函数的每一段的单调性，从而得到函数的单调性，再利用函数的单调性转化为,最后利用二次函数的图像性质得解.详解:,由于-1+1=ln(-1+2)=0,,因为函数,,,.故答案为：B,,个解.对于函数的零点问题常用的是图像法.11. 且边长为四边形的外接球的半径为D.【答案】D【解析】分析: 首先把平面图形转换为空间图形，进一步利用球的中心和勾股定理的应用求出结果．详解: 如图所示：菱形ABCD的∠A=60°，沿BC折叠，得到上图，则E、F分别是△ABC和△BCD的中心，球心O为△ABC和△BCD的过中心的垂线的交点，则：OE=OF=1，EC=2，利用勾股定理得：故答案为：D点睛: (1)本题主要考查空间几何体的外接球问题，考查二面角，意在考查学生对这些基础知识的掌握能力及空间想象能力. (2)解答本题的关键是找到球心,由于E、F分别是△ABC和△BCD的中心，所以球心O为△ABC 和△BCD的过中心的垂线的交点.12. 为数列对任意的【答案】C【解析】分析：根据数列{a n}求解S n，利用不等式的性质求解．详解：由a12a n+1+3S n=3（n∈N*），则2a n+3S n﹣1=3．两式相减，可得2a n+1﹣2a n+3a n=0，∵a1=，∴a n=﹣n．那么．要使n∈N*恒成立．根据勾勾函数的性质，当S n∴实数M故答案为：C点睛：（1）本题考查了等差数列与等比数列的通项公式及其前n项和公式，意在考查了学生对这些基础知识的掌握能力及推理能力与计算能力．（2S n项都大于1，单调递减，偶数项都小于1，单调递增..二、填空题（每题5分，满分20分，将答案填在答题纸上）13. _______．【解析】分析：直接把.故的夹角为.故答案为：点睛：本题主要考查向量的数量积及向量的运算，考查向量的夹角，意在考查学生对这些基础知识的掌握能力及基本的运算能力.14. 为焦点的双曲线______．【解析】分析：根据题意，由双曲线的标准方程可得a、b的值，由双曲线的定义可得||PF1|﹣|PF2||=2a=2，又由|PF1|=3|PF2|，计算可得|PF1|=3，|PF2|=1，又由|F1F2详解：根据题意，双曲线C的方程为x2﹣y2=1，则a=1，b=1，则则||PF1|﹣|PF2||=2a=2，又由|PF1|=3|PF2|，则|PF1|=3，|PF2|=1，又由|F1F2则△PF1F2的周长l=|PF1|+|PF2|+|F1F2故答案为：4点睛：(1)本题主要考查双曲线的简单几何性质，考查双曲线的定义,意在考查学生对这些基础知识的掌握能力. (2)在圆锥曲线种，只要看到焦半径就要联想到曲线的定义分析解答，这是一个解题技巧，学生要掌握.15. 我国南北朝时期的数学家张丘建是世界数学史上解决不定方程的第一人，他在《张丘建算经》中给出一个解不定方程的百鸡问题，问题如下：鸡翁一，值钱五，鸡母一，值钱三，鸡雏三，值钱一．百钱买百鸡，为______．【答案】4y=25，结合x=4t，可得框图中正整数m的值．得：y=25，故x必为4的倍数，当x=4t时，y=25﹣7t，由y=25﹣7t＞0得：t的最大值为3，故判断框应填入的是t＜4？，即m=4，故答案为：4点睛:本题考查的知识点是程序框图，根据已知分析出y与t的关系式及t的取值范围，是解答的关键．16.______．【解析】分析：求出f（x）的解析式为f（x）=e x，结合函数图象即可得出a的范围．详解：0，∴f（x）为增函数，∴f（f（x）﹣e x）=1，∴存在唯一一个常数x0，使得f（x0）=1，∴f（x）﹣e x=x0，即f（x）=e x+x0，令x=x00=1，∴x0=0，故而f（x）=e x，∵f（x）≥ax+a恒成立，即e x≥a（x+1）恒成立．∴y=e x的函数图象在直线y=a（x+1）上方，不妨设直线y=k（x+1）与y=e x的图象相切，切点为（x0，y0），k=1．∴当0≤a≤1时，y=e x的函数图象在直线y=a（x+1）上方，即f（x）≥ax+a恒成立，：故答案为：[0，1]．三、解答题：本大题共6小题，满分70分．解答须写出文字说明证明过程和演算步骤．17.（1（2【答案】（1（2【解析】分析：（1）先利用正弦定理边化角得到A的大小.(2)先利用余弦定理求c，再利详解：（1（2由余弦定理有：，或（舍去）点睛：（1）本题主要考查正弦定理、余弦定理解三角形，意在考查学生对这些基础知识的掌握能力及分析转化能力.(2)数学的解题必须严谨，在得到后，不能简单两边同时除以sinC,必须说明sinC.在有的地方容易出错.18. 为响应绿色出行，某市在推出“共享单车”后，又推出“新能源租赁汽车”．每次租车收费的标准由两部分组成：①里程计费：1元/公里；②/，现统计了50次路上开车所用时间，在各时间段内频数分布情况如下表所示分．（1（2，并说明理由.（同一时段，用该区间的中点值作代表）【答案】（1（2）见解析【解析】分析：（1）利用对立事件的概率公式求陈先生一次租用新能源租赁汽车的时间不低于30分钟的概率.(2).详解：（1）设“陈先生一次租用新能源租赁汽车的时间不低于30分钟”所以陈先生一次租用新能源租赁汽车的时间不低于（2每次租用新能源租赁汽车的平均费用为因此公车补贴够上下班租用新能源分时租赁汽车.点睛：本题主要考查对立事件的概率，考查平均值的计算等知识，意在考查学生对这些基础知识的掌握能力及分析能力.19. ，（1（2（i（ii【答案】（1）见解析；（2）见解析，【解析】分析: (1)再证明连接证明四边形.（ii）先分别计算出两部分的体积，再求它们的比.详解：（1）证明：(1)连接(2)(i),理由如下:、，四边形.：（1）本题主要考查空间平行垂直位置关系的证明，考查空间几何体体积的计算，意在考查学生对这些基础知识的掌握能力和空间想象转化能力.（2）对于空间平行垂直位置关系的证明有几何法和向量法两种方法，空间几何体体积的计算有公式法、割补法和体积变换法三种方法.20. 的离心率为（1的方程；（2两点，求【答案】（12【解析】分析：（1）根据已知列出方程组解方程组即得椭圆.(2)t的值，即得直线的方程.详解：（1联立①②得（2）由（1依题意,的方程为,的距离为,当且仅当时,即时取等号,,此时直线的方程为．点睛：（1）本题主要考查椭圆标准方程的求法，考查直线和椭圆的位置关系，意在考查学生对这些基础知识的掌握能力及分析推理能力和计算能力. (2)数的最大值，本题是利用基本不等式求的最大值,简洁明了,解题效率高.21.（1（2【答案】（1）见解析；（2）见解析【解析】分析：（1）先求导，再对a.(2)详解：,则或,时,,,综上所述：,.,.（2）由(1)；,.的极小值为有三个零点,则需,要证明：即要证：证明如下：构造函数令∴．22.．（1的极坐标方程；（2【答案】（12）1【解析】分析：（1）直接代极坐标公式化极坐标为直角坐标，利用三角恒等式消参得到再化为极坐标方程.(2)利用直线参数方程t.详解：（1，曲线化为一般方程为：化为极坐标方程为：（2）及联立得，点睛：（1）本题主要考查直角坐标、极坐标和参数方程的互化，考查直线参数方程t的几何意义，意在考查学生对这些基础知识的掌握能力及运算能力. (2)就表示点的距离（2）由直线参数方程中参数的几何意义得：如果求直线上两点在哪里，总有23. 已知实数x, y（1）解关于x；（2【答案】（1；（2）9【解析】分析：（1）先消去y利用基本不等式详解：（1）时，原不等式化为时，原不等式化为（2.当且仅当“=”.点睛：（1）本题主要考查零点讨论法解绝对值不等式，考查不等式的证明，意在考查学生对这些基础知识的掌握能力和分类讨论能力.(2)第（2换之后才方便利用基本不等式证明.。

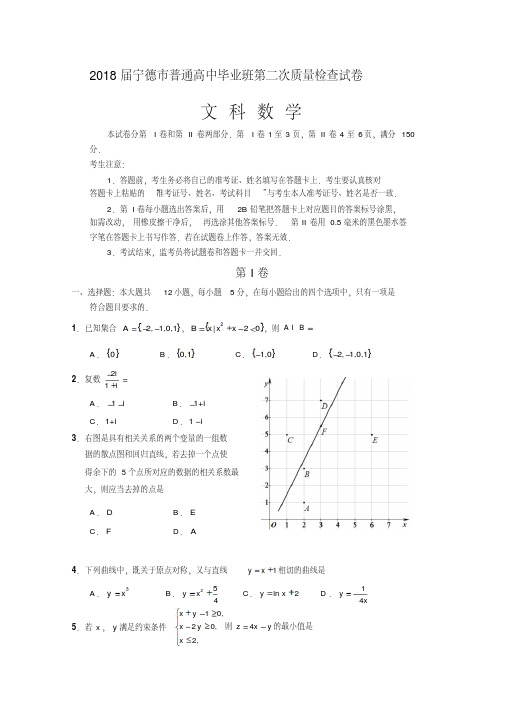
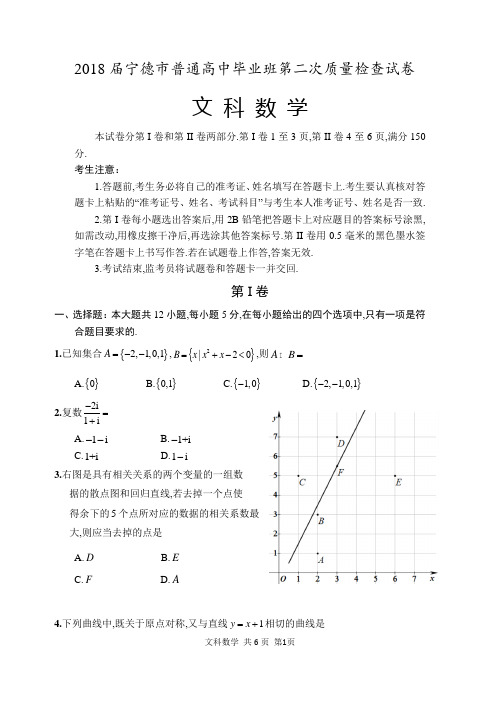
2018届宁德市普通高中毕业班第二次质量检查试卷文 科 数 学本试卷分第I 卷和第II 卷两部分.第I 卷1至3页,第II 卷4至6页,满分150分. 考生注意：1.答题前,考生务必将自己的准考证、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致.2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.第II 卷用0.5毫米的黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答,答案无效.3.考试结束,监考员将试题卷和答题卡一并交回.第I 卷一、选择题：本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2,1,0,1A =--,{}2|20B x x x =+-<,则A B =IA.{}0B.{}0,1C.{}1,0-D.{}2,1,0,1-- 2.复数2i1i-=+ A.1i -- B.1+i - C.1+i D.1i -3.右图是具有相关关系的两个变量的一组数 据的散点图和回归直线,若去掉一个点使 得余下的5个点所对应的数据的相关系数最 大,则应当去掉的点是A.DB.EC.FD.A4.下列曲线中,既关于原点对称,又与直线1y x =+相切的曲线是A.3y x =B.254y x =+ C.ln 2y x =+ D.14y x =-5.若x ,y 满足约束条件10,20,2,x y x y x +-≥⎧⎪-≥⎨⎪≤⎩则4z x y =-的最小值是A.43 B.73C.7D.9 6.已知等差数列{}n a 满足3514a a +=,2633a a =,则17a a =A.33B.16C.13D.127.如右图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的表面积为A.25B.24C.23D.228.将周期为π的函数ππ())cos()(0)66f x x x ωωω+++> 的图象向右平移π3个单位后,所得的函数解析式为 A.π2sin(2)3y x =- B.2cos(2)3y x π=-C.2sin 2y x =D.2π2cos(2)3y x =- 9.过抛物线24y x =的焦点F 作一倾斜角为3π的直线交抛物线于A ,B 两点（A 点在x 轴上方）,则AF BF=A.2B.52C.3D.4 10.已知ln(2),1,()1,1,x x f x x x x +≥-⎧⎪=⎨-<-⎪⎩若函数2(2)(2)y f x f x k =--+只有一个零点,则实数k 的值为A.4B.3C.2D.1 11.将一个内角为3π且边长为的菱形沿着较短的对角线折成一个二面角为2π的空间四边形,则此空间四边形的外接球的半径为B.2C.3 12.记n S 为数列{}n a 的前n 项和,满足132a =,1233()n n a S n *++=∈N ,若2n n S M S +≤对任意的n *∈N 恒成立,则实数M 的最小值为A. B.176 C.4112D.42018届宁德市普通高中毕业班第二次质量检查试卷文 科 数 学第II 卷注意事项：用0.5毫米黑色签字笔在答题卡上书写作答.在试题卷上作答,答案无效. 本卷包括必考题和选考题两部分.第13～21题为必考题,每个试题考生都必须做答.第22、23题为选考题,考生根据要求做答. 二、填空题（每题5分,满分20分,将答案填在答题纸上） 13.已知两个单位向量a ,b ,且|2|-=a b 则a ,b 的夹角为_______.14.已知点P 是以1F ,2F 为焦点的双曲线22:1C x y -=上的一点,且12=3PF PF ,则12PF F ∆的周长为______.15.我国南北朝时期的数学家张丘建是世界数学史上解决不定方程的第一人,他在《张丘建算经》中给出一个解不 定方程的百鸡问题,问题如下：鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一.百钱买百鸡,问鸡翁母 雏各几何？用代数方法表述为：设鸡翁、鸡母、鸡雏的 数量分别为x ,y ,z ,则鸡翁、鸡母、鸡雏的数量即为方程组53100,3100z x y x y z ⎧++=⎪⎨⎪++=⎩的解.其解题过程可用框图 表示如右图所示,则框图中正整数m 的值为 ______. 16.已知定义在R 上的函数()f x 满足()0f x '>且(()e )1x f f x -=,若()f x ax a ≥+恒成立,则实数a 的取值范围为______.三、解答题：本大题共6小题,满分70分.解答须写出文字说明证明过程和演算步骤.17.（12分）ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,且(sin cos )b a C C =+. （１）求角A 的大小；（２）若a b ==求AC 边上高BD 的长. 18.（12分）为响应绿色出行,某市在推出“共享单车”后,又推出“新能源租赁汽车”.每次租车收费的标准由两部分组成：①里程计费：1元/公里；②时间计费：0.12元/分.已知陈先生的家离上班公司12公里,每天上、下班租用该款汽车各一次.一次路上开车所用的时间记为t （分）,现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示：将各时间段发生的频率视为概率,一次路上开车所用的时间视为用车时间,范围为[)20,60错误！未找到引用源。

2018年宁德市普通高中毕业班质量检查 数学（文科）试题参考答案及评分标准说明：一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解法不同，可根据试题的主要考查内容比照评分标准指定相应的评分细则． 二、对计算题，当考生的解答在某一部分解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数． 四、只给整数分数，选择题和填空题不给中间分．一、选择题：本题考查基础知识和基本运算，每小题5分，满分60分．1. D2. A3. B4. A5.C6. C7. C8. B9. D 10. B 11. D 12.A二、填空题：本题考查基础知识和基本运算，每小题5分，满分20分．13. 12i 55-- 14. 13 15. 36π 16. (1)22n n -+三、解答题：本大题共6小题，满分70分，解答须写出文字说明、证明过程和演算步骤． 17.本小题主要考查正弦定理、余弦定理等基础知识，考查运算求解能力，考查化归与转化思想、函数与方程思想等．满分12分． （Ⅰ）1BC =,4B π=,1sin 2BCDS BC BD B ∆=⨯⨯⨯………….….1分11122BD ⨯⨯=……………………….…2分BD = ……………………………………3分在BCD ∆中，由余弦定理得2222cos CD BC BD BC BD B =+-⨯⨯……….…………....4分21211=+-⨯=………………………………...5分∴1CD = ………………………………………………. ....6分(Ⅱ)在ACD ∆中，由正弦定理得sin sin AD CDACD A=∠…………....7分 ∴sin sin AD AACD CD⋅∠=sin62AD AD CD CDπ⋅== …………....8分 在BCD ∆中，由正弦定理得sin sin DB CDDCB B=∠ .………..9分∴sin sin 4sin DB DB BDCB CDCDπ⋅⋅∠===…………..10分∴sin 1sin 3ACD DCB ∠===∠………….………..12分18.本小题主要考查空间直线与直线、直线与平面的位置关系、平面与平面位置关系，几何体的体积等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查化归与转化思想等．满分12分．解法一：,.AB O CO DO I ()证明：取中点，连接……………..1分∵ABC ∆为等边三角形CO AB ∴⊥ ……………....2分 ∵0ABCD DBA ∠四边形为菱形，=60 ∴DAB ∆为等边三角形∴DO AB ⊥……………………………….3分 又∵CODO O =∴AB DOC ⊥面…………………………..5分 ∵DC DOC ⊂面∴AB CD ⊥………………………………..6分 （Ⅱ）∵,,ABDE ABC CO AB ABDEABC AB CO ABC ⊥⊥⊂面面面面=,面∴CO ABDE ⊥面 ∵OD ABDE ⊂面∴CO OD ⊥…………………………………….……...8分∵OD OC =在Rt COD ∆中，CD =由（1）得AB CD ⊥， 因为//,ED AB ED DC ⊥且11222CDE S CD ED ∆=⨯⋅=⨯...9分∵0122sin1202BDE S ∆=⨯⨯⨯..…..10分.B CDE h 设点到面的距离为∵B CDE C BDE V V --=即1133CDE BDE S h S CO ∆∆⨯⋅=⨯⋅.…….11分即1133h =∴h =.…….12分 解法二：（Ⅰ）同解法一（Ⅱ）∵在菱形ABDE 中,//,AB DE DE ⊂平面CDE ,AB ⊄平面CDE∴//AB 平面CDE∴B 点到平面CDE 的距离等于O 点到平面CDE 的距离……………7分 由（Ⅰ）知, AB ⊥平面ODC ∴DE ⊥平面ODC ∵DE ⊂平面CDE ∴平面ODC ⊥平面CDE过O 作OH DC ⊥于H ,则OH ⊥平面CDE , 且OH DC ⊥……………8分 ∵,DO AB CO AB ⊥⊥DOC ∠为二面角D AB C --的平面角∵平面ABC ⊥平面ABDEDO OC ⊥……………10分DO OC DC ==又DC OH OD OC ⋅=⋅………………………………………………..…11分∴OH =..…12分 19. 本小题主要考查了频率分布直方图，平均数，函数，不等式等基础知识，考查数据分析能力、运算求解能力，考查化归与转化思想等．满分12分 （Ⅰ）…. ………2分解：设年需求量平均数为x ，/t则650.05750.15850.5950.21050.186.5x =⨯+⨯+⨯+⨯+⨯= ……………6分 (注:列式2分,错一个扣1分,错两个及以上不得分;答案2分) （Ⅱ）设今年的年需求量为x 吨、年获利为y 万元 当0100x ≤≤时，0.40.3(100)0.730y x x x =-⨯-=- 当100x >时，40y =故0.730,6010040,100110x x y x -≤≤⎧=⎨<≤⎩………………………………………8分0.73027.4x -≥则82x ≥ ……………………………………………………………………9分9082(8290)(8090)10P x P x -≤<=⨯≤<，40.50.45=⨯=………………………………………………..………………10分 (90100)0.2P x ≤<=(100110)0.1P x ≤≤=………………………………………………………..11分(82)(8290)(90100)(100110)P x P x P x P x ≥=≤<+≤<+≤<0.40.20.10.7=++=所以今年获利不少于27.4万元的概率为0.7………………………………12分20. 本题主要考查直线、圆、抛物线、直线与圆，直线与抛物线的位置关系等基础知识，考查运算求解能力、推理论证能力，考查函数与方程思想、化归与转化思想，考查考生分析问题和解决问题的能力，满分12分．解：（I ）因为抛物线焦点F 坐标为(,0)2p , 则:2AB pl x =联立 222y px px ⎧=⎪⎨=⎪⎩∴112p x y p ⎧=⎪⎨⎪=⎩或222p x y p ⎧=⎪⎨⎪=-⎩ 故122AB y y p =-= ……………………………………………………2分 ∴213326222MAB S p p p ∆=⨯⨯== ……………………………………….3分即2p = …………………………………………………………………..4分∴抛物线方程为：24y x =圆方程为：()2224x y ++=…………………………………………….5分(注:错一个不给分)(II) 解法一：显然1l 、2l 的斜率必须存在且均不为0，设1l 的方程为y kx =，则2l 方程为1y x k =-…………………………………….6分(注:末说明斜率不给分)由24y x y kx ⎧=⎨=⎩得0x =，或24x k =∴244(,)C k k 同理可求得2(4,4)E k k -………….7分由22(2)4x y y kx ⎧++=⎨=⎩得0x =，或241x k =-+∴2244(,)11kD k k --++同理可求得22244(,)11k k G k k -++…………….8分∴422224(4)2144()11COE C E DOGD Gk S y y k k k k k Sy y k k k -⋅++===-⋅++………….10分221224k k =++≥=…….11分 当且仅当1k =±时， COE ∆与DOG ∆的面积比的取到最小值4.…………….12分 解法二：显然1l 、2l 的斜率必须存在且均不为0，设1l 的方程为y kx =，则2l 方程为1y x k =-…………………………………….6分(注:末说明斜率不给分)由24y x y kx⎧=⎨=⎩得x =0，或24x k =∴244(,)C k k 同理可求得2(4,4)E k k -………….7分则1002COEC E SOC OE x x ==-- ()22228111442k k k k k k ++=⋅⋅⋅=…………………………………….8分 设(2,0)M -到1l 、2l 的距离分别为1d 、2d则1d =2d =……………………………………….9分则1228122221DOGk Sd d k =⋅⋅==+………………..10分∴()22422228112112248COE DOG k Skk k k S kk k k ++++=⋅==++≥=…….11分 当且仅当1k =±时， COE ∆与DOG ∆的面积比的取到最小值4.…………….12分21.本小题主要考查导数及其应用、不等式等基础知识，考查推理论证能力、运算求解能力、创新意识等，考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想等．满分12分．解：（Ⅰ）函()y f x =的定义域为(0,)+∞………………………...……1分2()(1)a b f x x x'=-++………………………………………………..2分 把(1,(1))f 代入方程10x y -+=中，得1(1)10f -+=即(1)2f =，∴4a =…………………………………….…………3分又因为(1)1f '=，∴14a b -+= 故2b =…………………………………………………………...…4分 （Ⅱ）由（Ⅰ）可知4()2ln 1f x x x =++，当1x >时 ln ()21k x f x x >++恒成立等价于22(22)ln 0x x k x -++->..……5分 设()22(22)ln g x x x k x =-++-， 则1()22ln (22)g x x x k x '=-+++-⋅ 22ln k x x-=+………………………………………..……7分 由于1,ln 0x x >>当2k ≤时，()0g x '>，则()y g x =在(1,)+∞上单调递增，()(1)0g x g >=恒成立.………………………………………8分当2k >时，设()()h x g x '=,则222()0k h x x x-'=->…….…..9分 则()y g x '=为(1,)+∞上单调递增函数，又由(1)20g k '=-<………………………………….10分即()g x 在(1,)+∞上存在0x ，使得0()0g x '=，当0(1,)x x ∈时，()g x 单调递减，当0(,)x x ∈+∞时， ()g x 单调递增；则0()(1)0g x g <=，不合题意，舍去.……………………….11分综上所述，实数k 的取值范围是(,2]-∞.……………………12分22.选修44-；坐标系与参数方程本小题考查直线和圆的极坐标方程、参数方程等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想等．满分10分．解：（1）设(,)P ρθ，1(,)M ρθ，则由,OP OM 成等比数列，可得20OP OM ⋅=，………………………………1分 即1=20ρρ⋅，120=ρρ．………………………………2分又1(,)M ρθ满足14sin ρθ=，即204sin θρ=，………………………………3分 ∴sin 5ρθ=，………………………………4分化为直角坐标方程为5y =．………………………………5分（Ⅱ）依题意可得(2,5)B ，故1AB k =，即直线AB 倾斜角为4π，………………………………6分∴直线AB的参数方程为,23,x y ⎧=⎪⎪⎨⎪=+⎪⎩………………………………7分代入圆的直角坐标方程22(2)4x y +-=，得230t -=，………………………………8分故12t t +=，1230t t =-<，………………………………9分∴12AD AE t t -=+=………………………………10分23．选修45-：不等式选讲本小题考查绝对值不等式的解法与性质等基础知识，考查运算求解能力、推理论证能力，考查分类与整合思想、化归与转化思想等． 满分10分．解：(1)当4a =-时，()()f x g x ≥化为2412x x x -≥++- ，…………1分当1x ≤-，不等式化为2+250x x -≥，解得1x ≤-或1x ≥-+故1x ≤-；…………2分当12x -<<时，不等式化为27x ≥，解得x ≤x ≥，故x ∈∅； …………3分当2x ≥，不等式化为2230x x --≥，解得1x ≤-或3x ≥故3x ≥； …………4分所以()f x x ≤解集为{|1x x x ≤-}3x ≥． …………5分(2) 由题意可知，即为[0,3]x ∈时，()()f x g x ≤恒成立． …………6分当02x ≤≤时，23x a +≤，得()2min 31a x ≤-=-；…………8分 当23x ≤≤时，221x a x +≤-，得()2min +214a x x ≤--=-，综上，4a ≤-．…………10分。

2018年福建省普通高中毕业班质量检查文 科 数 学一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．I4IeOCFw4D 1．已知全集U =R ，集合{}31|<≤-=x x A ，{}0,2,4,6B =，则A B ⋂等于A ．{}0,2B ．{}1,0,2- C ．{}|02x x ≤≤ D ．{}|12x x -≤≤ 2．执行如图所示的程序框图，若输入的x 的值为3，则输出的y 的值为A ．4B ．5C ．8D ．103．某几何体的俯视图是正方形，则该几何体不可能是 Ａ．圆柱 Ｂ．圆锥 Ｃ．三棱柱 Ｄ．四棱柱4．函数()f x =的定义域是 A ．()0,2 B ．[]0,2 C ．()()0,11,2⋃ D ．[)(]0,11,2⋃ 5．“1a =”是“方程22220x y x y a +-++=表示圆”的 Ａ．充分而不必要条件 Ｂ．必要而不充分条件 Ｃ．充要条件 Ｄ．既不充分也不必要条件6．向圆内随机投掷一点，此点落在该圆的内接正n ()3,n n N ≥∈边形内的概率为n P ，下列论断正确的是A ．随着n 的增大，n P 减小B ．随着n 的增大，n P 增大C ．随着n 的增大，n P 先增大后减小D ．随着n 的增大，n P 先减小后增大7．已知0ω>，2π<ϕ，函数()sin()f x x =+ωϕ的部分图象如图所示．为了得到函数()sin g x x =ω的图象，只要将()f x 的图象 A ．向右平移4π个单位长度 B ．向右平移8π个单位长度C ．向左平移4π个单位长度 D ．向左平移8π个单位长度8．已知)(x f 是定义在R 上的奇函数，且在),0[+∞单调递增，若(lg )0f x <，则x 的取值范围是A ．(0,1)B ．(1,10)C ．(1,)+∞D ．(10,)+∞9．若直线ax by ab +=<0,0a b >>）过点()1,1，则该直线在x 轴，y 轴上的截距之和的最小值为A ． 1B ．2C ．4D ． 810．若ABC ∆满足2A π∠=，2AB =，则下列三个式子：①AB AC ，②BA BC ，③CA CB 中为定值的式子的个数为 A ．0 B ．1 C ．2 D ．311．已知双曲线()22122:10,0x y C a b a b-=>>，一条渐近线为l ，抛物线2C ：24y x =的焦点为F ，点P 为直线l 与抛物线2C 异于原点的交点，则PF = A ．2 B ． 3 C ．4 D ．512．已知()g x '是函数()g x 的导函数，且()()f x g x '=，下列命题中，真命题是A ．若()f x 是奇函数，则()g x 必是偶函数B ．若()f x 是偶函数，则()g x 必是奇函数C ．若()f x 是周期函数，则()g x 必是周期函数D ．若()f x 是单调函数，则()g x 必是单调函数第Ⅱ卷<非选择题 共90分）二、填空题:本大题共4小题，每小题4分，共16分．把答案填在答题卡相应位置．13．复数()1i i +=__________．14．已知1sin 3α=，则cos2α=__________．15．已知y x ,满足4000x y x y y +-≤⎧⎪-≥⎨⎪≥⎩，则2z x y =-的最大值是__________．16．在平面直角坐标系xOy 中， Ω是一个平面点集，如果存在非零平面向量a ，对于任意P ∈Ω，均有Q ∈Ω，使得OQ OP a =+，则称a 为平面点集Ω的一个向量周期．现有以下四个命题：yscqAJo3Va ①若平面点集Ω存在向量周期a ，则ka (),0k k ∈≠Z 也是Ω的向量周期； ②若平面点集Ω形成的平面图形的面积是一个非零常数，则Ω不存在向量周期；③若平面点集(){},0,0x y x y Ω=>>，则()1,2b =为Ω的一个向量周期； ④若平面点集()[][]{},0x y y x Ω=-=<[]m 表示不大于m 的最大整数），则()1,1c =为Ω的一个向量周期．其中真命题是＿＿＿＿<写出所有真命题的序号）．三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．17．(本小题满分12分>已知等比数列{}n a 的前n 项和为n S ，432a a =，26S =。

开始1n =2a =-2018n ≤11a a=-a 输出1n n =+结束是否2018年宁德市普通高中毕业班第一次质量检查试卷文 科 数 学本试卷分第I 卷和第II 卷两部分．第I 卷1至3页，第II 卷4至6页，满分150分．第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知集合{320}A x x =-<,2{2}B x x x =≤，则AB =A ．3[0,)2B ．3[0,]2C ．3(,2)2D ．3(,2]22．已知双曲线2221y x b-=的离心率为2,则双曲线的渐近线方程为A ．3y x =±B ．5y x =±C ．3y =D ．3y = 3．福建省第十六届运动会将于2018年在宁德召开，组委会预备在会议期间从3女2男共5名志愿者中任选2名志愿者参与接待工作，则选到的都是女性志愿者的概率为 A ．110 B ．310C ．12D ．354．已知等差数列{}n a 的前n 和为n S ，若1239a a a ++=，636S =,则12a 为 A ．23B ．24C ．25D ．265．已知命题p :“若E 是正四棱锥P ABCD -棱PA 上的中点,则CE BD ⊥”;命题q :“1x >是2x >的充分不必要条件”，则下列命题为真命题的是A ．p q ⌝∧B ．p q ⌝∧⌝C ．p q ∨⌝D ．p q ⌝∨ 6．执行如图所示的程序框图,运行相应的程序，则输出的a 的值为A ． 32B ． 23C ．13D ．2-7．已知0.41.9a =，0.4log 1.9b =， 1.90.4c =，则A ．a b c >>B ．b c a >>C ．a c b >>D ．c a b >>8．我国古代数学名著《孙子算经》中有如下问题：“今有筑城， 上广二丈，下广五丈四尺，高三丈八尺，长五千五百五十尺， 秋程人功三百尺．问：须工几何？” 意思是：“现要筑造底 面为等腰梯形的直棱柱的城墙，其中底面等腰梯形的上底为2丈、下底为5.4丈、高为3.8丈，直棱柱的侧棱长为5550尺．如果一个秋天工期的单个人可以筑出300立方尺，问：一个秋天工期需要多少个人才能筑起这个城墙？”（注：一丈等于十尺）A ．24642B ．26011C ．52022D ．78033 9．已知函数2()23cos 2cos 1(0)f x x x x ωωωω=⋅+->的最小正周期为2π,则当[0,]4x π∈时，函数()y f x =的值域是A ．[2,1]-B ．[2,2]-C ．[1,1]-D ．[1,2]-10．已知三角形ABC 中, 22AB AC ==3DB AD =，连接CD 并取线段CD 的中点F ,则AF CD ⋅的值为A ．5-B ．154-C ．52- D ．2-11．已知1F 、2F 分别是椭圆C ：22221(0)x y a b a b+=>>的左、右焦点，若椭圆C 上存在点A ，满足1223AF AF a -=, 则椭圆的离心率取值范围是A ．)1,21( B ．1[,1)5 C ．2(,1)5 D ．2[,1)512．已知函数3(1),0()(1)e ,0xx x f x x x ⎧-≥⎪=⎨-+<⎪⎩，若函数()()g x f x a =-有3个零点，则实数a 的取值范围是 A ．21(0,)e B ．21(1,)e - C ．2(e ,1)-- D ．(,1)-∞-2018年宁德市普通高中毕业班第一次质量检查试卷文 科 数 学第II 卷注意事项：用0.5毫米黑色签字笔在答题卡上书写作答．在试题卷上作答，答案无效．本卷包括必考题和选考题两部分．第13～21题为必考题，每个试题考生都必须做答．第22、23题为选考题，考生根据要求做答． 二、填空题：本大题共4小题，每小题5分．13．若复数z 满足(2i)i z -=，其中i 为虚数单位，则z =_______． 14．设,x y 满足约束条件12136x y x y x y -≤⎧⎪+≥⎨⎪+≤⎩，则23z x y =+的最小值为_______．15．在三棱锥D ABC -中，DC ⊥平面ABC ，150ACB ∠=︒，7AB =22DC =，则此三棱锥D ABC -的外接球的表面积为_______．16．今要在一个圆周上标出一些数，第一次先把圆周二等分，在这两个分点处分别标上1，如图（1）所示；第二次把两段半圆弧二等分，在这两个分点处分别标上2，如图（2）所示；第三次把4段圆弧二等分，并在这4个分点处分别标上3，如图（3）所示．如此继续下去，当第n 次标完数以后，该圆周上所有已标出的数的总和是_______． 三、解答题：解答须写出文字说明、证明过程和演算步骤． 17．(本小题满分12分)如图，ABC ∆中，D 为AB 边上一点, 1BC =, 4B π=． （Ⅰ）若BCD ∆的面积为12，求CD 的长;（Ⅱ）若6A π=，13AD DB = ，求sin sin ACD DCB ∠∠的值． 18． (本小题满分12分)在多面体CABDE 中， ABC ∆为等边三角形，四边形ABDE 为菱形，平面ABC ⊥平面ABDE ，2AB ，3DBA π∠=． （Ⅰ）求证:AB CD ⊥;（Ⅱ）求点B 到平面CDE 距离． 19． (本小题满分12分)某海产品经销商调查发现, 该海产品每售出1吨可获利0.4万元, 每积压1吨则亏损0.3万元．根据往年的数据,得到年需求量的频率分布直方图如下图所示，将频率视为概率． (Ⅰ)请补齐[90,100]上的频率分布直方图，并依据该图估计年需求量的平均数；(Ⅱ) 今年该经销商欲进货100吨，以x （单位：吨，[60,110]x ∈）表示今年的年需求量，以y （单位：万元）表示今年销售的利润，试将y 表示为x 的函数解析式；并求今年的年利润不少于27.4万元的概率． 20．(本小题满分12分)已知抛物线Γ：22(0)y px p =>的焦点为F ，圆M ：222()x p y p ++=，过F 作垂直于x 轴的直线交抛物线Γ于A 、B 两点，且MAB ∆的面积为6． （Ⅰ）求抛物线Γ的方程和圆M 的方程；(Ⅱ) 若直线1l 、2l 均过坐标原点O ，且互相垂直，1l 交抛物线Γ于C , 交圆M 于D , 2l 交抛物线Γ于E ，交圆M 于G , 求COE ∆与DOG ∆的面积比的最小值． 21．(本小题满分12分) 已知函数()ln 1af x b x x =++，曲线()y f x =在点(1,(1))f 处的切线方程为10x y -+=. （Ⅰ）求a ，b 的值；DCBA（Ⅱ）当(1,)x ∈+∞时，ln ()21k xf x x >++恒成立，求实数k 的取值范围. 请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题记分．做答时请写清题号． 22．（本小题满分10分）选修4—4：坐标系与参数方程在平面直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线1C 的极坐标方程为4sin ρθ=，M 为曲线1C 上异于极点的动点，点P 在射线OM 上，且,25,OP OM 成等比数列．（Ⅰ）求点P 的轨迹2C 的直角坐标方程；（Ⅱ）已知(0,3)A ,B 是曲线2C 上的一点且横坐标为2，直线AB 与1C 交于,D E 两点，试求AD AE -的值．23．（本小题满分10分）选修4—5：不等式选讲已知2()()f x x a a =+∈R ，()12g x x x =++- （Ⅰ）若4a =-，求不等式()()f x g x ≥的解集；（Ⅱ）若[0,3]x ∈时，()()f x g x >的解集为空集，求a 的取值范围．2018年宁德市普通高中毕业班质量检查数学（文科）试题参考答案及评分标准说明：一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解法不同，可根据试题的主要考查内容比照评分标准指定相应的评分细则．二、对计算题，当考生的解答在某一部分解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数． 四、只给整数分数，选择题和填空题不给中间分．一、选择题：本题考查基础知识和基本运算，每小题5分，满分60分．1. D2. A3. B4. A5.C6. C7. C8. B9. D 10. B 11. D 12.A二、填空题：本题考查基础知识和基本运算，每小题5分，满分20分．13. 12i 55-- 14. 13 15. 36π 16. (1)22n n -+三、解答题：本大题共6小题，满分70分，解答须写出文字说明、证明过程和演算步骤．17.本小题主要考查正弦定理、余弦定理等基础知识，考查运算求解能力，考查化归与转化思想、函数与方程思想等．满分12分． （Ⅰ）1BC =,4B π=,1sin 2BCDS BC BD B ∆=⨯⨯⨯………….….1分 121122BD ⨯⨯=……………………….…2分 2BD =……………………………………3分 在BCD ∆中，由余弦定理得DCBA2222cos CD BC BD BC BD B =+-⨯⨯……….…………....4分2212121=+-⨯=………………………………...5分∴1CD = ………………………………………………. ....6分(Ⅱ)在ACD ∆中，由正弦定理得sin sin AD CDACD A=∠…………....7分 ∴sin sin AD AACD CD⋅∠=sin62AD AD CD CDπ⋅== …………....8分 在BCD ∆中，由正弦定理得sin sin DB CDDCB B=∠ .………..9分 ∴sin sin 24sin 2DB DB BDBDCB CDCDCDπ⋅⋅∠===…………..10分 ∴sin 122sin 32ACD DCB DB∠===∠………….………..12分18.本小题主要考查空间直线与直线、直线与平面的位置关系、平面与平面位置关系，几何体的体积等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查化归与转化思想等．满分12分．解法一：,.AB O CO DO I ()证明：取中点，连接……………..1分∵ABC ∆为等边三角形CO AB ∴⊥ ……………....2分 ∵0ABCD DBA ∠四边形为菱形，=60 ∴DAB ∆为等边三角形∴DO AB ⊥……………………………….3分 又∵CODO O =∴AB DOC ⊥面…………………………..5分 ∵DC DOC ⊂面∴AB CD ⊥………………………………..6分 （Ⅱ）∵,,ABDE ABC CO AB ABDEABC AB CO ABC ⊥⊥⊂面面面面=,面∴CO ABDE ⊥面 ∵OD ABDE ⊂面∴CO OD ⊥…………………………………….……...8分 ∵3OD OC ==，DAO在Rt COD ∆中，226CD OD OC =+由（1）得AB CD ⊥， 因为//,ED AB ED DC ⊥且1126622CDE S CD ED ∆=⨯⋅=⨯……………...9分∵0122sin12032BDE S ∆=⨯⨯⨯=..…..10分∵B CDE C BDE V V --=即1133CDE BDE S h S CO ∆∆⨯⋅=⨯⋅.…….11分即1163333h =∴6h =.…….12分 解法二：（Ⅰ）同解法一（Ⅱ）∵在菱形ABDE 中,//,AB DE DE ⊂平面CDE ,AB ⊄平面CDE∴//AB 平面CDE∴B 点到平面CDE 的距离等于O 点到平面CDE 的距离……………7分 由（Ⅰ）知, AB ⊥平面ODC ∴DE ⊥平面ODC ∵DE ⊂平面CDE ∴平面ODC ⊥平面CDE过O 作OH DC ⊥于H ,则OH ⊥平面CDE , 且OH DC ⊥……………8分 ∵,DO AB CO AB ⊥⊥DOC ∠为二面角D AB C --的平面角∵平面ABC ⊥平面ABDEDO OC ⊥……………10分又DC OH OD OC ⋅=⋅………………………………………………..…11分∴6OH =..…12分 19. 本小题主要考查了频率分布直方图，平均数，函数，不等式等基础知识，考查数据分析能力、运算求解能力，考查化归与转化思想等．满分12分 （Ⅰ）DAO H…. ………2分 解：设年需求量平均数为x ，则650.05750.15850.5950.21050.186.5x =⨯+⨯+⨯+⨯+⨯= ……………6分 (注:列式2分,错一个扣1分,错两个及以上不得分;答案2分) （Ⅱ）设今年的年需求量为x 吨、年获利为y 万元 当0100x ≤≤时，0.40.3(100)0.730y x x x =-⨯-=- 当100x >时，40y =故0.730,6010040,100110x x y x -≤≤⎧=⎨<≤⎩………………………………………8分则82x ≥ ……………………………………………………………………9分9082(8290)(8090)10P x P x -≤<=⨯≤<， 40.50.45=⨯=………………………………………………..………………10分 (100110)0.1P x ≤≤=………………………………………………………..11分所以今年获利不少于27.4万元的概率为0.7………………………………12分20. 本题主要考查直线、圆、抛物线、直线与圆，直线与抛物线的位置关系等基础知识，考查运算求解能力、推理论证能力，考查函数与方程思想、化归与转化思想，考查考生分析问题和解决问题的能力，满分12分．解：（I ）因为抛物线焦点F 坐标为(,0)2p , 则:2AB pl x =联立 222y px px ⎧=⎪⎨=⎪⎩∴112p x y p ⎧=⎪⎨⎪=⎩或222p x y p ⎧=⎪⎨⎪=-⎩ 故122AB y y p =-= ……………………………………………………2分∴213326222MAB S p p p ∆=⨯⨯== ……………………………………….3分即2p = …………………………………………………………………..4分 ∴抛物线方程为：24y x =圆方程为：()2224x y ++=…………………………………………….5分(注:错一个不给分)(II) 解法一：显然1l 、2l 的斜率必须存在且均不为0，设1l 的方程为y kx =，则2l 方程为1y x k=-…………………………………….6分(注:末说明斜率不给分)由24y x y kx ⎧=⎨=⎩得0x =，或24x k =∴244(,)C k k 同理可求得2(4,4)E k k -………….7分由22(2)4x y y kx⎧++=⎨=⎩得0x =，或241x k =-+∴2244(,)11kD k k --++同理可求得22244(,)11k kG k k -++…………….8分∴422224(4)2144()11COE C E DOGD Gk S y y k k k k k Sy y k k k -⋅++===-⋅++………….10分 2222112224k k k k=++≥⋅=…….11分 当且仅当1k =±时， COE ∆与DOG ∆的面积比的取到最小值4.…………….12分解法二：显然1l 、2l 的斜率必须存在且均不为0，设1l 的方程为y kx =，则2l 方程为1y x k=-…………………………………….6分(注:末说明斜率不给分)由24y x y kx⎧=⎨=⎩得x =0，或24x k =∴244(,)C k k 同理可求得2(4,4)E k k -………….7分则22111101022COEC E SOC OE k x x k=+-+- ()22228111442k k k k k k++=⋅⋅⋅=…………………………………….8分 设(2,0)M -到1l 、2l 的距离分别为1d 、2d 则1221k d k =+；221d k +9分则122222812222111DOGk k Sd d k k k =⋅⋅==+++………………..10分∴()224222222811211122248COE DOGk Sk k k k k Sk k k k k++++=⋅==++≥⋅=…….11分 当且仅当1k =±时， COE ∆与DOG ∆的面积比的取到最小值4.…………….12分21.本小题主要考查导数及其应用、不等式等基础知识，考查推理论证能力、运算求解能力、创新意识等，考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想等．满分12分． 解：（Ⅰ）函()y f x =的定义域为(0,)+∞………………………...……1分2()(1)a bf x x x'=-++………………………………………………..2分把(1,(1))f 代入方程10x y -+=中，得1(1)10f -+= 即(1)2f =，∴4a =…………………………………….…………3分 又因为(1)1f '=，∴14ab -+=故2b =…………………………………………………………...…4分 （Ⅱ）由（Ⅰ）可知4()2ln 1f x x x =++，当1x >时 ln ()21k xf x x >++恒成立等价于22(22)ln 0x x k x -++->..……5分 设()22(22)ln g x x x k x =-++-， 则1()22ln (22)g x x x k x'=-+++-⋅22ln kx x-=+………………………………………..……7分 由于1,ln 0x x >>当2k ≤时，()0g x '>，则()y g x =在(1,)+∞上单调递增， ()(1)0g x g >=恒成立.………………………………………8分当2k >时，设()()h x g x '=,则222()0kh x x x-'=->…….…..9分 则()y g x '=为(1,)+∞上单调递增函数， 又由(1)20g k '=-<………………………………….10分 即()g x 在(1,)+∞上存在0x ，使得0()0g x '=， 当0(1,)x x ∈时，()g x 单调递减， 当0(,)x x ∈+∞时， ()g x 单调递增；则0()(1)0g x g <=，不合题意，舍去.……………………….11分 综上所述，实数k 的取值范围是(,2]-∞.……………………12分 22.选修44-；坐标系与参数方程本小题考查直线和圆的极坐标方程、参数方程等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想等．满分10分． 解：（1）设(,)P ρθ，1(,)M ρθ，则由,25,OP OM 成等比数列，可得20OP OM ⋅=，………………………………1分即1=20ρρ⋅，120=ρρ．………………………………2分又1(,)M ρθ满足14sin ρθ=，即204sin θρ=，………………………………3分∴sin 5ρθ=，………………………………4分化为直角坐标方程为5y =．………………………………5分 （Ⅱ）依题意可得(2,5)B ，故1AB k =，即直线AB 倾斜角为4π，………………………………6分 ∴直线AB 的参数方程为2,23,x y ⎧=⎪⎪⎨⎪=⎪⎩………………………………7分代入圆的直角坐标方程22(2)4x y +-=， 得2230t t +-=，………………………………8分故122t t +=-1230t t =-<，………………………………9分 ∴122AD AE t t -=+．………………………………10分 23．选修45-：不等式选讲本小题考查绝对值不等式的解法与性质等基础知识，考查运算求解能力、推理论证能力，考查分类与整合思想、化归与转化思想等． 满分10分．解：(1)当4a =-时，()()f x g x ≥化为2412x x x -≥++- ，…………1分当1x ≤-，不等式化为2+250x x -≥，解得16x ≤-或16x ≥- 故16x ≤--…………2分当12x -<<时，不等式化为27x ≥，解得7x ≤-7x ， 故x ∈∅； …………3分当2x ≥，不等式化为2230x x --≥，解得1x ≤-或3x ≥ 故3x ≥； …………4分所以()f x x ≤解集为{|16x x x ≤-}3x ≥． …………5分(2) 由题意可知，即为[0,3]x ∈时，()()f x g x ≤恒成立． …………6分 当02x ≤≤时，23x a +≤，得()2min31a x ≤-=-；…………8分当23x ≤≤时，221x a x +≤-，得()2min+214a x x ≤--=-，综上，4a ≤-．…………10分。