数学史作业
- 格式:doc
- 大小:51.50 KB
- 文档页数:6

09数学史作业题7一、选择题1.最先建立“非欧几何”理论的数学家是( B )。
A.高斯 B.罗巴契夫斯基 C.波约 D.黎曼2.提出“集合论悖论”的数学家是(B)。
A.康托尔B.罗素C.庞加莱D.希尔伯特3.提出“集合论悖论”的数学家罗素是( A )A.英国数学家;B.法国数学家;C.德国数学家;D.巴西数学家4.1900 年,德国数学家希尔伯特在巴黎国际数学家大会上提出的著名数学问题共有(B)。
A.18 个B.23 个C.32 个D.40 个5.证明了π的超越性,从而确立了化圆为方不可能性的数学家是(D)A.旺泽尔B.牛顿C.伽罗瓦 D.林德曼6.大数学家欧拉出生于(A)A.瑞士B.奥地利C.德国D.法国7.最先明确定义无穷级数收敛性的数学家是(D)A.高斯B.欧拉C.魏尔斯特拉斯D.柯西8.在1900年巴黎国际数学家大会上提出了23个著名的数学问题的数学家是(A)A.希尔伯特B.庞加莱C.罗素D.克莱因9.射影几何的开创者是(B)A.笛卡尔和费马等;B.德沙格和帕斯卡等;C.庞斯列和斯坦纳等;D.施陶特和默比乌斯等10.射影几何产生于文艺复兴时期的( D)A.音乐演奏B.服装设计C.雕刻艺术D.绘画艺术11.在射影几何的诞生过程中,对于透视画法所产生的问题从数学上直接给予解答的第一个人是( C )A.达·芬奇;B.笛卡儿;C.德沙格;D.牛顿12.对于透视法所产生的问题从数学上直接给予解答的第一个人是(D)。
A.达·芬奇B.笛卡儿C.帕斯卡D.德沙格13.最早提出对数方法的是英国数学家(A)A.纳皮尔B.布里格斯C.斯蒂弗尔 D.比尔吉14.对数方法的发明者是数学家( C )。
A.拉普拉斯 B.布里格斯 C.纳皮尔 D.帕斯卡15.集合论的创立者是( D )A.希尔伯特B.戴德金C.庞加莱D.康托尔43.建立无理数理论基础方面最有贡献的是(D)A.笛卡尔和费马;B.欧拉和韦达;C.柯西和黎曼;D.康托和戴德金。

数学史作业题3一、选择题1.世界上第一个把π计算到3.1415926<π<3.1415927的数学家是(B) A.刘徽B.祖冲之C.阿基米德D.卡瓦列利2.我国古代十部算经中年代最晚的一部(C)A.《孙子算经》B.《张邱建算经》C.《缉古算经》D.《周髀算经》3.在中算史上,刘徽首先建立了可靠的理论来推算圆周率,他所算得的“徽率”是(B)。
A.3.1B.3.14C.3.142 D.3.14159264.“一尺之棰,日取其半,万世不竭”出自我国古代名著(D)。
A.《考工记》B.《墨经》C.《史记》D.《庄子》5.祖冲之的代表作是(C)A.《考工记》B.《海岛算经》C.《缀术》D.《缉古算经》6.世界上讲述方程最早的著作是(A)A.中国的《九章算术》B.阿拉伯花拉子米的《代数学》C.卡尔丹的《大法》D.牛顿的《普遍算术》7.《九章算术》的作者是(D)。
A.刘徽B.张苍、耿寿昌C.秦九韶D.作者不详8.用以发现球体积公式的“平衡法”的数学家是(B)。
A.刘徽B.阿基米德C.莱布尼茨D.牛顿9.《九章算术》的“少广”章主要讨论(D)。
A.比例术B.面积术C.体积术D.开方术10.《九章算术》中的“阳马”是指一种特殊的(B)A.棱柱B.棱锥C.棱台D.楔形体二、填空题1.在现存的中国古代数学著作中,《__九章算术_________》是最早的一部。
卷上叙述的关于荣子与陈方的对话,包含了____勾股定理_______的一般形式。
2.我国古代著作《周髀算经》中的“髀”是指___竖立的表或杆子___________。
3.中国历史上最早叙述勾股定理的著作是《_周髀算经_____》,中国历史上最早完成勾股定理证明的数学家是三国时期的_赵爽_____。
4.《墨经》是我国试图对数学进行理论探讨的著作,它的诞生时代是__战国时期_______。
5.我国古代文献《墨经》一书中的“端”、“直”,“平”、”厚”,就是现代几何课本中的_____点_________、_____直线_________、_____平行______、__体积__________。

《数学史》作业选《数学史》作业选第五讲文艺复兴时期的数学1、学习珠算有现实意义吗?对于这个问题,每个人都有自己的看法。
在我的观点中,学习珠算是有现实作用的。
中国珠算是中华民族的一项伟大的发明,珠算作为一门应用学科对基础数学,对发展生产,适应生活需要起了推动作用。
珠算内涵非常丰富,不但有良好的计算功能,它是中国应用数学。
珠算是独立的学科,因而它应具有系统的体系。
一是从算史上看,算盘计教原理是我国最早创造的。
它是数形结合,以算为主。
二是使用算盘具有中国数学的显著特点。
中国古代数学体系是以它的应用性、直观性,算法的结构化、机械化,寓算理于算法之中的,而珠算正是这种特征的体现。
珠算作为中华民族的优秀文化瑰宝是凭借其计算功能才得以流传千百年至今,并在全世界传播的。
然而在当今计算机时代,算盘的应用领域将发生变化。
这就好比有了飞机还要有自行车,自行车要发展,要进入健身房。
同样,有了计算机。
也还要有算盘,算盘的功能将得到拓展,还要进入健脑房。
我们有理由相信,在新的世纪中,计算机和算盘会长期共存,互助互补,各尽其职。
珠算是中华民族的优秀文化遗产,它有着数千年的光辉里程,在历史的进程中,珠算作为经济数学,为发展社会生产、经济,推进人类进步做出重大贡献,当今电子时代,由于珠算已起到变化,有其独特的功能将起著巨大的经济核算,学校教育,启迪人们智力水平的重要作用,但这一项古老又新生的科技产物,是利国利民的技术。
珠算科技是随着这会经济的发展而发展。
因此,关于培养经济核算人才,不单是培养计算的准快高水平问题,而应该理解为智慧的核算人才,珠算,珠心算不仅培养了计算高水平者,而且事实证明,由于学珠算,脑手眼并举,使人们更加脑明起,这就是所谓一科突出,多科受益的道理所在。
当今世界,经济在发展,社会在前进,人才在极需,而传统的珠算科技必然在发展。
学习珠算,在方法上调动左右脑,特别脑印象活动,给右脑以激动的刺激,左右脑同时并用,这样可以起到很大潜力的脑力的开发,起到数学教育,启迪智力的良好的作用。
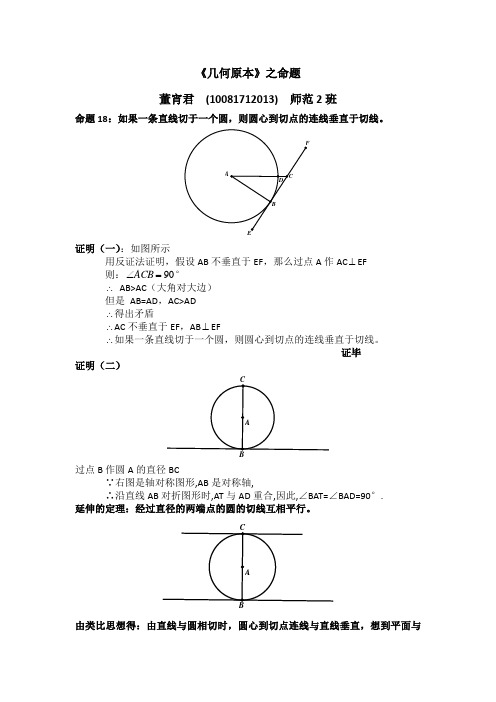
《几何原本》之命题董宵君 (10081712013) 师范2班命题18:如果一条直线切于一个圆,则圆心到切点的连线垂直于切线。
证明(一):如图所示用反证法证明,假设AB 不垂直于EF ,那么过点A 作AC ⊥EF 则:90=∠ACB °∴ AB>AC (大角对大边)但是 AB=AD ,AC>AD∴得出矛盾∴AC 不垂直于EF ,AB ⊥EF∴如果一条直线切于一个圆,则圆心到切点的连线垂直于切线。
证毕 证明(二)过点B 作圆A 的直径BC∵右图是轴对称图形,AB 是对称轴,∴沿直线AB 对折图形时,AT 与AD 重合,因此,∠BAT=∠BAD=90°.延伸的定理:经过直径的两端点的圆的切线互相平行。
由类比思想得:由直线与圆相切时,圆心到切点连线与直线垂直,想到平面与球相切时,球心与切点连线与平面垂直。
命题8:如果在直角三角形中,由直角顶点向底边作垂线,则与垂线相邻的两个三角形都与原三角形相似且它们两个彼此相似。
证明:如图所示在ABC ∆和ACD ∆中90=∠=∠ADC ACB °A A ∠=∠ABC ∆∴和ACD ∆相似。
一下同理。
延伸定理:如果在直角三角形中,由直角顶点向底边作垂线,则AD AB AC ∙=2,BD AB BC ∙=2,BD AD CD ∙=2。
命题22:内接于圆的四边形其对角的和等于两直角。
证明:如图所示在ABC ∆中,180=∠+∠+∠BAC ACB ABC °B DC C A B ∠=∠(同弧所对的圆周角相等)A DB AC B ∠=∠(同弧所对的圆周角相等)B DC AD B A D C ∠+∠=∠A∴ABCADC°180∠+=∠∴内接于圆的四边形其对角的和等于两直角。
证毕延伸命题:命题47:在直角三角形中,直角所对的边上的正方形的面积等于两直角边上的正方形面积之和。
证明:如图所示AC AF = ,AD AB =,=∠FAB GAD ∠∴G A D F A B ∆≅∆F A B ∆的面积等于221a G A D ∆的面积等于矩形ADJI 的面积的一半∴2a S A D J I =,2b S IJEB ==A D E B S I J E BA D J I S S + ∴222b a c +=∴在直角三角形中,直角所对的边上的正方形的面积等于两直角边上的正方形面积之和。

数学史习题第一、二讲同步练习一、填空题1.古埃及的数学知识常常记载在( A )。
A.纸草书上B.竹片上C.木板上D.泥板上2.关于古埃及数学的知识,主要来源于( B )。
A.埃及纸草书和苏格兰纸草书B.莱茵德纸草书和莫斯科纸草书C.莫斯科纸草书和希腊纸草书D.莱茵德纸草书和尼罗河纸草书3.对古代埃及数学成就的了解主要来源于( A )A.纸草书B.羊皮书C.泥版D.金字塔内的石刻4.最早采用六十进制位值记数法的国家或民族是( A )A.美索不达米亚B.埃及C.印度D.中国5.古代美索不达米亚的数学成就主要体现在( A )A.代数学领域B.几何学领域C.三角学领域D.解方程领域6.最早采用位值制记数的国家或民族是( D )。
A.美索不达米亚B.埃及C.阿拉伯D.印度7.在现存的中国古代数学著作中,最早的一部是( D )A.《孙子算经》B.《墨经》C.《算数书》D.《周髀算经》8.古代将数学知识记载于泥版上的国家或民族是( C )A.中国B.埃及C.美索不达米亚D.印度二、选择题1.最早采用位值制记数的国家或民族是____印度____,最早采用十进位值制记数的国家或民族是____中国____。
2.在代数和几何这两大传统的数学领域,古代美索不达米亚的数学成就主要在代数方面,他们能够卓有成效地处理相当一般的解三次二项方程。
3.古代美索不达米亚的数学常常记载在__泥版文书__上,在代数与几何这两个传统领域,他们成就比较高的是___代数___领域。
4.古代埃及的数学知识常常记载在__ 纸草书 _上,在代数和几何这两大传统的数学领域,古代埃及的数学成就主要在_ 几何 _方面。
5.在代数和几何这两大传统的数学领域,古代埃及的数学成就主要是几何方面,现存的____纸草___书中可以找到一些图形面积或体积的正确计算公式。
6.在代数和几何这两大传统的数学领域,古代埃及的数学成就主要在__几何__方面,美索不达米亚的数学成就主要在___代数____方面。

一、为什么在早期的古希腊数学成就中几乎看不到代数即解方程的研究?试从古希腊人的观点、数学态度及社会背景进行分析。
古希腊人的观念数和几何图形是人类进行符号化思维达到理性高度的重要标志。
“符号化的思维和符号化的行为是人类生活中最富于代表性的特征,并且人类文化的全部发展都依赖于这些条件,这一点无可争辩。
”古希腊在与古埃及和巴比伦的交流过程中,在对数学和几何图形的研究中,逐步形成了一种与其他文明截然不同的的数学观念。
由于这种观念导致古希腊人对几何研究情有独钟。
希腊人非常好辩,他们惟“法”是从,遇事辩理,慢慢形成一种“法”和“理”的信念,而只有几何知识比较有利于解决实际中问题,故而导致了古希腊人对几何学的偏爱。
希腊人在和古埃及、古巴比伦的接触过程中,把数学特别是几何学从一门经验科学转变成抽象和演绎程度较高的理论科学。
在巴比伦和埃及文明中,早已形成了很多初级的数学知识,在几何学方面出现了很多基本的定律、公式和法则, 但都只是停留在经验和应用层面,数学还只是一种解决日常生活中所遇到的问题的工具,并没有成为一门抽象的纯理论学科。
“几乎还没有成套的记号,几乎没有意识的抽象思维,没有搞出一般的方法论,没有证明甚或直观推理的想法,使人能深信他们所作的运算步骤或所用的公式是正确的。
希腊人把抽象和演绎的方法引进数学中,建立了较为完整的体系,将数学变成一个纯粹推理演绎的抽象领域,这种抽象演绎的思维是形成数学观念和数学精神的前提。
由于纯理论的古希腊数学几何占据这统治地位,希腊人相信的只是那些十分清楚的解释和概念,并建立直观的几何模型来解决问题,从而推动了几何学的形成和发展。
但是他们忽略了代数解方程的讲解,由于这种观念,导致古希腊在代数学及解方程方面少之又少。
古希腊人的数学态度古希腊人只是把数学作为一种解决日常生活中所遇到问题的工具,在遇到问题时总是建立几何模型,并运用逻辑的演绎来研究,而缺乏对具体代数的运用,如古希腊人对“三大几何问题”的求解。
11数学史作业题111数学史作业题1一、选择题1.最早采用位值制记数的国家或民族是( A )。
A.美索不达米亚B.埃及C.阿拉伯D.印度2.古代美索不达米亚的数学成就主要体现在( B )A.几何学领域B.代数学领域C.三角学领域D.体积计算方面3.对古代埃及数学成就的了解主要来源于( A )A.纸草书B.羊皮书C.泥版D.金字塔内的石刻4.古代美索不达米亚的数学常常记载在( A )。
A.纸草书上B.竹片上C.木板上D.泥板上5.古希腊数学家泰勒斯创立的学派是( A )A.伊利亚学派B.爱奥尼亚学派C.诡辩学派6.发现不可公度量的是( B )。
A.爱奥尼亚学派;B.毕达哥拉斯学派;C.诡辩学派;D.伊利亚学派7.以“万物皆数”为信条的古希腊数学学派是( D )。
A.爱奥尼亚学派;B.伊利亚学派;C.诡辩学派;D.毕达哥拉斯学派8.建立新比例理论的古希腊数学家是( C )。
A.毕达哥拉斯B.希帕苏斯C.欧多克斯D.阿基米德 D.吕园学派9.数学的第一次危机的产生是由于( B )A.负数的发现B.无理数的发现C.虚数的发现D.超越数的发现10.古希腊数学家帕波斯的唯一传世之作《数学汇编》被认为是( C )A.古希腊论证数学的发端;C.古希腊数学的安魂曲;二、填空题11.古希腊开论证几何学先河的是___爱奥尼亚___________学派。
12.古希腊三大著名几何问题是___画圆为方________、____倍立方体_______和三等分角。
13.古希腊数学家___丢番图______的《算术》是一本问题集,特别以不定方程的求解而著称。
所谓“不定方程”是指____未知数个数多于方程个数的代数方程_____。
14.古希腊亚历山大时期的数学家__阿波罗尼奥斯____在前人工作的基础上创立了相当完美的圆锥曲线理论,其著作《__圆锥曲线论____》代表了希腊演绎几何的最高成就。
15.阿基米德通常用_______平衡______法发现求积公式,然后用_______穷竭______法进行严格的证明。
09 数学史作业题4一、选择题1.印度一位数学家在其著作《肯德卡迪亚格》中,利用二次插值法结构了间隔为15 度的正弦函数表 ,这位数学家是 ( B 。
A.阿耶波多 ;B.婆罗摩笈多 ;C.马哈维拉 ;D.婆什迦罗。
2.印度古代数学著作《计算方法大纲》的作者是( C 。
A.阿耶波多 ;B.婆罗摩笈多 ;C.马哈维拉 ;D.婆什迦罗3.印度数学家婆什迦罗在其数学著作中完好阐述了零的运算法例,并对零作除数的问题给出了存心义的解说,以为分母为零的分数表示一个无穷大批。
该数学著作是( C 。
A.《肯德卡迪亚格》 ;B.《计算方法大纲》 ;C.《算法根源》 ;D.《莉拉沃蒂》4.以下著作中 ,为印度数学家马哈维拉所著的是( BA.《圆锥曲线论》 ;B.《计算方法大纲》 ;C.《算经》D.《算法根源》5.中世纪《代数学》一书的著作是阿拉伯人( BA.比鲁尼 ;B.花拉子米 ;C.奥马·海亚母 ;D.纳尔西·丁二、填空题1.“代数学”一词发源于阿拉伯人 ____花拉子米 ______的著作。
2.因为天文计算的需要 ,阿拉伯天文学家都致力于高精度三角函数表的编制 ,特别是比鲁尼利用二次插值法拟订了 ______正弦 _______函数表。
(题目有错3.阿拉伯数学的突出成就第一表此刻____代数 _______方面。
4.阿拉伯数学家 ___ __花拉子米 _______的《复原与抵消计算纲要》第一次给出了___一元二次 ____方程的一般解法 ,并用 ______几何 ____方法对这一解法给出了证明。
三、简答题1.阿拉伯数学的历史地位答:花拉子米是阿拉伯早期最主要的数学家,他编写了第一本用阿拉伯语在伊斯兰世界介绍印度数字和记数法的著作。
公元十二世纪后 ,印度数字、十进制值制记数法开始传入欧洲 ,又经过几百年的改革 ,这类数字成为我们今日使用的印度─阿拉伯数码。
花拉子米的另一名著《 ilmal-jabr wa'lmugabalah》(《代数学》系统地议论了一元二次方程的解法 ,该种方程的求根公式即是在此书中第一次出现。
数学史作业题3一、选择题1.世界上第一个把π计算到3.1415926<π<3.1415927的数学家是(B) A.刘徽B.祖冲之C.阿基米德D.卡瓦列利2.我国古代十部算经中年代最晚的一部(C)A.《孙子算经》B.《张邱建算经》C.《缉古算经》D.《周髀算经》3.在中算史上,刘徽首先建立了可靠的理论来推算圆周率,他所算得的“徽率”是(B)。
A.3.1B.3.14C.3.142 D.3.14159264.“一尺之棰,日取其半,万世不竭”出自我国古代名著(D)。
A.《考工记》B.《墨经》C.《史记》D.《庄子》5.祖冲之的代表作是(C)A.《考工记》B.《海岛算经》C.《缀术》D.《缉古算经》6.世界上讲述方程最早的著作是(A)A.中国的《九章算术》B.阿拉伯花拉子米的《代数学》C.卡尔丹的《大法》D.牛顿的《普遍算术》7.《九章算术》的作者是(D)。
A.刘徽B.张苍、耿寿昌C.秦九韶D.作者不详8.用以发现球体积公式的“平衡法”的数学家是(B)。
A.刘徽B.阿基米德C.莱布尼茨D.牛顿9.《九章算术》的“少广”章主要讨论(D)。
A.比例术B.面积术C.体积术D.开方术10.《九章算术》中的“阳马”是指一种特殊的(B)A.棱柱B.棱锥C.棱台D.楔形体二、填空题1.在现存的中国古代数学著作中,《__九章算术_________》是最早的一部。
卷上叙述的关于荣子与陈方的对话,包含了____勾股定理_______的一般形式。
2.我国古代著作《周髀算经》中的“髀”是指___竖立的表或杆子___________。
3.中国历史上最早叙述勾股定理的著作是《_周髀算经_____》,中国历史上最早完成勾股定理证明的数学家是三国时期的_赵爽_____。
4.《墨经》是我国试图对数学进行理论探讨的著作,它的诞生时代是__战国时期_______。
5.我国古代文献《墨经》一书中的“端”、“直”,“平”、”厚”,就是现代几何课本中的_____点_________、_____直线_________、_____平行______、__体积__________。
数学史习题介绍数学是一门古老而又深奥的学科,它以逻辑推理和数学符号为基础,研究数量、结构、变化以及空间的关系。
通过解决问题和应用于实际情境,数学帮助我们理解世界的运行方式。
在数学史上,我们可以追溯到古代人类对数学问题的思考和解决方法。
以下是一些数学史习题,用以挑战你的数学思维能力。
1. 古代埃及的图像文字系统是一种非常有趣的表达方式,其中包含了数学符号。
请从以下线描图像中,尝试找出代表数字的符号:─────────│││─────────││───────────2. 古希腊人开创了几何学,其中最著名的问题之一是希俄斯岛上的“中值定理”。
在一个三角形中,通过连接一个角的顶点到对边的中点,将三角形划分为两个面积相等的小三角形。
请证明这个定理。
3. 著名的欧几里德几何学有着丰富的数学问题,其中之一是“平行公设”。
在几何学中,我们一直认为平行线永远不会相交。
然而,在19世纪初,这个公设被质疑,并且后来被证明是无法从其他公设中推导出来的。
请尝试找到一种方法,通过欧几里德几何学中的其他公设来证明平行线不会相交。
4. 中国古代数学在代数方面也有很大的贡献。
请试着解决以下古老的中国算术题:“有三种商品,一种每个10个卖1元,一种每个3个卖1元,一种每个2个卖1元,现在有20元,请问你最多可以买到几个商品?”5. 在17世纪,法国数学家皮埃尔·德费马提出了著名的费马大定理。
这个定理声称a^n + b^n = c^n在n大于2时没有正整数解。
这个问题困扰了数学界很长时间,直到1994年被英国数学家安德鲁·怀尔斯证明。
请尝试提出你自己的证明或解释怀尔斯的证明。
6. 经典力学是数学和物理学的结合。
牛顿第二定律F=ma描述了力、质量和加速度之间的关系。
请使用这个公式解决以下问题:一个物体质量为2kg,施加在它上面的力为5N,求它的加速度。
7. 概率论是数学中的一个重要分支,它研究随机事件的发生概率。
我看古中国数学古中国数学,和天文学以及其他许多科学技术一样,在中国历史上占有重要的地位,并且取得了极其辉煌的成就。
可以毫不夸张地说,直到明代中叶以前,在数学的许多分支领域里,中国一直处于遥遥领先的地位。
,根据古中国数学发展的特点,可以分为六个时期:萌芽;体系的形成;发展;繁荣和中西方数学的融合,衰落。
古中国数学具有悠久的历史,丰富的内容,重大的成就,它持续不断,长期发达,成就辉煌,呈现出鲜明异常的“东方数学”的色彩,对于世界数学发展的历史进程有着深远的影响,时至今日,仍影响着我们生活的方方面面,并且有重要的现实意义和应用价值。
关键词:产生特点发展衰落价值一古中国数学的产生古中国数学思想扎根于中国古人的社会实践之中,体现着中国古代生产方式、生活方式和思维方式的特点。
反过来数学思想也推动着生产和其他社会实践的发展,促进着中国古代文化的发展。
可以通过中国数学思想产生的文化背景,历史文物以及古代典籍探讨中国古代数学思想的产生。
1、古中国数学思想产生的文化背景当代历史学中,文明起源的“挑战和应战”学说占有重要的地位,正是人类的应战促使了人类的创造性行为,开创了文明,与此相应的则是文明未必在宜于人类生活的各种有利环境中产生。
2、中国文明产生的自然、历史条件中国东部和东南部面临着浩瀚的海洋,西部蜿蜒着巍峨的高山及号称“世界屋脊”的青藏高原,北部是蒙古高原的戈壁瀚海。
这些地理环境在古代交通不发达的条件下,形成了相对的封闭状态,使我们的祖先与外界交往存在着困难,因而使中国的古代文化在相当长的时期内保持不变。
并且受当时的哲学、理学、历史学等文明的的发展的影响,独具特色。
二、古中国数学的特点1.浓厚的人文色彩和鲜明的社会性。
为社会实际服务是中国古代数学的传统,也是它的特色。
外国古代数学著作相比较,中国传统数学在学以致用方面可以独树一帜。
这主要表现在中国古代数学典籍具有浓厚的应用数学色彩,与古希腊腊人数学看做纯理念的精神活动形成鲜明的对照,中国古代数学家的知识更注重来源于社会实践。
例如,九章算术更是秦汉之际封建统一帝国形成过程中政治,经济,军事文化各领域的映射;方田反映了土地分配的需要,粟米反映了易物交换的本源,商功来自水利和土木工程,均输来自官派劳役制度;总之,中代数中学的格局与时代的政治,经济,乃至学术思想休戚相关2. 便捷的记数制和计算工具中国是最早发明和使用10进位制计数法的国家。
春秋时代发展起来的筹算不但是10进位制得以完善,而且为我们的祖先提供了便捷的技术和运算工具,利用筹算的纵横捭阖,中国古代数学家可以相当迅速而准确的进行计算。
3..不拘一格的推理模式;与古希腊唯一接受的演绎的逻辑推理有别,中学是一种从实际出发,进过分析提高而概括出一般原里和方法,以求最终解决一打类问题的体系。
与此格局相适应,中国数学经典尤其独特的表达形式,其中术和相应的注就体现了中国古代数学家对一般方法的重视以及对逻辑推理的追求。
中国古代数学的推理方式是丰富多彩的4.经典著作的示范作用如同西方学者把《原本》看做“科学的圣经”中算家把《九章算术》连同他的注文奉为从事研究和著述的“楷模”。
从《数学九章》《九章翼》《九章通明法算》….可以看出,都已成为中算家这一科学共同体的主要学术规范。
5.土生土长,独具中国特色,呈现出鲜明异常的“东方数学”的色彩,6.涉及范围广,影响深远,对人类文明具有特殊的贡献。
《九章算术》标志以筹算为基础的中国古代数学体系的正式形成。
它对以后中国古代数学发展所产生的影响巨大,在中国,它在一千几百年间被直接用作数学教育的教科书。
它还影响到国外,朝鲜和日本也都曾拿它当作教科书。
古中国数学,是一个延续了近两千年的知识体系,它有丰富的内涵的并且经历了不同的发展阶段,因而以上概括出开的特征只能是就整体而言三古中国数学的发展、成就、衰落从公元前后至公元14世纪,中国古典数学先后经历了三次发展高潮,即两汉时期、魏晋南北朝时期和宋元时期,并在宋元时期达到顶峰。
1.先秦奠基时期先秦时期中国古代数学已经取得多方面的成就,逐渐形成系统的初等数学体系,这是我国古代数学的奠基时期。
当时筹算作为一种计算工具已经得到初步的普及,四则运算也得到发展,并且计算口诀的出现,也是中国数学的特色所在,这在《孙子算经》中有所体现。
早期的农业生产和生活的需要也促进了我国古代几何的发展。
当时极限思想,排列组合,干支记日,对策论也都体现了我国先秦数学的显著成就。
2.汉唐初创时期汉唐时期是中国封建社会的上升时期,经济,文化和科技都得到了迅速的发展。
《九章算术》标志以筹算为基础的中国古代数学体系的正式形成。
它对古代数学的各个方面全面完整地进行叙述,是十部算书中最重要的一部,它对以后中国古代数学发展所产生的影响深远。
在中国,它在一千几百年间被直接用作数学教育的教科书。
它还影响到国外,朝鲜和日本也都曾拿它当作教科书。
同时,《杜忠算数》,《许商算数》是最早见于著录的数学专著。
同时随着天文学,历法等的发展,我国数学知识也不断丰富起来,并确立了自己的体系。
3.三国两晋南北朝中国古代数学在三国及两晋时期侧重于理论研究,其中以赵爽与刘徽为主要代表人物。
赵爽是三国时期吴人,在中国历史上他是最早对数学定理和公式进行证明的数学家之一,其学术成就体现于对《周髀算经》的阐释。
在《勾股圆方图注》中,他还用几何方法证明了勾股定理,其实这已经体现“割补原理”的方法。
用几何方法求解二次方程也是赵爽对中国古代数学的贡献。
南北朝是中国古代数学的蓬勃发展时期,计有《孙子算经》、《夏侯阳算经》、《张丘建算经》等算学著作问世。
祖冲之、祖暅父子的工作在这一时期最具代表性。
根据史料记载,其著作《缀术》(已失传)取得如下成就:圆周率精确到小数点后第六位,《大衍历》中将其发展为不等间距二次内插公式。
4.宋元全盛时期宋元时期中国古代数学的发展达到了一个高峰,其数学思想绽放出了惊人的异彩。
这一时期的数学思想继承和发扬了刘徽的数学思想的同时,进行了数学思想理论化、抽象化的转换,这是世界上不多见的群体性全方位的数学成果。
中国古代数学,经过从汉到唐一千多年间的发展,已经形成了更加完备的体系。
在这基础上,到了宋元时期(公元十世纪到十四世纪)又有了新的发展。
宋元数学,从它的发展速度之快、数学著作出现之多和取得成就之高来看,都可以说是中国古代数学史上最光辉的一页。
从公元11世纪到14世纪的宋、元时期,是以筹算为主要内容的中国古代数学的鼎盛时期,其表现是这一时期涌现许多杰出的数学家和数学著作。
中国古代数学以宋、元数学为最高境界。
在世界范围内宋、元数学也几乎是与阿拉伯数学一道居于领先集团的。
例如,《数书九章》主要讲述了两项重要成就:高次方程数值解法和一次同余式解法。
宋元算书中的这些成就,和西方同类成果相比:高次方程数值解法比霍纳(1786—1837)方法早出五百多年,四元术要比贝佐(1730—1783)①早出四百多年,高次招差法比牛顿(1642—1727)等人早出近四百年。
宋元算书中所记载的辉煌成就再次证明:直到明代中叶之前,中国科学技术的许多方面,是处在遥遥领先地位的。
5.明清时期整理,融合阶段宋元以后,明清时期也有很多算书。
此时我国数学基本上进入大规模整理阶段,融合,衰落阶段。
例如明代就有著名的算书《算法统宗》。
这是一部风行一时的讲珠算盘的书。
入清之后,虽然也有不少算书,但是像《算经十书》、宋元算书所包含的那样重大的成就便不多见了。
特别是在明末清初以后的许多算书中,有不少是介绍西方数学的。
这反映了在西方资本主义发展进入近代科学时期以后我国科学技术逐渐落后的情况,同时也反映了中国数学逐渐融合到世界数学发展总的潮流中去的一个过程。
由于演算天文历法的需要,自16世纪末开始,来华的西方传教士便将西方一些数学知识传入中国。
数学家徐光启向意大利传教士利马窦学习西方数学知识,而且他们还合译了《几何原本》中国数学发展的历史表明:中国数学曾经为世界数学的发展作出过卓越的贡献,只是在近代才逐渐落后了。
我们深信,经过努力,中国数学一定能迎头赶上世界先进水平四古中国数学的贡献和时代价值1.古中国数学对世界数学发展的贡献古中国数学有其自身的历史渊源和独特的发展道路。
它持续不断,长期发达,成就辉煌,对于世界数学发展的历史进程有着深远的影响。
数学的发展包括了两大主要活动:证明定理和创造算法。
在数学史上,算法倾向与演绎倾向总是交替地取得主导地位。
东方数学在文艺复兴前夕通过阿拉伯传播到欧洲,对近代数学兴起产生了深刻影响。
事实上,作为近代数学诞生标志的解析几何与微积分,从思想方法的渊源看都不能说是演绎倾向而是算法倾向的产物。
现在再来看一看更早的解析几何的诞生。
通常认为,笛卡儿发明解析几何的基本思想,是用代数方法来解几何问题。
这同欧氏演绎方法已经大相径庭了。
而事实上如果我们去阅读笛卡儿的原著,就会发现贯穿于其中的彻底的算法精神。
任何问题→数学问题→代数问题→方程求解而笛卡儿的《几何学》,正是他上述方案的一个具体实施和示范,解析几何在整个方案中扮演着重要的工具作用。
这与上面介绍的古代中国数学家解决问题的路线可以说是一脉相承。
2.对当前人类社会的影响数学无处不在,它影响着我们生活的方方面面,对当前人类经济、文化、政治、甚至生态建设都有着重大的影响。
以电子计算机为例,随着电子计算机的广泛应用和进一步发展,构造性理念和算法传统将日益显示出重要性。
例如《九章算术》中的消元法在计算机中解线性方程组,就远比克莱姆方法简捷。
即使撇开计算机不谈,即使仍使用价值。
例如有亮亮连环求等计算若干整数的最小公倍数和最大公约数,在数学较大较多的情况下就远比素因数分解法来的简介。
至于,中算家于理于算的思想,无疑是现代机器证明的先声,当代数学家已在该领域勾画出了逻辑与算法两大传统并驾齐驱的美妙途径。
3.古为今用,创新价值研究科学的历史,其重要意义之一就是从历史的发展中获得借鉴和汲取教益,促进现实的科学研究,通俗地说就是“古为今用”。
:“假如你对数学的历史发展,对一个领域的发生和发展,对一个理论的兴旺和衰落,对一个概念的来龙去脉,对一种重要思想的产生和影响等这许多历史因素都弄清了,我想,对数学就会了解得更多,对数学的现状就会知道得更清楚、更深刻,还可以对数学的未来起一种指导作用,也就是说,可以知道数学究竟应该按怎样的方向发展可以收到最大的效益”数学的发展呈现出算法创造与演绎证明两大主流交替繁荣、螺旋式上升过程:演绎传统——定理证明活动算法传统——算法创造活动中国古代数学家对算法传统的形成与发展做出了毋容置疑的巨大贡献。
数学机械化方法已使中国在数学机械化领域处于国际领先地位,这便是古代中国数学的启发与创新。
其中,“吴方法”,是中国古代数学算法化、机械化精髓的发扬光大。