浙教版-数学-七年级上册-一元一次方程的应用之储蓄浓度问题

一元一次方程的应用【考点透视】一、考纲指要1．了解用一元一次方程解决实际问题的一般步骤.2．能根据具体问题中的数量关系，列出一元一次方程，解决实际问题。

3．能根据具体问题中的数量关系，列出可化为一元一次的分式方程，解决实际问题。

二、命题落点1．有关数字、行程、工程等常规问题，如例1和例2。

2．有关配套、利息等与生产生活有关类型题，如例3和例4。

3．有关打折销售、利润等与营销决策有关类型题，如例5。

【典例精析】例1：某桥长1000米，一列火车从桥上通过，测得火车从开始上桥到过完桥共用1分钟，而整列火车完全在桥上的时间为40秒，求火车的速度和长度．分析 本题根据火车的速度不变列方程.解：1分钟=60秒，设火车的长度为x 米，由题意得601000401000x x +=- 解得 x=200 ∴火车的速度20401000=-x （米/秒 答：火车的速度为20米/秒，火车的长度为200米．例2：（2005.马尾区）如图是2005年6月份的日历，如图中那样，用一个圈竖着圈住3圈的三个数的和为39，则这三个数中最大的一个为．解析 本题关键是找出日历中存在的数量关系，即：在日历中，每一竖排相邻两个数字之间差7.设一竖列上的相邻的3个数的中间一个数为x ，则最小一个数为（7-x ），最大一个数为(7+x )，有：39)7()7(=+++-x x x ，解得：x=13，∴最大一个数为20. 答案：20 例3：（2004.某某）购某种三年期国债x 元，到期后可得本息和y 元，已知y=kx ，则这种国债的年利率为（ ） A ．k B ．3k C ．k-1 D ．13k - 解析 解决利息问题的关键是抓住两个等量关系：利息=本金×利率×期数， 本息和=本金+利息. 这种国债的年利率为a 元，由题意得：3x （1+a ）=y,因为y=kx ，所以 k=3（1+a ），解得：31-=k a ，故选D 2x ×2．25％×(1－20％)=540． 答案：D例4：（2005.某某省）X 新和李明相约到图书城去买书,请你根据他们的对话内容(如图),求出李明上次所买书籍的原价.分析 本题中的等量关系是：售价=标价×10折数. 解：设李明上次购买书籍的原价是x 元，由题意得：,12208.0-=+x x 160:=x 解得. 答：李明上次所买书籍的原价是160元.例5：（2004.某某）某市今年1月10起调整居民用水价格，每立方米水费上涨25％，小明家去年12月份的水费是18元，而今年5月份的水费是36元，已知小明家今年5月份的用水量比去年12月份多6 m 3，求该市今年居民用水的价格．分析 本题是一道和收水费有关的实际问题．解决本题的关键是根据题意找到相等关系：今年5月份的用水量一去年12月份的用量=6m 3. 同时分式方程应注意验根．解：设该市去年居民用水的价格为x 元/m 3， 则今年用水价格为（1＋25%）x 元/m 3 根据题意得： 36186(125%)x x-=+ 解得：x 经检验：x =1.8是原方程的解 (125%) 2.25x ∴+=3【常见误区】列方程解决实际问题常见的思维误区是：由于审题不清，找不到“等量关系”或找错，诸如（1）利润=售价×利润率，（2）打几折就是标价乘几，（3）在得到方程的解后，不检验它是否符合实际意义等错误类型；在列方程解应用题时，我们可以采用画图，列表格的方法展示数量之间的关系，更形象、直观地帮助理解问题．。

（2）求溶剂
例、要把浓度为 90％的酒精溶液 500克，稀 释成浓度为75％的酒精溶液，需加水多少 克． 解：设需加水x克，因为加水前后溶质数量 不变，依题意得方程 75％(x+500)=90％ ×500． 化简得15x=1500． 解这个方程得x=100． 答：需加水100克．
（3）求溶液
例、有若干克4％的盐水蒸发了一些水分后，变成 10 ％的盐水，接着加进 4 ％的盐水 300 克，混合 后变为6.4％的盐水， 问:最初有盐水多少克？ 解：设最初有盐水x克，注意混合后的含盐量，依 题意得方程 4% x
一元一次方程应用题专题
——百分比浓度问题
有关溶液的浓度应用题是初中 代数中列方程解应用题的一类基本 题．解这类应用题，关键的问题是： 抓住不变量 ( 如稀释前溶质重量等 于稀释后溶质重量)列方程．
（1）求溶质
例、现有浓度为 20％的盐水300 克和浓度为 30％的 盐水 200 克，需配制成浓度为 60 ％的盐水，问两 种溶液全部混合后，还需加盐多少克？ 解：设两种溶液全部混合后，还需加盐 x克，注意 混合前后溶质总量不变，依题意得方程： 20％×300+30％×200+x=60％(300+200+x)． 化简得2x=900．解这个方程得x=450． 答：两种溶液全部混合后，还需加盐450克．
4% x 4% 300 6.4%(
10%
0).
化简得 1.44x=720． 解这个方程得x=500． 答：最初有盐水500克．
（4）求浓度
例、甲种硫酸溶液含硫酸的百分数是乙种硫酸溶液的 1.5 倍，甲种硫酸溶液 5 份与乙种硫酸溶液 3 份混合成的硫 酸溶液含硫酸 52.5 ％，求两种硫酸溶液含硫酸的百分 数． 解：设乙种硫酸溶液含硫酸的百分数为 x，则甲种硫酸溶 液含硫酸的百分数为1.5x，依题意得方程 5×1.5x+3x=52.5％×8． 化简得105x=42．解这个方程得x=0.4=40％， 则 1.5x=1.5×0.4=0.6=60％． 答：甲种硫酸溶液含硫酸的百分数是 60 ％，乙种硫酸溶 液含硫酸的百分数是40％．

知识点一 方程的概念 含有未知数的等式叫方程方程必须具备两个条件 一是等式，二是含有未知数注意：方程中的未知数可以用x 表示，也可以用其他字母表示，方程中的未知数的个数不一定是一个，可以是两个或两个以上。

知识点二 解方程和方程的解1.解方程就是求出使方程中等号左右两边相等的未知数的值，这个值就是方程的解。

2解方程是一个过程，方程的解是一个结果。

3检验一个数是不是方程的解，只需要将这个数代入原方程即可。

若方程两边相等，则这个数是方程的解，反之则不是。

例2 x=5方程23)36(3)42(=-++x x 的解吗？解：将x=5代入原方程，两边成立，所以，x=5是原方程的解。

解一元一次方程的一般步骤（重点）解一元一次方程的步骤是：去分母，去括号，移项，合并同类项，系数化为1．这些步骤不是固定不变的，有时可以省略某个步骤，主要是根据方程的特点灵活选用。

解含分数系数的一元一次方程的一般步骤总结如下表：注意(1)解一元一次方程时，应灵活运用一般步骤中的各种做法，采取哪些步骤要看解什么样的方程，有分母则去分母，有括号就去括号(2)解一元一次方程时，不一定是按照上表中自上而下的顺序解方程，有时要根据方程的形式、特点灵活安排求解步骤，熟练后还可以合并或简化某些步骤． 解方程2.04.05.05.15.05.0-x 2.0x+=+ 知识点三 一元一次方程的特点一元一次方程的定义：只有一个未知数，未知数的次数都是1的方程。

特点：1只有一个未知数； 2未知数的次数是1；3可带分母，但分母不能带有未知数。

如421=-x 就不是一元一次方程。

例3下列各式哪些是一元一次方程？①56-1=55；②2x+6=0；③6x=0；④8y-3=12；⑤0532=+-x x ；⑥2x 十5z=23；⑦11-x 22x 1=++例4已知43654=+-n x 是一元一次方程，求n 的值。

【变式2】若关于的方程是一元一次方程，则_______【变式3】若关于的方程()523=+--mx x m m 是一元一次方程，则_______． 【变式4】若关于的方程()5)2()2(22=+++-x m x m m 是一元一次方程，则_______．知识点四 等式的性质等式的性质1 等式两边加（或减）同一个数（或式子），结果仍相等。

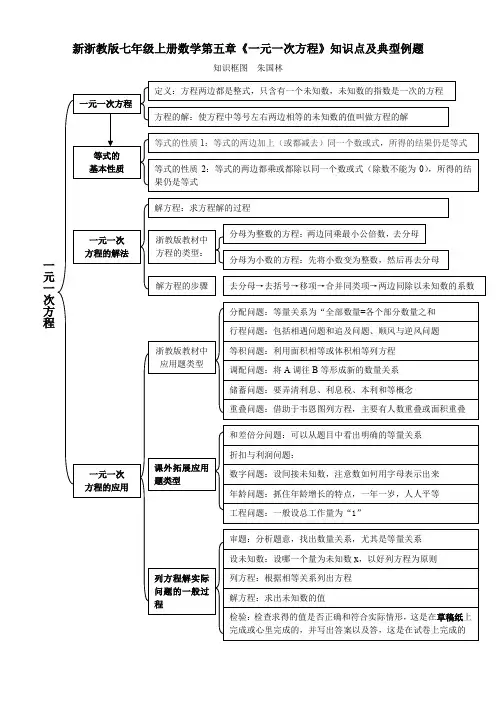
新浙教版七年级上册数学第五章《一元一次方程》知识点及典型例题知识框图朱国林关于一元一次方程概念的拓展教材中的概念：方程两边都是整式，只含有一个未知数，未知数的指数是一次的方程是一元一次方程，那么 x+2=x+3是一元一次方程吗？从概念上来看，是一元一次方程，但稍作变形，就是2=3，是不是觉得很可笑？因此，一元一次方程的概念应该是：方程两边都是整式，只含有一个未知数，未知数的指数是一次，并且能变形为ax=b （a ≠0，a 、b 均为常数）的方程是一元一次方程，也就是说，一元一次方程一定只有一个解。

关于用方程解应用题的秘诀：相关条件设未知数，剩余条件列方程考点一、判断方程是不是一元一次方程及一元一次方程概念的简单应用 考点二、关于在解方程过程中的某些变形问题，只能以选择题的形式出现 考点三、解一元一次方程考点四、列一元一次方程解与实际生活无关的题目（可以是选择题、填空题、解答题） 考点五、列一元一次方程解与实际生活有关的题目（可以是选择题、填空题、解答题）将考点与相应习题联系起来考点一、判断方程是不是一元一次方程及一元一次方程概念的简单应用 1、下列等式中是一元一次方程的是（ ）A ．3x=y-1B ．2(1)21x x -=+C ．3(x-1)= -2x-3D ．3x 2-2=3E ．11x x=+ 2、在方程23=-y x ，021=-+x x ，2121=x ，0322=--x x 中一元一次方程的个数为（ ） A ．1个 B ．2个 C ．3个 D ．4个 3、如果06312=+--a x是一元一次方程，那么=a ，方程的解为 。

（特别注意）考点二、关于在解方程过程中的某些变形问题，只能以选择题的形式出现 1、已知等式523+=b a ，则下列等式中不一定．．．成立的是（ ） （A ）;253b a =- （B ）;6213+=+b a （C ）;523+=bc ac （D ）.3532+=b a 2、解方程2631xx =+-，去分母，得（ ） （A ）133x x --= （B ）633x x --= （C ）633x x -+= （D ）133x x -+=3、下列方程变形中，正确的是（ ）（A ）方程1223+=-x x ，移项，得;2123+-=-x x （B ）方程()1523--=-x x ，去括号，得;1523--=-x x （C ）方程2332=t ，未知数系数化为1，得;1=t （D ）方程110.20.5x x --=化成101010125x x --= 考点三、解一元一次方程（1）x x 3.15.67.05.0-=-； （2）；（3）1676352212--=+--x x x ； （4）4.06.0-x 3.011.0+x .考点四、列一元一次方程，解与实际生活无关的题目（可以是选择题、填空题、解答题） 1、方程432-=+x m x 与方程6)16(21-=-x 的解相同，则m 的值为__________. 2、已知5x+3=8x －3和65a x +=37这两个方程的解是互为相反数，则a= . 3、某数的4倍减去3比这个数的一半大4，则这个数为__________.4、若与互为相反数，则的值是 .5、一个两位数，个位上的数字是十位上的数字的3倍，它们的和是12，那么这个两位数是 .6、写出一个以x=－21为解的一元一次方程7、小明在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程是：11222y y -=- 怎么办呢？小明想了一想，便翻看书后答案，此方程的解是53y =-，于是很快就补好了这个常数，你能补出这个常数吗？它应是（ ） A.1 B.2 C.3 D.48、已知21=x 是方程32142m x m x -=--的根，求代数式()⎪⎭⎫ ⎝⎛---+-121824412m m m 的值.★★★已知关于x 的一元一次方程b x x +=+2301121的解为2=x ，那么关于y 的一元一次方程b y y ++=++）（）（123101121的解为 ． 考点五、列一元一次方程解与实际生活有关的题目（可以是选择题、填空题、解答题） 1、日历上竖列相邻的三个数，它们的和是39，则第一个数是（ ）A.6B.12C.13D.142、有m 辆客车及n 个人，若每辆客车乘40人，则还有10人不能上车；若每辆客车乘43人，则还有1人不能上车．有下列四个等式：①4010431m m +=-；②1014043n n ++=；③1014043n n --=；④4010431m m +=+．其中正确的是（ ） A.①② B.②④ C.②③ D.③④ 3、某商店卖出两件衣服，每件60元，其中一件赚25%，另一件亏25%，那么这两件衣服卖出后，商店是 （ ） A.不赚不亏 B.赚8元 C.亏8元 D. 赚15元4、一件商品提价25%后发现销路不是很好，欲恢复原价，则应降价（ ） A.40% B.20% C.25% D.15%5、小强比他叔叔小30岁，而两年前，小强的年龄是他叔叔的41，则小强的叔叔今年____________岁. 6、一项工程甲独做10天完成，乙的工作效率是甲的2倍，两人合做了2天未完成，剩下的工作量由乙完成，还需的天数为 ( )(A)．1 天 (B)2 天 (C)3 天 (D)4天 7、小明存入100元人民币，存期一年，年利率为2％，到期应缴纳所获利息的20％的利息税，那么小明存款到期交利息税后共得款 （ ）A.106元B.102元C.111.6元D.101.6元8、银行教育储蓄的年利率如右下表：小明现正读七年级，今年7月他父母为他在银行存款30000元，以供3年后上高中使用. 要使3年后的收益最大，则小明的父母应该采用（ ） （A ）直接存一个3年期；（B ）先存一个1年期的，1年后将利息和自动转存一个2年期； （C ）先存一个1年期的，1年后将利息和自动转存两个1年期； （D ）先存一个2年期的，2年后将利息和自动转存一个1年期.9、某酒店为招揽生意，对消费者实施如下优惠：凡订餐5桌以上，多于5桌的部分按定价的7折收费.小叶集团公司组织工会活动，预定了10桌，缴纳现金2550元，那么每桌定价是 元.10、某商店将彩电按成本价提高50%，然后在广告上写“大酬宾，八折优惠”，结果每台彩电仍获利270元，那么每台彩电成本价是___________。

例2：有含盐8%的盐水40kg，要使盐水含盐20%， 如果蒸发掉水分，需蒸发掉多少千克的水？ 注意：两种盐水所含的盐不变 解：设需蒸发掉x千克的水。
盐+水=盐水
原盐水40kg
含盐率=
现盐水（40-x）kg
盐 盐水
含盐率： 8% 含 盐： 40 × 8%
等量关系：
20% (40-x) × 20%
8%盐水的含盐量=20%盐水的含盐量
40 × 8%= ( 40-x) × 20%
例3：现有浓度为10%.及浓度为20%的两种酒精溶 液.问各取多少可配制成浓度为14%的酒精溶液100 升?
含酒精率：10% 20% 14% 总升数：10%的升数+20%的升数=14%的升数 100-x x 100 酒精含量：10%的含量+20%的含量 =14%的含量 20%(100-x) 10%x 14 %×100 10% x +20%(100-x）=14%×100
课堂作业
1、有含盐15%的盐水30千克,要使盐水含盐10%, 需要加水多少千克?
2、现有糖水20千克,浓度为22%,问需加多少千克糖 后可使浓度变为40%? 3、有两种合金，第一种含铜90％，第二含铜80％， 现要熔炼一种含铜82.5%的合金240千克。两种合金 应各取多少千克？ 4、从每千克0.8元的苹果中取出一部分,又从每千克 0.5元的苹果中取出一部分混合后共15千克,每千克要 卖0.6元,问需从两种苹果中各取出多少千克?
盐+水=盐水 原盐水40;x）kg 20% 含盐率： 8% 含 盐： 40 × 8% ( 40+x) × 20% 含 水： 40- 40 × 8% ( 40+x) -(40+x) × 20% 等量关系： 8%盐水的含水量=20%盐水的含水量

12/8/2021
第六页，共七页。
内容(nèiróng)总结
义务教育课程标准实验教科书。本息和：本金与利息的和。利率：每个期数内的利息与本 金的比。计算公式：利息=本金×利率×期数。春节过后，小明将压岁钱1000元存入银行，银行
No 的定期年利率如下所示：。（2）若按定期一年，且现在银行要收利息税（所得利。小颖的妈妈
盐的质量分数+水的质量分数=1
12/8/2021
第五页，共七页。
有盐的质量(zhìliàng)分数为16%的盐水质量800克， 如果要得到盐的质量分数为10%的盐水，应加水多少克？
变式1：如果要得到(dé dào)盐的质量分数为20%的盐水，
应加盐多少克？
变式2：如果要得到盐的质量分数为20%的盐水， 应蒸发水多少克？
为了准备小颖6年后上大学(dàxué)的学费5000元，她的父母现在就参加了教育储蓄．下面有两种 储蓄方式：。x×2.7%×3。x+ x×2.7%×3。1.081x ×2.7% ×3
Image
12/8/2021
第七页，共七页。
（2）若按定期一年，且现在银行要收利息税（所得利 息×20 %），小明实际只拿到利息______.
12/8/2021
第三页，共七页。
小颖的妈妈为了准备小颖6年后上大学的学费5000元，
她的父母现在就参加了教育储蓄．下面有两种储蓄方式：
(1)直接(zhíjiē)存一个6年期，年利率为2.88%．
(2)先存一个3年期，3年后将本息和自动转存一个3 年期，年利率为2.70%。
你认为哪种储蓄方式开始存入的本金比较少？
本金
第一个 x 3年期
第二个 3年期 1.081x
12/8/2021

第五章 一元一次方程
5.4 一元一次方程的应用
第6课时 用一元一次方程解 销售、储蓄问题
精选ppt
1
1 课堂讲解 销售问题 、储蓄问题、数量重叠问题
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
精选ppt
2
精选ppt
3
知识点 1 销售问题
知1－讲
【例1】一件商品按成本价提高20%后标价，又以9折 销售，售价为270元，则这件商品的成本价是 多少？
知3－讲
原理和方法： (1)如图①，C＝A＋B－AB(相交部分)； (2)如图②，D＝A＋B＋C－AB(相交部分)－AC(相交
部分)－BC(相交部分)＋ABC(三集合圈相交部分)．
精选ppt
（来自《点拨》）
21
知3－讲
【例5】某班共有48人，参加书法兴趣小组的有30人， 参加生物兴趣小组的有26人，其中这两个兴 趣小组都参加的有13人，在这个班上有多少 人没有参加这两个兴趣小组？
（来自《典中点》）
精选ppt
16
知2－练
3 若一种3年期国库券的年利率为2.89%.如果要在 3年后获得本息和10 867元，现在应购买国库券 多少元？
（来自《典中点》）
精选ppt
17
知识点 3 数量重叠问题
知3－讲
【例4】七年级二班有45人报名参加了文学社或书画社. 已知参加文学 社的人数比参加书画社的人数多 5人，两个社都参加的有20人，问参加书 画社 的有多少人？
解析：设住房公积金贷款x元，则普通住房贷款(250 000 －x)元，依题意找出等量关系，列方程求解．
精选ppt
12
知2－讲
解：设住房公积金贷款x元， 由题意得0.036x＋0.047 7(250 000－x)＝10 170， 解得x＝150 000. ∴250 000－x＝100 000. 答：王老师的住房公积金贷款是150 000元，普 通住房贷款是10 0000元．

xuekewangzxxk
？
变式：
七年级二班有45人报名参加了 文学社或书画社。已知参加文 学社的人数比参加书画社的人 数多5人，两个社都参加的有23 人，问参加书画社的有多少人 ？
• 5.4(4)一元一次方程的应用
例1 小明把压岁钱按定期一年 存入银行。当时一年期定期 存款的年利率为1.98%，利息 税的税率为20%，到期支取时，扣除利息税后小明实得本利 和为507.92元，问小明存入 银行的压岁钱有多少元？
例2 七年级二班有45人报名参加 了文学社或书画社。已知参加文 学社的人数比参加书画社的人数 多5人，两个社都参加的有20人， 问参加书画社的有多少人

浙教版初一数学一元一次方程 的应用ppt演示课件
目
CONTENCT
录
• 引言 • 一元一次方程的基本概念 • 一元一次方程的解法 • 一元一次方程的应用举例 • 一元一次方程与实际问题的结合 • 课堂互动与练习
01
引言
目的和背景
帮助学生理解一元一次方程的概念和应用
通过演示课件，学生可以更直观地了解一元一次方 程的定义、性质和解法，以及在实际问题中的应用 。
设定未知数
根据问题背景，合理设定 未知数，并用字母表示。
建立方程
根据问题中的等量关系， 建立一元一次方程。
方程解的合理性讨论
解的存在性
根据方程的形式和性质，判断方 程是否有解。
解的合理性
将方程的解代入实际问题中，检验 是否符合实际情况。
解的唯一性
根据方程的解和实际情况，判断方 程的解是否唯一。
实际问题的解决方案
骤。
利润问题
利润问题基本要素
介绍利润问题中的基本要素，包括进价、售价、利润和折扣等。
利润问题方程的建立
通过实例展示如何根据利润问题的基本要素建立一元一次方程。
利润问题方程的解法
详细解释如何解这类一元一次方程，包括列方程、解方程等步骤。
05
一元一次方程与实际问题的结合
建立数学模型
实际问题抽象化
将实际问题中的关键信息 抽象出来，用数学语言进 行描述。
练习题目
老师应当提供一些与一元一次方程应用相关的练 习题目，供学生在课堂上进行练习。
3
及时反馈
对于学生的测验和练习结果，老师应当及时给予 反馈，指出学生的不足之处，并提供相应的指导。
小组合作与讨论
分组合作
老师可以将学生分成若干小组，让每组学生共同 讨论和解决与一元一次方程应用相关的问题。

2.创设轻松、愉快的学习氛围，鼓励学生积极参与课堂讨论，敢于提出问题。
3.注重启发式教学，引导学生主动探究，培养学生的创新意识。
4.加强与学生的情感沟通，关注学生的心理需求，帮助他们建立自信心。
四、教学内容与过程
（一）导入新课
1.教师以谈话方式引入新课，询问学生：“同学们，你们知道储蓄是什么吗？在我们的生活中，储蓄有什么作用呢？”通过这个问题，让学生结合自己的生活经验，思考储蓄的意义。
（二）过程与方法
1.引导学生从现实生活情境中发现储蓄问题，培养学生观察问题、提出问题的能力。
2.通过小组合作、讨论交流，引导学生分析储蓄问题中的数量关系，培养学生合作学习、共同探究的能力。
3.指导学生运用一元一次方程的解法解决储蓄问题，强调列方程的步骤和注意事项，提高学生解决问题的条理性和准确性。
4.设计丰富的例题和练习题，让学生在实际操作中巩固所学知识，提高解题能力。
5.适时反馈，查漏补缺。在教学过程中，教师应及时关注学生的学习情况，给予反馈，帮助学生查漏补缺，提高学习效果。
6.情感教育，培养价值观。结合储蓄问题，引导学生树立正确的消费观念和理财观念，培养学生的节约意识。
在教学过程中，教师应注意以下几点：
1.关注学生的个体差异，因材施教，让每个学生都能在原有基础上得到提高。
3.教师巡回指导，关注学生的讨论过程，适时给予提示和指导，帮助学生解决问题。
4.各小组汇报讨论成果，教师对每组的表现进行点评，总结解题方法。
（四）课堂练习
1.教师设计难易程度不同的储蓄问题，要求学生独立解决。
2.学生在规定时间内完成练习，巩固所学知识。
3.教师对学生的练习情况进行反馈，针对共性问题进行讲解，帮助学生查漏补缺。
3.讲解一元一次方程的解法，包括移项、合并同类项、化简等基本运算，让学生掌握解题方法。

《一元一次方程的应用》讲义一元一次方程是数学中的重要基础知识，在实际生活中有着广泛的应用。

通过建立一元一次方程模型，我们可以解决许多有趣且实用的问题。

一、行程问题行程问题是一元一次方程常见的应用类型之一。

比如，甲、乙两人分别从 A、B 两地同时出发相向而行，甲的速度为每小时 x 千米，乙的速度为每小时 y 千米，经过 t 小时后两人相遇。

已知 A、B 两地的距离为 s 千米，那么可以根据路程＝速度×时间这个公式，得到方程：（x ＋ y)t ＝ s 。

再比如，某人骑自行车以每小时 15 千米的速度从甲地到乙地，回来时因逆风，速度变为每小时 10 千米，设甲地到乙地的距离为 s 千米，去时所用时间为 s÷15 小时，回来时所用时间为 s÷10 小时，因为来回的路程相同，所以可列方程：s÷15 ＋ 1 ＝ s÷10 （假设回来时多用 1 小时）。

二、工程问题工程问题也是常考的类型之一。

例如，一项工程，甲单独做需要 x天完成，乙单独做需要 y 天完成，两人合作需要 z 天完成。

把工作总量看作单位“1”，甲每天的工作效率就是 1/x ，乙每天的工作效率就是1/y ，两人合作每天的工作效率就是 1/z 。

根据工作效率×工作时间＝工作总量，可得到方程：（1/x ＋ 1/y)z ＝ 1 。

又如，某工厂要生产一批零件，原计划每天生产 a 个，实际每天多生产 b 个，提前 c 天完成任务。

设原计划生产 d 天，那么工作总量为ad 个。

实际每天生产（a ＋ b) 个，实际用的天数为 d c 天，可列方程：a×d ＝（a ＋ b)×（d c) 。

三、销售问题在销售问题中，经常会涉及到进价、售价、利润、利润率等概念。

比如，某商品进价为 x 元，售价为 y 元，利润为 z 元，那么利润＝售价进价，即 z ＝ y x 。

如果已知商品的进价为 a 元，利润率为 b%，售价为 c 元，因为利润率＝（利润÷进价）× 100% ，所以可列方程：（c a)÷a × 100% ＝b% 。

80%)销售，售价为2 080元．设该电器的成本价为x元，根据题意，下面
所列方程正确的是( A )
A．x(1＋30%)×80%＝2 080
B．x·30%·80%＝2 080
C．2 080×30%×80%＝x
D．x·30%＝2 080×80%
C C
6．(4分)小彬把暑假勤工俭学挣的300元钱，按活期存入银行，如果月
解：(1)这件衣服的进价是250元 (2)小明的妈妈没有捡到便宜，她比在公平买 卖时多付20元
解：设每次应付款x元，则(8 224－x)×(1＋5.6%)＝x，解得x＝4 224， 所以每次应付款4 224元
【综合运用】 14．(15分)一天，小明的妈妈从个体服装店买回一件衣服，回家后高兴地对小明 说：“今天我捡了个大便宜，碰上服装八折优惠酬宾，平时要花400元的衣服我 只花了320元就买回来了．” 资料：一般情况下，个体服装店只要高出进价的20%销售(公平买卖)便可盈利， 但经销商们常常以高出进价的60%～100%标价，然后进行打折销售，或者与顾 客讨价还价． 探究：(1)如果该件衣服是商家在进价的基础上加价60%标价，再打八折卖给小 明妈妈的，请你帮小明妈妈计算一下，这件衣服的进价是多少元？ (2)在第(1)小题的前提下，小明的妈妈真的捡便宜了吗？若没有，请你帮她计算 一下，她比在公平买卖(加价20%)时多付多少元？
解：(1)投资者选择方案二所获的投资收益率更高 (2)甲投资了62.5万元，乙投 资了53.125万元
13．(10分)某商店为了促销某空调机，2014年五一这天购买该机可分两 期付款，在购买时先付一笔款，余下部分及利息(年利率为5.6%)在2015 年五一付清，该空调机每台售8 224元，若两次付款数相同，则每次应 付款多少元？

第5章
5.4
Байду номын сангаас
一元一次方程
一元一次方程的应用(4)
知识点1：储蓄问题 1．某储户去年8月份存入定期为1年的人民币5 000元，存款利率为1.5%， A 设到期后银行应向储户支付现金x元，则所列方程正确的是( ) A．x－5 000＝5 000×1.5% B．x＋5 000＝5 000×1.5% C．x＋5 000＝5 000×(1＋1.5%) D．x＋5 000×1.5%＝5 000×(1＋1.5%)
＋3.24%×3)＝15 000，解得x≈12 460.如果按照第二种储蓄方式有 x(1＋3.60%×6)＝15 000，解得x≈12 336.∵12 460>12 336，∴第
二种储蓄方式开始存入的本金少．
10 ． (2016 秋 •江干区期末 ) 按国家2011 年 9 月1 日起实施的有关个人 所得税的规定，个人月工资(薪金)中，扣除国家规定的免税部分 3 500 元后的剩余部分为应纳税所得额．全月应纳税所得额不超过 1 500元的税率为3%，超过1 500元至4 500元部分的税率为10%. (1)若每月工资4 500元，则每月应纳税所得额为多少元？应缴多少 个人所得税？ (2) 每月工资为 x 元，且3 500<x≤5 000 ，用x 的代数式表示应缴个 人所得税． (3)小聪妈妈每月缴纳个人所得税95元，她每月的工资是多少？
9．为了准备小颖6年后上大学的学费15 000元，她的父母现在就参加了 教育储蓄，下面有两种储蓄方式．
期数 三年 六年
年期的．
教育储蓄年利率/% 3.24 3.60
①先存一个3年期，3年后将本息和自动转存一个3年期；②直接存一个6
你认为哪种储蓄方式开始存入的本金比较少？

一元一次方程应用题专题讲解列方程解应用题，是初中数学的重要内容之一。

许多实际问题都归结为解一种方程或方程组，所以列出方程或方程组解应用题是数学联系实际，解决实际问题的一个重要方面；同时通过列方程解应用题，可以培养我们分析问题，解决问题的能力。

因此我们要努力学好这部分知识。

一、列方程解应用题的一般步骤（解题思路）（1）审——审题：认真审题，弄清题意，找出能够表示本题含义的相等关系（找出等量关系）．（2）设——设出未知数：根据提问，巧设未知数．（3）列——列出方程：设出未知数后，表示出有关的含字母的式子，然后利用已找出的等量关系列出方程．（4）解——解方程：解所列的方程，求出未知数的值．（5）答——检验，写答案：检验所求出的未知数的值是否是方程的解，是否符合实际，检验后写出答案．（注意带上单位）二、各类题型解法分析一元一次方程应用题归类汇集：行程问题，工程问题，和差倍分问题（生产、做工等各类问题），等积变形问题，调配问题，分配问题，配套问题，增长率问题，数字问题，方案设计与成本分析，古典数学，浓度问题等。

（一）和、差、倍、分问题——读题分析法这类问题主要应搞清各量之间的关系，注意关键词语。

仔细读题，找出表示相等关系的关键字，例如：“大，小，多，少，是，共，合，为，完成，增加，减少，配套……”，利用这些关键字列出文字等式，并且据题意设出未知数，最后利用题目中的量与量的关系填入代数式，得到方程.1.倍数关系：通过关键词语“是几倍，增加几倍，增加到几倍，增加百分之几，增长率……”来体现。

2.多少关系：通过关键词语“多、少、和、差、不足、剩余……”来体现。

增长量＝原有量×增长率现在量＝原有量＋增长量例1．某单位今年为灾区捐款2万5千元，比去年的2倍还多1000元，去年该单位为灾区捐款多少元？例2．旅行社的一辆汽车在第一次旅程中用去油箱里汽油的25%，第二次旅程中用去剩余汽油的40%，这样油箱中剩的汽油比两次所用的汽油少1公斤，求油箱里原有汽油多少公斤？（二）等积变形问题等积变形是以形状改变而体积不变为前提。

长方形的宽： 4 3 4 11 长方形的面积：1311 143
练6
如图，一块长5厘米、宽2厘米的长方形纸板，一块长4厘米、宽1厘米的长方形纸 板，一块小正方形以及另两块长方形的纸板，恰好拼成一个大正方形，求大正方形 的面积.
ENDING
丙三台机器同时生产，刚好在10小时25分钟完成任务．
（1）求乙、丙两台机器每小时各生产多少个？
（2）由于
个循环中只能生产1小时，即每个循环需要3小时．
①若生产次序为甲、乙、丙，则最后一个芭比娃娃由 机器生产完成，整个生
产过程共需
小时；
②若想使完成生产任务的时间最少，直接写出三台机器的生产次序及完成生产任
5.4一元一次方程 的应用习题课
主讲老师：x老师
列方程解决实际问题步骤
01 审题，找出题目中的数量关系以及等量关系 02 设元，选择合适的未知数用字母表示
03 列方程，根据题目中的等量关目系列录出方程
04 解方程，求出未知数的值 05 检验，检查计算出来的值是否符合题意
常见题型
浙教版七年级数学上册一元一次方程 的应用 习题课 教学课 件
x6 答：用 6 立方米木材生产桌面．
浙教版七年级数学上册一元一次方程 的应用 习题课 教学课 件
浙教版七年级数学上册一元一次方程 的应用 习题课 教学课 件
练2
某车间每天能制作甲种零件500个，或者制作乙种零件250个，甲乙两种零件各 一个配成一套产品，现要在30天内制作最多的成套产品，则甲种零件制作多少天?
行程问题 某行军纵队以7千米/时的速度行进，队尾的通讯员以11千米/时的速度赶到队伍前 送一封信，送到后又立即返回队尾，共用13.2分钟，求这支队伍的长度.
答案
解：设这支队伍的长度为 x 千米． x + x = 13.2 ，

年前儿子的年龄。
解：设今年儿子的年龄是岁。
由题意可得3 − 6 = 4( − 6)，
解这个方程，得 = 18。
检验： = 18是方程的解，且符合题意。
答：今年儿子的年龄是18岁。
问题
总人（物）数。
注意事项
注意调配的方向
和数量。
合作效率=各单独
工程
工作量=工作时间 做的效率和；
一般情况下把总
问题
×工作效率。
工作量设为“1”。
总工作量=各部分
工作量之和。
涉及公式
储蓄
问题
等量关系
本金×利率×存期=利息。
售价=标价×
折扣数
；
10
注意事项
注意题中利率和存期要
对应。
打几折后的价格就是标
量。
注意事项
弄清“倍、分”关
系及“多、少”关
系。
涉及公式
长方体的体积
等积变
形问题
=长×宽×
高；
圆柱的体积=
底面积×高。
等量关系
注意事项
（1）面积变
了，周长没
变；
（2）原料体
积=成品体
积。
分清是“形”变“积”不
变，还是“形”变“积”也
变，但质量不变。
涉及公式
等量关系
甲处人（物）数+
调配
乙处人（物）数=
销售
售价-进价=利润；
问题
价乘十分之几或百分之
利润率=（售价-进价）÷ 进价
几十。
× 100%。
典例2 (杭州西湖区一模)今年父亲的年龄是儿子年龄的3倍，6年前
父亲的年龄是儿子年龄的4倍。今年儿子的年龄是多少岁？
分析：等量关系为“父亲今年的年龄−6 =父亲6年前的年龄”。

七年级上册应用题专题讲解一、列方程解应用题的一般步骤〔解题思路〕〔1〕审—审题：认真审题，弄清题意，找出能够表示此题含义的相等关系〔找出等量关系〕．〔2〕设—设出未知数：根据提问，巧设未知数．〔3〕列—列出方程：设出未知数后，表示出有关的含字母的式子，然后利用已找出的等量关系列出方程．〔4〕解—解方程：解所列的方程，求出未知数的值．〔5〕答—检验，写答案：检验所求出的未知数的值是否是方程的解，是否符合实际，检验后写出答案．〔注意带上单位〕二、各类题型解法分析一元一次方程应用题归类聚集：行程问题，工程问题，和差倍分问题〔生产、做工等各类问题〕，等积变形问题，调配问题，分配问题，配套问题，增长率问题，数字问题，方案设计与本钱分析，古典数学，浓度问题等。

〔一〕和、差、倍、分问题——读题分析法这类问题主要应搞清各量之间的关系，注意关键词语。

仔细读题，找出表示相等关系的关键字，例如：“大，小，多，少，是，共，合，为，完成，增加，减少，配套……〞，利用这些关键字列出文字等式，并且据题意设出未知数，最后利用题目中的量与量的关系填入代数式，得到方程.1.倍数关系：通过关键词语“是几倍，增加几倍，增加到几倍，增加百分之几，增长率……〞来表达。

2.多少关系：通过关键词语“多、少、和、差、缺乏、剩余……〞来表达。

增长量＝原有量×增长率现在量＝原有量＋增长量例1．某单位今年为灾区捐款2万5千元，比去年的2倍还多1000元，去年该单位为灾区捐款多少元？解：设去年该单位为灾区捐款x元，那么2x+1000=25000 2x=24000 x=12000答：去年该单位为灾区捐款12000元.例2．旅行社的一辆汽车在第一次旅程中用去油箱里汽油的25%，第二次旅程中用去剩余汽油的40%，这样油箱中剩的汽油比两次所用的汽油少1公斤，求油箱里原有汽油多少公斤？解：设油箱里原有汽油x公斤,那么x-[25%x+40%×(1-25%)x]+1=25%x+40%×(1-25%)x即10%x=1 x=10答：油箱里原有汽油10公斤.等积变形是以形状改变而体积不变为前提。