【数学】云南省宣威市2012届高三第二次调研统一模拟考试(理)

2012届高三模拟考试数学试题数学试题（理科）本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项：1.答卷前,考生要务必填写答题卷上密封线内的有关项目.2.选择题每小题选出答案后，用铅笔把答案代号填在答题卷对应的空格内.3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.请考生保持答题卷的整洁.考试结束后，将答题卷和答题卡交回. 参考公式:锥体的体积公式13V Sh =，其中S 为锥体的底面面积，h 为锥体的高. 一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数(1)i ai ⋅+是纯虚数，则实数a 的值是（ ）A. 1B. 1-C.0D. 0或1-2．已知集合{||2,A x x x =≤∈R },{2,B x x =≤∈Z },则A B = （ ）A. (0,2)B. [0,2]C. {0, 2}D. {0,1,2}3．设25025..12,25,()2.a b c ===，则,,a b c 的大小关系是（C ）A.a c b >>B. c a b >>C. a b c >>D.b a c >>4．一空间几何体的三视图如图所示，则该几何体的体积为. A. 1 B. 3 C 6 D. 25．设向量(1,0)a = ，11(,)22b = ，则下列结论正确的是 ( )A.a b =B.2a b ⋅= C. a ∥b D. a b - 与b 垂直6．执行如图1所示的程序框图后，输出的值为5，则P 的取值范围（ ）A.715816P <≤ B. 1516P > C. 715816P ≤< D.3748P <≤ 7. 下列四个判断：①某校高三一班和高三二班的人数分别是,m n ，某次测试数学平均分分别是,a b ，则这两个班的数学平均分为2a b+； ②10名工人某天生产同一零件，生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a ,中位数为b ,众数为c ，则有b a c >>； ③从总体中抽取的样本12221111(,),(,),,(,),,n nn n i i i i x y x y x y x x y y n n ====∑∑ 若记，则回归直线y =bx a +必过点（,x y ）④已知ξ服从正态分布(0N ,2)σ，且(20)0.4P ξ-≤≤=，则(2)0.2P ξ>= 其中正确的个数有： （ ）A ．0个B ． 1 个C ．2 个D ．3个8. 定义符号函数1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩，设111sgn()1sgn()122()()22x x f x f x -+-+=⋅+2()f x ⋅，[0,1]x ∈，其中1()f x =12x +, 2()f x ⋅=2(1)x -, 若1[()][0,)2f f a ∈，则实数a 的取值范围是（ ）A. 1(0,]4B. 11(,)42C. 11(,]42D. 3[0,]8二、填空题:本大共7小题,考生作答6小题,每小题5分，满分30分.(一)必做题(9～13题)9．. 已知A 是单位圆上的点，且点A 在第二象限，点B 是此圆与x 轴正半轴的交点，记AOB α∠=, 若点A的纵坐标为35．则s i n α=_____________;tan(2)πα-=_______________.10．以抛物线24y x =的焦点为圆心，且被y 轴截得的弦长等于2的圆的方程为__________________.11．从如图所示的长方形区域内任取一个点()y x M ,，则点M 取自阴影部分的概率为____________.12．已知,x y 满足约束条件5000x y x y y ++⎧⎪-⎨⎪⎩≥≤≤，则24z x y =+的最小值是_________.13.设()11f x x x =-++，若不等式121()a a f x a+--≥对任意实数0a ≠恒成立，则x 取值集合是_______________________.(二)选做题(14～15题,考生只能从中选做一题) 14．（几何证明选讲选做题）如图，AB 是圆O 的直径，DE AD =，6,8==BD AB ,则ADAC= ;15．(坐标系与参数方程选做题) 已知直线l 方程是11x ty t =+⎧⎨=-⎩(t 为参数），,以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，圆C 的极坐标方程为1ρ=，则圆C 上的点到直线l 的距离最小值是 三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 16. (本小题满分12分)已知等比数列{}n a 的前n 项和为n S ， 11a =，且1S ，22S ，33S 成等差数列. （1）求数列{}n a 通项公式；（2）设n n b a n =+，求数列{}n b 前n 项和n T ．17．(本小题满分14分) 有一个3×4×5的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成60个1×1×1的小正方体，从这些小正方体中随机地任取1个，设小正方体涂上颜色的面数为ξ. （１）求0ξ=的概率； （２）求ξ的分布列和数学期望.18．(本小题满分14分)如图5(1)中矩形ABCD 中，已知2AB =，AD =MN 分别为AD 和BC 的中点，对角线BD 与MN 交于O 点，沿MN 把矩形ABNM 折起，使平面ABNM 与平面MNCD 所成角为60 ，如图5(2).（1） 求证：BO DO ⊥；（2） 求AO 与平面BOD 所成角的正弦值.OABDC MNABDCMNO图6B A19．(本小题满分12分)在ABC ∆中，三个内角A ，B ，C 的对边分别为a ，b ，c ，其中2c =，且cos cos 1A bB a == (1)求证：ABC ∆是直角三角形；(2)如图6，设圆O 过,,A B C 三点，点P 位于劣弧AC ︿上，求PAC ∆面积最大值.20.(本小题满分14分)在直角坐标系xOy 中，动点P 与定点(1,0)F 的距离和它到定直线2x =的距离之比是2，设动点P 的轨迹为1C ，Q 是动圆2222:C x y r +=(12)r <<上一点. （1）求动点P 的轨迹1C 的方程； （2）设曲线1C上的三点1122(,),(,)A x y B C x y 与点F 的距离成等差数列，若线段AC 的垂直平分线与x 轴的交点为T ，求直线BT 的斜率k ；（3）若直线PQ 与1C 和动圆2C 均只有一个公共点，求P 、Q 两点的距离PQ 的最大值.21．(本小题满分14分)已知函数()ln(1)f x x mx =++，当0x =时，函数()f x 取得极大值. （１）求实数m 的值；（２）已知结论：若函数()ln(1)f x x mx =++在区间(,)a b 内导数都存在，且1a >-，则存在0(,)x a b ∈，使得0()()()f b f a f x b a-'=-.试用这个结论证明：若121x x -<<，函数121112()()()()()f x f x g x x x f x x x -=-+-，则对任意12(,)x x x ∈，都有()()f x g x >；（３）已知正数12,,,n λλλL ，满足121n λλλ+++=L ，求证：当2n ≥，n N ∈时，对任意大于1-，且互不相等的实数12,,,nx x x L ，都有1122()n n f x x x λλλ+++>L 1122()()()n n f x f x f x λλλ+++L .2012届高考模拟测试数学试题(理科)参考答案和评分标准一．选择题：CACBD ABB二填空题：9.35（2分）247（3分） 10. 22(1)2x y -+= 11. 13 12. 15- 13. 33(,][,)22-∞-+∞ 14. 4315.1三、解答题： 本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．16．(本题满分14分)解：（1）设数列{}n a 的公比为q ，……………1分若1q =，则111S a ==，21244S a ==，31399S a ==，故13231022S S S +=≠⨯，与已知矛盾，故1q ≠，………………………………………………2分从而得1(1)111n nn a q q S q q--==--，………………………………………………4分由1S ，22S ，33S 成等差数列，得132322S S S +=⨯，即321113411q q q q--+⨯=⨯--， 解得13q =……………………………………………5分 所以11113n n n a a q--⎛⎫=⋅= ⎪⎝⎭.………………………………………………6分（2）由（１）得，11()3n n n b a n n -=+=+，………………………………7分 所以12(1)(2)()n n T a a a n =++++++1(1)(1)(12)12n n b q n nS n q -+=++++=+- ………………………………10分2111()(1)333.12213n n n n n n --+++-=+=-……………………………12分 17．(本题满分12分)（１）60个1×1×1的小正方体中，没有涂上颜色的有6个，61(0)6010P ξ=== … （3分） （２）由（1）可知1(0)10P ξ==；11(1)30P ξ==；2(2)5P ξ==；2(3)15P ξ== … （7分）… （10分）E ξ=0×110+1×1130+2×25+3×215=4730 …（12分）18(本题满分14分)解：（1）由题设，M ，N 是矩形的边AD 和BC 的中点，所以AM ⊥MN, BC ⊥MN, 折叠垂直关系不变，所以∠AMD 是平面ABNM 与平面MNCD 的平面角，依题意，所以∠AMD=60o ， ………………………………………………………………………………………………………２分 由AM=DM ，可知△MAD 是正三角形，所以AD=2，在矩形ABCD 中，AB=2,AD=所以，，由题可知，由勾股定理可知三角形BOD 是直角三角形，所以BO ⊥DO ……………………………………………………………………………………… 5分解（２）设E ，F 是BD ，CD 的中点，则EF ⊥CD, OF ⊥CD, 所以，CD ⊥面OEF, OE CD⊥ 又BO=OD ，所以OE ⊥BD, OE⊥面ABCD, OE ⊂面BOD , 平面BOD ⊥平面ABCD过A 作AH ⊥BD ，由面面垂直的性质定理,可得AH ⊥平面BOD ，连结OH ，…………………… 8分 所以OH 是AO 在平面BOD 的投影，所以∠AOH 为所求的角,即AO 与平面BOD 所成角。

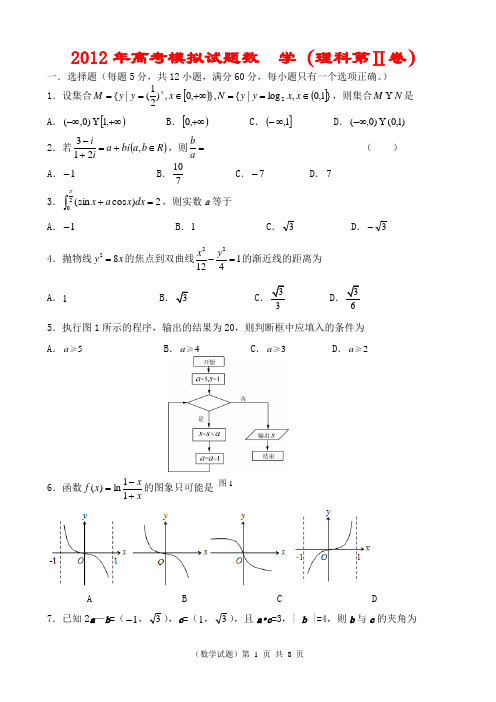
图12012年高考模拟试题数 学（理科第Ⅱ卷）一．选择题（每题5分，共12小题，满分60分，每小题只有一个选项正确。

） 1．设集合[)(]}1,0,log |{},,0,)21(|{2∈==+∞∈==x x y y N x y y M x ，则集合N M 是A ．[)+∞-∞,1)0,(B ．[)+∞,0C ．(]1,∞-D ．)1,0()0,( -∞ 2．若()R b a bi a ii ∈+=+-,213，则=a b（ ）A ．1-B ．710C ．7-D ．73．⎰=+202)cos (sin πdx x a x ，则实数a 等于A ．1-B ．1C ．3D ．3- 4．抛物线28y x =的焦点到双曲线221124xy-=的渐近线的距离为A ．1 BC3D65．执行图1所示的程序，输出的结果为20，则判断框中应填入的条件为 A ．5a ≥ B ．4a ≥ C ．3a ≥ D ．2a ≥6．函数xx x f +-=11ln)(的图象只可能是A B C D7．已知2a —b =（1-，3），c =（1，3），且a •c =3，| b |=4，则b 与c 的夹角为A ．6πB ．3πC ．65π D ．32π8．下列四个命题中真命题的个数是①若[]1,0,∈b a ，则不等式422<+b a 成立的概率是4π；②命题“∈∃x R ，02>-x x ”的否定是“∈∀x R ，02≤-x x ”； ③“若22bm am <，则b a <”的逆命题为真④命题[]1,0:∈∀x p ，1≥x e ，命题∈∃x q :R ，012<++x x ，则q p ∨为真 A ．0 B ．1 C ．2 D ．39．将圆⎩⎨⎧+==θθsin 1cos y x 的中心到直线y =kx 的距离记为d =f (k )给出下列判断①数列{nf (n )}是递增数列②数列})(1{2n f 的前n 项和是6)732(2++n n n③1])(1)1(1[lim 1=-+-∞→n f n f n ④2)1()()1()(211++<++--n fn fn f n f其中正确的结论是A ．①①②③④B ．①②③C ．①③D ．①10．现有4种不同颜色要对如图所示的四个部分进行着色，要求有公共边界的两块不能用同一种颜色，则不同的着色方法共有A ．24种B ．30种C ．36种D ．48种11．设O 为坐标原点，点M 坐标为)2,3(，若点(,)N x y 满足不等式组：⎪⎪⎩⎪⎪⎨⎧≤+≤+≥≥4200x y s y x y x ， 当3≤s ≤5时，则ON OM ⋅的最大值的变化范围是 A ．[7，8] B ．[7，9] C ．[6，8] D ．[7，15]12．若AB 是过椭圆)0(12222>>=+b a by ax 中心的一条弦，M 是椭圆上任意一点，且AM ，BM 与坐标轴不平行，AM k ，BM k 分别表示直线AM ，BM 的斜率，则AM k =BM k A ．22ac -B ．22ab -C ．22bc -D ．22ba -二．填空题（本大题共4小题，每小题5分，共20分）13．若n m x x x f )31()21()(+++=（m , n 为正整数）的展开式中x 的系数为13，则2x 的系数是 。

宁夏石嘴山市回民高级中学xx ～xx 学年第二学期高三第二次模拟考试理科数学参考答案及评分标准一．选择题：题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DBBDCDABAACB二．填空题：13． 214．1.415． 216．①②④三．解答题：17、解:(1)()2sin()2cos 2sin cos 2cos sin 2cos 666f x a b x x x x x πππ=⋅=+-=+-r r …2分3sin cos 2sin()6x x x π=-=-.…………………………………………5分 由22262k x k πππππ-+≤-≤+ 得 22233k x k ππππ-+≤≤+ …………………………………………7分所以2[2,2]33x k k ππππ∈-++（ k Z ∈）时， ()f x 为增函数………………8分(Ⅱ)由(Ⅰ)知6()2sin()65f x x π=-=，即3sin()65x π-=,.……………………………10分∴27cos(2)12sin ()3625x x ππ-=--=-。

………………………………………12分18、解：（Ⅰ）记“恰好选到1个曾经参加过数学研究性学习活动的同学”为事件的A ，则其概率为.74)(271314==C C C A P …………………………………4分 （Ⅱ）随机变量X=2，3，4。

24272(2);7C P X C === ……………………6分 1143274(3);7C C P X C === …………………………8分23271(4);7C P X C === ………………………………10分∴随机变量X 的分布列为X 234P72 74 71 ∴2347777EX =⨯+⨯+⨯=…………………………12分 19、解：如图，以A 为坐标原点建立空间直角坐标系A xyz -，设1BC =，则1(0,0,0),(0,0,2),(2,0,0),(2,1,0),(1,,1),(0,2,0)2A PBC MD .…………………………3分（I ） 因为3(2,0,2)(1,,1)2PB DM ⋅=-⋅-u u u r u u u u r 0=，所以.PB DM ⊥…………………………6分（II ） 因为(2,0,2)(0,2,0)PB AD ⋅=-⋅u u u r u u u r 0=， 所以PB AD ⊥，又因为PB DM ⊥，所以PB ⊥平面.ADMN …………………………8分 设CD 与平面ADMN 所成的角为θ， 则sinθ=|cos ,|||||||PB DCPB DC PB DC ⋅<>=⋅u u u r u u u ru u u r u u u r u u u r u u u r 10=，…………11分所以CD 与平面ADMN 所成的角正弦值为10。

云南省2012届高三第二次高中毕业生复习统一检测数学理试题word版.pdf云南省2012年第二次高中毕业生复习统一检测数学试题（理科）本试卷分第I卷（选择题）和第II卷（非选择题）两部分，考试结束后，将本试卷和答题卡一并交回。

满分150分，考试用时120分钟。

第I卷（选择题，共60分）注意事项：1．答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚，并认真核准条形码上的准考证号、姓名、考场号、座位号及科目，在规定的位置贴好条形码。

2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其它答案标号，答在试卷上的答案无效。

本卷共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

一、选择题1．已知i是虚数单位，则复数等于A．B．C．D．2．已知直线与圆相交于M、N两点，则|MN|等于A．B．C．D．3．已知随机变量X服从正态分布N（0，1），在某项测量中，若X在（-1.96，1.96）内取值的概率等于0.95，则X在内取值的概率等于A．0.025B．0.05C．0.95D．0.9754．已知等于A．B．C．D．5．设由直线围成的封闭图形的面积等于S，则S等于A．B．1C．2D．π6．已知的定义域是集合P，如果，那么的最小值等于A．B．C．D．π7．在棱长为2的正方体ABCD—A1B1C1D1中，点E、F分别是棱AB、BC的中点，则点C1到平面B1EF的距离等于A．B．C．D．8．设R是实数集，平面向量，等于A．4B．C．D．9．已知的渐近线，则m等于A．B．C．D．10．已知平面向量的夹角的正切值等于的值为A．B．2C．—2D．—2，11．已知椭圆E上存在点P，在P与椭圆E的两个焦点F1、F2构成的△F1PF2中，则椭圆E的离心率等于A．B．C．D．12．已知公差不等于0的等差数列的等比中项，那么在数列中，数值最小的项是A．第4项B．第3项C．第2项D．第1项第II卷（非选择题，共90分）本卷包括必考题和选考题两部分，第（13）题~第（21）题为必考题，每个试题考生都必须作答。

2023年高考物理模拟试卷考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、单项选择题：本题共6小题，每小题4分，共24分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、如图所示， 理想变压器的原副线圈的匝数比为10：1， 在原线圈接入u =302sin(100πt) V 的正弦交变电压。

若闭合开关后灯泡L 正常发光，且灯泡L 正常发光时的电阻为1.5Ω，电压表和电流表均为理想交流电表，则下列说法正确的是（ ）A ．副线圈中交变电流的频率为5HzB ．电压表的示数为3VC ．电流表的示数为20AD ．灯泡L 的額定功率为3W2、如图所示为某稳定电场的电场线分布情况，A 、B 、C 、D 为电场中的四个点，B 、C 点为空心导体表面两点，A 、D 为电场中两点。

下列说法中正确的是（ ）A ．D 点的电势高于A 点的电势B ．A 点的电场强度大于B 点的电场强度C ．将电子从D 点移到C 点，电场力做正功D ．将电子从B 点移到C 点，电势能增大3、质量为m 的长木板放在光滑的水平面上，质量为12m 的物块放在长木板上，整个系统处于静止状态.若对物块施加水平拉力（如图甲），使物块能从长木板上滑离，需要的拉力至少为F 1；若对长木板施加水平拉力（如图乙），也使物块能从长木板上滑离，需要的拉力至少为F 2，则12F F 为A．12B．2 C．23D．324、下列说法正确的是（）A．β射线是高速电子流，它的穿透能力比α射线和γ射线都弱B．在核反应中，比结合能小的原子核变成比结合能大的原子核时，会释放核能C．根据玻尔理论可知，氢原子辐射出一个光子后，核外电子的动能减小D．当紫外线照射到金属锌板表面时能发生光电效应，则当改为红光照射时，也能发生光电效应，但从锌板表面逸出的光电子的最大初动能减小5、一质点做匀加速直线运动连续经历了两段相等的时间。

云南省宣威五中2024届高三下学期第二次教学质量监测数学试题注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．双曲线的离心率为，则其渐近线方程为 A ．B ．C ．D ．2．已知非零向量a ，b 满足()2a b a -⊥，()2b a b -⊥，则a 与b 的夹角为（ ） A ．6π B ．4π C ．3π D ．2π 3．已知函数()ln xf x x =，()xg x xe -=.若存在()10,x ∈+∞，2x R ∈使得()()()120f x g x k k ==<成立，则221kx e x ⎛⎫ ⎪⎝⎭的最大值为（ ） A ．2e B ．eC ．24eD ．21e4．在ABC ∆中，D 为BC 中点，且12AE ED =，若BE AB AC λμ=+，则λμ+=（ ） A ．1 B ．23-C ．13-D ．34-5．若复数21iz =+，其中i 为虚数单位，则下列结论正确的是（ ） A ．z 的虚部为i -B ．2z =C ．z 的共轭复数为1i --D ．2z 为纯虚数6．圆柱被一平面截去一部分所得几何体的三视图如图所示，则该几何体的体积为（ ）A ．12πB ．32π C ．2π D ．3π7．已知双曲线2222:1(0,0)x y C a b a b-=>>的左，右焦点分别为1F 、2F ，过1F 的直线l 交双曲线的右支于点P ，以双曲线的实轴为直径的圆与直线l 相切，切点为H ，若113F P F H =，则双曲线C 的离心率为（ ） A ．132B ．5C ．25D ．138．已知定义在R 上的偶函数()f x 满足()()11f x f x +=-，当[]0,1x ∈时，()1f x x =-+，函数()1x g x e --=（13x -≤≤），则函数()f x 与函数()g x 的图象的所有交点的横坐标之和为（ ） A ．2B ．4C ．5D ．69．在ABC 中，点P 为BC 中点，过点P 的直线与AB ，AC 所在直线分别交于点M ，N ，若AM AB λ=，(0,0)AN AC μλμ=>>，则λμ+的最小值为（ ）A ．54B ．2C ．3D ．7210．过抛物线22(0)y px p =>的焦点作直线交抛物线于A B ，两点，若线段AB 中点的横坐标为3，且8AB =，则抛物线的方程是( ) A ．22y x =B ．24y x =C ．28y x =D ．210y x =11．已知数列{}n a 是以1为首项，2为公差的等差数列，{}n b 是以1为首项，2为公比的等比数列，设n n b c a =，12n n T c c c =+++()*n ∈N ，则当2020n T <时，n 的最大值是（ ）A ．8B ．9C ．10D ．1112．某几何体的三视图如图所示，若侧视图和俯视图均是边长为2的等边三角形，则该几何体的体积为A ．83B 43C ．1D ．2二、填空题：本题共4小题，每小题5分，共20分。

2023-2024学年云南省宣威市高二下学期第二次月考数学模拟试题一、单选题1．已知集合{}220A x x x =+-≤，{}31xB x =<，则R A B = ð（）A ．{}0x x <B ．{}2x x ≥-C ．{}20x x -≤<D ．{}01x x ≤≤【正确答案】D【分析】解一元二次不等式、指数不等式求集合A 、B ，应用集合的交补运算，求R A B ð即可.【详解】{}220={|(1)(2)0}={|21}A x x x x x x x x =+-≤-+≤-≤≤，{}31={|0}xB x x x =<<，∴{|0}R B x x =≥ð，故{|01}R A B x x =≤≤ ð.故选：D.2．在复平面内，复数1z ，2z 对应的点分别是(0,2)，(1,1)-，则复数21z z 的虚部为（）A ．12B ．1i2C ．i -D ．1-【正确答案】A【分析】根据复数的几何意义和复数的除法计算法则即可计算.【详解】易得12i z =，21i z =-+，∴211i 11i 2i 22z z -+==+，虚部为12.故选：A ．3．已知R λ∈，向量()3,a λ= ，()1,2b λ=- ，则“3λ=”是“//a b”的（）A ．必要不充分条件B ．充分不必要条件C ．充分必要条件D ．既不充分也不必要条件【正确答案】B【分析】首先利用向量平行的坐标表示求λ，再根据充分，必要条件的定义判断.【详解】若向量//a b，则()3210λλ⨯--=，即260λλ--=解得：2λ=-或3λ=,所以“3λ=”是“//a b”的充分不必要条件.故选：B 4．已知2tan 3α=，则1sin 2cos 2αα+=（）A ．5B ．5-C ．15D ．15-【正确答案】A【分析】利用三角恒等变换，将问题由弦化切计算即可.【详解】22221sin2sin cos 2sin cos cos2cos sin αααααααα+++=-，分子分母同时除以2cos α可得：22222222sin cos 2sin cos tan 2tan 1cos cos sin 1tan cos ααααααααααα++++=--=5，故选：A.5．已知等差数列{}n a 满足1471010a a a a +++=，3691230a a a a +++=，则811a a +=（）A ．25B ．35C ．40D ．50【正确答案】A【分析】根据等差数列的通项公式以及性质求得答案即可.【详解】设等差数列的公差为d .由1471010a a a a +++=，得1105a a +=，即1295a d +=①；由3691230a a a a +++=，得31215a a +=，121315a d +=②；由①②得1355,42a d -==，则811121725a a a d ++==.故选：A.6．在ABC 中，D 为线段BC 上一点，且2AE ED =，若ED xAB y AC =+ ，则19x y+的最小值为（）A ．163B ．16C ．48D ．60【正确答案】C【分析】先由2,AE ED =得出13ED AD =再得出331x y +=,最后常值代换应用基本不等式可解.【详解】12,3AE ED ED AD =∴=,13AD x AB y AC =+,33AD xAB y AC =+ ，又B ，D ，C 三点共线，331,0,0,x y x y ∴+=>>()1919327333273048y x x y x y x y x y ⎛⎫∴+=++=+++≥= ⎪⎝⎭,1948x y ∴+≥,当且仅当327,y x x y =即当11,412y x ==时取最小值.故选:C.7．将6名实习医生分配到4所医院进行培训，每名实习医生只能分配到1所医院，每所医院至少分配1名实习医生，则不同的分配方案共有（）A ．480种B ．1080种C ．2520种D ．1560种【正确答案】D【分析】根据部分均匀分组问题结合先分组后分配原则解决即可.【详解】由题知，6名实习医生分4组，有两种分法：第一种：1，1，1，3，有36C 20=种分法，第二种：1，1，2，2；有226422C C45A =种分法，所以共有204565+=种分法，再分配到4个医院，可得4465A 1560⨯=种.故选：D.8．设双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为1F ，2F ，过1F 的直线l 分别与双曲线左、右两支交于M ，N 两点，且22F M F N ⊥，22F M F N =，则双曲线C 的离心率为（）AB ．3CD1【正确答案】A【分析】根据双曲线的定义以及给定的条件，分析几何关系即可.【详解】由题意作下图：设双曲线C 的半焦距为c ，M ，N 的中点为G ，则2MNF 是等腰直角三角形，21GF GF ⊥，设2MF m =，根据双曲线的定义有：211222MF MF a NF NF a ⎧-=⎪⎨-=⎪⎩ ①②，并且2222,2,NF MF m MN m GF ====，由①得：12MF m a =-，1122NF MF MN m a m =+=-+，由②得：2222,4m a m m a a m --=∴=，在12R t GF F 中，2221212F F GF GF =+，()2222222c m m a ⎫⎛⎫∴=++-⎪ ⎪⎪ ⎪⎝⎭⎝⎭，解得64c =，∴双曲线C 的离心率3==ce a；故选：A.二、多选题9．关于函数()23sin cos 3sin 1,R f x x x x x =-+∈,下列说法正确的有（）A ．()f x 132-，最小值为132B ．()f x 的单调递增区间为5πππ,π,Z1212k k k ⎡⎤-+∈⎢⎥⎣⎦C ．()f x 的最小正周期为2πD ．()f x 的对称中心为ππ1,,Z622k k ⎛⎫-+-∈ ⎝⎭【正确答案】ABD【分析】根据三角函数恒等变换化简()f x ，结合正弦函数的性质可求得()f x D..D..A ；同理结合正弦函数的单调性、周期以及对称中心可判断B ，C ，D..【详解】由题意得()()231cos233sin cos 3sin 1sin2122x f x x x x x -=-+=-+31π1sin2cos2222232x x x ⎛⎫=+-+- ⎪⎝⎭，则()f x 12-，最小值为12，A 正确；令πππ2π22π,Z 232k x k k -+≤+≤+∈，即5ππππ,Z 1212k x k k -≤≤+∈，故()f x 单调递增区间为5πππ,π,Z 1212k k k ⎡⎤-+∈⎢⎥⎣⎦，B 正确；()f x 的最小正周期为2ππ2=，C 错误；令πππ2π,Z,,Z 326k x k k x k +=∈∴=-∈，故()f x 的对称中心为ππ1,,Z 622k k ⎛⎫-+-∈ ⎪⎝⎭，D 正确，故选：ABD.10．在71x ⎛⎫- ⎪⎝⎭的展开式中，下列叙述中正确的是（）A ．二项式系数之和为128B ．各项系数之和为1C ．常数项为15D ．4x -的系数为-48【正确答案】AB【分析】根据展开式的二项式系数的性质，可判定A 正确，令1x =，求得展开式的各项系数和，可判定B 正确，求得展开式的通项，结合通项，可判定C 、D 错误.【详解】在71x ⎛⎫ ⎝⎭的展开式中，二项式系数的和为72128=，所以A 正确；令1x =，可得展开式的各项系数的和为()7211-=，所以B 正确；又由二项式71x ⎛⎫ ⎝⎭展开式的通项为737721771C ()(1)2C rr r r r r rr T x x ---+=-=-⋅，因为N r ∈，所以7302r-≠，所以展开式没有常数项，所以C 错误；令7342r-=-，可得=5r ，所以站开始的4x -的系数为5257(1)2C 84-⋅=-，所以D 错误.故选：AB.11．如图，在正方体1111ABCD A B C D -中，E ，F 分别是11A D ，11C D 的中点，G 为线段BC 上的动点(不含端点)，则下列结论中正确的是（）A ．//AC 平面EFGB ．存在点G 使得EF FG⊥C ．存在点G 使得异面直线AB 与EG 所成的角为60°D ．三棱锥1G EFD -的体积为定值【正确答案】ABD【分析】对于A ，转证线线平行即可；对于B ，转证线面垂直即可；对于C ，把异面直线所成角转为相交直线所成角问题，借助边间关系即可判断；对于D ，利用面面平行可知点到平面距离为定值.【详解】如图，易证//EF AC ，AC ⊄平面EFG ，则有//AC 平面EFG ，故A 正确；设CD 中点为M ，若G 为BC 中点，则有AC MG ⊥，AC MF ⊥，MG MF M ⋂=，则AC ⊥平面MFG ，则AC FG ⊥，因为//EF AC ，所以EF FG ⊥，故B 正确；设正方体棱长为2，取11B C 中点为N ，连接EN ，因为//EN AB ，所以异面直线AB 与EG 所成的角即为NEG α∠=，在直角三角形NEG 中，5tan 32NG NB EN EN α=<=<，即60α<︒，故C 错误；易知点G 到平面1EFD 的距离为定值，则三棱锥1G EFD -的体积为定值，故D 正确.故选：ABD12．已知函数()f x 满足()()221ln x f x xf x x '+=+，()1e ef =.则当0x >时，下列说法中正确的是（）A ．1ee f ⎛⎫= ⎪⎝⎭B ．()f x 只有一个零点C ．()f x 有两个零点D ．()f x 有一个极大值【正确答案】BD【分析】令()()2g x x f x =，则()()()221ln g x xf x x f x x ''=+=+，于是()ln g x x x C =+，()2ln x x Cf x x +=，根据()1e e f =，解出C 的值.然后利用导数研究函数的单调性，即可推得结论.【详解】令()()2g x x f x =，则()()()221ln g x xf x x f x x ''=+=+，所以，()ln g x x x C =+()R C ∈，所以，()2ln x x Cf x x +=.又()1e e f =，则()2e 1e e eC f +==，解得0C =.所以，()2ln ln x x xf x x x==.则，()21ln x f x x -'=，且1ln1e e 1e ef ⎛⎫==- ⎪⎝⎭，A 项错误.当0e x <<时，()0f x ¢>，则()ln xf x x=在()0,e 上单调递增；当e x >时，()0f x '<，则()ln xf x x=在()e,+∞上单调递减.所以，()ln x f x x =在e x =处有极大值为()1e 0ef =>，且()f x 只有一个极值点，D 正确.且1x >时，有()0f x >恒成立.又()10f =，所以()f x 只有一个零点，B 项正确，C 项错误.故选：BD.三、填空题13．已知直线210ax y +-=与直线2350x y -+=垂直，则=a _________．【正确答案】3【分析】根据两直线垂直的等价条件即可得到结果.【详解】∵直线210ax y +-=与直线2350x y -+=垂直，∴260a -=∴3a =.故3.14．已知a ，b 均为单位向量，且22a b -= ，则a 与b a -的夹角为__________．【正确答案】64π-/64π-+【分析】利用向量数量积的运算律及向量的模公式，结合向量的夹角公式即可求解.【详解】||||1,|2|2,a b a b ==-=22|2|||4||41444a b a b a b a b ∴-=+-⋅=+-⋅=，14a b ⋅= .213()||144a b a a b a ∴⋅-=⋅-=-=- ,22216||()2222b a b a b a a b ∴-=-=+-⋅=-=,3()64cos ,4||||62a b a a b a a b a ⋅-∴<->=-=--,0,π,a b a ≤<->≤a ∴ 与b a -的夹角为π-故答案为.π-15．一个数学兴趣小组共有2名男生3名女生，从中随机选出2名参加交流会，在已知选出的2名中有1名是男生的条件下，另1名是女生的概率为______．【正确答案】67【分析】首先求出男女生各1名的概率，再应用对立事件概率求法求至少有1名男生的概率，最后应用条件概率公式求概率.【详解】若A 表示“2名中至少有1名男生”，B 表示“2名中有1名女生”，所以2名中有1名是男生的条件下，另1名是女生的概率为()(|)()P AB P B A P A =，而112325C C 3()C 5P AB ==，2325C 7()1C 10P A =-=，故6(|)7P B A =.故6716．过点()0,16P 作曲线33y x x =-的切线，则切点的横坐标为_______.【正确答案】2-【分析】设出切点，利用导数求得切线斜率，写出切线方程，根据其过点P ，代值求得参数m 的值，则问题得解.【详解】设切点为3(,3)m m m -，3()3f x x x =-的导数为2()33f x x '=-，可得切线斜率233k m =-，由点斜式方程可得切线方程为323(33)()y m m m x m -+=--，代入点(0,16)P 可得32163(33)(0)m m m m -+=--，解得2m =-，故答案为.2-四、解答题17．在ABC 中，角,,A B C 对应的边分别是,,a b c，且sin cos a B A =．(1)求角A 的大小；(2)若4b =，ABC的面积S =ABC 的周长．【正确答案】(1)2π3(2)6+【分析】（1）利用正弦定理化边为角即可求解；（2）根据三角形的面积公式和余弦定理即可求解.【详解】（1）在ABC 中，由正弦定理2sin sin sin a b cR A B C===得:2sin ,2sin a R A b R B ==代入式子sin cos a B A =，化简得，sin sin sin cos A B B A =，sin 0B ≠ ，sin A A ∴=，即tan A =因为(0,π)A ∈，所以2π3A =.（2）112sin 4sin223S bc A c π==⨯== 2c ∴=由余弦定理得2222212cos 42242(282a b c bc A =+-=+-⨯⨯⨯-=，a ∴=426abc ∴++=+=+ABC ∴ 的周长为6+18．已知数列{}n a 满足.()117,3122n n a a a n -==-≥(1)求证：数列12n a ⎧⎫-⎨⎬⎩⎭是等比数列；(2)求数列{}n a 的通项公式及其前n 项和n S 的表达式.【正确答案】(1)证明见解析；(2)11333,22n nn n na S +-+=+=；【分析】（1）由等比数列的定义证明即可；（2）由（1）得出数列{}n a 的通项公式，再由等差和等比的求和公式计算n S .【详解】（1）由题意可知131,1n n a a n +=-≥，1111313()2223111222n n n n n n a a a a a a +----===---所以数列12n a ⎧⎫-⎨⎬⎩⎭是以3为首项，公比为3的等比数列.（2）由（1）可知，132n n a -=，即132n n a =+前n 项和13(13)331322n n n n nS +--+=+=-.19．为庆祝党的二十大的胜利召开，培养担当民族复兴的时代新人，某高校在全校开展“不负韶华，做好社会主义接班人”的宣传活动，为进一步了解学生对党的“二十大”精神的学习情况，学校开展了“二十大”相关知识的竞赛活动，现从参加该活动的学生中随机抽取100人，将他们的竞赛成绩（满分为100分）分为5组：[)[)[)[)[]50,60,60,70,70,80,80,90,90,100，得到如图所示的频率分布直方图：(1)估计这100名学生的竞赛成绩的中位数（结果保留整数）；(2)若采用分层抽样的方法从竞赛成绩在[80,90)和[90,100]内的学生中抽取6人，再从这6人中随机抽取2人，这2人中在[90,100]的人数设为随机变量X ，请求出随机变量X 的分布列与数学期望.【正确答案】(1)72(2)分布列见解析，()23E X =【分析】（1）根据中位数的求法求得中位数.（2）根据分层抽样求得[80,90)和[90,100]抽取的人数，然后按照超几何分布的知识求得分布列并求得数学期望.【详解】（1）因为()0.0100.030100.40.5,0.40.045100.850.5+⨯=<+⨯=>，所以竞赛成绩的中位数在[)70,80内.设竞赛成绩的中位数为m ，则()700.0450.40.5m -⨯+=，解得72m ≈.所以估计这100名学生的竞赛成绩的中位数为72.（2）[80,90)和[90,100]的频率分别为0.1,0.05，所以在[80,90)的学生中抽取4人，在[90,100]的学生中抽取2人，X 的可能取值为0,1,2，()022426C C 620C 155P X ====，()112426C C 81C 15P X ===，()202426C C 12C 15P X ===,所以随机变量X 的分布列为:X012P25815115数学期望()8121215153E X =⨯+⨯=.20．如图，在四棱锥P ABCD -中，底面ABCD 是矩形，PD ⊥平面ABCD ，2PD DA ==，1DC =，M 是BC 的中点，点Q 在PM 上，且2PQ QM =.(1)证明：DQ ⊥平面PAM ；(2)求平面PAM 与平面PDC 的夹角的余弦值.【正确答案】(1)证明见解析【分析】(1)利用坐标法或几何法利用线面垂直的判定定理证明；(2)利用空间向量计算面面角.【详解】（1）证明：由题PD ⊥平面ABCD ，底面ABCD 为矩形，以D 为原点，直线DA ，DC ，DP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系D xyz -如图：则()2,0,0A ，()0,0,0D ，()0,1,0C ，()1,1,0M ，()002P ,,，222,,333Q ⎛⎫⎪⎝⎭，222,,333DQ ⎛⎫= ⎪⎝⎭ ，()1,1,0AM =-，()2,0,2AP =- ，∵0DQ AM ⋅=∴DQ AM ⊥，∵0DQ AP ⋅=，∴⊥DQ AP ，∵AM AP A = ,且,AM AP ⊆平面PAM ，∴DQ ⊥平面PAM .（法二）证明：由题PD ⊥平面ABCD ，底面ABCD 为矩形，以D 为原点，直线DA ，DC ，DP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系D xyz -如图：则()2,0,0A ，()0,0,0D ，()0,1,0C ，()1,1,0M ，()002P ,,，222,,333Q ⎛⎫⎪⎝⎭，设(),,n x y z = 是平面PAM 的一个法向量.()1,1,0AM =-，()2,0,2AP =- ..0.220n AM x y n AP x z ⎧=-+=⎪⎨=-+=⎪⎩ 取1x =，有111x y z =⎧⎪=⎨⎪=⎩∴()1,1,1n =，222,,333DQ ⎛⎫= ⎪⎝⎭，则23DQ n = ，DQ n ∥ .∴DQ ⊥平面PAM .（法三）证明：连接DM∵PD ⊥平面ABCD ，AM ⊂平面ABCD ,∴PD AM ⊥.在AMD中，AM DM ==2AD =.∵222AM DM AD +=，∴AM DM ⊥，且PD DM D ⋂=，∴AM ⊥平面PDM ，又∵DQ ⊂平面PDM ，∴AM DQ ⊥.∵cos 3DMPDM PM∠==，又∵cos 3QM DMQ DM ∠===，∴PDM DQM △△∽，∴DQ PM ⊥.且AM PM M = ，且,AM PM ⊆平面PAM ，∴DQ ⊥平面PAM .（2）（接向量法）由（1）可知平面PAM 的法向量为222,,333DQ ⎛⎫= ⎪⎝⎭（也可为()1,1,1n =）.平面PCD 的一个法向量为()1,0,0m =.23cos ,m DQ m DQ m DQ⋅=⋅∴平面PAM 与平面PDC的夹角的余弦值为3.（法二）延长AM ，DC ，交于点N ，连接PN.∵N AM ∈，∴N ∈平面PAM ，∵N CD ∈，∴N ∈平面PCD .∴平面PAM ⋂平面PCD PN =.过D 做DT PN ⊥于T ，连接AT .∵PD ⊥平面ABCD ，∴PD AD ⊥.又AD CD ⊥，CD PD D = ，∴AD ⊥平面PCD ，又PN ⊂平面PCD ，∴⊥AD PN .又∵DT PN ⊥，DT AD D ⋂=，,DT AD ⊂平面ADT ,∴PN ^平面ADT ，∴PN AT ⊥，∴ATD ∠为二面角A PN D --的平面角.在Rt ATD △中，AT =∴cos DT ATD AT ∠=∴平面PAM 与平面PDC21．在直角坐标系xOy 上，椭圆2222:1(0)x yC a b a b+=>>的右焦点为)F，C 的上、下顶点与F(1)求C 的方程；(2)已知过点F 的直线l 与C 相交于A ，B 两点，问C 上是否存在点Q ，使得OA OB OQ +=？若存出，求出l 的方程．若不存在，请说明理由【正确答案】(1)2214x y +=(2)(44y x y x ==-或.【分析】（1）利用待定系数法求出椭圆的方程；（2）分类讨论：①当l 的斜率不存在时和②当l 的斜率存在时，设l 的方程为(y k x =，()()()112233,,,,A x y B x y Q x y ，，利用“设而不求法”求解.【详解】（1）依题意得Δ122S b =⨯=1b =，另由2224a b c =+=，c =24a =，所以椭圆的标准方程为程为2214x y +=.（2）①当l的斜率不存在时，则11,22A B ⎫⎫-⎪⎪⎭⎭，()OA OB += ，因为OA OB OQ +=，所以点()Q ，而点()Q 不在椭圆上，故不存在点Q 符合题意.②当l 的斜率存在时，设l的方程为(y k x =，()()()112233,,,,A x y B x y Q x y ，，联立(2214x y y k x ⎧+=⎪⎨⎪=⎩得()2222141240k x x k +-+-=，则21228314x x k+=+，而(1212214y y k x x k -+=+-=+，因为OA OB OQ +=，则121233(,)(,)x x y y x y ++=，所以Q ⎝⎭，而Q在曲线上，所以2214⎝⎭+=⎝⎭，即218k =，所以4k =，符合题意.综上所述，存在点Q 满足题意，此时直线l的方程为(44y x y x ==-或22．已知函数()32f x x ax bx c =+++在3x =-和1x =处取得极值.（1）求a b 、的值及()f x 的单调区间；（2）若对[]1,2x ∈-，不等式()2f x c <恒成立，求c 的取值范围.【正确答案】（1）3a =，9b =-，函数()f x 的递增区间是(,3)-∞-和(1,)+∞，递减区间是(3-，1)；（2）cc >【分析】（1）先求导，再解方程组(3)2760(1)320f a b f a b '-=-+=⎧⎨'=++=⎩即得a b 、的值，再求函数的单调区间；（2）求出()f x 的最大值，再解不等式211c c >+即得解.【详解】解；（1）32()f x x ax bx c =+++，2()32f x x ax b '=++由(3)2760(1)320f a b f a b '-=-+=⎧⎨'=++=⎩解得，3a =，9b =-，2()3693()++3(1)f x x x x x '=-=-，函数()f x 的单调区间如下表：x(,3)-∞-3-(3-，1)1(1,)+∞()f x '+0-0+()f x极大值极小值所以函数()f x 的递增区间是(,3)-∞-和(1,)+∞，递减区间是(3-，1)．（2）32()39f x x x x c =+-+，[1x ∈-，2]，当=1x -时，(1)11f c -=+，f （2）2c =+，(1)5f c =-所以f (-1)11c =+为最大值．要使2()f x c <对[1x ∈-，2]恒成立，须且只需211c c >+．解得c <c。

xy O32π- 2 34π－4云南省部分名校高2012届第二次统一考试（玉溪一中、楚雄一中、昆明三中）理 科 数 学一、单项选择题（每小题5分，共60分）1．设全集{}1,2,3,4,5U =，集合{1,2,4}A =，{4,5}B =，则图中的阴影部分表示的集合为A ．{}5B ．{}4C ．{}1,2D ．{}3,52．已知非零向量a 、b 满足b a =，那么向量b a +与向量b a -的夹角为A ．6π B ．3π C ．2π D ．23π3．61()2x x -的展开式中第三项的系数是 A ．154- B ．154 C ．15 D ．52-4．圆22420x y x +-+=与直线l 相切于点(3,1)A ，则直线l 的方程为A ．250x y --=B ．210x y --=C ．20x y --=D ．40x y +-=5．某单位员工按年龄分为A ，B ，C 三组，其人数之比为5：4：1，现用分层抽样的方法从总体中抽取一个容量为20的样本，已知C 组中甲、乙二人均被抽到的概率是,451则该单位员工总数为 A ．110 B ．100 C ．90 D ．806、右边程序框图的程序执行后输出的结果是（ ）. A ，24， B ，25， C ，34， D ，357.已知函数sin()y A x B ωφ=++ (0,0,||2A ωφπ>><) 的周期为T ，在一个周期内的图象如图所示， 则正确的结论是（ ）.A.3,2A T ==πB.2,1=-=ωB开始1n =0S =10?n >输出S2n n =+S S n=+结束是 否C.4,6T φπ=π=-D.3,6A φπ== 8.将函数sin()3y x =-π的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得图像向左平移3π个单位，则所得函数图像对应的解析式为A.1sin()26y x =-πB.1sin()23y x =-πC.1sin 2y x = D.sin(2)6y x =-π9．长方体ABCD —A 1B 1C 1D 1中，12,AB AD AA ===1D 到直线AC 的距离是 A ．3 B．．410. 设双曲线12222=-by a x （a ＞0,b ＞0)的一条渐近线与抛物线12+=x y 有且只有一个公共点，则双曲线的离心率为. A.45 B. 5 C. 25 D.5 11，设a ，b 是不同的直线，α、β是不同的平面，则下列命题： ①若,,//;ab a b αα⊥⊥则②若//,,;aa ααββ⊥⊥则③若βαβ⊥⊥,a ，则a ∥α④若,,,.a b a b αβαβ⊥⊥⊥⊥则其中正确命题的个数是A ．0B ．1C ．2D ．312.设函数[],0(),(1),0x x x f x f x x -≥⎧=⎨+<⎩其中][x 表示不超过x 的最大整数，如]2.1[-=-2，]2.1[=1，]1[=1，若直线y=)0(>+k k kx 与函数y=)(x f 的图象恰有三个不同的交点，则k 的取值范围是A ．]31,41(B ．]41,0(C ．]31,41[D ．)31,41[二、填空题（每小题5分，共20分）13、已知满足约束条件⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x ，则2z x y =+的最小值是14．与椭圆1422=+y x 有相同的焦点且过点P )1,2(的双曲线方程是15．一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积是π332，那么这个三棱柱的体积是 .16．对于复数=z i -1，有下面4个命题：①它在复平面上对应的点在第二象限；②它的平方是一个纯虚数；③它的模是2；④0)(22=+z z 。

高考数学期末测试卷必考（重点基础题）含解析注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．向量1,tan 3a α⎛⎫= ⎪⎝⎭，()cos ,1b α=，且//a b ，则cos 2πα⎛⎫+=⎪⎝⎭（ ）A ．13B ．C ．D ．13-2．正三棱柱111ABC A B C -中，1AA =，D 是BC 的中点，则异面直线AD 与1A C 所成的角为（ ） A ．6π B ．4π C ．3π D ．2π 3．已知函数()f x 满足当0x ≤时，2(2)()f x f x -=，且当(2,0]x ∈-时，()|1|1f x x =+-；当0x >时，()log (0a f x x a =>且1a ≠).若函数()f x 的图象上关于原点对称的点恰好有3对，则a 的取值范围是（ ）A ．(625,)+∞B ．(4,64)C ．(9,625)D ．(9,64)4．已知三棱锥P ABC -的四个顶点都在球O 的球面上,PA ⊥平面ABC ,ABC ∆是边长为,若球O 的表面积为20π,则直线PC 与平面PAB 所成角的正切值为( )A ．34B C D 5．已知函数()f x 在R 上都存在导函数()f x '，对于任意的实数都有2()e ()x f x f x -=，当0x <时，()()0f x f x '+>，若e (21)(1)af a f a +≥+，则实数a 的取值范围是( )A ．20,3⎡⎤⎢⎥⎣⎦B ．2,03⎡⎤-⎢⎥⎣⎦C ．[0,)+∞D ．(,0]-∞6．已知集合{}1,3,5,7A =，{}2,3,4,5B =，则A B =A ．{}3B ．{}5C ．{}3,5D ．{}1,2,3,4,5,77．已知正项等比数列{}n a 的前n 项和为2317,,927n S S S ==，则12n a a a 的最小值为（ ） A ．24()27B ．34()27C ．44()27D ．54()278．不等式42,3x y x y -⎧⎨+⎩的解集记为D ，有下面四个命题：1:(,),25p x y D y x ∀∈-；2:(,),22p x y D y x ∃∈-；3:(,),22p x y D y x ∀∈-；4:(,),24p x y D y x ∃∈-.其中的真命题是（ ）A ．12,p pB ．23,p pC ．13,p pD ．24,p p9．已知等比数列{}n a 满足21a =，616a =，等差数列{}n b 中54b a =，n S 为数列{}n b 的前n 项和，则9S =（ ） A ．36B ．72C ．36-D ．36±10．中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”，主要指德育；“乐”，主要指美育；“射”和“御”，就是体育和劳动；“书”，指各种历史文化知识；“数”，指数学.某校国学社团开展“六艺”课程讲座活动，每艺安排一节，连排六节，一天课程讲座排课有如下要求：“数”必须排在第三节，且“射”和“御”两门课程相邻排课，则“六艺”课程讲座不同的排课顺序共有（ ） A ．12种B ．24种C ．36种D ．48种11．复数2(1)i i +的模为（ ）． A ．12B ．1C ．2D ．2212．设过抛物线()220y px p =>上任意一点P (异于原点O )的直线与抛物线()280y px p =>交于,A B 两点，直线OP 与抛物线()280y px p =>的另一个交点为Q ，则ABQ ABOS S=（ ）A ．1B ．2C ．3D ．4二、填空题：本题共4小题，每小题5分，共20分。

云南省宣威市二中2012届高三2月模拟考理科数学试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第22－24题为选考题，其它题为必考题．考生作答时，将答案答在答题卡上．在本试卷上答题无效．考试结束后，将本试卷和答题卡一并交回． 注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上．2．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚．3．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效． 4．保持卡面清洁，不折叠，不破损．5．做选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的题号涂黑．参考公式：如果事件A 、B 互斥，那么球的表面积公式 P(A+B)=P(A)+P(B) 24R S π=如果事件A 、B 相互独立，那么其中R 表示球的半径 P(A·B)=P(A)·P(B)球的体积公式如果事件A 在一次试验中发生的概率是343V R π=P ，那么n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径()(1)(0,1,2,,)k kn k n n P k C P P k n -=-=第Ⅰ卷一、选择题：本大题共12小题，每小题5分，满分60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知复数1z =2+i ，2z =3-i ，其中i 是虚数单位，则复数21z z 的实部与虚部之和为（ ）A ．0B ．21 C ．1D ．22．已知集合M={x|x 2-2008x-2009>0},N={x|x 2+ax+b ≤0},若M ∪N=R ，M ∩N=(2009,2010]，则（ ）A ．a=2009,b=-2010B ．a=-2009,b=2010C ．a=2009,b=2010D ．a=-2009,b=-2010 3．已知条件p ：011>+x 和条件q:)11lg(2x x -++有意义，则⌝p 是⌝q 的( ) A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．等差数列{a n }的前n 项和为S n (n=1,2,3…)，若当首项a 1和公差d 变化时，a 5+a 8+a 11是一个定值，则下列选项中为定值的是( )A ．S 17B ．S 18C ．S 15D ．S 16 5．某连队身高符合建国60周年国庆阅兵标准的士兵共有 45人，其中18岁～21岁的士兵有15人，22岁～25岁的士 兵有20人，26岁～29岁的士兵有10人，若该连队有9个 参加国庆阅兵的名额，如果按年龄分层选派士兵，那么，该 连队年龄在26岁～29岁的士兵参加国庆阅兵的人数为A ．5B ．4C ．3D ．26．执行如图所示的程序框图，若输出的b 的值为16， 则图中判断框内①处应填( )A ．3B ．4C ．5D ．2 7．在区间[-1,1]上随机取一个数x ，则4sinx π的值介于21-与22之间的概率为( ) A ．41 B ．31 C ．32 D ．658．已知函数f(x)=2sin(ωx+ϕ)(其中ω>0，|ϕ|<2π)的相邻两条对称轴之间的距离为2π，f(0)=3,则( )A ．6,21πϕω==B ．3,21πϕω==C ．6,2πϕω==D ．3,2πϕω== 9．已知函数f(x)=x 2+bx 的图象在点A(1，f(1))处的切线l 与直线3x-y+2=0平行，若数列})(1{n f 的前n 项和为S n ,则S 2009的值为( ) A ．20082007 B ．20102009 C ．20092008 D ．2011201010．△ABC 满足32=⋅AC AB ，∠BAC=30°，设M 是△ABC 内的一点(不在边界上)，定义f(M)=(x,y,z)，其中x,y,z 分别表示△MBC ，△MCA,△MAB 的面积，若f(M)=(x,y,21)，则yx 41+的最小值为( )A ．9B ．8C ．18D ．1611．若函数y=f(x)(x ∈R)满足f(x+2)=f(x)且x ∈(-1,1]时f(x)=1-x 2,函数g(x)=⎩⎨⎧=≠)0( 1)0( ||lg x x x ，则函数h(x)=f(x)-g(x)在区间[-5,10]内零点的个数为( )A ．12B ．14C ．13D ．812．若f(a)=(3m-1)a+b-2m ，当m ∈[0,1]时，f(a)≤1恒成立，则a+b 的最大值为( )A ．31 B ．32 C ．35 D ．37第Ⅱ卷本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第24题为选考题，考生根据要求做答． 二、填空题：本大题共4小题，每小题5分，共20分.13．已知向量a =(sin α,2)与向量b =(cos α,1)互相平行，则tan2α的值为_______。