MATLAB数值计算-第4章-方程求根
- 格式:docx
- 大小:46.41 KB
- 文档页数:5


实验四 MATLAB数值计算与符号计算一、实验目的1.掌握数据插值和曲线拟合的方法2.掌握求数值导数和数值积分的方法3.掌握代数方程数值求解的方法4.掌握常微分方程数值求解的方法5.掌握求解优化问题的方法6.掌握求符号极限、导数和积分的方法7.掌握代数方程符号求解的方法8.掌握常微分方程符号求解的方法二、实验原理1.数据插值a) 一维数据插值 Y1=interp1(X,Y,X1,’method’)b) 二维数据插值 Z1=interp2(X,Y,Z,X1,Y1,’method’)2.曲线拟合[P,S]=polyfit(X,Y,m)3.符号对象的建立(1)符号量名=sym(符号字符串):建立单个的符号变量或常量;(2)syms arg1 arg2,…,argn:建立n个符号变量或常量。
4.基本符号运算(1)基本四则运算:+,-,*,\,^(2)分子与分母的提取:[n,d]=numden(s)(3)因式分解与展开:factor(s),expand(s)(4)化简:simplify, simple(s)5.符号函数及其应用(1)求极限:limit(f,x,a)(2)求导数:diff(f,x,a);(3)求积分:int(f,v)三、实验内容1.按下表用3次样条方法插值计算0~900范围内整数点的正弦值和0~750范围内整数点的正切值,然后用5次多项式拟合方法计算相同的函数值,并将两种计算结果进行比较。
x2=0:75;y1=sin(pi.*x1./180);y2=tan(pi.*x2./180);;a=interp1(x1,y1,45,'cublic')b=interp1(x1,y1,45,'cublic')p1=polyfit(x1,y1,5)p2=polyfit(x2,y2,5)c1=polyval(p1,x1);c2=polyval(p2,x2);subplot(2,1,1);plot(x1,c1,':o',x1,y1,'r');subplot(2,1,2);plot(x2,c2,':o',x2,y2,'r');10203040506070802.(1)求函数33()sin cos f x x x =+在点,,,6432x ππππ=的数值导数。

第七讲 MATLAB 中求方程的近似根(解)教学目的:学习matlab 中求根命令,了解代数方程求根求解的四种方法,即图解法、准解析法、数值方法以及迭代方法,掌握对分法、迭代法、牛顿切法线求方程近似根的基本过程;掌握求代数方程(组)的解的求解命令.教学重点:求方程近似解的几种迭代方法,代数方程(组)的解的求解命令的使用方法.利用所学的编程知识,结合具体的实例,编制程序进行近似求根.掌握相关的代数方程(组)的求解命令及使用技巧.教学难点:方程的近似求解和非线性方程(组)的求解.一、问题背景和实验目的求代数方程0)(=x f 的根是最常见的数学问题之一(这里称为代数方程,主要是想和后面的微分方程区别开.为简明起见,在本实验的以下叙述中,把代数方程简称为方程),当)(x f 是一次多项式时,称0)(=x f 为线性方程,否则称之为非线性方程.当0)(=x f 是非线性方程时,由于)(x f 的多样性,尚无一般的解析解法可使用,但如果对任意的精度要求,能求出方程的近似根,则可以认为求根的计算问题已经解决,至少能满足实际要求.同时对于多未知量非线性方程(组)而言,简单的迭代法也是可以做出来的,但在这里我们介绍相关的命令来求解,不用迭代方法求解.通过本实验,达到下面目的:1. 了解对分法、迭代法、牛顿切线法求方程近似根的基本过程;2. 求代数方程(组)的解.首先,我们先介绍几种近似求根有关的方法: 1. 对分法对分法思想:将区域不断对分,判断根在某个分段内,再对该段对分,依此类推,直到满足精度为止.对分法适用于求有根区间内的单实根或奇重实根.设)(x f 在],[b a 上连续,0)()(<⋅b f a f ,即 ()0f a >,()0f b <或()0f a <,()0f b >.则根据连续函数的介值定理,在),(b a 内至少存在一点 ξ,使()0f ξ=.下面的方法可以求出该根:(1) 令0()/2x a b =+,计算0()f x ;(2) 若0()0f x =,则0x 是()0f x =的根,停止计算,输出结果0x x =.若 0()()0f a f x ⋅<,则令1a a =,10b x =,若0()()0f a f x ⋅>,则令10a x =,1b b =;111()/2x a b =+.……,有k a 、k b 以及相应的()/2k k k x a b =+.(3) 若()k f x ε≤ (ε为预先给定的精度要求),退出计算,输出结果()/2k k k x a b =+; 反之,返回(1),重复(1),(2),(3).以上方法可得到每次缩小一半的区间序列{[,]}k k a b ,在(,)k k a b 中含有方程的根. 当区间长k k b a -很小时,取其中点()/2k k k x a b =+为根的近似值,显然有2111()/2()/(2)()/2k k k k k k x b a b a b a ξ+---≤-=-==-以上公式可用于估计对分次数k .分析以上过程不难知道,对分法的收敛速度与公比为12的等比级数相同.由于1021024=,可知大约对分10次,近似根的精度可提高三位小数.对分法的收敛速度较慢,它常用来试探实根的分布区间,或求根的近似值. 2. 迭代法a) 松弛法:由方程()0f x =构造一个等价方程()x x φ=.则迭代方程是:1(1)()k k k k k x x x ωωφ+=-+,1/(1'())k k x ωφ=-,其中'()1x φ≠.松弛法的加速效果是明显的 (见附录4),甚至不收敛的迭代函数经加速后也能获得收敛.b) Altken 方法:松弛法要先计算'()k x φ,在使用中有时不方便,为此发展出以下的 Altken 公式:(1)()k k x x φ= ;(2)(1)()k k x x φ=;(2)(2)(1)2(2)(1)1()/(2)k k k k k k k x x x x x x x +=---+, ,2,1,0=k这就是Altken 公式,它的加速效果也是十分明显的,它同样可使不收敛的迭代格式获得收敛(见附录5).3. 牛顿(Newton)法(牛顿切线法)()0f x =是非线性方程其迭代公式为:1(()/'())k k k k x x f x f x +=- ,2,1,0=k即为牛顿法公式.牛顿法的缺点是:(1)对重根收敛很慢;(2)对初值0x 要求较严,要求0x 相当接近真值*x .因此,常用其他方法确定初值0x ,再用牛顿法提高精度. 以下是本实验中的几个具体的实验 具体实验1:对分法先作图观察方程:3310x x -+=的实根的分布区间,再利用对分法在这些区间上分别求出根的近似值.程序如下: function [y,p]=erfen()clc, x=[];a=[];b=[]; a(1)=1;b(1)=2; i=1;x(i)=(a(i)+b(i))/2; e=abs(f(x(i))); ezplot('x^3-3*x+1',[a(1),b(1)]);hold on, plot([a(i),b(i)],[0,0]) while e>10^(-5)plot([a(i),a(i)],[0,100],[x(i) x(i)],[0 100],[b(i) b(i)],[0 100]),pause(0.5) if f(a(i))*f(x(i))<0a(i+1)=a(i);b(i+1)=x(i);x(i+1)=(a(i+1)+b(i+1))/2; elsea(i+1)=x(i);b(i+1)=b(i);x(i+1)=(a(i+1)+b(i+1))/2; ende=abs(f(x(i)));i=i+1; endy=x(i);p=[a;x;b]' function u=f(x) u=x^3-3*x+1; end end图形如下:结果为:1.5321具体实验2:普通迭代法采用迭代过程:1()k k x x φ+=求方程3310x x -+=在 0.5 附近的根,精确到第 4 位小数.构造等价方程:3(1)/3x x =+用迭代公式: 31(1)/3k k x x +=+, ,2,1,0=k 具体实验3:迭代法的加速1——松弛迭代法3()(1)/3x x φ=+,2()'x x φ=,21/(1)k k x ω=-迭代公式为31(1)(1)/3k k k k k x x x ωω+=-++clc;x=[];w=[]; x(1)=1;w(1)=1/(1-x(1)); for i=1:10w(i)=1/(1- x(i)); x(i+1)=(1-w(i))*x(i)+ w(i)*(x(i)^3+1)/3; end x另外有程序可以参考,详见参见附录4. 具体实验4:迭代法的加速2——Altken 迭代法迭代公式为:(1)3(1)/3k k x x =+,(2)(1)3(1)/3k k x x =+(2)(2)(1)2(2)(1)1()/(2)k k k k k k k x x x x x x x +=---+, ,2,1,0=k%(符号计算)syms x fx gx;gx=(x^3+1)/3;fx=x^3-3*x+1; disp('k x x1 x2') x=0.5;k=0; ffx=subs(fx, 'x', x); while abs(ffx)>0.0001;u=subs(gx, 'x', x);v=subs(gx, 'x', u);disp([num2str(k), ' ', num2str(x), ' ', num2str(u), ' ', num2str(v)]) x=v-(v-u)^2/(v-2*u+x);k=k+1;ffx=subs(fx, 'x', x); enddisp([num2str(k), ' ', num2str(x), ' ', num2str(u), ' ', num2str(v)]) %(数值计算)function [y,p]=althken() % 求方根的迭代程序 clc,format long e , x(1)=6; i=1;p=[];ezplot('x^3-3*x+1',[x(1)-9,x(1)+1]);hold on plot([x(1)-20,x(1)+2],[0,0]) while abs(f(x(i)))>=10^(-5) plot(x(i),0,'*')t1=phi(x(i));t2=phi(t1); x(i+1)=t2-(t2-t1)^2/(t2-2*t1+x(i)+eps); p=[p;[i, x(i),t1,t2]]; i=i+1; pause(0.1) endp,y=x(i), i, format function u=phi(x) u=(x^3+1)/3; endfunction u=f(x) u=x^3+1-3*x; end end具体实验5:牛顿法用牛顿法计算方程3310x x -+=在-2到2之间的三个根. 提示:3()31f x x x =-+,2'()33f x x =-迭代公式:2321(31)/(33)k k k k k x x x x x +=--+-function [y,p]=newton() % 求方根的迭代程序 clc,format long e , x(1)=6; i=1; p=[]; ezplot('x^3-3*x+1',[x(1)-9,x(1)+1]);hold on plot([x(1)-20,x(1)+2],[0,0]) while abs(f(x(i)))>=10^(-5)plot(x(i),0,'*'), x(i+1)=x(i)-f(x(i))/(df(x(i))+eps); p=[p;[i, x(i)]]; i=i+1; pause(0.1) endformat short , p,y=x(i), i, function u=df(x) u=3*x^2-3; endfunction u=f(x) u=x^3+1-3*x; end end 结果:结果为: 1.5321※进一步思考:用迭代法求3的平方根. 迭代公式为1(3/)/2n n n x x x +=+. 编写M 函数文件My_sqrt.m, 求3正的平方根x . 要求误差小于510-.仅要求写出源程序.试使用以上介绍的迭代法来相互比较 参考程序:function y=my_sqrt(a) % 求方根的迭代程序if nargin~=1|~isa(a,'double') , error('输入数字为一个正数!'),end if a<0, error('输入数字为正数!'), endif a>0format long e , x(1)=0; x(2)=1; i=1; while abs(x(i+1)-x(i))>=10^(-5)i=i+1;x(i+1)=1/2*(x(i)+a/(x(i)+eps));endy=x(i+1);i,format end现在我们简单介绍图解法如何来求解一元方程和二元方程的根: 例:exp(-3*t)*sin(4*t+2)+4*exp(-0.5*t)*cos(2*t)=0.5>>ezplot('exp(-3*t)*sin(4*t+2)+4*exp(-0.5*t)*cos(2*t)-0.5',[0 5]) >>hold on, line([0,5],[0,0])验证:t=3.5203 >>syms x; t=3.5203;vpa(exp(-3*t)*sin(4*t+2)+4*exp(-0.5*t)*cos(2*t)-0.5) ans =-.43167073997540938989914138801396e-4例::x^2*exp(-x*y^2/2)+exp(-x/2)*sin(x*y)=0y^2 *cos(y+x^2) +x^2*exp(x+y)=0>> ezplot('x^2*exp(-x*y^2/2)+exp(-x/2)*sin(x*y)')>> hold onezplot('y^2 *cos(y+x^2) +x^2*exp(x+y)')具体的结果请大家自己下来运行二、关于直接利用函数(命令)求解方程及简介(1) solve('f(x)'),f(x)为一个具体的表达式.(2) roots(A),A为某个多项式按x降幂排列的系数矩阵(3) fzero('f(x)', x0),f(x)为一个具体的表达式,x0为一个具体的数值(4) linsolve(A,b),A为一方程组的系数矩阵,b为方程组右端的常数矩阵.1.单变量的多项式方程求根:命令格式:roots(A)例:x^3-6*(x^2)-72*x-27=0;>>p=[1 -6 -72 -27]>>r=roots(p)r=12.1229-5.7345-0.38842. 多项式型方程的准解析解法命令格式:[x,…]=solve(eqn1,eqn2,…)例:x^2+y^2-1=00.75*x^3-y+0.9=0>>syms x y;>> [x,y]=solve('x^2+y^2-1=0', '75*x^3/100-y+9/10=0')检验:>>[eval('x.^2+y.^2-1'), eval('75*x.^3/100-y+9/10')]具体结果就请大家下来自己运行3. 线性方程组的求解例:求线性方程组b⋅的解,已知m=[1 2 3 4 5;2 3 4 5 6;3 4 5 6 7 8;4 5 6 7 8 ;5 6 7 8 0],m=xb=[1;2;3;4;5]for i=1:5for j=1:5m(i, j)=i+j-1;endendm(5, 5)=0;b=[1:5]'; linsolve(m, b)4. 非线性方程数值求解(1)单变量非线性方程求解在MATLAB中提供了一个fzero函数,可以用来求单变量非线性方程的根.该函数的调用格式为:z=fzero('fname',x0,tol,trace)其中fname是待求根的函数文件名,x0为搜索的起点.一个函数可能有多个根,但fzero 函数只给出离x0最近的那个根.tol控制结果的相对精度,缺省时取tol=eps,trace•指定迭代信息是否在运算中显示,为1时显示,为0时不显示,缺省时取trace=0.例:求f(x)=x-10x+2=0在x0=0.5附近的根.步骤如下:(a) 建立函数文件funx.m.function fx=funx(x)fx=x-10.^x+2;(b)调用fzero函数求根.z=fzero('funx',0.5)z = 0.3758(2)非线性方程组的求解对于非线性方程组F(X)=0,用fsolve函数求其数值解.fsolve函数的调用格式为: X=fsolve('fun',X0,option)其中X为返回的解,fun是用于定义需求解的非线性方程组的函数文件名,X0是求根过程的初值,option为最优化工具箱的选项设定.最优化工具箱提供了20多个选项,用户可以使用optimset命令将它们显示出来.如果想改变其中某个选项,则可以调用optimset()函数来完成.例如,Display 选项决定函数调用时中间结果的显示方式,其中‘off’为不显示,‘iter’表示每步都显示,‘final’只显示最终结果.optim set(‘Display’,‘off’)将设定Display 选项为‘off’. 例: 求下列非线性方程组在(0.5,0.5) 附近的数值解.(a) 建立函数文件myfun.m . function q=myfun(p) x=p(1);y=p(2);q(1)=x-0.6*sin(x)-0.3*cos(y);q(2)=y-0.6*cos(x)+0.3*sin(y); (b) 在给定的初值x0=0.5,y0=0.5下,调用fsolve 函数求方程的根. x=fsolve('myfun',[0.5,0.5]',optimset('Display','off')) x = 0.6354 0.3734将求得的解代回原方程,可以检验结果是否正确,命令如下: q=myfun(x) q = 1.0e-009 * 0.2375 0.2957 可见得到了较高精度的结果.精品案例:螺旋线与平面的交点问题:螺旋线与平面相交的情况多种多样, 根据螺旋线与平面方程的不同可以相交, 也可以不相交. 在相交的情况下, 可以交于一点, 也可以交于好多点. 对于各种相交的情况, 要求其交点的坐标并不是一件容易的事. 本次实验就以此为背景讨论下面的具体问题:已知螺旋线的参数方程为4cos ,4sin ,,08x y z θθθθπ===≤≤.平面的方程为:0.520x y z ++-=. 求该螺旋线与平面的交点. 要求:1)求出所有交点的坐标;2)在同一图形窗口画出螺旋线、平面和交点. 实验过程: 1.1 问题分析可以采用多种方法求螺旋线与平面的交点坐标, 包括fsolve 等. 先对方程化简,减少变量个数,使用图解方法求方程的根.再分别画出螺旋线,平面,及其交点. 1.2 算法描述与分析先对方程化简,减少变量个数,再利用fsolve, 选择适当的初值, 求其数值解;再分别会出图形;最后对图形作出必要的修饰. 1.3 源程序及注释将螺旋线的参数方程代入平面方程后可得: 等价变形得 : 建立下面M 文件intersect_point.m %使用图解法求交点,并且三维图 %画图确定解的个数和大概位置 theta=0:0.01:8*pi;y1=4*(cos(theta)+sin(theta)); y2=2-0.5*theta;plot(theta,y1,theta,y2) %画出两个函数的图形%画螺旋线%theta=0:pi/100:8*pi; x=4*cos(theta); y=4*sin(theta); z=theta;figure %新建图形窗口plot3(x,y,z) %画含有参数的空间曲线 hold on %透明的画平面%x1=-5:0.1:5; %取值和螺旋线的范围[-4,4]有关. y1=x1;[X1 Y1]=meshgrid(x1,y1);%网格化,画曲面 Z1=4-2*X1-2*Y1;surf(X1,Y1,Z1) %或者使用mesh(X1,Y1,Z1)25.0sin 4cos 4=-++θθθθθθ5.02sin 4cos 4-=+shading flatalpha(0.5) %设置透明度alpha('z') %设置透明度方向%求交点坐标,为避免变量混淆和覆盖,这里用t 代替theta%i=1for n=[2,5,9,11] %根据画图确定解的大概位置作为初值t(i)=fsolve(inline('4*cos(t)+4*sin(t)+0.5 *t-2'),n)%选择不同初值求交点 x0(i)=4*cos(t(i));y0(i)=4*sin(t(i));z0(i)=t(i);i=i+1;endplot3(x0,y0,z0,'ro')1.4 测试结果(写清输入输出情况)从图形可见在 内与三角曲线有4个交点.交点坐标为:theta 的数值解为:t=[2.1961 5.3759 9.1078 11.1023]四个交点的近似坐标为:x0 =[-2.3413 2.4635 -3.8007 0.4261]y0 =[3.2432 -3.1514 1.2468 -3.9772] z0 =[2.1961 5.3759 9.1078 11.1023]1.5 调试和运行程序过程中产生的问题及采取的措施求交点的时候会出现重根和漏根的情形,通过选择适当的初值避免了上述情况.1.6 对算法和程序的讨论、分析, 改进设想及其它经验教训solve 函数只能求解一个数值解,不能全部求出;用fsolve 函数好; 为了满足更好的视觉πθ80≤≤效果,可以对图形进行进一步的修饰.习题1.已知多项式323)(2345+++-=x x x x x f2.解方程组:sin()0x x y ye +-=(1)22x y -= (2)3.求解方程: ex x x =)cos( 4.求解多项式方程 0189=++x x5.求下列代数方程(组)的解:(1) 510x x -+=(2) 230x y += ①2431x y += ②6.选择适当的迭代过程,分别使用:(1)普通迭代法;(2)与之相应的松弛迭代法和 Altken 迭代法.求解方程0133=+-x x 在 1.4 附近的根,精确到4位小数,请注意迭代次数的变化.7.分别用对分法、普通迭代法、松弛迭代法、Altken 迭代法、牛顿切法线等5种方法,求方程 sin()t x x ⋅= 的正的近似根,10≤<t .(建议取 5.0=t .时间许可的话,可进一步考虑 25.0=t 的情况.)五、附录为供近似求根的算法附录1:对分法程序(fulu1.m )syms x fx; a=0;b=1;fx=x^3-3*x+1;x=(a+b)/2;k=0;ffx=subs(fx, 'x', x);if ffx==0;disp(['the root is:', num2str(x)])else disp('k ak bk f(xk)')while abs(ffx)>0.0001 & a<b;disp([num2str(k), ' ', num2str(a), ' ', num2str(b), ' ', num2str(ffx)]) fa=subs(fx, 'x', a);ffx=subs(fx, 'x', x);if fa*ffx<0b=x;elsea=x;endk=k+1;x=(a+b)/2;enddisp([num2str(k), ' ', num2str(a), ' ', num2str(b), ' ', num2str(ffx)])end注:实验时,可将第 2 行的 a、b 改为其它区间端点进行其它实验.附录2:普通迭代法(fulu2.m)syms x fx gx; gx=(x^3+1)/3;fx=x^3-3*x+1; disp('k x f(x)')x=0.5;k=0; ffx=subs(fx, 'x', x);while abs(ffx)>0.0001;disp([num2str(k), ' ', num2str(x), ' ', num2str(ffx)]);x=subs(gx, 'x', x);ffx=subs(fx, 'x', x);k=k+1;enddisp([num2str(k), ' ', num2str(x), ' ', num2str(ffx)])附录3:收敛/发散判断(fulu3.m)syms x g1 g2 g3 dg1 dg2 dg3;x1=0.347;x2=1.53;x3=-1.88;g1=(x^3+1)/3;dg1=diff(g1, 'x');g2=1/(3-x^2);dg2=diff(g2, 'x');g3=(3*x-1)^(1/3);dg3=diff(g3, 'x');disp(['1 ', num2str(abs(subs(dg1, 'x', x1))), ' ', ...num2str(abs(subs(dg1, 'x', x2))), ' ', num2str(abs(subs(dg1, 'x', x3)))]) disp(['2 ', num2str(abs(subs(dg2, 'x', x1))), ' ', ...num2str(abs(subs(dg2, 'x', x2))), ' ', num2str(abs(subs(dg2, 'x', x3)))]) disp(['3 ', num2str(abs(subs(dg3, 'x', x1))), ' ', ...num2str(abs(subs(dg3, 'x', x2))), ' ', num2str(abs(subs(dg3, 'x', x3)))])附录4:松弛迭代法(fulu4.m)syms fx gx x dgx;gx=(x^3+1)/3;fx=x^3-3*x+1;dgx=diff(gx, 'x');x=0.5;k=0;ggx=subs(gx, 'x', x);ffx=subs(fx, 'x', x);dgxx=subs(dgx, 'x', x);disp('k x w')while abs(ffx)>0.0001;w=1/(1-dgxx); disp([num2str(k), ' ', num2str(x), ' ', num2str(w)]) x=(1-w)*x+w*ggx;k=k+1;ggx=subs(gx, 'x', x);ffx=subs(fx, 'x', x);dgxx=subs(dgx, 'x', x);enddisp([num2str(k), ' ', num2str(x), ' ', num2str(w)])附录5: Altken 迭代法(fulu5.m)syms x fx gx; gx=(x^3+1)/3;fx=x^3-3*x+1;disp('k x x1 x2') x=0.5;k=0;ffx=subs(fx, 'x', x);while abs(ffx)>0.0001;u=subs(gx, 'x', x);v=subs(gx, 'x', u);disp([num2str(k), ' ', num2str(x), ' ', num2str(u), ' ', num2str(v)]) x=v-(v-u)^2/(v-2*u+x);k=k+1;ffx=subs(fx, 'x', x);enddisp([num2str(k), ' ', num2str(x), ' ', num2str(u), ' ', num2str(v)])附录6:牛顿法(fulu6.m)syms x fx gx;fx=x^3-3*x+1;gx=diff(fx, 'x');x1=-2;x2=0.5;x3=1.4;k=0;disp('k x1 x2 x3')fx1=subs(fx, 'x', x1);fx2=subs(fx, 'x', x2);fx3=subs(fx, 'x', x3);gx1=subs(gx, 'x', x1);gx2=subs(gx, 'x', x2);gx3=subs(gx, 'x', x3);while abs(fx1)>0.0001|abs(fx2)>0.0001|abs(fx3)>0.0001;disp([num2str(k), ' ', num2str(x1), ' ', num2str(x2), ' ', num2str(x3)])x1=x1-fx1/gx1;x2=x2-fx2/gx2;x3=x3-fx3/gx3;k=k+1;fx1=subs(fx, 'x', x1);fx2=subs(fx, 'x', x2);fx3=subs(fx, 'x', x3);gx1=subs(gx, 'x', x1);gx2=subs(gx, 'x', x2);gx3=subs(gx, 'x', x3);enddisp([num2str(k), ' ', num2str(x1), ' ', num2str(x2), ' ', num2str(x3)])。


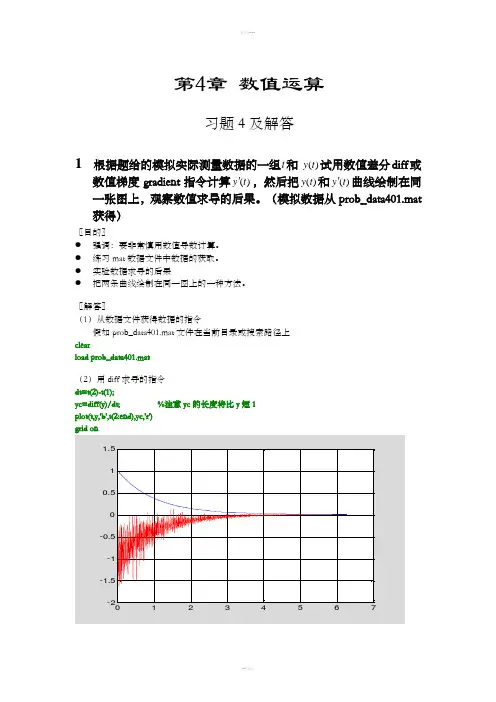
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat 获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')grid on(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
实验四 方程求根实验一. 实验目的(1)深入理解方程求根的迭代法的设计思想,学会利用校正技术和松弛技术解决某些实际的非线性方程问题,比较这些方法解题的不同之处。
(2)熟悉Matlab 编程环境,利用Matlab 解决具体的方程求根问题。
二. 实验要求用Matlab 软件实现根的二分搜索、迭代法、Newton 法、快速弦截法和弦截法,并用实例在计算机上计算。
三. 实验内容1. 实验题目(1)早在1225年,古代人曾求解方程020102)(23=-++=x x x x f 并给出了高精度的实根368808107.1*=x ,试用Newton 法和弦截法进行验证,要求精度610-=ε,并绘制方程的图形。
答:A.Newton 法:a .编写文件Newton.m 、func4.m 内容如下所示:b.运行,如下所示A为矩阵,由上面可知,对于初值为5,运行7次即可得到所需的精度,验证结果为古人给出的解释正确的;c.作图,编写下面的文件photo1.m.然后运行即可:注意下面中的x矩阵即为刚才计算出来的x系列,k为迭代的次数:a.编写文件Chord.m内容如下所示:b.运行结果如下所示:由上表可知,在精度为10^-6时有7位有效数字,古人的结果还是正确的c.作图,在上面运行后,即运行newton法时写的photo1.m文件即可出现图像:可以看到图中两条曲线基本重合; (2)取5.00=x ,用迭代法求方程x e x -=的根,然后用Aitken 方法加速,要求精度为结果有4为有效数字。
答:a. 编写文件func7.m 和Aiken.m ,内容如下所示:b .运行:具有四位有效数字 (3)用快速弦截法求解方程01)(=-=x xe x f ,要求精度为610-=ε,取6.05.010==x x ,作为开始值,并绘制1)(-=x xe x f 的图形。
答:对照可知,书本后面的程序已经正确,运行即可:下面为快速弦截法的主程序文件:函数文件如下:运行如下:作图,编写下面的文件:运行该文件就可以y=x*exp(x)-1函数和插值函数的图:可以看到两条直线基本重合在一起了,扩大图片可以看到两条直线是不重合的:2. 设计思想要求针对上述题目,详细分析每种算法的设计思想。




实验一方程根的近似计算一、问题求非线性方程的根二、实验目的1、学会使用matlab中内部函数roots、solve、fsolve、fzero求解方程,并用之解决实际问题。
4、熟悉Matlab的编程思路,尤其是函数式M文件的编写方法。
三、预备知识方程求根是初等数学的重要内容之一,也是科学和工程中经常碰到的数值计算问题。
它的一般形式是求方程f(x)=0的根。
如果有x*使得f(x*)=0,则称x*为f(x)=0的根,或函数f(x)的零点。
并非所有的方程都能求出精确解或解析解。
理论上已经证明,用代数方法可以求出不超过3次的代数方程的解析解,但对于次数大于等于5的代数方程,没有代数求根方法,即它的根不能用方程系数的解析式表示。
至于超越方程,通常很难求出其解析解。
不存在解析解的方程就需要结合具体方程(函数)的性质,使用作图法或数值法求出近似解。
而计算机的发展和普及又为这些方法提供了广阔的发展前景,使之成为科学和工程中最实用的方法之一。
下面介绍几种常见的求近似根的方法。
1. 求方程近似解的简单方法1.1 图形方法—放大法求根图形的方法是分析方程根的性态最简洁的方法。
不过,不要总是想得到根的精确值。
这些值虽然粗糙但直观,多少个根,在何范围,一目了然。
并且还可以借助图形局部放大功能,将根定位得更加准确一些。
例1.1 求方程x5+2x2+4=0的所有根及其大致分布范围。
解(1)画出函数f(x)=x5+2x2+4的图形,确定方程的实数根的大致范围。
为此,在matlab命令窗中输入clfezplot x-x,grid onhold onezplot('x^5+2*x^2+4',[-2*pi,2*pi])1-1 函数f(x)=x5+2x2+4的图形clfx=-2*pi:0.1:2*pi;y1=zeros(size(x));y2= x.^5+2*x.^2+4;plot(x,y1,x,y2)grid onaxis tighttitle('x^5+2x^2+4')xlabel('x')从图1-1可见,它有一个实数根,大致分布在-2与2之间。
Matlab 7.0使用说明(数值计算部分(数值计算部分))华中科技大学国家机械基础课程教学基地2010年 9月代号9-06A 模块计算机辅助设计层次基础型目录第一部分基本操作 (1)§1.Matlab的使用 (1)1-1.直接输入命令 (1)1-2.用M文件开发程序 (1)§2.M文件程序的主要语句和主要函数 (2)2-1.Matlab的数字特征 (2)2-2.主要语句 (3)2-3.常用函数 (4)2-4.几个常用的命令 (5)§3.矩阵的有关计算 (5)3-1.矩阵的输入 (5)3-2.矩阵/向量的运算 (6)3-3.矩阵的范数 (6)3-4.向量的范数 (7)3-5.矩阵的条件数 (7)3-6.矩阵的特征值和特征向量 (8)§4.Matlab绘图 (9)4-1.绘图的基本命令 (9)4-2.图形的交互编辑 (11)第二部分数值计算 (12)§1.方程求根 (12)1-1.牛顿迭代法 (12)1-2.图解法确定迭代的初始点 (13)§2.线性方程组 (13)2-1.迭代法的收敛性 (13)2-2.线性方程组的病态问题 (14)2-3.求解线性方程组 (15)§3.插值和拟合 (16)grange插值 (16)3-2.代数多项式插值 (17)3-3.插值误差 (17)3-4.分段线性插值 (18)3-5.数据的曲线拟合 (18)§4.数值积分 (20)4-1.复合梯形求积公式 (20)4-2.复合Simpson求积公式 (20)§5.常微分方程的数值解法 (21)5-1.Euler方法 (21)5-2.改进的Euler方法 (23)5-3.四阶龙格-库塔方法 (24)习题 (27)一、方程求根 (27)二、线性方程组 (27)三、插值与拟合 (28)四、数值积分 (29)五、常微分方程 (30)《计算方法》实验报告 (31)一、方程求根 (31)二、线性方程组 (31)三、插值与拟合 (32)四、数值积分 (32)五、常微分方程 (33)第一部分基本操作§1.1.MatlabMatlab 的使用Matlab 的使用方法有两种:(1)在Matlab 的命令窗口(Matlab Command Windows )中直接输入命令,即可得到结果;(2)在Matlab 的编辑窗口(Matlab Editor )内编写M 文件,然后在命令窗口执行该文件,得到所需的结果。
matlab第四章课后作业解答第四章习题解答1、求下列多项式的所有根,并进⾏验算。
(3)267235865x x x x-+-(4)4)32(3-+x 解:>> p=zeros(1,24);>> p(1)=5;p(17)=-6;p(18)=8;p(22)=-5;>> root=roots(p)root =0.97680.9388 + 0.2682i0.9388 - 0.2682i0.8554 + 0.5363i0.8554 - 0.5363i0.6615 + 0.8064i0.6615 - 0.8064i0.3516 + 0.9878i0.3516 - 0.9878i-0.0345 + 1.0150i-0.0345 - 1.0150i-0.4609 + 0.9458i-0.4609 - 0.9458i-0.1150 + 0.8340i-0.1150 - 0.8340i-0.7821 + 0.7376i-0.7821 - 0.7376i-0.9859 + 0.4106i-0.9859 - 0.4106i-1.0416-0.7927>> polyval(p,root)ans =1.0e-012 *-0.07120.0459 - 0.0081i0.0459 + 0.0081i-0.0419 + 0.0444i-0.0419 - 0.0444i0.0509 + 0.0929i0.0509 - 0.0929i-0.2059 + 0.0009i-0.2059 - 0.0009i-0.0340 + 0.0145i-0.0340 - 0.0145i0.1342 + 0.0910i0.1342 - 0.0910i0.0025 + 0.0027i0.0025 - 0.0027i-0.0077 + 0.4643i-0.0077 - 0.4643i-0.3548 - 0.1466i-0.3548 + 0.1466i-0.0251-0.0073(4) >> p1=[2 3];>> p=conv(conv(p1,p1),p1)-[0 0 0 4];>> root=roots(p)root =-1.8969 + 0.6874i-1.8969 - 0.6874i-0.7063>> polyval(p,root)ans =1.0e-014 *-0.7105 - 0.6217i-0.7105 + 0.6217i6、求解下列⽅程组在区域1,0<<βα内的解-=+=.sin 2.0cos 7.0,cos 2.0sin 7.0βαββαα解:以初值)5.0,5.0(),(00=βα进⾏求解>> fun=inline('[0.7*sin(x(1))+0.2*cos(x(2))-x(1),0.7*cos(x(1))-0.2*sin(x(2))-x(2)]');>> [x,f,h]=fsolve(fun,[0.5 0.5])Optimization terminated: first-order optimality is less than options.TolFun.x =0.5265 0.5079f =1.0e-007 *-0.1680 -0.2712h =1因⽽,该⽅程组的近似根为5079.0,5265.0==βα。
MATLAB数值计算
(读书日记及程序编写)
第四章方程求根 (2)
第四章 方程求根
#二分法 求2的值
转化成方程02-2
=x
最慢的方法是取初值1001=x 02-21>x ,取502=x
这样得到
也可以x0=a, x1=x0+h, 进行扫描,若f(x0)*f(x1)<0, 则扫描成功,有根区间为[x0,x1],否则继续扫描,如果出现x1>b ,表面扫描失败,再缩小步长h, 再次扫描。
>> format long %让显示的值为
M=2,a=1,b=2,k=0;
while b-a>eps
x=(a+b)/2;
if x^2>M
b=x
else
a=x
end
k=k+1
end
执行后得到的值为:
k =
50
b =
1.414213562373095
k =
51
b =
1.414213562373095
k =
52
最后得到的值就是Matlab 能表达的最接近的值。
#牛顿法
求解f(x)=0的牛顿法是在f(x)画一条切线,确定切线与x 轴的焦点,通过迭代 )
(x f )f(x -n n 1'=+n n x x 对于平方根的问题,牛顿法简洁有效,
换成f(x)=x^2-M, )(x f n '
=2x 这样
⎪⎪⎭
⎫ ⎝⎛+==+n n n n x M x M x x 212x -x -n 2n 1 该算法就是反复求x 和M/x 的平均值,Matlab 的程序为:
format long %让显示的值为
xprev=2; %取的不等于初值x 的一个值,让判断能继续
x=100; %取的初值为3
while abs(x-xprev)>eps*abs(x)
xprev=x;
x=0.5*(x+2/x)
end
x = 1.833333333333333
x = 1.462121212121212
x = 1.414998429894803
x = 1.414213780047198
x = 1.414213562373112
x = 1.414213562373095
x = 1.414213562373095
可见6步很快就收敛
然而,若f(x)不具有连续的、有界的一阶、二阶导数,牛顿法的收敛将变得很慢。
#fzero 函数直接求根
求x^3-1在区间[0,10]上的根
fzero(@(x)x^3-1,[0,10])
ans =
1
fzerogui(@(x)x^3-1,[0,10])
可以通过在图形界面上选择割点来得到
>> fzerogui(@(x)x^3-1,[0,10])
ans =
start 0.0000000000000000
start 10.0000000000000000
secant 0.0100000000000000
bisect 5.0049999999999999
secant 0.0498403198384075
bisect 2.5274201599192034
secant 0.2032825426923320
bisect 1.3653513513057676
secant 0.6575071192259432
bisect 1.0114292352658554
secant 0.9950727548572595
secant 0.9999439297147387
iqi 1.0000000052288878
secant 0.9999999999997068
secant 1.0000000000000000
(bisect:二分,secant:交点,可见,经过多次迭代,非常接近真实解x=1
同理,要求贝塞尔函数的根,输入直接得到
>> fzero(@(x)besselj(0,x),[0,3.83])
ans =
2.4048
输入图形求解,可以得到:
>> fzerogui(@(x)besselj(0,x),[0,3.83])。