连续梁的整体刚度矩阵

第12章 结构矩阵分析习题解答习题12-1 图示连续梁，不及轴向变形。

求引入支承条件后的结构刚度矩阵。

习题12-1图解： 单元刚度矩阵：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=i i i i i i i i k k k k k k k k 844842241111①22①21①12①11①22①22①12①11①k；⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=i i i i i i i i k k k k k k k k 2661242242222②22②21②12②11②33②32②23②22②k采用“直刚法”组集结构刚度矩阵：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=i i i i i i i k k k k k k k k k k k k k k k k 126062040480000②22②21②12②11①22①21①12①11②33②32②23②22①22①21①12①11K 引入支承条件后的结构刚度矩阵：⎥⎦⎤⎢⎣⎡=i i i i 126620K习题12-2 用先处理法写出图示连续梁的整体刚度矩阵K 。

习题12-2图解： 单元刚度矩阵：[][]1①11①4i k==k；⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=2222②22②21②12②11②4224i i i i k k k k k； ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=3333③33③32③23③22③4224i i i i k k k k k引入支承条件后的结构刚度矩阵：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++=333322221③33③32③23③22②22②21②12②11①114202442024400i i i i i i i i i k k k k k k k k k K 习题12-3 图示刚架，不考虑轴向变形，仅以转角为未知量，求引入支承条件前的结构刚度矩阵K 。

习题12-3图解： 单元刚度矩阵：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=i i i i k k k k 8448①22①22①12①11①k；⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=i i i i k k k k 126612②33②32②23②22②k ； 引入支承条件前的结构刚度矩阵：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=i i i i i i i k k k k k k k k k k k k k k k k 126061240480000②22②21②12②11①22①21①12①11②33②32②23②22①22①21①12①11K 习题12-4 图示刚架，不考虑轴向变形，仅以转角为未知量，求引入支承条件前的结构刚度矩阵K 中的各主元素。

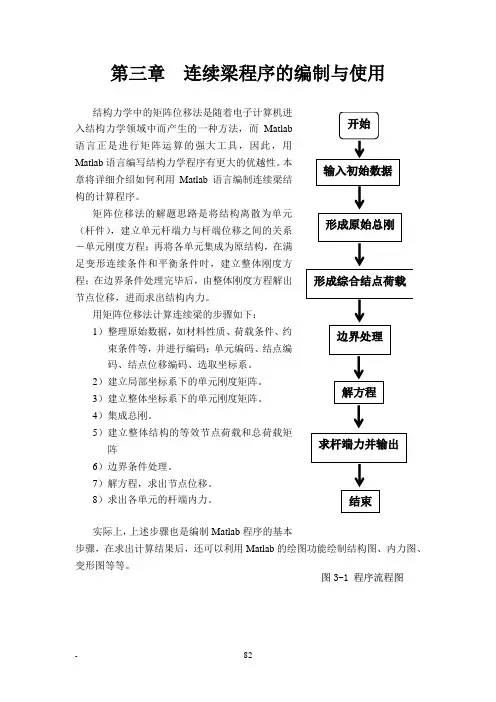
第三章连续梁程序的编制与使用入结构力学领域中而产生的一种方法，而Matlab语言正是进行矩阵运算的强大工具，因此，用Matlab语言编写结构力学程序有更大的优越性。

本章将详细介绍如何利用Matlab语言编制连续梁结构的计算程序。

矩阵位移法的解题思路是将结构离散为单元（杆件），建立单元杆端力与杆端位移之间的关系－单元刚度方程；再将各单元集成为原结构，在满足变形连续条件和平衡条件时，建立整体刚度方程；在边界条件处理完毕后，由整体刚度方程解出节点位移，进而求出结构内力。

用矩阵位移法计算连续梁的步骤如下：1）整理原始数据，如材料性质、荷载条件、约束条件等，并进行编码：单元编码、结点编码、结点位移编码、选取坐标系。

2）建立局部坐标系下的单元刚度矩阵。

3）建立整体坐标系下的单元刚度矩阵。

4）集成总刚。

5）建立整体结构的等效节点荷载和总荷载矩阵6）边界条件处理。

7）解方程，求出节点位移。

8）求出各单元的杆端内力。

实际上，上述步骤也是编制Matlab程序的基本步骤，在求出计算结果后，还可以利用Matlab的绘图功能绘制结构图、内力图、变形图等等。

图3-1程序流程图3.1 程序说明%******************************************************************* % 矩阵位移法解连续梁主程序%******************************************************************* ●功能：运用矩阵位移法解连续梁的基本原理编制的计算主程序。

●基本思想：结点（结点位移）编码默认为从左至右，从1开始顺序进行；杆端弯矩的方向默认为逆时针。

●荷载类型：可计算结点荷载，每单元作用的跨中集中力和均布荷载。

●说明：主程序的作用是通过赋值语句、读取和写入文件、函数调用等完成算法的全过程，即实现程序流程图的程序表达。

%----------------------------------------------------------------------------------------------------- 1 程序准备format short e %设定输出类型clear all %清除所有已定义变量clc %清屏●说明：format short e －设定计算过程中显示在屏幕上的数字类型为短格式、科学计数法；clear all －清除所有已定义变量，目的是在本程序的运行过程中，不会发生变量名相同等可能使计算出错的情况；clc －清屏，使屏幕在本程序运行开始时%----------------------------------------------------------------------------------------------------- 2 打开文件FP1=fopen('input.txt','rt'); %打开输入数据文件存放初始数据FP2=fopen('output.txt','wt'); %打开输出数据文件存放计算结果●说明：FP1=fopen('input.txt','rt'); －打开已存在的输入数据文件input.txt，且设置其为只读格式，使程序在执行过程中不能改变输入文件中的数值，并用文件句柄FP1来FP2=fopen('output.txt','wt'); －打开输出数据文件，该文件不存在时，通过此命令创建新文件，该文件存在时则将原有内容全部删除。

第七章 矩阵位移法一、就是非题1、单元刚度矩阵反映了该单元杆端位移与杆端力之间得关系。

2、单元刚度矩阵均具有对称性与奇异性。

3、局部坐标系与整体坐标系之间得坐标变换矩阵T 就是正交矩阵。

4、结构刚度矩阵反映了结构结点位移与荷载之间得关系。

5、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵 作 坐 标 变 换。

6、结 构 刚 度 矩 阵 就是 对 称 矩 阵 ,即 有K i j = K j i ,这 可 由 位 移 互 等 定 理 得 到 证 明 。

7、结构刚度方程矩阵形式为:,它就是整个结构所应满足得变形条件。

8、在直接刚度法得先处理法中,定位向量得物理意义就是变形连续条件与位移边界条件。

9、等效结点荷载数值等于汇交于该结点所有固端力得代数与。

10、矩阵位移法中,等效结点荷载得“等效原则”就是指与非结点荷载得结点位移相等。

11、矩阵位移法既能计算超静定结构,也能计算静定结构。

二、选择题1、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号就是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.21341234123412342、平面杆件结构一般情况下得单元刚度矩阵,就其性质而言,就是:A.非对称、奇异矩阵;B.对称、奇异矩阵;C.对称、非奇异矩阵;D.非对称、非奇异矩阵。

3、单元i j 在图示两种坐标系中得刚度矩阵相比:A.完全相同;B.第2、3、5、6行(列)等值异号;C.第2、5行(列)等值异号;D.第3、6行(列)等值异号。

4、矩阵位移法中,结构得原始刚度方程就是表示下列两组量值之间得相互关系:A.杆端力与结点位移;B.杆端力与结点力;C.结点力与结点位移;D.结点位移与杆端力。

第七章 矩阵位移法一、是非题1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。

2、单元刚度矩阵均具有对称性和奇异性。

3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。

4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。

5、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵 作 坐 标 变 换。

6、结 构 刚 度 矩 阵 是 对 称 矩 阵 ，即 有K i j = K j i ，这 可 由 位 移 互 等 定 理 得 到 证 明 。

7、结构刚度方程矩阵形式为：[]{}{}K P ∆=，它是整个结构所应满足的变形条件。

8、在直接刚度法的先处理法中，定位向量的物理意义是变形连续条件和位移边界条件。

9、等效结点荷载数值等于汇交于该结点所有固端力的代数和。

10、矩阵位移法中，等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。

11、矩阵位移法既能计算超静定结构，也能计算静定结构。

二、选择题1、已知图示刚架各杆EI = 常数，当只考虑弯曲变形，且各杆单元类型相同时，采用先处理法进行结点位移编号，其正确编号是：2、平面杆件结构一般情况下的单元刚度矩阵[]k 66⨯，就其性质而言，是： A ．非对称、奇异矩阵； B ．对称、奇异矩阵； C ．对称、非奇异矩阵； D ．非对称、非奇异矩阵。

3、单元i j 在图示两种坐标系中的刚度矩阵相比：A ．完全相同；B ．第2、3、5、6行(列)等值异号；C ．第2、5行(列)等值异号；D ．第3、6行(列)等值异号。

4、矩阵位移法中，结构的原始刚度方程是表示下列两组量值之间的相互关系： A ．杆端力与结点位移； B ．杆端力与结点力； C ．结点力与结点位移； D ．结点位移与杆端力 。

5、单 元 刚 度 矩 阵 中 元 素 k ij 的 物 理 意 义 是 ：A ．当 且 仅 当 δi =1 时 引 起 的 与 δj 相 应 的 杆 端 力 ；B ．当 且 仅 当 δj =1时 引 起 的 与 δi 相 应 的 杆 端 力 ；C ．当 δj =1时 引 起 的 δi 相 应 的 杆 端 力 ；D ．当 δi =1时 引 起 的 与 δj 相 应 的 杆 端 力。

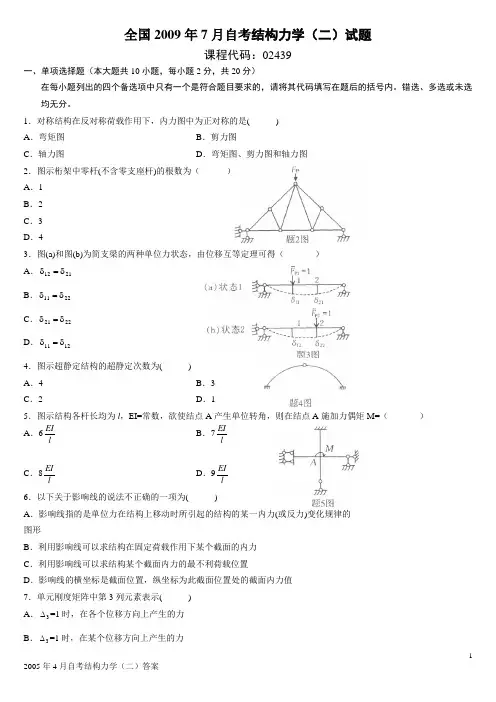
全国2009年7月自考结构力学（二）试题课程代码：02439一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．对称结构在反对称荷载作用下，内力图中为正对称的是( ) A ．弯矩图 B ．剪力图C ．轴力图D ．弯矩图、剪力图和轴力图2．图示桁架中零杆(不含零支座杆)的根数为（ ） A ．1 B ．2 C ．3 D ．43．图(a)和图(b)为简支梁的两种单位力状态，由位移互等定理可得（ ） A ．2112δ=δ B ．2211δ=δ C ．2221δ=δ D ．1211δ=δ4．图示超静定结构的超静定次数为( ) A ．4 B ．3 C ．2D ．15．图示结构各杆长均为l ，EI=常数，欲使结点A 产生单位转角，则在结点A 施加力偶矩M=（ ）A ．6l EIB ．7l EIC ．8lEID ．9lEI 6．以下关于影响线的说法不正确的一项为( )A ．影响线指的是单位力在结构上移动时所引起的结构的某一内力(或反力)变化规律的 图形B ．利用影响线可以求结构在固定荷载作用下某个截面的内力C ．利用影响线可以求结构某个截面内力的最不利荷载位置D ．影响线的横坐标是截面位置，纵坐标为此截面位置处的截面内力值 7．单元刚度矩阵中第3列元素表示( ) A ．3∆=1时，在各个位移方向上产生的力 B ．3∆=1时，在某个位移方向上产生的力C ．在各个位移方向上发生单位位移时，在3∆方向上产生的力D ．在某个位移方向上发生单位位移时，在3∆方向上产生的力 8．不计杆的分布质量，图示体系的动力自由度为 A ．1 B ．2 C ．3D ．49．为提高单自由度体系的自振频率可采取的措施有( ) A ．减小外荷载 B ．增大体系的刚度 C ．增大阻尼D ．增大质量10．AB 梁为矩形截面梁，截面高为h ，上侧温度升高10℃，下侧温度下降2℃，B 点的竖向位移(以向下为正)为( ) A ．3h l 2αB ．-3h l 2αC ．6hl 2αD ．-6hl 2α二、填空题（本大题共10小题，每小题2分，共20分） 请在每小题的空格中填上正确答案。

回顾Î局部坐标系下单元刚度方程{[]{eeek F Δ=Î单元坐标转换矩阵{}[]{}eeeF T F ={[]{}eeeT Δ=Δ[][][][]T kT k eTe=Î整体坐标系下单元刚度方程Î整体坐标系下单元刚度方程{}[]{}eeeF k =Δ9-4 连续梁的整体刚度矩阵教学目标：理解单元定位向量的物理意义； 掌握连续梁的整体刚度矩阵的计算。

教学内容：传统位移法 单元集成法 单元定位向量 连续梁的整体刚度矩阵1. 传统位移法11EI i l =22EI i l =①②1Δ2Δ3Δ2F 1F 3{}123Δ⎧⎫⎪⎪Δ=Δ⎨⎬⎪⎪Δ⎩⎭节点整体力向量{}123F F F F ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭节点整体位移向量例：求图示结构整体刚度矩阵。

1Δ2Δ3Δ2F 1F 3由△1引起的结点力偶1Δ114i Δ0112i Δ由△2引起的结点力偶122i Δ()12244i i +Δ2Δ222i Δ0232i Δ3Δ34i Δ由△3引起的结点力偶分别考虑每个结点位移对{F }的单独贡献叠加原理：{}111121122232234202442024F i i F F i i i i F i i Δ⎧⎫⎧⎫⎡⎤⎪⎪⎪⎪⎢⎥==+Δ⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪Δ⎢⎥⎣⎦⎩⎭⎩⎭{}[]{}F K =Δ[]111122224202442024i i K i i i i i i ⎡⎤⎢⎥=+⎢⎥⎢⎥⎣⎦整体刚度矩阵4224eei i k i i ⎡⎤⎡⎤=⎢⎥⎣⎦⎣⎦分别考虑每个单元对[F ]的单独贡献，然后进行叠加。

单元①的贡献1Δ2Δ3Δ2F 1F 3①②20i =0=1Δ2Δ3Δ2F 1F 3①②1i 2i []11114224i i k i i ⎡⎤=⎢⎥⎣⎦①111121124224F i i F i i Δ⎧⎫⎡⎤⎧⎫=⎨⎬⎨⎬⎢⎥Δ⎩⎭⎣⎦⎩⎭①123300000F Δ⎧⎫⎤⎪⎪⎪⎪⎥=Δ⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪Δ⎢⎥⎣⎦⎩⎭⎩⎭2. 单元集成法1111211233420240000F i i F i i F Δ⎧⎫⎧⎫⎡⎤⎪⎪⎪⎪⎢⎥=Δ⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪Δ⎢⎥⎣⎦⎩⎭⎩⎭①{}[]{}F K =Δ①①[]1111420240000i i K i i ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦①单元①的贡献矩阵单元②的贡献1Δ2Δ3Δ2F 1F 3①②10i =0=[]22224224i i k i i ⎡⎤=⎢⎥⎣⎦②{}[]{}F K =Δ②②[]2222000042024K i i i i ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦②222233224224F i i F i i Δ⎧⎫⎧⎫⎡⎤=⎨⎬⎨⎬⎢⎥Δ⎣⎦⎩⎭⎩⎭①1122223223000042024F i i F i i Δ⎧⎫⎤⎪⎪⎪⎪⎥=Δ⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪Δ⎢⎥⎣⎦⎩⎭⎩⎭①②叠加原理：{}{}{}[][](){}F F F K K =+=+Δ①②①②[][][][]eeK K K K =+=∑①②[]1111420240000i i K i i ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦①[]2222000042024K i i i i ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦②111122224202442024i i i i i i i i ⎡⎤⎢⎥=+⎢⎥⎢⎥⎣⎦ek ⎡⎤⎣⎦[]ek 思路：[]K局部码——单元分析中，每个单元的结点位移编码。