电路 第四版 答案
- 格式:doc
- 大小:1.92 MB
- 文档页数:26
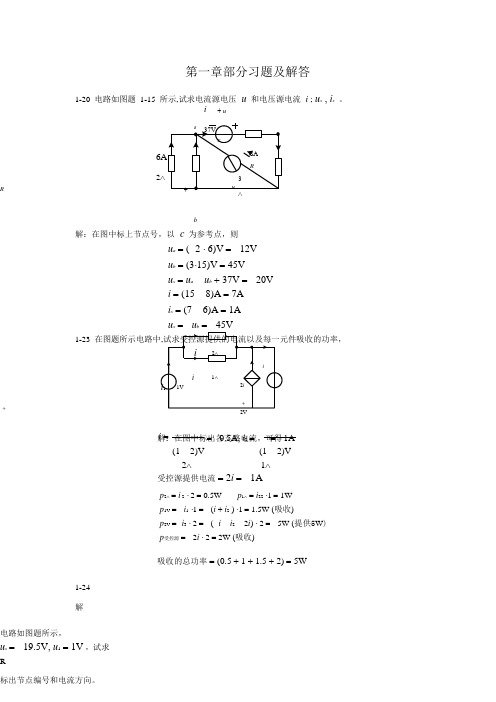
i = = 0.5A, i 2 = =1A 第一章部分习题及解答1-20 电路如图题 1-15 所示,试求电流源电压 u 和电压源电流 i ; u x , i x 。
i+ u2Rb解:在图中标上节点号,以 c 为参考点,则u a = ( 2 ⋅ 6)V = 12V u b = (3⋅15)V = 45V u x = u a u b + 37V = 20V i = (15 8)A = 7A i x = (7 6)A = 1A x b 1-23+解:在图中标出各支路电流,可得(1 2)V (1 2)V 2∧ 1∧受控源提供电流 = 2i = 1Ap 2∧ = i 2 ⋅ 2 = 0.5Wp 1∧ = i 22 ⋅1 = 1Wp 1V = i 1 ⋅1 = (i + i 2 ) ⋅1 = 1.5W (吸收)p 2V = i 3 ⋅ 2 = ( i i 2 2i ) ⋅ 2 = 5W (提供5W ) p 受控源 = 2i ⋅ 2 = 2W (吸收)吸收的总功率 = (0.5 + 1 + 1.5 + 2) = 5W1-24 解电路如图题所示,u s = 19.5V, u 1 = 1V ,试求R标出节点编号和电流方向。
ai +3∧u∧b+ui2∧4∧i+10ucRiiei1 =u11= 1A, u bc = u1 10u1 = 9Vu bc2u ab = i s ⋅ 3 = 10.5Vu ce = u cb + u ba + u s = (9 + 10.5 19.5) = 0V为确定R,需计算i4,u ce = u cd + u de = 0 ® u de = u cd = 10u1 = 10V故1-33 试用支路电流法求解图题所示电路中的支路电流i1, i2 , i3。
a 1∧ci+6Vb解求解三个未知量需要三个独立方程。
由KCL可得其中之一,即i1 + i2 + i3 = 5对不含电流源的两个网孔,列写KVL方程,得网孔badb网孔bdacb2i1 3i2 + 8 = 08 + 3i2 i3 + 6 = 0i 2 = = 4.5A, i s = i 1 + i 2 = 3.5Ai 3 = = 2.5A, i 4 = i s i 3 = ( 3.5 + 2.5)A = 1A整理得: ♦ 2i 1 2 = 8+ 3i ® ♦i 2 = 2A♥♥♣i 1 + i 2 + i 3 = 5 ♣i 1 = 1A ♠ ♠♠3i 2 i 3 = 2 ♠i 3 = 4A♦ i1 + 8i2 3i3 = 9 ® ♦i2 = 1A♥i3 = 1A® ♦♠(R +R)i M2 R1i M 1 R2i M 3 =u ♠♠♠==0♣i M 1 = 24 u® ♦(3 + 4)i M 3 = u ® ♦ ♥i M 3 i M 1 = 8♥ 第二章部分习题及解答2-1试用网孔电流法求图题所示电路中的电流i和电压u ab。

第1章直流电路习题解答1.1 求图1.1中各元件的功率,并指出每个元件起电源作用还是负载作用。
图1.1 习题1.1电路图解 W 5.45.131=×=P (吸收);W 5.15.032=×=P (吸收) W 15353−=×−=P (产生);W 5154=×=P (吸收); W 4225=×=P (吸收);元件1、2、4和5起负载作用,元件3起电源作用。
1.2 求图1.2中的电流I 、电压U 及电压源和电流源的功率。
图1.2 习题1.2电路图解 A 2=I ;V 13335=+−=I I U电流源功率:W 2621−=⋅−=U P (产生),即电流源产生功率6W 2。
电压源功率:W 632−=⋅−=I P (产生),即电压源产生功率W 6。
1.3 求图1.3电路中的电流1I 、2I 及3I 。
图1.3 习题1.3电路图解 A 1231=−=I ;A 1322−=−=I由1R 、2R 和3R 构成的闭合面求得:A 1223=+=I I 1.4 试求图1.4所示电路的ab U 。
图1.4 习题1.4电路图解 V 8.13966518ab −=×+++×−=U 1.5 求图1.5中的I 及S U 。
图1.5 习题1.5电路图解 A 7152)32(232=×+−×+−=IV 221021425)32(22S =+−=×+−×+=I U1.6 试求图1.6中的I 、X I 、U 及X U 。
图1.6 习题1.6电路图解 A 213=−=I ;A 31X −=−−=I I ; V 155X −=⋅=I UV 253245X X −=×−−⋅=I U1.7 电路如图1.7所示:(1)求图(a)中的ab 端等效电阻;(2)求图(b)中电阻R 。
图1.7 习题1.7电路图解 (1) Ω=+=+++×+×+×+=1046418666661866666ab R (2) Ω=−−=712432383R1.8 电路如图1.8所示:(1)求图(a)中的电压S U 和U ;(2)求图(b)中V 2=U 时的电压S U 。


电路第四版课后习题答案第一章:电路基础1. 确定电路中各元件的电压和电流。
- 根据基尔霍夫电压定律和电流定律,我们可以列出方程组来求解未知的电压和电流值。
2. 计算电路的等效电阻。
- 使用串联和并联电阻的计算公式,可以求出电路的等效电阻。
3. 应用欧姆定律解决实际问题。
- 根据欧姆定律 \( V = IR \),可以计算出电路中的电压或电流。
第二章:直流电路分析1. 使用节点电压法分析电路。
- 选择一个参考节点,然后对其他节点应用基尔霍夫电流定律,列出方程组并求解。
2. 使用网孔电流法分析电路。
- 选择电路中的网孔,对每个网孔应用基尔霍夫电压定律,列出方程组并求解。
3. 应用叠加定理解决复杂电路问题。
- 将复杂电路分解为简单的子电路,然后应用叠加定理计算总的电压或电流。
第三章:交流电路分析1. 计算交流电路的瞬时值、有效值和平均值。
- 根据交流信号的表达式,可以计算出不同参数。
2. 使用相量法分析交流电路。
- 将交流信号转换为复数形式,然后使用复数运算来简化电路分析。
3. 计算RLC串联电路的频率响应。
- 根据电路的阻抗,可以分析电路在不同频率下的响应。
第四章:半导体器件1. 分析二极管电路。
- 根据二极管的伏安特性,可以分析电路中的电流和电压。
2. 使用晶体管放大电路。
- 分析晶体管的共发射极、共基极和共集电极放大电路,并计算放大倍数。
3. 应用场效应管进行电路设计。
- 根据场效应管的特性,设计满足特定要求的电路。
第五章:数字逻辑电路1. 理解逻辑门的工作原理。
- 描述不同逻辑门(如与门、或门、非门等)的逻辑功能和电路实现。
2. 使用布尔代数简化逻辑表达式。
- 应用布尔代数的规则来简化复杂的逻辑表达式。
3. 设计组合逻辑电路。
- 根据给定的逻辑功能,设计出相应的组合逻辑电路。
第六章:模拟集成电路1. 分析运算放大器电路。
- 根据运算放大器的特性,分析电路的增益、输入和输出关系。
2. 设计滤波器电路。

第八章 相量法求解电路的正弦稳态响应,在数学上是求非齐次微分方程的特解。
引用相量法使求解微分方程特解的运算变为复数的代数运运算,从儿大大简化了正弦稳态响应的数学运算。
所谓相量法,就是电压、电流用相量表示,RLC 元件用阻抗或导纳表示,画出电路的相量模型,利用KCL,KVL 和欧姆定律的相量形式列写出未知电压、电流相量的代数方程加以求解,因此,应用相量法应熟练掌握:(1)正弦信号的相量表示;(2)KCL,KVL 的相量表示;(3)RLC 元件伏安关系式的相量形式;(4)复数的运算。
这就是用相量分析电路的理论根据。
8-1 将下列复数化为极坐标形式:(1)551j F --=;(2)342j F +-=;(3)40203j F +=; (4)104j F =;(5)35-=F ;(6)20.978.26j F +=。
解:(1)a j F =--=551θ∠ 25)5()5(22=-+-=a 13555arctan-=--=θ(因1F 在第三象限) 故1F 的极坐标形式为 135251-∠=F(2) 13.1435)43arctan(3)4(34222∠=-∠+-=+-=j F (2F 在第二象限) (3) 43.6372.44)2040arctan(40204020223∠=∠+=+=j F (4) 9010104∠==j F (5) 180335∠=-=F(6) 19.7361.9)78.220.9arctan(20.978.220.978.2226∠=∠+=+=j F注:一个复数可以用代数型表示,也可以用极坐标型或指数型表示,即θθj ae a ja a F =∠=+=21,它们相互转换的关系为:2221a a a += 12arctan a a =θ和 θcos 1a a = θsin 2a a =需要指出的,在转换过程中要注意F 在复平面上所在的象限,它关系到θ的取值及实部1a 和虚部2a 的正负。

` 第六章 一阶电路当电路除了电阻元件以外,还含有电容和电感这样的动态元件时,称为动态电路。
动态电路的特征是:(1)当电路的结构或元件的参数发生变化(称为换路),其工作状态的转变需要经历一个过渡时期。
(2)由于动态元件的伏安关系式对时间变量t 的微分或积分关系,因此,描述动态电路的方程是微分方程或积分方程,且方程的阶数由电路中动态元件的个数决定。
对于仅含一个动态元件的电阻电路,电路方程是一阶线性常微分方程,也称一阶电路。
分析动态电路的前提是掌握动态元件和动态电路的特性,常用的分析方法是经典法,它是一种在时间域中进行的分析方法。
其步骤为:(1)利用KCL 和KVL 及元件的伏安关系式建立以时间为自变量的线性常微分方程;(2)确定电路中待求量的初始值;(3)求解方程得所求电压和电流。
6-1 图(a ),(b )所示电路中开关S 在(t = 0) 时动作,试求电路在t =+0时刻电压,电流的初始值。
解(a ):第一步:求t > 0时,即开关S 动作前的电容电压c u (-0)。
由于开关闭合前,电路处于稳定状态,对直流电路有,0=dtdu c电容看作开路。
-=0t 时的电路如题解图(a1)所示。
由图(a1)可得10)0(=-c u V第二步:根据换路时,电容电压c u 不会跃变,所以有=+)0(c u V u c 10)0(_=应用替代定理,用电压等于=+)0(c u V 10的电压源代替电容元件,画出+0等效电路如题解图(a2)所示。
第三步:由+0等效电路,计算得A i c 5.110510)0(-=+-=+ 15)5.1(10)0(10)0(-=-⨯=⨯=++c r i u V换路后,c i 和r u 发生了跃变。
解(b ):第一步:由t<0时的电路,求)0(-l i 的值。
由于t<0时电路处于稳定状态,电感电流l i 为常量,故0=dtdi l,即l u 0=,电感可以看作短路,-=0t 时的电路如题解图(b1)所示,由图可知)0(-l i A 15510=+=第二步:根据换路时,电感电流l i 不会越变,所以有 A i i l l 1)0()0(==-+应用替代定理,用电路等于A i l 1)0(=+的电流源替代电感元件,画出0,等效电路如题解图(b2)所示。
第1章思考题与习题解答1-3 I 1的实际方向向下,I 2的实际方向向左,I 3的实际方向向上;U 1的实际方向下正上负,U 2的实际方向向右正左负,U 3的实际方向下正上负;W 360111-==I U P 释放功率 W 210222=-=I U P 吸收功率 W 150333==I U P 吸收功率1-4 (a )W 162A V 8=⨯=P(b )W 123A V 4-=⨯-=P (c )W 51A V 5=⨯=P (d )W 183A V 6-=⨯-=P 1-6 V 600==RI U W 1802==RI P 1-7 []900kWh kWh 30)(3100)10100(3=⨯⨯⨯⨯==-Pt W1-8 (a )A 1A 268=-=I V 2V )12(bc -=⨯-=U (b )8V V )152512(S =⨯++-⨯+U 4V S =U 1-9 (a )V 1V 2V 3ab =-=U(b )1)V 2(V 5⨯+-=R Ω=7R1-10 (a )A 2)A 221(=+=I电压源功率:W 42)W 2(US -=⨯-=P 电流源功率:W 21)W 2(IS =⨯=P电阻功率:W 2W 222R =⎥⎦⎤⎢⎣⎡=P(b )1V V )211(=⨯+-=U电压源功率:W 22)W 1(US -=⨯-=P电流源功率:[]W 2W 2)1(2)W (IS -=⨯--=⨯-=U P 电阻功率:[]W 4W 122R =⨯=P 1-11 0521=-+I I I0645=--I I I 0236=-+I I I0134=--I I I0S11144S455=-++-U I R I R U I R 0S44433S366=+--+U I R I R U I R05566S222=--+-I R I R U I R 其他回路电压方程略1-12 5V 2)V 756366(-=⨯-+⨯+=U 1-13 0321=-+I I I0S13311=-+U I R I R0S23322=-+U I R I R将已知数据代入方程,得:A 121=I ,A 42-=I ,A 83=I 以b 点位参考点, 0b =V0V 1233a ==I R V 0V 18S1c ==U V 0V 8S2d ==U V 0V 10d c cd =-=V V U以d 点位参考点, 0d =V0V 422a =-=I R V 0V 8S2b -=-=U V 0V 10S2S1c =-=U U V 0V 10d c cd =-=V V U第2章思考题与习题解答2-1 (a )图中四个电阻并联,Ω=2R(b )图中两个2Ω电阻并联后与3Ω电阻串联,然后与4Ω电阻并联,再与6Ω电阻串联,最后与 8Ω电阻并联,Ω=4R 2-2 开关打开A 91.2A 2624)2(6)2(410=++++⨯+=I开关闭合A 94.2A 2222646410=+⨯++⨯=I2-3 (a )(b )6V(c2-4 将电路进行等效变换,可求出电流。
电路理论基础第四版孙立山陈希有主编答案1. 引言《电路理论基础(第四版)》是一本系统介绍电路基本理论和基本分析方法的教材。
本文档是《电路理论基础(第四版)》的答案,提供了教材中习题的解答。
通过这些答案,学生可以检验自己对电路理论的理解,巩固知识点,提高解题能力。
2. 电路理论基础答案2.1 第一章网孔法和节点法的基本概念2.1.1 习题1-1a)略b)略c)略…2.2 第二章电阻网络的基本性质2.2.1 习题2-1a)略b)略c)略…2.3 第三章基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)2.3.1 习题3-1a)略b)略c)略…2.4 第四章电流和电压的计算2.4.1 习题4-1a)略b)略c)略…2.5 第五章电阻串联与并联的简化2.5.1 习题5-1a)略b)略c)略…2.6 第六章电流分压和电压分流2.6.1 习题6-1a)略b)略c)略…2.7 第七章网格分析法2.7.1 习题7-1a)略b)略c)略…2.8 第八章直流电路的戴维南定理2.8.1 习题8-1a)略b)略c)略…2.9 第九章交流电路频率特性2.9.1 习题9-1a)略b)略c)略…2.10 第十章交流电阻、电感和电容的阻抗2.10.1 习题10-1a)略b)略c)略…2.11 第十一章交流电路的功率2.11.1 习题11-1a)略b)略c)略…2.12 第十二章交流电路分析方法2.12.1 习题12-1a)略b)略c)略…3. 结语本文档提供了《电路理论基础(第四版)》的答案,涵盖教材中的习题。
通过阅读答案,学生可以巩固和检验自己的理论知识和解题能力。
希望本答案对学生学习电路理论有所帮助。
第三章电阻电路的一般分析电路的一般分析是指方程分析法,它是以电路元件的约束特性(VCR)和电路的拓扑约束特性(KCL,KVL)为依据,建立以支路电流或回路电流,或结点电压为变量的回路方程组,从中解出所要求的电流、电压、功率等。
方程分析法的特点是:(1)具有普遍适用性,即无论线性和非线性电路都适用;(2)具有系统性,表现在不改变电路结构,应用KCL,KVL,元件的VCR建立电路变量方程,方程的建立有一套固定不变的步骤和格式,便于编程和用计算机计算。
本章的重点是会用观察电路的方法,熟练运用支路法、回路法和结点电压法的“方程通式”写出支路电流方程、回路方程和结点电压方程,并加以求解。
3-1 在一下两种情况下,画出图示电路的图,并说明其节点数和支路数(1)每个元件作为一条支路处理;(2)电压源(独立或受控)和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理。
解:(1)每个元件作为一条支路处理时,图(a)和(b)所示电路的图分别为题解3-1图(a1)和(b1)。
图(a1)中节点数6b==n,支路数11图(b1)中节点数7=bn,支路数12=(2)电压源和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理时,图(a)和图(b)所示电路的图分别为题解图(a2)和(b2)。
图(a2)中节点数4b=n,支路数8=图(b2)中节点数15b=n,支路数9=3-2指出题3-1中两种情况下,KCL,KVL独立方程数各为多少?解:题3-1中的图(a)电路,在两种情况下,独立的KCL方程数分别为(1)51==4n1--1=6-1-=n (2)3独立的KVL方程数分别为(1)61=84+--n+=1b1=111b (2)5+6+--n=图(b)电路在两种情况下,独立的KCL方程数为(1)61=5-=1n-7n (2)41=1-=-独立的KVL方程数分别为(1)6+1=95b1-n+=-=1271b (2)51=-n++-3-3对题图(a)和(b)所示G,各画出4个不同的树,树支数各为多少?解:一个连通图G 的树T 是这样定义的:(1) T 包含G 的全部结点和部分支路;(2) T 本身是连通的且又不包含回路。
根据定义,画出图(a)和(b)所示图G 的4个树如题解3-3图(a)和(b)所示。
树支数为结点数减一。
故图(a)的数有树支,图(b)的树有树支1615n -=-=o3-4 图示桥形电路共可画出16个不同的树,试一一列出(由于节点树为4,故树支为3,可按支路号递减的方法列出所有可能的组合,如123,124,…,126,134,135,…等,从中选出树)。
解:图示电路,16个不同的树的支路组合为:(123),(124),(125),(136),(145),(146),(156),(234),(235),(236),(246),(256),(345),(346),(456)3-5 对题图3-3所示的1G 和2G ,任选一树并确认其基本回路组,同时指出独立回路数和网孔数各为多少?解:在连通图G 中,由树支和一个连支组成的回路称为G 的基本回路(或单连支回路),基本回路是独立回路,网孔也是独立回路,因此,基本回路数=独立回路数+网孔数。
对一个节点数为n ,支路数为b 的连通网,其独立回路数)1(+-=n b l 。
从题图3-3所示的1G 和2G 中任选一树,(见题解3-5图(a)和(b)中粗线所示),对应于这一树的基本回路分别为6,521==l l 。
3-6 对图示非平面图,设:(1)选择支路(1,2,3,4)为树;(2)选择支路(5,6,7,8)为树,问独立回路各有多少?求其基本回路组。
解:图中有结点数5=n ,支路数10=b ,故独立回路树为615101=+-=+-n b(1)选择支路(1,2,3,4)为树,对应的基本回路组为:(1,2,3,4,5),(1,2,3,7),(1,2,6),(2,3,4,8),(2,3,9),(3,4,10)(2)选择支路(5,6,7,8)为树,对应的基本回路组为:(1,5,8),(2,5,6,8),(3,6,7),(4,5,7),(5,7,8,9),(5,6,10)3-7 图示电路中V u V u R R R R R R s s 40,20,2,8,4,1063654321==Ω=Ω==Ω=Ω==,用支路电流法求解电流5i 。
解:本题电路有4个节点,6条支路,独立回路数为6-4+1=3。
设各支路电流和独立回路绕行方向如图所示,由KCL 列方程,设流出节点的电流取正号。
节点① 0621=++i i i节点② 0432=++-i i i节点③ 0654=-+-i i i由KVL 列方程回路Ⅰ 401082246-=--i i i回路Ⅱ 2041010321-=++-i i i回路Ⅲ 20884543=++-i i i联立求解以上方程组,得电流 A i 956.05-=注:由本题的求解过程可以归纳出用支路电流法分析电路的步骤如下:(1)选定各支路电流的参考方向;(2)任取(n-1)个结点,依 KCL 列独立结点电流方程;(3)选定(b-n+1)个独立回路(平面回路可选网孔),指定回路的绕行方向,根据KVL 列写独立回路电压方程;(4)求解联立方程组,得到个支路电流,需要明确:以上支路电流法求解电路的步骤只适用于电路中每一条支路电压都能用支路电流表示的情况,若电路中含有独立电流源或受控电流源,因其电压不能用支路电流表示,故不能直接使用上述步骤。
此外,若电路中含有受控源,还应将控制量用支路电流表示,即要多加一个辅助方程。
3-8 用网孔电流法求解题图3-7中电流5i 。
解:设网孔电流为1,23,l l l i i i ,其绕行方向如题图3-7中所标。
列写网孔方程⎪⎩⎪⎨⎧=+---=-+--=--20204820424104081020321321321l l l l l l l l l i i i i i i i i i应用行列式法解上面方程组 48802048202410401020,5104204842410810203-=------=∆=------=∆ 所以 A i i l 956.051044880335-=-=∆∆== 注:网孔电流法是以假想的网孔电流作为求解量,它仅适用于平面电路。
从本题的求解可以归纳出用网孔电流法求解电路的步骤是:(1)选取网孔电流1,23,l l l i i i ,如网孔电流方向即认为是列网孔 KVL 方程的绕行方向。
(2)列网孔电流方程。
观察电路求自电阻1122,R R L (一个网孔中所有电阻之和称该网孔的自电阻,如本题中11223320,24,20R R R =Ω=Ω=Ω,自电阻总为正值);互电阻121323,,R R R L (两网孔公共支路上的电阻之和,如本题中12132310,8,4R R R =-=-=-,当流过互电阻的两网孔电流方向一致,互电阻为正值,否则为负值),等效电压源数值(方程右方为各回路中电压源的代数和,与网孔电流方向一致的电压源前取负号,否则取正号)。
3-9 用回路电流法求解题图3-7中电流3i 。
解法一:取回路电流为网孔电流,如题图3-7中所示。
回路方程同题3-8中方程。
故有488051043-=∆=∆ 128002020842010840203-=------=∆所以A i i i A i A i l l l l 5517.19561.05078.29561.0510448805078.25104128003233322-=+-=-=-=-=∆∆=-=-=∆∆=解法二:取回路电流如题解3-9图所示。
仅让Ⅱ号回路电流流经3i 所在的支路。
列写回路方程。
⎪⎩⎪⎨⎧=++--=++--=--03620182020241040181020321321321l l l l l l l l l i i i i i i i i i用行列式法求上面方程组792036018202010184020,51043620182024101810202-=-----=∆=----=∆ 所以 A i i l 5517.151047920223-=-=∆∆== 显然解法二中回路电流的选取法使计算量减小。
注:回路电流法适用于平面或非平面电路,比网孔法更具灵活性。
回路法分析电路时,首先要确定一组基本回路,表定回路电流的绕行方向,其余步骤与网孔法类似。
需要指出的是回路电流法中两回路的共有支路有时会有多条,因而互有电阻的确定要特别细心。
否则会发生遗漏互有电阻的错误。
3-10 用回路电流法求解题图中Ω5电阻中的电流i 。
解:选取网孔为基本回路,回路电流的绕行方向如图中所示。
列回路方程⎪⎩⎪⎨⎧=+-=-+-=+-=-016848817601648326123232121l l l l l l l i i i i i i i 应用行列式法 4608080481760612,19201680817606123=---=∆=----=∆ 所以 A i i l 4.21920460833==∆∆== 3-11 用回路电流法求解图示电路中电压o U 。
解:回路电流如图中所标。
因A 3电流源仅与回路Ⅰ相关,即有,A i l 31=其余两回路的方程为865013620101813610508321321=-=++-=++-l l l l l l i i i i i i把A i l 31=带入两个方程中,加以整理得 ⎩⎨⎧=+=+140201016010503232l l l l i i i i解得 A i l 22=电压 V i U l o 80240402=⨯=⨯=3-12 用回路电流法求解图示电路中电压U 。
解:按图示设网孔电流为回路电流。
因受控电流源仅和Ⅲ号回路相关,故有1615n -=-=,对回路Ⅰ和Ⅱ列方程,并代入131.0l l i i -=有⎩⎨⎧-=⨯++-=⨯+-4201.0510401.010*********l l l l l l i i i i i i整理得⎩⎨⎧-=+-=-420105.304352121l l l l i i i i 解得 Ai i A i i i l l l l l 5.0)5(1.01.053575.43435475.4313222=-⨯-=-=-=⨯-=⨯=-= 选外层回路列KVL 方程 042012021=-+⨯+U i i l l从中解出 V U 25.276420)75.43(1)5(20=+-⨯+-⨯=3-13 用回路电流法求解题图(a),(b)两电路中每个元件的功率,并做功率平衡检验。
解(a):选取(a)图中网孔为基本回路,回路电流方向如图中所标,列回路方程 ⎪⎪⎩⎪⎪⎨⎧==++⨯-=ϕU i i i i i l l l l l 41102311533211 )3()2()1(式中ϕU 为受控电流源的控制量,需要用回路电流加以表示,所以增补一个方程 3324)(2l l l i i i U =+⨯=ϕ )4(从中解得 32l l i i =把方程)1(和)4(代入方程)2(中,有 10231522=++-l l i i即 A i i l l 552532=== 各元件的功率分别为V 10电压源发出的功率W i p l 505101021=⨯=⨯=A 15电流源发出功率[][]Wi i i i p l l l l 105010120315 )(1)(31521312=⨯+⨯⨯=-⨯++⨯⨯=受控电流源发出功率 [][]W i i U i i U p l l l l 400)2060(54203 )(34133313=+⨯=⨯+⨯⨯=++⨯⨯=ϕϕWi i i i i i p l l l l l l 1500203102101 )(3)(2)(12223132221=⨯+⨯+⨯=+⨯++⨯+-⨯=吸电路共发出功率 W p p p p1500400105050321=++=++=发满足 吸发p p=解(b):解法一:取网孔为基本回路,电路电流如图(b)中所标。