MATLAB和PDE工具箱

（整理）matlab部分工具箱.1)通讯工具箱(Communication Toolbox)。

令提供100多个函数和150多个SIMULINK模块用于通讯系统的仿真和分析——信号编码——调制解调——滤波器和均衡器设计——通道模型——同步可由结构图直接生成可应用的C语言源代码。

2)控制系统工具箱(Control System Toolbox)。

鲁连续系统设计和离散系统设计* 状态空间和传递函数* 模型转换* 频域响应：Bode图、Nyquist图、Nichols图* 时域响应：冲击响应、阶跃响应、斜波响应等* 根轨迹、极点配置、LQG3)财政金融工具箱(FinancialTooLbox)。

* 成本、利润分析，市场灵敏度分析* 业务量分析及优化* 偏差分析* 资金流量估算* 财务报表4)频率域系统辨识工具箱(Frequency Domain System ldentification Toolbox* 辨识具有未知延迟的连续和离散系统* 计算幅值／相位、零点／极点的置信区间* 设计周期激励信号、最小峰值、最优能量诺等5)模糊逻辑工具箱(Fuzzy Logic Toolbox)。

* 友好的交互设计界面* 自适应神经—模糊学习、聚类以及Sugeno推理* 支持SIMULINK动态仿真* 可生成C语言源代码用于实时应用(6)高阶谱分析工具箱(Higher—Order SpectralAnalysis Toolbox * 高阶谱估计* 信号中非线性特征的检测和刻画* 延时估计* 幅值和相位重构* 阵列信号处理* 谐波重构(7)图像处理工具箱(Image Processing T oolbox)。

* 二维滤波器设计和滤波* 图像恢复增强* 色彩、集合及形态操作* 二维变换* 图像分析和统计(8)线性矩阵不等式控制工具箱(LMI Control Toolbox)。

* LMI的基本用途* 基于GUI的LMI编辑器* LMI问题的有效解法* LMI问题解决方案(9)模型预测控制工具箱(ModelPredictive Control Toolbox* 建模、辨识及验证* 支持MISO模型和MIMO模型* 阶跃响应和状态空间模型(10)u分析与综合工具箱(u-Analysis and Synthesis Toolbox)* u分析与综合* H2和H无穷大最优综合* 模型降阶* 连续和离散系统* u分析与综合理论(11)神经网络工具箱(Neursl Network T oolbox)。

MATLAB R2009a\help\product help\Partial Differential Equation Toolbox\Graphical User Interface this chapter discusses the graphical user interface (GUI) pdetool. The main components of theGUI are the menus, the dialog boxes, and the toolbar.PDE Toolbox 求解椭圆、抛物、双曲方程的基本步骤第一步：在MATLAB命令窗口，输入命令>> pedtool进入PDE Toolbox窗口第二步：建立几何模型在toolbar中选择几何图形，如建立单位圆，则点击第3或第4个按钮，用鼠标的右键，click-and-drag，创立一个圆c1双点击圆c1，弹出dialog box，输入几何参数第三步：输入边界条件点击输入边界条件。

若所有边界条件都是齐次的第一类边界条件，此步可省略。

第四步：输入偏微分方程参数点击输入偏微分方程参数。

第五步：划分网格点击一次，初步划分网格。

点击多次，细划网格。

单元圆细化两次的结果第六步：输入初始条件若方程是椭圆的，此步可省略。

点击菜单中的 Parameters 选项。

若方程是抛物的，则需输入初始位移条件及计算参数若方程是双曲的，则需输入初始位移条件、初始速度条件及计算参数第七步：求解有限元方程点击求解有限元方程。

第八步：绘图点击绘图。

利用绘图选项，将计算结果进行可视化输出。

下面是两个编程算例。

泊松方程边值问题单位圆域内泊松方程齐次边值问题其精确解为试求泊松方程问题的数值解并与精确解比较。

解 (1) 建立有限元模型在MATLAB 命令窗口，输入命令>> pedtool进入PDE Toolbox 窗口在toolbar 中点击第3或第4个按钮，用鼠标的右键，click-and-drag ，创立一个圆c1()⎪⎩⎪⎨⎧=+=<+=+-1,01,12222y x u y x u u yy xx ()22141y x u --=双点击圆c1，输入几何参数输入边界条件（略）。

实验六：使用偏微分方程工具箱对电磁场的仿真一、实验目的与要求1.掌握微分方程工具箱的使用方法；2.掌握使用偏微分方程工具箱分析电磁场。

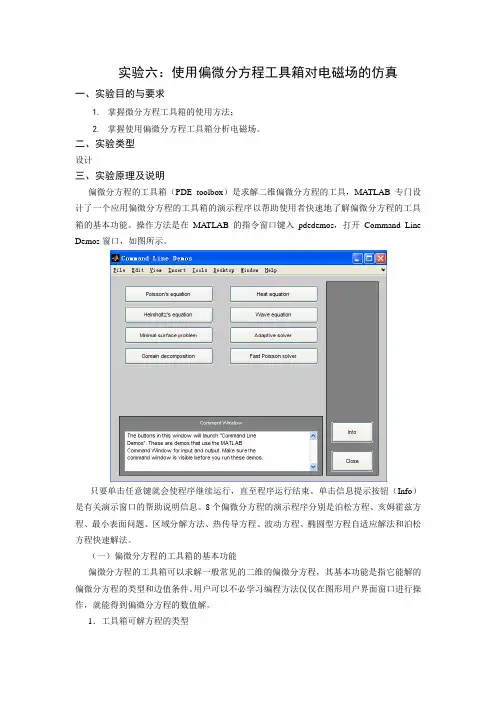
二、实验类型设计三、实验原理及说明偏微分方程的工具箱（PDE toolbox）是求解二维偏微分方程的工具，MA TLAB专门设计了一个应用偏微分方程的工具箱的演示程序以帮助使用者快速地了解偏微分方程的工具箱的基本功能。

操作方法是在MA TLAB的指令窗口键入pdedemos，打开Command Line Demos窗口，如图所示。

只要单击任意键就会使程序继续运行，直至程序运行结束。

单击信息提示按钮（Info）是有关演示窗口的帮助说明信息。

8个偏微分方程的演示程序分别是泊松方程、亥姆霍兹方程、最小表面问题、区域分解方法、热传导方程、波动方程、椭圆型方程自适应解法和泊松方程快速解法。

（一）偏微分方程的工具箱的基本功能偏微分方程的工具箱可以求解一般常见的二维的偏微分方程，其基本功能是指它能解的偏微分方程的类型和边值条件。

用户可以不必学习编程方法仅仅在图形用户界面窗口进行操作，就能得到偏微分方程的数值解。

1．工具箱可解方程的类型定义在二维有界区域Ω上的下列形式的偏微分方程，可以用偏微分方程工具箱求解：椭圆型()f au u c =+∇∙∇- 抛物型()f au u c tu d =+∇∙∇-∂∂ 双曲型()f au u c tu d =+∇∙∇-∂∂22 本征值方程()du au u c λ=+∇∙∇-式中，u 是偏微分方程的解；c 、a 、d 、f 是标量复函数形式的系数，在抛物型和双曲型方程中，它们也可以是t 的函数，λ是待求的本征值。

当c 、a 、f 是u 的函数时，称之为非线性方程，形式为()()()()u f u u a u u c =+∇∙∇-也可以用偏微分方程工具箱求解。

2．工具箱可解方程的边值条件解偏微分方程需要的边值条件一般为下面两种之一：狄里赫利(Diriclet)边值条件 hu=r广义诺曼(Generalized Neumann)边值条件 ()g qu u c n =+∇∙式中，n为边界外法向单位向量；h 、q 、r 、g 是在边界上定义的复函数。

Hamilton 算子:(,)i j x y x y∂∂∂∂∇=+=∂∂∂∂ Laplace 算子:2222()x y∂∂∆=∇∇=+∂∂ MATLAB 的PDE 工具箱能解的方程类型:椭圆型PDE:() in c u au f -∇∇+=ΩΩ为有界平面.c, a, f,和 未知量u 是标量,且是定义在Ω上的 复函数. c 可以是 Ω上的2×2的矩阵函数.抛物型PDE() in u d c u au f t∂-∇∇+=Ω∂双曲型PDE22() in u d c u au f t∂-∇∇+=Ω∂特征值问题() in c u au du λ-∇∇+=Ωd 是 Ω上的复函数, λ 是未知的特征值.对于抛物和双曲型 PDE ,参数 c, a, f, 和d 可依赖时间t. 非线性求解器可解非线性椭圆 PDE所谓非线性椭圆 PDE 就是椭圆PDE 中的参数 c, a 和 f 是(未知函数)u 的函数.对于如何使用非线性求解器,还需做特别的介绍.还能求方程组等其他一些的问题.下面是针对标量u 而定义的边界条件:狄利克雷边界条件: hu=r on ∂ΩDirichlet: hu = r广义黎曼条件Generalized Neumann: ()n c u qu g ∇+= on ∂Ω . n 是边界∂Ω上单位向外法向量. g, q, h 和r 是定义在Ω上的复值函数.(特征值问题是齐次条件问题,即 g = 0, r = 0.)在非线性情形下,系数g, q, h 和r 可以依赖于u,对于双曲和抛物型PDE,系数可以依赖于时间t.对于2维方程组系统, Dirichlet 边界条件是:11112212112222h u h u r h u h u r +=+=广义Neumann 条件是:11112211112212112222112222()()()()n c u n c u q u q u g n c u n c u q u q u g ∇+∇++=∇+∇++=混合边界条件是:1111221h u h u r +=111122111122111211222211222212()()()()n c u n c u q u q u g h n c u n c u q u q u g h μμ∇+∇++=+∇+∇++=+此处 µ 的计算要满足 Dirichlet 边界条件.典型方程的计算实例1. 单位圆上的Possion 方程的边值问题:10u u∂Ω-∆=⎧⎪⎨∣=⎪⎩ (此问题有精确解22(1)(,)4x y u x y --=)2. 散射问题一块圆形金属片,中心挖去一正方形,外边界满足Neumann 条件,内边界满足Dirichlet 条件,考虑以-x 方向的入射波.得到求解此入射波的反射问题:2600 on 60 i x r k r r e r n-⎧⎪∆+=Ω⎪=-⎨⎪∂⎪=-∂⎩内边界上外边界上3. 最小曲面问题平面上一圆形区域22{(,)1}x y x y Ω=∣+<,求此区域上具有最小面积的函数u(x,y),且在区域边界上满足2u x =.此问题可转化为如下的偏微分方程问题: 20, in 1u u u x ∂Ω⎧⎛⎫⎪ ⎪-∇=Ω⎪ ⎪⎨+∇⎭⎪⎪∣=⎩4. 设区域为单位圆,求解() in u=0. onu ⎧-∇∇=-Ω⎪⎨∂Ω⎪⎩ 此问题的精确解为:222()1u x y =+-5. 热传导方程:带有矩形孔的矩形金属板的热传导问题 0100, u 1, n u 0, n u0u d u t u 0τ=τ∂⎧-∆=⎪∂⎪=⎪⎪∂⎪=-⎨∂⎪∂⎪=⎪∂⎪∣=⎪⎩左边界上右边界上其它边界上 外边界顶点坐标(-0.5,-0.8),(0.5,-0.8),(0.5,0.8),(-0.5,0.8).内边界顶点坐标(-0.05,-.4),(0.05,-0.4),(0.05,0.4),(-0.05,0.4).6. 二维波动方程的定解问题:(,){(,),11,11}x y x y x y ∈Ω=-<<-<<2211sin()20,000,arctan{cos()}2u 3sin().n x x y u u t u u n t u x x e πππ=±=±⎧∂-∆=⎪∂⎪⎪∣=⎪∂⎪∣=⎨∂⎪⎪==⎪⎪∂⎪=∂⎩7 特征值问题的例0u u u λ∂Ω-∆=⎧⎪⎨∣=⎪⎩ (,){(,)0,1}x y x y x y ∈Ω=∣<< 此问题的精确解为:特征值222,(),,1,2,3,,m n m n m n λπ=+= 对应的特征函数为:,sin sin m n u mx ny ππ=练习: (1)222204030,04,03(3),0,sin ,0;4x x y y u ux y x y u y y u u x u π====⎧∂∂+=<<<<⎪∂∂⎪⎪⎨∣=-∣=⎪⎪∣=∣=⎪⎩ (2) 222201011,01,011,1,0,1;y y x x u ux y x y u u uu u x ====⎧∂∂+=-<<<<⎪∂∂⎪⎪⎨∣=∣=⎪∂⎪(+∣=∣=⎪∂⎩ (3) 222222220,4;uu x y x y u x y Γ⎧∂∂+=+<⎪∂∂⎨⎪∣=⎩ (4) 111,1,130,()0,40x x y u u x y u u u n un λ=-==±-∆=-<<⎧⎪∂⎪∣=-∣=⎨∂⎪∂⎪∣=∂⎩(5) 12222220,0,75,0,x u u x y u u u un =-ΓΓ⎧∂∂+=⎪∂∂⎪⎪⎨∣=∣=∣=⎪∂⎪∣=⎪∂⎩在其余边界参考书偏微分方程的MATLAB解法武汉大学出版社。

MATLAB偏微分方程工具箱使用手册一、Matlab偏微分方程工具箱介绍Matlab偏微分方程工具箱是Matlab中用于求解偏微分方程（PDE）问题的工具。

它提供了一系列函数和工具，可以用于建立、求解和分析PDE问题。

PDE是许多科学和工程领域中的重要数学模型，包括热传导、扩散、波动等现象的数值模拟、分析和优化。

Matlab偏微分方程工具箱为用户提供了丰富的功能和灵活的接口，使得PDE问题的求解变得更加简单和高效。

二、使用手册1. 安装和启用在开始使用Matlab偏微分方程工具箱前，首先需要确保Matlab已经安装并且包含了PDE工具箱。

确认工具箱已经安装后，可以通过以下命令启用PDE工具箱：```pdetool```这将打开PDE工具箱的图形用户界面，用户可以通过该界面进行PDE 问题的建立、求解和分析。

2. PDE建模在PDE工具箱中，用户可以通过几何建模工具进行PDE问题的建立。

用户可以定义几何形状、边界条件、初值条件等，并选择适当的PDE方程进行描述。

PDE工具箱提供了各种几何建模和PDE方程描述的选项，用户可以根据实际问题进行相应的设置和定义。

3. 求解和分析一旦PDE问题建立完成，用户可以通过PDE工具箱提供的求解器进行求解。

PDE工具箱提供了各种数值求解方法，包括有限元法、有限差分法等。

用户可以选择适当的求解方法，并进行求解。

求解完成后，PDE工具箱还提供了丰富的分析功能，用户可以对结果进行后处理、可视化和分析。

4. 结果导出和应用用户可以将求解结果导出到Matlab环境中，并进行后续的数据处理、可视化和分析。

用户也可以将结果导出到其他软件环境中进行更进一步的处理和应用。

三、个人观点和理解Matlab偏微分方程工具箱是一个非常强大的工具，它为科学和工程领域中的PDE问题提供了简单、高效的解决方案。

通过使用PDE工具箱，用户可以快速建立、求解和分析复杂的PDE问题，从而加快科学研究和工程设计的进程。

利用Matlab中的PDE工具箱进行偏微分方程求解！在科学技术各领域中，有很多问题都可以归结为偏微分方程问题。

在物理专业的力学、热学、电学、光学、近代物理课程中都可遇见偏微分方程。

偏微分方程，再加上边界条件、初始条件构成的数学模型，只有在很特殊情况下才可求得解析解。

随着计算机技术的发展，采用数值计算方法，可以得到其数值解。

下面的几个简单例子，将为大家介绍如何利用Matlab中的PDE 工具箱进行偏微分方程的求解！抛物线型受热金属块的热传导问题：一块受热的有矩形裂纹的金属块。

金属块的左侧被加热到100℃，右侧热量则以恒定速率降低到周围空气的温度，所有其他边界都是独立的，于是边界条件为：初始温度为0℃。

指定起始时间为0，研究5s的热扩散问题。

求解结果如下：具体步骤：1.建模。

先画一个起点为(-0.5,-0.8)，终点为(0.5,0.8)的矩形，再建另一个矩形，起点(-0.05,-0.4)，终点(0.05,0.4)，然后在设置公式中输入R1-R2；2.设置边界条件；3.PDE中设置参数，d=1,c=1,a=0,f=0；4.初始化网格并细化一次；5.在Solve Parameter中，设置u0=0，时间为[0:0.5:5]，然后求解。

注意到金属块的温度升高很快，可试着改变时间列表的表达式为logspace(-2,0.5,20)以便观察。

双曲线型方形薄膜横向波动问题（波动方程）：薄膜左侧和右侧固定（u=0），上端和下端自由：满足边界条件的初值为：求解结果如下：具体步骤：1.建模，画出起点(-1,-1)，终点(1,1)的矩形；2.确定边界条件；3.PDE Specification对话框中选择双曲线型，参数设为c=1,a=0,f=0,d=1；4.初始化网格，并细化一次；5.在Solve Parameters对话框的时间中输入linspace(0,5,31)，u的初值为atan(cos(pi/2*x))，一次偏导的初值为3*sin(pi*x).*exp(sin(pi/2*y))，然后求解。

Matlab各工具箱功能简介(部分)Ｔoolbo某工具箱序号工具箱备注一、数学、统计与优化1 Symbolic Math Toolbo某符号数学工具箱Symbolic Math Toolbo某? 提供用于求解和推演符号运算表达式以及执行可变精度算术的函数。

您可以通过分析执行微分、积分、化简、转换以及方程求解。

另外，还可以利用符号运算表达式为 MATLAB?、Simulink? 和Simscape? 生成代码。

Symbolic Math Toolbo某包含 MuPAD? 语言，并已针对符号运算表达式的处理和执行进行优化。

该工具箱备有 MuPAD 函数库，其中包括普通数学领域的微积分和线性代数，以及专业领域的数论和组合论。

此外，还可以使用 MuPAD 语言编写自定义的符号函数和符号库。

MuPAD 记事本支持使用嵌入式文本、图形和数学排版格式来记录符号运算推导。

您可以采用 HTML 或 PDF 的格式分享带注释的推导。

2 Partial Differential Euqation Toolbo某偏微分方程工具箱偏微分方程工具箱?提供了用于在2D，3D求解偏微分方程（PDE）以及一次使用有限元分析。

它可以让你指定和网格二维和三维几何形状和制定边界条件和公式。

你能解决静态，时域，频域和特征值问题在几何领域。

功能进行后处理和绘图效果使您能够直观地探索解决方案。

你可以用偏微分方程工具箱，以解决从标准问题，如扩散，传热学，结构力学，静电，静磁学，和AC电源电磁学，以及自定义，偏微分方程的耦合系统偏微分方程。

3 Statistics Toolbo某统计学工具箱Statistics and Machine Learning Toolbo某提供运用统计与机器学习来描述、分析数据和对数据建模的函数和应用程序。

您可以使用用于探查数据分析的描述性统计和绘图，使用概率分布拟合数据，生成用于Monte Carlo 仿真的随机数，以及执行假设检验。

Using the MATLAB PDE TOOLBOXThe MATLAB PDE Toolbox is a tool for solving two-dimensional linear partial differential equations by finite element methods. This document is intended to guide you through the use of the graphical user interface for interactive use. It assumes that the reader is running MATLAB and the PDE toolbox in a graphical environment.At the MATLAB prompt, type pdetool. You should see a window like the one below pop up.We will work through the solution of Laplace's equation with Dirichlet boundary conditions. Solutions of Laplace's equation, called harmonic functions, describe situations in which forces are balanced, as might occur in electrostatics or thermal equilibria. This is an example which might be first encountered in an elementary PDE course, and which you might solve by Fourier series methods, by hand; you will find that you obtain the solution faster with the PDE Toolbox, and that you also obtain a visual representation, which may contribute to the more important goal of understanding. We will then modify the example, to one which might not be so easily done by hand.1.Draw the region of interest: suppose we want the rectangle (x,y) = [0, 3] X [0, 1].o In the Options menu, select Grid and Snap; then set the Axes' Limits to [-1 4] and [-1 2]. When finished, click Apply and Close the Axes' Limits window.1.o In the Draw menu, select Rectangle/Square (not centered).o In the drawing region, click and hold with the cursor at the origin, and drag it to the point with coordinates (3,1). The region will be shaded and marked R1.2.Set up the boundary conditions: suppose we want the unknown solution function u to be -1 on the long horizontal sides, and +1 on the short vertical sides.o In the Boundary menu, select Boundary Mode. The window changes to this:o In the drawing region, double click on the left edge of the rectangle. The boundary condition window pops up. The default Dirichlet condition h*u=r isOK, the default h=1 is OK; change the value of r to +1.3.o Do the same thing with the right edge: double-click, set the value. On the top and bottom edges, set r to -1. Be patient and careful. When the boundary conditionsare correctly set, you should be able to click on any edge, and see the correctvalue for r.4.Specify the particular PDE of interest:o In the PDE menu, select PDE specification. The pde specification window pops up; we are doing the default type of problem, elliptic, of the form -div(c*grad(u))+ a*u = f, wherea=0, f=0, and c=1. Change the values as needed, and click onOK.4.Generate the mesh:o In the Mesh menu, select Initialize Mesh. This time we will use the default mesh.5.Solve the Finite Element problem:o In the Solve menu, select Solve PDE. The figure in the main drawing area changes.6.Generate other plots:o In the Plot menu, select Parameters. The plot parameter window pops up; click on the check boxes for color, contour, and height, then on the Plot button.A new figure window pops up, with the appropriate plot.Click the Done button [the height plot will remain the default].The contours are pretty jagged, you may wish to get a better result. Go back to the Mesh menu, and select Refine mesh; Solve again; if you wish, repeat the process. You can click and hold with the left mouse button, and then drag to change the viewing angle.Let's solve a similar problem: Laplace's equation on the same rectangle, with different boundary conditions.1.Go back to Boundary mode.o Make the boundary conditions on the short vertical sides be 4*sin(pi*y).^2 .On the long horizontal sides make it -.05 * x.^4 .* (3 - x).^2 on the bottom, -.05*x.^2.*(3 - x).^4 on the top.2.Then solve and plot, again. This time we have set the plot parameters to color andcontour, but not height:In the figure below, we have again checked the height box in the Plot Parameters window, and under Property, we have made the color vary with abs(grad(u)). You can click on the figure window and drag to obtain a different point of view.You may want to save your work; click on File, then Save As... Save your session in your own directory, as pdeintro.m. Then you can quit MATLAB, and at some later time restart it and enterpdeintro at the MATLAB command prompt to return to the current state.The PDE Toolbox can be used from the command prompt without using the GUI interface illustrated above, or in batch mode using m-files. For example, several demonstration files are included with the package; at the MATLAB command prompt,type pdedemo1 [alternatively, pdedemos brings up a menu window].The code may be examined, in the $MATLAB/toolbox/pde directory.The MATLAB PDE Toolbox is a product of Computer Solutions Europe AB.。

Introduction to the Matlab Partial DifferentialEquation Toolbox——PDETOOLMatlab PDE Toolbox介绍(1) 可以求解(非)线性椭圆型PDE,以及线性抛物,双曲问题。

可以求解单个方程，也可以求解方程组：(2) 自适应网格加密, 区域分裂(如Lshape区域分为3部分进行计算, matlab有演示算例)(3) 有两种方式调用偏微分方程工具箱中的函数：⏹matlab script⏹GUI(by >>pdetool)如果采用GUI方式,一般的求解过程是：Starting the PDE Toolbox 开启工具箱Specifying the Domain 指定二维求解区域Specifying the Boundary Conditions 指定边界条件Specifying the PDE 指定PDE方程(椭圆、抛物、双曲)Specifying the Initial Mesh 指定初始网格Mesh Refinement 设置网格加密Solving boundary value problem and plotting solution 求解(初)边值问题并绘图 Working in the MA TLAB workspace (export data｛p,e,t,u｝) 对变量空间进行操作 Post-Processing the Solution 后处理数值解比如tri2grid(p,t,u,x,y)Visualization Commands 比如绘图命令pdemesh(p,e,t), pdesurf(p,t,u) (4) 非结构三角网格的网格数据结构下面是一个半圆形区域的非结构网格的剖分结果：(5) 一般的椭圆问题的系数矩阵c的输入法则：注意c可以写成Matlab PDE Toolbox 允许这样。

注意上面每个,,{1,1}ij c i j ∈都是一个22⨯的矩阵, 在GUI 中输入时写在一行按照(1,1),(2,1),(1,2),(2,2)的顺序输入(因为Matlab 的二维数组是按列优先存放的).(6) 非线性问题的2个例子, 非线性是指中的函数c,a,f 依赖于u ，ux 或者uy 。

Matlab 实例教程：PDE工具箱函数用法讲解Matlab工具箱中任何功能都能用命令行的形式解决，对于一些复杂的问题，gui形式是解决不了的，这时就必须用命令行形式自己编程来解决问题。

最近查看了一些pde工具箱中的函数，对两个函数的用法做一些说明。

PDE解决问题流程与一般的fam方法一样，先画出几何模型，再画网格，加边界、载荷，求解。

MATLAB中的画几何命令有两种方式，其中一种方式是自己编写m文件，MATLAB中的命令是pdegeom，实际上这不是一个命令，而是要用户自己编写的一个几何m文件。

在网上找了半天，也没见有人介绍过这个函数的用法，网上大多数只是列出pde中的函数而已，感叹一下….这个函数名可以任意，假设为tt，参数有两个（bs,s）如果输入参数为0，1时，函数也必须要能有返回值。

函数的意义为：参数为0个，即没有参数时，返回边界总共段数。

参数为1个是，即只有bs，返回边界指定段的参变量范围。

参数为2个时，返回每段边界长度为s时的坐标。

函数参数意义bs表示几何边界段数，如矩形，边界为四段，三角开边界肯定为三段….s为第bs段时的长度，bs与s可以为向量，但是要一一对应，即bs为几个值，s也得为几个值。

下面具体来讲下函数如何实现当参数为2时的返回值。

其实函数中实现的内容是指用一个参变量来控制指定段的边界坐标，也就是说对任意一段边界，上面的坐标设为参变量的函数，假设参变量为t,则对任一边界，坐标为(x(t),y(t))，参变量的范围由用户自己定义。

由以上可以看出，参变量其实有无穷多种取法，看自己怎么设定而已。

例如：一个矩形，四条边，返回每一段对应长度的坐标，m文件为：function [x,y]=tt(bs,s);ux=1;uy=1;nbs=4; //表示有四段if nargin==0x=nbs;returnenddl=[0,0,0,0; //参变量t范围，第一行为起始值，第二行为结束值，这两个值理论3,1,2,3; //可以任意设置，只要后面能对应求出边界上坐标(x(t),y(t))就行1,1,1,1; //第三行指面积在边界左侧0,0,0,0,]; //第四行指面积在边界右侧if nargin==1x=dl(:,bs);return;endx=zeros(size(s));y=zeros(size(s));[m,n]=size(bs);if m==1 & n==1bs=bs*ones(size(s));endii=find(bs==1);if ~isempty(ii)x(ii)=interp1([dl(1,1),dl(2,1)],[0 3],s(ii));y(ii)=interp1([dl(1,1),dl(2,1)],[0,0],s(ii));//其实这一段是一条水平直线，//x=(3-0)/(dl(2,1)-dl(1,1))*s(1)=s(1)//y=(0-0)/(dl(2,1)-dl(1,1))*s(1)=0,//如果dl(2,1)由3变成1，那么//x(ii)=interp1([dl(1,1),dl(2,1)],[0 3],s(ii));结果也是一样的。

作业：电机电磁场有限元分析——用MA TLAB偏微分方程工具箱求解空载磁场电机与电器 2009级张华一、电机数据的选取：电机的设计数据选自Ansoft Rmxprt 11软件中自带的电机实例，数据文件位于该软件主程序文件夹下的Examples\rmxprt5\syng3\bjs7-6-1.pjt中。

该实例是一台6极同步发电机。

从Rmxprt的Design Output中可以找出该电机的一系列的工作参数。

为了得到空载磁场，要从中找出空载励磁电流--No-Load Exciting Current (A)：735.793为绘制求解区域其机构，要得到其尺寸数据，其迭片结构如图1所示。

（具体尺寸在打开文件bjs7-6-1.pjt后可以看到）图1 求解电机的迭片图二、确定求解区域为了简化分析，选用一个极下的区域进行求解，根据半周期条件，可以求得整个区域的解。

三、使用有限元软件进行求解这里采用MA TLAB PDE toolbox进行空载磁场的有限元求解，求解后并与Ansoft 2D所生成的同一电机的解进行了一致性的比较。

1．MA TLAB PDE toolbox的介绍。

MA TLAB的偏微分工具箱提供了图形用户界面的解法工具，此优点使偏微分方程工具箱在实际中得到了很多的应用。

图形用户界面可以画出二维图形,从而定义偏微分方程的边界条件,可以定义偏微分方程,建立、细分网格,并通过计算在计算机上显示最终结果。

2．求解区域的绘制。

根据电机的结构数据和迭片结构，编写MA TLAB程序在PDE toolbox的GUI中精确绘制出求解区域。

①绘制电机轮廓图利用基本封闭曲线（如椭圆、多变形）的绘图函数绘制出电机的轮廓如图2所示。

图2 PDE toolbox 中的电机轮廓图将求解问题确定为Magnetostatics(静磁场求解)，再把Set formula改为：REC1*(DELTA1+S1+S2+R2+R1+R3 +POLEBODY+P1+P2+P3+P4+P5+P6+P7+P8+P9+P10+P11+P12+D1+D2+D3+D4+D5+D6+P13+P14+P15+P16+P17+P18)即可得到求解区域范围。

Matlab PDE工具箱在电动力学教学中的辅助应用
刘思平
【期刊名称】《廊坊师范学院学报（自然科学版）》
【年(卷),期】2017(017)001
【摘要】电动力学是高校物理专业及相关专业的一门重要的理论基础课,教学内容中涉及了大量偏微分方程,求解过程复杂,难以理解,阻碍了学生的学习兴趣.Matlab 中偏微分方程工具箱(PDE Toolbox)是一个求解各类偏微分方程很好的平台,可以直观地显示物理规律和物理现象,便于学生对知识点的理解和掌握,值得在教学和科研中推广.
【总页数】3页(P110-112)
【作者】刘思平
【作者单位】湖北文理学院,湖北襄阳441053
【正文语种】中文
【中图分类】G642.3
【相关文献】
1.MATLAB R2010a PDE工具箱在瓦斯治理中的应用分析 [J], 卢卫永
2.MATLAB PDE工具箱在地下水科学实验教学中的应用 [J], 牛宏;梁杏;尼胜楠;孙蓉琳
3.基于MATLAB PDE工具箱的土体冻结温度场模拟 [J], 夏锦红;张勋程;夏元友;李顺群;李岩
4.MATLAB PDE工具箱在半导体器件中的应用研究 [J], 马宁;王振宇;朱子君;
5.Matlab PDE工具箱在电动力学教学中的辅助应用 [J], 刘思平
因版权原因，仅展示原文概要，查看原文内容请购买。