小学四年级数学知识点旋转与角

四年级数学教案——《旋转与角》教案（精选13篇）四年级——《旋转与角》教案篇1教学目标：1.通过操作活动，认识平角、周角。

2.能说出生活中的平角与周角。

教学要求：学生已经认识了锐角、直角与钝角，也感知了图形的旋转。

再此基础上，教材从旋转入手，使学生体会旋转过程中角的变化，从而引入平角和周角。

在开展活动时，可以让每个学生准备一个简单的教具，并让他们摆出经过旋转后的各种角，说说他们已经认识的角的名称，然后引出平角和周角。

教学过程：活动一：旋转角。

1、让学生用活动角演示各种角。

2、观察旋转过程中形成的各种角，与同学们进行交流。

3、引出平角，周角，说明是如何构成的。

4、生活中还有哪些自己看到的平角和周角。

活动二：练一练。

1、观察表面上时针和分针组成的角是什么角（p24）。

2、画锐角、直角、钝角和平角。

活动三：交流本节课的体会和感受。

第5课时：角的度量教学目标：1、体会引入量角器的必要性，认识量角器。

2、会用量角器测量各种角的度数。

教学重难点：会用量角器测量各种角的度数。

活动一：创设情景，解决问题教学要求在二年级时，学生已经学习了两个角的大小比较（直观地进行比较），在学习本知识时，可以从两个角的大小比较着手，在比较中，可能有些角的大小在比较接近时无法进行比较，这时引出量角器。

量角器的认识可以先由学生自己进行观察，然后交流观察的结果。

在学生交流的过程中，教师可以逐步引导学生认识量角器上计量单位与排列特点。

量角时，重点突出“点与点重合、边与边重合”的量角方法。

开始时可以先让学生尝试，交流量角的方法，随后让学生自己总结量角的经验，并概括出基本的方法。

活动二：实践练习在学生独立完成的基础上，进行全班的交流，老师进行指导（1）第2题在量角时，先让学生估一估所量的角是什么角？大约是多少度？这是培养学生估计能力的一个载体，也是学生直觉思维的基础。

因此，在量角时，先让学生估一估就显得十分的重要。

（2）数学游戏本活动的目的是提高学生估计角度的能力。

小学数学知识归纳旋转的性质旋转是小学数学中一个重要的概念，它涉及到图形的变化和性质。

在本文中，我们将归纳总结小学数学中与旋转有关的一些重要性质。

希望通过本文的阅读，读者能够更加深入地理解旋转的概念，提升数学能力。

1. 旋转的定义旋转是指以某个点为中心，将图形绕着这个点旋转一定角度。

我们常常使用“顺时针”和“逆时针”来描述旋转的方向。

顺时针旋转是指图形向右旋转，逆时针旋转是指图形向左旋转。

2. 旋转的角度旋转可以是90度、180度、270度，也可以是任意角度。

根据旋转的角度，我们可以将旋转分为四个类别：顺时针旋转90度、逆时针旋转90度、顺时针旋转180度、逆时针旋转180度。

需要注意的是，顺时针旋转n度等价于逆时针旋转360度-n度。

3. 旋转的特点旋转不改变图形的大小和形状，但会改变图形的方向。

如果将一个图形旋转180度，得到的仍然是与原图形完全相同的图形，只是位置发生了变化。

如果将一个图形旋转90度或270度，得到的图形是与原图形完全相同的镜像图形。

4. 图形的旋转对称性有些图形在旋转一定角度后，仍然与原图形相同。

这种性质称为旋转对称性。

正方形、圆、正多边形都具有旋转对称性，它们旋转一定角度后可以得到与原图形完全相同的图形。

5. 图形的旋转中心图形的旋转中心是旋转过程中的固定点，也是旋转的中心轴。

对于圆，旋转中心是圆心；对于正方形，旋转中心是正方形的中心点；对于正多边形，旋转中心是正多边形的中心。

图形的旋转中心对于保持图形形状不变很重要。

6. 旋转的应用旋转在日常生活中有很多应用。

比如，钟表上的指针就是旋转运动，它们以钟表的中心点为旋转中心，通过旋转来指示时间。

另外，旋转还广泛应用于机械领域、建筑设计等方面。

通过以上对小学数学中旋转的性质的归纳，我们可以更好地理解旋转的概念和特点。

旋转不仅仅是一种图形变化，更是一种思维的训练和观察力的培养。

希望读者通过学习旋转的知识，能够在解决问题时灵活运用旋转的性质，提高数学解题的能力。

北师大版数学四年级上册《旋转与角》说课稿2一. 教材分析《旋转与角》是北师大版数学四年级上册的一章节，本章主要让学生初步认识旋转现象，了解旋转的概念，理解旋转的性质，能运用旋转知识解决一些简单问题。

同时，本章还介绍了角的概念及分类，让学生了解角的度量，学会用角度来描述角的大小。

二. 学情分析四年级的学生已经具备了一定的空间观念和几何直观能力，对于生活中的旋转现象有一定的认知。

但是，学生对于旋转的数学定义和性质还不够理解，需要通过实例和操作活动来加深认识。

在角的部分，学生需要进一步理解角的概念，学会用角度来描述角的大小。

三. 说教学目标1.知识与技能：学生能理解旋转的概念，了解旋转的性质，能运用旋转知识解决一些简单问题；学生能了解角的分类，学会用角度来描述角的大小。

2.过程与方法：学生通过观察、操作、思考、交流等活动，培养空间观念和几何直观能力。

3.情感态度价值观：学生体验数学与生活的联系，培养学习数学的兴趣和信心。

四. 说教学重难点1.教学重点：旋转的概念和性质，角的概念和分类。

2.教学难点：旋转的数学定义，角的大小比较。

五. 说教学方法与手段本节课采用情境教学法、探究教学法、合作学习法等教学方法，结合多媒体课件、实物模型、操作活动等教学手段，引导学生主动参与，提高学习效果。

六. 说教学过程1.导入：通过展示生活中的旋转现象，如旋转门、风车等，引导学生初步认识旋转，激发学习兴趣。

2.新课导入：介绍旋转的定义和性质，让学生理解旋转的基本概念。

3.实例讲解：通过具体的实例，让学生学会运用旋转知识解决问题。

4.角的认识：介绍角的概念和分类，让学生学会用角度来描述角的大小。

5.课堂练习：设计一些练习题，让学生巩固所学知识，提高解决问题的能力。

6.总结与反思：对本节课的内容进行总结，引导学生思考旋转和角在实际生活中的应用。

七. 说板书设计板书设计要清晰、简洁，突出本节课的主要内容，包括旋转的定义、性质，角的分类和度量。

《旋转与角》（教案教学反思）四年级上册数学北师大版在今天的数学课上，我们将探讨一个有趣的概念——旋转与角。

这是一个与我们日常生活密切相关的概念，例如我们打开门、翻转书本等，都是旋转的例子。

一、教学内容我们使用的教材是北师大版四年级上册的数学教材。

今天我们将学习第七章第一节“旋转与角”。

这部分内容主要包括旋转的定义、旋转的性质以及如何计算旋转后的图形。

二、教学目标通过本节课的学习，我希望学生们能够理解旋转的定义，掌握旋转的性质，并能够运用这些性质解决实际问题。

三、教学难点与重点本节课的重点是旋转的定义和性质，难点是如何运用这些性质解决实际问题。

四、教具与学具准备为了更好地讲解旋转的概念，我准备了一些图片和实物，如风扇、地球仪等，以便学生们能够更直观地理解旋转。

同时，我也准备了一些练习题，以便随堂练习。

五、教学过程1. 引入：我向学生们展示了风扇和地球仪，并询问它们是如何运动的。

学生们回答说是旋转，然后我引出了旋转的概念。

2. 讲解：接着，我详细讲解了旋转的定义和性质，并通过示例进行了说明。

3. 练习：然后，我给出了几个练习题，让学生们运用旋转的性质进行计算。

六、板书设计我在黑板上写下了旋转的定义和性质，以及一些关键的点，以便学生们能够清晰地理解旋转的概念。

七、作业设计我布置了一道作业题：一个矩形绕着它的一个顶点旋转90度，求旋转后的矩形的面积。

答案是旋转后的矩形的面积仍然是原来的面积。

八、课后反思及拓展延伸通过本节课的教学，我发现学生们对旋转的概念有一定的理解，但在运用旋转的性质解决实际问题时，还存在一些困难。

在今后的教学中，我将继续强调旋转的性质，并通过更多的练习题来帮助学生们掌握这一概念。

我还可以引入一些更高级的旋转问题，如三维空间的旋转等，以拓展学生的思维。

总的来说，我对今天的教学感到满意。

学生们积极参与，课堂气氛良好。

我相信通过不断的练习和引导，学生们能够更好地理解和运用旋转的概念。

重点和难点解析在上述教学过程中，有几个关键的细节是需要重点关注的。

小学-数学-上册-打印版
角之间的关系
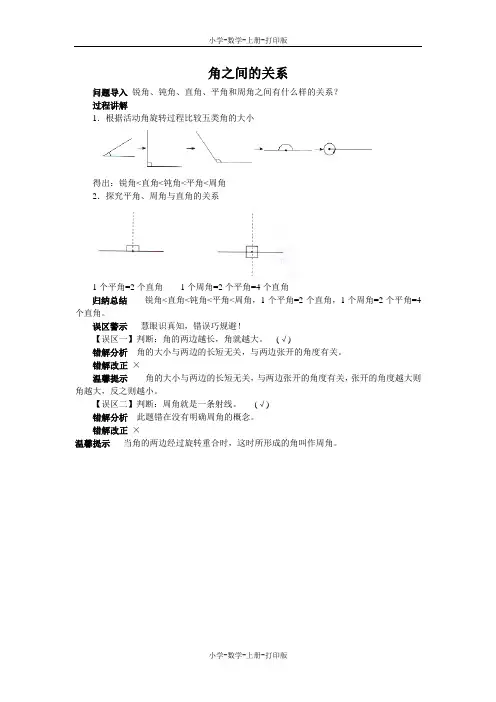
问题导入锐角、钝角、直角、平角和周角之间有什么样的关系？
过程讲解
1．根据活动角旋转过程比较五类角的大小
得出：锐角<直角<钝角<平角<周角
2．探究平角、周角与直角的关系
1个平角=2个直角1个周角=2个平角=4个直角
归纳总结锐角<直角<钝角<平角<周角，1个平角=2个直角，1个周角=2个平角=4个直角。

误区警示慧眼识真知，错误巧规避！
【误区一】判断：角的两边越长，角就越大。

(√)
错解分析角的大小与两边的长短无关，与两边张开的角度有关。

错解改正×
温馨提示角的大小与两边的长短无关，与两边张开的角度有关，张开的角度越大则角越大，反之则越小。

【误区二】判断：周角就是一条射线。

(√)
错解分析此题错在没有明确周角的概念。

错解改正×
温馨提示当角的两边经过旋转重合时，这时所形成的角叫作周角。

小学-数学-上册-打印版。

旋转知识点总结小学一、旋转的基本概念旋转是物体围绕某个点或轴线进行的运动。

在旋转运动中，物体的各个部分绕着固定的轴线或点进行转动，如地球围绕着太阳旋转，风车的叶片围绕着轴线旋转等。

旋转的基本概念包括：1. 旋转的轴线：旋转围绕的固定轴线，如地球的轴线、风车的轴线等。

2. 角速度：表示旋转运动每秒转过的角度，通常用符号ω表示，单位是弧度/秒。

3. 角加速度：表示旋转运动的速度变化率，通常用符号α表示，单位是弧度/秒²。

4. 旋转惯量：表示物体对于旋转运动的惯性，通常用符号I表示，单位是千克·米²。

5. 转动力矩：使物体发生旋转运动的力的力矩，通常用符号τ表示，单位是牛·米(N·m)。

6. 绕轴转动的动能：物体绕某个轴线旋转所具有的动能，通常用符号K表示，单位是焦耳(J)。

二、旋转的运动规律旋转运动有一些基本的运动规律，包括：1. 角速度与线速度的关系：物体任意一点的线速度与角速度之间存在着简单的函数关系，即线速度等于半径乘以角速度。

2. 角加速度与力矩的关系：牛顿第二运动定律对旋转运动的表达式是τ=Iα，它表示物体的角加速度与受到的力矩成正比。

3. 转动动能：转动的动能是由于物体的旋转而产生的动能，它与物体的质量、半径和角速度有关，通常用K=1/2Iω²表示。

4. 动能定理：对旋转运动来说，力对物体做功，能够改变物体的角动量，因此动能定理可以表示为W=ΔK=I(ω²-ω₁²)/2，其中W表示对物体做功，ΔK表示动能的增量，ω和ω₁表示物体的角速度。

三、旋转平衡和力矩1. 平衡条件：如果物体受到的合外力矩为零，则物体处于平衡状态。

2. 杠杆原理：杠杆原理是一个重要的物理原理，它描述了杠杆的力矩平衡条件。

根据杠杆原理，如果一个杠杆处于平衡状态，那么左右两边的力矩之和必须相等。

3. 平衡陀螺：平衡陀螺是一种利用陀螺的自旋来保持稳定平衡的物理装置，它利用了陀螺的自旋动能和角动量守恒原理来保持平衡状态。

旋转与角（教案）-四年级上册数学北师大版一、教学目标1. 让学生理解旋转的概念，知道旋转的三要素：旋转中心、旋转方向和旋转角度。

2. 培养学生的空间想象能力，能够根据旋转的特征判断图形的变化。

3. 培养学生运用旋转知识解决实际问题的能力。

二、教学内容1. 旋转的概念2. 旋转的三要素3. 旋转的应用三、教学重点与难点1. 教学重点：旋转的概念，旋转的三要素。

2. 教学难点：旋转的应用。

四、教学过程1. 导入新课通过生活中的旋转现象，如转动的风车、旋转木马等，引导学生观察并思考这些现象的共同特征，从而引出旋转的概念。

2. 讲解旋转的概念旋转是指将一个图形绕着某一点转动一个角度的图形变换。

这个点称为旋转中心，转动的角度称为旋转角度，转动的方向可以是顺时针或逆时针。

3. 讲解旋转的三要素（1）旋转中心：旋转中心是图形旋转的中心点，可以是图形内部的点，也可以是图形外部的点。

（2）旋转方向：旋转方向可以是顺时针或逆时针，取决于旋转的角度是正数还是负数。

（3）旋转角度：旋转角度是指图形旋转的角度，可以是任意角度，通常用度数表示。

4. 演示旋转的过程通过实际操作，演示旋转的过程，让学生直观地理解旋转的概念和三要素。

5. 练习旋转的应用提供一些旋转的应用题，让学生运用旋转知识解决实际问题，如旋转时钟的时针和分针，旋转地图等。

6. 总结与拓展总结旋转的概念和三要素，并引导学生思考旋转在生活中的应用，如旋转门、旋转楼梯等。

五、作业布置1. 完成练习册上的旋转练习题。

2. 观察生活中的旋转现象，并记录下来。

六、教学反思本节课通过生活中的实例，让学生理解旋转的概念和三要素，并通过实际操作和练习，培养学生的空间想象能力和解决问题的能力。

在教学过程中，要注意引导学生观察和思考，激发学生的学习兴趣，提高教学效果。

需要重点关注的细节是“旋转的应用”。

这是因为在学生理解了旋转的概念和三要素之后，能够将理论知识运用到实际情境中，解决实际问题，是教学目标中非常重要的一部分。

北师大版数学四年级上册2.4《旋转与角》说课稿1一. 教材分析《旋转与角》是北师大版数学四年级上册第2.4节的内容。

这部分内容是在学生已经掌握了角的含义、分类以及量角器量角的基础上进行的。

本节课主要让学生初步理解旋转的意义，学会用旋转来解释生活中的现象，感受数学与生活的联系。

二. 学情分析四年级的学生已经具备了一定的空间观念和几何直观能力，他们对角的概念和分类有一定的了解。

但是，对于旋转的意义和如何在实际问题中运用旋转来解决问题可能还比较模糊。

因此，在教学过程中，我需要注重引导学生通过观察、操作、思考、交流等活动，体会旋转的意义，提高解决问题的能力。

三. 说教学目标1.知识与技能：学生能够理解旋转的含义，学会用旋转来解释生活中的现象。

2.过程与方法：学生通过观察、操作、思考、交流等活动，培养空间观念和几何直观能力。

3.情感态度与价值观：学生感受数学与生活的联系，提高学习数学的兴趣。

四. 说教学重难点1.教学重点：学生能够理解旋转的含义，学会用旋转来解释生活中的现象。

2.教学难点：学生能够在实际问题中运用旋转来解决问题。

五. 说教学方法与手段1.教学方法：引导发现法、合作交流法、实践操作法。

2.教学手段：多媒体课件、实物模型、量角器。

六. 说教学过程1.创设情境，引入新课通过多媒体课件展示生活中的旋转现象，如风扇转动、车轮转动等，引导学生观察、思考这些现象的特点。

然后提问：这些现象都有一个共同的特点，那就是什么？引出旋转的概念。

2.自主探究，理解旋转学生分组讨论，每组选择一个旋转现象，用彩纸、剪刀等工具制作一个旋转的模型，并展示给全班同学。

通过观察、操作、思考，引导学生理解旋转的意义。

3.实践应用，解决问题出示一些实际问题，如旋转后的图形发生了什么变化？旋转了多少度？引导学生运用旋转的知识解决问题。

4.总结提升，内化新知通过学生自主总结和教师引导，使学生明确旋转的意义，并能应用于实际问题中。

5.布置作业，拓展延伸设计一些富有思考性的作业，让学生在课后进一步巩固旋转的知识，提高解决问题的能力。

数学四年级旋转知识点总结一、旋转的概念在数学中，旋转是指以某一点为中心，按照一定的规则使图形或物体绕着这一中心点转动的运动。

在二维平面中，旋转可以是顺时针方向或逆时针方向的。

旋转可以用角度来描述，通常以逆时针旋转为正角度，顺时针旋转为负角度。

二、旋转的基本概念1. 中心：旋转的中心点，图形绕中心点旋转。

2. 角度：表示图形旋转的角度大小，通常用度来表示。

3. 顺时针和逆时针：用来描述旋转的方向。

4. 图形的对称性：旋转会改变图形的位置，但不改变图形的形状。

三、旋转的性质1. 图形旋转后的性质：旋转不改变图形的大小和形状，只是改变了位置和方向。

2. 旋转与对称性：如果一个图形在旋转之后能够重合自身，说明这个图形具有旋转对称性。

3. 旋转和角度：旋转的角度可以是正数、负数、0或360°，负数表示顺时针旋转，正数表示逆时针旋转，0表示不旋转，360°表示一周旋转。

四、旋转的应用1. 时钟：时钟指针围绕表盘中心进行旋转，表示时间的变化。

2. 几何图形：在几何学中常常用旋转来研究图形的性质和对称性。

3. 机械运动：旋转也是机械运动中常见的一种形式，如摩托车轮子的旋转等。

五、常见旋转的图形和作图方法1. 点的旋转：以坐标原点为中心，按照规定的角度进行旋转，可以得到旋转后的点的坐标。

2. 直线的旋转：以直线上的一点为中心，按照规定的角度进行旋转，可以得到旋转后的直线。

3. 三角形的旋转：以三角形的重心为中心，按照规定的角度进行旋转，可以得到旋转后的三角形。

六、数学实践中的旋转问题1. 如何确定旋转的中心和角度？2. 旋转后的图形如何和原图形相对应？3. 旋转对图形的性质有何影响？4. 如何利用旋转对称性解决问题？七、数学实践中的旋转思维1. 在解决问题时，可以考虑使用旋转对称性来简化问题。

2. 通过对图形进行旋转，可以发现图形的隐藏性质或规律。

3. 旋转可以帮助我们理解几何图形的对称性和性质。

四年级数学旋转与角知识点
1、角的概念。

由一点引出两条射线所组成的图形叫做角。

角是由一个顶点和两条边组成的.。

2、认识平角、周角。

平角：角的两边在同一直线上，(像一条直线)，平角等于
180°，等于两个直角。

周角：角的两边重合，(像一条射线)，周角等于360°，等于两个平角，四个直角。

3、角的分类：
小于90度的角叫做锐角;
等于90度的角叫做直角;
大于90度小于180度的角叫做钝角;
等于180度的角叫做平角;
大于180度小于270度叫做优角(此为补充内容);
等于360度的角叫做周角。

4、动手画平角、周角。

【四年级数学旋转与角知识点】。