结构力学第5章__影响线

结构力学（祁皑）课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。

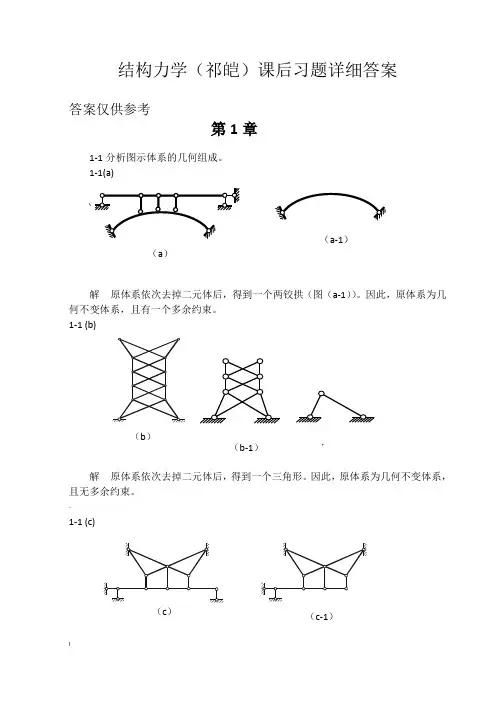
1-1(a)(解原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。

因此，原体系为几何不变体系，且有一个多余约束。

1-1 (b)解原体系依次去掉二元体后，得到一个三角形。

因此，原体系为几何不变体系，且无多余约束。

1-1 (c)[（c-1）（a）（a-1）（b）（b-1）*（c-2） （c-3）解 原体系依次去掉二元体后，得到一个三角形。

因此，原体系为几何不变体系，且无多余约束。

1-1 (d)!（d-1） （d-2） （d-3）解 原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。

因此，原体系为几何不变体系，且无多余约束。

注意：这个题的二元体中有的是变了形的，分析要注意确认。

1-1 (e)~解 原体系去掉最右边一个二元体后，得到（e-1）所示体系。

在该体系中，阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体，也可以去掉，得到（e-2）所示体系。

在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。

因此，原体系为几何可变体系，缺少一个必要约束。

1-1 (f)[解 原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相（d ）（e ）（e-1）AB}AB （e-2）（f ）（f-1）连，符合几何不变体系的组成规律。

因此，可以将该刚片和相应的约束去掉只分析其余部分。

很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。

因此，原体系为几何不变体系，且无多余约束。

1-1 (g)解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变体系的组成规律。

因此，可以将该刚片和相应的约束去掉，只分析其余部分。

余下的部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。

因此，原体系为几何不变体系，且无多余约束。

结构力学（祁皑）课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。

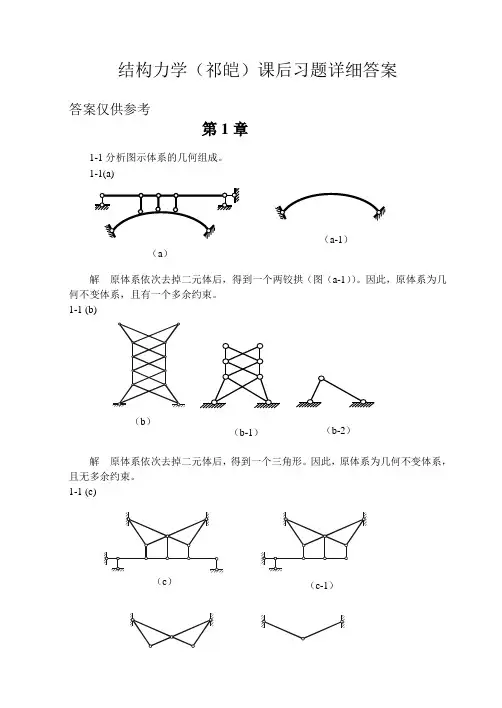
1-1(a)解 原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。

因此，原体系为几何不变体系，且有一个多余约束。

1-1 (b)解 原体系依次去掉二元体后，得到一个三角形。

因此，原体系为几何不变体系，且无多余约束。

1-1 (c)（c-1）（a ）（a-1）（b ）（b-1）（b-2）（c-2） （c-3）解 原体系依次去掉二元体后，得到一个三角形。

因此，原体系为几何不变体系，且无多余约束。

1-1 (d)（d-1） （d-2） （d-3）解 原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。

因此，原体系为几何不变体系，且无多余约束。

注意：这个题的二元体中有的是变了形的，分析要注意确认。

1-1 (e)解 原体系去掉最右边一个二元体后，得到（e-1）所示体系。

在该体系中，阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体，也可以去掉，得到（e-2）所示体系。

在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。

因此，原体系为几何可变体系，缺少一个必要约束。

1-1 (f)解原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连，符合几何不变体系的组成规律。

因此，可以将该刚片和相应的约束去掉只分析其余部分。

很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。

因此，原体系为几何不变体系，且无多余约束。

1-1 (g)（d ） （e ）（e-1）A（e-2）（f ）（f-1） （g ） （g-1） （g-2）解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变体系的组成规律。

因此，可以将该刚片和相应的约束去掉，只分析其余部分。

余下的部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。

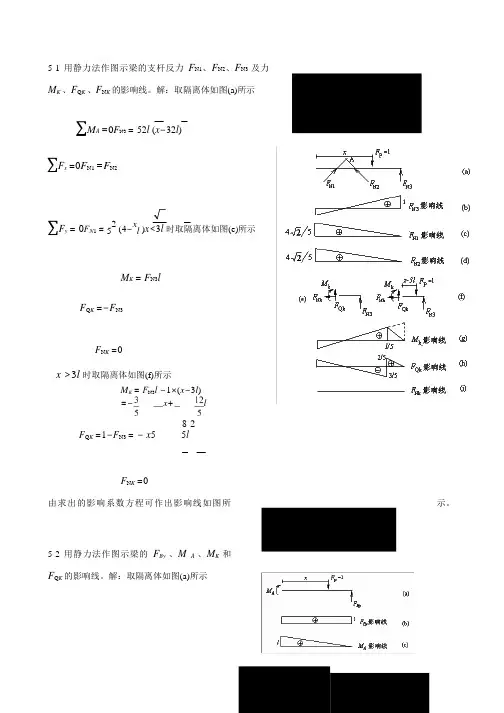
5-1 用静力法作图示梁的支杆反力F N1、F N2、F N3及力M K 、F Q K 、F N K 的影响线。

解：取隔离体如图(a)所示∑M A =0F N3 = 52l (x−32l)∑F x =0F N1 =F N2∑F y = 0F N1 = 52 (4−x l )x<3l 时取隔离体如图(e)所示M K = F N3lF Q K =−F N3F N K =0x >3l 时取隔离体如图(f)所示M K = F N3l −1×(x−3l)=−x+l8 2F Q K =1−F N3 = − x5 5lF N K =0由求出的影响系数方程可作出影响线如图所示。

5-2 用静力法作图示梁的F By 、M A 、M K 和F Q K 的影响线。

解：取隔离体如图(a)所示∑F y =0F By =1∑M B =0M A =x x <l/2时, 取隔离体如图(f)所示M K =l/2F Q K =−1x >l/2时, 取隔离体如图(e)所示M K =l −xF Q K =0由影响系数方程可作出影响线如图所示。

5-3 用静力法作图示斜梁的F Ay、F Ax、F By 、M C 、F Q C 和F N C 的影响线。

（1）解：∑M A =0F By = x/l∑F y =0F Ay =1−x/l∑F x =0F Ax =0x<a，取右侧∑M c =0 M C= bx/l∑F r =0 F Q C =−x l cosα∑Fβ=0 F N C = x l sinαx>a，取左侧∑M c =0 M C = a(1−x/l)∑F r =0 F Q C = (1−x l )cosαx ∑Fβ=0 F N C =−(1−l )sinα由影响系数方程可作出影响线如图所示。

5-3（2）解：∑M A =0F By = x l tanαx∑F y = 0F Ay =− l tanα∑F x =0 F Ax =−1x<a，取右侧∑M c =0 M C = b l x tanα∑F r =0 F Q C =−x l sinα∑Fβ= 0 F N C = x l sinα⋅tanαx>a，取左侧∑M c =0 M C = tanα⋅a(1−x/l)∑F r =0 F Q C = sinα−x l sinα∑Fβ= 0 F N C = cosα+ x l tanα⋅sinα由影响系数方程可作出影响线如图所示。

对图示体系进行几何组成分析.
答题说明：简单给出分析过程。

最后给出结论。

问题反馈
【教师释疑】
正确答案：【去除基础，再去除二元体后，小三角形、大三角形用三根链杆相连，故体系为无多余约束的几何不变体系。

】
2、
试对图示体系进行几何构造分析。

答题说明：简单给出分析过程。

最后给出结论。

3、
对图示体系进行几何组成分析。

答题说明：简单给出分析过程。

最后给出结论。

问题反馈
【教师释疑】
正确答案：【依次去除二元体A、B、C、D、E、F、G后剩下大地，故该体系为无多余约束的几何不变体系。

】
4、试对图示体系进行几何构造分析。

问题反馈
【教师释疑】
正确答案：【依次去除二元体DGF,FHE,DFE,ADC,CEB后，B点少一个约束。

该体系为有一个自由度的几何常变体系】
问题反馈
【教师释疑】
正确答案：【 23、34、49、89、59、96、65、57共8根零杆。

】
2、
找出图示桁架中的零杆。

答题说明：按你的分析结果，给出零杆总数和零杆编号（以两端结点编号表示）。

问题反馈
3、
找出图示桁架中的零杆。

答题说明：按你的分析结果，给出零杆总数和零杆编号（以两端结点编号表示）。

问题反馈
【教师释疑】
正确答案：【 EA、EB、AF、AC、BG、GD共有6根零杆。

】
矩图对应的是某一固定荷载。

结构力学课程作业答案第一章绪论1、按照不同的构造特征和受力特点，平面杆件结构可分为哪几类？2、何为静定结构和超静定结构？从几何构造分析的角度看，结构必须是几何不变体系。

根据多余约束 n ，几何不变体系又分为：有多余约束( n > 0)的几何不变体系——超静定结构；无多余约束( n = 0)的几何不变体系——静定结构。

从求解内力和反力的方法也可以认为：静定结构：凡只需要利用静力平衡条件就能计算出结构的全部支座反力和杆件内力的结构。

超静定结构：若结构的全部支座反力和杆件内力，不能只有静力平衡条件来确定的结构。

3、土建、水利等工程中的荷载，根据其不同的特征，主要有哪些分类？第二章平面结构的几何组成分析作业题：1、何为平面体系的几何组成分析？按照机械运动及几何学的观点，对平面结构或体系的组成情况进行分析，称为平面体系的几何组成分析。

2、何为几何不变体系？何为几何可变体系？几何不变体系—若不考虑材料的应变，体系的位置和形状不会改变。

几何可变体系—若不考虑材料的应变，体系的位置和形状是可以改变的。

3、几何组成分析的目的是什么？1）保证结构的几何不变性,以确保结构能承受荷载和维持体系平衡.2）判别某一体系是否为几何不变,从而决定它能否作为结构.3）研究几何不变体系的组成规则,以保证所设计的结构是几何不变体系,从而能承受荷载而维持平衡.4）根据体系的几何组成分析,正确区分静定结构和超静定结构,从而选择适当的计算方法进行结构的反力和内力计算.5）通过几何组成分析,明确结构的构成特点,从而选择结构受力分析的顺序以简化计算.4、何为一个体系的自由度？知悉体系计算自由度的公式。

5、试对下图所示体系进行几何组成分析。

图1图2图3图46、试求图示各体系的计算自由度数W。

7、例2-1 例2-28、习题 2.1～2.12 试对图示体系作几何组成分析。

第三章静定梁、静定平面刚架和三角拱的计算作业题：1、单跨静定梁有简支梁、外伸梁、悬臂梁等形式。

第二章：平面体系几何构造分析一．判断题1．几何可变体系在任何荷载作用下都不能平衡。

〔〕2．三个刚片由三个铰相连的体系一定是静定构造。

〔〕3．有多余约束的体系一定是超静定构造。

〔〕4．有些体系是几何可变体系，但却有多与约束存在。

〔〕5．在任意荷载作用下，仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。

〔〕6．图1－16所示体系是几何不变体系。

〔〕图1－16 图1－17 图1－18 7．图1－17所示体系是几何不变体系。

〔〕8．几何瞬变体系的计算自由度一定等于零。

〔〕9．图1－18所示体系按三刚片法那么分析，三铰共线故为几何瞬变。

〔〕10．图中链杆1和2的交点O可视为虚铰。

〔〕1O22．8多余约束的体系一定是几何可变体系。

〔〕2．9 只有无多余约束的几何不变体系才能作构造。

〔〕2．10 图示2－10铰结体系是无多余约束的几何不变体系。

〔〕图2－10 题2－112．11 图示2－11铰结体系是有多余约束的几何不变体系。

〔〕2．12 图示2－12体系是无多余约束的几何不变体系。

〔〕题2－12 题2－132．13 图示体系是有多余约束几何不变的超静定构造。

〔〕2．14 图示体系在给定荷载下可维持平衡，因此，此体系可作为构造承当荷载。

〔〕2．15 图示体系是有多余约束的超静定构造。

〔〕题2－14 题2－15答案：1 ×2 ×3 ×4 √5 √6 ×7 √8 ×9 ×10×；2.8 ×2.9×2.10√2.11×2.12 × 2.13× 2.14 × 2.15 ×二、分析题：对以下平面体系进展几何组成分析。

3、4、C D B C DB5、 6、 A C D BEAB CDE7、 8、 A B C D G E F A B C D E F GHK9、 10、11、 12、 1234513、 14、15、 16、17、 18、19、 20、 1245321、 22、 123456781234523、 24、12345625、 26、27、 28、29、 30、31、 32、33、A CB DE F三、在以下体系中添加支承链杆，使之成为无多余约束的几何不变体系。

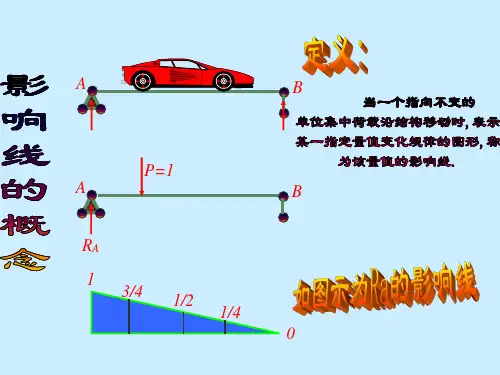
项目四 移动荷载作用下结构的内力计算子项目一　绘制影响线1. 掌握影响线的概念。

2. 能够熟练绘制单跨静定梁的影响线。

学习能力目标项目表述对如图 4 – 1 所示简支梁进行受力分析，引入对影响线概念的理解，掌握利用静力法绘制出单跨静定梁的影响线，并了解移动荷载作用对结构的影响。

学习进程知识链接1．静定单跨梁的计算（1）静定单跨梁的类型静定单跨梁在工程中应用十分广泛，是组成各种结构的基本构件之一。

单跨静定梁有简支梁（图 2 – 1a）、外伸梁（图 2 – 1b）、悬臂梁（图 2 – 1c）三种基本形式。

知识链接前面内容中所讨论的荷载，其大小、方向和作用点都是固定不变的，称为固定荷载。

在这种荷载作用下，结构中支座反力和任一截面上的内力数值和方向均固定不变。

但在工程实际中，还存在大量的活载问题。

其中有许多活荷载大小和作用方向都保持不变，但作用位置却不断变化，通常称为移动荷载。

1．移动荷载的概念常见的移动荷载有两类：（1）移动的集中荷载指一组排列、间距和数值保持不变的共同移动的集中力系，又叫行列荷载。

例如图 4 – 2a所示的工业厂房中，当吊车起吊重物沿吊车桥架行走时，小车的轮压为移动荷载；当吊车桥架在吊车梁上沿厂房纵向移动时，则吊车轮压就是作用在吊车梁上的移动荷载。

知识链接知识链接（2）移动的均布荷载指作用位置可以变动或断续分布的均布荷载，如图 4 – 3 所示。

如履带式起重机、拖拉机，材料的任意堆放，人群的任意走动。

知识链接2．影响线的概念在移动荷载作用下，即使不考虑结构的振动，结构的支座反力、各截面的内力和位移等（通常称为量值 S）也将随荷载位移 x而变化。

因此为结构设计和验算提供依据，需考虑以下三方面的问题：① 找出各量值S随荷载位置 x变化的规律。

若用函数表示，即为影响线方程S= f(x)； 若用图形表示，即为下面将讨论的影响线。

知识链接② 从以上各量值的变化规律中，找出使某一量值达到最大值时的荷载位置，称为荷载的最不利位置，并求出相应的最大值。

结构力学—影响线【例2-13】求图2-27b所求简支梁在中一活载作用下截面K的弯矩最大值。

图2-27中一活载（图2-27a）是中华人民共和国铁路标准活荷载的简称，它是我国铁路桥涵设计使用的标准荷载。

与前例吊车荷载不同的是要考虑左行、右行两种情况。

作出影响线如图2-27c所示，各段直线的坡度为由式（2-7）确定临界位置。

1、列车由右向左开行时的情况将轮4置于D点试算（图2-27d）：荷载左移荷载右移不满足判别条件，故轮4处于D点不是临界位置。

由于左移时，而，故，即荷载左移会使值增加。

因此荷载应继续左移才会使达到最大值。

将轮2置于C点（图2-27e）试算，有荷载左移荷载右移满足判别条件，轮2位于C点时是临界位置。

在此位置算得值为继续试算，没有其它临界位置。

2、列车从左向右开行情况将轮4置于D点（图2-27f）试算，有荷载左移荷载右移满足判别条件，故从左向右开行时轮4位于D点时是临界位置。

相应的值为继续试算，没有其它临界位置。

3、比较可得的最大值为发生于从右向左开行，轮2处于C点时。

以上讨论的是如何求最大值，若求最小值，则把判别式中的大于号改成小于号，小于号改成大于即可。

如果影响线是直角三角形或竖标有突变，则前述判别式不适用。

此时的最不利荷载位置可按前面提到的试算原则由试算确定。

【例2-14】求图2-28a所示简支梁K截面剪力的最大值和最小值。

荷载运行方向不变。

图2-28解：作出影响线如图2-28b所示。

使发生最大或最小值的荷载位置只有（图2-28c、d）两种可能性。

1、处于K点（图2-28c），有2、F P2位于K点（图2-28d），有3、经比较，得的最大值和最小值分别为伸臂梁的影响线内力影响线的量纲影响线与内力图的区别影响线绘制举例（1）伸臂梁跨中截面内力影响线跨中截面是指两支座间的截面。

在不动荷载作用下求这种截面内力时要先求支座反力，然后通过支座反力求内力。

作影响线时也是这样，先绘支座反力的影响线，然后通过它，绘内力影响线。

弯矩与影响线的竖坐标在结构力学中，弯矩和影响线是两个重要的概念。

弯矩描述了梁的弯曲程度，而影响线则反映了结构上力或力矩的分布情况。

本文将重点探讨弯矩与影响线的竖坐标之间的关系。

一、弯矩的概述弯矩是描述梁弯曲程度的物理量，其值的大小与力的方向、作用点以及梁的弯曲形状有关。

在静力学中，弯矩的计算通常采用“力矩”的概念，即力与力臂的乘积。

弯矩可以表示为M(x)，其中x为横截面上的点到梁的对称轴的距离。

当梁上作用有分布载荷时，弯矩图呈抛物线形状。

二、影响线的概念影响线是在结构上作用有分布载荷的情况下，表示结构上力或力矩分布情况的图线。

影响线可以是竖直的，也可以是水平的，其值的大小反映了相应力或力矩的分布情况。

影响线的竖坐标即为该力或力矩在结构上的作用点距离对称轴的距离。

三、弯矩与影响线的竖坐标的关系弯矩与影响线的竖坐标之间存在密切的关系。

在静力学中，对于一个给定的分布载荷，如果知道弯矩图上的某一点的横坐标x，就可以通过影响线的竖坐标来求出该点处的弯矩值。

这是因为弯矩图和影响线在横截面上是对称的，即它们具有相同的形状和变化规律。

四、应用实例以简支梁为例，简支梁在均布载荷作用下，其弯矩图呈抛物线形状。

当知道简支梁上某一点的横坐标x时，就可以通过影响线的竖坐标来求出该点处的弯矩值。

例如，当x=0.5米时，根据影响线的竖坐标可以求出该点处的弯矩值为M=2.5kN·m。

五、结论综上所述，弯矩与影响线的竖坐标之间存在密切的关系。

在结构力学中，这种关系为解决实际问题提供了重要的理论依据。

通过弯矩图和影响线的相互参照，可以更准确地掌握结构的受力情况，从而为结构的优化设计和安全评估提供有力的支持。