当前位置：文档之家 › 5.7用二元一次方程组确定一次函数的表达式课件ppt

5.7用二元一次方程组确定一次函数的表达式课件ppt

  • 格式：ppt
  • 大小：4.60 MB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

北师大版数学八年级上册用二元一次方程组确定一次函数表达式课件

北师大版数学八年级上册用二元一次方程组确定一次函数表达式课件

对点范例
1.一次函数y=kx+b，经过（1，1），（2，-4），则k与b的值为（
）C k=3，
A. b=-2
k=-3， B. b=4
k=-5， C. b=6
k=6， D. b=-5
知识重点 知识点二：根据实际问题求一次函数表达式 根据实际问题给出的条件选取___两__个____等量关系，再用待定系数 法求出一次函数的表达式.
对点范例 3. 已知一次函数的图象如图5-7-1，则此函数的解析式为 _____y_=_2_x_-_8_______.
课堂演练 典例精析 【例1】如图5-7-2，直线AB对应的函数 表达式是___y_=_____x_+_2______.
思路点拨：根据图象上两个特殊点的坐标，利用待定系数法即 可确定直线的函数表达式.
对点范例 2.有一段导线，在0 ℃时电阻为2 Ω，温度每增加1 ℃，电阻增 加0.008 Ω，那么电阻R(Ω)表示为关于温度t(℃)的函数关系式 为( A ) A. R=2＋0.008t B. R=2-0.008t C. t=2＋0.008R D. t=2-0.008R
知识重点 知识点三：根据图象求一次函数表达式 选取图象上的___两__个____特殊点，再用待定系数法求出一次函数的 表达式.
举一反三
2. 某商场经营一批进价为2元的小商品，在市场营销中发现此商 品的日销售单价x（元）与日销售量y（件）之间有如下关系：
x/元
3
5
9
11
y/件
18
14
6
2
（1）求日销售量y与日销售单价x的函数关系式； （2）根据（1）中所求的函数关系式计算当日销售单价为6元时 ，日销售量是多少件.
解：（1）由题意，知y与x是一次函数关系，设y与x的函数关系

《用二元一次方程组确定一次函数表达式》优秀ppt课件

《用二元一次方程组确定一次函数表达式》优秀ppt课件

间的关系，观察图象，回答下列问题： L2
（1）途中乙发生了什么事？ s
（2）他们几时相遇？
L1
P
D
12
E
10
AB
8
0 0.5 1 1.2
t
10
例：某长途汽车客运站规定，乘客可以免费携带一定 质量的行李，但超过该质量则需购买行李票，且行 李费y（元）是行李质量x（千克）的一次函数，现 知李明带了60千克的行李，交了行李费5元，王华 带了90千克的行李，交了行李费10元 （1）写出y与x之间的函数表达式 （2）旅客最多可免费携带多少千克的行李？
s 与t 之间的关系图象， 20 找出交点的横坐标就行了！
0
11 22(A)33 4 t
7
用方程 解 行程问题
A、B 两地相距150千米，
1 时后乙距A地
甲、乙两人骑自行车分别从A、
120千米,即乙的
B 两地同时相向而行。假设他 小彬 速度是 30千米/时,
们都保持匀速行驶，则他们各
自到A地的距离s(千米)都是骑 车时间t(时)的一次函数. 1 时后乙距A地120千米, 2 时后甲距A地 40千米.
12
2、仿例题，做习题， 完成P127的随堂练习1－2题。
13
课堂检测
1.已知一次函数 y kx 5与y 3x b的图象 交点为 P(2,3), 则k _1__, b -_9__ . 2.已知一次函数 y 2x a与y x b的图象都 经过点 A(2,0), 且与 y轴分别交于 B, C两点,则
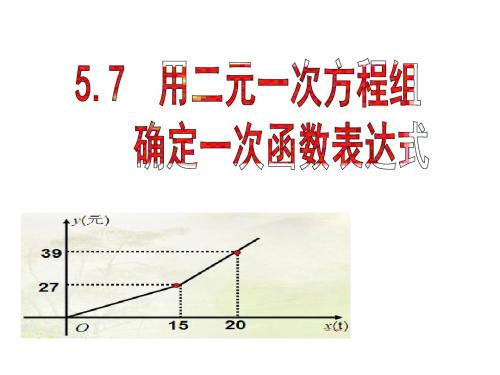
5.7 用二元一次方程组确 定一次函数表达式
1
任意一个二元一次方程都可以转 化成y=kx+b的形式,所以每个二 元一次方程都对应一个一次函数.

5.7用二元一次方程组确定一次函数表达式

5.7用二元一次方程组确定一次函数表达式

１）设关系式；
２）找Ｘ与Ｙ的对应值；
３）代入转化成方程（组）； ４）解方程（组）； ５）写出关系式。
课堂小结
确定关系式的方法： １）设关系式； ２）找Ｘ与Ｙ的对应值； ３）代入转化成方程（组） ４）解方程（组）； ５）写出关系式。 像这样，先设出函数关系式，再根据所给 条件确定表达式中未知数的系数，从而得到函 数表达式的方法，叫做待定系数法。
20 t 30 t 150
t=3
求出s与t之间的关系式，联立解方程组
A、B 两地相距150千米，甲、 乙两人骑自行车分别从A、B 两地相 向而行。假设他们都保持匀速行驶， 则他们各自到A 地的距离s (千米) 都 是骑车时间 t (时) 的一次函数. 1 时后乙距A地120千米, 2 时后甲距A地 40千米. 问 经过多长时间两人相遇 ? 对于乙，s 是t 的一次函数， 可设 s=kt+b。 小颖 当t=0时，s=150； 当t=1时，s=120。将它们分 别代入s=kt+b中，可以求出k 、b的值，也即可以求出乙 s 与t 之间的函数表达式。 同样可求出甲s与t之间的函 数表达式。 再联立这两个表达式，求解 方程组就行了。
甲 A
2时,40千米
120千米
1时
B 乙Βιβλιοθήκη s甲 20ts乙 150 30t
用图象法 解 行程问题
A、B 两地相距150千米，甲、 乙两人骑自行车分别从A、B 两地 相向而行。假设他们都保持匀速行 驶，则他们各自到A地的距离s(千米) 都是骑车时间t(时)的一次函数. 1 时后乙距A地120千米, 2 时后甲距A地 40千米. 问 经过多长时间两人相遇 ? 150 (B) 140
１、二元一次方程组与一次函数有何联系?

57用二元一次方程组确定一次函数表达式

57用二元一次方程组确定一次函数表达式

57用二元一次方程组确定一次函数表达式要确定一次函数的表达式，我们需要建立一个二元一次方程组。

一次函数的表达式通常具有以下形式：f(x) = ax + b其中，a是斜率，b是y轴截距。

为了确定这个一次函数的表达式，我们需要至少两个点的坐标。

假设我们已经有两个点(x1,y1)和(x2,y2)。

我们可以得到以下方程组：y1 = ax1 + by2 = ax2 + b我们可以利用这个方程组来求解a和b的值。

现在我们来具体解决一个问题。

假设有两个点A(2,3)和B(4,7)，我们要确定一条过这两个点的一次函数的表达式。

将这两个点的坐标带入到方程组中，我们得到以下方程组：3=2a+b7=4a+b现在我们可以通过消元法或代入法来解决这个方程组。

我们选择使用消元法。

我们可以将第一个方程两边乘以2，得到如下方程：6=4a+2b然后将第二个方程减去第一个方程，得到消去b的新方程：7-3=(4a+b)-(2a+b)4=2a解这个方程，我们得到：a=2将a的值代入到第一个方程中，我们可以解得：3=2(2)+b3=4+bb=-1因此，通过解决这个方程组，我们确定了一次函数的表达式为：f(x)=2x-1这个一次函数的斜率为2，y轴截距为-1，经过点A(2,3)和点B(4,7)。

我们可以验证一下，将x代入到表达式中应该得到相应的y值：f(2)=2(2)-1=3f(4)=2(4)-1=7我们可以看到，这些计算的结果与原来的点的坐标相匹配。

综上所述，我们可以通过解一个二元一次方程组来确定一次函数的表达式。

我们需要至少两个点的坐标来建立方程组。

通过求解方程组，我们可以得到斜率和y轴截距的值，并确定一次函数的表达式。

北师大版八年级上册5.7用二元一次方程组确定一次函数表达式课件(22张PPT)

北师大版八年级上册5.7用二元一次方程组确定一次函数表达式课件(22张PPT)
设同时出发后t小时相遇，则15t+20t=100，
解：设这个一次函数的解析式为y=kx+b.
b=-1.
根据题意，可得方程组
会应用方程与函数的联系解决实际问题.
水的冰点温度是0℃，用华氏温度度量为32 ℉.
小亮 二元一次方程组与一次函数有何联系?
小颖 用作图象的方法可以直观地获得问题的结果，但有时却难以准确，为了获得准确的结果，我们一般用代数方法. 小明 设同时出发后t小时相遇，则15t+20t=100，
若一客户购买400kg,单价是多少?
解 解：方解程这 组所个 得二挂元一物次方体程组的得k质，b.量为3kg时，弹簧长度为16cm.写出y与x之间的
（1）写出y与x之间的函数表达式；
关系式，并求当所挂物体的质量为4kg时弹簧的长度. 用作图象的方法可以直观地获得问题的结果，但有时却难以准确，为了获得准确的结果，我们一般用代数方法.
探究新知
方法点拨 确定一次函数关系式的方法：
１）设关系式； ２）找x与y的对应值； ３）代入转化成方程（组） ４）解方程（组）确定系数； ５）还原关系式.
巩固练习
变式训练
已知一次函数的图象过点（3，5）与（-4，-9），求 这个一次函数的解析式．
解：设这个一次函数的解析式为y=kx+b. 把点（3，5）与（-4，-9）分别代入，得： 3k+b=5， -4k+b=-9， 解方程组得 k=2， b=-1.
探究新知
解：（1）设此一次函数表达式为：y=kx+b（k≠0) . 根据题意，可得方程组
5 60k b 10 90k b
解得Leabharlann k 1 , 6b 5.
所以 y 1 x 5.

5.7 用二元一次方程组确定一次函数表达式-知识考点梳理 北师大版数学八年级上册课件

5.7 用二元一次方程组确定一次函数表达式-知识考点梳理 北师大版数学八年级上册课件
突
破 关系就可以求出a 值，再分别就 0≤x≤75，75＜x≤125 和
x＞125 运用待定系数法表示出 y 与 x 的函数关系式即可.
5.7 用二元一次方程组确定一次函数表达式
返回目录
［答案］ 解：（1）由题意，得 60×2.5＝150（元）
重
难
题 ；
型
（2）由题意，得 a＝（325-75×2.5）÷（125-75）＝
读
5.6 二元一次方程与一次函数
考
点
清
单
解
读
［解题思路］
［答案］ C
返回目录
5.6 二元一次方程与一次函数
考
点
清
单
解
读
■考点二
一次函数与二元一次方程组
二元一次
方程组与
一次函数
的关系
返回目录
5.6 二元一次方程与一次函数
考
点
清
单
解
读
返回目录
续表
已知两条直线 y=k1x+b1（k1≠0），y=k2x+b2
重
难
（2）调价后每月支付燃气费用 y（单位：元）与每月
题
型 用气量 x（单位：m3）的关系如图所示，求 y 与 x 的表
突
破 达式及 a 的值.
5.7 用二元一次方程组确定一次函数表达式
返回目录
［解析］（1）根据单价×数量＝总价就可以求出 3 月
重
难
题 应该缴纳的费用；
型
（2）（结合统计表的数据） 根据单价×数量＝总价的
= −，

ቊ
所以直线 l1：y＝x+5 与直线 l2：y＝- x-1

= .

北师版八年级上册数学精品教学课件 用二元一次方程组确定一次函数表达式


你明白他的想 法吗？用他的方法做 一做!
设同时出发后t小时 相遇，则 15t+20t=100
20
t=
7
对于乙，s 是t的一次函数，可设 s=kt+b. 当t=0时，s=100；当t=1时，s=80.将它们分 小颖 别代入s=kt+b中，可以求出k，b的值，也 即可以求出乙 s 与t 之间的函数表达式.
课后练习
见本课时练习
随堂练习
1.右图中的两直线l1 ，l2 的交点坐标可
以看作方程组
的解
y
4
l1
3
2
l2 1
-1 0 -1
1 2 3 4x
2. 在弹性限度内，弹簧的长度y（cm）是
所挂物体质量x（kg）的一次函数.当所挂 物体的质量为1kg时，弹簧长15厘米；当所 挂物体的质量为3 kg时，弹簧长16 cm.写 出 y 与 x 之间的关系式，并求出所挂物体 的质量为4 kg时弹簧的长度.
s/千米 图象表示
小明
可以分别作出两人s 与 120 t 之间的关系图象，找 100 (B)
出交点的横坐标就行了 80
60
40
你明白他的想法吗？用 20
他的方法做一做
(A)0
1 2 2.8 3 4 t/时
1 时后乙距A地 80千米,即乙的
速度是20千米/时
小 彬
2 时后甲距A 地 30千米,故甲 的速度是 15千米/时
们一般用代数方法.
小彬
小明
小颖
例2 某长途汽车客运站规定，乘客可以 免费携带一定质量的行李，但超过该质 量则需购买行李票，且行李费y（元）是 行李质量x（kg）的一次函数．现知李明 带了60 kg的行李，交了行李费5元；张 华带了90 kg的行李，交了行李费10 元．

5.7用二元一次方程组确定一次函数表达式

1 22.8 3 4 t/时
(A)0
求出s与t之间的关系式，联立解方程组
A、B 两地相距100千米，甲、乙 两人骑自行车分别从A、B 两地相向 而行。假设他们都保持匀速行驶， 则他们各自到A 地的距离s (千米) 都是骑车时间 t (时) 的一次函数. 1 时后乙距A地80千米, 2 时后甲距A地 30千米. 问 经过多长时间两人相遇 ? 对于乙，s 是t 的一次函数， 可设 s=kt+b。 小颖 当t=0时，s=100； 当t=1时，s=80。将它们分 别代入s=kt+b中，可以求出 k、b的值，也即可以求出乙 s 与t 之间的函数表达式。 同样可求出甲s与t之间的函 数表达式。 再联立这两个表达式，求解 方程组就行了。
解;（1）设此一次函数表达式为：y=kx+b,根据题意，得
5 60k b 10 90k b
解得：
1 k 6 b 5
1 ∴y= x—5 6
（2）当y=0时 , x=30；当x>30时， y>0。 所以旅客最多可免费携带30千克的行李。
学生展示一：P127
用一元一次方程的 方法可以解决问题
用图象法可以解决问题
小明
小亮 用作图象的方法可以 直观地获得问题的结果， 但有时却难以准确，为了 获得准确的结果，我们一 般用代数方法。
用方程组的方法 可以解决问题
小颖
合作探究
对于上面同一道题的三中哪种方法适用性更广一些。
k b 15, 3k b 16.
解得
k 0.5, b 14.5.
所以y与x之间的函数关系式y=0.5x+14.5 并且当x=4时，y=16.5
小结：
利用二元一次方程组确定一次函数表达式的一般步骤:

(完整版)5.7用二元一次方程组确定一次函数表达式

方法，叫做待定系数法.
利用二元一次方程组求一次函数表达式的一般步骤： 1.用含字母的系数设出一次函数的表达式：y=kx+b.
2.将已知条件代入上述表达式中得k，b的二元一次方程组. 3.解这个二元一次方程组得k，b.
4.进而求出一次函数的表达式.
巩固训练1：
例2 已知一次函数的图象过点（3，5）与（-4，-9）， 求这个一次函数的解析式．
达标检测：
典例精析
例1：某长途汽车客运站规定，乘客可以免费携带 一定质量的行李，但超过该质量则需购买行李票，
且行李费y（元）是行李质量x（kg）的一次函
数．已知李明带了60 kg的行李，交了行李费5元； 张华带了90 kg的行李，交了行李费10元．
（1）写出y与x之间的函数表达式；
（2）旅客最多可免费携带多少千克的行李？
由题意可知，
1 3k b 2 0 b
k 1, 解得 b 2.
所以过A，B两点的直线的表达式为y=x-2．
因为当x=4时，y=4-2=2．
所以点C（4，2）在直线y=x-2上．
所以三点A（3，1）， B（0，-2），C（4，2）在
同一条直线上．
巩固训练3：
3.在某个范围内,某产品的购买量y(单位:kg)与单价x(单位:元)
之间满足一次函数,若购买1000kg,单价.若一客户购买400kg,单价是多少?
解:设购买量y与单价x的函数解析式为y=kx+b， 根据题意得：
｛800k + b = 1000 700k + b = 2000 ｛k 10 解得: b =900
所以购买量y与单价x的函数解析式为 y =-10x + 9000 当 y = 400时代入y =-10x + 9000得 -10 x + 900 =400, x =860. 答:当客户购买400kg,单价是860元.

5.7用二元一次方程组确定一次函数表达式


自学检测1：
1.如图，L1和L2分别表示甲走路和乙骑自行车（在同 一条路上）行走的路程s（千米）与时间t（小时）之 间的关系，观察图象，回答下列问题： L2 （1）途中乙发生了什么事？ s
（2）他们几时相遇？
12 10 8 D
P
E
L1
A B
0
0.5
1 1.2
t
知识升华
利用二元一次方程组确定一次函数的表达式是求一次 函数表达式的主要方法，一般步骤如下： （1）设：设出函数表达式： y=kx+b （2）代：把已知条件代入，得到关于k、b的方程组 （3）解：解方程组，求出k、b的值 （4）还原：写出其表达式
求出s与t之间的关系式，联立解方程组
A、B 两地相距150千米，甲、 乙两人骑自行车分别从A、B 两地相 向而行。假设他们都保持匀速行驶， 则他们各自到A 地的距离s (千米) 都 是骑车时间 t (时) 的一次函数. 1 时后乙距A地120千米, 2 时后甲距A地 40千米. 问 经过多长时间两人相遇 ? 对于乙，s 是t 的一次函数， 可设 s=kt+b。 小颖 当t=0时，s=150； 当t=1时，s=120。将它们分 别代入s=kt+b中，可以求出k 、b的值，也即可以求出乙 s 与t 之间的函数表达式。 同样可求出甲s与t之间的函 数表达式。 再联立这两个表达式，求解 方程组就行了。
s
图象表示
120
100 80 60
s乙 150 30t
l2
l1
s甲 20t
可以分别作出两人 40 s 与t 之间的关系图象， 20 找出交点的横坐标就行了！ 1 2 3 0 (A) 4 t 1 2 3 你明白他的想法吗？ 用他的方法做一做， 小明的方法求出的 看看和你的结果一致吗？ 结果准确吗？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

甲：t=0时，s=0; t=2时，s=30. 乙：t=0时，s=100; t=1时，s=80. 可以分别作 出两人s 与t 之间 的关系图象，找 出交点的横坐标 就行了。
用作图象的方 法可以直观地获得 问题的结果，但有 时却难以准确。
小 明
你明白他的想法 吗？用他的方法 做一做！
例题： A ,B两地相距100千米，甲、乙两人骑自行车分别
确定关系式的方法
解：（1）设y＝kx+b 根据题意，得： 5=60k+b 10=90k+b １）设关系式； ２）找Ｘ与Ｙ的对应值；
解得：k=1/6,b=-5 ∴y与x的函数关系式是：y=1/6x-5 （2）当x=30时，y=0。即旅客最多可免费带30kg 的行李。
３）代入转化成方程（组） ４）解方程（组）；
２）找Ｘ与Ｙ的对应值；
３）代入转化成方程（组）； ４）解方程（组）； ５）写出关系式。
确定关系式的方法： １）设关系式；
２）找Ｘ与Ｙ的对应值； ３）代入转化成方程（组） ４）解方程（组）； ５）写出关系式。
像这样，先设出函数关系式，再根据所给条件确定表 达式中未知数的系数，从而得到函数表达式的方法，叫做 待定系数法。
某市自来水公司为鼓励居民节约用水，采取按月用水 量分段收费办法，若某户居民应交水费 y（元）与用水量x （t）的函数关系如图所示。 1）分别写出当0≤x≤15和x＞15时，y与x的函数关系式。 2）若某用户十月份用水量为10 t，则应交水费多少元？若 该用户十一月份交了51元的水费，则他该月用水多少吨？
小 亮
解：设同时出发后t小时相遇，则15t+20t=100
解得：t=
20 7
例题： A ,B两地相距100千米，甲、乙两人骑自行车分别
从A，B两地相向而行。假设他们都保持匀速行驶，则他们 各自到A地的距离 s(千米)都是骑车时间 t (时)的一次函数。 1小时后乙距A地80千米； 2小时后甲距A地30千米。问： 经过多长时间两人相遇 ?
从A，B两地相向而行。假设他们都保持匀速行驶，则他们 各自到A地的距离 s(千米)都是骑车时间 t (时)的一次函数。 1小时后乙距A地80千米； 2小时后甲距A地30千米。问： 经过多长时间两人相遇 ? 对于乙，s 是t的一次函数，可设 s=kt+b. 当t=0时，s=100；当t=1时，s=80。将它们分 别代入s=kt+b中，可以求出k，b的值，也即 可以求出乙 s 与t 之间的函数表达式。 你能求出甲的表达式吗？
正因如此，方程问 题可以通过函数知识来 解决，反之，函数问题 也可以通过方程知识来 解决。
方法三：图象法
例题： A ,B两地相们都保持匀速行驶，则他们 各自到A地的距离 s(千米)都是骑车时间 t (时)的一次函数。 1小时后乙距A地80千米； 2小时后甲距A地30千米。问： 经过多长时间两人相遇 ? 1 时后乙距A地 80千米，即乙的速度是20千米/时 2 时后甲距A 地 30千米,故甲的速度是 15千米/时 你明白他的想法吗？用他的方法做一做! 用一元一次方 程的方法可以解决 问题。
５）写出关系式。
已知函数y=2x+b的图象经过点（a, 7）和（－2，a）, 求这个函数表达式。
确定关系式的方法
１）设关系式；
在弹性限度内，弹簧的长度y（cm）是所挂物体质量x （kg）的一次函数.当所挂物体的质量为1kg时，弹簧长15 厘米；当所挂物体的质量为3 kg时，弹簧长16 cm.写出 y 与 x 之间的关系式，并求出所挂物体的质量为4 kg时弹簧 的长度。
小明
用图象法 可以解决 问题
小颖
用方程组的 方法可以解 决问题
用作图象的方法可以直观地获得问题的结果， 但有时却难以准确，为了获得准确的结果，我们一 般用代数方法。
例2 某长途汽车客运站规定，乘客可以免费携带一定质量的 行李，但超过该质量则需购买行李票，且行李费y（元）是行李质 量x（kg）的一次函数．现知李明带了60 kg的行李，交了行李费5 元；张华带了90 kg的行李，交了行李费10元． （1）写出y与x之间的函数表达式； （2）旅客最多可免费携带多少千克的行李？
s 15t s 100 20t
确定关系式的方法
１）设关系式； ２）找Ｘ与Ｙ的对应值； ４）解方程（组）； ５）写出关系式。
３）代入转化成方程（组）；
小 颖
解得：
300 Ｓ＝ 7 20 t 7
用方程组的方法 可以解决问题。
在以上的解题过程中你受到什么启发？
小亮
用一元一 次方程的 方法可以 解决问题
古之成大事 者,不惟有超 士之才,亦有 坚忍不拔之志。
教学目标
1.理解作函数 图像的方法与代数方 法各自的特点. 2.掌握利用二 元一次方程组确定一 次函数的表达式. 3.进一步理解 方程与函数的联系， 体会知识之间的普遍 联系和知识之间的相 互转化.
１、二元一次方程组与一次函数有何联系? 二元一次方程组的解是它们对应的两个一次函数图象 的交点坐标；反之，两个一次函数图象的交点也是它们所 对应的二元一次方程组的解。 ２、二元一次方程组有哪些解法？ 方法一：代入法 消元法 方法二：加减法 代数方法 数形结合方法
y(元)
确定关系式的方法
１）设关系式；
２）找Ｘ与Ｙ的对应值；
３）代入转化成方程（组）； ４）解方程（组）； ５）写出关系式。
39 27
O
15
20
x(t)