立体几何大题题库

立体几何解答题题库1.如图，在三棱锥P -ABC 中，P A ，PB ，PC 两两垂直，P A =AB =AC =3，平面//α平面P AB ，且α与棱PC ，AC ，BC 分别交于P 1，A 1，B 1三点．（1）过A 作直线l ，使得l BC ⊥，11l P A ⊥，请写出作法并加以证明；（2）若α将三棱锥P -ABC 分成体积之比为8:19的两部分（其中，四面体P 1A 1B 1C 的体积更小），D 为线段B 1C 的中点，求四棱锥A 1-PP 1DB 1的体积．2.如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形，俯视图为正方形，侧视图为直角三角形，尺寸如图所示)．(1)求四棱锥P -ABCD 的体积；(2)证明：BD ∥平面PEC ；(3)线段BC 上是否存在点M ，使得AE ⊥PM ？若存在，请说明其位置，并加以证明；若不存在，请说明理由．3.如图1所示，平面多边形CDEF 中，四边形ABCD 为正方形，EF ∥AB ，AB =2EF =2,沿着AB 将图形折成图2，其中AED ∠90,,AE ED H =︒=为AD 的中点.（Ⅰ）求证：EH ⊥BD ；（Ⅱ）求四棱锥D -ABFE 的体积.4.如图，四棱锥P -ABCD 中，侧面PAD 为等边三角形，且平面⊥PAD 底面ABCD ，121===AD BC AB ，090=∠=∠ABC BAD .（1）证明：：AB PD ⊥；（2）点M 在棱PC 上，且CP CM λ=，若三棱锥ACM D -的体积为31，求实数λ的值. 5.已知ABCD 是矩形，PD ⊥平面ABCD ，PD =DC =a ，2AD a =，M 、N 分别是AD 、PB 的中点。

（Ⅰ）求证：平面MNC ⊥平面PBC ；（Ⅱ）求点A 到平面MNC 的距离。

6.在直三棱柱ABC －A 1B 1C 1中，AB =AC ，E 是BC 的中点.（1）求证：平面AB 1E ⊥平面B 1BCC 1；（2）求证：A 1C ∥平面AB 1E ．7.如图，ABCD 为矩形，点A 、E 、B 、F 共面，且ABE ∆和ABF ∆均为等腰直角三角形，且BAE AFB ∠=∠=90°．（Ⅰ）若平面ABCD ⊥平面AEBF ，证明平面BCF ⊥平面ADF ；（Ⅱ）问在线段EC 上是否存在一点G ，使得BG ∥平面CDF ，若存在，求出此时三棱锥G -ABE 与三棱锥G -ADF 的体积之比．8.如图，四边形ABCD 为菱形，ACEF 为平行四边形，且平面ACEF ⊥平面ABCD ，设BD 与AC 相交于点G ，H 为FG 的中点.（Ⅰ）证明：BD ⊥CH ；（Ⅱ）若AB =BD =2，AE =3，CH =32，求三棱锥F -BDC 的体积.9.如图，四边形ABCD 是平行四边形，平面AED ⊥平面ABCD ，EF ∥AB ，AB =2,BC = EF =1,6AE =,DE =3,60BAD ∠=，G 为BC 的中点.（1）求证：FG ∥平面BED ；（2）求证：BD ⊥平面AED ；（3）求点F 到平面BED 的距离.10.如图，在底面为梯形的四棱锥S -ABCD 中，已知//AD BC ，60ASC ∠=，2AD DC ==，2SA SC SD ===.（1）求证：AC SD ⊥；（2）求三棱锥B -SAD 的体积.11.如图，在四棱锥P －ABCD 中，平面PCD ⊥平面ABCD ，112AB AD CD ===， ∠BAD ＝∠CDA ＝90°，2PC PD ==．（1）求证：平面P AD ⊥平面PBC ；（2）求直线PB 与平面P AD 所成的角；（3）在棱PC 上是否存在一点E 使得直线BE ∥平面P AD ，若存在求PE 的长，并证明你的结论． 12.如图，三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 是菱形，其对角线的交点为O ，且AB =AC 1，1AB B C ⊥.（1）求证：AO ⊥平面BB 1C 1C ；（2）若12BB =，且1160B BC B AC ∠=∠=︒，求三棱锥C 1-ABC 的体积.13.如图，在四棱锥P -ABCD 中，PA ⊥平面ABCD ，底面ABCD 是菱形，AB =2，60BAD ∠=︒．（1）求证：平面PBD ⊥平面P AC ；（2）若PA AB =，M 为线段PC 的中点，求三棱锥C -MBD 的体积。

立体几何大题专练1、如图，已知PA ⊥矩形ABCD 所在平面，M 、N 分别为AB 、PC 的中点； (1)求证：MNP ABC -,E F ,AC BC //EF PAB PAC ⊥ABC PA PC =90ABC ∠=︒PEF ⊥PBCEF Q E F AC BC //EF AB ∴ ……………………2分 又⊄EF 平面PAB ，⊆AB 平面PAB ，∴ EF ∥平面PAB . ……………………5分（2）PA PC =Q ，E 为AC 的中点，PE AC ∴⊥ ……………………6分 又Q 平面PAC ⊥平面ABCPE ∴⊥面ABC ……………………8分 PE BC ∴⊥……………………9分PAC EBF又因为F 为BC 的中点，//EF AB ∴090,BC EF ABC ⊥∠=∴Q ……………………10分EF PE E =Q IBC ∴⊥面PEF ……………………11分 又BC ⊂Q 面PBC∴面PBC ⊥面PEF ……………………12分3. 如图，在直三棱柱ABC —A 1B 1C 1中，AC=BC ，点D 是AB 的中点。

（1）求证：BC 1PC AB N M ABCD PA 、分别是、所在的平面，矩形⊥PAD MN 平面//CD MN ⊥图，正方形ABCD 所在的平面与三角形ＡD Ｅ所在平面互相垂直，△ＡＥＢ是等腰直角三角形，且ＡＥ＝ＥD 设线段BC 、AE 的中点分别为F 、M ，求证：（1）FM ∥ECD 平面； （2）求二面角Ｅ－ＢＤ—Ａ的正切值．（1）证明：取AD 的中点N,连结FN,MN,则MN ∥ED ，FN ∥CD∴平面FMN ∥平面ECD. ∵ MF 在平面FMN 内,∴ FM ∥平面ECD ......5分 （2）连接EN, ∵AE=ED ，N 为AD 的中点，NMPDCBA∴ EN⊥AD.又∵面ADE⊥面ABCD，∴EN⊥面ABCD.作NP⊥BD,连接EP,则EP⊥BD，∴∠EPN即二面角E-BD-A的平面角，设AD=a,∵ABCD为正方形，⊿ADE为等腰三角形，∴EN=12a,NP=24a.∴tan∠EPN=2. ......10分7.如图，一个圆锥的底面半径为2cm，高为6cm，其中有一个高为x cm的内接圆柱.(1)试用x表示圆柱的侧面积；（2）当x为何值时，圆柱的侧面积最大.19.（1）解：设所求的圆柱的底面半径为r则有662xr-=,即32xr-=.∴2324)32(22xxxxrxSππππ-=-==圆柱侧.......5分（2）由（1）知当3)32(24=--=ππx时，这个二次函数有最大值为π6所以当圆柱的高为3cm时，它的侧面积最大为26cmπ......10分8．（10分）如图，在三棱锥P ABC-中，⊿PAB是等边三角形，∠PAC=∠PBC=90 o.（1）证明：AB⊥PC；（2）若4PC=，且平面PAC⊥平面PBC，求三棱锥P ABC-体积.解：（1）因为PAB ∆是等边三角形，90PAC PBC ∠=∠=︒, 所以Rt PBC Rt PAC ∆≅∆,可得AC BC =。

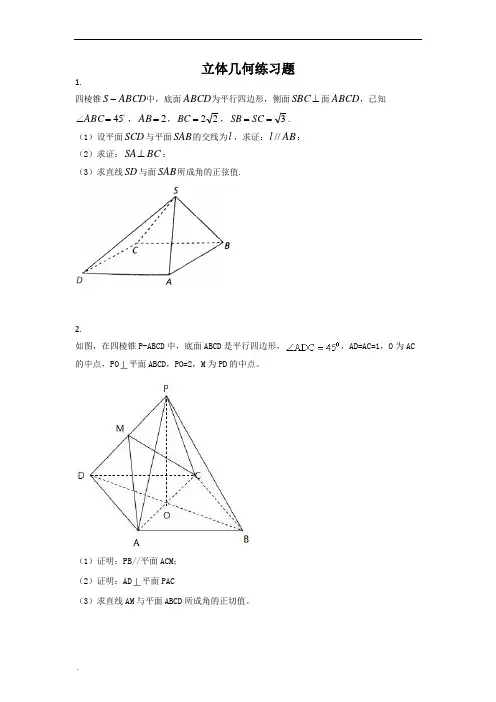
高中数学立体几何10道大题1.在四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC垂直于面ABCD，已知∠ABC=45°，AB=2，BC=22，SB=SC=3.1) 证明平面SCD与平面SAB的交线l平行于AB；2) 证明SA垂直于BC；3) 求直线SD与面SAB所成角的正弦值。

2.在四棱锥P-ABCD中，底面ABCD是平行四边形，P为其顶点，O为其中心，PO平行于AB且PO=2，M为PD的中点，AD=AC=1，O为AC的中点。

1) 证明PB平行于平面ACM；2) 证明AD在平面PAC上；3) 求直线AM与平面ABCD所成角的正切值。

3.在四棱锥P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD均为等边三角形。

1) 证明CD垂直于平面PBD；2) 求二面角CPBD的平面角的余弦值。

4.在四棱锥P-ABCD中，PA垂直于底面ABCD，AC垂直于AD，ABCD为梯形，AB平行于DC，AB垂直于BC，PA=AB=BC=3，点E在棱PB上，且PE=2EB。

Ⅰ) 证明平面PAB垂直于平面PCB；Ⅱ) 证明PD平行于平面EAC；Ⅲ) 求平面AEC和平面PBC所成锐二面角的余弦值。

5.在图中，矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB，平面ABCD与平面ABPE的交线为AB，且AB=BP=2，AD=AE=1，AE垂直于AB，且AE平行于BP。

1) 在面ABCD内是否存在点N，使得MN垂直于平面ABCD？若存在，请证明；若不存在，请说明理由；2) 求二面角D-PE-A的余弦值。

6.在直三棱柱ABC-A1B1C1中，平面A1BC垂直于侧面A1BB1，且AA1=AB=2.1) 证明AB垂直于BC；2) 若直线AC与平面A1BC所成角为α，求锐二面角AAC1B的大小。

7.在四棱锥V-ABCD中，底面ABCD为正方形，侧面VAD 为正三角形，平面VAD垂直于底面ABCD。

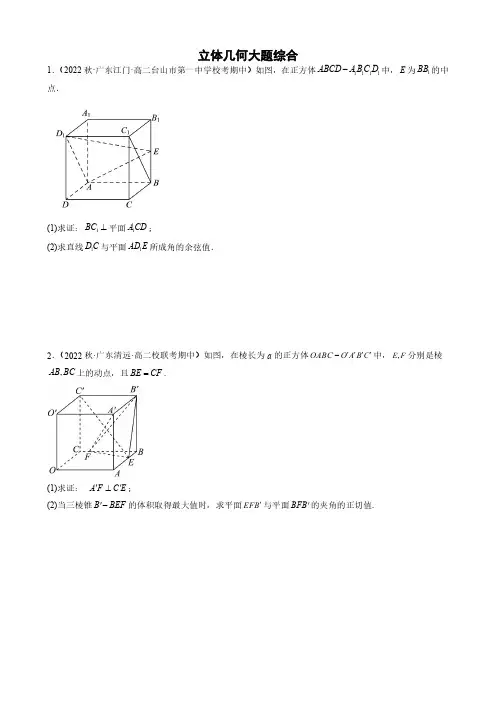
立体几何大题综合1．（2022秋·广东江门·高二台山市第一中学校考期中）如图，在正方体1111ABCD A B C D -中，E 为1BB 的中点．(1)求证：1BC ⊥平面1ACD ；(2)求直线1D C 与平面1AD E 所成角的余弦值．2．（2022秋·广东清远·高二校联考期中）如图，在棱长为a 的正方体OABC O A B C ''''-中，,E F 分别是棱,AB BC 上的动点，且BE CF =.(1)求证：A F C E ''⊥；(2)当三棱锥B BEF '-的体积取得最大值时，求平面EFB '与平面BFB '的夹角的正切值.3．（2022秋·广东肇庆·高二校考期中）如图在棱长为1的正方体1111ABCD A B C D -中，E 为11A B 的中点，F 为AB 的中点，H 为1DD 的中点，K 为1BB 的中点.(1)求直线1A H 到直线KC 的距离；(2)求直线FC 到平面1AEC 的距离.4．（2022秋·广东江门·高二校考期中）如图，在四棱锥P －ABCD 中，PD ⊥底面ABCD ，底面ABCD 是边长为2的正方形，PD CD =，F ，G 分别是PB ，AD 的中点．(1)求证：FG //平面PCD ；(2)求点C 到平面PGB 的距离．5．（2022秋·广东清远·高二校联考期中）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，AB ⊥平面PAD ，E 是AD 的中点，PAD 为等腰直角三角形，DP AP ⊥，2PA AB ==2(1)求证：PE BD ⊥；(2)求点A 到平面PBE 的距离．6．（2022秋·广东江门·高二新会陈经纶中学校考期中）如图，在直角梯形ABCD 中，,=90,AD BC ADC AE ∠︒⊥∥平面ABCD ，EF CD ∥，112BC CD AE EF AD =====．(1)求证：BE AF ⊥；(2)在线段BC 上是否存在点M ，使平面EMD 与平面AMD 的夹角的大小为π3若存在，求出CM 的长；若不存在，请说明理由．7．（2022秋·广东江门·高二台山市第一中学校考期中）如图，边长为1的正方形ABCD 所在平面与正方形ABEF 所在平面互相垂直，动点M 、N 分别在正方形对角线AC 和BF 上移动，且(0CM BN a a ==<<．(1)求证MN 与平面BCE 平行；(2)当a =A MN B --的余弦值．8．（2022秋·广东肇庆·高二肇庆市端州中学校考期中）如图在四棱锥P ABCD －中，侧面PAD ⊥底面ABCD ，侧棱PA PD ==ABCD 为直角梯形，其中BC AD ∥，AB AD ⊥，222AD AB BC ===，O 为AD 的中点．(1)求证：PO ⊥平面ABCD ；(2)求二面角C PD A --的正弦值．9．（2022秋·广东江门·高二江门市第二中学校考期中）如图，已知PA ⊥平面ABCD ，底面ABCD 为矩形，2,,PA AD AB M N ===分别为,AB PC 的中点.(1)求证：MN 平面PAD ；(2)求平面PMC 与平面PAD 的夹角的余弦值.10．（2022秋·广东阳江·高二校联考期中）图1是直角梯形ABCD ，//AB DC ，90,2,3,2D AB DC AD CE ED ︒∠====.以BE 为折痕将BCE 折起，使点C 到达C 1的位置，且1AC = 2.(1)证明：平面1BC E ⊥平面ABED ；(2)求直线1BC 与平面1AC D 所成角的正弦值.11．（2022秋·广东深圳·高二深圳外国语学校校考期中）如图所示，在四棱锥P ABCD -中，底面ABCD 为正方形，E 为侧棱PC的中点．(1)设经过A 、B 、E 三点的平面交PD 于F ，证明：F 为PD 的中点；(2)若PA ⊥底面ABCD ，且2PA AD ==，求点P 到平面ABE 的距离．12．（2022秋·广东阳江·高二校联考期中）如图，在四棱柱ABCD -A 1B 1C 1D 1中，四边形ABCD 是一个边长为2的菱形，∠DAB ＝60°.侧棱DD 1⊥平面ABCD ，DD 1＝3.(1)求二面角B -D 1C -D 的平面角的余弦值；(2)设E 是D 1B 的中点，在线段D 1C 上是否存在一点P ，使得AE ∥平面PDB ？若存在，请求出11D P D C的值；若不存在，请说明理由.13．（2022秋·广东茂名·高二统考期中）在直四棱柱1111ABCD A B C D -中，四边形ABCD 为平行四边形，M为1AA 的中点，1BC BD ==，1AB AA ==(1)求证：DM ⊥平面1BDC ；(2)求平面1MBC 与平面1D B C 夹角的余弦值.14．（2022秋·广东揭阳·高二惠来县第一中学校考期中）已知四棱锥P ABCD -中，底面ABCD 是矩形，且2=AD AB ，PAD 是正三角形，CD ⊥平面PAD ，E 、F 、G 、O 分别是PC 、PD 、BC 、AD 的中点．(1)求平面EFG 与平面ABCD 所成角的大小；(2)线段PA 上是否存在点M ，使得直线GM 与平面EFG 所成角的大小为π6，若存在，求出PM PA的值；若不存在，说明理由．15．（2022秋·广东佛山·高二顺德一中校考期中）如图，在直棱柱1111ABCD A B C D -中，底面ABCD 是边长为4的菱形，60BAD ∠= ，14AA =，P 是1AD 上的动点（不含端点）.(1)当P 为1AD 的中点时，求直线AD 到平面PBC 的距离；(2)求直线1AD 和平面BCP 所成角的正弦值的取值范围.16．（2022秋·广东佛山·高二顺德一中校考期中）如图，在直角梯形ABED 中，//BE AD ，DE AD ⊥，BC AD ⊥，4AB =，BC =BE =.将矩形BEDC 沿BC 翻折，使得平面ABC ⊥平面BCDE .(1)求DB 与平面ADE 所成角的正弦值.(2)求平面ADE 与平面ABC 所成的锐二面角的余弦值.17．（2022秋·广东珠海·高二珠海市第二中学校考期中）如图1，在MBC 中，24BM BC BM BC ==⊥，，,A D 分别为棱,BM MC 的中点，将△MAD 沿AD 折起到PAD 的位置，使90PAB ∠=︒，如图2，连接,PB PC .(1)求证：平面PAD ⊥平面ABCD ；(2)若E 为PC 中点，求直线DE 与平面PBD 所成角的正弦值；(3)线段PC 上是否存在一点G ，使二面角G AD P --求出PG PC 的值；若不存在，请说明理由.18．（2022秋·广东广州·高二广州市第八十九中学校考期中）如图，已知梯形ABCD ，AB //CD ，,120AD DC BC ADC ︒==∠=，四边形ACFE 为正方形，且平面ACFE ⊥平面ABCD ．(1)求证：BC ⊥平面ACFE ；(2)点M 在线段EF 上运动，求平面MAB 与平面ADE 夹角余弦值的取值范围．19．（2022秋·广东东莞·高二校考期中）如图，在长方体ABCD-A 1B 1C 1D 1中，E ，M 分别是BC ，AE 的中点，AD=AA 1=1，AB=2.(1)试问在线段CD 1上是否存在一点N ，使MN ∥平面ADD 1A 1?若存在，确定N 的位置；若不存在，请说明理由；(2)在（1）中，当MN ∥平面ADD 1A 1时，试确定直线BB 1与平面DMN 的交点F 的位置，并求BF 的长.20．（2022秋·广东湛江·高二湛江二十一中校考期中）如图，在长方体1111ABCD A B C D -中，11AD AA ==，2AB =，点E 在棱AB 上移动．(1)证明：11D E A D ⊥；(2)求平面1ACD 的法向量.(3)当E 为AB 的中点时，求点E 到面1ACD 的距离.21．（2022秋·广东广州·高二统考期中）如图，在四棱锥P —ABCD 中，PA ⊥平面ABCD ，底面ABCD 是边长为2的正方形，PA =，G 为CD 的中点，E ，F 是棱PD 上两点（F 在E 的上方），且2EF =．(1)若BF //平面AEG ，求DE ；(2)当点F 到平面AEC 的距离取得最大值时，求直线AG 与平面AEC 所成角的正弦值．22．（2022秋·广东广州·高二校联考期中）在多面体ABCDEF 中，平面ABCD 为正方形，2AB =，3AE =，DE =E AD C --//EF BD .(1)证明：平面ABCD ⊥平面DCE ；(2)若()0EF DB λλ=> ，求平面ABF 与平面CEF 所成锐二面角的余弦值的取值范围.23．（2022秋·广东佛山·高二佛山市顺德区容山中学校考期中）如图，圆柱的轴截面ABCD 为正方形，点E 在底面圆周上，且,BE CE M =为AE 上的一点，且,BM AC N ⊥为线段AC 上一动点（不与,A C 重合）(1)若2AN NC =，设平面BMN ⋂面BEC l =，求证：//MN l ；(2)当平面BMN 与平面DEC 夹角为π3，试确定N 点的位置.24．（2022秋·广东肇庆·高二肇庆市端州中学校考期中）如图，四棱锥P ABCD -的底面为菱形，,23ABC AB AP π∠===，PA ⊥底面ABCD ，,E F 分别是线段,PB PD 的中点，G 是线段PC 上的一点.(1)若G 是直线PC 与平面AEF 的交点，试确定PG CG的值；(2)若直线AG 与平面AEF 所成角的正弦值为35，求三棱锥P EFG -体积.25．（2022秋·广东江门·高二校考期中）如图甲，在矩形ABCD 中，2AB AD E ==为线段DC 的中点，ADE V 沿直线AE 折起，使得DC .(1)求证：BE ⊥平面ADE ；(2)线段AB 上是否存在一点H ，使得平面ADE 与平面DHC 所成的角为π4若不存在，说明理由；若存在，求出H 点的位置.26．（2022秋·广东惠州·高二统考期中）如图，在四棱锥P ABMN -中，PNM △是边长为2的正三角形，AN NP ⊥，AN BM ∥，3AN =，1BM =，AB =C ，D 分别是线段AB ，NP 的中点.(1)求证：平面ANMB ⊥平面NMP ；(2)求直线CD 与平面ABP 所成角的正弦值.27．（2022秋·广东广州·高二校联考期中）如图，在四棱锥P ABCD -中，平面PAD ⊥平面,2,4,ABCD PA AD BD AB ====，BD 是ADC ∠的平分线，且BD BC ⊥.(1)若点E 为棱PC 的中点，证明：BE 平面PAD ；(2)已知二面角P AB D --的大小为60 ，求平面PBD 和平面PCD 的夹角的余弦值.28．（2022秋·广东珠海·高二珠海市斗门区第一中学校考期中）如图，等腰直角△ACD 的斜边AC 为直角△ABC 的直角边，E 是AC 的中点，F 在BC 上．将三角形ACD 沿AC 翻折，分别连接DE ，DF ，EF ，使得平面DEF ⊥平面ABC ．已知2AC =，30B ∠=︒，(1)证明：EF ∥平面ABD ；(2)若DF =A BC D --的余弦值．29．（2022秋·广东阳江·高二统考期中）如图，在四面体ABCD 中，ABC 是正三角形，ACD 是直角三角形，ABD CBD ∠=∠，AB =BD ．(1)求证：平面ACD ⊥平面ABC ；(2)若DE mDB = ，二面角D AE C --的余弦值为17，求m ．30．（2022春·广东广州·高二执信中学校考期中）已知△ABC 是边长为6的等边三角形，点M ，N 分别是边AB ，AC 的三等分点，且13AM AB =，13CN CA =，沿MN 将△AMN 折起到A MN '△的位置，使90A MB '∠=︒．(1)求证：A M '⊥平面MBCN ；(2)在线段BC 上是否存在点D ，使平面A ND '与平面A MB '所成锐二面角的余弦值为13若存在，设()0BD BC λλ=> ，求λ的值；若不存在，说明理由．立体几何大题综合答案1．（2022秋·广东江门·高二台山市第一中学校考期中）如图，在正方体1111ABCD A B C D -中，E 为1BB 的中点．(1)求证：1BC ⊥平面1ACD ；(2)求直线1D C 与平面1AD E 所成角的余弦值．（2）以AD 方向为x 轴正方向，妨设正方体边长为1，则()0,0,0A 面1AD E 的法向量为(),,n x y z = ，则设直线1D C 与平面1AD E 所成角为2．（2022秋·广东清远·高二校联考期中）如图，在棱长为a 的正方体OABC O A B C ''''-中，,E F 分别是棱,AB BC 上的动点，且BE CF =.(1)求证：A F C E ''⊥；(2)当三棱锥B BEF '-的体积取得最大值时，求平面EFB '与平面BFB '的夹角的正切值.则()()()0,0,0,1,0,0,0,1,0,C O B B (,1,0),(0,,0)E m F m ，(1,A F '=- 则(1)(1)11A F C E m m ''⋅=-+-⨯+ ∴A F C E ''⊥ ，故A F C E ''⊥.（2）由（1）知1BB '=,而B BEF V '-故当S 取到最大值时，三棱锥111111的中点，F 为AB的中点，H为1DD的中点，K为1BB的中点.(1)求直线1A H到直线KC的距离；(2)求直线FC到平面1AEC的距离.【详解】（1）长为2的正方形，PD CD =，F ，G 分别是PB ，AD 的中点．(1)求证：FG //平面PCD ；(2)求点C 到平面PGB 的距离．【详解】（1）以D 为原点，DA ，DC ，DP 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，则(1,0,0),(0,0,2),(2,0,0),(2,2,0),(0,2,0),(1,1,1),G P A B C F 明显面PCD 的一个法向量为()1,0,0n =r ，又()0,1,1GF = ，()()1,0,00,1,10n GF ∴⋅=⋅= ，GF n ∴⊥ ，又GF ⊄面PCD ，//GF ∴面PCD ；（2）(1,0,2),(2,2,2)PG PB =-=- ，设平面PGB 的一个法向量为(,,)m a b c = ，00m PB m PG ⎧⋅=⎪∴⎨⋅=⎪⎩ ，即222020a b c a c +-=⎧⎨-=⎩，令1c =，则2,1a b ==-所以平面PGB 的一个法向量为(2,1,1)m =- ，又()2,0,0CB = ，所以点C 到平面PGB 的距离4263||411CB m d m ⋅===++ 5．（2022秋·广东清远·高二校联考期中）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，AB ⊥平面PAD ，E 是AD 的中点，PAD 为等腰直角三角形，DP AP ⊥，2PA AB ==2(1)求证：PE BD ⊥；(2)求点A 到平面PBE 的距离．【详解】（1）∵AB ⊥平面PAD ，PE ⊂平面PAD ，∴PE AB ⊥，又∵PAD 是等腰直角三角形，E 是斜边AD 的中点，∴PE AD ⊥，又∵AD ⊂平面ABCD ，AB ⊂平面ABCD ，AB AD A ⋂=，∴PE ⊥平面ABCD又∵BD ⊂平面ABCD ，∴PE BD ⊥；因为22PA AB ==，则()000E ，，，(0,1,1)B ，()010A ，，则(0,1,1)EB = ，(1,0,0)EP = ，PA 设平面PBE 的一个法向量为(n = 00EB n y z EP n x ⎧⋅=+=⎪⎨⋅==⎪⎩ ，取1y =，则z 设点A 到平面PBE 的距离为h ，则∴点A 到平面PBE 的距离为226．（2022秋·广东江门·高二新会陈经纶中学校考期中）如图，在直角梯形,=90,AD BC ADC AE ∠︒⊥∥平面ABCD ，EF CD ∥，112BC CD AE EF AD =====．(1)求证：BE AF ⊥；(2)在线段BC 上是否存在点M ，使平面EMD 与平面AMD 的夹角的大小为π3若存在，求出CM 的长；若不存在，请说明理由．【详解】（1）如图，作,FG EA AG EF ，连接EG ，AF ，BG ，∵EF CD ∥且EF AG ∥，AG CD ∴ ，即点G 在平面ABCD 内，所以四边形CDAG 为平行四边形，四边形AEFG 为平行四边形.又90ADC ∠=︒，BG AG ∴⊥，因为⊥AE 平面ABCD ，BG ⊂平面ABCD ，所以AE BG ⊥，又因为AG AE A = ，,AG AE ⊂平面AEFG ，∴BG ⊥平面AEFG ，因为AF ⊂平面AEFG ，BG AF ∴⊥．AE AG ⊥ ，所以平行四边形AEFG 为矩形，又因为AE EF =，所以矩形AEFG 为正方形，所以AF EG ⊥，又因为BG EG G = ，,BG EG ⊂平面BGE ，所以AF ⊥平面BGE ，因为BE ⊂平面BGE ，所以AF BE ⊥.（2）由（1）知AG ，AD ，AE 为三条两两互相垂直的直线，所以以A 为原点，AG 为x 轴，AD 为y 轴，AE 为z 轴建立空间直角坐标系A xyz -，如图，则(0,0,0),(1,0,0),(0,0,1),(0,2,0)A G E D ，设()001,,0,[1,2]M y y ∈，∴(0,2,1)ED =- ，()01,2,0DM y =- ，设平面EMD 的法向量为(,,)n x y z = ，则00n ED n DM ⎧⋅=⎪⎨⋅=⎪⎩，即()02020y z x y y -=⎧⎨+-=⎩，令1y =，得02,2z x y ==-，所以平面EMD 的法向量为()02,1,2n y =- ，又⊥AE 平面ABCD ，即⊥AE 平面AMD ，ABEF 所在平面互相垂直，动点M 、N 分别在正方形对角线AC 和BF 上移动，且(0CM BN a a ==<<．(1)求证MN 与平面BCE 平行；(2)当a =A MN B --的余弦值．8．（2022秋·广东肇庆·高二肇庆市端州中学校考期中）侧棱2PA PD ==，底面ABCD 为直角梯形，其中BC AD ∥，AB AD ⊥，222AD AB BC ===，O 为AD 的中点．(1)求证：PO ⊥平面ABCD ；(2)求二面角C PD A --的正弦值．【详解】（1）PA PD = ，O 为AD 的中点，PO AD ∴⊥，侧面PAD ⊥底面ABCD ，侧面PAD ⋂底面ABCD AD =，PO ⊂平面PAD ，PO ∴⊥平面ABCD ；（2） 底面ABCD 为直角梯形，其中BC AD ∥，AB AD ⊥，222AD AB BC ===，OC AD ∴⊥，又PO ⊥平面ABCD ，∴以O 为原点，OC 所在直线为x 轴，OD 所在直线为y 轴，OP 所在直线为z 轴，建立空间直角坐标系，易得平面PAD 的法向量(1,0,0m =设平面PCD 的法向量(,,n x y z = 设二面角C PD A --夹角为θ，则1cos 3m n m n θ⋅==⋅ ，则sin θ2,,PA AD AB M N ===分别为,AB PC 的中点.(1)求证：MN 平面PAD ；(2)求平面PMC 与平面PAD 的夹角的余弦值.（2）由题意，可构建如下图示的空间直角坐标系，令2x =，故(2,1,1)m =- ，又(1,0,0)n = 是面PAD 的一个法向量，所以26cos ,3||||6m n m n m n ⋅<>=== 故平面PMC 与平面PAD 的夹角的余弦值10．（2022秋·广东阳江·高二校联考期中）图90,2,3,2D AB DCAD CE ED ︒∠====.以BE 为折痕将BCE 折起，使点C 到达C 1的位置，且1AC = 2.(1)证明：平面1BC E ⊥平面ABED ；(2)求直线1BC 与平面1AC D 所成角的正弦值.（2）如图②，以D 为坐标原点，DA ，DE 的方向分别为空间直角坐标系.D xyz -则(0,0,0),(3,0,0),(3,2,0),(0,1,0)D A BE ，F 33(,,0)22，133(,,3)22C ，31(,,3)BC =-- ()3,0,0DA = ,DC = 正方形，E 为侧棱PC 的中点．(1)设经过A 、B 、E 三点的平面交PD 于F ，证明：F 为PD 的中点；(2)若PA ⊥底面ABCD ，且2PA AD ==，求点P 到平面ABE 的距离．【详解】（1）因为底面ABCD 为矩形，所以//AB CD .又AB ⊄平面PCD ，且CD ⊂平面PCD ，所以//AB 平面PCD .又AB ⊂平面ABE ，且平面ABE ⋂平面PCD EF =，所以//AB EF .又因为//AB CD ，所以//CD EF因为E 为PC 的中点，所以F 为PD 的中点.（2）如图所示，以A 为原点，,,AB AD AP 所在的直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系.则(2,0,0),(2,2,0),(0,0,2),(1,1,1)B C P E ，设(,,)n x y z = 是平面ABE 的法向量，则0,0n AE n AB ⋅=⋅= ，即200x x y z =⎧⎨++=⎩令1y =，则平面ABE 的一个法向量为(0,1,1)n =- 又因为(0,0,2)AP = ，所以点P 到平面ABE 的距离为222|||00+01+21|2||011AP n n ⋅⨯⨯⨯==++ （-），即点P 到平面ABE 的距离为2．12．（2022秋·广东阳江·高二校联考期中）如图，在四棱柱ABCD -A 1B 1C 1D 1中，四边形ABCD 是一个边长为2的菱形，∠DAB ＝60°.侧棱DD 1⊥平面ABCD ，DD 1＝3.(1)求二面角B -D 1C -D 的平面角的余弦值；(2)设E 是D 1B 的中点，在线段D 1C 上是否存在一点P ，使得AE ∥平面PDB ？若存在，请求出11D P D C 的值；若不存在，请说明理由.【详解】（1）如图1，连接BD ，由题意，△ADB 是正三角形，设M 是AB 的中点，则DM ⊥AB ，所以DM ⊥DC ，又DD 1⊥平面ABCD ，所以DM ⊥平面DD 1C 1C.以D 为原点，建立如图所示的空间直角坐标系，则D (0,0,0)，D 1(0,0,3)，C (0,2,0)，B (3,1,0)，则BC ＝(－3,1,0)，1BD ＝(－3,－1,3).显然，平面D 1CD 的一个法向量是()1,0,0m = ，设平面BD 1C 的法向量为n = (x ,y ,z )，则1=30,330,n BC x y n BD x y z ⎧⋅-+=⎪⎨⋅=--+=⎪⎩ 令x ＝3，得n = (3,3,2)，设二面角B -D 1C -D 的平面角为θ，由几何体的特征可知θ为锐角，则cos ||||m n m n θ⋅=⋅＝33941++⨯＝34.故二面角B -D 1C -D 的平面角的余弦值为34.（2）设11D P D C＝λ，即有11λD P D C ＝，其中01λ≤≤由（1）知D 1(0,0,3)，C (0,2,0)，则()10,2,3D C =- ，所以P (0,2,33)λλ-+，又D (0,0,0)，B (3,1,0)，1111为1AA的中点，1BC BD==，1AB AA==(1)求证：DM⊥平面1BDC；(2)求平面1MBC与平面1D B C夹角的余弦值.则()0,0,0D，21,0,2M⎛⎫⎪⎪⎝⎭，2=AD AB ，PAD 是正三角形，CD ⊥平面PAD ，E 、F 、G 、O 分别是PC 、PD 、BC 、AD 的中点．(1)求平面EFG 与平面ABCD 所成角的大小；(2)线段PA 上是否存在点M ，使得直线GM 与平面EFG 所成角的大小为π6，若存在，求出PMPA的值；若不存在，说明理由．【详解】（1）解：因为PAD 是正三角形，O 为AD 的中点，所以PO AD ⊥，因为CD ⊥平面PAD ，PO ⊂平面PAD ，PO CD ∴⊥，,,AD CD D AD CD Q Ç=Ì平面ABCD ，PO ∴⊥平面ABCD ，因为AD BC ∥且AD BC =，O 、G 分别为AD 、BC 的中点，所以AO BG ∥且AO BG =，所以四边形ABGO 为平行四边形，15．（2022秋·广东佛山·高二顺德一中校考期中）如图，在直棱柱1111为4的菱形，60BAD ∠= ，14AA =，P 是1AD 上的动点（不含端点）.(1)当P 为1AD 的中点时，求直线AD 到平面PBC 的距离；(2)求直线1AD 和平面BCP 所成角的正弦值的取值范围.则()0,0,0O ，()23,0,0A ，()10,2,4D -，()1123,2,0B C =-∴- ，AB P 为1AD 的中点，则(P()3,3,2BP =∴- ，(BC =- 则33202320n BP x y z n BC x y ⎧⋅=-+=⎪⎨⋅=--=⎪⎩4AB =，BC =BE =.将矩形BEDC 沿BC 翻折，使得平面ABC ⊥平面BCDE .(1)求DB 与平面ADE 所成角的正弦值.(2)求平面ADE 与平面ABC 所成的锐二面角的余弦值.【详解】（1） 平面ABC ⊥平面BCDE ，平面ABC ⋂平面BCDE BC =，CD BC ⊥，BE ⊂平面BCDE ，CD \^平面ABC ，则以C 为原点，,,CA CB CD正方向为,,x y z 轴，可建立如图所示的空间直角坐标系，则()0,0,0C ，()22,0,0A()22,0,23AD ∴=- ，DE设平面ADE 的法向量为n =则2223220AD n x z DE n y ⎧⋅=-+=⎪⎨⋅==⎪⎩DB n ⋅ ,A D 分别为棱,BM MC 的中点，将△MAD 沿AD 折起到PAD 的位置，使90PAB ∠=︒，如图2，连接,PB PC .(1)求证：平面PAD ⊥平面ABCD ；(2)若E 为PC 中点，求直线DE 与平面PBD 所成角的正弦值；(3)线段PC 上是否存在一点G ，使二面角G AD P --的余弦值为10若存在，求出PG PC 的值；若不存在，请说明理由.由题意得(0,1,0),(0,0,2),(2,0,0),(2,2,0),D P B C 所以(1,0,1)DE = ，(2,0,2),PB PD =-=设平面PBD 的法向量(,,)n x y z =，则22020PB n x z PD n y z ⎧⋅=-=⎪⎨⋅=-=⎪⎩ ，解得(1,2,1)n = 设直线DE 与平面PBD 所成角为θ，n DE ⋅,120AD DC BC ADC ︒==∠=，四边形ACFE 为正方形，且平面ACFE ⊥平面ABCD ．(1)求证：BC ⊥平面ACFE ；(2)点M 在线段EF 上运动，求平面MAB 与平面ADE 夹角余弦值的取值范围．令(03)FM λλ=≤≤，则(3,0,0),(0,1,0),(,0,3),(3,0,A B M E λ1111AD=AA 1=1，AB=2.(1)试问在线段CD 1上是否存在一点N ，使MN ∥平面ADD 1A 1?若存在，确定N 的位置；若不存在，请说明理由；(2)在（1）中，当MN ∥平面ADD 1A 1时，试确定直线BB 1与平面DMN 的交点F 的位置，并求BF 的长.延长DM交AB于点G，可证点G是线段再过点G作GF//AB1与线段BB1交于点20．（2022秋·广东湛江·高二湛江二十一中校考期中）如图，在长方体11111 AB=，点E在棱AB上移动．2(1)证明：11D E A D ⊥；(2)求平面1ACD 的法向量.(3)当E 为AB 的中点时，求点E 到面1ACD 的距离.【详解】（1）以D 为坐标原点，分别以1DA DC DD ､､所在直线为x y z ､､轴，建立如图的坐标系，则()()()()()110,0,0,1,0,1,0,0,1,1,0,00,2,0D A D A C ，，所以()11,0,1DA = ，设()1,,0E t ，所以()11,,1D E t =- ，所以11110DA D E ⋅=-= ，故11DA D E ⊥ 所以11D E A D ⊥；（2）设平面1ACD 的法向量为(),,n x y z =r，则()()11,0,1,1,2,0AD AC =-=-，由10,0n AD n AC ⋅=⋅=，得020x z x y -+=⎧⎨-+=⎩，令1x =得11,,12n ⎛⎫= ⎪⎝⎭；（3）当E 为AB 的中点时，()1,1,0E ，则()11,1,1D E =-，由点到平面的距离公式，得()12221111111231112n D E d n ⨯+⨯+⨯-⋅===⎛⎫++ ⎪⎝⎭，边长为2的正方形，PA=，G为CD的中点，E，F是棱PD上两点（F在E的上方），且2EF=．(1)若BF//平面AEG，求DE；(2)当点F到平面AEC的距离取得最大值时，求直线AG与平面AEC所成角的正弦值．则()0,0,0A ，()2,2,0C ，()1,2,0G ，因为2EF =，所以EFC 的面积为定值，又点A 到平面EFC 的距离为定值，所以三棱锥A -EFC 的体积为定值，即三棱锥所以要使点F 到平面AEC的距离最大，则AEC △即E 到AC 的距离最小时，点F 到平面AEC 的距离最大，设()0,2,3E t t -，则()0,2,3AE t t =- ，AC22AE AC⎛⎫⋅ DE =E AD C --//EF BD .(1)证明：平面ABCD ⊥平面DCE ；(2)若()0EF DB λλ=>，求平面ABF 与平面CEF 所成锐二面角的余弦值的取值范围.【详解】（1）∵2AB AD ==，3AE =，5DE =，∴222AD DE AE +=，即AD DE ⊥，又∵在正方形ABCD 中，AD DC ⊥，且DE DC D ⋂=，DE ⊂平面EDC ，DC ⊂平面EDC ，∴AD ⊥平面EDC ，又AD ⊂平面ABCD ，∴平面ABCD ⊥平面EDC ；（2）由（1）知，EDC ∠是二面角E AD C --的平面角，作OE CD ⊥于点O ，则cos 1OD DE EDC =⋅∠=，2OE =，且平面ABCD ⊥平面EDC ，平面ABCD ⋂平面EDC CD =，OE ⊂平面EDC ，∴OE ⊥平面ABCD ，取AB 中点M ，连接OM ，则OM CD ⊥，如图，建立空间直角坐标系，则()2,1,0A -，()2,1,0B ，()0,1,0D -，()0,1,0C ，()0,0,2E ，()2,2,0DB = ，()2,2,0EF λλ=，()0,1,2EC =- ，设平面CEF 的一个法向量为(),,m x y z=，则20220m EC y z m EF x y λλ⎧⋅=-=⎪⎨⋅=+=⎪⎩ ，取11,1,2m ⎛⎫=-- ⎪⎝⎭ ，()22,21,2BF λλ=--，()0,2,0AB = ，设平面ABF 的一个法向量为(),,n a b c =，在底面圆周上，且,BE CE M =为AE 上的一点，且,BM AC N ⊥为线段AC 上一动点（不与,A C 重合）(1)若2AN NC =，设平面BMN ⋂面BEC l =，求证：//MN l ；(2)当平面BMN 与平面DEC 夹角为π3，试确定N 点的位置.【详解】（1）由题知AB ⊥面,BEC EC ⊂面BEC ，则AB EC ⊥，由BC 为底面圆的直径，则EC BE ⊥，由BE AB B =I ，,BE AB ⊂面ABE ，则(220,,,1,33BM CA ⎛⎫=-=-+ ⎪ ⎪⎝⎭设()(,,2,CN CA λλλλλ==-∈设面BMN 的法向量为(,,n x y z =r 13λ-⎛⎫,23ABC AB AP π∠===，PA ⊥底面ABCD ，,E F 分别是线段,PB PD 的中点，G 是线段PC 上的一点.(1)若G 是直线PC 与平面AEF 的交点，试确定PGCG的值；(2)若直线AG 与平面AEF 所成角的正弦值为35，求三棱锥P EFG -体积.则()()(0,0,0,3,1,0,3,1,0A BC-()31,,1,0,1,122AE AF ⎛⎫=-= ⎪ ⎪⎝⎭ (0,0,AG AP PG AP PC λ=+=+=设平面AEF 的法向量(,,m a b =ADE V 沿直线AE 折起，使得DC .(1)求证：BE ⊥平面ADE ；(2)线段AB 上是否存在一点H ，使得平面ADE 与平面DHC 所成的角为π4若不存在，说明理由；若存在，求出H 点的位置.【详解】（1）证明：连接BE ，取线段AE 的中点O ，连接,DO OC ，在Rt ADE V 中，DA DE ==,1DO AE DO ∴⊥=，在OEC △中，11,2OE AE ==()()()1,0,1,1,1,0,2,0,0,D C A B -平面ADE 的法向量()10,1,0n =，在平面直角坐标系xOy 中，直线设H 的坐标为(),2,0t t -，()(。

1、如图，正方形所在平面与平面四边形所在平面互相垂直，△是等腰直角三角形，（1）线段的中点为，线段的中点为，求证：；（2）求直线与平面所成角的正切值.解：（1）取的中点为，连,,则,面/面, .............. 分5（2）先证出面，.............. 分8为直线与平面所成角，................ 分11................ 分142、己知多面体ABCDE中，DE平面ACD,, AC=AD=CD=DE=2 AB =1, O 为CD 的中点.（1）求证：AO平面CDE（2）求直线BD与平面CBE所成角的正弦值3、如图，在△中，，，点在上，交于，交于•沿将△翻折成△，使平面平面；沿将△翻折成△ ，使平面平面．（ 1 ）求证：平面；（2 ）若，求二面角的平面角的正切值.解：（1）因为，平面，所以平面.因为平面平面，且，所以平面. …2分同理，平面，所以，从而平面. …4分所以平面平面，从而平面.2)因为，，所以，，，．过E作，垂足为M，连结.由( 1)知，可得，所以，所以.所以即为所求二面角的平面角，可记为.在Rt△中，求得，所以. …4、如图，平面ABC,平面BCD, DE=DA=AB=AC,. M(1) 求直线EM与平面BCD所成角的正弦值；(2) P为线段DM上一点，且DM，求证：AP//DE. (12)分15 分为BC中点.解：(1) 平面,为在平面上的射影,为与平面所成角. …分2平面,, 设,又,. 在△中，，，又为中点，， ,.…5分在△中，，．……………………分 (7)2),为中点, ．又平面, ,平面．又平面,,分11 …分9又，平面. .............. 分13又平面，. .............. 分145、如图，已知ABCD是边长为1的正方形，AF丄平面ABCD, CE// AF,(1)证明：BD丄EF;(2)若AF= 1，且直线BE与平面ACE所成角的正弦值为,求的值.解：(1)连结BD、AC,交点为O. •/ ABCD是正方形/• BD丄AC ……2分•/ AF丄平面ABCD A AF丄BD ……4分••• BD丄平面ACEF (6)A BD丄EF ……7分(2)连结0E,由(1)知，BD丄平面ACEF所以/ BEO即为直线BE与平面ACE所成的角. ……10分•/ AF丄平面ABCD, CE// AF , • CE丄平面ABCD, CE1 BC,•/ BC =1 , AF= 1 ,贝U CE= , BE= , B0=,• RtA BEO 中，，…1盼因为解得. …… 15分6、如图在几何体中平面ABC分别是的中点.(1) 求证：平面CDE；(2) 求二面角的平面角的正切值.解：(1)连接ACR1R交EC于点F ,由题意知四边形ACCR1RE是矩形,贝U F是ACR1R的中连接DF, •/ D是AB的中点，•ABCR1R勺中位线，a BCR1R//DF， 4 分•/ BCR1RF面EDC DF平面EDC,• BCR1R//平面CDE. 7 分(2)作AH丄直线CD,垂足为H ,连接HE,•/ AAR1R丄平面ABC, • AAR1RL DC,CD丄平面AHE,CD丄EH ,••• AHE是二面角E -CD -A的平面角. 11分•/ D是AB的中点，• AH等于点B到CD的距离，在厶BCD中，求得：AH=, 在厶AEH中，即所求二面角的正切值为.7、如图，已知平面与直线均垂直于所在平面，且,( 1 )求证：平面；(2)若，求与平面所成角的正弦值.解：(1)证明：过点作于点，•••平面丄平面，•平面……2分又•••丄平面•- 〃 , ......... 分又•••平面• 〃平面 ......... 分(2) •••平面•,又•/••………………分8•点是的中点，连结，则•平面•//,•四边形是矩形………………分10设得：，又•••，•，从而，过作于点，则：•是与平面所成角…………………………………………分…… •，• 与平面所成角的正弦值为…………………………分14&如图，在直三棱柱中，是等腰直角三角形，，侧棱AA仁2, D, E分别为点，点E在平面ABD上的射影是的重心.(1) 求证：DE// 平面ACB；(2) 求A1B与平面ABD所成角的正弦值.12CC1 与A1B 的中9、如图，在侧棱垂直于底面的三棱柱ABC-A1B1中，底面△ ABC为等腰直角三角形，/ B=90°D为棱BB1的中点。

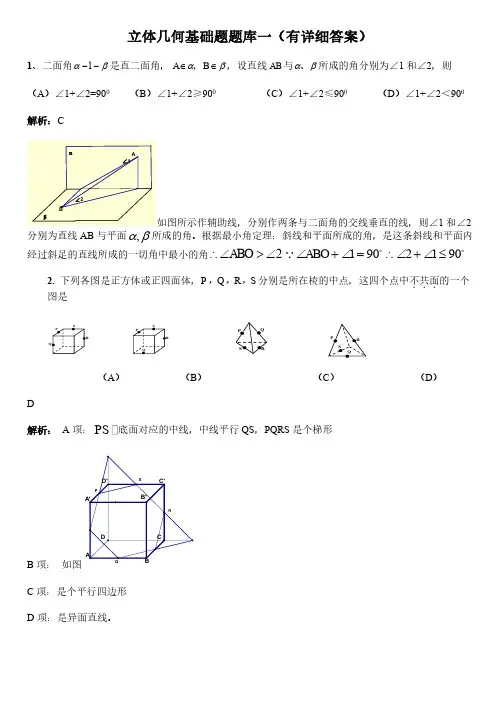
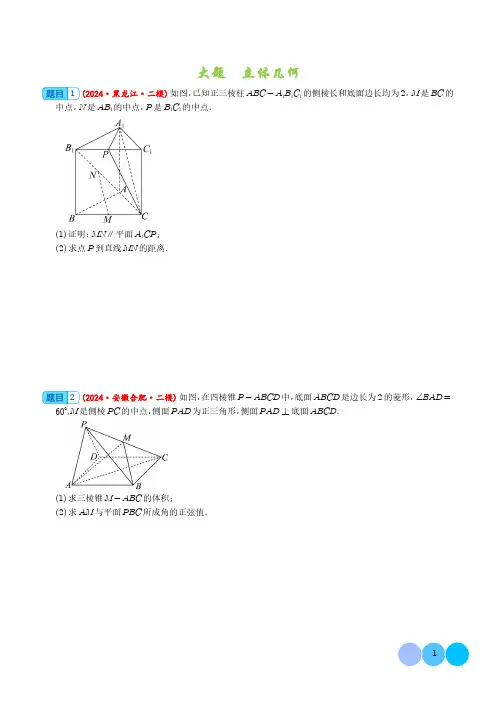
大题立体几何1(2024·黑龙江·二模)如图，已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2，M是BC的中点，N是AB1的中点，P是B1C1的中点．(1)证明：MN⎳平面A1CP；(2)求点P到直线MN的距离．2(2024·安徽合肥·二模)如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠BAD= 60°,M是侧棱PC的中点，侧面PAD为正三角形，侧面PAD⊥底面ABCD．(1)求三棱锥M-ABC的体积；(2)求AM与平面PBC所成角的正弦值．3(2023·福建福州·模拟预测)如图，在三棱柱ABC-A1B1C1中，平面AA1C1C⊥平面ABC,AB= AC=BC=AA1=2，A1B=6．(1)设D为AC中点，证明：AC⊥平面A1DB；(2)求平面A1AB1与平面ACC1A1夹角的余弦值．4(2024·山西晋中·三模)如图，在六面体ABCDE中，BC=BD=6，EC⊥ED，且EC=ED= 2，AB平行于平面CDE，AE平行于平面BCD，AE⊥CD.(1)证明：平面ABE⊥平面CDE；(2)若点A到直线CD的距离为22，F为棱AE的中点，求平面BDF与平面BCD夹角的余弦值．5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC-A1B1C1中，A1在平面ABC内的射影O在棱AC的中点处，P为棱A1B1(包含端点)上的动点．(1)求点P到平面ABC1的距离；(2)若AP⊥平面α，求直线BC1与平面α所成角的正弦值的取值范围．6(2024·重庆·模拟预测)在如图所示的四棱锥P-ABCD中，已知AB∥CD，∠BAD=90°，CD= 2AB，△PAB是正三角形，点M在侧棱PB上且使得PD⎳平面AMC．(1)证明：PM=2BM；(2)若侧面PAB⊥底面ABCD，CM与底面ABCD所成角的正切值为311，求二面角P-AC-B的余弦值．7(2024·安徽·模拟预测)2023年12月19日至20日，中央农村工作会议在北京召开，习近平主席对“三农”工作作出指示．某地区为响应习近平主席的号召，积极发展特色农业，建设蔬菜大棚．如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架，四边形ABCD是矩形，AB=8m，AD=4m，ED=CF=1m，且ED，CF都垂直于平面ABCD，GA=GB=5m，HE=HF，平面ABG⊥平面ABCD．(1)求点H到平面ABCD的距离；(2)求平面BFHG与平面AGHE所成锐二面角的余弦值．8(2024·重庆·模拟预测)如图，ACDE为菱形，AC=BC=2，∠ACB=120°，平面ACDE⊥平面ABC，点F在AB上，且AF=2FB，M，N分别在直线CD，AB上．(1)求证：CF⊥平面ACDE；(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线，若∠EAC=60°，MN为直线CD，AB的公垂线，求ANAF的值；(3)记直线BE与平面ABC所成角为α，若tanα>217，求平面BCD与平面CFD所成角余弦值的范围．9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°，使得CD 到EF 的位置，得到如图所示的几何体．(1)求证：平面ACF ⊥平面BDE ；(2)点M 为DF 上一点，若二面角C -AM -E 的余弦值为13，求∠MAD ．10(2024·安徽黄山·二模)如图，已知AB 为圆台下底面圆O 1的直径，C 是圆O 1上异于A ,B 的点，D 是圆台上底面圆O 2上的点，且平面DAC ⊥平面ABC ，DA =DC =AC =2，BC =4，E 是CD 的中点，BF =2FD ．(1)证明：DO 2⎳BC ；(2)求直线DB 与平面AEF 所成角的正弦值.11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22，A 1B 1=12AB ，M 为BC 中点，已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1 ，其中λ∈0,1 ．(1)求证D 1P ⊥AC ；(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37，当λ=23时，求直线DP 与平面AMC 1所成角的正弦值．12(2024·辽宁·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2，AB =1,BC =3，点E 为线段AC 的中点.(1)求证：AB 1∥平面BEC 1；(2)若∠A 1AC =π3，求二面角A -BE -C 1的余弦值.13(2024·广东广州·一模)如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，△DCP是等边三角形，∠DCB=∠PCB=π4，点M，N分别为DP和AB的中点.(1)求证：MN⎳平面PBC；(2)求证：平面PBC⊥平面ABCD；(3)求CM与平面PAD所成角的正弦值.14(2024·广东梅州·二模)如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，底面ABCD 为直角梯形，△PAD为等边三角形，AD⎳BC，AD⊥AB，AD=AB=2BC=2．(1)求证：AD⊥PC；(2)点N在棱PC上运动，求△ADN面积的最小值；(3)点M为PB的中点，在棱PC上找一点Q，使得AM⎳平面BDQ，求PQQC的值．15(2024·广东广州·模拟预测)如图所示，圆台O1O2的轴截面A1ACC1为等腰梯形，AC=2AA1= 2A1C1=4,B为底面圆周上异于A,C的点，且AB=BC,P是线段BC的中点.(1)求证：C1P⎳平面A1AB.(2)求平面A1AB与平面C1CB夹角的余弦值.16(2024·广东深圳·二模)如图，三棱柱ABC-A1B1C1中，侧面BB1C1C⊥底面ABC，且AB= AC，A1B=A1C．(1)证明：AA1⊥平面ABC；(2)若AA1=BC=2，∠BAC=90°，求平面A1BC与平面A1BC1夹角的余弦值．17(2024·河北保定·二模)如图，在四棱锥P -ABCD 中，平面PCD 内存在一条直线EF 与AB 平行，PA ⊥平面ABCD ，直线PC 与平面ABCD 所成的角的正切值为32，PA =BC =23，CD =2AB =4.(1)证明：四边形ABCD 是直角梯形.(2)若点E 满足PE =2ED ，求二面角P -EF -B 的正弦值.18(2024·湖南衡阳·模拟预测)如图，在圆锥PO 中，P 是圆锥的顶点，O 是圆锥底面圆的圆心，AC 是圆锥底面圆的直径，等边三角形ABD 是圆锥底面圆O 的内接三角形，E 是圆锥母线PC 的中点，PO =6,AC =4.(1)求证：平面BED ⊥平面ABD ；(2)设点M 在线段PO 上，且OM =2，求直线DM 与平面ABE 所成角的正弦值.19(2024·湖南岳阳·三模)已知四棱锥P -ABCD 的底面ABCD 是边长为4的菱形，∠DAB =60°，PA =PC ，PB =PD =210，M 是线段PC 上的点，且PC =4MC ．(1)证明：PC ⊥平面BDM ；(2)点E 在直线DM 上，求BE 与平面ABCD 所成角的最大值．20(2024·湖南·二模)如图，直四棱柱ABCD -A 1B 1C 1D 1的底面是边长为2的菱形，∠ABC =60°,BD 1⊥平面A 1C 1D .(1)求四棱柱ABCD -A 1B 1C 1D 1的体积；(2)设点D 1关于平面A 1C 1D 的对称点为E ，点E 和点C 1关于平面α对称(E 和α未在图中标出)，求平面A 1C 1D 与平面α所成锐二面角的大小.21(2024·山东济南·二模)如图，在四棱锥P-ABCD中，四边形ABCD为直角梯形，AB∥CD，∠DAB=∠PCB=60°,CD=1,AB=3,PC=23，平面PCB⊥平面ABCD，F为线段BC的中点，E为线段PF上一点.(1)证明：PF⊥AD；(2)当EF为何值时，直线BE与平面PAD夹角的正弦值为74.22(2024·山东潍坊·二模)如图1，在平行四边形ABCD中，AB=2BC=4，∠ABC=60°，E为CD 的中点，将△ADE沿AE折起，连结BD，CD，且BD=4，如图2．(1)求证：图2中的平面ADE⊥平面ABCE；(2)在图2中，若点F在棱BD上，直线AF与平面ABCE所成的角的正弦值为3010，求点F到平面DEC 的距离．23(2024·福建·模拟预测)如图，在三棱锥P-ABC中，PA⊥PB,AB⊥BC,AB=3,BC=6，已知二面角P-AB-C的大小为θ，∠PAB=θ.(1)求点P到平面ABC的距离；(2)当三棱锥P-ABC的体积取得最大值时，求：(Ⅰ)二面角P-AB-C的余弦值；(Ⅱ)直线PC与平面PAB所成角.24(2024·浙江杭州·二模)如图，在多面体ABCDPQ中，底面ABCD是平行四边形，∠DAB=60°, BC=2PQ=4AB=4,M为BC的中点，PQ∥BC,PD⊥DC,QB⊥MD．(1)证明：∠ABQ=90°；(2)若多面体ABCDPQ的体积为152，求平面PCD与平面QAB夹角的余弦值．25(2024·浙江嘉兴·二模)在如图所示的几何体中，四边形ABCD为平行四边形，PA⊥平面ABCD,PA∥QD，BC=2AB=2PA=2,∠ABC=60°.(1)证明：平面PCD⊥平面PAC；(2)若PQ=22，求平面PCQ与平面DCQ夹角的余弦值.26(2024·浙江绍兴·二模)如图，在三棱锥P-ABC中，AB=4，AC=2，∠CAB=60°，BC⊥AP.(1)证明：平面ACP⊥平面ABC；(2)若PA=2，PB=4，求二面角P-AB-C的平面角的正切值.27(2024·河北沧州·一模)如图，在正三棱锥A -BCD 中，BC =CD =BD =4，点P 满足AP =λAC ，λ∈(0,1)，过点P 作平面α分别与棱AB ，BD ，CD 交于Q ，S ，T 三点，且AD ⎳α，BC ⎳α.(1)证明：∀λ∈(0,1)，四边形PQST 总是矩形；(2)若AC =4，求四棱锥C -PQST 体积的最大值.28(2024·湖北·二模)如图1．在菱形ABCD 中，∠ABC =120°，AB =4，AE =λAD ，AF =λAB (0<λ<1)，沿EF 将△AEF 向上折起得到棱锥P -BCDEP ．如图2所示，设二面角P -EF -B 的平面角为θ．(1)当λ为何值时，三棱锥P -BCD 和四棱锥P -BDEF 的体积之比为95(2)当θ为何值时，∀λ∈0,1 ，平面PEF 与平面PFB 的夹角φ的余弦值为5529(2024·湖北·模拟预测)空间中有一个平面α和两条直线m ，n ，其中m ，n 与α的交点分别为A ，B ，AB =1，设直线m 与n 之间的夹角为π3，(1)如图1，若直线m ，n 交于点C ，求点C 到平面α距离的最大值；(2)如图2，若直线m ，n 互为异面直线，直线m 上一点P 和直线n 上一点Q 满足PQ ⎳α，PQ ⊥n 且PQ ⊥m ，(i )求直线m ，n 与平面α的夹角之和；(ii )设PQ =d 0<d <1 ，求点P 到平面α距离的最大值关于d 的函数f d ．30(2024·浙江绍兴·模拟预测)如图所示，四棱台ABCD -A 1B 1C 1D 1，底面ABCD 为一个菱形，且∠BAD =120°. 底面与顶面的对角线交点分别为O ，O 1. AB =2A 1B 1=2，BB 1=DD 1=392，AA 1与底面夹角余弦值为3737.(1)证明：OO 1⊥平面ABCD ；(2)现将顶面绕OO 1旋转θ角，旋转方向为自上而下看的逆时针方向. 此时使得底面与DC 1的夹角正弦值为64343，此时求θ的值(θ<90°)；(3)求旋转后AA 1与BB 1的夹角余弦值.。

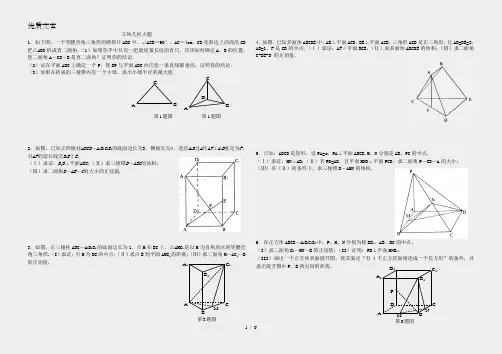
A BC第1题图ABCD第1题图立体几何大题1．如下图，一个等腰直角三角形的硬纸片ABC中，∠ACB＝90°，AC＝4cm，CD是斜边上的高沿CD 把△ABC折成直二面角．（1）如果你手中只有一把能度量长度的直尺，应该如何确定A，B的位置，使二面角A－CD－B是直二面角？证明你的结论．（2）试在平面ABC上确定一个P，使DP与平面ABC内任意一条直线都垂直，证明你的结论．（3）如果在折成的三棱锥内有一个小球，求出小球半径的最大值．2．如图，已知正四棱柱ABCD—A1B1C1D1的底面边长为3，侧棱长为4，连结A1B过A作AF⊥A1B垂足为F，且AF的延长线交B1B于E。

（Ⅰ）求证：D1B⊥平面AEC；（Ⅱ）求三棱锥B—AEC的体积；（Ⅲ）求二面角B—AE—C的大小的正弦值.3．如图，正三棱柱ABC—A1B1C1的底面边长为1，点M在BC上，△AMC1是以M为直角顶点的等腰直角三角形.（I）求证：点M为BC的中点；（Ⅱ）求点B到平面AMC1的距离；（Ⅲ）求二面角M—AC1—B 的正切值. 4．如图，已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，三角形ACD是正三角形，且AD=DE=2，AB=1，F是CD的中点．（Ⅰ）求证：AF∥平面BCE；（Ⅱ）求多面体ABCDE的体积；（Ⅲ）求二面角C-BE-D 的正切值．5．已知：ABCD是矩形，设PA=a，PA⊥平面ABCD.M、N分别是AB、PC的中点.（Ⅰ）求证：MN⊥AB；（Ⅱ）若PD=AB，且平面MND⊥平面PCD，求二面角P—CD—A的大小；（Ⅲ）在（Ⅱ）的条件下，求三棱锥D—AMN的体积.6．在正方体ABCD—A1B1C1D1中，P、M、N分别为棱DD1、AB、BC的中点。

（I）求二面角B1—MN—B的正切值；（II）证明：PB⊥平面MNB1；（III）画出一个正方体表面展开图，使其满足“有4个正方形面相连成一个长方形”的条件，并求出展开图中P、B两点间的距离。

专题20 立体几何综合大题必刷100题任务一:善良模式(基础)1-30题1．在棱长为1的正方体1111ABCD A B C D -中，E 为线段11A B 的中点，F 为线段AB 的中点.（1）求点B 到直线1AC 的距离；（2）求直线FC 到平面1AEC 的距离.2．如图，正方形11ABB A 的边长为2，11,AB A B 的中点分别为C ，1C ，正方形11ABB A 沿着1CC 折起形成三棱柱111ABC A B C -，三棱柱111ABC A B C -中，1,AC BC AD AA λ⊥=.（1）证明:当12λ=时，求证：1DC ⊥平面BCD ；（2）当14λ=时，求二面角1D BC C --的余弦值.3．如图，直三棱柱111ABC A B C -的底面为直角三角形，两直角边AB 和AC 的长分别为4和2，侧棱1AA 的长为5.（1）求三棱柱111ABC A B C -的体积；（2）设M 是BC 中点，求直线1A M 与平面ABC 所成角的正切值.4．如图，在三棱锥P ABC -中，PA ⊥底面ABC ，90.BAC ∠=︒点D ，E ，N 分别为棱P A ，PC ，BC 的中点，M 是线段AD 的中点，4PA AC ==，2AB =.（1）求证：//MN 平面BDE ；（2）求二面角C EM N --的正弦值；（3）已知点H 在棱P A 上，且直线NH 与直线BE ，求线段AH 的长.5．已知圆锥的顶点为P ，底面圆心为O ，半径为2.（1）设圆锥的母线长为4，求圆锥的体积；（2）设4PO =，OA 、OB 是底面半径，且90AOB ∠=︒，M 为线段AB 的中点，如图.求异面直线PM 与OB 所成的角的余弦值.6．如图所示，已知四棱锥P ABCD -中，四边形ABCD 为正方形，三角形PAB 为正三角形，侧面PAB ⊥底面ABCD ，M 是棱AD 的中点．（1）求证：PC BM ⊥；（2）求二面角B PM C --的正弦值．7．已知点E ，F 分别是正方形ABCD 的边AD ，BC 的中点.现将四边形EFCD 沿EF 折起，使二面角C EF B --为直二面角，如图所示.（1）若点G ，H 分别是AC ，BF 的中点，求证：//GH 平面EFCD ；（2）求直线AC 与平面ABFE 所成角的正弦值.8．已知如图1所示，等腰ABC 中，4AB AC ==，BC =D 为BC 中点，现将ABD 沿折痕AD 翻折至如图2所示位置，使得3BDC π∠=，E 、F 分别为AB 、AC 的中点．（1）证明：//BC 平面DEF ；（2）求四面体BCDE 的体积．9．在三棱柱ABC -A 1B 1C 1中，AB =2，BC =BB 1=4，1AC AB ==BCC 1=60°.（1）求证：平面ABC 1⊥平面BCC 1B 1：（2）设二面角C -AC 1-B 的大小为θ，求sinθ的值.10．如图，四棱锥P ABCD -中，底面ABCD 是直角梯形，//AD BC ，∠BAD =90°，已知PA PC ==，2,3AD AB BC ===.（1）证明：AC PD ⊥；（2）若二面角P AC B --的余弦值为13，求四棱锥P ABCD -的体积.11．如图，四棱柱ABCD —A 1B 1C 1D 1中，底面ABCD 和侧面BCC 1B 1都是矩形，E 是CD 的中点，D 1E ⊥CD ，AB ＝2BC ＝2．（1）求证：平面CC 1D 1D ⊥底面ABCD ；（2）若平面BCC 1B 1与平面BED 1所成的锐二面角的大小为3π，求线段ED 1的长度．12．如图，四棱锥P ABCD -的底面ABCD 是边长为2的正方形，平面PAD ⊥平面ABCD ，PAD △是斜边PA 的长为E ，F 分别是棱PA ，PC 的中点，M 是棱BC 上一点．（1）求证：平面DEM ⊥平面PAB ；（2）若直线MF 与平面ABCD E DM F --的余弦值．13．如图所示，四棱锥E ABCD -的底面ABCD 是边长为2的正方形，侧面EAB ⊥底面ABCD ，EA EB =，F 在侧棱CE 上，且BF ⊥平面ACE ．（1）求证：AE ⊥平面BCE ；（2）求点D 到平面ACE 的距离．14．在三棱锥B －ACD 中，平面ABD ⊥平面ACD ，若棱长AC ＝CD ＝AD ＝AB ＝1，且∠BAD ＝30°，求点D 到平面ABC 的距离．15．如图，在长方体1111ABCD A B C D -中，1AB BC ==，12BB =，E 为棱1AA 的中点.（1）证明：BE ⊥平面11EB C ；（2）求二面角1B EC C --的大小.16．如下图，在四棱锥S ABCD -中，底面ABCD 是正方形，平面SAD ⊥平面ABCD ，2SA SD ==，3AB =．（1）求SA 与BC 所成角的余弦值；（2）求证：AB SD ⊥．17．如图，四棱锥P ABCD -的底面是矩形，PD ⊥底面ABCD ，M 为BC 的中点，且PB AM ⊥．（1）证明：平面PAM ⊥平面PBD ；（2）若1PD DC ==，求四棱锥P ABCD -的体积．18．如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，120,1,4,ABC AB BC PA ∠=︒===M ，N 分别为,BC PC 的中点，,PD DC PM MD ⊥⊥.（1）证明：AB PM ⊥；（2）求直线AN 与平面PDM 所成角的正弦值.19．如图，.AB O PA O C O 是圆的直径，垂直圆所在的平面，是圆上的点（I ）求证BC PAC ⊥平面；（II ）设//.Q PA G AOC QG PBC ∆为的中点，为的重心，求证：平面20．如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，AB AD ⊥，点E 在线段AD 上，且CE AB ∥.（Ⅰ）求证：CE ⊥平面PAD ；（Ⅰ）若1==PA AB ，3AD =，CD =，45CDA ∠=︒，求四棱锥P ABCD -的体积.21．如图，直三棱柱ABC A B C '''-，90BAC ∠=，,AB AC AA λ'==点M ，N 分别为A B '和B C ''的中点． (∠)证明：MN ∠平面A ACC '';(∠)若二面角A MN C '--为直二面角，求λ的值．22．如图，在三棱锥S ABC -中, 侧面SAB 与侧面SAC 均为等边三角形,90,BAC ∠=︒O 为BC 中点. （∠）证明：SO ⊥平面;ABC（∠）求二面角A SC B --的余弦值.23．如图，在四棱锥P—ABCD 中，底面是边长为ⅠBAD ＝120°，且PAⅠ平面ABCD ，PA ＝M ，N 分别为PB ，PD 的中点．(1)证明：MNⅠ平面ABCD ；(2) 过点A 作AQⅠPC ，垂足为点Q ，求二面角A—MN—Q 的平面角的余弦值．24．如图，在三棱锥P ABC -中，AB BC ==4PA PB PC AC ====∠O 为AC 的中点． ∠1）证明：PO ⊥平面ABC ∠∠2）若点M在棱BC上，且2，求点C到平面POM的距离．MC MB25．如图，在三棱锥P∠ABC中，P A∠AB∠P A∠BC∠AB∠BC∠P A∠AB∠BC∠2∠D为线段AC的中点，E为线段PC上一点.(1)求证：P A∠BD∠(2)求证：平面BDE∠平面P AC∠(3)当P A∠平面BDE时，求三棱锥E∠BCD的体积．26．如图，在四棱锥P-ABCD中，PAⅠCD，ADⅠBC，ⅠADC=ⅠPAB=90°，BC=CD=1AD．2（Ⅰ）在平面PAD 内找一点M ，使得直线CMⅠ平面PAB ，并说明理由；（Ⅰ）证明：平面PABⅠ平面PBD ．27．如图，在三棱台ABC–DEF 中，平面BCFEⅠ平面ABC ，ⅠACB=90°，BE=EF=FC=1，BC=2，AC=3.（Ⅰ）求证：BFⅠ平面ACFD ；（Ⅰ）求直线BD 与平面ACFD 所成角的余弦值.28．如图，在直三棱柱ABC-A 1B 1C 1中，D ，E 分别为AB ，BC 的中点，点F 在侧棱B 1B 上，且11B D A F ⊥ ，1111AC A B ⊥.求证：（1）直线DE 平面A 1C 1F ；（2）平面B 1DEⅠ平面A 1C 1F.29．如图，在三棱锥111ABC A B C -中，11BAC 90AB AC 2,4,A AA ∠====，在底面ABC 的射影为BC 的中点，D 为11B C 的中点.∠1）证明：11D A BC A ⊥平面∠∠2）求直线1A B 和平面11B C B C 所成的角的正弦值.30．如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，,,60,AB AD AC CD ABC PA AB BC ⊥⊥∠===，E 是PC 的中点．（∠）证明CD AE ⊥；（∠）证明PD ⊥平面ABE ；--的大小．（∠）求二面角A PD C任务二:中立模式(中档)30-70题31．如图，在四棱锥P-ABCD中，底面ABCD为菱形，△P AD为正三角形，平面P AD⊥平面ABCD，E，F 分别是AD，CD的中点.（1）证明：BD⊥PF；（2）若AD=DB=2，求点C到平面PBD的距离；32．如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠P AD为正三角形，平面P AD⊥平面ABCD，E，F 分别是AD，CD的中点．（1）证明：BD⊥PF；（2）若∠BAD=60°，求直线PC与平面PBD所成角的正弦值；33．如图，在四棱锥E -ABCD 中，AB ⊥CE ，AE ⊥CD ，BC AD ∥，AB =3，CD =4，AD =2BC =10.（1）证明：∠AED 是锐角；（2）若AE =10，求二面角A -BE -C 的余弦值.34．如图，在直四棱柱1111ABCD A B C D -中，12A E EA =（1）若F 为1BB 的中点，试在11A B 上找一点P ，使//PF 平面1CD E ；（2）若四边形ABCD 是正方形，且1BB 与平面1CD E ，求二面角1E D C D --的余弦值.35．如图1，已知ADE 为等边三角形，四边形ABCD 为平行四边形，1,2,BC BD BA ===ADE 沿AD 向上折起，使点E 到达点P 位置，如图2所示；且平面PAD ⊥平面PBD ．（1）证明：PA BD ⊥；（2）在（1）的条件下求二面角A PB C --的余弦值．36．如图所示，在四棱锥P ABCD -中，PA ⊥平面ABCD ，2PA =，四边形ABCD 为梯形，//AB CD ，3AB =，1CD =，AD =60ABC ∠=，30BAD ∠=，点E 在AB 上，满足AD DE ⊥.（1）求证：平面PAD ⊥平面PBC ；（2）若点F 为PA 的中点，求平面PCD 与平面DEF 所成角的余弦值.37．在四棱锥P ABCD -中，PA ⊥平面ABCD ，22PA AB ==，90ABC ACD ∠=∠=，60BAC CAD ∠=∠=，E 为PD 的中点，在平面PCD 内作EF PC ⊥于点F .（1）求证：平面AEF ⊥平面PAC ；（2）求二面角P AC E --的余弦值.38．在正方体1111ABCD A B C D -中，点E 、F 分别在AB 、BC 上，且13AE AB =，13BF BC =．（1）求证：11A F C E ⊥；（2）求直线1A F 与平面1B EF 所成角的正弦值．39．如图，在多面体1111ABCD A B C D -中，1111,,,AA BB CC DD 均垂直于平面ABCD ，//AD BC ，11=2AB BC CD AA CC ====，1=1BB ，14AD DD ==.（1）证明：11A C ⊥平面11CDD C ；（2）求1BC 与平面11AA B B 所成角的余弦值.40．某商品的包装纸如图1，其中菱形ABCD 的边长为3，且60ABC ∠=︒，AE AF ==BE DF ==E ，F ，M ，N 汇聚为一点P ，恰好形成如图2的四棱锥形的包裹．（1）证明PA ⊥底面ABCD ；（2）设点T 为BC 上的点，且二面角B PA T --，试求PC 与平面P AT 所成角的正弦值．41．如图，在四棱锥P ABCD -中，底面ABCD 是菱形，侧面PAB ⊥底面ABCD ，且P A =AB ，90PAB ∠=.（1）证明：PC BD ⊥；（2）若60ABC ∠=，求直线PC 与平面PBD 所成角的正弦值.42．1.如图，正方形ABCD 所在平面与等边ABE △所在平面成的锐二面角为60，设平面ABE 与平面CDE 相交于直线l ．（1）求证：//l CD ；（2）求直线DE 与平面BCE 所成角的正弦值．43．如图，在四棱锥P ABCD -中，//AD BC ，AB AD ⊥，平面APD ⊥平面ABCD ，点E 在AD 上，且AB BC AE ED ===，PA PD ==.（1）求证：CE PD ⊥.（2）设平面PAB ⋂平面PCD l =，求二面角E l A --的余弦值.44．如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，120ADC =∠︒，4BC =，M ，N 分别为BC ，PC 的中点，1,,CD PD DC PM MD =⊥⊥．（1）证明：BC PM ⊥；（2）若PA =BN 与平面PDC 所成角的正弦值．45．如图，已知点P 在圆柱1OO 的底面圆O 上，120AOP ∠=，圆O 的直径4AB =，圆柱的高13OO =.（1）求点A到平面1A PO的距离；--的余弦值大小.（2）求二面角1A PB O46．如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=AA1=2，点P为棱B1C1的中点，点Q为线段A1B上的一动点.（1）求证:当点Q为线段A1B的中点时，PQ⊥平面A1BC；BA，试问:是否存在实数λ，使得平面A1PQ与平面B1PQ（2）设BQ=λ1在，求出这个实数λ；若不存在，请说明理由.47．如图，在三棱锥P ABC -中，PA ⊥底面ABC ，90ABC ∠=︒，2PA =，AC =（1）求证：平面PBC ⊥平面PAB ；（2）若二面角P BC A --的大小为45︒，过点A 作AN PC ⊥于N ，求直线AN 与平面PBC 所成角的大小．48．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是菱形，2PA AB ==，60BAD ∠=︒.（1）求证：直线BD ⊥平面PAC ；（2）设点M 在线段PC 上，且二面角C MB A --的余弦值为57，求点M 到底面ABCD 的距离.49．如图，在三棱锥P ABC -中，底面ABC 是边长2的等边三角形，PA PC ==F 在线段BC 上，且3FC BF =，D 为AC 的中点，E 为的PD 中点.(Ⅰ)求证：EF //平面PAB ；(Ⅱ)若二面角P AC B --的平面角的大小为2π3，求直线DF 与平面PAC 所成角的正弦值.50．如图，直四棱柱1111ABCD A B C D -的底面是菱形，侧面是正方形，60DAB ∠=︒，经过对角线1AC 的平面和侧棱1BB 相交于点F ，且12B F BF =．（1）求证：平面1AC F ⊥平面11BCC B ；（2）求二面角1F AC C --的余弦值．51．直角梯形11AA B B 绕直角边1AA 旋转一周的旋转的上底面面积为9π，下底面面积为36π，侧面积为，且二面角111B AA C --为90，P ，Q 分别在线段1CC ，BC 上．（∠）若P ，Q 分别为1CC ，BC 中点，求1AB 与PQ 所成角的余弦值；（∠）若P 为1CC 上的动点、Q 为BC 的中点，求PQ 与平面11AAC C 所成最大角的正切值，并求此时二面角Q AP C --的余弦值．52．正多面体也称柏拉图立体，被喻为最有规律的立体结构，其所有面都只由一种正多边形构成的多面体（各面都是全等的正多边形，且每一个顶点所接的面数都一样，各相邻面所成二面角都相等）．数学家已经证明世界上只存在五种柏拉图立体，即正四面体、正六面体、正八面体、正十二面体、正二十面体．已知一个正四面体QPTR 和一个正八面体AEFBHC 的棱长都是a （如图），把它们拼接起来，使它们一个表面重合，得到一个新多面体．（1）求新多面体的体积；（2）求二面角A BF C --的余弦值；（3）求新多面体为几面体？并证明．53．中国是风筝的故乡，南方称“鹞”，北方称“鸢”，如图，某种风筝的骨架模型是四棱锥P ABCD -，其中AC BD ⊥于O ，4OA OB OD ===，8OC =，PO ⊥平面ABCD ．（1）求证：PD AC ⊥；（2）试验表明，当12PO OA =时，风筝表现最好，求此时直线PD 与平面PBC 所成角的正弦值．54．在陕西汉中勉县的汉江河与定军山武侯坪一带，经常出土有铜、铁扎马钉等兵器文物.扎马钉（如题21图（1））是三国时蜀汉的著名政治家、军事家诸葛亮所发明的一种对付骑兵的武器，状若荆刺，故学名蒺藜，有铜、铁两种.扎马钉有四个锋利的尖爪，随手一掷，三尖撑地，一尖直立向上，推倒上尖，下尖又起，始终如此，使触者不能避其锋而被刺伤.即总有一个尖垂直向上，三尖对称支承于地.简化扎马钉的结构，如图（2），记组成该“钉”的四条等长的线段公共点为O ，钉尖为i A （1,2,3,4i =）．（Ⅰ）判断四面体1234A A A A -的形状特征； （Ⅱ）若某个出土的扎马钉因年代久远，有一尖爪受损，其长度仅剩其他尖爪长度的23（即4123OA OA '=），如图（3），将2A ，3A ，4A '置于地面，求1OA 与面234A A A '所成角θ的正弦值.55．正多面体也称柏拉图立体，被誉为最有规律的立体结构，其所有面都只由一种正多边形构成的多面体（各面都是全等的正多边形，且每一个顶点所接的面数都一样，各相邻面所成二面角都相等）.数学家已经证明世界上只存在五种柏拉图立体，即正四面体、正六面体、正八面体、正十二面体、正二十面体.已知一个正四面体QPTR 和一个正八面体AEFBHC 的棱长都是a （如图），把它们拼接起来，使它们一个表面重合，得到一个新多面体.（1）求新多面体的体积；（2）求正八面体AEFBH 中二面角A BF C --的余弦值；（3）判断新多面体为几面体？（只需给出答案，无需证明）56．如图，已知在四棱锥P ABCD -中，底面ABCD 为等腰梯形，//BC AD ，AB CD =，E 为棱PB 上一点，AC 与BD 交于点O ，且AC BD ⊥，1AD =，3BC PC PB ===，PO =（1）证明：AC DE ⊥；（2）是否存在点E ，使二面角B DC E --E 点位置，若不存在，请说明理由．57．如图，在三棱柱111ABC A B C ﹣中点，E 在棱1BB 上，点F 在棱CC 1上，且点,E F 均不是棱的端点，1,AB AC BB ⊥＝平面,AEF 且四边形11AA B B 与四边形11AAC C 的面积相等.（1）求证：四边形BEFC 是矩形；（2）若2,AE EF BE ＝＝ABC 与平面AEF 所成角的正弦值.58．如图，在三棱台111ABC A B C -中，11190,4,2,BAC AB AC A A A B ∠=︒====侧棱1A A ⊥平面,ABC 点D 在棱1CC 上，且1CD CC λ=（1）证明：1BB ⊥平面1AB C ；（2）当二面角C BD A --的余弦值为，求λ的值.59．在直四棱柱1111ABCD A B C D -中，底面ABCD 为平行四边形，1,45AB BC ABC ∠===，点M 在棱1CC 上，点N 是BC 的中点，且满足1AM B N ⊥.（1）证明：AM ⊥平面11A B N ；（2）若M 是1CC 的中点，求二面角111A B N C --的正弦值.60．在四棱锥P ABCD -中，四边形ABCD 是边长为4的菱形，PB BD PD ===PA =（1）证明：PC ⊥平面ABCD ；（2）如图，取BC 的中点为E ，在线段DE 上取一点F 使得23DF FE =，求二面角F PA C --的大小.61．如图，在底面是菱形的四棱柱1111ABCD A B C D -中，60ABC ∠=，1112,AA AC A B A D ====E 在1A D 上．（1）求证：1AA ⊥平面ABCD ；（2）当E 为线段1A D 的中点时，求点1A 到平面EAC 的距离．62．已知四棱锥P ABCD -的底面是菱形，对角线AC 、BD 交于点O ，4OP OA ==，3OB =，OP ⊥底面ABCD ，设点M 满足()01PM MC λλ=<<．（1）若三棱锥P MBD -体积是169，求λ的值；（2）若直线PA 与平面MBD λ的值．63．光学器件在制作的过程中往往需要进行切割，现生产一种光学器件，有一道工序为将原材料切割为两个部分，然后在截面上涂抹一种光触媒化学试剂，加入纳米纤维导管后粘合.在如图所示的原材料器件直三棱柱ABC﹣A'B'C'中，AB⊥AC，AB＝AC＝AA'＝a，现经过AB作与底面ABC所成角为θ的截面，且截面与B'C'，A'C'分别交于不同的两点E，F．（1）试求截面面积S随θ变化的函数关系式S（θ）；（2）当E和F分别为B C''和A C''的中点时，需要在线段AF上寻找一个点Q，用纳米纤维导管连接EQ，使得EQ与AB'所在直线的夹角最小，试求出纤维导管EQ的长．64．如图，四棱锥P﹣ABCD的底面ABCD为菱形，∠ABC＝60°，P A⊥平面ABCD，且E，M分别为BC，PD的中点，点F为棱PC上一动点．（1）证明：平面AEF ⊥平面P AD ．（2）若AB ＝P A ，在线段PC 上是否存在一点F ，使得二面角F ﹣AE ﹣M 定F 的位置；若不存在，说明理由．65．如图，三棱柱111ABC A B C -中，111AA B C =，11120BB C ∠=︒，1190AB C ∠=︒．（1）求证：ABC 为等腰三角形；（2）若11111AB C B AC ∠=∠，11B AB B BA ∠=∠，点M 在线段11B C 上，设111102B M B C λλ⎛⎫=<< ⎪⎝⎭，若二面角11A CM C --λ的值．66．如图，四棱锥P ABCD -中，底面ABCD 为菱形，2AB AD ==，60ABC ∠=︒，PA ⊥平面ABCD ，PA =（1）点E 在线段PC 上，37PE PC =，点F 在线段PD 上，35PF PD =，求证：PC ⊥平面AEF ； （2）设M 是直线AC 上一点，求CM 的长，使得MP 与平面PCD 所成角为45︒．67．如图，在四棱锥P ABCD -中，底面ABCD 为正方形，侧棱PA ⊥底面ABCD ，1AB =，2PA =，E 为PB 的中点，点F 在棱PC 上，且PF PC λ=．（1）求直线CE 与直线PD 所成角的余弦值；（2）当直线BF 与平面CDE 所成的角最大时，求此时λ的值．68．如图，在四棱锥P ABCD ﹣中，四边形ABCD 为直角梯形，//AD BC ，90BAD ∠=︒，且1AB BC ==，2AD =，PA PD =，M 为AD 的中点，平面PAD ⊥平面ABCD ，直线PB 与平面ABCD 所成角的正切值为（1）求四棱锥PABCD ﹣的体积；（2）在棱CD 上(不含端点)是否存在一点Q ，使得二面角C AP Q --？若存在，请确定点Q 的位置；若不存在，请说明理由.69．已知四棱锥P ABCD -P 中，底面ABCD 是平行四边形，PA AB =，PAD BAD ∠=∠，,E F 分别是,AB DC 的中点，2,3,AD PF PE ===（1）求证：AD ⊥平面PAB ；（2）若PB =B PC A --的余弦值.70．如图，矩形ABCD 中，AB ADλ=()1λ>，将其沿AC 翻折，使点D 到达点E 的位置，且二面角C AB E --为直二面角.（1）求证：平面ACE ⊥平面BCE ；（2）设F 是BE 的中点，二面角E AC F --的平面角的大小为θ，当[]2,3λ∈时，求cos θ的取值范围.任务三:邪恶模式(困难)70-100题71．如图，在四棱锥P ABCD -中，底面ABCD 是正方形，侧面PAD ⊥底面ABCD ，E ，F 分别为,PA BD 中点，2PA PD AD ===．（1）求证：//EF 平面PBC ；（2）求二面角E DF A --的余弦值；（3）在棱PC 上是否存在一点G ，使GF ⊥平面EDF ？若存在，指出点G 的位置；若不存在，说明理由．72．请从下面三个条件中任选一个，补充在下面的横线上，并作答.∠()0BA PA PD ⋅+=；∠PC ∠点P 在平面ABCD 的射影在直线AD 上.如图，平面五边形PABCD 中，PAD △是边长为2的等边三角形，//AD BC ，22AB BC ==，AB BC ⊥，将PAD △沿AD 翻折成四棱锥P ABCD -，E 是棱PD 上的动点（端点除外），F M 、分别是AB CE 、的中点，且___________.（1）求证：AB FM ⊥；（2）当EF 与平面PAD 所成角最大时，求平面ACE 与平面PAD 所成的锐二面角的余弦值.注：如果选择多个条件分别解答，按第一个解答计分.73．蜂房是自然界最神奇的“建筑”之一，如图1所示．蜂房结构是由正六棱柱截去三个相等的三棱锥H ABC -，J CDE -，K EFA -，再分别以AC ，CE ，EA 为轴将ACH ∆，CEJ ∆，EAK ∆分别向上翻转180︒，使H ，J ，K 三点重合为点S 所围成的曲顶多面体（下底面开口），如图2所示．蜂房曲顶空间的弯曲度可用曲率来刻画，定义其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和，而每一顶点的曲率规定等于2π减去蜂房多面体在该点的各个面角之和（多面体的面角是多面体的面的内角，用弧度制表示）．（1）求蜂房曲顶空间的弯曲度；（2）若正六棱柱的侧面积一定，当蜂房表面积最小时，求其顶点S 的曲率的余弦值．74．2022年北京冬奥会标志性场馆——国家速滑馆的设计理念来源于一个冰和速度结合的创意，沿着外墙面由低到高盘旋而成的“冰丝带”，就像速度滑冰运动员高速滑动时留下的一圈圈风驰电掣的轨迹，冰上划痕成丝带，22条“冰丝带”又象征北京2022年冬奥会.其中“冰丝带”呈现出圆形平面、椭圆形平面、马鞍形双曲面三种造型，这种造型富有动感，体现了冰上运动的速度和激情这三种造型取自于球、椭球、椭圆柱等空间几何体，其设计参数包括曲率、挠率、面积体积等对几何图形的面积、体积计算方法的研究在中国数学史上有过辉煌的成就，如《九章算术》中记录了数学家刘徽提出利用牟合方盖的体积来推导球的体积公式，但由于不能计算牟合方盖的体积并没有得出球的体积计算公式直到200年以后数学家祖冲之、祖眶父子在《缀术》提出祖暅原理：“幂势既同，则积不容异”，才利用牟合方盖的体积推导出球的体积公式原理的意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等.（Ⅰ）利用祖暅原理推导半径为R 的球的体积公式时，可以构造如图②所示的几何体M ，几何体M 的底面半径和高都为R ，其底面和半球体的底面同在平面α内.设与平面α平行且距离为d 的平面β截两个几何体得到两个截面，请在图②中用阴影画出与图①中阴影截面面积相等的图形并给出证明；（Ⅱ）现将椭圆()222210x y a b a b+=>>所围成的椭圆面分别绕其长轴、短轴旋转一周后得两个不同的椭球A ，B （如图），类比（Ⅰ）中的方法，探究椭球A 的体积公式，并写出椭球A ，B 的体积之比.75．如图，已知边长为2的正方形材料ABCD ，截去如图所示的阴影部分后，可焊接成一个正四棱锥的封闭容器.设FCB θ∠=.（1）用θ表示此容器的体积；（2）当此容器的体积最大时，求tan θ的值.76．如图，在四面体ABCD 中，AB AC ⊥，平面ACD 与平面BCD 垂直且CD =（1）若2AB AC ==，证明：45BCD ∠<︒；（2）若33AB AC ==，当ACD △与BCD 面积之和最大时，求二面角C AB D --的余弦值.77．某人设计了一个工作台，如图所示，工作台的下半部分是个正四棱柱ABCD ﹣A 1B 1C 1D 1，其底面边长为4，高为1（1）当圆弧E 2F 2（包括端点）上的点P 与B 1的最短距离为DB 1Ⅰ平面D 2EF ．（2）若D 1D 2＝3．当点P 在圆弧E 2E 2（包括端点）上移动时，求二面角P ﹣A 1C 1﹣B 1的正切值的取值范围．78．平面凸六边形11MBB NC C 的边长相等,其中11BB C C 为矩形,1190BMC B NC ∠=∠=︒．将BCM ,11B C N △分别沿BC ,11B C 折至ABC ,111A B C ,且均在同侧与平面11BB C C 垂直,连接1AA ,如图所示,E ,G 分别是BC ,1CC 的中点．（1）求证：多面体111ABC A B C -为直三棱柱；（2）求二面角1A EG A --平面角的余弦值．79．如图，AB 是圆O 的直径，点C 是圆O 上异于,A B 的点，直线PC ⊥平面ABC ，,E F 分别是,PA PC 的中点.（1）记平面BEF 与平面ABC 的交线为l ，试判断直线l 与平面PAC 的位置关系，并加以证明；（2）设（1）中的直线l 与圆O 的另一个交点为D ，且点Q 满足12DQ CP =.记直线PQ 与平面ABC 所成的角为θ，异面直线PQ 与EF 所成的角为α，二面角E l C --的大小为β，求证：sin sin sin θαβ=.80．已知，图中直棱柱1111ABCD A B C D -的底面是菱形，其中124AA AC BD ===.又点,,,E F P Q 分别在棱1111,,,AA BB CC DD 上运动，且满足：BF DQ =，1CP BF DQ AE -=-=.（1）求证：,,,E F P Q 四点共面，并证明EF Ⅰ平面PQB .（2）是否存在点P 使得二面角B PQ E --？如果存在，求出CP 的长；如果不存在，请说明理由.81．如图1，ADC ∆与ABC ∆是处在同-个平面内的两个全等的直角三角形，30ACB ACD ︒∠=∠=90ABC ADC ︒∠=∠=，2AB =，连接是,BD E 边BC 上一点，过E 作// EF BD ，交CD 于点F ，沿EF 将CEF ∆向上翻折，得到如图2所示的六面体,P ABEFD -（1）求证：;BD AP ⊥（2）设),(BE EC R λλ=∈若平面PEF ⊥底面ABEFD ，若平面PAB 与平面PDF λ的值；（3）若平面PEF ⊥底面ABEFD ，求六面体P ABEFD -的体积的最大值.82．设三棱锥P ABC -的每个顶点都在球O 的球面上，PAB ∆是面积为AC BC ⊥，AC BC =，且平面PAB ⊥平面ABC .（1）确定O 的位置（需要说明理由），并证明：平面POC ⊥平面ABC .（2）与侧面PAB 平行的平面α与棱AC ，BC ，PC 分别交于D ，E ，F ，求四面体ODEF 的体积的最大值.83．如图，在三棱柱111ABC A B C -中，1AA ⊥平面ABC ，D 是AB 的中点，BC AC =，2AB DC ==，14AA =.（Ⅰ）求证：1//BC 平面1A CD ；（Ⅰ）求平面11BCC B 与平面1A CD 所成锐二面角的平面角的余弦值.84．如图，P 为圆锥的顶点，O 是圆锥底面的圆心，AC 为底面直径，ABD △为底面圆O 的内接正三角E 在母线PC 上，且1,AE CE EC BD ==⊥．（1）求证：平面BED ⊥平面ABD ；（2）设线段PO 上动点为M ，求直线DM 与平面ABE 所成角的正弦值的最大值．85．如图，三棱柱111ABC A B C -的底面是边长为4的正三角形，侧面11ACC A ⊥底面ABC ，且侧面11ACC A 为菱形，160A AC ∠=.（1）求二面角1A AB C 所成角θ的正弦值.（2）,M N 分别是棱11A C ，11B C 的中点，又2AP BP =.求经过,,M N P 三点的平面截三棱柱111ABC A B C -的截面的周长.86．如图，在三棱台111ABC A B C -中，底面ABC 是边长为2的正三角形，侧面11ACC A 为等腰梯形，且1111AC AA ==，D 为11A C 的中点．（1）证明：AC BD ⊥；（2）记二面角1A AC B --的大小为θ，2,33ππθ⎡⎤∈⎢⎥⎣⎦时，求直线1AA 与平面11BB C C 所成角的正弦值的取值范围．87．如图，在四棱锥P ABCD -中，M ，N 分别是AB ，AP 的中点，AB BC ⊥，MD PC ⊥，//MD BC ，1BC =，2AB =，3PB =，CD =PD =（Ⅰ）证明：//PC 平面MND ；（Ⅱ）求直线PA 与平面PBC 所成角的正弦值．88．设P 为多面体M 的一个顶点，定义多面体M 在点P 处的离散曲率为12231111()2k k k Q PQ Q PQ Q PQ Q PQ π--∠+∠++∠+∠，其中Q i （i ＝1，2，…，k ，k ≥3）为多面体M 的所有与点P 相邻的顶点，且平面Q 1PQ 2，平面Q 2PQ 3，…，平面Q k ﹣1PQ k 和平面Q k PQ 1遍历多面体M 的所有以P 为公共点的面．（1）如图1，已知长方体A 1B 1C 1D 1﹣ABCD ，AB ＝BC ＝1，1AA =P 为底面A 1B 1C 1D 1内的一个动点，则求四棱锥P ﹣ABCD 在点P 处的离散曲率的最小值；（2）图2为对某个女孩面部识别过程中的三角剖分结果，所谓三角剖分，就是先在面部取若干采样点，然后用短小的直线段连接相邻三个采样点形成三角形网格．区域α和区域β中点的离散曲率的平均值更大的是哪个区域？（确定“区域α”还是“区域β”）89．如图，四棱锥P ABCD -的底面ABCD 是边长为2的正方形，3PA PB ==．（1）证明：PAD PBC ∠=∠；（2）当直线PA 与平面PCD 所成角的正弦值最大时，求此时二面角P AB C 的大小．90．北京大兴国际机场的显著特点之一是各种弯曲空间的运用．刻画空间的弯曲性是几何研究的重要内容．用曲率刻画空间弯曲性，规定：多面体顶点的曲率等于2π与多面体在该点的面角之和的差（多面体的面的内角叫做多面体的面角，角度用弧度制），多面体面上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和．例如：正四面体在每个顶点有3个面角，每个面角是3π，所以正四面体在各顶点的曲率为233πππ-⨯=，故其总曲率为4π．（1）求四棱锥的总曲率；（2）若多面体满足：顶点数-棱数+面数2=，证明：这类多面体的总曲率是常数．91．已知四棱锥T ABCD -的底面是平行四边形，平面α与直线AD ，TA ，TC 分别交于点P ，Q ，R 且AP TQ CRx AD TA CT===，点M 在直线TB 上，N 为CD 的中点，且直线//MN 平面α.（1）设TA a =，TB b =，TC c =，试用基底{},,a b c 表示向量TD ；（2）证明，四面体T ABC -中至少存在一个顶点从其出发的三条棱能够组成一个三角形；（3）证明，对所有满足条件的平面α，点M 的线段上.92．如图，在四棱台ABCD -A 1B 1C 1D 1中，底面ABCD 是菱形，ⅠABC =3π，ⅠB 1BD =6π，11,B BA B BC ∠=∠11122,3AB A B B B ===。

立体几何练习题1.四棱锥ABCD S -中，底面ABCD 为平行四边形，侧面⊥SBC 面ABCD ，已知45=∠ABC ，2=AB ，22=BC ，3==SC SB .（1）设平面SCD 与平面SAB 的交线为l ，求证：AB l //； （2）求证：BC SA ⊥；（3）求直线SD 与面SAB 所成角的正弦值.2.如图，在四棱锥P-ABCD 中，底面ABCD 是平行四边形，，AD=AC=1，O 为AC的中点，PO平面ABCD ，PO=2，M 为PD 的中点。

（1）证明：PB//平面ACM ； （2）证明：AD平面PAC（3）求直线AM 与平面ABCD 所成角的正切值。

如图，四棱锥P ABCD -中，90ABC BAD ∠=∠=︒，2BC AD =，△PAB 与△PAD 都是等边三角形． （1）证明：CD ⊥平面PBD ；（2）求二面角C PB D --的平面角的余弦值．4.如图，四棱锥P ﹣ABCD 中，PA ⊥底面ABCD ，AC ⊥AD ．底面ABCD 为梯形，AB ∥DC ，AB ⊥BC ，PA=AB=BC=3，点E 在棱PB 上，且PE=2EB ． （Ⅰ）求证：平面PAB ⊥平面PCB ； （Ⅱ）求证：PD ∥平面EAC ；（Ⅲ）求平面AEC 和平面PBC 所成锐二面角的余弦值．5.如图，已知矩形ABCD 所在平面垂直于直角梯形ABPE 所在平面于直线AB ，平面ABCD 平面ABPE AB =，且2AB BP ==，1AD AE ==，AE AB ⊥，且//AE BP ．（1）设点M 为棱PD 中点，在面ABCD 内是否存在点N ，使得MN ⊥平面ABCD ？若存在，请证明；若不存在，请说明理由； （2）求二面角D PE A --的余弦值.如图，在直三棱柱ABC﹣A1B1C1中，平面A1BC⊥侧面A1ABB1，且AA1=AB=2．（1）求证：AB⊥BC；（2）若直线AC与平面A1BC所成的角为，求锐二面角A﹣A1C﹣B的大小．7.在四棱锥V﹣ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD．（1）求证AB⊥面VAD；（2）求面VAD与面VDB所成的二面角的大小．8.如图，在五面体ABCDEF中，四边形ABCD为菱形，且∠BAD=，对角线AC与BD相交于O，OF⊥平面ABCD，BC=CE=DE=2EF=2．（Ⅰ）求证：EF∥BC；（Ⅱ）求面AOF与平面BCEF所成锐二面角的正弦值．如图，在四棱锥P ﹣ABCD 中，底面为直角梯形，AD ∥BC ，∠BAD=90°，PA ⊥底面ABCD ，且PA=AD=AB=2BC ，M 、N 分别为PC 、PB 的中点． （Ⅰ）求证：PB ⊥DM ；（Ⅱ）求BD 与平面ADMN 所成的角．10.如图，在等腰梯形ABCD 中，//AB CD ，1AD DC CB ===，60ABC ∠=，四边形ACFE为矩形，平面ACFE ⊥平面ABCD ，1CF =. （1）求证：BC ⊥平面ACFE ；（2）点M 在线段EF 上运动，设平面MAB 与平面FCB 二面角的平面角为(90)θθ≤，试求cos θ的取值范围.立体几何试卷答案（2）证明：连接AC ，45222ABC AB BC ∠===，，，由余弦定理得2AC =，AC AB ∴= 6分 取BC 中点G ，连接,SG AG ，则AG BC ⊥.,,,SB SC SG BC SG AG G =∴⊥=BC ∴⊥面,.SAG BC SA ∴⊥ …………………8分（Ⅲ）如图，以射线OA 为x 轴，以射线OB 为y 轴，以射线OS 为z 轴，以O 为原点，建立空间直角坐标系xyz O -,B ySCAD2、试题解析：（1）证明：为AC的中点，即O为BD的中点，且 M为PD的中点，又平面ACM，平面ACM,所以PB//平面ACM。