1.3.1 奇妙的一笔画

所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢？下面，我们就来探求解决这个问题的方法．什么样的图形能一笔画成呢？这就是一笔画问题，它是一种有名的数学游戏．我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点． 一笔画问题：(1)能一笔画出的图形必须是连通的图形；(2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点； (3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点； (4)奇点个数超过两个的图形，一定不能一笔画． 多笔画问题：我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n 个奇点(n 为自然数)，那么这个图一定可以用n 笔画成．模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点？哪些点是奇点？J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答 【解析】 奇点： D H J O 偶点：A B C E F G I 【答案】奇点： D H J O 偶点：A B C E F G I【例 2】 同学们野营时建了9个营地，连接营地之间的道路如图所示，贝贝要给每个营地插上一面旗帜，要求相邻营地的旗帜色彩不同，则贝贝最少需要 种颜色的旗子，如果贝贝从某营地出发，不走重复路线就 （填“能”或“不能”）完成任务.【考点】一笔画问题 【难度】2星 【题型】填空 【关键词】华杯赛，六年级，初赛，第10题 【解析】 最少需要3种颜色的旗子。

因为中间的三点连成一个三角形，要使这三点所代表营地两粮相邻，要使相邻营地没有相同颜色的旗子，必须各插一种与其它两点不同颜色的旗子。

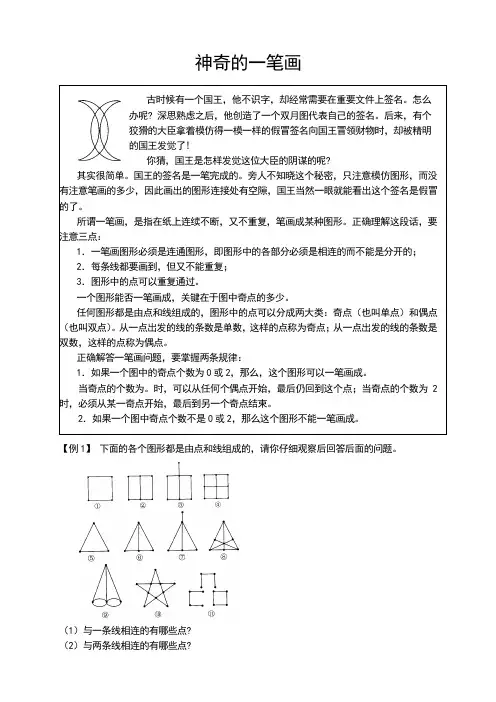
神奇的一笔画古时候有一个国王，他不识字，却经常需要在重要文件上签名。

怎么办呢? 深思熟虑之后，他创造了一个双月图代表自己的签名。

后来，有个狡猾的大臣拿着模仿得一模一样的假冒签名向国王冒领财物时，却被精明的国王发觉了!你猜，国王是怎样发觉这位大臣的阴谋的呢?其实很简单。

国王的签名是一笔完成的。

旁人不知晓这个秘密，只注意模仿图形，而没有注意笔画的多少，因此画出的图形连接处有空隙，国王当然一眼就能看出这个签名是假冒的了。

所谓一笔画，是指在纸上连续不断，又不重复，笔画成某种图形。

正确理解这段话，要注意三点：1．一笔画图形必须是连通图形，即图形中的各部分必须是相连的而不能是分开的；2．每条线都要画到，但又不能重复；3．图形中的点可以重复通过。

一个图形能否一笔画成，关键在于图中奇点的多少。

任何图形都是由点和线组成的，图形中的点可以分成两大类：奇点（也叫单点）和偶点（也叫双点）。

从一点出发的线的条数是单数，这样的点称为奇点；从一点出发的线的条数是双数，这样的点称为偶点。

正确解答一笔画问题，要掌握两条规律：1．如果一个图中的奇点个数为0或2，那么，这个图形可以一笔画成。

当奇点的个数为。

时，可以从任何个偶点开始，最后仍回到这个点；当奇点的个数为2时，必须从某一奇点开始，最后到另一个奇点结束。

2．如果一个图中奇点个数不是0或2，那么这个图形不能一笔画成。

【例1】下面的各个图形都是由点和线组成的，请你仔细观察后回答后面的问题。

（1）与一条线相连的有哪些点?（2）与两条线相连的有哪些点?（3）与三条线相连的有哪些点?（4）与四条或四条以上的线相连的有哪些点?（5）若把与奇数条线相连的点叫奇点，把与偶数条线相连的叫偶点，那么有0个奇点（即全部是偶点）的图形有哪些? 有2个奇点的图形有哪些? 有3个或3个以上奇点的图形有哪些? 分析先找出图中的点，再数一数从这点出发的线有几条，根据从一个点出发的线的条数的多少就能确定这个点是奇点还是偶点了。

奇妙的一笔画例题精讲所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢下面，我们就来探求解决这个问题的方法．什么样的图形能一笔画成呢这就是一笔画问题，它是一种有名的数学游戏．我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点．一笔画问题：(1)能一笔画出的图形必须是连通的图形；(2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点；(3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点；(4)奇点个数超过两个的图形，一定不能一笔画．多笔画问题：我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n个奇点(n为自然数)，那么这个图一定可以用n笔画成．【例 1】我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点哪些点是奇点【解析】奇点：J D H F偶点：A E B C G I【例 2】判断下列图a、图b、图c能否一笔画．【解析】图a能，因为有2个奇点，图b不能，因为图形不是连通的，图c能，因为因为图中全是奇点【例 3】下面图形能不能一笔画成若果能，应该怎样画【解析】图1能因为图中全是偶点，图2能因为图中全是偶点，图3不能因为有4个奇点．【例 4】下面的图形，哪些能一笔画出哪些不能一笔画出【解析】第1个能，2、3不能【例 5】下图中不能一笔画成，请你在下图中添加最少的线段，将其改成一笔画的图形，并画出路线图．【解析】不能一笔画出，因为图中有E H G F四个奇点，连结EH就可以使图形一笔画出．【例 6】下图中的线段表示小路，请你仔细观察，认真思考，能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁该怎样爬【解析】要想不重复爬出，需要图形能一笔画出，由于图中有两个奇点，所以应该从奇点出发才能一笔画出图形，所以甲蚂蚁能够．【例 7】能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形【解析】可以．【例 8】下图是儿童乐园的道路平面图，要使游客走遍每条路并且不重复，那么出、入口应设在哪里【解析】要想不重复，需要路线能一笔画出，由于图中有两个奇点，所以入口和出口应该分别放在两个奇点出，即F和I点．【例 9】邮递员叔叔向11个地点送信一次信，不走重复路，怎样走最合适【解析】不走重复路，一笔能画出路线图，图中有2个奇点，应该从奇点处出发，下面有一种参考路线：4-1-2-5-8-9-6-【例 10】观察下面的图，看各至少用几笔画成【解析】图(1)有8个奇点，所以要4笔画出，图(2)有12个奇点，所以要一笔画出，图(3)能一笔画出．【例 11】判断下列图形能否一笔画．若能，请给出一种画法；若不能，请加一条线或去一条线，将其改成可一笔画的图形．【解析】图(1)不能一笔画出，因为图中有4个奇点，连结BD，或者去掉BF都可以使图形能一笔画出．图(2)不能一笔画出，因为图中有4个奇点，去掉KL，或者BK都可以使图形能一笔画出．图(3)不能一笔画出，因为图中有4个奇点，去掉AB可以使图形能一笔画出．一个K(K＞1)笔画最少要添加几条连线才能变成一笔画呢我们知道K笔画有2K个奇点，如果在任意两个奇点之间添加一条连线，那么这两个奇点同时变成了偶点．如左下图中的B，C两个奇点在右下图中都变成了偶点．所以只要在K笔画的2K个奇点间添加(K-1)笔就可以使奇点数目减少为2个，从而变成一笔画．【例 12】18世纪的哥尼斯堡城是一座美丽的城市，在这座城市中有一条布勒格尔河横贯城区，这条河有两条支流在城市中心汇合，汇合处有一座小岛A和一座半岛D，人们在这里建了一座公园，公园中有七座桥把河两岸和两个小岛连接起来(如图a)．如果游人要一次走过这七座桥，而且对每座桥只许走一次，问如何走才能成功【解析】欧拉解决这个问题的方法非常巧妙．他认为：人们关心的只是一次不重复地走遍这七座桥，而并不关心桥的长短和岛的大小，因此，岛和岸都可以看作一个点，而桥则可以看成是连接这些点的一条线．这样，一个实际问题就转化为一个几何图形(如下图)能否一笔画出的问题了．而图B中有4个奇点显然不能一笔画出．【巩固】如下图所示，两条河流的交汇处有两个岛，有七座桥连接这两个岛及河岸．问：一个散步者能否一次不重复地走遍这七座桥【解析】能【例 13】右图是某展览厅的平面图，它由五个展室组成，任两展室之间都有门相通，整个展览厅还有一个进口和一个出口，问游人能否一次不重复地穿过所有的门，并且从入口进，从出口出【解析】将图形中的6个区域看成6个点，每个门看成连结他们的线段，显然6个点都是偶点，所以有人能一次不重复的走过所有的门．【巩固】右图是某展览馆的平面图，一个参观者能否不重复地穿过每一扇门如果不能，请说明理由．如果能，应从哪开始走【解析】不能【例 14】一条小虫沿长6分米，宽4分米，高5分米的长方体的棱爬行．如果它只能进不能退，并且同一条棱不能爬两次，那么它最多能爬多少分米【解析】8个定点都是奇点，所以至少需要4笔．多画长和高能保证总路程最长，为A－B－G－H－A－D－C－F－E－D总长为6×4＋5×4 ＋4×1＝48分米．【巩固】一只木箱的长、宽、高分别为5，4，3厘米(见右图)，有一只甲虫从A点出发，沿棱爬行，每条棱不允许重复，则甲虫回到A点时，最多能爬行多少厘米【解析】最多34厘米【例 15】如图是某餐厅的平面图，共有五个小厅，相邻两厅之间有门相通，并且设有入口．请问你能否从入口进入一次不重复地穿过所有的门．如果可以，请指明穿行路线，如果不能，应关闭哪个门就可以办到【解析】可以将图中的五个小厅以及厅外的部分都抽象成点，为方便解题，给它们分别编号．这时，连通厅与厅之间的门就相当于各点之间的连线．于是题目中餐厅的平面图就抽象成为一个连通的图形，求穿形路线的问题就转化成一笔画的问题．在抽象出的图形中，我们可以找到四个奇点，即①、④、③和厅外，所以图形不能一笔画出也就是说，从入口进入不可能一次不重复的穿过所有的门．但根据一笔画问题的知识，只要关闭门，把③、④变为偶点，就可以办到，可行路线如下图：B【例 16】在3×3的方阵中每个小正方形的边长都是100米．小明沿线段从A点到B 点，不许走重复路，他最多能走多少米【解析】这道题大多数同学都采用试画的方法，实际上可以用一笔画原理求解．首先，图中有8 个奇点，在8 个奇点之间至少要去掉4 条线段，才能使这8 个奇点变成偶点；其次，从A点出发到B 点，A，B 两点必须是奇点，现在A，B 都是偶点，必须在与A，B 连接的线段中各去掉1 条线段，使A，B 成为奇点．所以至少要去掉6 条线段，也就是最多能走1800 米，走法如图【例 17】一个邮递员投递信件要走的街道如右图所示，图中的数字表示各条街道的千米数，他从邮局出发，要走遍各街道，最后回到邮局．怎样走才能使所走的行程最短全程多少千米【解析】图中共有8 个奇点，必须在8 个奇点间添加4 条线，才能消除所有奇点，成为能从邮局出发最后返回邮局的一笔画．在距离最近的两个奇点间添加一条连线，如左下图中虚线所示，共添加4 条连线，这4 条连线表示要重复走的路，显然，这样重复走的路程最短，全程30 千米．走法参考右下图(走法不唯一)．。

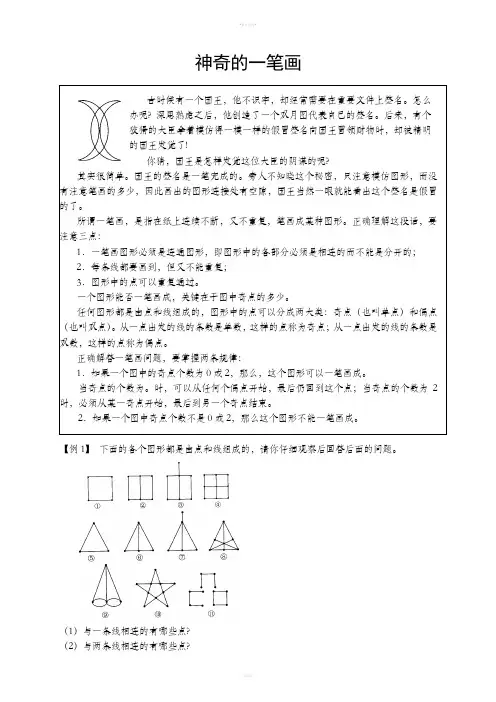
神奇的一笔画古时候有一个国王，他不识字，却经常需要在重要文件上签名。

怎么办呢? 深思熟虑之后，他创造了一个双月图代表自己的签名。

后来，有个狡猾的大臣拿着模仿得一模一样的假冒签名向国王冒领财物时，却被精明的国王发觉了!你猜，国王是怎样发觉这位大臣的阴谋的呢?其实很简单。

国王的签名是一笔完成的。

旁人不知晓这个秘密，只注意模仿图形，而没有注意笔画的多少，因此画出的图形连接处有空隙，国王当然一眼就能看出这个签名是假冒的了。

所谓一笔画，是指在纸上连续不断，又不重复，笔画成某种图形。

正确理解这段话，要注意三点：1．一笔画图形必须是连通图形，即图形中的各部分必须是相连的而不能是分开的；2．每条线都要画到，但又不能重复；3．图形中的点可以重复通过。

一个图形能否一笔画成，关键在于图中奇点的多少。

任何图形都是由点和线组成的，图形中的点可以分成两大类：奇点（也叫单点）和偶点（也叫双点）。

从一点出发的线的条数是单数，这样的点称为奇点；从一点出发的线的条数是双数，这样的点称为偶点。

正确解答一笔画问题，要掌握两条规律：1．如果一个图中的奇点个数为0或2，那么，这个图形可以一笔画成。

当奇点的个数为。

时，可以从任何个偶点开始，最后仍回到这个点；当奇点的个数为2时，必须从某一奇点开始，最后到另一个奇点结束。

2．如果一个图中奇点个数不是0或2，那么这个图形不能一笔画成。

【例1】下面的各个图形都是由点和线组成的，请你仔细观察后回答后面的问题。

（1）与一条线相连的有哪些点?（2）与两条线相连的有哪些点?（3）与三条线相连的有哪些点?（4）与四条或四条以上的线相连的有哪些点?（5）若把与奇数条线相连的点叫奇点，把与偶数条线相连的叫偶点，那么有0个奇点（即全部是偶点）的图形有哪些? 有2个奇点的图形有哪些? 有3个或3个以上奇点的图形有哪些?分析先找出图中的点，再数一数从这点出发的线有几条，根据从一个点出发的线的条数的多少就能确定这个点是奇点还是偶点了。

所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢？下面，我们就来探求解决这个问题的方法．什么样的图形能一笔画成呢？这就是一笔画问题，它是一种有名的数学游戏． 我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点．一笔画问题：(1)能一笔画出的图形必须是连通的图形；(2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点；(3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点；(4)奇点个数超过两个的图形，一定不能一笔画． 多笔画问题：我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n 个奇点(n 为自然数)，那么这个图一定可以用n 笔画成．模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点？哪些点是奇点？J O I H G FED CBA【例 2】 同学们野营时建了9个营地，连接营地之间的道路如图所示，贝贝要给每个营地插上一面旗帜，要求相邻营地的旗帜色彩不同，则贝贝最少需要 种颜色的旗子，如果贝贝从某营地出发，不走重复路线就 （填“能”或“不能”）完成任务.例题精讲知识点拨4-1-5.奇妙的一笔画【例 3】 判断下列图a 、图b 、图c 能否一笔画．NML KF DECBA 图bODCBAGFECBA【例 4】 下面图形能不能一笔画成？若果能，应该怎样画？（1）（2）（3）【例 5】 下面的图形，哪些能一笔画出？哪些不能一笔画出？【例 6】 右图是某展览厅的平面图，它由五个展室组成，任两展室之间都有门相通，整个展览厅还有一个进口和一个出口，问游人能否一次不重复地穿过所有的门，并且从入口进，从出口出？【巩固】右图是某展览馆的平面图，一个参观者能否不重复地穿过每一扇门？如果不能，请说明理由．如果能，应从哪开始走？E CDB A【例 7】 下图中的线段表示小路，请你仔细观察，认真思考，能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁？该怎样爬？乙甲【例 8】 能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形？【例 9】 下图是儿童乐园的道路平面图，要使游客走遍每条路并且不重复，那么出、入口应设在哪里？IHGFEDC BA【例 10】 邮递员叔叔向11个地点送信一次信，不走重复路，怎样走最合适？【例 11】 观察下面的图，看各至少用几笔画成？（1）A ED HCF GB （2）（3）【例 12】 在3×3的方阵中每个小正方形的边长都是100 米．小明沿线段从A 点到B 点，不许走重复路，他最多能走多少米？【例 13】 有16个点排成的44 方阵。

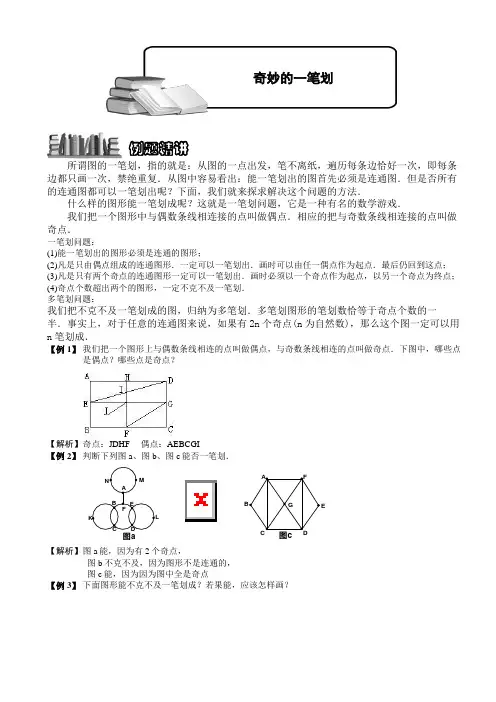
所谓图的一笔划，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，禁绝重复．从图中容易看出：能一笔划出的图首先必须是连通图．但是否所有的连通图都可以一笔划出呢？下面，我们就来探求解决这个问题的方法．什么样的图形能一笔划成呢？这就是一笔划问题，它是一种有名的数学游戏．我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点．一笔划问题：(1)能一笔划出的图形必须是连通的图形；(2)凡是只由偶点组成的连通图形．一定可以一笔划出．画时可以由任一偶点作为起点．最后仍回到这点； (3)凡是只有两个奇点的连通图形一定可以一笔划出．画时必须以一个奇点作为起点，以另一个奇点为终点； (4)奇点个数超出两个的图形，一定不克不及一笔划． 多笔划问题：我们把不克不及一笔划成的图，归纳为多笔划．多笔划图形的笔划数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n 个奇点(n 为自然数)，那么这个图一定可以用n 笔划成．【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点？哪些点是奇点？【解析】 奇点：JDHF 偶点：AEBCGI 【例 2】 判断下列图a 、图b 、图c 能否一笔划．图aNML KF DECBA 图cGFEDCBA【解析】 图a 能，因为有2个奇点，图b 不克不及，因为图形不是连通的， 图c 能，因为因为图中全是奇点【例 3】 下面图形能不克不及一笔划成？若果能，应该怎样画？例题精讲奇妙的一笔划【解析】图1能因为图中全是偶点，图2能因为图中全是偶点，图3不克不及因为有4个奇点．【例 4】下面的图形，哪些能一笔划出？哪些不克不及一笔划出？【解析】第1个能，2、3不克不及【例 5】下图中不克不及一笔划成，请你在下图中添加最少的线段，将其改成一笔划的图形，并画出路线图．【解析】不克不及一笔划出，因为图中有EHGF四个奇点，连结EH就可以使图形一笔划出．【例 6】下图中的线段暗示小路，请你仔细观察，认真思考，能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁？该怎样爬？【解析】要想不重复爬出，需要图形能一笔划出，由于图中有两个奇点，所以应该从奇点出发才干一笔划出图形，所以甲蚂蚁能够．【例 7】能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形？【解析】可以．【例 8】下图是儿童乐园的道路平面图，要使游客走遍每条路而且不重复，那么出、入口应设在哪里？【解析】要想不重复，需要路线能一笔划出，由于图中有两个奇点，所以入口和出口应该分别放在两个奇点出，即F和I点．【例 9】邮递员叔叔向11个地点送信一次信，不走重复路，怎样走最合适？【解析】 不走重复路，一笔能画出路线图，图中有2个奇点，应该从奇点处出发，下面有一种参考路线：4-1-2-5-8-9-6-10-11-7-4-3【例 10】 观察下面的图，看各至少用几笔划成？【解析】 图(1)有8个奇点，所以要4笔划出，图(2)有12个奇点，所以要一笔划出， 图(3)能一笔划出．【例 11】 判断下列图形能否一笔划．若能，请给出一种画法；若不克不及，请加一条线或去一条线，将其改成可一笔划的图形．IH G FED CBA 图aH G I KLJ F EDCBA 图bDC HG EFBA图c【解析】 图(1)不克不及一笔划出，因为图中有4个奇点，连结BD ，或者去掉BF 都可以使图形能一笔划出．图(2)不克不及一笔划出，因为图中有4个奇点，去掉KL ，或者BK 都可以使图形能一笔划出． 图(3)不克不及一笔划出，因为图中有4个奇点，去掉AB 可以使图形能一笔划出．一个K(K ＞1)笔划最少要添加几条连线才干酿成一笔划呢？我们知道K 笔划有2K 个奇点，如果在任意两个奇点之间添加一条连线，那么这两个奇点同时酿成了偶点．如左下图中的B ，C 两个奇点在右下图中都酿成了偶点．所以只要在K 笔划的2K 个奇点间添加(K-1)笔就可以使奇点数目减少为2个，从而酿成一笔划．【例 12】 18世纪的哥尼斯堡城是一座美丽的城市，在这座城市中有一条布勒格尔河横贯城区，这条河有两条支流在城市中心汇合，汇合处有一座小岛A 和一座半岛D ，人们在这里建了一座公园，公园中有七座桥把河两岸和两个小岛连接起来(如图a)．如果游人要一次走过这七座桥，而且对每座桥只许走一次，问如何走才干成功？【解析】 欧拉解决这个问题的方法非常巧妙．他认为：人们关心的只是一次不重复地走遍这七座桥，而其实不关心桥的长短和岛的大小，因此，岛和岸都可以看作一个点，而桥则可以看成是连接这些点的一条线．这样，一个实际问题就转化为一个几何图形(如下图)能否一笔划出的问题了．而图B 中有4个奇点显然不克不及一笔划出．【巩固】如下图所示，两条河流的交汇处有两个岛，有七座桥连接这两个岛及河岸．问：一个散步者能否一次不重复地走遍这七座桥？【解析】能【例 13】右图是某展览厅的平面图，它由五个展室组成，任两展室之间都有门相通，整个展览厅还有一个进口和一个出口，问游人能否一次不重复地穿过所有的门，而且从入口进，从出口出？【解析】将图形中的6个区域看成6个点，每个门看成连结他们的线段，显然6个点都是偶点，所以有人能一次不重复的走过所有的门．【巩固】右图是某展览馆的平面图，一个观赏者能否不重复地穿过每一扇门？如果不克不及，请说明理由．如果能，应从哪开始走？【解析】不克不及【例 14】一条小虫沿长6分米，宽4分米，高5分米的长方体的棱爬行．如果它只能进不克不及退，而且同一条棱不克不及爬两次，那么它最多能爬多少分米？【解析】8个定点都是奇点，所以至少需要4笔．多画长和高能包管总路程最长，为A－B－G－H－A－D－C－F－E－D总长为6×4＋5×4 ＋4×1＝48分米．【巩固】一只木箱的长、宽、高分别为5，4，3厘米(见右图)，有一只甲虫从A点出发，沿棱爬行，每条棱不允许重复，则甲虫回到A点时，最多能爬行多少厘米？【解析】最多34厘米【例 15】如图是某餐厅的平面图，共有五个小厅，相邻两厅之间有门相通，而且设有入口．请问你能否从入口进入一次不重复地穿过所有的门．如果可以，请指明穿行路线，如果不克不及，应关闭哪个门就可以办到？【解析】可以将图中的五个小厅以及厅外的部分都抽象成点，为方便解题，给它们分别编号．这时，连通厅与厅之间的门就相当于各点之间的连线．于是题目中餐厅的平面图就抽象成为一个连通的图形，求穿形路线的问题就转化成一笔划的问题．在抽象出的图形中，我们可以找到四个奇点，即①、④、③和厅外，所以图形不克不及一笔划出也就是说，从入口进入不成能一次不重复的穿过所有的门．但根据一笔划问题的知识，只要关闭门，把③、④变成偶点，就可以办到，可行路线如下图：B【例 16】在3×3的方阵中每个小正方形的边长都是100 米．小明沿线段从A点到B点，禁绝走重复路，他最多能走多少米？【解析】这道题大多数同学都采取试画的方法，实际上可以用一笔划原理求解．首先，图中有8个奇点，在8个奇点之间至少要去掉4条线段，才干使这8个奇点酿成偶点；其次，从A点出发到B点，A，B两点必须是奇点，现在A，B都是偶点，必须在与A，B连接的线段中各去掉1条线段，使A，B成为奇点．所以至少要去掉6条线段，也就是最多能走1800米，走法如图【例 17】一个邮递员投递信件要走的街道如右图所示，图中的数字暗示各条街道的千米数，他从邮局出发，要走遍各街道，最后回到邮局．怎样走才干使所走的行程最短？全程多少千米？【解析】图中共有8个奇点，必须在8个奇点间添加4条线，才干消除所有奇点，成为能从邮局出发最后返回邮局的一笔划．在距离最近的两个奇点间添加一条连线，如左下图中虚线所示，共添加4条连线，这4条连线暗示要重复走的路，显然，这样重复走的路程最短，全程30千米．走法参考右下图(走法不唯一)．。

所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢？下面，我们就来探求解决这个问题的方法．什么样的图形能一笔画成呢？这就是一笔画问题，它是一种有名的数学游戏．我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点． 一笔画问题：(1)能一笔画出的图形必须是连通的图形；(2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点； (3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点； (4)奇点个数超过两个的图形，一定不能一笔画． 多笔画问题：我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n 个奇点(n 为自然数)，那么这个图一定可以用n 笔画成．模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点？哪些点是奇点？J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答 【解析】 奇点： D H J O 偶点：A B C E F G I 【答案】奇点： D H J O 偶点：A B C E F G I【例 2】 同学们野营时建了9个营地，连接营地之间的道路如图所示，贝贝要给每个营地插上一面旗帜，要求相邻营地的旗帜色彩不同，则贝贝最少需要 种颜色的旗子，如果贝贝从某营地出发，不走重复路线就 （填“能”或“不能”）完成任务.【考点】一笔画问题 【难度】2星 【题型】填空 【关键词】华杯赛，六年级，初赛，第10题 【解析】 最少需要3种颜色的旗子。

因为中间的三点连成一个三角形，要使这三点所代表营地两粮相邻，要使相邻营地没有相同颜色的旗子，必须各插一种与其它两点不同颜色的旗子。

所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢？下面，我们就来探求解决这个问题的方法．什么样的图形能一笔画成呢？这就是一笔画问题，它是一种有名的数学游戏．我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点．一笔画问题：(1)能一笔画出的图形必须是连通的图形；(2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点；(3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点；(4)奇点个数超过两个的图形，一定不能一笔画．多笔画问题：我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n个奇点(n为自然数)，那么这个图一定可以用n笔画成．【例 1】我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点？哪些点是奇点？【例 2】判断下列图a、图b、图c能否一笔画．N MLKFDECBA图bODCBAGFECBA【例 3】下面图形能不能一笔画成？若果能，应该怎样画？例题精讲奇妙的一笔画【例 4】下面的图形，哪些能一笔画出？哪些不能一笔画出？【例 5】下图中不能一笔画成，请你在下图中添加最少的线段，将其改成一笔画的图形，并画出路线图．【例 6】下图中的线段表示小路，请你仔细观察，认真思考，能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁？该怎样爬？【例 7】能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形？【例 8】下图是儿童乐园的道路平面图，要使游客走遍每条路并且不重复，那么出、入口应设在哪里？【例 9】邮递员叔叔向11个地点送信一次信，不走重复路，怎样走最合适？【例 10】观察下面的图，看各至少用几笔画成？【例 11】判断下列图形能否一笔画．若能，请给出一种画法；若不能，请加一条线或去一条线，将其改成可一笔画的图形．IFCA图aHGIK LJCADCHGFBA图c【例12】 18世纪的哥尼斯堡城是一座美丽的城市，在这座城市中有一条布勒格尔河横贯城区，这条河有两条支流在城市中心汇合，汇合处有一座小岛A 和一座半岛D ，人们在这里建了一座公园，公园中有七座桥把河两岸和两个小岛连接起来(如图a )．如果游人要一次走过这七座桥，而且对每座桥只许走一次，问如何走才能成功？【巩固】如下图所示，两条河流的交汇处有两个岛，有七座桥连接这两个岛及河岸．问：一个散步者能否一次不重复地走遍这七座桥？【例 13】 右图是某展览厅的平面图，它由五个展室组成，任两展室之间都有门相通，整个展览厅还有一个进口和一个出口，问游人能否一次不重复地穿过所有的门，并且从入口进，从出口出？【巩固】右图是某展览馆的平面图，一个参观者能否不重复地穿过每一扇门？如果不能，请说明理由．如果能，应从哪开始走？E CDB A【例 14】一条小虫沿长6分米，宽4分米，高5分米的长方体的棱爬行．如果它只能进不能退，并且同一条棱不能爬两次，那么它最多能爬多少分米？【巩固】一只木箱的长、宽、高分别为5，4，3厘米(见右图)，有一只甲虫从A点出发，沿棱爬行，每条棱不允许重复，则甲虫回到A点时，最多能爬行多少厘米？【例 15】如图是某餐厅的平面图，共有五个小厅，相邻两厅之间有门相通，并且设有入口．请问你能否从入口进入一次不重复地穿过所有的门．如果可以，请指明穿行路线，如果不能，应关闭哪个门就可以办到？【例 16】在3×3的方阵中每个小正方形的边长都是100米．小明沿线段从A点到B点，不许走重复路，他最多能走多少米？【例 17】一个邮递员投递信件要走的街道如右图所示，图中的数字表示各条街道的千米数，他从邮局出发，要走遍各街道，最后回到邮局．怎样走才能使所走的行程最短？全程多少千米？。

神奇的一笔画的讲义学法指导星期天到了，小伙伴们都来到小红家集合，准备出发去放风筝。

这时，小王提议：“我们为什么不利用这个星期天，把小红家附近的每条路都转一圈，说不定还会有很多惊喜等着我们呢！”小方立即说道：“对呀，每条路上都值得去看一看，百货商店、儿童乐园、少年宫、肯德基……这些地方我都想去。

”可是，从小红家出发，怎样走才能不重复地走遍每一条路，最后到达人民公园呢？小朋友们，你们知道怎么走吗？实际上这样的问题就是“一笔画问题”。

所谓一笔画，就是从图形上某点出发，笔不离纸，而且每条线都只画一次不重复。

什么样的图形可以一笔画成呢？我们知道，任何图形都是由点和线组成的，图形中的点可以分为两大类：1．从一点出发的线的条数是双数，这点称为双数点．2．从一点出发的线的条数是单数，这点称为单数点．一个图形能否一笔画成，关键在于图中单数点的多少、l．图形中没有单数点，可一笔画成。

画时，任意一个双数点既是起点，又是终点。

2．图形中有两个单数点，可一笔画成。

画时以一个单数点为起点，另一个单数点为终点其他情况的图形都不能一笔画成。

下列图形能一笔画成吗？为什么？【分析与解答】先找出图中的点，再数‘数从这点出发的线有几条就能确定能不能一笔画了。

图1有2个双数点，可一笔画成。

图2有2个双数点、2个单数点，可一笔画成图3有5个双数点、4个单数点，不可一笔画成试一试1下列图形能一笔画成吗？为什么？观察下列图形，哪个图形可一笔画成？为什么？【分析与解答】图1可一笔画成，因为只有两个单数点：A、B：画法为：A一头部一翅膀一尾部一翅膀一嘴一B。

图2不能一笔两成，因为图中有4个单数点：A、B、C、D。

试一试2观察下列图形，哪个图形可一笔画成？为什么下图是王叔叔每天送牛奶所走的路线图：为了让居民们早点喝到新鲜的牛奶，王叔叔准备设计一种最好的方案，使自己不重复地走遍每条路。

小朋友们，你们有什么办法吗？【分析与解答】要想不重复地走遍每条路，就得转化成一道一笔画的题目来思考一图中共有9个点，都是双数点，所以可一笔面成一任何一个双数点都可以作为起点，最后仍以这一点作为终点。