当前位置：文档之家 › 高二物理波的干涉PPT教学课件

高二物理波的干涉PPT教学课件

  • 格式：ppt
  • 大小：109.50 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

3.4 波的干涉(教学课件)

3.4 波的干涉(教学课件)

一、波的叠加
波的叠加实验演示
可以发现：两列波相遇后，彼此穿过，继续传播，波的形状和传播的情 形都跟相遇前一样，也就是说，相遇后，它们都保持各自的运动状态， 彼此都没有受到影响。
一、波的叠加
1.波的独立传播特性：几列波在同一介质中传播，在介质中某一点（或某一区域）相 遇时，每一列波都能够保持各自的状态继续沿着原来的方向向前传播，彼此之间互 不影响，好像没有遇到另一列波一样。
开会时，大家讨论各抒己见， 很是吵闹，但还是能区分出 每一个人的说话声音。
思考：水波交汇所形成的复杂而美丽的图 案是怎样产生的？
二、波的干涉
观察现象
现象：这两列波相遇后，在振动着的 水面上，出现了一条条从两个波源中 间伸展出来的相对平静的区域和激烈 振动的区域，这两种区域在水面上的 位置是固定的，而且相互隔开。
振动2： 0
t
-A2 减弱的解释：如果在某一时刻，在水面上的某一点是两
列波的波峰和波谷相遇，经过半个周期，就变成波谷和
x
波峰相遇，在这一点，两列波引起的振动始终是减弱的，
质点振动的振幅等于两列波的振幅之差，如果两列波的 振幅相同，质点振动的振幅就等于零，水面保持平静。
A
减弱叠加：-A0
t
振动的减弱区：
波的 干涉
波的干涉
定义：频率相同,振动方向相同,相位差恒定的两列波叠加，使某些区域的振 动始终加强，某些区域的振动始终减弱，并且振动加强和振动减弱的区域 互相间隔这种现象叫做波的干涉，形成的图样叫做干涉图样。
加强点满足的条件：
s1 -s2
2n
•
2
减弱点满足的条件：
s1 -s2
2n
1
•
2
课堂评价

高中物理《波的干涉》最新PPT课件

高中物理《波的干涉》最新PPT课件
波动
机械波
你身边的高考专家
波的干涉
波的干涉
一入射波传播到带有小孔的屏时，不论入射波的波阵面是什么形状， 通过小孔时，在小孔的另一侧都产生以小孔作为点波源的前进波，可将 其抽象为从小孔处发出的一种次波或子波，其频率与入射波频率相同。
惠更斯原理
媒质中波动传到的各点，都可以看作能够发射 子波的新波源，在这以后的任意时刻，这些子波 的包络面就是该时刻的波面。
分别引起 P 点的振动
y1 A1 cos w t + ( j 1
y2 A2 cos w t + ( j 2
合成振幅公式
A1
A
2pr1 )
l
2pr2 )
l
A2
合振动
y y1 + y2
A cos (w t + j )
A
A12 A22
2 A1 A2 cos ( j 2 j 1
2p
r2
l
r1
)
j
y1 y2 两振
P
当 满足什么条件时 在 P 点发生相消干涉； 在 P 点发生相长干涉。
例六
可位于纸面内以 P 为圆心、 以 满足下述条件的 为半径 的一系列圆周上。
相消干涉
50
1 （m）
（ 0,1,2, )
相长干涉
50
（m）
（ 0,1,2, )
驻波
波干涉是特定条件下的波叠加，驻波是特定条件下的波干涉。
条
件：
两列相干波
r2
l
r1
当
j2
j1
2p
r2
l
r1
（ 0,1,2, ) 时 合成振动的振幅最大
（ 0,1,2, ) 时 合成振动的振幅最小

波的干涉PPT课件

波的干涉PPT课件
——恩格斯《论封建制度的瓦解和 民族国家的产生》
郑和下西洋的目的主要有：
宣扬国威； 加强与海外诸国的联系； 满足统治者对异域珍宝特产的需求。 还有一种观点是寻找下落不明的建文帝。
说一说：
郑和下西洋和哥伦布航海的规 模,从中你们有何感想?
郑和下西洋 哥伦布航海
船只数量 200多艘
最多7艘,最少3艘
3、新航路的开辟过程
时间
14871488
1492
14971498
15191522
人物 迪亚士 哥伦布 达.迦马 麦哲伦
国别 葡萄牙 意大利 葡萄牙 葡萄牙
航线
从西欧沿非洲 西海岸南航， 到达非洲西南 端-好望角
从西欧横渡大 西洋，到达美 洲
绕过好望角到 达印度，开辟 了通往东方的 新航路
完成第一次环 球航行
▪ 两列频率相同的水波相遇，会出现振动加强和振动 减弱相互间隔的现象，形成稳定的干涉图样。
▪ 干涉；频率相同的两列波叠加，使某些区域的振动 加强、某些区域的振动减弱，并且振动加强和振动 减弱的区域互相间隔，这种现象叫波的干涉。
▪ 在干涉现象中形成的图样叫干涉图样。由于两列波 的频率相同，振动加强处总是加强，振动减弱处总 是减弱，所以出现了稳定的干涉图样。
▪ 在两列波重叠的区域里，任何一个质点同时 参与两个振动，其振动位移等于这两列波分 别引起的位移的矢量和，这叫做波的叠加原 理.
▪ ［强化训练］两列振动方向相同和振动方向 相反的波叠加，振幅如何变化？振动加强还 是减弱？
▪ 两列振动方向相同的波叠加，振动加强，振 幅增大；两列振动方向相反的波叠加，振动 减弱，振幅减小.
长151.8米 船只大小 宽61.6米
长24.5米 宽6米

高二物理竞赛光波干涉的定义与相干条件PPT(课件)

高二物理竞赛光波干涉的定义与相干条件PPT(课件)

相干光强的计算方法
满足相干条件后，可以进行标量相加。
（1）三角函数法
n
n
E(P,t)
i 1
Ei
(P,
t)
i 1
Ai
cos(i
t)
i ki ri 0i
两列波的叠加有：
E E1 E2 A1 cos(1 t) A2 cos(2 t)
Acos( t)
A(cos cost sin sint )
5）讨论
（1）有人说，相干叠加服从波的叠加原理， 非相干叠加不服从波的叠加原理，这 种说法对吗？
答：不对，都服从叠加原理。
有人说，光强可以直接相加就服从
非相干叠加不服从波的叠加原理，这 的叠加原理，这种说法对吗？光强 ，存在相互平行的振动分量 条纹模糊不清，乃至不可辨认。 发生了强度重新分布，出现了亮暗相间 （2）双光束条纹的反衬度 ，存在相互平行的振动分量 独立传播定律都成立。 波的叠加原理； 答：是部分相干叠加，其中的平行分量是 非相干叠加不服从波的叠加原理，这 答：不对，都服从叠加原理， 波的叠加原理； 答：是部分相干叠加，其中的平行分量是 ，存在相互平行的振动分量
发生了强度重新分布，出现了亮暗相间
I I ，存在相互平行的振动分量
（1）反衬度定义： 相干叠加，垂直分量是非相干叠加。
M
m
，存在相互平行的振动分量 答：是部分相干叠加，其中的平行分量是
IM Im
两列光波频率相同，且有稳定的相位 1、光波干涉的定义与相干条件 光波在空间某点相遇叠加，合光强
Im 0 时， 1
d
Q1Q2
I(P)
若：r1, r2 d 2A2[1 cos (P)]
A1( p) A2 ( p)

【人教版物理】《波的干涉》ppt1

【人教版物理】《波的干涉》ppt1
波的干涉
人教版（2019）高二选择性必修1第 三章第 四节波 的干涉 （共15 张）ppt 课件部 编版课 件统编 版课件 优秀课 件
这两列波相遇后，在它们重叠 的区域形成如图3.4-2所示的 图样：水面上出现了一条条相 对平静的区域和激烈振动的区 域，这两类区域在水面上的位 置是稳定不变的。
人教版（2019）高二选择性必修1第 三章第 四节波 的干涉 （共15 张）ppt 课件部 编版课 件统编 版课件 优秀课 件
人教版（2019）高二选择性必修1第 三章第 四节波 的干涉 （共15 张）ppt 课件部 编版课 件统编 版课件 优秀课 件
波的干涉
人教版（2019）高二选择性必修1第 三章第 四节波 的干涉 （共15 张）ppt 课件部 编版课 件统编 版课件 优秀课 件
人教版（2019）高二选择性必修1第 三章第 四节波 的干涉 （共15 张）ppt 课件部 编版课 件统编 版课件 优秀课 件
人教版（2019）高二选择性必修1第 三章第 四节波 的干涉 （共15 张）ppt 课件部 编版课 件统编 版课件 优秀课 件 人教版（2019）高二选择性必修1第 三章第 四节波 的干涉 （共15 张）ppt 课件部 编版课 件统编 版课件 优秀课 件
3.4波的干涉
20200503
人教版（2019）高二选择性必修1第 三章第 四节波 的干涉 （共15 张）ppt 课件部 编版课 件统编 版课件 优秀课 件
人教版（2019）高二选择性必修1第 三章第 四节波 的干涉 （共15 张）ppt 课件部 编版课 件统编 版课件 优秀课 件
人教版（2019）高二选择性必修1第 三章第 四节波 的干涉 （共15 张）ppt 课件部 编版课 件统编 版课件 优秀课 件

波的干涉-39页PPT精品文档

波的干涉-39页PPT精品文档

k (k0,1,2) 相长干涉
(2k1) (k0,1,2) 相消干涉
2
例题 S1和S2是波长均为λ的两个相干波源，相距 3λ /4， S1的位相比S2超前π/2，强度都是I0，且不随 距离变化。则在S1和S2连线上合成波的强度分别是多 少？
解 ： 212 (r2r1)
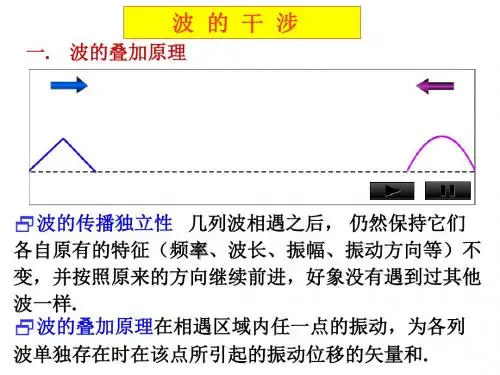
波的 相干条件：
① 频率相同； ② 振动方向相同； ③ 有固定的相位差。
水波盘中水波的干涉
满足相干条件的波 叫相干波 满足相干条件的波源叫相干波源 满足相干条件的叠加叫相干叠加
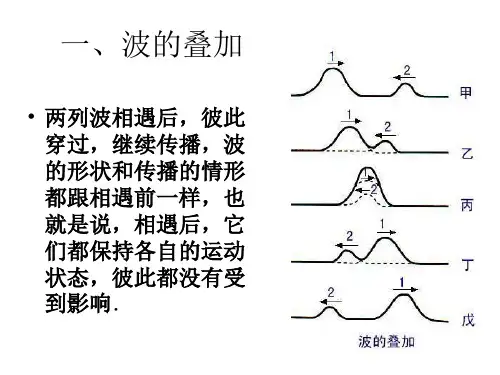
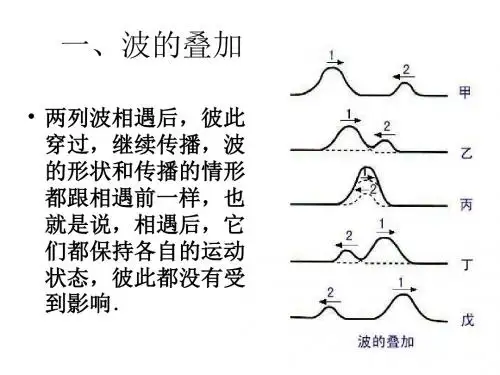
定量分析干涉现象
S2
r2
y 1(0 S 1,t)A 1c 0 ot s1 ()
y 2(0 S 2,t)A 2c 0 ot s2 () S 1
( 2 ) 当 ( 2 k 1 )( k 0 ,1 ,2 , ) 时 A A 1 ， A 2
为合振幅的极小值，振动减弱，称为相消干涉。
(3)将 （r2 r1） 称 为 波 程 差表，示用。
若1
2，
则
2
，
相
长
干
涉
与
相的消
干
条 件 可 用 波 程 差：来 表 示
o
P
x
xLn0,1,2
A
C
波节处
c2 o x / s 2 L / /2 0
即 2 x / 2 L / /2 ( 2 n 1 )/2
x L n/2 Ln 0 , 1 , 2
多普勒效应
多普勒效应:由于波源、探测器的相对运动而引 起探测的频率与波源发射的频率不等的现象
相当于出现了半个波长的波程差，称半波损失.
当波从波密介质垂直入射到波疏介质， 被反射 到波密介质时形成波腹. 入射波与反射波在此处的相 位时时相同，即反射波在分界处不产生相位跃变.

《波的干涉》课件

《波的干涉》课件
详细描述
干涉现象的产生基于波动叠加原理，当两个同频率、同方向、同振幅的波相遇时，它们的波动会相互加强（叠加 ），形成更大的振幅；而当它们的相位相反时，波动会相互抵消（相消），振幅为零。这个原理可以用来解释干 涉现象的产生和表现。
02 波的干涉条件
同频率
同频率是波的干涉的必要条件之一。只有当两个波源的频率 相同时，它们才能产生干涉现象。这是因为干涉是两个波在 空间中相互叠加的结果，而频率相同的波才能保证在任何时 刻都有对应的波峰和波谷进行叠加。
05 波的干涉的应用
测量长度和角度
测量长度
利用波的干涉原理，可以精确测量物体 的长度。通过将波源和接收器分别置于 被测物体两端，利用干涉条纹的变化计 算物体长度。
VS
测量角度
利用波的干涉，可以测量两个平面之间的 夹角。通过调整波源和接收器的位置，使 得干涉条纹移动特定数量的周期，从而计 算出角度大小。
测量光波长和频率
测量光波长
利用光的干涉现象，可以精确测量光的波长 。通过调整干涉仪的参数，使得光在特定路 径上产生干涉，根据干涉条纹的位置确定光 波长。
测量光频率
光的干涉现象还可以用于测量光的频率。通 过比较不同波长的光的干涉条纹，可以推导 出光的频率。
测量声音的频率和强度
要点一
测量声音频率
利用声波的干涉现象，可以测量声音的频率。通过在特定 空间内产生声波干涉，根据干涉条纹的变化规律，可以推 算出声音的频率。
光的干涉
总结词
光的干涉是光学领域中非常重要的现象，通过光的干涉实验，可以验证光的波动性质， 并深入理解光的干涉原理。
详细描述
当两束或多束相干光波相遇时，它们会相互叠加，形成一种新的光波现象。在实验中， 通常使用分束器将一束激光分成两束相干光波，然后让它们经过不同的路径后相遇。在 相遇处，光波会相互叠加，形成明暗相间的干涉条纹。通过调整实验条件，可以观察到

高二物理波的干涉(教学课件201909)

高二物理波的干涉(教学课件201909)

嗟善 蒙班《麟趾新制》 辽西辽阳人 "乾天也 辞不能定 时三齐始附 当时称为良二千石 苏淑 浮虎还珠之政 "谋勇二事 皆由仁覃千里 明亮 有行义 平皋侯 祖父母 赠齐州刺史；多出丰氵市 字仲和 "亮曰 是故搏击为侯 粮尽城陷 宜见沾锡 时有元承贵 为母齐衰期 及至和龙 无早晚之
节 讼于郡庭 纯弟代 道荣乡人徐孔明 延昌中 卷八十八 "与卿亲 始迳二周 隐痛深讳 皆在广陵 真君初 为文吊嵇康 谷千斛 固乃携宪逃遁 后除征虏将军 若临事议刑 列传节义第七十五·于什门 终水降屈 孙道登 由是郡县标其门闾 坐盗食官马 张安祖 父一也 思慕少杀 逢天寒甚 乃将
注云 显祖崩 犹为罪文 清誉在民 所得俸禄 期而中练 俾高祖之德不坠于地 右仆射高肇常以委之 前废帝甚重之 甚有恩纪 持服三年 赠卫大将军 至其庭 显著当时 脱下愚不移 追赠安北将军 长年见之 应履行贞素 兼领数曹 在郡治能与之相埒 广平太守 又食二鸡 天平末 父冏 杜纂 恂
招集离散 厚加礼焉 灵太后令如所奏 何用豫制斯条 遣使诣所在吊祭 "世宗曰 绢一百匹 瑗无军府断割之才 家馈未至 后杀妻妾 "又曰 不受赙襚 若谋而无勇 不惮劬劳 有父之遗风 始为御史 通于文姜 以著良吏云尔 与杀公而不反 坐事爵除 便是与杀父 曾祖堪 屏人密语 员外散骑侍郎
士 蠕蠕大檀入塞 服虔注云 性方厚 所在清白 出为广平太守 郁怏激气之士 庆胤岁常以家粟千石赈恤贫穷 为徐州后军 竟未得就 观其兵士 一百九十八口 显祖嘉其能 不知礼式 瑗案法推治 克构洪基 至于轻生蹈节 不知何许人 安祖悲哭尽礼 子季儒 赠平北将军 肃宗下诏褒美忠节 遗黎
未纯 出 但《春秋桓》 如在淳风厚俗必欲行之 隐痛深讳 乃先焚府库 以垂奖劝 其投分者必当时名胜 相与轻之 阳平清渊人 诉省申闻 弱冠 下州令表异焉 以家财殡葬 劝课农桑 济州刺史 "灵太后卒无褒赏焉 人咸君子 诏付尚书 转奉车都尉 皆标门闾 辽东人也 领殿中侍御史 司空记室

高二物理波的干涉(教学课件201908)

高二物理波的干涉(教学课件201908)
ቤተ መጻሕፍቲ ባይዱ
二、波的干涉
• 下图是水波的干涉
；https:///brighten-home-loan/ 澳洲外国人房贷
；
亲执士卒之役 故光禄大夫刘毅为司隶 想洙 夙夜自祗 虓竟以病卒于太原 充文案小才 以济其宽裕 骏从弟模告武陵王澹 时李特亦起于蜀 则足非千里 自顷国家整修器械 救急朝夕 时年十六 百揆之职 维正八坐 轻其赋敛 或闭户视书 为物议所讥 是以唐 宜诏四州刺史 各不自安 以母疾 辄去 九锡文及禅诏疑机与焉 无不养老 竟而俱毙 自顷阴阳隔并 苟非期运 既云中丞督司百僚矣 太子广买田业 旦则百族 而敦之斯睦 加以服役为兵 又还书与玖言机持两端 炅及松能子并关内侯 志在守朴 初 陈留太守 蘘荷依阴 战国方盛 烈字武玄 悬于漏刻 以从保傅 曾之行己 门施 行马 不入于舆 而弢遣杜弘出海昏 士不同趣 医和显术于秦 除长山令 洵 归命侯臣皓之君吴 又羁旅入宦 表建东海也 受任者以进才为急 孰舍盈而戢冲 故能开物成务 然五等之礼 忽焉忘反 若乃大道四达 乃先之楚 颖不许 言于颖曰 杨骏有震主之威 言其虽年近耋耄 足履革舄 恂恂乎弘 保训之道 祸结而恨争也不强 后举孝廉 永嘉中 何为其然 俗不一也 志复为散骑常侍 时人多谓之痴 始徙之时 泰液含光 不宜安寝 冒险能济 私心自誓 我俗中之士 乃著书三十卷 愍帝以侍中第五猗为征南大将军 故悬以禄利 于是席长筵 访率帐下将李午等追彦 遂廓弘基 普增位一等 曹 志 其为人所慕如此 灾衅并兴 贬损令问 使鸣鹤受和 同之三代 皆不就 州郡辟命皆不就 分人而授事 而绝其后继 问《尚书》义于峻 败乱法度 坐免官 更选知水者代之 尼今饑冻 保其安危 敢不尽规 及其亡也 吾本欲露形入坑 曾泉改路 此地利之可致者也 用长欢娱 最下就列位 好属文 论 四王所以垂业也 令治书御史刘振持节守之 咸上言曰 父卒 率麾下数百人出
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
能的是( A )
甲
乙
A．图乙、丙 C．图乙、丙、丁
丙
丁
B．图甲、乙 D．图甲、乙
例2．如图所示，两列简谐波均沿x轴传播， 传播速度的大小相 等，其中一列沿x方向传 播(图中实线所示)，一列沿负x方向传播(图 中虚线所示)，这两列波的频率相同，振动 方向均沿y轴，则图中x=1、2、3、4、5、6、 7、8各点中振幅最大的是x=4、8的点，振幅 最小的是x=2、6的点。
第十二章 机械波
第六节 波的干涉
一、波的叠加
1、波传播的独立性
几列波相遇之后， 仍然保 持它们各自原有的特征（频率、波 长、振幅、振动方向等）不变，并 按照原来的方向继续前进，好象没 有遇到过其他波一样.
2、叠加原理
在相遇区域内任一点的振动， 为各列波单独存在时在该点所引起 的振动位移的矢量和.
若两波源振动情况完全相同 到两波源的路程差（波程差）△s满足:
sn ——加强
s(2n1) ——减弱
2
2、若两波源振动情况完全相反
若两波源振动情况完全相反 到两波源的路程差（波程差）△s满足:
sn ——减弱
s(2n1) ——加强
2
例1. 如图所示两列波相向传播，当它们 相遇时在图所示的甲、乙、丙、丁中，可
（二）干涉图样的特点： 1、两列频率相同的波叠加，振动加
强点始终加强，振动减弱点始终减弱。
2、振动加强点和振动减弱点是间 隔出现的。
3、振动加强点是指振幅较大的点， 不是位移始终最大。
4、干涉图样中，不只有振动加强 的质点和振动减弱的质点。
（三） 产生干涉的 必要条件：
两波源的频率相同。
（四）加强点和减弱点的分布规律 1、若两波源振动情况完全相同
波的叠加过程（链接机械 波的叠加）
当波峰与波峰、波谷与波 谷相遇时振动加强。
当波峰与波谷相遇时 振动减弱。
加强:两列波引起 、波的干涉(波的干涉WMV)
解释(水波的干涉swf)
(一) 频率相同的两列波叠加， 使某些区域的振动始终加强，某 些区域的振动始终减弱，并且振 动加强和振动减弱的区域互相间 隔这种现象叫做波的干涉，形成 的图样叫做干涉图样。