【八年级】2018北师大版数学八年级下册63三角形的中位线

6.3三角形的中位线教案设计一、教材分析《三角形的中位线》是义务教育北师大版八年级（下）第六章《平行四边形》的第三节，教材安排一个学时完成。

此节内容是平面几何知识的综合应用，实用性很高，也是近几年中考的难点。

七年级在教学过程中，学生对中位线的有关知识有了初步了解。

本课时在教学中注重新旧知识的联系，强调直观与抽象的结合，鼓励学生大胆猜想，大胆探索新颖独特的证明方法和思路，让学生经历“探索—发现—猜想—证明”这一过程，同时渗透归纳、类比、转化等数学思想方法。

通过本节课的学习，应使学生理解三角形中位线性质，不但能指出了三角形的中位线与第三边的位置关系和数量关系，而且还为证明线段之间的位置关系和数量关系提供了新的思路。

二、学情分析针对本班学生基础知识不够扎实，新知识接受能力不强，数学思想方法运用不够灵活的现状,本节课着眼于基础，注重能力的培养，积极引导学生首先通过实际操作获得结论，然后借助于平行四边形的有关知识进行探索和证明。

在此过程中注重知识渗透转化、类比、归纳的数学思想方法，使学生能充分参与到教学过程中去，从而提高本节课的教学效果。

三、教学目标●知识与技能1、理解三角形的中位线的概念，会区别三角形的中线；掌握三角形中位线性质。

2、能正确应用三角形中位线定理进行有关的计算和证明。

●过程与方法经历探索、猜想、证明的过程，进一步发展推理论证的能力。

●情感、态度与价值观（1）经历从认识发现三角形的中位线到推理的三角形的中位线的性质的过程，体会探索发现的乐趣。

（2）通过观察、讨论、比较，研究三角形的中位线的图象和性质，培养学生收集提取信息的意识和推理能力，使学生会将复杂问题转化为简单问题。

（3）培养学生的数形结合的思想。

四、教学重点、难点教学重点：经历三角形中位线的性质定理的形成过程，并能利用它解决简单的问题。

教学难点：三角形中位线性质的证明。

五、教学方法●教法分析设计思想：对于中位线的应用问题，关键是由实际问题向数学问题的转化过程。

第02讲_三角形的中位线知识图谱三角形的中位线知识精讲一．三角形的中位线三角形中位线定义 连接三角形两边中点的线段 叫做三角形的中位线性质DE ∥BC ， 12DE BC =如图，在△ABC 中，D 、E 分别是AB 、AC 边的中点，则线段DE 是△ABC 的中位线．求证：DE ∥BC ， 12DE BC =证明过程：延长DE 到F ，使EF = DE ，连接 FC 、DC 、AF 1）证明四边形ADCF 是平行四边形 2）证明四边形BCFD 是平行四边形∴DE// BC 且DE=EF=12BC 2．任意两点的中点坐标公式：平面直角坐标系内的任意两点()11A x y ， ，()22B x y ，，线段AB 的中点C 的坐标为121222x xy y ++⎛⎫ ⎪⎝⎭，．ABCD EABCDEF出现两个中点，无三角形→构造三角形如图，四边形ABCD 中，点E 、F 、G 、H分别为四边中点连接对角线AC 、BD ，则HG 为△ADC的中位线，HG ∥AC 且HG ＝12AC 。

最后可证四边形HEFG 为平行四边形三．易错点（1）注意中线与中位线的区分 （2）中位线的辅助线构造三点剖析一．考点：1．中位线定理．二．重难点： 构造中位线，解决相关的角度线段问题．三．易错点：中线与中位线的区别．中位线定理例题1、 如图，▱ABCD 中，对角线AC 、BD 交于点O ，点E 是BC 的中点．若OE=3cm ，则AB 的长为（ ）A.3 cmB.6 cmC.9 cmD.12 cm【答案】 B【解析】 解：∵四边形ABCD 是平行四边形， ∴OA=OC ；又∵点E 是BC 的中点， ∴BE=CE ，∴AB=2OE=2×3=6（cm ） 故选：B ．例题2、 如图，在Rt △ABC 中，△A=30°，BC=1，点D ，E 分别是直角边BC ，AC 的中点，则DE 的长为（ ）A.1B.2C.D.1+【答案】 A【解析】 如图，△在Rt △ABC 中，△C=90°，△A=30°， △AB=2BC=2．又△点D 、E 分别是AC 、BC 的中点， △DE 是△ACB 的中位线， △DE=AB=1．例题3、 如图，在Rt △ABC 中，∠B ＝90°，AB ＝5，BC ＝12，点D 在BC 上，以AC 为对角线的所有平行四边形ADCEH GFEA BCD中，DE 的最小值是（ ）A.5B.6C.12D.13【答案】 A【解析】 ∵在Rt △ABC 中，∠B ＝90°， ∴BC ⊥AB ．∵四边形ADCE 是平行四边形， ∴OD ＝OE ，OA ＝OC ．∴当OD 取最小值时，DE 线段最短，此时OD ⊥BC ． ∴OD 是△ABC 的中位线，∴12.52OD AB ==，∴ED ＝2OD ＝5．例题4、 已知：如图，△ABC 中，∠ACB=90°，点D 、E 分别是AC 、AB 的中点，点F 在BC 的延长线上，且CF=DE ，求证：∠CDF=∠A ．【答案】 见解析【解析】 证明：∵D 、E 分别是AC 、AB 的中点， ∴DE ∥BC ，∵点F 在BC 的延长线上， ∴DE ∥CF ， ∵DE=CF ，∴四边形CEDF 为平行四边形， ∴DF ∥CE ，∴∠CDF=∠ECA ，∵∠ACB=90°，E 为AB 的中点， ∴CE=21AB=AE ， ∴∠A=∠DCE ， ∴∠CDF=∠A ．例题5、 （1）如图1，在四边形ABCD 中，E 、F 分别是AD 、BC 的中点，连接EF 并延长，分别与BA 、CD 的延长线交于点M 、N ，则BME CNE ∠=∠，求证：AB CD =．（提示取BD 的中点H ，连接FH ，HE 作辅助线） （2）如图2，在ABC ∆中，且O 是BC 边的中点，D 是AC 边上一点，E 是AD 的中点，直线OE 交BA 的延长线于点G ，若5AB DC ==，60OEC ∠=︒，求OE 的长度．【答案】 （1）见解析（2）52【解析】 连结BD ，取DB 的中点H ，连结EH 、FH ． E 、F 分别是AD 、BC 的中点，∴EH AB ∥，12EH AB =，FH CD ∥，12FH CD =BME CNE ∠=∠，∴HE HF =， ∴AB CD =；（2）解：连结BD ，取DB 的中点H ，连结EH 、OH ， AB CD =，∴HO HE =，∴HOE HEO ∠=∠，60OEC ∠=︒，∴60HEO AGO ∠=∠=︒， ∴OEH ∆是等边三角形， 5AB DC ==∴52OE =随练1、 一个三角形的周长是36，则以这个三角形各边中点为顶点的三角形的周长是（ ） A.6 B.12 C.18 D.36 【答案】 C【解析】 根据题意，画出图形如图示， 点D 、E 、F 分别是AB 、AC 、BC 的中点，∴DE=12BC ，DF=12AC ，EF=12AB ，∵AB+CB+AC=36，∴DE+DF+FE=36÷2=18． 故选C ．随练2、 如图，△ABC 中，已知AB=8，△C=90°，△A=30°，DE 是中位线，则DE 的长为（ ）A.4B.3C.D.2【答案】 D【解析】 △△C=90°，△A=30°， △BC=AB=4， 又△DE 是中位线， △DE=BC=2．故选D ．随练3、 如图，已知ABC △是锐角三角形，分别以AB 、AC 为边向外侧作两个等边三角形ABM △和CAN △，D 、E 、F 分别MB 、BC 、CN 的中点，连结DE 、FE ，求证：DE EF =.【答案】 证明见解析【解析】 连接MC 、BN ，ABM ∵△和CAN △是等边三角形，60BAM CAN ∠=∠=︒∴，MA BA =，AN AC =， BAM BAC CAN BAC ∠+∠=∠+∠∴， 即MAC BAN ∠=∠， 在MAC △与BAN △中 MA BA MAC BAN AN AC =⎧⎪∠=∠⎨⎪=⎩， MAC BAN ∴△≌△， MC NB =∴，D ∵、E 、F 分别是MB 、BC 、CN 的中点，12DE MC =∴，12EF BN =，DE EF =∴.随练4、 如图所示，在△ABC 中，M 是BC 的中点，AN 平分∠BAC ，BN ⊥AN ．若AB=14，AC=19，则MN 的长度为__________．【答案】 2.5【解析】 延长BN 交AC 于D ，∵AN ⊥BN ，AN 平分∠BAC ，∴AN 是BD 的垂直平分线，∵点M 是BC 的中点，∴MN 是△BCD 的中位线，111 2.5222MN CD AC AD AC AB ==-=-=（）（） 随练5、 已知，如图，四边形ABCD 中AD BC =，E 、F 分别是AB 、CD 的中点，延长AD 、EF 和BC 的延长线分别交于M 、N 两点，求证：AME BNE ∠=∠．ABCMN ABC D EFMNNMFD C BA【选项】【答案】见解析【解析】证明：连接BD，取BD的中点G，连接EG、FGE、F、G分别是AB、CD、BD的中点//FG BC∴，//EG AD且1=2FG BC，1=2EG ADAME FEG∴∠=∠,BNE GFE∠=∠AD BC=FG EG∴=FEG EFG∴∠=∠AME BNE∴∠=∠．拓展1、如图，在△ABC中，从A点向∠ACB的角平分线作垂线，垂足为D，E是AB的中点，已知AC＝4，BC＝6，则DE的长为（）A.1B.43C.32D.2【答案】A【解析】如图，延长AD交BC于F，∵CD是∠ACB的角平分线，CD⊥AD，∴AD＝DF，AC＝CF，（等腰三角形三线合一），又∵E是AB的中点，∴DE是△ABF的中位线，∴12DE BF=，∵AC＝4，BC＝6，∴BF＝BC－CF＝6－4＝2，∴1212DE=⨯=．2、如图，△ABC中，D、E分别是BC、AC的中点，BF平分∠ABC，交DE于点F，若BC=6，则DF的长是（）A.2B.3C.52D.4【答案】 B【解析】 在△ABC 中，D 、E 分别是BC 、AC 的中点 ∴DE ∥AB∴∠EDC=∠ABC ∵BF 平分∠ABC ∴∠EDC=2∠FBD在△BDF 中，∠EDC=∠FBD+∠BFD ∴∠DBF=∠DFB∴FD=BD=12BC=12×6=3．3、 如图，已知△ABC 中，AB ＝10，AC ＝8，BC ＝6，DE 是AC 的垂直平分线，DE 交AB 于点D ，连接CD ，则CD ＝________．【答案】 5【解析】 ∵AB ＝10，AC ＝8，BC ＝6， ∴BC 2＋AC 2＝AB 2，∴△ABC 是直角三角形， ∵DE 是AC 的垂直平分线，∴AE ＝EC ＝4，DE ∥BC ，且线段DE 是△ABC 的中位线， ∴DE ＝3， ∴225AD DC AE DE ==+=．4、 如图，点A ，B 为定点，定直线l △AB ，P 是l 上一动点，点M ，N 分别为PA ，PB 的中点，对下列各值： ①线段MN 的长；②△PAB 的周长；③△PMN 的面积；④直线MN ，AB 之间的距离；⑤△APB 的大小． 其中会随点P 的移动而变化的是（ ）A.②③B.②⑤C.①③④D.④⑤【答案】 B【解析】 △点A ，B 为定点，点M ，N 分别为PA ，PB 的中点， △MN 是△PAB 的中位线， △MN=AB ，即线段MN 的长度不变，故①错误； PA 、PB 的长度随点P 的移动而变化，所以，△PAB 的周长会随点P 的移动而变化，故②正确；△MN 的长度不变，点P 到MN 的距离等于l 与AB 的距离的一半， △△PMN 的面积不变，故③错误；直线MN ，AB 之间的距离不随点P 的移动而变化，故④错误； △APB 的大小点P 的移动而变化，故⑤正确． 综上所述，会随点P 的移动而变化的是②⑤． 故选：B5、 如图，分别以Rt △ABC 的直角边AC 及斜边AB 为边向外作等边△ACD 、等边△ABE ，EF ⊥AB ，垂足为F ，连接DF ，当ACAB=______时，四边形ADFE 是平行四边形．【答案】32【解析】 当ACAB =32时，四边形ADFE 是平行四边形．理由：∵ACAB =32，∴∠CAB=30°，∵△ABE 为等边三角形，EF ⊥AB ，∴EF 为∠BEA 的平分线，∠AEB=60°，AE=AB ， ∴∠FEA=30°，又∠BAC=30°， ∴∠FEA=∠BAC ， 在△ABC 和△EAF 中， ACB EFA BAC AEF AB AE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△ABC ≌△EAF （AAS ）； ∵∠BAC=30°，∠DAC=60°， ∴∠DAB=90°，即DA ⊥AB ， ∵EF ⊥AB ， ∴AD ∥EF ，∵△ABC ≌△EAF ， ∴EF=AC=AD ，∴四边形ADFE 是平行四边形6、 如图所示，在梯形ABCD 中，AD BC ∥，AD BC <，F ，E 分别是对角线AC ，BD 的中点．求证：()12EF BC AD =-【答案】 见解析【解析】 如图所示，连接AE 并延长，交BC 于点G ． AD BC ∥，∴ADE GBE ∠=∠，EAD EGB ∠=∠，又E 为BD 中点，∴AED GEB ∆∆≌．∴BG AD =，AE EG =． 在AGC ∆中，F ，E 分别是对角线AC ，BD 的中点∴F 、E 是AGC ∆的为中位线，∴EF BC ∥，()()111222EF GC BC BG BC AD ==-=-，即()12EF BC AD =-。

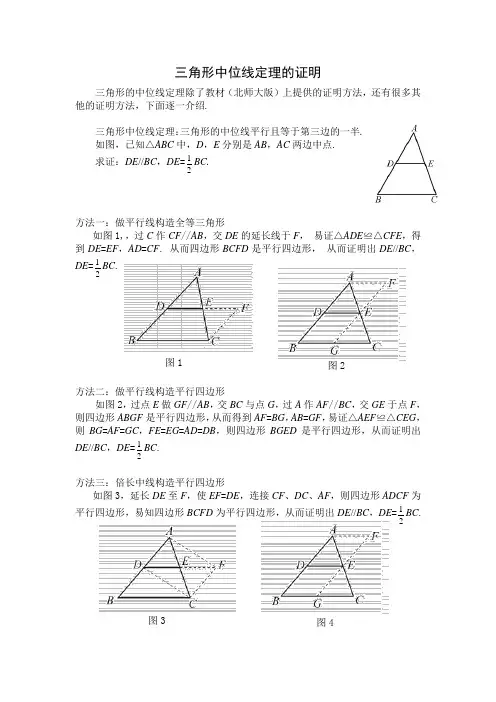
图3 图 4三角形中位线定理的证明三角形的中位线定理除了教材（北师大版）上提供的证明方法，还有很多其他的证明方法，下面逐一介绍.三角形中位线定理：三角形的中位线平行且等于第三边的一半.如图，已知△ABC 中，D ，E 分别是AB ，AC 两边中点.求证：DE //BC ，DE =21BC.方法一：做平行线构造全等三角形如图1,，过C 作CF //AB ，交DE 的延长线于F ， 易证△ADE ≌△CFE ，得到DE =EF ，AD =CF . 从而四边形BCFD 是平行四边形， 从而证明出DE //BC ，DE =21BC .方法二：做平行线构造平行四边形如图2，过点E 做GF //AB ，交BC 与点G ，过A 作AF //BC ，交GE 于点F ，则四边形ABGF 是平行四边形，从而得到AF =BG ，AB =GF ，易证△AEF ≌△CEG ，则BG =AF =GC ，FE =EG =AD =DB ，则四边形BGED 是平行四边形，从而证明出DE //BC ，DE =21BC .方法三：倍长中线构造平行四边形如图3，延长DE 至F ，使EF =DE ，连接CF 、DC 、AF ，则四边形ADCF 为平行四边形，易知四边形BCFD 为平行四边形，从而证明出DE //BC ，DE =21BC .图1 图2B C E D A y xO (0,a)(b,0)(c,0)图5-1 图5-2 图6图7 方法四：取中点截长线如图4，取BC 的中点G ，连接GE 并延长，使得FE =EG ，连接AF .易证△AEF ≌△CEG ，从而得到AF ∥GC ，AF =GC .所以AF ∥BG ，AF =BG ，易知四边形ABGF 和四边形DBFE 是平行四边形，从而证明出DE //BC ，DE =21BC .方法五:作垂线如图5-1，分别过点A ，B ，C 向DE 作垂线，垂足分别为F ，M ，N.易证△ADF ≌△BDM ，△AEF ≌△CEN ，从而MD =DF ，NE =EF ，则MN =2DE ，又由BM =AF =CN ，MB //NC ，得到四边形MBCN 为矩形，所以MN =BC ，从而证明出DE //BC ，DE =21BC . 如图5-2过点D 作DF ⊥BC 于F ，过点E 作EG ⊥BC 于G ，过A 作MN //BC ，分别与FD 、GE 的延长线交于M 、N.显而易见四边形MFGN 为矩形，于是MN =FG ,又可易证△MDA ≌△FDB ，△NEA ≌△GEC ，所以MD =DF =NE =EG ，AM =BF ，AN =CG 得到四边形DFGE 为矩形，FG =21BC .所以DE =FG .从而证明出DE //BC ，DE =21BC .方法六：面积法如图6：连接BE ，CD ，则CD 是△ABC 的中线，所以ABC BDC S S ∆∆=21，同理ABC BEC S S ∆∆=21，所以BEC BDC S S ∆∆=，故DE //BC (两三角形同底等高)，又因为DE 是△ABE 的中线，所以BEC ABE BDE S S S ∆∆∆==2121，故BC DE 21=（△BDE 和△BEC 等高）,从而证明出DE //BC ，DE =21BC . F N A B C D E M F N A B C D E MG方法七：建立平面直角坐标系如图7，建立平面直角坐标系，设A (0,a )，B (b ,0)，C (c ,0)则.2,2,2,2⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛a c E a b D 显然DE 平行于x 轴，即DE //BC .因为BC =c -a ，2-2a c DE = 所以BC DE 21=,从而证明出DE //BC ，DE =21BC . 证明三角形中位线定理的不同方法中有很多值得我们借鉴的地方:1.教材提供的证明是倍长中线做辅助线，本文方法一平行法做辅助线和本文方法五作垂直做辅助线，都能构造全等三角形，但它们都是利用了旋转变换，其本质思想一样.2.教材提供的证明中和方法三的倍长中线，方法四取中点截长线，是解决线段倍分问题的有效途径.3.方法七：建立平面直角坐标系是用代数方法解决几何问题，以后结合函数问题可以进一步探究.。

、定理1.三角形的中位线平行于第三边(不与中位线接触)，并且等于第三边的一半。

2.连接三角形两边中点的线段，叫做三角形的中位线。

逆定理逆定理一：在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线。

逆定理二：在三角形内，经过三角形一边的中点，且与另一边平行的线段，是三角形的中位线。

注意：在三角形内部，经过一边中点，且等于第三边一半的线段不一定是三角形的中位线。

（微课精讲）三角形中的三条重要线段：中线、角平分线、高线概念中线在三角形中，连接一个顶点与它对边中点的线段，叫做这个三角形的中线（median）。

三角形的三条中线交于一点，这点称为三角形的重心。

如图，AD是边BC上的中线，BE是边AC上的中线，CF是边AB上的中线三条中线交于点O，点O称为△A BC的重心角平分线在三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线。

如图，AD平分∠BAC，BE平分∠ABC，CF平分∠ACB，三角形三条角平分线交于点O点O称为△ABC的内心高线从三角形的一个顶点向它的对边所在直线作垂线，定点和垂足之间的线段叫做三角形的高线，简称三角形的高。

如图，AD⊥BC，BE⊥AC，CF⊥AB三角形三条高线交于点O点O称为△ABC的垂心以上是我们在初一时所学的三角形三条重要线段，今天，我们将学习三角形中第四条重要的线段——中位线（知识点精讲)中位线概念：连接三角形两边中点的线段叫做三角形的中位线性质：三角形的中位线平行于第三边，且等于第三边的一半。

如图，E、F分别是三角形AB、AC边上的中点，所以，EF是三角形BC 边所对的中位线，则EF∥BC且EF=1/2BC三角形的中位线衍生出很多重要的图形，其中最重要的就是中点四边形（微课堂精讲）中点四边形任意画一个四边形，以四边形的中点为顶点组成一个新四边形，这个新四边形称为——中点四边形中点四边形一定是平行四边形证明：连接AC因为E、F分别为AB、BC的中点，所以EF平行且等于AC的一半同理，GH平行且等于AC的一半因此，EF∥HG，EF=HG所以，四边形EFGH是平行四边形思考：四边形ABCD满足什么条件时，四边形EFGH是菱形？矩形？正方形？三角形中位线的解题策略三角形的中位线定理，既有线段的位置关系，又有线段的数量关系，它是一个在三角形中遇到中点，必须联想到的重要定理之一。

6.3 三角形的中位线教学设计其面积相等的平行四边形吗？怎样将一张三角形纸片剪成两部分，使分成的两部分能拼成一个平行四边形？操作：（1）剪一个三角形，记为△ABC（2）分别取AB,AC中点D,E，连接DE（3）沿DE将△ABC剪成两部分，并将△ABC绕点E旋转180°，得四边形BCFD.从小明的做法中，你能猜想出三角形两边中点的连线与第三边有怎样的关系？能证明你的猜想吗？连结三角形两边中点的线段叫三角形的中位线三角形有三条中位线注意：三角形的中位线和三角形的中线不同猜一猜：△ ABC的中位线DE与BC的关系怎样？（从位置和数量关系猜想）三角形的中位线平行于第三边，并且等于第三边的一半。

已知：在△ABC中，D是AB的中点，E是AC的中点。

求证：DE∥BC DE= 1/2BC.活动探究二：做一做 :小组活动，回答下列问题。

（小组讨论，3min）如图,任意画一个四边形，顺次连结四边形四条边的中点，所得的四边形有什么特点？请证明你的结论，并与同伴交流。

活动探究三：小组活动，回答下列问题。

（小组讨论，3min）（1）顺次连结对角线相等的四边形各边中点所得的四边形是什么？（2）顺次连结对角线垂直的四边形各边中点所得的四边形是什么？（3）顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么？变式1：如图, MN 为△ABC 的中位线,若∠ABC =59°则∠AMN =_______,若MN =13 ,则BC=_______.变式2：如图,已知△ABC中,AB = 4㎝,BC=4.6 ㎝AC=6㎝且D,E,F分别为 AB,BC,AC边的中点,则△DEF的周长是_______㎝.变式3：如下图：在Rt △ ABC中，∠A=90°,D、E、F分别是各边中点, AB=9cm，AC=12cm，则△DEF的周长=______cm。

变式4：如图：工人师傅要把一块三角形的钢板，通过切割焊接成一个与其面积相等的平行四边形．请你设计一种方案并在图中标出焊接线，然后证明你的结论．拓展提高：在△ABC中，∠BAC=90°，延长BA到点D，使AD=1/2AB，点E,F分别为BC,AC的中点，试说DF=BE理由。