特殊的平行四边形专题(题型详细分类)

特殊平行四边形重点题型一、题型概述特殊平行四边形是初中数学中经常出现的一个重要概念，它具有特殊的性质，常用于解决几何问题。

本文将介绍特殊平行四边形的定义、性质以及解题方法，并通过一些典型题目进行分析和讲解。

二、特殊平行四边形的定义特殊平行四边形是指具有特殊性质的平行四边形，包括矩形、正方形、菱形和长方形。

下面将逐个介绍这些特殊平行四边形的定义。

1.矩形矩形是一种特殊的平行四边形，具有以下特点：-所有内角均为直角；-两对相对边长度相等；-对角线相等且相互平分。

2.正方形正方形是一种特殊的矩形，具有以下特点：-所有内角均为直角；-所有边长相等；-对角线相等且相互平分。

3.菱形菱形是一种特殊的平行四边形，具有以下特点：-所有边长相等；-对角线相等且相互平分。

4.长方形长方形是一种特殊的矩形，具有以下特点：-所有内角均为直角；-两对相对边长度相等；-对角线相等且相互平分。

三、特殊平行四边形的性质特殊平行四边形具有一些独特的性质，这些性质是解决几何问题的重要依据。

下面将详细介绍这些性质。

1.矩形的性质-矩形的对角线相等且互相平分；-矩形的内角均为直角；-矩形的邻边互相垂直；-矩形的任意两边长度相等。

2.正方形的性质-正方形的对角线相等且互相平分；-正方形的内角均为直角；-正方形的任意两边长度相等。

3.菱形的性质-菱形的对角线相等且互相平分；-菱形的内角不一定为直角；-菱形的邻边互相垂直。

4.长方形的性质-长方形的对角线相等且互相平分；-长方形的内角均为直角；-长方形的邻边互相垂直。

四、特殊平行四边形的解题方法解决特殊平行四边形的问题，通常需要运用它们的特殊性质。

下面将介绍一些常见的解题方法。

1.利用对角线性质对于特殊平行四边形的问题，我们经常可以利用对角线的性质来解题。

例如，求特殊平行四边形的面积，可以先求出对角线的长度，然后利用面积公式计算。

2.利用内角性质特殊平行四边形的内角性质也是解题中常用的方法。

【单元复习】第一章特殊平行四边形知识精讲第一章特殊平行四边形一、平行四边形1.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形。

2.平行四边形的性质（1）平行四边形的对边平行且相等。

（对边）（2）平行四边形相邻的角互补，对角相等（对角）（3）平行四边形的对角线互相平分。

（对角线）（4）平行四边形是中心对称图形，对称中心是对角线的交点。

常用点：（1）若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段的中点是对角线的交点，并且这条直线二等分此平行四边形的面积。

（2）推论：夹在两条平行线间的平行线段相等。

3.平行四边形的判定（1）定义：两组对边分别平行的四边形是平行四边形。

（对边）（2）定理1：两组对边分别相等的四边形是平行四边形。

（对边）（3）定理2：一组对边平行且相等的四边形是平行四边形。

（对边）（4）定理3：两组对角分别相等的四边形是平行四边形。

（对角）（5）定理4：对角线互相平分的四边形是平行四边形。

（对角线）4.两条平行线的距离两条平行线中，一条直线上的任意一点到另一条直线的距离，叫做这两条平行线的距离。

注意：平行线间的距离处处相等。

5.平行四边形的面积: S平行四边形=底边长×高=ah二、菱形1.菱形的定义：有一组邻边相等的平行四边形叫做菱形2.菱形的性质（1）菱形的四条边相等，对边平行。

（边）（2）菱形的相邻的角互补，对角相等。

（对角）（3）菱形的对角线互相垂直平分，并且每一条对角线平分一组对角。

（对角线）（4）菱形既是中心对称图形又是轴对称图形；对称中心是对角线的交点（对称中心到菱形四条边的距离相等）；对称轴有两条，是对角线所在的直线。

3.菱形的判定（1）定义：有一组邻边相等的平行四边形是菱形。

（2）定理1：四边都相等的四边形是菱形。

（边）（3）定理2：对角线互相垂直的平行四边形是菱形。

（对角线）（4）定理3：对角线垂直且平分的四边形是菱形。

（对角线）4.菱形的面积：S菱形=底边长×高=两条对角线乘积的一半三、矩形1.矩形的定义:有一个角是直角的平行四边形叫做矩形。

专题1特殊平行四边形题型总结知识归纳掌握矩形、菱形、正方形的概念,了解它们之间的关系；探索并掌握矩形、菱形、正方形的有关性质和常用判别方法,并能运用这些知识进行有关的证明和计算；掌握三角形中位线定理是本章知识的重点。

特殊平行四边形在中招考试中会与三角形、圆、函数、平面直角系等知识点结合考试。

本专题主要对特殊平形四边形的题型进行总结，对其解法进行归纳总结，所选题型为近几年期末考试中的常考题型。

知识点梳理一、菱形1.定义：有一组邻边相等的平行四边形叫做菱形.2．性质：（1）具有平行四边形的一切性质；（2）四条边相等；（3）两条对角线互相平分且垂直，并且每一条对角线平分一组对角；（4）中心对称图形，轴对称图形.3．面积：2对角线对角线高＝＝底菱形⨯⨯S 4．判定：（1）一组邻边相等的平行四边形是菱形；（2）对角线互相垂直的平行四边形是菱形；（3）四边相等的四边形是菱形；（4）对角线垂直且平分的四边形是菱形。

知识点梳理二、矩形1．定义：有一个角是直角的平行四边形叫做矩形.2．性质：（1）具有平行四边形的所有性质；（2）四个角都是直角；（3）对角线互相平分且相等；（4）中心对称图形，轴对称图形.3．面积：宽＝长矩形⨯S ４．判定：（1)有一个角是直角的平行四边形是矩形.（2）对角线相等的平行四边形是矩形.（3）有三个角是直角的四边形是矩形.特别说明：由矩形得直角三角形的性质：（1）直角三角形斜边上的中线等于斜边的一半；（2）直角三角形中，30度角所对应的直角边等于斜边的一半．知识点梳理三、正方形1.定义：四条边都相等，四个角都是直角的四边形叫做正方形.2．性质：（1）对边平行；（2）四个角都是直角；（3）四条边都相等；（4）对角线互相垂直平分且相等，对角线平分对角；（5)两条对角线把正方形分成四个全等的等腰直角三角形；（6）中心对称图形，轴对称图形.3．面积：=S 正方形边长×边长＝12×对角线×对角线4．判定：（1）有一个角是直角的菱形是正方形；（2）一组邻边相等的矩形是正方形；（3）对角线相等的菱形是正方形；（4）对角线互相垂直的矩形是正方形；（5）对角线互相垂直平分且相等的四边形是正方形；（6）四条边都相等，四个角都是直角的四边形是正方形.常考题型专练一、选择题1.菱形不具备的性质是（）A.四边都相等 B.对角线一定相等 C.是轴对称图形 D.每一条对角线平分一组对角2．如图，以正方形ABCD 的一边AD 为边向外作等边三角形ADE ，则∠BED 等于（）A ．30°B ．37.5°C ．45°D ．50°3.下列四边形中，对角线互相垂直平分的是（）A.平行四边形、菱形 B.矩形、菱形 C.矩形、正方形 D.菱形、正方形4.在四边形ABCD 中，AB ＝BC ＝CD ＝DA ，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（）A.AC ⊥BDB.AB ∥CDC.∠A ＝90°D.∠A ＝∠C 5.如图，在ABCD Y 中，AD AB >，按以下步骤作图：（1）以点A 为圆心，AB 的长为半径作弧，交AD 于点E ；（2）分别以点B 、E 为圆心，大于12BE 的长为半径作弧，两弧在∠BAD 的内部交于点G ，连接AG 并延长交BC 于点F ．若AB ＝5，BE ＝6，则AF 的长是（）A.4B.6C.8D.106.如图1，ABCD Y 中，AD AB >，ABC ∠为锐角．要在对角线BD 上找点N ，M ，使四边形ANCM 为平行四边形，现有图2中的甲、乙、丙三种方案，则正确的方案（）A.甲、乙、丙都是B.只有甲、乙才是C.只有甲、丙才是D.只有乙、丙才是7.如图，点P 是▱ABCD 边AD 上的一点，E ，F 分别是BP ，CP 的中点，已知▱ABCD 面积为16，那么△PEF 的面积为（）A.8B.6C.4D.28.如图，已知菱形OABC 的顶点O (0，0)，B (2，2)，菱形的对角线的交于点D ；若将菱形OABC 绕点O 逆时针旋转，每秒旋转45°，从如图所示位置起，经过60秒时，菱形的对角线的交点D 的坐标为（）A.(1，1)B.(﹣1，﹣1)C.(-1，1)D.(1，﹣1)9．如图，菱形ABCD 的对角线AC 与BD 相交于点O ，E 为AD 的中点，连接OE ，60ABC ∠=︒，BD =，则OE =（）A ．4B ．C ．2D10.如图，已知菱形ABCD 的顶点(2,0)B -，且60ABC ∠=︒，点A 在y 轴的正半轴上．按以下步骤作图：①以点B 为圆心，适当长度为半径作弧，分别交边AB 、BC 于点M 、N ；②分别以点M 、N 为圆心，大于12MN 的长为半径作弧，两弧在ABC ∠内交于点P ；③作射线BP ，交菱形的对角线AC 于点E ，则点E 的坐标（）A.(B.(1,2)C.1,12⎛⎫ ⎪⎝⎭D.12⎛ ⎝二、填空题1.如图，在矩形ABCD 中，AB =，对角线AC 与BD 机交于点O ，BE AC ⊥，垂足为E ，且BE 平分∠CBD ，则BE 的长为____________．2.如图，菱形ABCD 的对角线AC ，BD 相交于点O ，点P 为AB 边上一动点（不与点A ，B 重合），PE OA ⊥于点E ，PF OB ⊥于点F ，若20AC =，10BD =，则EF 的最小值为____________．3.如图，BD 是正方形ABCD 的一条对角线，E 是BD 上一点，F 是CB 延长线上一点，连接CE ，EF ，AF ．若DE DC =，EF EC =，则BAF ∠的度数为__________．4．如图，菱形ABCD 中，点E 是边CD 的中点，EF 垂直AB 交AB 的延长线于点F ，若:1:2,BF CE EF ==，则菱形ABCD 的边长是______．5.如图，正方形ABCD 和正方形AEFG 的边长分别为5cm 和3cm ，点E 、G 分别为AB 、AD 边上的点，H 为CF 的中点，连接HG ，则HG 的长为______．三、解答题1.如图，在四边形ABCD 中，90ACB CAD ∠=∠=︒，点E 在BC 上，//,AE DC EF AB ⊥，垂足为F ．（1）求证：四边形AECD 是平行四边形；（2）若AE 平分4,5,cos 5BAC BE B ∠==，求BF 和AD 的长．2．如图，在□ABCD 中，∠ABC 的平分线交AD 于点F ，EF AB ∥交BC 于点E ．(1)求证；四边形ABEF 是菱形；(2)若AB ＝5，BF ＝8，12CE AE ，求□ABCD 的面积．3.如图，在矩形ABCD 中，沿EF 将矩形折叠，使A 、C 重合，AC 与EF 交于点H.(1)求证：△ABE ≌△AGF ；(2)若AB=6，BC=8，求△ABE 的面积．4．如图，ABCD 中，2BC AB =，AB AC ⊥，分别在边BC 、AD 上的点E 与点F 关于AC 对称，连接EF 、AE 、CF 、DE ．（1）试判定四边形AECF 的形状，并说明理由；（2）求证：AE DE⊥5.和3的两个正方形放置在直线l 上，如图a ,他连接AD 、CF ，经测量发现AD =CF ．（1）他将正方形ODEF 绕O 点逆时针针旋转一定的角度，如图b ，试判断AD 与CF 还相等吗？说明理由．（2）他将正方形ODEF 绕O 点逆时针旋转，使点E 旋转至直线l 上，如图c ，请求出CF 的长．6.已知：在△ABC年，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合）.以AD为边作正方形ADEF，连接CF.=-.（1）如图1，当点D在线段BC上时，求证：①BD⊥CF.②CF BC CD（2）如图2，当点D在线段BC的延长线上时，其它条件不变，请直接写出CF、BC、CD三条线段之间的关系；（3）如图3，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC的两侧，其它条件不变：①请直接写出CF、BC、CD三条线段之间的关系，②若连接正方形对角线AE，DF，交点为0，连接OC，探究△AOC的形状，并说明理由.。

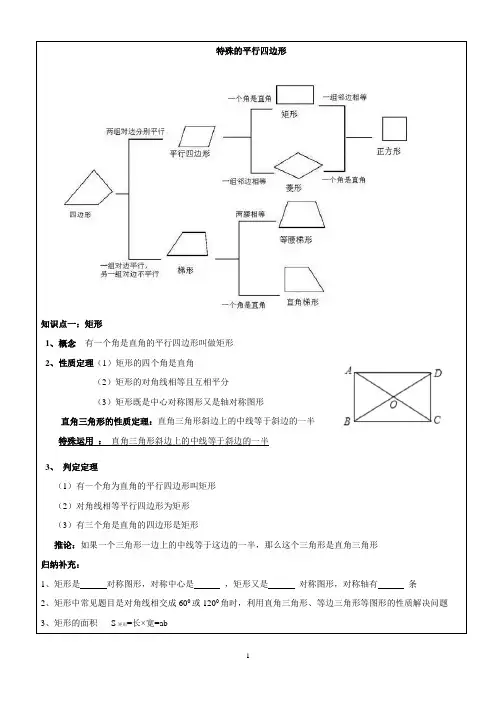
特殊的平行四边形知识点一：矩形1、概念有一个角是直角的平行四边形叫做矩形2、性质定理（1）矩形的四个角是直角（2）矩形的对角线相等且互相平分（3）矩形既是中心对称图形又是轴对称图形直角三角形的性质定理：直角三角形斜边上的中线等于斜边的一半特殊运用：直角三角形斜边上的中线等于斜边的一半3、判定定理（1）有一个角为直角的平行四边形叫矩形（2）对角线相等平行四边形为矩形（3）有三个角是直角的四边形是矩形推论：如果一个三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形归纳补充：1、矩形是对称图形，对称中心是，矩形又是对称图形，对称轴有条2、矩形中常见题目是对角线相交成600或1200角时，利用直角三角形、等边三角形等图形的性质解决问题3、矩形的面积S矩形=长×宽=ab知识点二：菱形1、定义：一组邻边相等的平行四边形叫做菱形2、性质定理：（1）菱形的四条边都相等（2）菱形的对角线互相垂直平分，且每条对角线平分一组对角（3）菱形是轴对称图形，两条对角线所在的直线是都是它的对称轴菱形是中心对称图形，对角线的交点是它的对称中心2、判定定理：（1）一组邻边相等的平行四边形是菱形（2）对角线互相垂直的平行四边形是菱形（3）四条边都相等的四边形是菱形※注意：对角线互相垂直的四边形不一定是菱形，对角线互相垂直平分的四边形才是菱形归纳补充:1、菱形被对角线分成四个全等的三角形和两对全等的三角形2、菱形的面积可以用平行四边形面积公式计算，也可以用两对角线积的来计算3、菱形常见题目是内角为1200或600时，利用等边三角形或直角三角形的相关知识解决题目知识点三：正方形1、定义：有一组邻边相等的矩形叫正方形2、性质定理（1）正方形的四条边都相等，四个角是直角。

（2）正方形的两条对角线相等且互相垂直平分，每一组对角线平分一组对角（3）正方形既是中心对称图形，又是轴对称图形3、判定定理（1）有一组邻边相等的矩形是正方形（2）对角线相互垂直的矩形是正方形（3）对角线相等的菱形是正方形（4）有一个角是直角的菱形是正方形方法总结：（1）判定一个四边形是正方形的主要依据是定义，途径有两种：先证它是矩形，再证有一组邻边相等。

平行四边形知识点归纳和题型归类平行四边形知识点归纳和题型归类要点梳理】要点一、平行四边形1.定义：有两组对边分别平行的四边形叫做平行四边形。

2.性质：（1）对边相等；（2）同位角相等；（3）相邻角互补；（4）是中心对称图形。

3.面积：S = 底 ×高。

4.判定：边：（1）有两组对边分别平行的四边形是平行四边形；（2）对边相等的四边形是平行四边形；（3）对角线互相平分的四边形是平行四边形。

角：（4）有一组对边平行，且同位角相等的四边形是平行四边形。

对角线：有一组对边相等，且互相平分的四边形是平行四边形。

要点诠释：平行线的性质：（1）平行线间的距离相等；（2）等底等高的平行四边形面积相等。

要点二、矩形1.定义：有四个角都是直角的平行四边形叫做矩形。

2.性质：（1）对边相等；（2）相邻角互补；（3）对角线相等；（4）是中心对称图形，也是轴对称图形。

3.面积：S = 长 ×宽。

4.判定：有四个角都是直角的平行四边形是矩形。

要点诠释：由矩形得直角三角形的性质：（1）直角三角形斜边上的中线等于斜边的一半；（2）直角三角形中，30度角所对应的直角边等于斜边的一半。

要点三、菱形1.定义：有四个边都相等的平行四边形叫做菱形。

2.性质：（1）对边相等；（2）相邻角互补；（3）对角线相等；（4）是中心对称图形，也是轴对称图形。

3.面积：S = 对角线之积的一半。

4.判定：有一组对边平行且相等的四边形是菱形。

要点四、正方形1.定义：四条边都相等，四个角都是直角的平行四边形叫做正方形。

2.性质：（1）对边相等；（2）相邻角互补；（3）对角线相等；（4）是中心对称图形，也是轴对称图形；（5）两条对角线把正方形分成四个全等的等腰直角三角形。

3.面积：S = 边长的平方，也可以用对角线的平方的一半求解。

4.判定：（1）有一组对边平行且相等的菱形是正方形；（2）有四个角都是直角的矩形是正方形；（3）对角线互相垂直平分且相等的四边形是正方形；（4）四条边都相等，四个角都是直角的四边形是正方形。

特殊的平行四边形章末重难点题型汇编【考点1 菱形的性质】【方法点拨】菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线都平分一组对角。

【例1】（2019春•卧龙区期末）如图，已知菱形ABCD 的周长为24，对角线AC 、BD 交于点O ，且16AC BD +=，则该菱形的面积等于( )A ．6B ．8C ．14D ．28【分析】首先根据题意求出AD 的长度，然后利用菱形的性质以及勾股定理的知识求出AO •BO 的值，最后结合三角形的面积公式即可求出答案．【答案】解：∵四边形ABCD 是菱形，∴AC ⊥BD ，AB ＝BC ＝CD ＝DA ，∵菱形ABCD 的周长为24，∴AD ＝AB ＝6，∵AC +BD ＝16，∴AO +BO ＝8，∴AO 2+BO 2+2AO •BO ＝64，∵AO 2+BO 2＝AB 2，∴AO •BO ＝14，∴菱形的面积＝4×三角形AOD 的面积＝4××14＝28，故选：D ．【点睛】本题主要考查了菱形的性质，解题的关键是利用菱形的性质以及勾股定理的知识求出AO •BO 的值．【变式1-1】（2019春•定远县期末）如图，菱形ABCD 中，AC 交BD 于点O ，DE BC ⊥于点E ，连接OE ，若50BCD ∠=︒，则OED ∠的度数是( )A．35︒B．30︒C．25︒D．20︒【分析】根据直角三角形的斜边中线性质可得OE＝BE＝OD，根据菱形性质可得∠DBE＝∠ABC＝65°，从而得到∠OEB度数，再依据∠OED＝90°﹣∠OEB即可．【答案】解：∵四边形ABCD是菱形，∠BCD＝50°，∴O为BD中点，∠DBE＝∠ABC＝65°．∵DE⊥BC，∴在Rt△BDE中，OE＝BE＝OD，∴∠OEB＝∠OBE＝65°．∴∠OED＝90°﹣65°＝25°．故选：C．【点睛】本题主要考查了菱形的性质、直角三角形斜边中线的性质，解决这类问题的方法是四边形转化为三角形．【变式1-2】（2019春•宝应县期末）如图，四边形ABCD是菱形，6AC=，8BD=，AH BC⊥于H，则AH 等于()A．125B．4C．245D．5【分析】根据菱形的性质得出BO、CO的长，在Rt△BOC中求出BC，利用菱形面积等于对角线乘积的一半，也等于BC×AH，即可得出AH的长度．【答案】解：∵四边形ABCD是菱形，∴CO＝AC＝3，BO＝BD＝4，AO⊥BO，∴BC＝5，∴S菱形ABCD＝AC•BD＝×6×8＝24，∵S菱形ABCD＝BC×AH，∴BC×AH＝24，∴AH＝故选：C．【点睛】本题考查了菱形的性质，也涉及了勾股定理，要求我们掌握菱形的面积的两种表示方法，及菱形的对角线互相垂直且平分．【变式1-3】（2018秋•巴南区期末）如图，菱形ABCD中，135D⊥于E，交AC于F，FG BC⊥∠=︒，BE CD于G．若BFG∆的周长为4，则菱形ABCD的面积为()A．42B．82C．16D．162【分析】根据菱形的性质得到∠BCD＝45°，推出△BFG与△BEC是等腰直角三角形，根据全等三角形的性质得到FG＝FE，CG＝CE，设BG＝FG＝EF＝x，得到BF＝x，根据△BFG的周长为4，列方程x+x+x＝4，即可得到结论．【答案】解：∵菱形ABCD中，∠D＝135°，∴∠BCD＝45°，∵BE⊥CD于E，FG⊥BC于G，∴△BFG与△BEC是等腰直角三角形，∵∠GCF＝∠ECF，∠CGF＝∠CEF＝90°，CF＝CF，∴△CGF≌△CEF（AAS），∴FG＝FE，CG＝CE，设BG＝FG＝EF＝x，∴BF＝x，∵△BFG的周长为4，∴x+x+x＝4，∴x＝4﹣2，∴BE＝2，∴BC＝BE＝4，∴菱形ABCD的面积＝4×2＝8，故选：B．【点睛】本题考查了菱形的性质，等腰三角形的性质，求FG的长是本题的关键．【考点2 矩形的性质】【方法点拨】矩形具有平行四边形的一切性质；矩形的四个角都是直角；矩形的对角线相等。

特殊平行四边形知识点总结及题型特殊平行四边形知识点总结及题型特殊平行四边形是几何学中的重要概念，它包括矩形、菱形和正方形。

这些特殊平行四边形具有一些独特的性质和特征，它们在几何学、晶体学和工程学等领域都有广泛的应用。

本文将总结特殊平行四边形的定义、性质、判定方法和典型题型，以帮助读者更好地理解和掌握这些知识。

一、定义1、矩形：一个内角为直角的平行四边形叫做矩形。

2、菱形：一个内角为锐角的平行四边形叫做菱形。

3、正方形：内角均为直角的平行四边形叫做正方形。

二、性质1、对边平行且相等。

2、对角线互相平分且相等。

3、四个内角均为90度。

4、邻角互补。

5、对角线与邻边组成的三角形为等腰直角三角形。

三、判定方法1、矩形 (1) 内角为直角。

(2) 对边平行且相等。

2、菱形 (1) 内角为锐角。

(2) 对边平行且相等。

3、正方形 (1) 内角均为直角。

(2) 对边平行且相等。

四、典型题型1、求特殊平行四边形的角度和周长。

2、证明特殊平行四边形的性质和判定方法。

3、解决与特殊平行四边形相关的实际问题。

五、扩展知识1、空间几何中的特殊平行四边形，如空间双面平行四边形等。

2、立体几何中的特殊平行四边形，如平行六面体等。

3、相关知识点，如三角函数、向量等在特殊平行四边形中的应用。

总之，特殊平行四边形是一个具有丰富内容和广泛应用的知识点。

理解和掌握这些特殊形状的特点和性质，对于解决相关问题以及进一步学习几何学、物理学等学科都具有重要意义。

希望读者通过阅读本文，能够对这些特殊平行四边形的定义、性质、判定方法和典型题型有更深入的理解和掌握，为进一步学习打下坚实的基础。

平行四边形知识点总结平行四边形知识点总结一、定义平行四边形是一种几何图形，具有两条相互平行的对边和两条对角线。

它是人类生活中常见的形状，具有广泛的应用价值。

二、性质1、平行四边形的对边平行且相等。

2、平行四边形的对角相等。

3、平行四边形的内角和为360度。

专题04 特殊的平行四边形压轴题型汇总一、单选题1．（2021·临沂第九中学）如图，在□ABCD中，对角线BD⊥AD，AB=10，AD=6，O为BD的中点，E为边AB上一点，直线EO交CD于点F，连接DE、BF，下列结论不成立的是（）A．四边形DEBF为平行四边形B．若AE=3.6，则四边形DEBF为矩形C．若AE=5，则四边形DEBF为菱形D．若AE=4.8，则四边形DEBF为正方形【答案】D【分析】根据平行四边形的判定方法，矩形的判定方法，菱形的判定方法，正方形的判定方法解答即可．【详解】解：∵O为BD的中点，∵OB＝OD，∵四边形ABCD为平行四边形，∵DC//AB，∵∵CDO＝∵EBO，∵DFO＝∵OEB，∵∵FDO∵∵EBO（AAS），∵OE＝OF，∵四边形DEBF为平行四边形，故A选项不符合题意，若AE＝3.6，AD＝6，∵3.6365AEAD==，又∵63105ADAB==，∵AE ADAD AB=，∵∵DAE＝∵BAD，∵∵DAE∵∵BAD，压轴题型汇总1∵∵AED＝∵ADB＝90°．∵四边形DEBF为矩形．故B选项不符合题意，∵AB＝10，AE＝5，∵BE＝5，又∵∵ADB＝90°，AB＝5，∵DE＝12∵DE＝BE，∵四边形DEBF为菱形．故C选项不符合题意，∵AE＝3.6时，四边形DEBF为矩形，AE＝5时，四边形DEBF为菱形，∵AE＝4.8时，四边形DEBF不可能是正方形．故选项D符合题意．故选：D．【点睛】本题考查了矩形的判定、菱形的判定、平行四边形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质、正方形的判定等知识；熟练掌握矩形的判定和菱形的判定，证明三角形全等是解题的关键．2．（2021·河南八年级期末）如图，菱形ABCD的边长是8，对角线交于点O，⊥ABC=120°，若点E是AB的中点，点M是线段AC上的一个动点，则BM+EM的最小值为（）A．4B．C．8D．16【答案】B【分析】连接DE交AC于M，由菱形的对角线互相垂直平分，可得B和D关于AC对称，则MD = MB，ME十MB=ME+MD≥DE，即DE就是ME十M B的最小值．【详解】解：连接DE交AC于M，由菱形的对角线互相垂直平分，可得B、D关于AC对称，则MD = MB，ME 十MB =ME +MD ≥DE ，即DE 就是ME 十MB 的最小值，∵∵ABC =120°，∵BAD = 60°，AD ＝ AB ＝8，∵ABD 是等边三角形，∵点E 是AB 的中点，∵AE = BE ＝4，DE ∵AB (等腰三角形三线合一的性质)，在Rt ∵ADE 中，由勾股定理可得： DE =，故选：B ．【点睛】本题考查菱形的性质，轴对称-最短路线问题，勾股定理的应用，解题的关键确定M 的位置． 3．（2021·连云港市新海实验中学）如图，在Rt ABC 中，⊥ACB =90°，BC =2，⊥BAC =30°，将ABC 绕顶点C 逆时针旋转得到⊥A 'B 'C '， M 是BC 的中点，P 是A 'B '的中点， 连接PM ，则线段PM 的最大值是（ ）A ．4B ．2C ．3D ．【答案】C【分析】连接PC ，分别求出PC ，CM 的长，然后根据PM MC PC ≤+即可得到答案．【详解】解：如图所示，连接PC ，∵∵ACB =90°，BC =2，∵BAC =30°，∵AB =2BC =4，由旋转的性质可知：=90A CB ACB ''=∠∠，4A B AB ''==，∵P 、M 分别是A B ''、BC 的中点， ∵122PC A B ''==，112CM BC ==， ∵3PM MC PC ≤+=，∵PM 的最大值为3，且此时P 、C 、M 三点共线，故选C ．【点睛】本题主要考查了旋转的性质，直角三角形斜边的中线，三角形三边的关系，解题的关键在于能够熟练掌握相关知识进行求解．4．（2021·山东济宁学院附属中学九年级）如图，矩形纸片ABCD ，6cm AB =，8cm BC =，E 为边D 上一点，将BCE 沿BE 所在的直线折叠，点C 恰好落在AD 边上的点F 处，过点F 作FM BE ⊥，垂足为点M ，取AF 的中点N ，连接MN ，则MN =（ ）cm ．A ．5B ．6C ．245D ．【答案】A【分析】 连接AC ，MC ，可求得M 为CF 的中点，根据中位线的性质可得12MN AC =，勾股定理求得AC 即可．【详解】解：连接AC ，MC由折叠的性质可得CF EB ⊥，CE EF =又∵FM BE ⊥∵点M 在线段FC 上，90EMF EMC ∠=∠=︒又∵ME ME =∵()EMF EMC HL △≌△∵FM MC =又∵AF 的中点N∵MN 为ACF 的中位线 ∵12MN AC =在Rt ACB 中，10cm AC =∵5cm MN =故选A【点睛】此题考查了折叠的性质，矩形的性质以及三角形中位线的性质，熟练掌握相关基本性质是解题的关键．5．（2021·珠海市九洲中学）如图所示，矩形ABCD 中，AE 平分BAD ∠交BC 于E ，15CAE ∠=︒，则下面的结论：①ODC △是等边三角形；②2BC AB =；③AOB BOC S S =△△；④AOE COE S S =，其中正确的有（ ）A ．①②③B ．①②④C ．①③④D ．②③④【答案】C【分析】 由矩形的性质得OA ＝OD ＝OC ＝OB ，再证∵ACD ＝60°，得∵ODC 是等边三角形，故①正确；然后由含30°角的直角三角形的性质得AC ＝2AB ，则2AB ＞BC ，故②错误；然后由OA ＝OC得AOB BOC S S =△△，AOE COE SS =，故③④正确．【详解】 解：∵四边形ABCD 是矩形，∵AD //BC ，∵BAD ＝∵ABC ＝∵ADC ＝90°，OA ＝OC ，OD ＝OB ，AC ＝BD ，∵OA ＝OD ＝OC ＝OB ，∵AE 平分∵BAD ，∵∵DAE ＝45°，∵∵CAE ＝15°，∵∵DAC ＝45°−15°＝30°，∵∵ACD ＝90°−∵DAC ＝90°−30°＝60°，∵OD ＝OC ，∵∵ODC 是等边三角形，故①正确；∵AD //BC ，∵∵ACB ＝∵DAC ＝30°，∵∵ABC ＝90°，∵AC ＝2AB ，∵2AB ＞BC ，故②错误；∵OA ＝OC ，∵AOB BOC S S =△△，AOE COE SS =，故③④正确；故答案为：C.【点睛】本题考查了矩形的性质、等边三角形的判定与性质、含30°角的直角三角形的性质以及三角形面积等知识；熟练掌握矩形的性质，证出OA ＝OD ＝OC 是解题的关键．6．（2021·西安市铁一中学九年级开学考试）如图，在平面直角坐标系xoy 中，()4,4P ，A 、B 分别是x 轴正半轴、y 轴正半轴上的动点，且ABO 的周长是8，则P 到直线AB 的距离是（ ）A ．4B ．3C ．2.5D ．2【答案】A【分析】 构造正方形DPCO ，将∵PA 'C 沿PA'折叠得到∵PA 'E ，再证明∵PB 'D ∵∵PB 'E ，得到''A B O 的周长等于8，于是∵A 'B'O 即∵ABO ，故可得到P 到直线AB 的距离为PE =4，即可求解．【详解】如图，∵()4,4P∵构造正方形DPCO ，边长等于4，故PD =PC =4将∵PA 'C 沿PA'折叠得到∵PA 'E ，延长A'E 交y 轴于点B'，∵PC =PE ，A 'C =A 'E ，∵PCA'=∵PEA'=90°，∵PD =PE又∵PDB'=∵PEB'=90°，PB'=PB'∵∵PB 'D ∵∵PB'E （HL ）∵B 'D =B'E∵''A B O 的周长等于A 'O +OB'+A 'B'=A'O +B'O +B'E +A'E = A 'O +B'O +B'D +A 'C =OC +DO =8故∵A 'B 'O 符合题意中的∵ABO ，∵P 到直线AB 的距离为PE =4故选A ．【点睛】此题主要考查正方形的判定与性质，解题的关键是根据题意构造正方形，利用全等三角形的性质求解．7．（2021·浦江县教育研究和教师培训中心）如图，在正方形ABCD 中，点E 、F 分别在边BC 、CD 上，AE BF ⊥，交点为G ，CH BF ⊥，交BF 于点H ．若CH HG =，1CFH S =△，那么正方形的面积为（ ）A ．15B ．20C ．22D ．24【答案】B【分析】 根据AE BF ⊥，利用同角的余角相等得出EAB FBC ∠=∠，再根据AAS 即可证出ABG BCH ≌△△，得BG CH =，设CH x =，算出BC ，设FH 为y ，分别在CFH △和CFB 中使用勾股定理得12y x =，再由1CFH S =△得2x =，即可求出正方形的面积．【详解】 解：四边形ABCD 是正方形，AB BC ∴=，90ABE BCF ∠=∠=︒， AE BF ⊥，90ABC ∠=︒，90BAE GBA ∴∠+∠=︒，90FBC GBA ∠+∠=︒，BAE CBF ∴∠=∠，CH BF ⊥，90BHC AGB ∴∠=︒=∠，在ABG 与BCH 中，BGA BHC BAE CBF AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()ABG BCH AAS ∴△≌△，BG CH ∴=，设CH x =，则HG BG x ==，2BH x ∴=，BC ∴，设FH 为y ，CH BF ⊥，在CFH △中，22222CF FH CH x y =+=+，在CFB 中，22222(2)5CF BF BC x y x =-=+-，2222(2)5x y x y x ∴+=+-， 解得：12y x =， ∴211124CFH S FH CH x =⋅==△，2x ∴=（舍负），∴正方形的面积为2220BC ==．故选：B ．【点睛】本题主要考查了正方形的性质、全等三角形的判定与性质、勾股定理，分别在CFH △和CFB 中使用勾股定理是本题的关键．8．（2021·四川绵阳市·中考真题）如图，在等腰直角ABC 中，90C ∠=︒，M 、N 分别为BC 、AC 上的点，50CNM ∠=︒，P 为MN 上的点，且12PC MN =，117BPC ∠=︒，则ABP ∠=（ ）A ．22︒B ．23︒C ．25︒D ．27︒【答案】A【分析】作辅助线，构建矩形，得P 是MN 的中点，则MP ＝NP ＝CP ，根据等腰三角形的性质和三角形外角的性质可解答．【详解】解：如图，过点M 作MG ∵BC 于M ，过点N 作NG ∵AC 于N ，连接CG 交MN 于H ，∵∵GMC＝∵ACB＝∵CNG＝90°，∵四边形CMGN是矩形，∵CH＝12CG＝12MN，∵PC＝12MN，存在两种情况：如图，CP＝CP1＝12MN，①P是MN中点时，∵MP＝NP＝CP，∵∵CNM＝∵PCN＝50°，∵PMN＝∵PCM＝90°−50°＝40°，∵∵CPM＝180°−40°−40°＝100°，∵∵ABC是等腰直角三角形，∵∵ABC＝45°，∵∵CPB＝117°，∵∵BPM＝117°−100°＝17°，∵∵PMC＝∵PBM＋∵BPM，∵∵PBM＝40°−17°＝23°，∵∵ABP ＝45°−23°＝22°．②CP 1＝12MN ，∵CP ＝CP 1，∵∵CPP 1＝∵CP 1P ＝80°，∵∵BP 1C ＝117°，∵∵BP 1M ＝117°−80°＝37°，∵∵MBP 1＝40°−37°＝3°，而图中∵MBP 1＞∵MBP ，所以此种情况不符合题意．故选：A ．【点睛】此题主要考查了等腰直角三角形的性质，矩形的性质和判定，等腰三角形的性质等知识，作出辅助线构建矩形CNGM 证明P 是MN 的中点是解本题的关键．9．（2021·四川绵阳市·中考真题）如图，在边长为3的正方形ABCD 中，30∠=︒CDE ，DE CF ⊥，则BF 的长是（ ）A ．1B C D ．2【答案】C【分析】 由正方形的性质得出DC CB =，90DCE CBF ∠=∠=︒，由ASA 证得DCE CBF △≌△，即可得出答案．【详解】 解：四边形ABCD 是正方形，90FBC DCE ∴∠=∠=︒，3CD BC ==，∵在Rt DCE 中，30∠=︒CDE ，12CE DE ∴=， 设CE x =，则2DE x =，根据勾股定理得：222DC CE DE +=，即2223(2)x x +=，解得：x =， 3CE ，DE CF ⊥，90DOC ∴∠=︒，60DCO ∴∠=︒，906030BCF CDE ∴∠=︒-︒=︒=∠，DCE CBF ∠=∠，CD BC =，()DCE CBF ASA ∴△≌△，BF CE ∴=故选：C ．【点睛】 本题考查了正方形的性质，全等三角形的判定与性质，勾股定理，含30角的直角三角形的性质等知识，证明DCE CBF △≌△是解题的关键．10．（2021·河南濮阳县·八年级期中）如图，AD 是ABC 的中线，过点A 作//AM BC ，在AM 上截取AE DC =，连接CE ，则下列命题中，假命题是（ ）A ．若AB AC =，则四边形ADCE 是矩形B ．若AD 平分BAC ∠，则四边形ADCE 是矩形C ．若ABC ∠与ACB ∠互余，则四边形ADCE 是菱形D ．若222AB BC AC +=，则四边形ADCE 是菱形【答案】D【分析】先推出四边形ADCE 是平行四边形，结合等腰三角形的性质，可得AD ∵BC ，进而即可判断A ；过点D 作DG ∵AB ，DH ∵AC ，推出ABC 是等腰三角形，进而可判断B ，根据直角三角形的性质，可判断C ；先推出ABC 是直角三角形且∵B =90°，进而判断D ．【详解】解：∵//AM CD ，AE DC =，∵四边形ADCE 是平行四边形，∵当AB AC =时，AD 是ABC 的中线，∵AD ∵BC ，即∵ADC =90°，∵四边形ADCE 是矩形，故A 是真命题；∵当AD 平分BAC ∠，过点D 作DG ∵AB ，DH ∵AC ，∵DG =DH ，∵AD 是ABC 的中线，∵BD =CD ，∵BDG CDH ≌（HL ），∵∵ABC =∵ACB ，∵ABC 是等腰三角形，∵AD ∵BC ，即：∵ADC =90°，∵平行四边形ADCE 是矩形，故B 是真命题；∵ABC ∠与ACB ∠互余，即ABC ∠+ACB ∠=90°，∵ABC 是直角三角形，∵AD 是ABC 的中线，∵AD =12BC =DC ，∵平行四边形ABCD 是菱形，故C 是真命题；∵当222AB BC AC +=时，∵ABC 是直角三角形且∵B =90°，∵AD 是ABC 的中线，∵AD ≠12BC =DC ，∵四边形ABCD 不是菱形，故D 是假命题【点睛】本题主要考查平行四边形的判定和性质，矩形，菱形的判定定理，直角三角形的性质，等腰三角形的性质，熟练掌握平行四边形的判定和性质，矩形，菱形的判定定理是解题的关键．11．（2021·诸暨市开放双语实验学校八年级期中）如图，正方形ABCD的面积为s，ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（）A B．C D．s【答案】A【分析】由于点B与D关于AC对称，所以连接BD，BE与AC的交点即为P点．此时PD+PE=BE最小，而BE是等边∵ABE的边，BE=AB，由正方形ABCD的面积为s，可求出AB的长，从而得出结果．【详解】解：连接BD，设BE与AC交于点F，连接PD∵点B与D关于AC对称，∵PD=PB，∵PD+PE=PB+PE=BE最小．∵正方形ABCD的面积为s，∵AB又∵∵ABE是等边三角形，∵BE=AB∵故选：A．此题主要考查了轴对称--最短路线问题，难点主要是确定点P 的位置．注意充分运用正方形的性质：正方形的对角线互相垂直平分．再根据对称性确定点P 的位置即可．要灵活运用对称性解决此类问题．二、填空题12．（2021·哈尔滨市第四十七中学八年级月考）ABCD 的对角线AC 、BD 相交于点O ，若5AB =，8AC =，6BD =，则DCO 的周长为________．【答案】12【分析】首先由勾股定理的逆定理证明∵AOB 为直角三角形，从而得到AC ∵BD ，然后根据对角线相互垂直的平行四边形是菱形判定进而解答即可．【详解】解：∵四边形ABCD 是平行四边形，且AC ＝8，BD ＝6，∵AO ＝4，BO ＝3，∵AB ＝5，∵AB 2＝AO 2＋BO 2．∵∵OAB 是直角三角形．∵AC ∵BD ．又∵四边形ABCD 为平行四边形，∵四边形ABCD 为菱形．∵∵DCO 的周长＝CD ＋OC ＋OD ＝5＋4＋3＝12，故答案为：12【点睛】 本题主要考查的是菱形的判定、平行四边形的性质等知识，掌握勾股定理的逆定理的应用、菱形的判定是解题的关键．13．（2021·哈尔滨德强学校八年级月考）在矩形ABCD 中，12AB =，7BC =，点E 在CD 边上，点F 在AB 边上，连接EF 、DF ，若3CE DE =，EF =DF 的长为_______．【分析】根据矩形的性质及勾股定理的应用对该问题进行分类讨论，分点E 在点G 的左边和点E 在点G 的右边讨论．【详解】解：如图所示，作FG DC ⊥于点G ，则90FGC ∠=︒，四边形ABCD 为矩形，12,90DC AB B C ∴==∠=∠=︒，∴四边形FGCB 为矩形，7FG BC ∴==， 5EF =1EG ∴==， 3CE DE =，1112344DE DC ∴==⨯=， 314DG DE EG ∴=+=+=，DF ∴==如图，作FG DC ⊥于点G ，则90FGC ∠=︒，四边形ABCD 为矩形，12,90DC AB B C ∴==∠=∠=︒，∴四边形FGCB 为矩形，7FG BC ∴==， 5EF =1EG ∴==， 3CE DE =，1112344DE DC ∴==⨯=， 312DG DE EG ∴=-=-=，DF ∴【点睛】本题考查了矩形的性质、勾股定理的应用，解题的关键是掌握相关的性质定理，利用分类讨论的思想进行求解．14．（2021·哈尔滨德强学校八年级月考）如图，四边形ABCD 是正方形，以CD 为边向外作等边CDE △，BE 与AC 相交于点M ，则AMB ∠的度数是________°．【答案】60【分析】易得ABM ∆与ADM ∆全等，AMD AMB ∠=∠，因此只要求出15CBE ∠=︒的度数即可．【详解】解：连接DM ，四边形ABCD 是正方形．AB AD ∴=，BAM DAM ∠=∠．又AM=AMABM ∴∆与ADM ∆全等．AMD AMB ∴∠=∠．CB CE =，CBE CEB ∴∠=∠．9060150BCE BCD DCE ∠=∠+∠=︒+︒=︒，15CBE ∴∠=︒．45ACB =︒∠，60AMB ACB CBE ∴∠=∠+∠=︒．故答案为：60．【点睛】此题考查正方形的性质，三角形的外角的性质、三角形全等，解题的关键是熟练掌握正方形及等边三角形的性质，会运用其性质进行一些简单的转化．15．（2021·江苏姑苏区·苏州市振华中学校）如图，矩形ABCD 中，2AC AB =，将矩形ABCD 绕点A 旋转得到矩形AB C D '''，使点B 的对应点B '落在AC 上，在'B C '上取点F ，使'B F AB =．则'FBB ∠的度数为_________°．【答案】15【分析】连接BB '，根据矩形的性质及旋转的性质得到90ABC AB C ''∠=∠=︒，AB AB '=，由已知条件及直角三角形的性质得到BB AB B C AB '''===，可证ABB '是等边三角形，再由已知证明B F BB ''=，最后由等腰三角形的性质求解即可．【详解】如图，连接BB '，∵四边形ABCD 是矩形，∵∵ABC =90°，由旋转的性质可知：90ABC AB C ''∠=∠=︒，AB AB '=，∵AC =2AB ，∵2AC AB AB B C '''==+，∵AB B C ''=，∵∵ABC =90°，∵BB AB B C AB '''===，∵ABB '是等边三角形，∵60AB B '∠=︒，∵150BB F '∠=︒，∵B F AB '=，∵B F BB ''=，∵15B BF B FB ''∠=∠=︒．故答案为：15．【点睛】本题考查了矩形的性质，旋转的性质，等边三角形的判定和性质，等腰三角形的判定与性质，熟练运用各性质及判定定理进行推理是解题的关键．16．（2021·重庆实验外国语学校）如图，在矩形ABCD 中，点E 是线段AB 上的一点，AE AB <，DE CE ⊥，将BCE 沿CE 翻折，得到FCE △，连接DF ，若3AD =，10AB =，则线段DF 的长度为______．【分析】过点F 作FH CD ⊥，根据矩形和折叠的性质得到FEC BEC GCE ∠=∠=∠，从而得到G 为CD 的中点，求得EG 、FG 的长度，勾股定理求得GC ，等面积法求得FH ，勾股定理即可求得DF ．【详解】解：过点F 作FH CD ⊥，如下图：在矩形ABCD 中，10CD AB ==，3AD BC ==，//CD AB ，90B ∠=︒ ∵BEC GCE ∠=∠由折叠的性质可得：3CF BC ==，FEC BEC ∠=∠，90GFC B ∠=∠=︒ ∵FEC BEC GCE ∠=∠=∠∵=EG CG又∵DE CE ⊥∵90DEC ∠=︒∵90,90GEC DEG GDE DCE ∠+∠=︒∠+∠=︒∵GDE DEG ∠=∠ ∵152DG GE GC CD ====，即G 为CD 的中点在Rt GFC 中，由勾股定理得4FG = 1122GFC S FC FG GC FH =⨯=⨯△得125FC FG FH GC ⨯==由勾股定理得165GH =415DH DG GH =+=由勾股定理得DF【点睛】此题考查了矩形的性质，折叠的性质，直角三角形的性质，勾股定理，等腰三角形的性质，熟练掌握相关基本性质是解题的关键．17．（2021·哈尔滨市虹桥初级中学校八年级期中）如图，在正方形ABCD 中，E 为BC 边上一点，AF AE ⊥交CD 延长线于点F ，2BE =，EFD BAE ∠=∠，则BG =_________．【答案】2+【分析】先证明∵EAF 是等腰直角三角形，过点E 作EH ∵BC 于点E ，交BD 于点H ，证明∵AEH =∵HEG =12∵AEF =22.5°，得到EG =HG =BE =2，即可求解．【详解】解：∵正方形ABCD 中，AF ∵AE ，∵∵BAD =∵EAF =90°，AB =AD ，∵∵BAE+∵EAD =∵DAF+∵EAD =90°，∵∵BAE =∵DAF ，又∵∵ABE =∵ADF =90°，∵∵BAE ∵∵DAF (ASA )，∵AE =AF ，∵∵EAF 是等腰直角三角形，∵∵AEF =∵AFE =45°，过点E 作EH ∵BC 于点E ，交BD 于点H ，如图：∵四边形ABCD 是正方形，∵∵HBE =45°，∵∵HBE 是等腰直角三角形，且BE =EG =2，∵HB BE∵EH ∵BC ，∵EFD =∵BAE ，∵∵FEC =∵AEB ，∵∵AEH =∵HEG =12∵AEF =22.5°，∵∵BHE =∵HEG +∵HGE =45°，∵∵HEG =∵HGE =22.5°，∵HG =HE =BE =2，∵BG故答案为：【点睛】本题考查了正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识，解题的关键是证明∵AEH =∵HEG =12∵AEF =22.5°．18．（2021·苏州高新区实验初级中学八年级月考）如图，在Rt ABC △中，90BAC ∠=︒，5AB =，12AC =，P 为边BC 上一动点（P 不与B 、C 重合），PE AB ⊥于E ，PF AC ⊥于F ，M 为EF 中点，则AM 的取值范围是______．【答案】30613AM < 【分析】首先连接AP ，由在Rt ABC ∆中，90BAC ∠=︒，PE AB ⊥于E ，PF AC ⊥于F ，可证得四边形AEPF 是矩形，即可得AP EF =，即2=AP AM ，然后由当⊥AP BC 时，AP 最小，可求得AM 的最小值，又由AP AC <，即可求得AM 的取值范围．【详解】解：连接AP ，PE AB ⊥，PF AC ⊥，90AEP AFP ∴∠=∠=︒，90BAC ∠=︒，∴四边形AEPF 是矩形，AP EF ∴=，90BAC ∠=︒，M 为EF 中点，1122AM EF AP ∴==， 在Rt ABC ∆中，90BAC ∠=︒，5AB =，12AC =，13BC ∴=，当⊥AP BC 时，AP 值最小， 此时115121322BAC S AP ∆=⨯⨯=⨯⨯，6013AP ∴=， 即AP 的范围是6013AP， 60213AM ∴， AM ∴的范围是3013AM ，AP AC <，即12AP <，6AM ∴<， ∴30613AM <． 故答案为：30613AM <． 【点睛】此题考查了矩形的判定与性质、勾股定理以及直角三角形的面积问题．注意掌握辅助线的作法，注意当⊥AP BC 时，AP 最小，且AP AC <．三、解答题19．（2021·吉林德惠市·七年级期末）如图，点E 是正方形ABCD 的边AB 上一点，4AB =， 1.5AE =，DAE △逆时针旋转后能够与DCF 重合．（1）旋转中心是哪一点，旋转角为多少度？（2）请你判断DFE △的形状，并说明理由；（3）求四边形ABFD 的面积．【答案】（1）点D ，90°；（2）等腰直角三角形，理由见解析；（3）19【分析】（1）依据DAE △逆时针旋转后能够与DCF 重合，即可得到旋转中心以及旋转角的度数；（2）根据旋转可得DE DF =，90EDF ADC ∠=∠=︒，即可得到DFE △是等腰直角三角形； （3）根据旋转的性质可得ADE CDF ≌，再由CDF ABCD ABFD S S S =+△正方形四边形即可得到答案．【详解】解：（1）DAE △旋转后能与DCF 重合，∴旋转中心是点D ，四边形ABCD 是正方形，90ADC ∴∠=︒，∴旋转角为90︒；（2）DFE △是等腰直角三角形．理由如下：根据旋转可得DE DF =，90EDF ADC ∠=∠=︒，所以DFE △是等腰直角三角形．（3）四边形ABCD 是正方形，90A BCD ∴∠=∠=︒，4AD AB ==，4416ABCD S =⨯=正方形，根据旋转可得：ADE CDF ≌，90DCF DAE ∴∠=∠=︒，180DCF BCD ∴∠+∠=︒，114 1.5322CDF ADE S S AD AE ∴==⋅=⨯⨯=△△， 16319CDF ABCD ABFD S S S ∴=+=+=△正方形四边形．【点睛】本题是四边形综合题，主要考查了旋转的性质，正方形的性质，等腰直角三角形的判定，掌握“旋转不改变图形的形状与大小，只改变图形的位置，旋转前后两个图形全等”是解题的关键．20．（2021·海南海口市·）如图1，在正方形ABCD 中，点P 是线段BC 上一个动点（与点B 、C 不重合），将线段AP 绕着点P 顺时针旋转90°得到线段PE ，连接DE ，过点D 作//DF EP ，交AB 于点F ，交AP 于点G ，连接FP ．（1）求证：①ABP DAF ≅△△；②四边形PEDF 是平行四边形；（2）如图2，点M 是BC 延长线上一点，当点P 在线段BC 上运动时，求证：点E 始终在DCM ∠的角平分线上．【答案】（1）①见解析；②见解析；（2）点E 始终在DCM ∠的角平分线上，见解析．【分析】（1）由正方形的性质得出AB DA =，90B DAF ∠=∠=︒，推出//DF EP ，证得BAP ADF ∠=∠，根据ASA 即可证得答案；（2）由全等三角形的性质可得AP DF =，等量代换可得DF PE =，再根据平行四边形的判定定理即可证得答案；（3）过点E 作EH DC ⊥于点H ，EI BM ⊥于点I ，先证明四边形CIEH 是矩形，根据AAS 证ABP PIE ≅，得到AB PI =，BP IE =，再通过证四边形CIEH 是正方形．即可证得答案．【详解】（1）①证明：∵四边形ABCD 是正方形，∵AB DA =，90B DAF ∠=∠=︒．∵90APE ∠=︒，//DF EP ，∵90AGD ∠=︒，∵ADF DAP BAP DAP ∠+∠=∠+∠，∵BAP ADF ∠=∠，∵()ASA ABP DAF ≅．②由ABP DAF ≅△△，可知AP DF =．∵AP PE =，∵DF PE =．∵//DF EP ，∵四边形PEDF 是平行四边形．（2）如图，过点E 作EH DC ⊥于点H ，EI BM ⊥于点I ，则90EHC CIE ∠=∠=︒，∵90HCI ∠=︒，∵四边形CIEH 是矩形．∵90APE ∠=︒，∵90APB EPI ∠+∠=︒，∵90PEI EPI ∠+∠=︒，∵APB PEI ∠=∠．∵90B PIE ∠=∠=︒，AP PE =，∵()AAS ABP PIE ≅．∵AB PI =，BP IE =．∵AB BC =，∵BC PI =，即BP PC CI PC +=+，∵BP CI =，∵IE CI =，∵四边形CIEH 是正方形．∵点E 始终在DCM ∠的角平分线上．【点睛】本题考查了四边形的综合题：熟练掌握三角形全等的判定和性质，正方形的判定与性质以及平行四边形、矩形的判定是解题的关键．21．（2021·新余市第一中学九年级）如图，在正方形ABCD 中，点E 、F 分别在边BC 和CD 上，且BE CF =，连接AE 、BF ，其相交于点G ，将BCF △沿BF 翻折得到BC F '△，延长FC '交BA 延长线于点H ．（1）求证：AE BF =；（2）若3AB =，2EC BE =，求BH 的长．【答案】（1）见解析；（2）5．【分析】（1）根据正方形的性质得到BA BC =，90ABC BCD ∠=∠=︒，利用SAS 定理证明ABE BCF △△≌，根据全等三角形的性质证明结论；（2）根据折叠的性质得到C BF CBF ∠'=∠，90BC F BCF ∠'=∠=︒，证明HB HF =，根据勾股定理列式计算即可．【详解】（1）证明：四边形ABCD 是正方形，BA BC ∴=，90ABC BCD ∠=∠=︒，在ABE △和BCF △中，AB BC ABE BCF BE CF =⎧⎪∠=∠⎨⎪=⎩，()ABE BCF SAS ∴△≌△，AE BF ∴=；（2）解：3BC AB ==，2EC BE =，2EC ∴=，1BE =，1C F CF ∴'==，由折叠的性质可知，C BF CBF ∠'=∠，90BC F BCF ∠'=∠=︒，90C FB C BF ∠'+∠'=︒，90HBF FBC ∠+∠=︒，C FB HBF ∴∠'=∠，HB HF ∴=，312HC HF C F HB C F AH AH ∴'=-'=-'=+-=+，在Rt HBC '△中，222HB C B C H ='+'，即222(3)3(2)AH AH +=++，解得：2AH =，5BH AH AB ∴=+=．【点睛】本题考查的是正方形的性质、全等三角形的判定和性质、折叠的性质、勾股定理的应用，掌握全等三角形的判定定理和性质定理、正方形的性质定理是解题的关键．22．（湖北省黄冈市2020-2021学年八年级下学期期末数学试题）我们给出如下定义：顺次连接任意一个四边形各边中所得的四边形叫中点四边形．（1）如图1，在四边形ABCD 中，点E ，F ，G ，H 分别为边AB ，BC ，CD ，DA 的中点，中点四边形EFGH 是 ．（2）如图2，点P 是四边形ABCD 内一点，且满足PA ＝PB ，PC ＝PD ，⊥APB ＝⊥CPD ，点E ，F ，G ，H 分别为边AB ，BC ，CD ，DA 的中点．猜想中点四边形EFGH 的形状，并证明你的猜想．（3）若改变（2）中的条件，使⊥APB ＝⊥CPD ＝90°，其他条件不变，直接写出中点四边形EFGH 的形状（不必证明）．【答案】（1）平行四边形；（2）菱形，见解析；（3）正方形【分析】（1）连接BD ，根据三角形中位线定理证明EH ∵FG ，EH =FG ，根据平行四边形的判定定理证明即可；（2）证明∵APC∵∵BPD，根据全等三角形的性质得到AC=BD，再证明EF=FG，根据菱形的判定定理证明结论；（3）证明∵EHG=90°，利用∵APC∵∵BPD，得到∵ACP=∵BDP，即可证明∵COD=∵CPD=90°，再根据平行线的性质证明∵EHG=90°，根据正方形的判定定理证明即可．【详解】解：（1）如图1，连接BD，∵点E，H分别为边AB，DA的中点，∵EH∵BD，EH=12 BD，∵点F，G分别为边BC，CD的中点，∵FG∵BD，FG=12 BD，∵EH∵FG，EH=GF，∵中点四边形EFGH是平行四边形，故答案为：平行四边形；（2）结论：四边形EFGH是菱形，理由：如图2，连接AC，BD．∵∵APB=∵CPD，∵∵APB+∵APD=∵CPD+∵APD，即∵APC=∵BPD，在∵APC和∵BPD中，AP BP APC BPD PC PD =⎧⎪∠=∠⎨⎪=⎩，∵∵APC ∵∵BPD （SAS ），∵AC =BD ，∵点E ，F ，G 分别为边AB ，BC ，CD 的中点，∵EF =12AC ，FG =12BD ， ∵EF =FG ，由（1）知中点四边形EFGH 是平行四边形，∵平行四边形EFGH 是菱形；（3）结论：四边形EFGH 是正方形，理由：如图2，设AC 与BD 交于点O ．AC 与PD 交于点M ，∵∵APC ∵∵BPD ，∵∵ACP =∵BDP ，∵∵DMO =∵CMP ，∵∵COD =∵CPD =90°，∵EH ∵BD ，AC ∵HG ，∵∵EHG =∵DOC =90°，由（2）知中点四边形EFGH 是菱形，∵菱形EFGH 是正方形．【点睛】本题考查的是平行四边形的判定和性质、全等三角形的判定和性质、菱形的判定和性质、正方形的判定和性质，解题的关键是灵活应用三角形中位线定理，学会添加常用辅助线． 23．（2021·吉林梅河口市·八年级期末）如图，在矩形ABCD 中，E 是边AD 上的点，ABE △沿BE 折叠，点A 的对应点为点G ．（1）如图1，当点G 恰好在BC 边上时，四边形ABGE 的形状是_______；（2）如图2，当E是AD的中点，G在矩形ABCD内部时，延长BG交DC边于点F．①求证：BF AB DF=+；②若AD=，试探索线段DF与FC的数量关系．【答案】（1）正方形；（2）①见解析；②CF=DF，理由见解析【分析】（1）先根据有三个角是直角得四边形ABGE是矩形，根据折叠的性质和矩形的性质可以得到AE=BG=AB，从而得四边形ABGE是正方形；（2）①连接EF，在矩形ABCD中，AB＝CD，AD＝BC，∵A＝∵C＝∵D＝90°，由∵ABE沿BE折叠得到∵GBE，可得BG＝AB，EG＝AE＝ED，∵A＝∵BGE＝90°，进而可证∵EGF∵∵EDF，由此求解即可；②设AB＝DC＝a，则DF＝b，在Rt∵BCF中，由勾股定理可得4ab＝2a²，进而可得2=，CD DF =．则DF FC【详解】解：（1）正方形，理由如下：∵四边形ABCD是矩形，∵∵A＝∵ABC＝90°，由折叠得：∵BGE＝∵A＝90°，∵ABE＝∵EBG＝45°，AB=BG∵四边形ABGE是矩形，∵AE=BG=AB，∵矩形ABGE是正方形；故答案为：正方形；（2）①证明：如图，连接EF，在矩形ABCD 中，AB ＝CD ，AD ＝BC ，∵A ＝∵C ＝∵D ＝90°，∵E 是AD 的中点，∵ AE ＝ DE ，∵∵ABE 沿BE 折叠得到∵GBE ，∵BG ＝ AB ， EG ＝ AE ＝ ED ，∵A ＝∵BGE ＝90°，∵∵EGF ＝∵D ＝90°，在Rt ∵EGF 和Rt ∵EDF 中，∵EG ＝ED ，EF ＝EF ，∵∵EGF ∵∵EDF （HL ）∵GF =DF ，∵BF =BG +GF =AB +DF ；②DF FC =，理由如下设AB ＝DC ＝a ，DF ＝b ，∵AD ＝BC ，由①得：BF ＝AB ＋DF ，∵BF ＝a ＋b ，CF ＝a -b ，在Rt ∵BCF 中，由勾股定理得：222BC B F F C =+，∵())()222a b a b +=+-，∵4ab ＝2a ²，∵a ≠0，∵2b ＝a ，∵2DF=CD ，∵CF CD DF DF =-=．【点睛】此题属于四边形综合题，涉及的知识有：矩形的性质与判定，折叠的性质，正方形的判定，全等三角形的判定与性质，勾股定理，熟练掌握判定与性质是解本题的关键．1．如图，正方形ABCD 中，2AB =，E 为BC 中点，两个动点M 和N 分别在边CD 和AD 上运动，且1MN =，若ABE △与以D 、M 、N 为顶点的三角形相似，则DM =（ ）A ．13BC ．13或23D 【答案】D【分析】根据条件求出AE ，再根据相似三角形的性质求解即可；【详解】∵E 为BC 中点，∵1BE =．由勾股定理得，AE =当ABE MDN ∽时，AB AE DM MN =，即21DM =，解得5DM =；∽时，DM=同理，当ABE NDM∵DM．故选D．【点睛】本题主要考查了相似三角形的判定与性质、勾股定理、正方形的性质，准确计算是解题的关键．2．如图，正方形ABCD的边长为4cm，点E是边AD的中点，P为对角线BD上一动点，则+的最小值为（）AP PEA B．C．D．【答案】B【分析】连接EC，PC，由AP＋PE＝PC＋PE≥EC得EC就是AP＋PE的最小值，求出EC即可．【详解】解：如图，连接EC，PC，∵AP＋PE＝PC＋PE≥EC，∵EC就是AP＋PE的最小值，∵正方形ABCD的边长为4cm，点E是边AD的中点，∵CD＝4cm，ED＝2cm，∵CE＝2225+=，ED CD cm∵AP＋PE的最小值是25cm．故选：B．【点睛】本题考查正方形的性质、最短路径问题，解决此题的关键是将AP＋PE转化为PC＋PE．3．如图是将正方形ABCD 和正方形CEFG 拼在一起的图形，点B ，C ，E 在同一条直线上，连结BD ，BF ．若阴影部分BDF ∆的面积为8，则正方形ABCD 的边长为（ ）A ．2B ．3C ．4D ．6【答案】C【分析】 连接CF ，根据题意可得DB //CF ，再利用平行线之间的距离都相等可得：S ∵BDF =S ∵BDC =8，进而可得出边长．【详解】如图，连接CF ，∵四边形ABCD 和四边形CGFE 都是正方形，∵∵BDC =45°，∵GCF =45°，∵∵BDC =∵GCF ，∵BD ∵CF ，∵S ∵BDF =S ∵BCD =8，∵S ∵BDF =BC ×BC ÷2=8．∵BC =4，故选：C ．【点睛】本题考查了正方形的性质、平行线、等腰三角形的性质，三角形面积公式等知识，能根据平行线之间的距离相等进而得出三角形面积相等是解题的关键．4．如图，在矩形AOBC 中，()()4,0,0,2A B -，若正比例函数y kx =的图象经过点C ，则k 的值为（ ）A．2-B．12-C．52D．5【答案】B【分析】根据矩形的性质得出点C的坐标，再将点C坐标代入解析式求解可得．【详解】解：∵A（−4，0），B（0，2）．∵OA＝4、OB＝2，∵四边形AOBC是矩形，∵AC＝OB＝2、BC＝OA＝4，则点C的坐标为（−4，2），将点C（−4，2）代入y＝kx，得：2＝−4k，解得：k＝12 -，故选：B．【点睛】本题主要考查一次函数图象上点的坐标特征，解题的关键是掌握矩形的性质和待定系数法求函数解析式．5．在正方形ABCD中，AD＝6，点M在边DC上，连接AM，⊥ADM沿直线AM翻折后点D 落到点N，过点N作NE⊥CD，垂足为点E．如图，如果ED＝2EC，则DM＝（）A．B．C．9﹣D．6﹣【答案】C【分析】过点N 作NH ∵AD 于H ，先证明四边形NEDH 为矩形，得到HD =NE ，NH =DE ，根据ED =2EC ，ED +EC =CD =6，可以得到ED =HN =4，再利用勾股定理求出AH ，即可得到NE 的值，最后再直角三角形MNE 中用勾股定理求解即可.【详解】解：如图所示，过点N 作NH ∵AD 于H ，∵四边形ABCD 是正方形，AD =6∵AD =CD =6，∵D =90°，∵NE ∵CD ，NH ∵AD ，∵∵NED =∵NHD =∵NHA =90°，∵四边形NEDH 为矩形，∵HD =NE ，NH =DE ，∵ED =2EC ，ED +EC =CD =6，∵ED =HN =4，由翻折的性质可得AD =AN =6，DM =MN∵AH ==∵6NE DH ==-设DM =MN =x ，则ME =4-x ,则222MN NE ME =+,∵(()22264x x =-+-， 解得9x =-∵9DM =-故选C.【点睛】本题主要考查了矩形的性质与判定，正方形的性质，折叠的性质，勾股定理，解题的关键在于能够熟练掌握相关知识进行求解.6．在正方形ABCD 中，90AEB CFD ∠=∠=︒，3AE CF ==，8BE DF ==，则点E 、F 之间的距离是（ ）A．B．C ．5 D ．6【答案】A【分析】 由正方形的性质得出90BAD ABC BCD ADC ∠=∠=∠=∠=︒，AB BC CD AD ===，由SSS 证明ABE CDF ∆≅∆，得出ABE CDF ∠=∠，证出ABE DAG CDF BCH ∠=∠=∠=∠，由AAS 证明ABE ADG ∆≅∆，得出AE DG =，BE AG =，同理：3AE DG CF BH ====，8BE AG DF CH ====，得出EG GF FH EF ===，证出四边形EGFH 是正方形，即可得出结果．【详解】解：如图所示：四边形ABCD 是正方形，90BAD ABC BCD ADC ∴∠=∠=∠=∠=︒，AB BC CD AD ===，90BAE DAG ∴∠+∠=︒，在ABE ∆和CDF ∆中，AB CD AE CF BE DF =⎧⎪=⎨⎪=⎩， ()ABE CDF SSS ∴∆≅∆，ABE CDF ∴∠=∠，90AEB CFD ∠=∠=︒，90ABE BAE ∴∠+∠=︒，ABE DAG CDF ∴∠=∠=∠，同理：ABE DAG CDF BCH ∠=∠=∠=∠，90DAG ADG CDF ADG ∴∠+∠=∠+∠=︒，即90DGA ∠=︒，同理：90CHB ∠=︒，在ABE ∆和ADG ∆中，90ABE DAG AEB DGA AB DA ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ()ABE ADG AAS ∴∆≅∆，AE DG ∴=，BE AG =，同理：3AE DG CF BH ====，8BE AG DF CH ====，835EG GF FH EF ∴====-=，1809090GEH ∠=︒-︒=︒，∴四边形EGFH 是正方形，EF ∴=故选：A ．【点评】本题考查了正方形的判定与性质、全等三角形的判定与性质；解题的关键是熟练掌握正方形的判定与性质，证明三角形全等．7．如图，矩形ABCD 中，AE BD ⊥垂足为E ，若4DAE BAE ∠=∠，则EAC ∠的度数为（ ）A ．54°B ．45°C ．36°D ．18°【答案】A【分析】 由矩形的性质和已知条件得出OA =OB ，∵OAB =∵OBA ，∵BAE =15∵BAD =18°，再求出∵OAB ，即可得出∵EAC 的度数．【详解】解：∵四边形ABCD 是矩形，∵∵BAD =90°，OA =12AC ，OB =12BD ，AC =BD ，。

特殊平行四边形（易错必刷36题8种题型专项训练）➢直角三角形斜边上的中线有理数➢菱形的性质➢矩形的性质➢矩形的判定➢矩形的判定与性质➢正方形的性质➢正方形的判定➢轴对称-最短路线问题一．直角三角形斜边上的中线（共1小题）1．已知：如图，在四边形ABCD 中，∠BCD ＝∠BAD ＝90°，E ，F 分别是对角线BD ，AC 的中点．（1）请判断线段EF 与AC 的位置关系，并说明理由；（2）若∠ADC ＝45°，请判断EF 与AC 的数量关系，并说明理由．【答案】（1）EF ⊥AC ，理由见解答；（2）EF ＝AC ，理由见解答．【解答】解：（1）EF ⊥AC ，理由：连接AE ，EC，∵∠BCD＝90°，点E是BD的中点，∴CE＝BD，∵∠BAD＝90°，点E是BD的中点，∴AE＝BD，∴AE＝CE，∵点F是AC的中点，∴EF⊥AC；（2）EF＝AC，理由：∵∠BCD＝90°，点E是BD的中点，∴CE＝DE＝BD，∴∠ECD＝∠CDE，∵∠BAD＝90°，点E是BD的中点，∴AE＝DE＝BD，∴∠EAD＝∠ADE，∵∠ADC＝45°，∴∠AEC＝∠AEB+∠BEC＝∠EAD+∠ADE+∠ECD+∠EDC＝2∠ADE+2∠CDE＝2（∠ADE+∠CDE）＝2∠ADC＝90°，∵点F是AC的中点，∴EF＝AC．二．菱形的性质（共3小题）2．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA＝10，S＝100，则OH的长为（ ）菱形ABCDA．B．10C．5D．【答案】C【解答】解：∵四边形ABCD是菱形，∴AC＝2AO＝20，＝×AC×BD＝20×BD＝100，又∵S菱形ABCD∴BD＝10，∵DH⊥AB，∴在Rt△BHD中，点O是BD的中点，∴OH＝BD＝10＝5．故选：C．3．如图，边长为1的菱形ABCD中，∠DAB＝60°，连接对角线AC，以AC为边作第二个菱形ACC1D1，使∠D1AC＝60°；连接AC1，再以AC1为边作第三个菱形AC1C2D2，使∠D2AC1＝60°，…，按此规律所作的第2023A．B．C．D．【答案】B【解答】解：连接BD，交AC于点O，∵四边形ABCD是菱形，∴∠AOB＝90°，OB＝BD，OA＝AC，DA＝AB＝1，∵∠DAB＝60°，∴△ADB是等边三角形，∴BD＝AB＝AD＝1，∴OB＝BD＝，∴AO＝＝＝，∴AC＝2AO＝，同理可得：AC1＝3，∴第1个菱形的边长＝1＝（）0，第2个菱形的边长＝＝（1，第3个菱形的边长＝3＝（）2，…∴第2023个菱形的边长＝（）2022，故选：B．4．如图，菱形ABCD中，∠A＝60°，边AB＝8，E为边DA的中点，P为边CD上的一点，连接PE、PB，当PE＝EB时，线段PE的长为 ．【答案】4．【解答】解：连接BD，∵四边形ABCD是菱形，∴AB＝AD＝8，且∠A＝60°，∴△ABD是等边三角形，且点E是AD的中点，∴BE⊥AD，且∠A＝60°，∴AE＝4，BE＝AE＝4，∴PE＝BE＝4．故答案为：4．三．矩形的性质（共10小题）5．如图，矩形ABCD的对角线AC，BD交于点O，AB＝6，BC＝8，过点O作OE⊥AC，交AD于点E，过点E作EF⊥BD，垂足为F，则OE+EF的值为（ ）A．B．C．D．【答案】C【解答】解：∵AB＝6，BC＝8，∴矩形ABCD的面积为48，AC＝＝10，∴AO＝DO＝AC＝5，∵对角线AC，BD交于点O，∴△AOD的面积为12，∵EO⊥AO，EF⊥DO，∴S△AOD ＝S△AOE+S△DOE，即12＝AO×EO+DO×EF，∴12＝×5×EO+×5×EF，∴5（EO+EF）＝24，∴EO+EF＝，故选：C．6．定义：如果一个三角形有一边上的中线等于这条边的一半，那么称三角形为“智慧三角形”．如图，在平面直角坐标系xOy中，矩形OABC的边OA＝3，OC＝4，点M（2，0），在边AB存在点P，使得△CMP 为“智慧三角形”，则点P的坐标为（ ）A．（3，1）或（3，3）B．（3，）或（3，3）C．（3，）或（3，1）D．（3，）或（3，1）或（3，3）【答案】D【解答】解：由题意可知，“智慧三角形”是直角三角形，∠CPM＝90°或∠CMP＝90°，∴设P（3，a），则AP＝a，BP＝4﹣a；①若∠CPM＝90°，在Rt△BCP中，由勾股定理得：CP2＝BP2+BC2＝（4﹣a）2+9，在Rt△MPA中，由勾股定理得：MP2＝MA2+AP2＝1+a2，在Rt△MPC中，由勾股定理得：CM2＝MP2+CP2＝1+a2+（4﹣a）2+9＝2a2﹣8a+26，又∵CM2＝OM2+OC2＝4+16＝20，∴2a2﹣8a+26＝20，∴（a﹣3）（a﹣1）＝0，解得：a＝3或a＝1，∴P（3，3）或（3，1）；②若∠CMP＝90°，在Rt△BCP中，由勾股定理得：CP2＝BP2+BC2＝（4﹣a）2+9，在Rt△MPA中，由勾股定理得：MP2＝MA2+AP2＝1+a2，∵CM2＝OM2+OC2＝20，在Rt△MCP中，由勾股定理得：CM2+MP2＝CP2，∴20+1+a2＝（4﹣a）2+9，解得：a＝．∴P（3，）．综上，P（3，）或（3，1）或（3，3）．故选：D．7．如图，∠MON＝90°，矩形ABCD在∠MON的内部，顶点A，B分别在射线OM，ON上，AB＝4，BC ＝2，则点D到点O的最大距离是（ ）A．2﹣2B．2+2C．2﹣2D．【答案】B【解答】解：取AB中点E，连接OE、DE、OD，∵∠MON＝90°，∴OE＝AB＝2．在Rt△DAE中，利用勾股定理可得DE＝2．在△ODE中，根据三角形三边关系可知DE+OE＞OD，∴当O、E、D三点共线时，OD最大为OE+DE＝2+2．故选：B．8．如图，矩形ABCD中，AB＝6，AD＝8，且有一点P从B点沿着BD往D点移动，若过P点作AB的垂线交AB于E点，过P点作AD的垂线交AD于F点，则EF的长度最小为多少（ ）A．B．C．5D．7【答案】B【解答】解：如图，连接AP、EF，∵PE⊥AB，PF⊥AD，∴∠AEP＝∠AFP＝90°．∵四边形ABCD是矩形，∴∠BAD＝90°．∴四边形AEPF为矩形．∴AP＝EF．∴要求EF的最小值就是要求AP的最小值．∵点P从B点沿着BD往D点移动，∴当AP⊥BD时，AP取最小值．下面求此时AP的值，在Rt△BAD中，∵∠BAD＝90°，AB＝6，AD＝8，∴BD＝＝＝＝10．∵S＝＝，△ABD∴AP＝＝＝．∴EF的长度最小为：．故本题选B．9．如图，矩形ABCD中，AD＝18，AB＝24．点E为边DC上的一个动点，△AD'E与△ADE关于直线AE 对称，当△CD'E为直角三角形时，DE的长为　9或18　．【答案】9或18．【解答】解：（1）当∠CED′＝90°时，如图（1），∵∠CED′＝90°，根据轴对称的性质得∠AED＝∠AED′＝×90°＝45°，∵∠D＝90°，∴△ADE是等腰直角三角形，∴DE＝AD＝18；（2）当∠ED′A＝90°时，如图（2），根据轴对称的性质得∠AD′E＝∠D＝90°，AD′＝AD，DE＝D′E，△CD'E为直角三角形，即∠CD′E＝90°，∴∠AD′E+∠CD′E＝180°，∴A、D′、C在同一直线上，根据勾股定理得AC＝＝30，∴CD′＝30﹣18＝12，设DE＝D′E＝x，则EC＝CD﹣DE＝24﹣x，在Rt△D′EC中，D′E2+D′C2＝EC2，即x2+144＝（24﹣x）2，解得x＝9，即DE＝9；综上所述：DE的长为9或18；故答案为：9或18．10．如图，将矩形ABCD沿直线EF对折，点D恰好与BC边上的点H重合，∠GFP＝62°，那么∠EHF 的度数等于 °．【答案】见试题解答内容【解答】解：∵矩形ABCD沿直线EF对折，点D恰好与BC边上的点H重合，∴∠CFP＝∠GFP，HE∥GF∴∠CFG＝2∠GFP＝124°，∴∠HFG＝180°﹣∠CFG＝56°，∴∠EHF＝∠HFG＝56°．故答案为56．11．如图，在矩形AOBC中，点A的坐标是（﹣2，1），点C的纵坐标是4，则B点的纵坐标是 ．【答案】见试题解答内容【解答】解：如图，过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，过点C作CF∥y轴，过点A作AF∥x轴，交点为F，则AF⊥CF，延长CA交x轴于点H，∵四边形AOBC是矩形，∴OB＝AC，AC∥OB，∴∠CAF＝∠CHO＝∠BOE，∵∠AFC＝∠OEB＝90°，∴△AFC≌△OEB（AAS），∴CF＝BE＝4﹣1＝3，故答案为：3．12．如图，在长方形ABCD中，，AD＝4，E，F分别为AD，BC上的两个动点，且∠EFC＝60°，连接AF、CE，那么AF+CE的最小值为 ．【答案】．【解答】解：如图，过点E作EH⊥BC于点H，则四边形ABHE是矩形，∴EH＝AB＝．∵∠EHF＝90°，∠EFH＝60°，∴∠FEH＝30°．∴EF＝2FH．∴FH＝1，EF＝2．设BF＝x，则CH＝4﹣x﹣1＝3﹣x，∴AF+EC＝+．欲求AF+EC的最小值，相当于在x轴上寻找一点P（x，0），使得P到M（0，），N（3，）的距离和最小（如图1中），作点M关于x轴的对称点F，连接FN，∵F（0，﹣），N（3，），∴直线FN的解析式为y＝x﹣．令y＝0，可得x＝，∴x＝时，PM+PN的值最小，此时NF＝AF+EC＝．故答案为：．13．如图，A，B，C，D为矩形的四个顶点，AB＝4cm，AD＝2cm，动点P、Q分别从点A，C同时出发，都以1cm/s的速度运动，其中点P由A运动到B停止，点Q由点C运动到点D停止．（1）求四边形PBCQ的面积；（2）P、Q两点从出发开始到几秒时，点P、Q、D组成的三角形是等腰三角形？【答案】见试题解答内容【解答】解：（1）设运动时间为t，则AP＝t，CQ＝t，∵四边形ABCD是矩形，∴CD＝AB＝4cm，BC＝AD＝2，∠B＝∠C＝90°，∴BP＝4﹣t，∴四边形PBCQ的面积＝（PB+CQ）•BC＝4×2＝4（cm）2；（2）设P、Q两点从出发开始到t秒时，点P、Q、D组成的三角形是等腰三角形，∵CQ＝t，∴DQ＝4﹣t，①当PQ＝DQ＝4﹣t时，如图1，过P作PH⊥DQ于H，则PH＝AD＝2，DH＝AP＝t，∵CQ＝t，∴HQ＝4﹣2t，∵PH2+HQ2＝PQ2，∴22+（4﹣2t）2＝（4﹣t）2，解得：t＝2，t＝，②当PQ＝PD时，如图2，过P作PH⊥DQ于H，则PH＝AD＝2，DH＝AP＝HQ＝t，∵CQ＝t，∴HQ＝4﹣2t，∴4﹣2t＝t，∴t＝，③当DQ＝PD时，∴DQ＝4﹣t，∴PD＝DQ＝4﹣t，∵AP2+AD2＝PD2，∴t2+22＝（4﹣t）2，∴t＝，综上所述，当t＝2秒或t＝秒或t＝秒或t＝秒时，点P、Q、D组成的三角形是等腰三角形．14．如图，在矩形ABCD中，O是AB的中点，点P在线段AM上（不与点A重合），OP＝AB，连接CP 并延长，交AD于点N．（1）判断△ABP的形状，并说明理由．（2）若M为DC的中点，求证：PN＝AN．【答案】（1）△ABP是直角三角形；（2）证明见解析．【解答】（1）解：△ABP是直角三角形．理由如下：∵点O是AB的中点，∴AO＝OB＝AB．∵OP＝AB，∴OP＝OA＝OB．∴∠OBP＝∠OPB，∠OAP＝∠APO．∵∠OAP+∠APO+∠OBP+∠BPO＝180°，∴∠APO+∠BPO＝90°．∴∠APB＝90°．∴△ABP是直角三角形．（2）证明：如图，延长AM，BC交于点Q，∵M是CD的中点，∵∠D＝∠MCQ＝90°，∠AMD＝∠QMC，∴△ADM≌△QCM（ASA）．∴AD＝CQ＝BC．∵∠BPQ＝90°．∴PC＝BQ＝BC．∴∠CPB＝∠CBP．∵∠OPB＝∠OBP，∴∠OBC＝∠OPC＝90°．∴∠OPN＝∠OPA+∠APN＝90°．∵∠OAP+∠PAN＝90°，∠OAP＝∠OPA，∴∠APN＝∠PAN．∴PN＝AN．四．矩形的判定（共1小题）15．如图，线段DE与AF分别为△ABC的中位线与中线．（1）求证：AF与DE互相平分；（2）当线段AF与BC ADFE为矩形？请说明理由．【答案】见试题解答内容【解答】（1）证明：∵点D是AB的中点，∴AD＝AB，∵点E是AC的中点，点F是BC的中点，∴EF是△ABC的中位线，∴EF∥AB，EF＝AB，∴四边形ADFE是平行四边形，∴AF与DE互相平分；（2）解：当AF＝BC时，四边形ADFE为矩形，理由：∵线段DE为△ABC的中位线，∴DE＝BC，∵AF＝BC，∴AF＝DE，由（1）得：四边形ADFE是平行四边形，∴四边形ADFE为矩形．五．矩形的判定与性质（共1小题）16．下列命题错误的是（ ）A．平行四边形的对边相等B．两组对边分别相等的四边形是平行四边形C．对角线相等的四边形是矩形D．矩形的对角线相等【答案】C【解答】解：平行四边形的性质有平行四边形的对边相等，故A选项错误；平行四边形的判定定理有两组对边分别相等的四边形是平行四边形，故B选项错误；C、对角线相等的平行四边形是矩形，故C选项正确；D、矩形的性质有矩形的对角线相等，故D选项错误；故选：C．六．正方形的性质（共18小题）17．如图，四边形ABCD是正方形，以CD为边作等边三角形CDE，BE与AC相交于点M，则∠AMD的度数是（ ）A．75°B．60°C．54°D．67.5°【答案】B【解答】解：如图，连接BD，∵∠BCE＝∠BCD+∠DCE＝90°+60°＝150°，BC＝EC，∴∠EBC＝∠BEC＝（180°﹣∠BCE）＝15°∵∠BCM＝∠BCD＝45°，∴∠BMC＝180°﹣（∠BCM+∠EBC）＝120°，∴∠AMB＝180°﹣∠BMC＝60°∵AC是线段BD的垂直平分线，M在AC上，∴∠AMD＝∠AMB＝60°故选：B．18．将n个边长都为1cm的正方形按如图所示的方法摆放，点A1，A2，…，A n分别是正方形对角线的交点，则n个正方形重叠形成的重叠部分的面积和为（ ）A．cm2B．cm2C．cm2D．（）n cm2【答案】B【解答】解：由题意可得阴影部分面积等于正方形面积的，即是，5个这样的正方形重叠部分（阴影部分）的面积和为×4，n个这样的正方形重叠部分（阴影部分）的面积和为×（n﹣1）＝．故选：B．19．如图，以边长为4的正方形ABCD的中心O为端点，引两条相互垂直的射线，分别与正方形的边交于E、F两点，则线段EF的最小值为（ ）A．2B．4C．D．2【答案】D【解答】解：如图，连接EF，∵四边形ABCD为正方形，∴∠EAO＝∠FDO＝45°，AO＝DO；∵∠EOF＝90°，∠AOD＝90°，∴∠AOE＝∠DOF；在△AOE与△DOF中，，∴△AOE≌△DOF（ASA），∴OE＝OF（设为λ）；∴△EOF是等腰直角三角形，由勾股定理得：EF2＝OE2+OF2＝2λ2；∴EF＝OE＝λ，∵正方形ABCD的边长是4，∴OA＝2，O到AB的距离等于2（O到AB的垂线段的长度），由题意可得：2≤λ≤2，∴2≤EF≤4．所以线段EF的最小值为2．故选：D．20．如图，在正方形ABCD和正方形CEFG中，点G在CD上，BC＝8，CE＝4，H是AF的中点，那么CH的长为（ ）A．4B．2C．4D．2【答案】B【解答】解：连接AC、CF，如图：∵四边形ABCD和四边形CEFG是正方形，∴∠ACG＝45°，∠FCG＝45°，∴∠ACF＝90°，∵BC＝8，CE＝4，∴AC＝8，CF＝4，由勾股定理得，AF＝＝4，∵H是AF的中点，∠ACF＝90°，∴CH＝AF＝2，故选：B．21．如图所示，正方形ABCD的边长为2，AB在x轴的正半轴上，以A（1，0）为圆心，AC为半径作圆交x轴负半轴于点P，则点P的横坐标是（ ）A．B．C．﹣1D．【答案】D【解答】解：∵四边形ABCD是边长为2的正方形，∴AB＝BC＝2，∴AC＝，∵以A为圆心，AC为半径画圆交x轴负半轴于点P，∴AP＝AC＝，又∵点A（1，0），∴OP＝﹣1，∴点P（1﹣，0），故选：D．22．如图，在正方形ABCD的外侧，作等边△ADE，则∠ABE为（ ）A．10°B．15°C．20°D．25°【答案】B【解答】解：∵四边形ABCD为正方形，△ADE为等边三角形，∴AB＝BC＝CD＝AD＝AE＝DE，∠BAD＝90°，∠DAE＝60°，∴∠BAE＝∠BAD+∠DAE＝150°，又∵AB＝AE，∴∠ABE＝（180°﹣150°）＝15°．故选：B．23．有5张边长为2的正方形纸片，4张边长分别为2、3的矩形纸片，6张边长为3的正方形纸片，从其中取出若干张纸片，且每种纸片至少取一张，把取出的这些纸片拼成一个正方形（原纸张进行无空隙、无重叠拼接），则拼成正方形的边长最大为（ ）A．6B．7C．8D．9【答案】D【解答】解：设大正方形的边为a，小正方形的边长为b，矩形的边长为a、b，如图所示：∵大正方形，有6张，小正方形有5张，矩形有4张，∴构成边长最大是为9正方形，其中有两边为9，则需要5个边长为3的正方形，另外两边的边长都为3+2+2+2＝9也可以满足3a＝3b+a，即2a＝3b．故选：D．24．在直线l上依次摆放着7个正方形，已知斜放置的3个的面积分别是a、b、c，正放置的4个正方形的面积依次是S1，S2，S3，S4，则S1+S2+S3+S4的值为（ ）A．a+b+c B．a+c C．a+2b+c D．a﹣b+c【答案】B【解答】解：∵∠ACB+∠DCE＝90°，∠BAC+∠ACB＝90°，∴∠DCE＝∠BAC，∵AC＝CE，∠ABC＝∠CDE∴△ABC≌△CDE，∴BC＝DE，在直角△ABC中，AB2+BC2＝AC2，即，AB2+DE2＝AC2，∵S3＝AB2，S4＝DE2∴S3+S4＝c同理S1+S2＝a故可得S1+S2+S3+S4＝a+c，故选：B．25．如图，正方形ABCD中，点M是边BC异于点B、C的一点，AM的垂直平分线分别交AB、CD、BD 于E、F、K，连接AK、MK．下列结论：①EF＝AM；②AE＝DF+BM；③BK＝；④∠AKM＝90°．其中正确的结论有 个．【答案】见试题解答内容【解答】解：如图，作FG⊥AB于G，则AD＝GF＝AB，∵AM⊥EF，∴∠BAM＝∠GFE，∵∠BAM＝∠GFE，∠ABM＝∠EGF，GF＝AB，∴△ABM≌△FGE，∴EF＝AM，故①正确；由题可得：AG＝DF，GE＝BM，∴AE＝AG+GE＝DF+BM；故②正确；如图，过K作KQ⊥AB于Q，KT⊥BC于T，∵∠KBQ＝45°，∴△BQK是等腰直角三角形，∴BK＝KQ＜AK，故③错误；∵DB平分∠ABC，∴KQ＝KT，又∵AM的垂直平分线交BD于K，∴KA＝KM，∴Rt△AQK≌Rt△MTK，∴∠AKQ＝∠MKT，又∵∠QKT＝∠MKT+∠MKQ＝90°，∴∠AKQ+∠MKQ＝90°，即∠AKM＝90°，故④正确；故答案为：3．26．如图，已知正方形ABCD中，AD＝6，∠DAE＝30°，点F为AE的中点，过点F作直线分别与AD、BC相交于点M、N，若MN＝AE，则AM的长等于 ．【答案】4或2．【解答】解：在正方形ABCD AD＝6，∠DAE＝30°，设DE＝x，则AE＝2x，由勾股定理x2+62＝（2x）2，解得：x＝2（负值舍去），∴AE＝4，∵点F为AE的中点，∴AF＝EF＝2，分两种情况：①过M作MG⊥BC，G为垂足，则MG＝DC＝AD，在Rt△MGN和Rt△ADE中，，∴Rt△MGN≌Rt△ADE（HL），∴∠NMG＝∠EAD，∴∠NMG+∠AMF＝90°，∴∠EAD+∠AMF＝90°，∴∠AFM＝90°，在Rt△AFM中，∠DAE＝30°，AF＝2，设MF＝m，则AM＝2m，由勾股定理，得4m2﹣m2＝12，解得m＝2（负值舍去），则AM＝4；②方法一：根据对称性由①可知：AM＝6﹣4＝2，方法二：如图，过N作NG⊥AD于G，过M作MH⊥AE于H，则NG＝CD＝AD，在Rt△ADE和Rt△NGM中，，∴Rt△ADE≌Rt△NGM（HL），∴∠GNM＝∠DAE＝30°，∴∠GMN＝60°，△AMF中，∠GMN＝∠MAF+∠AFM，∴∠AFM＝∠DAE＝30°，∴AM＝MF，∵MH⊥AF，∴AH＝FH，设MH＝x，则AM＝2x，AH＝FH＝x，∵F是AE的中点，∴AE＝2AF＝4AH＝4x，Rt△ADE中，∠DAE＝30°，∴DE＝AE＝2x，AD＝DE＝6x，∵AD＝6，即6x＝6，x＝1，即AM＝2x＝2；故答案为：4或2．27．如图，若正方体的棱长为a，M是AB的中点，则图中阴影部分的面积为 ．【答案】见试题解答内容【解答】解：找到CD的中点N，连接BN．正方形ABCD中，AC为BD的垂直平分线，∴OB＝OD，∵在△OAD和△OAB中，AB＝AD，OA＝OA∴△OAD≌△OAB，又∵，所以阴影部分面积为△OAD和△OAB的面积和．根据中位线定理M、N分别为AB、CD的中点，∴CE＝EO＝OA，∴O到AD的距离为CD长度的．∴S△ADO +S△ABO＝2S△ADO＝2××a×＝．故答案为．28．如图，分别以△ABC的边AB，AC为边往外作正方形ABDE和正方形ACFG，连接BG，CE，EG，若AB＝3，AC＝1，则BC2+EG2的值为 ．【答案】20．【解答】解：如图，连接BE，CG，∵正方形ABDE和正方形ACFG，∴AB＝AE，AG＝AC，∠BAE＝∠CAG＝90°，∴∠BAG＝∠CAE，∴△BAG≌△EAC（SAS），∴∠ABG＝∠AEC，∵∠AHB＝∠OHE，∴∠EOH＝∠BAH＝90°，∴∠EOG＝∠BOC＝90°，∴BC2+EG2＝OB2+OC2+OE2+OG2＝BE2+CG2，∵AB＝3，AC＝1，∴BE2＝32+32＝18，CG2＝12+12＝2，∴BE2+CG2＝18+2＝20，∴BC2+EG2＝20．故答案为：20．29．如图，正方形MNKT由8个全等的直角三角形和正方形EFGH拼接而成，记图中正方形MNKT，正方形ABCD，正方形EFGH的面积分别为S1，S2，S3，若S1﹣S2+S3＝10，则边AB的长度为 ．【答案】．【解答】解：将四边形EFGH的面积设为x，将其余八个全等的三角形面积一个设为y，∵正方形MNKT，正方形ABCD，正方形EFGH的面积分别为S1，S2，S3，若S1﹣S2+S3＝10，∴S1＝8y+x，S2＝4y+x，S3＝x，∴S1﹣S2+S3＝8y+x﹣（4y+x）+x＝10，故x+4y＝10，所以S2＝x+4y＝10，∴AB＝．故答案为：．30．如图，在正方形ABCD中，E为对角线AC上一点，连接DE，过点E作EF⊥DE，交BC延长线于点F，以DE，EF为邻边作矩形DEFG，连接CG．在下列结论中：①DE＝EF；②△DAE≌△DCG；③AC⊥CG；④CE＝CF．其中正确的结论序号是 ．【答案】①②③．【解答】解：过E作EM⊥BC于M点，过E作EN⊥CD于N点，如图所示：∵四边形ABCD是正方形，∴∠BCD＝90°，∠ECN＝45°，∴∠EMC＝∠ENC＝∠BCD＝90°，∴NE＝NC，∴四边形EMCN为正方形，∵四边形DEFG是矩形，∴EM＝EN，∠DEN+∠NEF＝∠MEF+∠NEF＝90°，∴∠DEN＝∠MEF，又∠DNE＝∠FME＝90°，在△DEN和△FEM中，，∴△DEN≌△FEM（ASA），∴ED＝EF，故①正确；∴矩形DEFG为正方形；∴DE＝DG，∠EDC+∠CDG＝90°，∵四边形ABCD是正方形，∵AD＝DC，∠ADE+∠EDC＝90°，∴∠ADE＝∠CDG，在△ADE和△CDG中，，∴△ADE≌△CDG（SAS），故②正确；∴AE＝CG，∠DAE＝∠DCG＝45°，∴∠ACG＝90°，∴AC⊥CG，故③正确；当DE⊥AC时，点C与点F重合，∴CE不一定等于CF，故④错误，综上所述：①②③．故答案为：①②③．31．如图，正方形ABCD中，点E是AD边的中点，BD，CE交于点H，BE，AH交于点G，则下列结论：①∠ABE＝∠DCE；②AG⊥BE；③S△BHE＝S△CHD；④∠AHB＝∠EHD．其中正确的结论有： （请填上序号）．【答案】①②③④．【解答】解：∵点E是AD边的中点，∴AE＝DE，而AB＝DC，∠BAE＝∠CDE，∴△BAE≌△CDE（SAS），∴∠ABE＝∠DCE，故①正确；∵DH＝DH，AD＝CD，∠ADH＝∠CDH，∴△ADH≌△CDH（SAS），∴∠EAG＝∠DCE，而∠ABE＝∠DCE，∠ABE+∠AEB＝90°，∴∠EAG+∠AEB＝90°，∴AG⊥BE，故②正确；∵△CDE和△BDE同底等高，∴S△CDE ＝S△BDE，而S△CDE ﹣S△EHD＝S△BDE﹣S△EHD，∴S△BHE ＝S△CHD，故③正确；∵△ADH≌△CDH，∴AH＝CH，而AB＝CB，∠EAG＝∠DCE，∴∠HAB＝∠HCB，∴△ABH≌△CBH（SAS），∴∠AHB＝∠CHB，而∠EHD＝∠CHB，∴∠AHB＝∠EHD，故④正确，故答案为：①②③④．32．如图1，在正方形ABCD AEF＝90°，且EF交正方形外角的平分线CF于点F．（1）若点E是BC边上的中点，求证：AE＝EF；（2）如图2，若点E是BC的延长线上（除C点外）的任意一点，其他条件不变，那么结论“AE＝EF”是否仍然成立，若成立，请写出证明过程；若不成立，请说明理由；（3）如图3，若点E是BC边上的任意点一，在AB边上是否存在点M，使得四边形DMEF是平行四边形？若存在，请给予证明；若不存在，请说明理由．【答案】见试题解答内容【解答】（1）证明：取AB的中点H，连接EH；如图1所示∵四边形ABCD是正方形，AE⊥EF；∴∠1+∠AEB＝90°，∠2+∠AEB＝90°∴∠1＝∠2，∵BH＝BE，∠BHE＝45°，且∠FCG＝45°，∴∠AHE＝∠ECF＝135°，AH＝CE，在△AHE和△ECF中，，∴△AHE≌△ECF（ASA），∴AE＝EF；（2）解：AE＝EF成立，理由如下：如图2，延长BA到M，使AM＝CE，∵∠AEF＝90°，∴∠FEG+∠AEB＝90°．∵∠BAE+∠AEB＝90°，∴∠BAE＝∠FEG，∴∠MAE＝∠CEF．∵AB＝BC，∴AB+AM＝BC+CE，即BM＝BE．∴∠M＝45°，∴∠M＝∠FCE．在△AME与△ECF中，，∴△AME≌△ECF（ASA），∴AE＝EF．（3）存在，理由如下：如图3，作DM⊥AE于AB交于点M，则有：DM∥EF，连接ME、DF，在△ADM与△BAE中，，∴△ADM≌△BAE（ASA），∴DM＝AE，由（2）AE＝EF，∴DM＝EF，∴四边形DMEF为平行四边形．33．如图，正方形ABCD边长为4，点E在边AB上（点E与点A、B不重合），过点A作AF⊥DE，垂足为G，AF与边BC相交于点F．（1）求证：△ADF≌△DCE；（2）若△DEF的面积为，求AF的长；（3）在（2）的条件下，取DE，AF的中点M，N，连接MN，求MN的长．【答案】（1）证明见解答部分；（2）AF＝5或．（3）MN的长度为或．【解答】（1）证明：∵AF⊥DE，∠B＝90°，∴∠AED＝∠AFB，在△ABF与△DAE中，，∴△ABF≌△DAE（AAS），∴AF＝DE，∵∠ADE+∠CDE＝∠ADE+∠DAG＝90°，∴∠CDE＝∠DAF，在△ADF和△DCE中，，∴△ADF≌△DCE（SAS）．（2）解：∵△ABF≌△DAE，∴AE＝BF＝x，∴BE＝CF＝4﹣x，∴△DEF的面积＝S正方形﹣S△ADE﹣S△EBF﹣S△DCF＝4×4﹣×4•x﹣（4﹣x）•x﹣×4•（4﹣x）＝8﹣2x+x2，∴y＝x2﹣2x+8＝，解得，x1＝3，x2＝1，∴AE＝3或AE＝1，∴AF＝DE＝5或．（3）解：如图，连接AM并延长交CD于点P，连接PF，∵点M是DE的中点，∴DM＝ME，∵AB∥CD，∴∠PDM＝∠AEM，∠DPM＝∠EAM，∴△DPM≌△EAM（AAS），∴PM＝AM，DP＝AE＝3或1，当AE＝3时，BF＝DP＝3，∴CF＝CP＝1，∴PF＝，∴MN＝PF＝；当AE＝1时，BF＝EP＝1，∴CF＝CP＝3，∴PF＝3，∴MN＝PF＝；综上，MN的长度为或．34．如图，点G是正方形ABCD对角线CA的延长线一点，对角线BD与AC交于点O，以线段AG为边作一个正方形AEFG，连接EB、GD．（1）求证：EB＝GD；（2）若AB＝5，AG＝2，求EB的长．【答案】见试题解答内容【解答】（1）证明：在△GAD和△EAB中，∠GAD＝90°+∠EAD，∠EAB＝90°+∠EAD，∴∠GAD＝∠EAB，在△GAD和△EAB中，，∴△GAD≌△EAB，∴EB＝GD；（2）∵四边形ABCD是正方形，AB＝5，∴BD⊥AC，AC＝BD＝5，∴∠DOG＝90°，OA＝OD＝BD＝，∵AG＝2，∴OG＝OA+AG＝，由勾股定理得，GD＝＝，∴EB＝．七．正方形的判定（共1小题）35．如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F（1）线段OE与OF的数量关系 ．（填空）；（2）若CE＝8，CF＝6，则OC＝ ．（填空）；（3）当点O运动到 ，且∠BCA等于 时，四边形AECF是正方形．（填空）【答案】见试题解答内容【解答】解：（1）∵CE是∠ACB的平分线，∴∠1＝∠2．∵MN∥BC，∴∠1＝∠3．∴∠2＝∠3．∴OE＝OC．同理可证OC＝OF．∴OE＝OF．故答案为：OE＝OF．（2）∵MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F，∴∠2＝∠ACB，∠5＝∠ACD，∴∠ECF＝∠2+∠5＝（∠ACB+∠ACD）＝90°，∴△ECF是直角三角形，又∵CE＝8，CF＝6，∴由勾股定理得EF＝10，∵OE＝OF，∴Rt△CEF中，CO＝EF＝5，故答案为：5；（3）当点O运动到AC ACB＝90°时，四边形AECF是正方形．理由如下：∵O为AC中点，∴OA＝OC，∵由（1）可得OE＝OF，∴四边形AECF为平行四边形；由（2）可得∠ECF＝90°，∴四边形AECF为矩形，∠5＝∠6＝45°，∠2＝∠3＝45°，∴∠3＝∠6，∴CE＝CF，∴平行四边形AECF是正方形．故答案为：AC的中点处，90°．八．轴对称-最短路线问题（共1小题）36．如图，在矩形ABCD中，AB＝6，AD＝5，点P在AD上，点Q在BC上，且AP＝CQ，连接CP，QD，则PC+QD的最小值为（ ）A．10B．11C．12D．13【答案】D【解答】解：如图，连接BP，在矩形ABCD中，AD∥BC，AD＝BC，∵AP＝CQ，∴AD﹣AP＝BC﹣CQ，∴DP＝QB，DP∥BQ，∴四边形DPBQ是平行四边形，∴PB∥DQ，PB＝DQ，则PC+QD＝PC+PB，则PC+QD的最小值转化为PC+PB的最小值，在BA的延长线上截取AE＝AB＝6，连接PE，∵PA⊥BE，∴PA是BE的垂直平分线，∴PB＝PE，∴PC+PB＝PC+PE，连接CE，则PC+QD＝PC+PB＝PC+PE≥CE，∵BE＝2AB＝12，BC＝AD＝5，∴CE＝＝13．∴PC+PB的最小值为13．故选：D．。

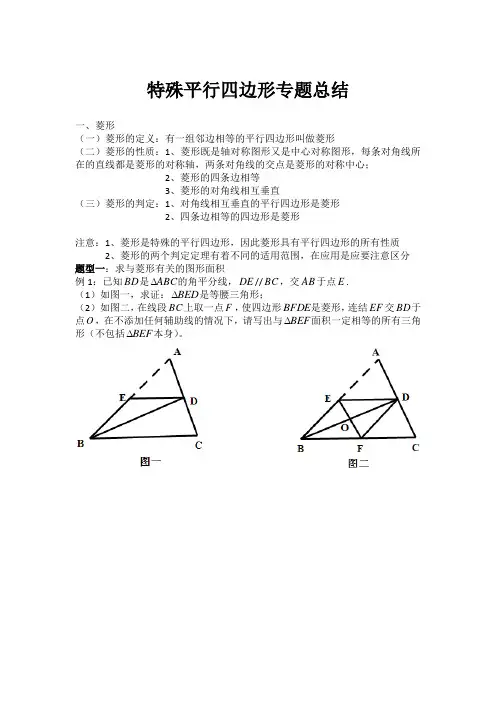
特殊平行四边形专题总结一、菱形（一）菱形的定义：有一组邻边相等的平行四边形叫做菱形（二）菱形的性质：1、菱形既是轴对称图形又是中心对称图形，每条对角线所在的直线都是菱形的对称轴，两条对角线的交点是菱形的对称中心；2、菱形的四条边相等3、菱形的对角线相互垂直（三）菱形的判定：1、对角线相互垂直的平行四边形是菱形2、四条边相等的四边形是菱形注意：1、菱形是特殊的平行四边形，因此菱形具有平行四边形的所有性质2、菱形的两个判定定理有着不同的适用范围，在应用是应要注意区分题型一：求与菱形有关的图形面积例1：已知BD是ABC∆的角平分线，DE//BC，交AB于点E.（1）如图一，求证：BED∆是等腰三角形；（2）如图二，在线段BC上取一点F，使四边形BFDE是菱形，连结EF交BD于点O，在不添加任何辅助线的情况下，请写出与BEF∆面积一定相等的所有三角形（不包括BEF∆本身）。

1、如图，四边形ABCD 是菱形，AB DH DB AC ⊥==，，68与点H ，则=DH （ ） 524.A 512.B 12.C 24.D题型二：综合运用菱形的性质与判定解题例2：如图，F E ,为线段BD 的两个三等分点，四边形AECF 是菱形。

（1）试判断四边形ABCD 的形状，并加以证明；（2）若菱形AECF 的周长为20，BD 的长为24，试求四边形ABCD 的面积。

2、如图，已知F E ,分别是平行四边形ABCD 的边AD BC ,的中点，且︒=∠90BAC（1）求证：四边形AECF 是菱形；（2）若1035==BC AB ，,求菱形AECF 的面积。

题型三：与菱形有关的图形变换问题例3：如图，在ABC ∆和EDC ∆中，︒=∠=∠===09,DCE ACB CD CB CE AC ,AB 与CE 交于点F ，BC AB ED 、与分别交于H M 、.（1）求证：CH CF =；（2）如图2，ABC ∆不动，将EDC ∆绕点C 旋转到︒=∠45BCE 时，试判断四边形ACDM 是什么四边形，并证明你的结论。