正弦定理证明上课讲义
- 格式:doc
- 大小:261.00 KB
- 文档页数:6


《正弦定理》说课讲稿唐山市丰南区第二中学李立春一、学情分析:(一)教材分析:本节知识是人教版必修五第一章《解三角形》的第一节内容,与初中学习的三角形的边和角关系、判定三角形的全等有密切联系,在日常生活和工农业生产中也时常有解三角形的问题,而且解三角形问题在高考当中是必考内容,因此,正弦定理和余弦定理的知识非常重要。
根据上述分析,故确定本节:教学重点:1、正弦定理的证明、内容;2、定理的基本应用;教学难点:1、正弦定理的探索及证明;2、已知两边和其中一边的对角判断解的个数问题。
(二)学生情况分析:学生在此之前已经学习了函数、三角函数有关知识,初步掌握了利用函数研究问题的重要方法,并且在初中学习三角形知识及勾股定理的基础上去探索正弦定理做好了铺垫。
经过一个学期的高中学习,学生已经初步能够从特殊的情况中发现一些规律,从而推广为一般情况。
关键是学生在这个方面的应用意识还比较淡漠,所以本节课要做好这种引导工作,学生是比较容易理解的。
这也是本节课要突出的“从特殊到一般”的课堂设计的原因,能够使学生充分地参与进来,体会到成功的喜悦。
二、教学目标:根据上述学情分析,制定如下教学目标:认知目标:在创设的问题情境中,引导学生发现正弦定理的内容,推证正弦定理,简单运用正弦定理与三角形的内角和定理解三角形的两类问题。
能力目标:引导学生通过观察、推导、比较,由特殊到一般归纳出正弦定理,培养学生的创新意识、观察能力与逻辑思维能力,体会利用所学知识向量作为数形结合的工具,将几何问题转化为代数问题。
情感目标:培养学生勇于探索、善于研究的精神,挖掘其非智力因素资源,培养其良好的数学学习品质。
调动学生的主动性和积极性,给学生成功的体验,激发学生学习的兴趣。
三、教学方法:(一)教法:1、遵循“数学学习的本质是主体(学生)在头脑中建构和发展数学认知结构的过程,是主体的一种再创造行为”的理论,遵循以学生为主体,教师为主导的指导思想,采用探究式教学法,即在教学过程中,在教师的启发引导下,以学生独立自主和合作交流为前提,以“正弦定理的发现”为基本探究内容,以生活实际为参照对象,让学生的思维由问题开始,到猜想的得出,猜想的探究,定理的推导,并逐步得到深化。



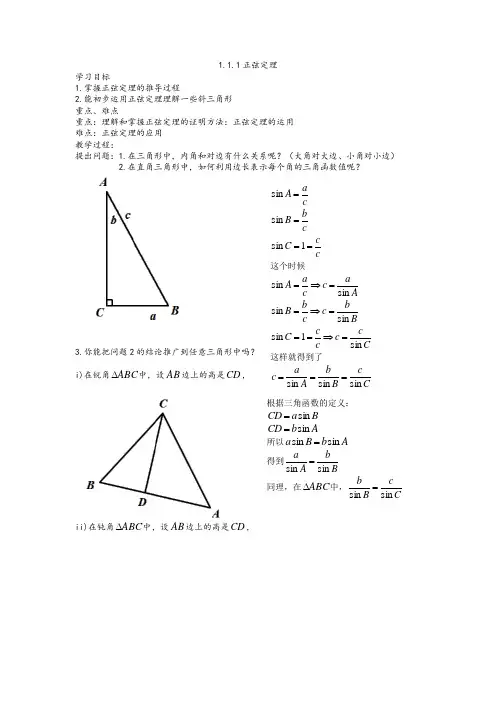
1.1.1正弦定理学习目标1.掌握正弦定理的推导过程2.能初步运用正弦定理理解一些斜三角形 重点、难点重点:理解和掌握正弦定理的证明方法:正弦定理的运用 难点:正弦定理的应用 教学过程:提出问题:1.在三角形中,内角和对边有什么关系呢?(大角对大边、小角对小边) 2.在直角三角形中,如何利用边长表示每个角的三角函数值呢?3.你能把问题2的结论推广到任意三角形中吗?i)在锐角ABC ∆中,设AB 边上的高是CD ,ii)在钝角ABC ∆中,设AB 边上的高是CD ,c a A =sin c bB =sinccC ==1sin这个时候A ac c a A sin sin =⇒=B bc c b B sin sin =⇒= C cc c c C sin 1sin =⇒== 这样就得到了C c B b A a c sin sin sin === 根据三角函数的定义: B a CD sin = A b CD sin =所以A b B a sin sin = 得到BbA a sin sin =同理,在ABC ∆中,CcB b sin sin =正弦定理:在一个三角形中,个边和它所对角的正弦的比相等,即CcB b A a sin sin sin == 定理理解:1)正弦定理说明同一三角形中,边与其对角的正弦成正比,且比例系数为同一正数,即存在正数k 使A k a sin =,B k b sin =,C k c sin = 2)CcA aB bC c B b A a C c B b A a sin sin ,sin sin ,sin sin sin sin sin ===⇔== 定理的作用:①已知三角形的任意两角及其一边可以求出三角形的其他元素,如B Ab a sin sin =例1:已知在中,,求解:根据三角形内角和定理:根据正弦定理:②已知三角形的任意两边与其中一边的对角可以求三角形的其他元素,如B b aA sin sin =例2:在中,已知,求解:由正弦定理得:ABC ∆10,45,105c A B ==︒=︒,,a b C 1801804510530C A B =︒--=︒-︒-︒=︒()sin sin105sin 6045sin 60cos 45cos 60sin 454B =︒=︒+︒=︒︒+︒︒=10sin 21sin 2c Aa C⨯===10sin 41sin 2c Bb C===ABC∆45a b B ===︒,,A Cc sin sin a BA b===根据三角函数的定义: B a CD sin =()A b A b CD sin sin =-=π所以A b B a sin sin =得到BbA a sin sin =同理,在ABC ∆中,CcB b sin sin =所以当时,,当时,,一般的,已知三角形某些边和角,求其它边和角的过程叫做解三角形3)在ABC ∆中,已知A b a ,,时解三角形的情况:当A ∠为锐角时,在A ∠的一条边上作b AC =,以点C 为圆心,以a 为半径作圆,观察与A ∠另一边交点个数,连接交点和点C ,就确定了三角形的形状。

《正弦定理》讲义一、正弦定理的引入在三角形中,边和角之间存在着一定的关系。
为了探究这种关系,我们引入正弦定理。
想象一下,你站在一个三角形的顶点,看着三条边和三个角。
我们想要找到一种数学表达式,能够将边的长度和角的正弦值联系起来。
二、正弦定理的定义正弦定理表述为:在任意一个三角形中,各边和它所对角的正弦值的比相等,且等于外接圆的直径。
即:\(\frac{a}{\sin A} =\frac{b}{\sin B} =\frac{c}{\sin C} = 2R\)(其中\(R\)为三角形外接圆的半径)三、正弦定理的推导我们以锐角三角形为例来推导正弦定理。
假设\(\triangle ABC\),角\(A\)、\(B\)、\(C\)所对的边分别为\(a\)、\(b\)、\(c\),作\(AD\perp BC\)于\(D\)。
在\(Rt\triangle ABD\)中,\(\sin B =\frac{AD}{c}\),则\(AD = c\sin B\)在\(Rt\triangle ACD\)中,\(\sin C =\frac{AD}{b}\),则\(AD = b\sin C\)所以\(c\sin B = b\sin C\),即\(\frac{b}{\sin B} =\frac{c}{\sin C}\)同理,我们可以通过作其他边上的高,推导出\(\frac{a}{\sin A} =\frac{b}{\sin B}\)这样就得到了正弦定理:\(\frac{a}{\sin A} =\frac{b}{\sin B} =\frac{c}{\sin C}\)对于钝角三角形,推导过程类似,只是需要注意高的位置。
四、正弦定理的应用1、已知两角和一边,求其他两边和一角例如,已知\(\triangle ABC\)中,\(A = 30^\circ\),\(B = 45^\circ\),\(c = 10\),求\(a\)和\(b\)。




正弦定理证明正弦定理的证明解读克拉玛依市高级中学 曾艳一、正弦定理的几种证明方法1.利用三角形的高证明正弦定理(1)当∆ABC 是锐角三角形时,设边AB 上的高是CD ,根据锐角三角函数的定义,有=sin CD a B ,sin CD b A =。
由此,得 sin sin a b A B =,同理可得 sin sin c b C B=, 故有 sin sin abA B =sin cC =.从而这个结论在锐角三角形中成立.(2)当∆ABC 是钝角三角形时,过点C 作AB 边上的高,交AB 的延长线于点D ,根据锐角三角函数的定义,有=∠=∠sin sin CD a CBD a ABC ,sin CD b A = 。
由此,得=∠sin sin a b A ABC ,同理可得 =∠sin sin c b C ABC 故有 =∠sin sin abA ABC sin c C =. 由(1)(2)可知,在∆ABC 中,sin sin abA B =sin cC = 成立.从而得到:在一个三角形中,各边和它所对角的正弦的比值相等,即sin sin abA B =sin cC =.1’用知识的最近生长点来证明:实际应用问题中,我们常遇到问题:已知点A ,点B 之间的距|AB|,可测量角A 与角B ,需要定位点C ,即:ab D A B CA B C Db a在如图△ABC 中,已知角A ,角B ,|AB |=c , 求边AC 的长b 解:过C 作CD ⊥AB 交AB 于D ,则 cos AD c A = sin sin cos sin tan sin cos BD c A c A C DC C C C C===sin cos (sin cos sin cos )sin cos sin sin sin c A C c C A A C c B b AC AD DC c A C C C +==+=+== 推论:sin sin b c B C = 同理可证:sin sin sin a b c A B C==2.利用三角形面积证明正弦定理已知△ABC,设BC =a, CA =b,AB =c,作AD ⊥BC,垂足为 D.则Rt △ADB中,ABAD B =sin ,∴AD=AB·sinB=csinB. ∴S △ABC =B ac AD a sin 2121=•.同理,可证 S △ABC =A bc C ab sin 21sin 21=. ∴ S △ABC =B ac A bc C ab sin 21sin 21sin 21==.∴absinc=bcsinA=acsinB, 在等式两端同除以ABC,可得b B a A c C sin sin sin ==.即Cc B b A a sin sin sin ==. 3.向量法证明正弦定理(1)△ABC 为锐角三角形,过点A 作单位向量j 垂直于AC ,则j 与AB 的夹角为90°-A ,j 与CB 的夹角为90°-C .由向量的加法原则可得AB CB AC =+, 为了与图中有关角的三角函数建立联系,我们在上面向量等式的两边同取与向量j 的数量积运算,得到AB j CB AC j •=+•)(由分配律可得AB j CB j AC •=•+. B ∴|j |AC Co s90°+|j |CB Co s(90°-C )=|j |AB Co s(90°-A ). jD C B A C∴asinC=csinA.∴C c A a sin sin =. A 另外,过点C 作与CB 垂直的单位向量j ,则j 与AC 的夹角为90°+C ,j 与AB 的夹角为90°+B ,可得Bb Cc sin sin =. (此处应强调学生注意两向量夹角是以同起点为前提,防止误解为j 与AC 的夹角为90°-C ,j 与AB 的夹角为90°-B )∴C c B b A a sin sin sin ==.(2)△ABC 为钝角三角形,不妨设A >90°,过点A 作与AC 垂直的单位向量j ,则j 与AB 的夹角为A -90°,j 与CB 的夹角为90°-C .由AB CB AC =+,得j ·AC +j ·CB =j ·AB , j 即a·Cos(90°-C)=c·Cos(A-90°),∴asinC=csinA.∴Cc A a sin sin = 另外,过点C 作与CB 垂直的单位向量j ,则j 与AC 的夹角为90°+C ,j 与AB 夹角为90°+B .同理,可得C c B b sin sin =.∴ Cc B b simA a sin sin == 4.外接圆证明正弦定理 在△ABC 中,已知BC=a,AC=b,AB=c,作△ABC 的外接圆,O 为圆心,连结BO 并延长交圆于B′,设BB′=2R.则根据直径所对的圆周角是直角以及同弧所对的圆周角相等可以得到∠BAB′=90°,∠C =∠B′,∴sin C =sin B′=R c B C 2sin sin ='=.∴R Cc 2sin =. 同理,可得R B b R A a 2sin ,2sin ==.∴R Cc B b A a 2sin sin sin ===. 这就是说,对于任意的三角形,我们得到等式Cc B b A a sin sin sin ==. 二、剖析四种证明方法的本质联系虽然正弦定理的有四种证明方法(也可以看成5种,对于第一种证明方法也可以用向量的形式来表示,可以看成向量、向量在向量方向上的投影相等),虽然每种证明方法都用不同的数学知识从不同的角度去证明了正弦定理,但是仔细观察会发现有一条纽带一直联系在正弦定理的各种证明方法A CB A之间,可以说每一种证明方法离开这条纽带都是没办法成立的,这条纽带就是:直角三角形思想。
正弦定理的四种证明方法(在正弦定理的第一种证明方法中,用到的就是最基本的通过三角形作高把斜三角形转化为直角三角形。
第二面积法,三角形的面积等于低乘高,也是把一般的三角形问题转化为垂直关系来研究。
第三种向量法用到的也是向量的垂直关系。
第四种外接圆法也借助了直径所对的圆周角等于090这个特殊的直角三角形)都是利用了直角三角形;余弦定理的平面几何证明方法,也是利用三角形做高转化成直角三角形来证明;在没学正余弦定理之前,学生直接利用初中的知识来解斜三角形,也是转化成直角三角形来解。
从这其中我们可以发现直角三角形它那不可替代的特殊作用。
所以,我觉得正弦定理的四种证明方法的本质联系就是:直角三角形。
其实,研究正余弦定理就是为了解斜三角形,在没有正余弦定理之前,我们只能够解直角三角形。
而正弦定理的发现也是借助于直角三角形,通过直角三角形边角的关系发现了正弦定理。
而我们要证明正弦定理必须得借助已经学过的知识,而在没有学习正余弦定理之前,我们仅能解得就是直角三角形,所以正弦定理的各种证明方法都是通过建立构造和解直角三角形的基础之上,所以正弦定理的各种证明方法都会或多或少的借助“垂直”的关系。
三、我对正弦定理证明的一点想法1、对于正弦定理的四种证明方法,我认为作高法和面积法是学生比较容易接受的方法,因为正弦定理的发现也好,或是初中同学们对三角形的认识也好,对于一般三角形问题通过作高转化成直角三角形问题是大家都很熟悉的,所以接受起来特别的容易,所以用作高来证明正弦定理是最容易被学生接受和掌握的方法。
而有了作高证明正弦定理的方法以后,要用面积法学生接受起来也就不会存在很大的困难,因为所有的学生都知道,三角形的面积等于低乘高,所以作出三角形的高以后,通过老师的恰当引导,学生很容易就能联想到三角形的面积等于低乘高,从而也就较容易接受和掌握面积法证明正弦定理。
而对于向量法证明几何问题学生相对比较生疏,所以不容易马上联想到,那么接受起来也就没有前面的方法那么容易。
所以,我觉得向量法是四种方法中学生比较不容易联想到的一种方法。
2、对于正弦定理的四种证明方法,没有必要让学生全部掌握,我们可以根据自己的教学特点和学生的实际需要选择合适的方法即可,但是,不管我们要选择那一种证明方法,都必须设置相应适合的教学活动,让学生能够更能理解定理的证明,并且能够培养学生一些分析问题解决问题的能力。
下面针对几种证明方法谈谈我自己的教学活动上的一些想法。
为了让学生能够理解为什么要通过做高来证明正弦定理,我们可以在讲定理之前设计一个斜三角形问题,然后引导学生利用做高转化为直角三角形问题来解。
例如:已知∆ABC中,10=,45A=︒,c kmB=︒,求边b和边a的长。
105学生通过对这个三角形的求解过程会发现斜三角形问题可以转化为直角三角形来求解。
那么通过直角三角形推导出正弦定理需要证明在锐角三角形和直角三角形中是否成立的时候,学生就会很自然的联想到斜三角形可以通过做高转化成直角三角形问题,从而,做高法证明正弦定理就很容的被学生接受和掌握。
而有了做高法做铺垫,可以引导学生联想到三角形的面积等于低乘高,从而引出面积法证明正弦定理,并能得到三角形ABC 的面积111sin sin sin 222S ab C bc A ac B ===。
如果要用外接圆法来证明正弦定理,我觉得从特殊的直角三角形入手是一个比较不错的方法:正弦定理sin sin sin a b c A B C==等于一个常数,那么这个常数是什么呢?它和三角形ABC 有什么关系?引导学生发现在直角三角形(C=090)中有sin sin sin a b c A B C===c ,这个常数刚好是直角三角形的斜边,从而可以引导学生发现直角三角形的斜边就是其外接圆的直径,从而引出外接圆法证明余弦定理,并得到sin sin sin a b c A B C==R 2= 对于要用向量的方法来证明正弦定理,我觉得设置这样的几个问题可能效果也不错。
问题1:在我们学过的知识当中,还有那些知识是和长度、角度之间有密切联系的?(学生马上会想到向量的数量积)问题2:在三角形ABC中,如果把三条边用向量来表示,他们之间会有什么样的关系?(学生会联想到向量加法的三角形法则)问题3:如何用向量的方法来证明正弦定理呢?(学生可能不会马上想到,那么可以再设置一个问题)问题4:从前面学过的证明方法会给你什么启示吗?(我觉得做高法这个比较容易接受的方法基本上老师都会讲,所以学生在做高法的引导下对于做垂直向量就比较容易接受了),有了这四个问题做铺垫,那么对于利用向量方法来证明正弦定理,学生接受起来应该不会难。