弧度制1
- 格式:doc
- 大小:63.00 KB
- 文档页数:3




题:4.2弧度制(一)教学目的:1.理解1弧度的角、弧度制的定义.2.掌握角度与弧度的换算公式并能熟练地进行角度与弧度的换算.3.熟记特殊角的弧度数教学重点:使学生理解弧度的意义,正确地进行角度与弧度的换算.教学难点:弧度的概念及其与角度的关系.授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪内容分析:讲清1弧度角的定义,使学生建立弧度的概念,理解弧度制的定义,达到突破难点之目的. 通过电教手段的直观性,使学生进一步理解弧度作为角的度量单位的可靠性、可行性.通过周角的两种单位制的度量,得到角度与弧度的换算公式. 使学生认识到角度制、弧度制都是度量角的制度,二者虽单位不同,但是互相联系的、辩证统一的.进一步加强对辩证统一思想的理解.教学过程:一、复习引入:1.角的概念的推广⑴“旋转”形成角一条射线由原来的位置OA,绕着它的端点O按逆时针方向旋转到另一位置OB,就形成角α.旋转开始时的射线OA叫做角α的始边,旋转终止的射线OB 叫做角α的终边,射线的端点O叫做角α的顶点.⑵.“正角”与“负角”“0角”我们把按逆时针方向旋转所形成的角叫做正角,把按顺时针方向旋转所形成的角叫做负角,如图,以OA为始边的角α=210°,β=-150°,γ=660°,定义的?规定周角的3601作为1°的角,我们把用度做单位来度量角的制度叫做角度制,有了它,可以计算弧长,公式为180rn l π=3.探究30°、60°的圆心角,半径r 为1,2,3,4,分别计算对应的弧长l ,再计算弧长与半径的比结论:圆心角不变,则比值不变,因此比值的大小只与角的大小有关,我们可以利用这个比值来度量角,这就是另一种度量角的制度——弧度制二、讲解新课:1. 定义:长度等于半径长的弧所对的圆心角称为1弧度的角它的单位是rad读作弧度,这种用“弧度”做单位来度量角的制度叫做弧度制.如下图,依次是1rad , 2rad , 3rad ,αrad探究:⑴平角、周角的弧度数,(平角=π rad 、周角=2π rad )⑵正角的弧度数是正数,负角的弧度数是负数,零角的弧度数是0 ⑶角α的弧度数的绝对值 rl=α(l 为弧长,r 为半径) ⑷角度制、弧度制度量角的两种不同的方法,单位、进制不同,就像度量长度一样有不同的方法,千米、米、厘米与丈、尺、寸,反映了事物本身不变,改变的是不同的观察、处理方法,因此结果就有所不同⑸用角度制和弧度制来度量零角,单位不同,但数量相同(都是0) 用角度制和弧度制来度量任一非零角,单位不同,量数也不同2. 角度制与弧度制的换算:∵ 360︒=2π rad ∴180︒=π rad∴ 1︒=rad rad 01745.0180≈π'185730.571801=≈⎪⎭⎫ ⎝⎛=πrad三、讲解范例:例1 把'3067化成弧度解:⎪⎭⎫⎝⎛=2167'3067∴ rad rad ππ832167180'3067=⨯=例2 把rad π53化成度 解: 1081805353=⨯=rad π 注意几点:1.度数与弧度数的换算也可借助“计算器”进行;2.今后在具体运算时,“弧度”二字和单位符号“rad ”可以省略 如:3表示3rad , sin π表示πrad 角的正弦;3.一些特殊角的度数与弧度数的对应值应该记住:4.应确立如下的概念:角的概念推广之后,无论用角度制还是弧度制都能在角的集合与实数的集合之间建立一种一一对应的关系任意角的集合 实数集R例3用弧度制表示:1 终边在x 轴上的角的集合2 终边在y 轴上的角的集合3 终边在坐标轴上的角的集合解:1 终边在x 轴上的角的集合 {}Z k k S ∈==,|1πββ 2 终边在y 轴上的角的集合 ⎭⎬⎫⎩⎨⎧∈+==Z k k S ,2|2ππββ 3 终边在坐标轴上的角的集合 ⎭⎬⎫⎩⎨⎧∈==Z k k S ,2|3πββ 四、课堂练习:1.下列各对角中终边相同的角是( )A.πππk 222+-和(k∈Z) B.-3π和322πC.-97π和911πD. 9122320ππ和2.若α=-3,则角α的终边在( )A.第一象限B.第二象限C.第三象限D.第四象限3.若α是第四象限角,则π-α一定在( )A.第一象限B.第二象限C.第三象限D.第四象限4.(用弧度制表示)第一象限角的集合为 ,第一或第三象限角的集合为 .5.7弧度的角在第 象限,与7弧度角终边相同的最小正角为 .6.圆弧长度等于截其圆的内接正三角形边长,则其圆心角的弧度数为 .7.求值:2cos4tan6cos6tan3tan3sinππππππ-+.8.已知集合A={α|2kπ≤α≤π+2kπ,k∈Z},B ={α|-4≤α≤4},求A ∩B .9.现在时针和分针都指向12点,试用弧度制表示15分钟后,时针和分针的夹角.参考答案: 1.C 2.C 3.C4.{α|2k π<α<2π+2k π,k ∈Z } {α|k π<α<2π+k π,k ∈Z } 5.一 7-2π 6.3 7.28.A ∩B ={α|-4≤α≤-π或0≤α≤π} 9.2411π五、小结 1.弧度制定义 2.与弧度制的互化 2.特殊角的弧度数 六、课后作业:已知α是第二象限角,试求:(1)2α角所在的象限;(2)3α角所在的象限;(3)2α角所在范围.解:(1)∵α是第二象限角,∴2π+2k π<α<π+2k π,k ∈Z ,即4π+k π<2α<2π+k π,k ∈Z .故当k =2m (m ∈Z )时,4π+2m π<2α<2π+2m π,因此,2α角是第一象限角;当k =2m +1(m ∈Z )时,45π+2m π<2α<23π+2m π,因此,2α角是第三象限角.综上可知,2α角是第一或第三象限角.(2)同理可求得:6π+32k π<3α<3π+32k π,k ∈Z .当k =3m (m ∈Z )时,ππαππm m 23326+<<+,此时,3α是第一象限角;当k =3m +1(m ∈Z )时,πππαπππ322333226++<<++m m ,即3265αππ<+m <π+2m π,此时,3α角是第二象限角; 当k =3m +2(m ∈Z )时,ππαππm m 2353223+<<+,此时,3α角是第四象限角.综上可知,3α角是第一、第二或第四象限角. (3)同理可求得2α角所在范围为:π+4k π<2α<2π+4k π,k ∈Z .评注:(1)注意某一区间内的角与象限角的区别.象限角是由无数个区间角组成的,例如0°<α<90°这个区间角,只是k =0时第一象限角的一种特殊情况.(2)要会正确运用不等式进行角的表达,同时会以k 取不同值,讨论形如θ=α+32k π(k ∈Z )所表示的角所在象限. (3)对于本例(3),不能说2α只是第一、二象限的角,因为2α也可为终边在y 轴负半轴上的角23π+4k π(k ∈Z ),而此角不属于任何象限. 七、板书设计(略)八、课后记:一般情况下,我们在研究圆中的角的弧度一般都是正数!除非题目有特别的要求!有两种方法可以解释,一是正的弧对的弧度为正,负的弧对的是负的弧度(解释稍显牵强!),二是无论是顺时针方向还是逆时针旋转的角度数值始终是正数,所以研究时弧度取正数!扇形的圆心角始终是正数!。

弧度制
➢教学重点:
1.理解并掌握弧度制定义;
2.熟练地进行角度制与弧度制地互化换算;
3.弧度制的运用.
➢教学难点:理解弧度制定义,弧度制的运用.
➢教学过程:
第一课时弧度制
一、引入新课
有人问:温州到杭州有多远时,我们回答约400公里,但也有人回答约250英里,请问哪一种回答是正确的?(已知1英里=1.6公里)
显然,两种回答都是正确的,但为什么会有不同的数值呢?那是因为所采用的度量制不同,一个是公制,一个是英制.它们的长度单位是不同的,但是,它们之间可以换算:1英里=1.6公里.
在角度的度量里面,也有类似的情况,一个是角度制,一个是弧度制.
角度制规定:将一个圆周分成360份,每一份叫做一度,故一周等于360度,半轴等于180度,直角等于90度等等.
弧度制是什么呢?弧度是什么意思?一周是多少弧度?半周呢?直角等于多少弧度?弧度制与角度制之间如何换算?
二、新课讲授
1.弧度制的定义
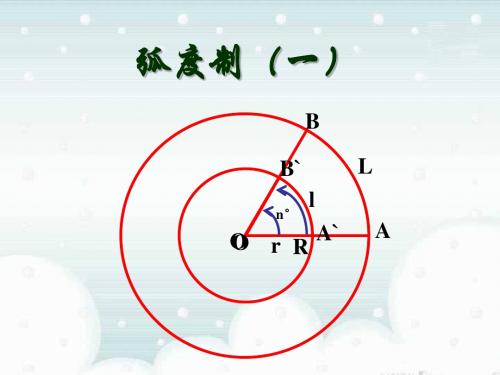
长度等于半径长的圆弧所对的圆心角叫做1弧度角,记作1rad,或1弧度,或1.
(1)长度等于直径的弧所对的圆心角的弧度数是多少?(画图示意,并写成2R/R 的形式)再举一个负角的例子.
(2)当圆心角是周角时,它的弧度数是多少?为什么?
(3)当圆心角是平角时,它的弧度数是多少?为什么?直角呢?
2.说明
(1) 我们知道,角有正负零角之分,它的弧度数也应该有正负零之分,如-π,-2
π等等,由角的旋转方向决定.
(2) 正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0,角α的弧度数的绝对值是:r
l =α,其中,l 是圆心角所对的弧长,r 是半径. (3) 以弧度作为单位来度量角的单位制,叫做弧度制.
3.角度制与弧度制的换算
(1)记住原理:
∵周角所对的弧是整个圆周,是2πr ,所以周角的弧度数是2π,但周角又等于360° ∴360°=2π rad
∴180°=π rad
∴1°=180
π rad ≈0.01745 rad (直接做4(1)(2)(3)) 1 rad=π
︒180≈57.3°=57°18/
三、例题练习:
(1)把下列各角从度化成弧度:(口答,并问为什么?)
360°,180°,90°,45°
30°, 60°,120°,135°,270°.
(2)把67°30/,化成弧度.
(3)把各角从弧度化成度:(口答,并问为什么)
2π,π21,π32,
6π (4)把π53化成度.
说明:弧度制与角度制的转换运算,关键要抓住180°=π rad .
四、巩固小结
1.小结
(1)圆心角的弧度数的绝对值等于它所对弧长与半径的比值:r
l =α;也可写成:r l α=;
(2)180°=π;也可写成:1801π=
︒; 1 rad=π︒180.
2.常用角的弧度角度换算
这些结果同学们应在理解的基础上熟记,在今后有很多的应用.
3.计算:
(1)sin 4
π (2)tan1.5 处理:A :解释tan 与初中的记号tg 不同,并要求参阅课本首页“本书部分数学符号”注意正切和余切的写法.
B :教师示范解答,并说明可以查表.
4.引出角度制与弧度制下的弧长计算公式:
角度制下的弧长公式:1802360r n r n l ππ=⨯=
(说明推导方法) 弧度制下的弧长公式:r l α=.。