标架与坐标
- 格式:ppt
- 大小:859.00 KB
- 文档页数:7

教学内容§1.5标架与坐标一、空间中的标架与坐标系的有关概念1. 标架仿射标架(简称为标架):是指空间中的一个定点O ,连同三个不共面的有序向量 321,,e e e 的全体,记为{O ;321,,e e e }。
笛卡尔标架:{O ;321,,e e e },其中321,,e e e 都是单位向量。
笛卡尔直角标架(简称为直角标架):{O ;321,,e e e },其中321,,e e e 都是单位向量,且两两垂直。
注:笛卡尔标架,直角标架是特殊的标架。
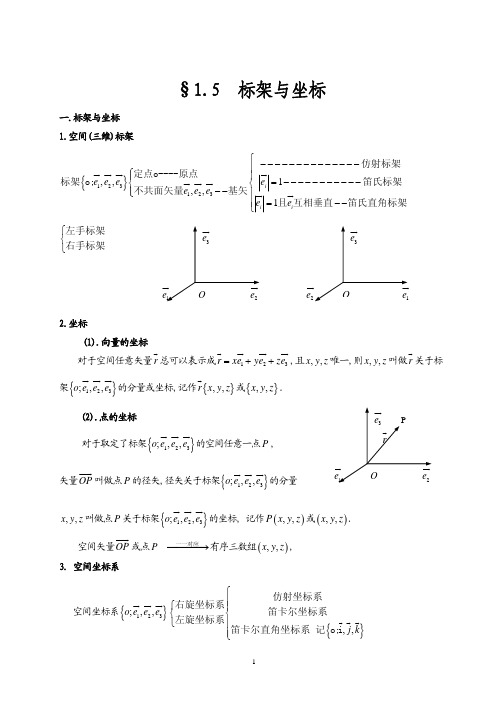
2. 左手标架与右手标架根据标架中321,,e e e 的相互关系,标架分左手标架与右手标架所谓右手标架入图所示,它的特征是:将右手的拇指和食指分别指向1e 和2e 的方向时中指的方向与3e 的方向在由1e 和2e 所在平面的同一侧。
3. 空间向量的坐标取定标架{O ;321,,e e e },r为空间向量,因321,,e e e 不共面,eeeOeeeO所以由定理 1.4.3 知,r 可分解为321,,e e e 的线性组合: r=321e z e y e x ++,这里x,y,z 是唯一确定的一组有序实数,上式中的x,y,z 叫做r 关于标架{O ;321,,e e e }的坐标或分量,记作r {x,y,z}或{x,y,z}。
4.空间中点的坐标: 取定标架{O ;321,,e e e },设P 为空间中的点,OP 叫做点P 的向径,向径OP 关于标架{O ;321,,e e e }的坐标x,y,z 叫做P 关于标架{O ;321,,e e e }的坐标,记为P(x,y,z)或(x,y,z)。
5. 坐标系定义:取定标架以后,由向量(点)的坐标概念可知,全体向量(点)的集合与全体有序三数组有一一对应关系,这种一一对应关系叫空间向量(点)的一个坐标系。
常用表示:显然,空间坐标系由标架{O ;321,,e e e },因此空间坐标系也用标架{O ;321,,e e e }来表示,这时O 称为坐标原点,321,,e e e 称为坐标向量。

课时教学实施方案课程:解析几何授课班级:13信本1班授课学期:2013-2014学年2学期复习提问:1•向量的线性组2. 向量的线性相关、线性无关3. 向量共线、共面与向量线性组合的关系4. 向量共线、共面与向量线性相关的关系约5分钟新课引入:前面向量的表示是°或万,那么有没有其他的方法表示向量呢?约5分钟讲解新课:一、 标架与坐标的概念标架就是空间一点和三个不共面向量组成的全体.坐标是在一个标架下,如果向量尸=疋】十)迭十疋3,此时这里的就 叫做向量F 的坐标.约15分钟二、 空间坐标系空间坐标系包括:坐标原点Q 坐标轴:x 轴,y 轴,z 轴,坐标面: xOy 面,面,zOx 面,卦限(八个)约15分钟三、 利用坐标作向量的运算在这一部分主要讲述了向量的坐标表示、向量的加减法、向量与数 量的乘法的坐标运算、向量共线与共面的条件的坐标表达式以及定比分 点的坐标.约55分钟教 学 进 程 设 计复习提问:1.向量的线性组合2.向量的线性相关、线性无关3.向量共线、共面与向量线性组合的关系4.向量共线、共面与向量线性相关的关系新课引入前面向量的表示是a或那么有没有其他的方法表示向量呢?前面我们己知道空间中任何矢量可由三个不共面的矢量來线性表示,于是在空间中任取一点0,再引出三个不共面的矢量盒迢,.那么空间中任何矢量戸可由爲,色,$线性表示,即r = xe1 + ye2 + % (1)并且这里的x, y, z是唯一的一组有序实数.所以就有了本节所学的概念.讲解新课:一、标架与坐标的概念标架的概念空间中一点0与三个不共面的向量可,乙,可的全体,叫做空间中的T T T一个标架.记做0©心启;如果也,乙都是单位向量,那么阳£可叫做笛卡尔标架;如果g,可两两互相垂直,那么[o.ZZe]叫做笛卡尔直角标架,简称直角标架;在一般情况下,可叫做仿射标架.对于标架[oZZeV如果可,爲,可间的相互关系和右手的拇指、食指、中指相同,那么这个标架叫做右旋标架或称右手标架.如果可,乙,可间的相互关系和左手的拇指、食指、中指相同,那么 这个标架叫做左旋标架或称左手标架.坐标的概念定义1在”=.馅十)运2十疋3式中,叫做向量戸关于标架T T T )〈。


第一章矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点;(3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点.解:2. 设点O是正六边形ABCDEF的中心,在矢量OA、OB、OC、OD、OE、OF、AB、BC、CD、DE、EF和FA中,哪些矢量是相等的?[解]:图1-13. 设在平面上给了一个四边形ABCD,点K、L、M、N分别是边AB、BC、CD、DA的中点,求证:KL=NM. 当ABCD是空间四边形时,这等式是否也成立?[证明]:.4. 如图1-3,设ABCD-EFGH是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB、CD; (2) AE、CG; (3) AC、EG;(4) AD、GF; (5) BE、CH.解:§1.2 矢量的加法1.要使下列各式成立,矢量b a ,应满足什么条件? (1=+ (2+=+ (3-=+ (4+=- (5= 解:§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出矢量→x ,→y .解:2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF . 解:3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 解:4 在四边形ABCD中,→→→+=baAB2,→→→--=baBC4,→→→--=baCD35,证明ABCD为梯形.解:6. 设L、M、N分别是ΔABC的三边BC、CA、AB的中点,证明:三中线矢量AL, BM, CN可以构成一个三角形.7. 设L、M、N是△ABC的三边的中点,O是任意一点,证明OBOA++OC=OL+OM+ON.解:8. 如图1-5,设M是平行四边形ABCD的中心,O是任意一点,证明OA+OB+OC+OD=4OM.解:9在平行六面体ABCDEFGH(参看第一节第4题图)中,证明→→→→=++AGAHAFAC2.证明:.10.用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半.解11. 用矢量法证明,平行四边行的对角线互相平分.解12. 设点O 是平面上正多边形A 1A 2…A n 的中心,证明: 1OA +2OA +…+n OA =0.解,13.在12题的条件下,设P 是任意点,证明 证明:§1.4 矢量的线性关系与矢量的分解1.在平行四边形ABCD 中,(1)设对角线,,b BD a AZ ==求.,,,DA CD BC AB 解(2)设边BC 和CD 的中点M 和N ,且q AN P AM ==,求CD BC ,。

§1.5 标架与坐标一、空间坐标系1. 空间中的一个定点O,连同三个不共面的有序矢量, , 的全体,叫做空间中的一个标架,记做{O;,}. 如果, , 都是单位矢量,那么{O;,,}叫做笛卡尔标架;, , 两两相互垂直的笛卡尔标架叫做笛卡尔直角标架,简称直角标架;在一般情况下,{O;,,}叫做仿射标架.2. 对于标架{O;,,},如果, , 间的相互关系和右手拇指、食指、中指相同,那么这个标架叫做右旋标架或称右手标架;如果, , 间的相互关系和左手的拇指、食指、中指相同,那么这个标架叫做左旋标架或称左手标架. 如图1-16.3. 表达式=x+y+z中的x, y, z叫做矢量关于标架{O;,,}的分量或称为坐标,记做{x, y, z}或{x, y, z}.4. 对于取定了标架{O;,,}的空间中任意点P,矢量叫做点P的径矢,径矢关于标架{O;,,}的分量x, y, z叫做点P关于标架{O;,,}的坐标,记做P (x, y, z)或(x, y, z).5. 当空间取定标架{O; ,, }之后,空间全体矢量的集合或者全体点的集合与全体有序三数组x, y, z的集合具有一一对应的关系,这种一一对应的关系叫做空间矢量或点的一个坐标系. 空间坐标系也常用{O;,,}来表示,此时点O叫做坐标原点,,, 都叫做坐标矢量.6. 由右(左)旋标架决定的坐标系叫做右(左)旋坐标系或右(左)手坐标系;仿射标架、笛卡尔标架与直角标架所确定的坐标系分别叫做仿射坐标系、笛卡尔坐标系与直角坐标系.二、平面坐标系1. 约定用{O;}表示直角坐标系,以后在讨论空间问题时所采用的坐标系,一般都是空间右手直角坐标系.2. 过点O沿着三坐标矢量, , 的方向引三轴Ox, Oy, Oz,可以用这三条具有公共点O的不共面的轴Ox, Oy, Oz来表示空间坐标系,记做O—x y z,此时点O叫做空间坐标系的原点,三条轴Ox, Oy, Oz都叫做坐标轴,且依次叫做x轴,y轴和z轴,每两条坐标轴所决定的平面叫做坐标面,分别叫做xOy平面,yOz平面与xOz平面. 三坐标平面把空间划分为八个区域,每一个区域都叫做卦限.3. 平面上一个定点O, 连同两个不共线的有序矢量, 的全体,叫做平面上的一个标架,记做{O;,},如果, 都是单位矢量,那么{O;,}叫做笛卡尔标架;与相互垂直的笛卡尔标架叫做笛卡尔直角标架,简称直角标架;在一般情况下,{O;,}叫做仿射标架.4. 对于标架{O;,},将绕O旋转,使的方向以最近的路径旋转到与的方向相合时,如果旋转方向是逆时针的,则这种标架叫做右旋标架或称右手标架;如果旋转方向是顺时针的,则这种标架叫做左旋标架或称左手标架. 如图1-17.5. 表达式=x+y中的x, y叫做矢量关于标架{O;,}的分量或称为坐标,记做{x, y}或{x, y}.6. 对于取定了标架{O;,}的平面上的任意点P,矢量叫做点P的径矢,径矢关于标架{O;,}的分量x, y叫做点P关于标架{O;,}的坐标,记做P(x, y)或(x, y).7. 当平面上取定标架{O;,}之后,平面上全体矢量的集合或者全体点的集合与全体有序数对x, y的集合具有一一对应的关系,这种一一对应的关系叫做平面上矢量或点的一个坐标系. 平面坐标系也常用{O;,}来表示,此时点O叫做坐标原点,, 都叫做坐标矢量.8. 由右(左)旋标架决定的坐标系叫做右(左)旋坐标系或右(左)手坐标系;仿射标架、笛卡尔标架与直角标架所确定的坐标系分别叫做仿射坐标系、笛卡尔坐标系与直角坐标系.15. 约定用{O;,}表示直角坐标系, 在讨论平面问题时所采用的坐标系,一般都是平面右手直角坐标系.9. 过点O沿着坐标矢量, 的方向引二轴Ox, Oy,可以用这二条具有公共点O的不共线的轴Ox,Oy来表示平面坐标系,记做O-x y,此时点O叫做平面坐标系的原点,Ox 叫做x轴,Oy叫做y轴. 两坐标轴把平面分成四个区域,每一个区域都叫做象限.例1. 在空间直角坐标系{O;}下,求P(2,-3,-1),M(a, b, c)关于 (1) 坐标平面;(2) 坐标轴;(3) 坐标原点的各个对称点的坐标.解:可按照“关于哪轴对称,哪轴不动,其余变号”的方法去考虑,有M (a, b, c)关于xOy平面的对称点坐标为(a, b, -c),M (a, b, c)关于yOz平面的对称点坐标为(-a, b, c),M (a, b, c)关于xOz平面的对称点坐标为(a,-b, c),M (a, b, c)关于x轴平面的对称点坐标为(a,-b,-c),M (a, b, c)关于y轴的对称点的坐标为(-a, b,-c),M (a, b, c)关于z轴的对称点的坐标为(-a,-b, c).类似考虑P (2,-3,-1)即可.例2. 已知矢量, , 的分量如下:(1) ={0, -1, 2},={0, 2, -4},={1, 2, -1};(2) ={1, 2, 3},={2, -1, 0},={0, 5, 6}.试判别它们是否共面?能否将表成,的线性组合?若能表示,写出表示式.解:(1) 因为=0,所以, , 三矢量共面, 由于, 的对应坐标成比例,即//,但,故不能将表成, 的线性组合.(2) 因为=0,所以, , 三矢量共面.由于, 的对应坐标不成比例,即,故可以将表成, 的线性组合.设=λ+μ, 即 {0, 5, 6}=λ{1, 2, 3}+μ{2, -1, 0}从而由此解得λ=2,μ=-1,所以=2-.例 3.证明:四面体每一个顶点与对面重心所连的线段共点,且这点到顶点的距离是它到对面重心距离的三倍. 用四面体的顶点坐标把交点坐标表示出来.证明:设四面体A1A2A3A4,A i对面重心为G i, 欲证A i G i交于一点(i=1, 2, 3, 4).在A i G i上取一点P i,使=3, 从而=,设A i (x i, y i, z i)(i=1, 2, 3, 4),则G1,G2,G3,G4,所以P1(,,)≡P1(,,).同理得P2≡P3≡P4≡P1,所以A i G i交于一点P,且这点到顶点距离等于这点到对面重心距离的三倍.作业题:1. 指出坐标满足下列条件的点(x, y, z)在空间的位置.(1)x=y; (2)y z<0; (3)x y z<0.2. 平行于z轴的矢量有什么特点?平行于x轴和y轴的矢量又分别有什么特点?3. 已知线段AB被点C(2, 0, 2)和D(5,-2, 0)三等分,试求这个线段两端点A与B 的坐标.。
第一章 矢量与坐标§1.1 矢量的概念1.下列情形中矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点; (3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点. [解]:(1)单位球面; (2)单位圆(3)直线; (4)相距为2的两点2. 设点O 是正六边形ABCDEF 的中心,在矢量OA 、、 OC 、、、 OF 、、BC 、CD 、 、EF 和FA 中,哪些矢量是相等的?[解]:如图1-1,在正六边形ABCDEF 中,相等的矢量对是: 图1-1 .DE OF CD OE AB OC FA OB EF OA 和;和;和;和;和3. 设在平面上给了一个四边形ABCD ,点K 、L 、M 、N 分别是边AB、BC、CD、DA的中点,求证:KL =. 当ABCD 是空间四边形时,这等式是否也成立?[证明]:如图1-2,连结AC , 则在∆BAC 中,21AC. KL 与AC 方向相同;在∆DAC 中,21AC . 与方向相同,从而KL =NM 且KL 与方向相同,所以KL =NM .4. 如图1-3,设ABCD -EFGH 是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB 、; (2) AE 、; (3) 、EG ;(4)、GF ; (5) 、CH .[解]:相等的矢量对是(2)、(3)和(5); 互为反矢量的矢量对是(1)和(4)。
§1.2 矢量的加法1.要使下列各式成立,矢量b a ,应满足什么条件? (1-=+ (2+=+ (3-=+ (4+=- (5=C[解]:(1),-=+;(2),+=+(3≥且,-=+ (4),+=-(5),≥-=-§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出矢量→x ,→y . 解 ⑴→→→→→→→→→→→→→→-=+-+---+=-⋅+--⋅-ay b x b y a y b x a x b y a y b x a x b a y x b a y x 22)()()()(⑵ →→→→→→→→→→+=+-+-+=+3132132142232e e e e e e e e b a ,→→→→→→→→→→→-+-=+---+=-321321321342)223(2e e e e e e e e e b a , →→→→→→→→→→→-+-=+---+=-3213213217103)223(2)2(323e e e e e e e e e b a . 2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF .解 →→→→→→→→→→→-+=-+-+=+=c b a c a c b a AB CD EF 533)2(21)865(212121.3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线,又∵B 为公共点,从而A 、B 、D 三点共线.4 在四边形ABCD 中,→→→+=b a AB 2,→→→--=b a BC 4,→→→--=b a CD 35,证明ABCD 为梯形.证明∵→→→→→→→→→→→→→=--=-+--++=++=BC b a b a b a b a CD BC AB AD 2)4(2)35()4()2(∴→AD ∥→BC ,∴ABCD 为梯形.6. 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点,证明:三中线矢量, ,可 以构成一个三角形.[证明]: )(21+=)(21BC BA BM +=)(21+=0)(21=+++++=++∴CB CA BC BA AC AB CN BM AL从而三中线矢量CN BM AL ,,构成一个三角形。