下载文档原格式
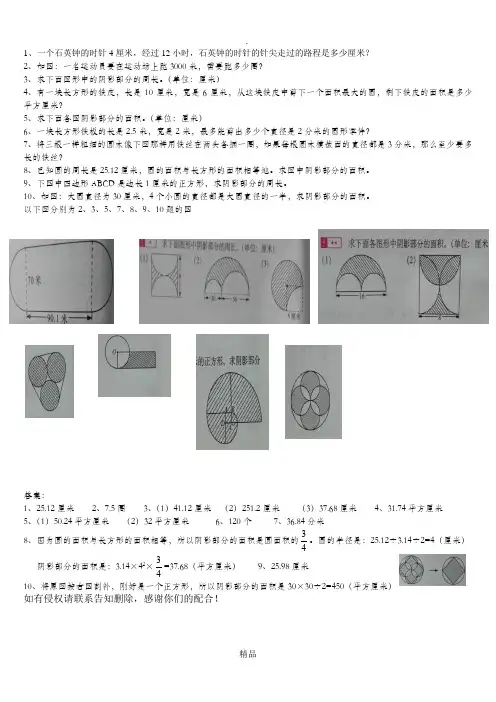
.精品 1、一个石英钟的时针4厘米，经过12小时，石英钟的时针的针尖走过的路程是多少厘米？2、如图：一名运动员要在运动场上跑3000米，需要跑多少圈？3、求下面图形中的阴影部分的周长。
（单位：厘米）4、有一块长方形的铁皮，长是10厘米，宽是6厘米，从这块铁皮中剪下一个面积最大的圆，剩下铁皮的面积是多少平方厘米？5、求下面各图阴影部分的面积。
（单位：厘米）6、一块长方形铁板的长是2.5米，宽是2米，最多能剪出多少个直径是2分米的圆形零件？7、将三根一样粗细的圆木像下图那样用铁丝在两头各捆一圈，如果每根圆木横截面的直径都是3分米，那么至少要多长的铁丝？8、已知圆的周长是25.12厘米，圆的面积与长方形的面积相等地。
求图中阴影部分的面积。
9、下图中四边形ABCD 是边长1厘米的正方形，求阴影部分的周长。
10、如图：大圆直径为30厘米，4个小圆的直径都是大圆直径的一半，求阴影部分的面积。
以下图分别为2、3、5、7、8、9、10题的图答案：1、25.12厘米2、7.5圈3、（1）41.12厘米 （2）251.2厘米 （3）37.68厘米4、31.74平方厘米5、（1）50.24平方厘米 （2）32平方厘米6、120个7、36.84分米8、因为圆的面积与长方形的面积相等，所以阴影部分的面积是圆面积的43。
圆的半径是：25.12÷3.14÷2=4（厘米） 阴影部分的面积是：3.14×42×43=37.68（平方厘米） 9、25.98厘米 10、将原图按右图割补，刚好是一个正方形，所以阴影部分的面积是30×30÷2=450（平方厘米）如有侵权请联系告知删除，感谢你们的配合！。
六年级圆的面积知识点圆是我们日常生活中常见的几何形状之一，它具有许多有趣的性质，其中之一就是它的面积。
在六年级的数学学习中，理解和计算圆的面积是非常重要的。
本文将介绍六年级学生需要掌握的圆的面积相关知识点。
1. 圆的定义和基本概念1.1 圆的定义圆是由平面上离一个固定点距离小于等于一定值的所有点组成的集合。
1.2 圆上的关键概念圆心：圆心是圆的中心点，通常用字母O表示。
半径：半径是从圆心到圆上任意一点的距离，通常用字母r表示。
2. 圆周长和圆的面积2.1 圆周长的计算公式圆的周长，也称为圆的周长，是圆周上的全部长度。
圆周长可以通过半径与圆周率的乘积来计算，公式如下：周长 = 2 ×半径 ×圆周率（π）2.2 圆的面积的计算公式圆的面积是圆内部所有点的集合，可以通过半径的平方与圆周率的乘积来计算，公式如下：面积 = 半径 ×半径 ×圆周率（π）3. 圆周率(π)的意义和计算3.1 圆周率的定义圆周率π是圆的周长与直径比值的恒定值，通常取近似值3.14。
3.2 圆周率的计算方法圆周率π的计算通常使用数学方法进行近似计算，可以通过分数的形式或无限小数来表达。
我们常用的近似值是3.14，或者更精确一些的3.14159。
4. 圆的面积计算示例让我们通过几个示例来计算圆的面积：示例一：已知圆的半径为5cm，求解其面积。
解：根据面积计算公式，面积 = 半径 ×半径× π代入数值，得到面积= 5cm × 5cm × 3.14 ≈ 78.5cm²示例二：已知圆的直径为10m，求解其面积。
解：首先要求得半径，半径 = 直径 ÷ 2 = 10m ÷ 2 = 5m代入面积计算公式，得到面积= 5m × 5m × 3.14 ≈ 78.5m²5. 圆的面积与其他图形的比较圆的面积与其他图形的面积可以进行比较，从而更好地理解圆的面积大小。
探索小学数学重点圆的周长与面积的计算与关系在数学学科中，圆是一个非常重要的概念和形状。
无论是在小学阶段还是更高级的阶段，圆的周长和面积计算一直都是一个关键的学习目标。
本文将探索小学数学的重点——圆的周长和面积的计算与关系。
一、圆的周长计算圆的周长是指圆的边界的长度，也即圆一周的长度。
圆的周长计算公式是C = 2πr，其中 C 表示圆的周长，π（pi）是一个数值近似为3.14的常数，r 表示圆的半径。
在小学阶段，教师可以通过引导学生绘制圆和测量圆的直径或半径来演示圆的周长计算。
学生可以使用直尺或计算器测量或计算圆的直径或半径，然后将其代入公式C = 2πr 来计算周长。
这样的实际操作可以帮助学生理解并掌握圆的周长的计算方法。
二、圆的面积计算圆的面积是指圆所覆盖的平面的大小。
圆的面积计算公式是A = πr²，其中 A 表示圆的面积，π（pi）是一个数值近似为3.14的常数，r 表示圆的半径。
小学阶段的学生可能没有涉及到π这个特殊的常数，教师可以根据学生的年级和理解能力，采用一些简化的方法来引导学生理解圆的面积计算。
比如，教师可以引导学生通过绘制圆并分割为多个等分的扇形，然后将这些扇形重新组合为一个与圆形相似的长方形，并将长方形的面积除以扇形的数量来近似计算圆的面积。
随着学生年级的增加，教师可以逐渐引入π这个常数的概念，帮助学生更准确地计算圆的面积。
三、圆的周长和面积的关系在学习圆的周长和面积的计算时，学生应该意识到周长和面积是两个不同的概念，其计算方法也不相同。
周长是描述圆边界的长度，面积则表示圆所覆盖的平面大小。
然而，周长和面积之间并不是完全独立的。
实际上，通过对圆的周长和面积的计算过程进行观察和探索，我们可以发现它们之间存在一定的关系。
一种简单的观察方法是比较两个圆的半径大小不同时，它们的周长和面积的变化情况。
当两个圆的半径不同时，可以发现周长的变化比面积的变化更为明显。
这是因为周长的计算采用了乘以2这个系数，而面积的计算则采用了平方的操作。
圆的周长与面积的关系1. 引言说到圆，很多人可能会想到足球、披萨或者是那些美丽的钟表。
圆，真的是一个神奇的形状！它既简单又复杂，既实用又美观。
今天咱们就来聊聊圆的周长和面积，看看它们之间究竟有什么关系，听起来是不是很有趣呢？2. 圆的基本知识2.1 周长和半径的关系首先，咱们得先搞清楚什么是圆的周长。
简单来说，圆的周长就是把圆的边边沿一圈量一遍，听起来是不是挺简单的？我们常用的公式是：周长= 2 × π × r，没错，r就是圆的半径。
要知道，π是个神秘的数字，约等于3.14。
就像古话说的，“三分天注定，七分靠打拼”，这里的π就像是个天生的数字，帮我们把周长和半径的关系联系起来。
2.2 面积的奥秘接下来聊聊圆的面积，面积就是圆里面那块“地盘”。
我们计算圆的面积用的是公式：面积= π × r²。
说白了，圆的面积和半径的平方成正比。
你可以想象成，半径越长，圆的“肚子”就越大，面积自然也就水涨船高了。
听起来是不是像是在说一个人的身材？哈哈，别笑，数学也有自己的身材标准嘛！3. 周长与面积的关系3.1 直观的理解现在，咱们来看看周长和面积之间的关系。
你会发现，虽然它们的计算公式不一样，但都和半径这个小家伙紧密相连。
半径一大，周长就像是喝了红牛一样，呼啦啦地涨起来；而面积也不甘示弱，直接用平方的方式追着周长跑。
这就好比是两个好朋友，一个爱跑步，一个爱健身，虽然各自的风格不同，但都是为了同一个目标，越变越强！3.2 实际应用说到这里，可能有人会问：“这跟我有什么关系呢？”其实，圆的周长和面积在我们的生活中可用得上，比如说你要买一块披萨，周长可以告诉你这块披萨的大小，面积则能告诉你能吃到多少好料。
再比如，园艺爱好者们种花时也会用到这些公式，周长可以帮助你围起花坛，而面积则能帮你计算种多少花才够美。
听着，是不是觉得这些公式有点儿生活气息了？4. 小结总而言之，圆的周长和面积就像是一对好搭档，一个负责“跑”，一个负责“吃”，虽然各自的职能不同，但却是不可或缺的。
第1讲 圆的周长和面积【学习目标】1、进一步学习圆的周长计算；2、进一步学习圆的面积计算。
【知识梳理】1、周长：围成圆的曲线的长度叫做圆的周长。
公式：C=πd 或 C=2πd2、面积：圆所占面积的大小叫圆的面积。
公式：Ｓ＝πｒ²3、半圆的周长公式：Ｃ＝πd ÷2＋d 或 Ｃ＝πr ＋2r圆周长的一半=πr4、半圆的面积：公式为：Ｓ＝πｒ²÷2（半圆面积＝圆的面积÷2）5、圆环的面积：S=πR ²－πｒ² 或 S=π（R ²－ｒ²）（其中R ＝r ＋环的宽度）。
6、扇形弧长：扇形中的曲线部分线条的长度，用L 表示弧长，L=r 180n π。
扇形面积：扇形的面积S=3602r n π（n 是扇形圆心角的度数）。
【典例精析】【例1】如图，有三根直径都是2分米的圆柱形木材，想用一根绳子把它们捆成一捆，捆三圈最短需要分米长的绳子。
（打结处强长不计，工取3.14)【趁热打铁-1】如图，春节时，商店出售直径为10厘米的图柱形礼花。
每7个用彩带捆成一捆，每捆需要彩带________厘米。
（接头不计，π取3.14)【例2】将两个半径分别为3cm 、5cm 的半圆如图放置,求涂色部分的周长.【趁热打铁-2】右图中每个小圆的半径是1厘米，阴影部分的周长是_____厘米(π=3.14)。
【例3】如图是有4个41扇形和1个正方形构成，如果正方形的边长为2，求这个图的周长。
【趁热打铁-3】有一只狗被拴在一建筑物的墙角A 处，这个建筑物是底面边长为8m 的正方形，栓狗的绳子长20米，现在狗从P 点出发（如图），将绳子拉紧按顺时针方向跑，可跑多少米？【例4】如右图把圆分成若干，等份拼剪拼成一个近似的长方形，已知长方形的宽为5厘米，长是厘米。
【趁热打铁-4】如图，把半径为3dm的圆分成若干等分后，拼成一个近似的长方形，则这个长方形的长是 dm，宽是 dm，该长方形的周长是 dm，面积是 dm²，该圆的周长是 dm，面积是 dm²。
圆及圆的周长一、圆的认识1、圆的定义：平面上到定点的距离等于定长的所有点组成的图形叫做圆。
如图，用圆规画圆时，针尖所在的点叫做圆心，一般用字母O表示。
连接圆心和圆上任意一点的线段叫做半径，一般用字母r表示，半径的长度就是圆规两个角之间的距离。
通过圆心并且两端都在圆上的线段叫做直径，一般用字母d表示。
在同一个圆里，有无数条直径，且所有的直径都相等。
在同一个圆里，有无数条半径，且所有的半径都相等。
直径与半径的关系：d=2r2、圆的对称性如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形是轴对称图形。
折痕所在的这条直线叫做对称轴。
如下图：练习：判断对错（1）半径的长短决定圆的大小。
（）（2）圆心决定圆的位置。
（）（3）同一个圆的直径是半径的2倍。
（）（4）圆的半径都相等。
（）3、圆的周长圆的周长测量方法：A、用一根线，绕圆一周，减去多余的部分，再拉直量出它的长度，即可得出圆的周长。
B 、把圆放在直尺上滚动一周，直接量出圆的周长。
以下是通过上述方法测得的圆的周长与直径的大致关系：一个固定的数，我们把它叫做圆周率，用字母π表示。
它是一个无限不循环小数， π⋅⋅⋅⋅⋅≈1415926535.3但在实际应用中常常只取它的近似值，例如π14.3≈。
如果用C 表示圆的周长，就有：C=πd 或C=2πr例1 求下列圆的周长练习：1、求下列圆的周长2、在一个长10厘米，宽8厘米的长方形中画一个最大的圆，这个圆的周长是（ ）厘米。
21d 121）π（4、看图填空（单位：cm ）正方形的周长是（ ）cm ，圆的周长是（ ）cm 。
其中一个圆的周长是（ ）cm ，长方形的周长是（ ）cm 。
例2：一个圆的半径是4厘米，求它的半圆周长是多少？练习：圆的直径是d ，下列表示半圆周长公式正确的是：A 、πdB πd C例3：圆形花坛的直径是20m ，它的周长是多少米？小自行车车轮的直径是50m ，绕花坛一 周车轮大约转动多少周？练习：1、一个圆形喷水池的半径是5m ，它的周长是多少米？2、在一个圆形亭子里，小丽沿着直径从一端走12步到达另一端，每步长大约是55cm 。
圆的面积与周长的关系公式圆的面积和周长之间的关系，其实就像是一对好朋友，形影不离。
想象一下，一个圆就像是那种有点神秘的蛋糕，外面光滑诱人，里面却藏着惊喜。
我们都知道，圆的周长就是一圈走下来，像是围着这个蛋糕转了一圈。
这个周长的公式是2πr，听起来有点高大上吧？其实只要记住这个小r，就是圆的半径就行了，没那么复杂。
然后，我们再来看看圆的面积，公式是πr²。
这里的r²就像是说，半径不仅仅是个单数，它还得自己乘以自己，变得更大，更美妙。
说到圆的周长和面积，它们就像是一对默契的双胞胎。
一个周长长了，面积也跟着水涨船高。
这就像我们在生活中，努力工作赚到的钱，花出去的也不少。
想象一下，你的朋友请你吃饭，点了个大披萨，圆圆的，一口气吃掉一整块，哇，那可是圆的面积在发挥作用啊。
吃的时候，心里想着，真是太满足了。
而当你把它吃完，周围的朋友们就开始讨论这个披萨有多大，周长多么诱人。
周长给人的第一感觉就是“哇”，一圈下去，仿佛把所有的美味都包裹在里面。
说到这，可能有些人会问，面积和周长到底有什么关系呢？嘿，别着急，咱们慢慢来聊。
想象一下，咱们从小到大学过的很多东西，很多时候都是相辅相成的。
比如说，刚学走路的时候，总是先跟着旁边的妈妈走，等熟悉了才敢自己跑。
圆的周长就像是那条路，让你能更好地认识这个形状，而面积就是那条路的宽度，让你可以在上面跑得更快。
长得好，才能更容易找到快乐，这不就是生活的真谛吗？为什么我们要关注这个圆呢？圆的形状在我们生活中无处不在，看看你的盘子、杯子，甚至是车轮，都是圆的。
圆形的设计不仅好看，还能让物体更加稳定。
比如说，开车的时候，轮子一转，整个车就能轻松地跑起来。
周长决定了轮子的周围，而面积则决定了轮子的大小和承载力。
哇，真是太有趣了，感觉像是在解开一个秘密的盒子。
当我们深入探讨这个关系时，似乎也能理解一些生活的哲理。
比如说，想要在生活中取得成功，光有努力的周长是不够的，咱们还得有足够的“面积”去容纳更多的知识和经验。
小学六年级奥数教材课程圆的周长和面积一条线段绕着它固定的一端在平面内旋转一周，它的另一端在平面内画出一条封闭的曲线，这条封闭的曲线就是圆。
画圆时，固定的一点叫做圆心，从圆心到圆上任意一点的线段叫做圆的半径，在同一个圆中，所有的半径都相等。
通过圆心，并且两端在圆上的线段叫做直径。
在同一个圆中，所有的直径都相等，且等于半径的2倍。
圆心决定圆的位置，半径决定圆的大小。
任意一个圆，它的周长除以直径的商总是一个固定的数，这个数叫圆周率。
如果用C 表示圆周的长度，d 表示这个圆的直径，r 表示它的半径，π表示圆周率，就有C dπ=或2C r。
π是一个无限不循环小数，π=3.14159265358979323846…。
圆的周长：C=2πr 或C=πd，圆的面积：S=πr 2。
圆的周长和面积计算的基本方法是仔细观察，发现特点，找出内在的联系，常常通过对图形的割补、旋转、平移、等积变形等方法加以解决。
需要精巧的构思和恰当的设计，把形象思维和抽象思维结合起来。
(本讲π均取 3.14)例1、上海外滩海关大钟钟面的直径是5.8米，钟面的面积是多少平方米？时针长2.7米，时针绕一圈时针尖端走过途径的长度是多少米？(得数保留一位小数)分析与解法：钟面的直径是5.8米这个条件是直接的，时针长指的是半径。
解：钟面的面积是：3.14×(5.8×2)2≈26.4(平方米)。
时针绕一圈时针尖端走过途径的长度是：2×3.14×2.7≈17.0(米)。
例2、如图所示，试比较大圆的面积与阴影部分的面积、大圆的周长与阴影部分的周长。
图图(1)分析与解法：本题有两问，一是比较阴影部分面积与大圆的面积；二是比较阴影部分周长与大圆的周长。
为了考虑问题方便，我们把图经过割补成图(1)，在图(1)中更容易看出大圆与小圆阴影部分的关系。
学习目标总结重点AOB解：先比较大圆面积与阴影部分的面积。
设大圆半径为r，则小圆半径为r，大圆面积为S 1=πr 2。
知识梳理：一根31.4米长的绳子，用它围成的正方形面积大，还是围成圆的面积大？大多少？围成的圆或正方形的周长是米，算出它们的面积再比较大小。
正方形的面积： ÷4=（米） ×≈（平方米） 圆的面积： ÷2÷=5（米） ×5×5=（平方米） 围成的圆面积大 －=（平方米）答：围成的圆面积大，大平方米。
一、圆的周长圆周长的意义：围成圆的曲线的长度叫作圆的周长。
直径大的圆，周长大；直径小的圆，周长小。
圆周长的计算公式：如果用字母C 表示圆的周长，那么=C d π或=2C r π。
圆周长计算公式的应用： 1 已知半径求周长：=2C r π。
2 已知直径求周长：=C d π。
3 已知周长求半径：2r C π=÷÷。
4 已知周长求直径：d C π=÷。
二、圆的面积圆面积的含义：圆形物体所占平面的大小或圆形物体表面的大小就是圆的面积。
圆面积的计算公式：如果用S 表示圆的面积，圆的面积计算公式可写成2S r π=。
圆面积的计算公式： 1 已知半径求面积：2S r π=。
2 已知直径求面积：因为2d r =，所以2()2d S π=或24S d π=。
3 已知周长求面积：因为2r C π=÷÷，所以2(2)S C ππ=÷÷。
典例精析例题1 在长6分米，宽4分米的长方形中画一个最大的半圆，半圆的周长和面积各是多少？ 解答过程：以长6分米为直径的半圆最大。
R=6÷2=3（分米）半圆周长=6×6÷2=（分米） 半圆面积=×3²÷2=（平方分米）答：半圆周长为分米，半圆面积为平方分米。
技巧点拨：半圆周长=直径半圆弧长，半圆面积=圆面积÷2。
例题2 用26米长的篱笆围成一个圆形苗圃，篱笆接头处用去米，苗圃的面积是多少？ 解答过程： 26－=（米） ÷2÷=4（米） ×4²=（平方米）答：苗圃的面积是平方米。
第十八章 圆的周长和面积知识要点如右图所示，当一条线段OA 绕着固定端点O 在平面内旋转一周，它的另一端点A 在平面内画出了一条封闭的曲线，这条封闭的曲线叫做圆。
围成圆的曲线叫做圆周，线段OA 叫做圆的半径，通常用r 或R 表示。
O 点是这个圆的圆心。
在同一个圆中，所有的半径都相等。
通过圆心，并且两端都在圆上的线段叫做直径。
在同一个圆内，所有直径都相等，且等于半径的2倍。
圆心决定圆的位置，半径决定圆的大小。
无论什么圆，它的周长除以直径的商是一个固定的数，这个数叫圆周率，用π表示。
如果用C 表示圆周的长度，d 表示这个圆的直径，那么，π＝C d 。
π是一个无限不循环小数：π＝3.14159265358979323846…圆的周长：C ＝2πr 或C ＝πd 圆的面积：S ＝πr 2＝π(2d )2＝π(2C π)2＝24C π 扇形是由圆心角的两条半径和圆心角所对的弧围成的图形。
如果扇形的圆心角是n ，那么当圆周长C ＝2πr 时，扇形的弧长计算方法：L ＝360n ×2πr ＝180n ×πr 例1 (第五届“希望杯”邀请赛试题)如图，ABCD 是边长为10厘米的正方形，且AB 是半圆的直径，则阴影部分的面积是 平方厘米。
(π取3.14)点拨 过E 点作AB 的垂线，垂足为O ，因为∠CAB＝45°，所以点O 是半圆的圆心，则阴影部分的面积等于梯形OECB 的面积，减去圆O 面积的14。
解 过E 点作AB 的垂线，垂足为0。
∵∠CAB ＝45°，∴点0是半圆的圆心。
则S 阴影＝S 梯形OECB －14S ⊙O＝(5＋10)×5÷2－ ×52＝17.875(平方厘米)例2 将半径分别是4厘米和3厘米的两个半圆，如图放置。
求阴影部分的周长。
点拨阴影部分的周长为小半圆的弧长加上大半圆的弧长，再加两条线段的长。
两个半圆的半径分别为4厘米和3厘米；两条线段分别是4厘米和3×2－4＝2(厘米)。
解 (1)两个半圆的弧长是：2×3.14×4÷2＋2×3.14×3÷2＝12.56＋9.42＝21.98(厘米)(2)两条线段的长：4＋(3×2－4)＝6(厘米)(3)阴影部分的周长为：21.98＋6＝27.98(厘米)答：阴影部分的周长是29.98厘米。
例3 直径均为1分米的四根管子被一根金属带紧紧地捆在一起，如下图。
试求金属带的长度和阴影部分的面积。
点拨要想求金属带的长度，我们必须把它分成8个部分来观察，金属带的长度正好是管子直径的4倍和一根管子圆周长度的总和。
中心阴影部分的面积等于中间正方形的面积减去一个圆的面积，其中正方形的边长等于直径。
解金属带的长度：1×4＋3.14×1＝7.14(分米)阴影面积：1×1－3.14×(1 2)2＝1－0.785＝0.215(平方分米)答：金属带的长度为7.14分米，阴影部分的面积为0.215平方分米。
说明我们在计算比较复杂的周长和面积时，要善于把这个圆形分解再重新组合，这样才会看得清楚明白。
例4 如图，圆的周长是12.56厘米，圆的面积是长方形面积的25，求阴影部分的周长。
点拨阴影部分的周长是半圆的弧长，加上两条长方形的长和一条宽。
已知圆的周长，容易求出半径，再求出圆的面积。
求出圆的面积，就可以求出长方形的面积，长方形的宽就是圆的直径，从而可以求出长方形的长，这样就可以求出阴影部分的周长了。
解半圆的弧长：12.56÷2＝6.28(厘米)长方形的面积：3.14×(12.56÷3.14÷2)2÷2 5＝3.14×4÷2 5＝31.4(平方厘米)长方形的长：31.4÷(12.56÷3.14)＝7.85(厘米)阴影部分的周长：6.28＋7.85×2＋12.56÷3.14＝6.28＋15.7＋4＝25.98(厘米)答：阴影部分的周长为25.96厘米。
例5 如右图，半圆的半径为15厘米，∠AOB＝90°，∠COD＝120°，CD＝26厘米，半圆中阴影部分的面积是多少平方厘米？点拨本题是一道比较复杂的问题，需要引辅助线和求扇形面积等方面的知识。
解三角形COD的面积：过点O作CD的垂线交互AB于F，交CD于E，连接DF，因为∠FOD＝60°，则△DFO 是正三角形。
DE为△DFO的对称轴，所以FE＝EO＝7.5(厘米)。
则三角形COD的面积为：26×7.5×12＝97.5(平方厘米)圆心角为120°的扇形的面积： 23.1415360⨯×120＝225 3.143⨯＝75×3.14＝235.5(平方厘米) 由弦CD 和弧CD 围成的弓形面积：235.5－97.5＝138(平方厘米)圆心角为90°的扇形面积：23.1415360⨯×90＝176.625(平方厘米) 三角形AOB 的面积：15×15×12＝112.5(平方厘米) 由弦AB 和弧AB 围成的弓形的面积：176.625－112.5＝64.125(平方厘米)阴影部分的面积：138－64.125＝73.875(平方厘米)答：阴影部分的面积是73.875平方厘米。
例6 如图，在半径AB 为20厘米，圆心角为45°的扇形中，以半径AB 的中点O 为圆心，以OA 为半径画一个半圆，交BC 于D 。
求阴影部分的面积。
点拨 图中阴影部分看似两个毫不相干的图形，但如果我们连接AD 就会发现：弓形BD 和弓形AD 的面积相等，如果用圆心角45°的扇形面积减去中间等腰直角三角形的面积，就可以求出两个阴影部分的面积的和。
解 圆心角45°的扇形的面积：23.1420360⨯×45＝157(平方厘米) 等腰直角三角形ADB 的面积：20×(20÷2)÷2＝100(平方厘米)阴影部分的面积：157－100＝57(平方厘米)答：阴影部分的面积是57平方厘米。
说明 在求两块或两块以上阴影部分的面积时，有时也把这几块合在一起求。
例7 如右图所示，大圆的直径是4厘米，黑色面积大还是阴影面积大？是黑色部分周长大，还是阴影部分的周长大？并求出各自的面积。
点拨大圆面积＝π×(42)2＝4π(平方厘米)，4个小圆面积＝π×(44)2×4＝4π(平方厘米)，由此我们可以看出，黑色部分面积之和正好等于四个小圆互相重叠的部分面积之和，所以这两部分的面积应相等。
黑色部分的周长应该等于大圆周长再加上8个14的小圆周长，而阴影部分的周长恰好等于8个14小圆的周长，所以黑色部分的周长大于阴影部分的周长。
解 S大圆＝π×(42)2＝4π(平方厘米)S小圆＝π×(44)2＝π(平方厘米)S阴＝8×(14π－1×1÷2)＝2π－4(平方厘米)＝2.28(平方厘米)S黑＝S大圆－(4S小圆－S阴)＝4π－(4π－2.28)＝2.28(平方厘米) S阴＝S黑C大圆＝π×4＝4πC小圆＝π×2＝2πC黑＝4π＋8×14×2π＝8πC阴＝8×14×2πC黑＞C阴解题技巧计算周长时，首先要分清围成这一图形的边有哪些，再正确计算。
计算组合图形的面积，有很多图形都是不规则的，很难直接用公式计算出它们的面积，必须将组合图形进行分解，看清组合图形是由哪几个基本图形合并起来的，或是从哪一个基本图形里去掉哪一个或几个基本图形得到的。
有时需要把其中的部分图形进行平移、翻转、添加辅助线、割补、等积变形等方法，化难为易，这需要精巧的构思和恰当的解题策略，从而提高自己的形象思维和抽象思维能力。
竞赛能级训练A级1.(第十一届“华罗庚金杯”邀请赛试题)如下左图，圆O中直径AB与CD互相垂直，AB＝10厘米，CA＝50厘米。
以C为圆心，CA为半径画弧AEB。
求月牙ADBEA(阴影部分)的面积。
2.(第五届“希望杯”邀请赛试题)如上右图，大圆直径上的黑点是五等分点，则A、B、C 三部分的面积比为。
3.如下左图所示，正方形的边长为10厘米，在正方形中画了两个四分之一圆，试求图中阴影面积。
4.如上右图，三角形ABC是直角三角形，阴影工的面积比阴影Ⅱ的面积小23平方厘米。
问BC的长度是多少厘米？( 取3)5.如下左图，直径AB为3厘米的半圆，绕A逆时针旋转60°，使AB到达AC位置。
求图中阴影部分的周长。
6.上右图中每个小圆的半径是1厘米，阴影部分的周长是多少厘米？7.如下左图所示，正方形的边长是6厘米，求图中阴影部分的面积。
8.如上右图所示，小明从家到学校有三条由半圆弧组成的路可以走，怎么走近？为什么？9.有一个长方形如下左图所示位置，在桌子上不滑动地每秒钟转动90°。
试回答下列问题：(1)如果长方形AB＝3厘米，AD＝4厘米，AC＝BD＝5厘米。
把长方形转动一周后，顶点A 所经过的痕迹的长是多少厘米？(2)13秒以后，长方形B点离A点开始位置的水平距离是多少厘米？10.如上右图所示，已知扇形的弧长为12.56厘米。
求阴影部分的面积。
11.右图是400米跑道的示意图，两头是两个半圆，每一个半圆的弧长是100米；中间是直线，长为100米。
求两个半圆的面积之和与跑道所围成的面积之比。
12.求下图中阴影部分的面积。
(单位：厘米)B 级1.将边长为1的正三角形放在一条直线上(如下左图)，让三角形绕顶点C顺时针转动到位置2，再继续这样转到3的位置。
求A点走过的痕迹的长度。
2.上右图中的三角板(等腰直角)、正方形纸板、圆形纸板的面积都是40cm2，阴影部分的面积总和是30cm2，三张纸板盖住的面积总和是70cm2。
求三张纸板重叠部分A的面积。
3.下左图是＝座古钟的示意图，有白、黄、蓝三部分。
试问白色部分的面积与蓝色扇形的面积谁更大一些？为什么？4.上右图中正方形的周长是圆环周长的3倍。
当圆环形绕正方形无滑动地滚动一周又回到原来位置时，这个圆环转了几圈？5.在右图中，直角三角形ABC的斜边AC长20厘米，∠A＝30°，以C点为固定点将直角三角形顺时针旋转使斜边AC与短边BC成一直线。
求图中阴影部分的面积。
6.已知下左图中半圆直径为10厘米，求图中阴影部分的面积。
7.在上右图中，AB长8cm，OB长5cm，求阴影部分的面积。
8.求下左图中阴影部分的面积。
