小学奥数圆的周长与面积精编版
- 格式:doc
- 大小:598.00 KB
- 文档页数:4
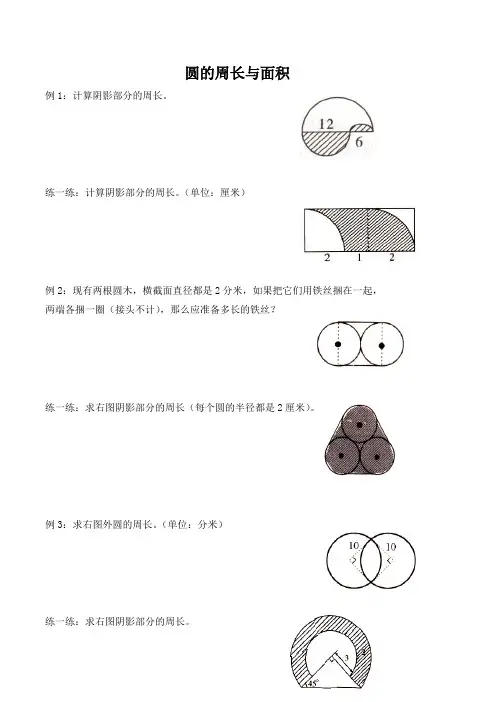
圆的周长与面积
例1:计算阴影部分的周长。
练一练:计算阴影部分的周长。
(单位:厘米)
例2:现有两根圆木,横截面直径都是2分米,如果把它们用铁丝捆在一起,两端各捆一圈(接头不计),那么应准备多长的铁丝?
练一练:求右图阴影部分的周长(每个圆的半径都是2厘米)。
例3:求右图外圆的周长。
(单位:分米)
练一练:求右图阴影部分的周长。
例4:如右图,已知正方形面积是60平方厘米,求圆的面积。
练一练:已知右图中阴影部分的面积是300平方厘米,求圆的面积。
例5:已知右图中阴影部分的面积是40平方厘米,求圆环的面积。
练一练:右图中平行四边形的面积是100平方厘米,求阴影部分的面积。
例6:有一个半圆形零件,周长是20.56厘米,求这个半圆形零件的面积。
练一练:如右图,一个扇形的圆心角是90°,它的周长是14.28厘米,求它的面积。
例7:图中ABCD是边长为4米的正方形,分别以AB、BC、CD、AD为直径画半圆,求这四个半圆弧所围成的阴影部分的面积。
练一练:图中三角形ABC是边长为6厘米的正三角形,求阴影部分的面积。
例8:计算阴影部分的面积。
练一练:计算阴影部分的面积。
(单位:厘米)
例9:求出右图中正方形面积与圆的面积比。
练一练:右图圆的面积是942平方分米,那么正方形的面积是多少?如果正方形的面积是360平方厘米,那么圆的面积是多少?。

附加专题2:圆的周长和面积一、填空:1、圆是平面上的一种()图形,围成圆的()的长叫做圆的周长。
在大大小小的圆中,它们的周长总是各自圆直径的()倍多一些,我们把这个固定的数叫做(),用字母()表示,它是一个()小数,在计算时,一般只取它的近似值()。
2、一个圆的直径扩大5倍,它的半径扩大()倍,它的周长扩大()倍,面积扩大()倍。
3、画一个周长12.56厘米的圆,圆规两脚间的距离是()厘米。
4、在一张长6厘米,宽4厘米的长方形纸片上画一个最大的圆,这个圆的半径是()厘米;如果画一个最大的半圆,这个圆的半径是()厘米,周长是(),面积是()。
5、()叫做圆的面积。
把圆沿着它的半径r分成若干等份,剪开后可以拼成一个近似的(),这个图形的长相当于圆周长的(),用字母表示是();宽相当于圆的(),用字母表示是()。
所以圆的面积S=( )×( ) =( )。
二、判断:1、圆的周长是这个圆的直径的3.14倍。
()2、小圆的圆周率比大圆的圆周率小。
()3、把一张圆形纸片对折若干次,所有折痕相交于圆心。
()4、圆的半径扩大3倍,它的直径就扩大6倍。
()5、半圆的周长等于圆周长的一半。
()6、经过一点可以画无数个圆。
()一、填空1、圆周率表示一个圆的()和()的倍数关系。
π约等于()。
2、在一个圆中,圆的周长是直径的()倍,是半径的()倍。
4、要画一个周长是31.4厘米的圆,圆规两角之间的距离是()厘米。
6、在一个正方形里面画一个最大的圆,这个圆的周长是6.28厘米,这正方形的面积是()平方厘米。
剩下的面积是()平方厘米。
7、大圆半径是3分米,小圆半径是2分米,小圆面积是大圆面积的()。
8、有大小两个圆,大圆直径是小圆半径的4倍,大圆周长是小圆的(),大圆面积是小圆的()。
9、用一根长12.56厘米的铁丝围成一个正方形,正方形的面积是()平方厘米;如果用这根铁丝围成一个圆,这个圆的面积是()平方厘米。
二、判断题(对的打√,错的打×)1,所有的直径都相等,所有的半径都相等. ()2,两端在圆上的线段,直径最长. ()3,经过圆心的线段就是直径. ()4,小圆的圆周率比大圆的圆周率小. ()5、圆的周长是6.28分米,那么半圆的周长是3.14分米。

第十讲 圆的周长和面积【知识概述】圆的认识:圆中心的一点叫做圆心,圆心一般用字母“o ”表示;连接圆心和圆上任意一点的线段叫做半径,半径一般用字母“r ”表示;通过圆心并且两端都在圆上的线段叫做直径,直径一般用字母“d ”表示。
d圆心决定圆的位置, O r 半径决定圆的大小。
圆的特征:(1)在同圆或等圆中,半径的长度都相等,直径的长度都相等,直径长度是半径长度的2倍,用字母表示是:d =2r 或r =2d。
(2)圆是轴对称图形,圆有无数条对称轴。
圆的对称轴是直径所在的直线。
圆的周长:围成圆的曲线的长。
周长一般用字母“C ”表示,C=πd=2πr .圆周率:圆的周长和直径的比值,用字母π表示。
(π≈3.14)圆的面积:圆所占平面的大小叫圆的面积,圆的面积一般用字母“S”表示, S =πr2.圆环的面积计算公式:S =πR2-πr2=π(R2-r2)扇形的面积公式: 360nr S n 360r S 22⨯=⨯=ππ或【典型例题】例1 求下面各圆的周长。
【学大名师】圆的周长是直径的π倍,是半径的2π倍。
解:(1) cm 3r =(2)d = 7dm84.18=(cm )98.21=(cm )例2 求下面各圆的面积。
(1)r = 4cm (2)d = 10dm (3)C = 18.84m【学大名师】圆的面积公式是2r S π=,要想求面积,要先求出半径。
解: (1)r=4cm 24.501614.3414.32=⨯=⨯(平方厘米)(2)d=10dm 10÷2=5(dm )5.782514.3514.32=⨯=⨯(2dm )(3)已知圆的周长,要先求出圆的半径,再利用2r S π=求面积。
C=18.84m3214.384.18=÷÷(m )26.28914.3314.32=⨯=⨯(2m )例3 小乌龟和小白兔又要比赛了,这一次小白兔沿大圆跑一圈,小乌龟沿两个小圆“∞”跑一圈,谁跑的路程长呢?好好想一想。

【奥数专题】精编人教版小学数学6年级上册工程问题(试题)含答案与解析奥数专题:精编人教版小学数学6年级上册工程问题(试题)含答案与解析工程问题是小学数学中常见的题型之一,能够锻炼学生的逻辑思维和综合运算能力。
本文将为大家精编人教版小学数学6年级上册的工程问题试题,并附带详细的答案与解析,希望能够帮助到同学们更好地理解和掌握这一题型。
1. 小明修建了一个半径为3米的圆形花坛,请问这个花坛的周长是多少米?答案与解析:圆的周长公式为C = 2πr,其中r为半径,π取近似值3.14。
代入已知数据,得C = 2 × 3.14 × 3 = 18.84(米),所以这个花坛的周长为18.84米。
2. 小红家的房屋正前方有一个边长为6米的正方形草坪,现在要在这个草坪上种植鲜花,请问这个草坪的面积是多少平方米?答案与解析:正方形的面积公式为A = a^2,其中a为边长。
代入已知数据,得A = 6^2 = 36(平方米),所以这个草坪的面积为36平方米。
3. 丽丽要制作一个高度为2米的三角形旗帜,其中底边长为4米,请问这个旗帜的面积是多少平方米?答案与解析:三角形的面积公式为A = 0.5 ×底边长 ×高,代入已知数据,得A = 0.5 × 4 × 2 = 4(平方米),所以这个旗帜的面积为4平方米。
4. 小华要铺设一条长为5米的沟渠,他计划将沟渠分为相等的5段,请问每段的长度是多少米?答案与解析:将沟渠分为相等的5段,则每段的长度为总长度除以段数,即5 ÷ 5 = 1(米)。
所以每段的长度为1米。
5. 小明用了21个园木将一条长20米的小路两侧都种满,请问每个园木之间的距离是多少米?答案与解析:将小路分为21段,则每个园木之间的距离为总长度除以段数减1,即20 ÷ (21-1) = 1(米)。
所以每个园木之间的距离为1米。
6. 小红需要用12个石板铺满一个长为3米的小路,请问每块石板的长度是多少米?答案与解析:将小路分为12段,则每块石板的长度为总长度除以段数,即3 ÷ 12 = 0.25(米)。

学之导教育中心教案学生: 钱文洛授课时间: 4月24日课时: 2 年级:六年级教师:陆老师课题圆的周长和面积教案构架:一、知识回顾二、知识检测三、知识新授四、知识小结教案内容:一、知识回顾运用正、反比例知识解答应用题的一般方法和步骤:1、分析题意,找出题中的定量和两种相关联的量。
2、判断题目中两种相关联的量是成正比例还是成反比例。
3、设未知量为x,并写明计量单位。
4、根据正、反比例的意义列出比例式,并解比例5、检查后写出答案。
二、知识检验1、甲、乙两修路队各修32千米的路,甲队比乙队迟6天开工,结果同时完成。
甲、乙两队工作效率的比是8: 5,乙队每天修多少千米?本次内容掌握情况总结教务老师签字学生签字2、张师傅、李师傅两人合作加工一批零件,由张师傅独做需20小时,李师傅每小时能加工48个零件,现由两位师傅同时加工,完成任务时,张师傅加工的个数是李师傅的1211,这批零件共有多少个?3、甲、乙两个长方体容器,底面积之比为4:3,甲容器中水深9厘米,乙容器中水深5厘米,再往两个容器注入同样多的水,直到水深相等。
这样甲容器的水面应上升多少厘米?4、客、货两车同时从甲、乙两地相向而行,相遇时客、货两车所行的路程比是8:7,相遇后货车每小时比相遇前每小时多走18千米,客车仍按原速前进,结果两车同时到达对方的出发站。
已知客车一共行15小时,甲、乙两地相距多少千米?5、客车以一定的速度从A 地到B 地去。
如果客车每小时比原来多行25千米,那么所用的时间只是原来的43。
如果每小时比原来少行25千米,那么所用的时间要比原来多用4小时,A 、B 两地相距多少千米?三、知识新授有关圆的问题,我们可以运用“化曲为直”的方法,可以将圆的周长转化为线段的长,将圆的面积转化为长方形的面积,这样计算更加简便。
例:计算阴影部分的周长。
练一练:计算阴影部分的周长。
(单位:厘米)例:现有两根圆木,横截面直径都是2分米,如果把它们用铁丝捆在一起,两端各捆一圈(接头不计),那么应准备多长的铁丝?练一练:求右图阴影部分的周长(每个圆的半径都是2厘米)。

第二讲平面图形、圆的周长面积一、课程引入正确而巧妙进行平面图形的周长面积计算、圆的周长面积计算二、基本理论理论点11.通过对平面图形的周长和面积的有关知识进行系统整理,进一步理解周长和面积,能正确计算常见平面图形的周长和面积。
理论点22.沟通几种基本图形的面积公式及其推导过程的内在联系,体会数学知识和方法的内在联系,体会转化、类比等数学思想方法,发展初步的推理能力。
理论点33.在整理和复习的过程中,通过多种活动,巩固所学知识,能综合运用学过的数学知识和方法解决生活中的现象,解决简单的实际问题,发展解决问题的能力和反思意识,发展三、例题精析【例题1】【题干】右图中的阴影部分BCGF 是正方形,线段FH 长18厘米,线段AC 长24厘米,则长方形ADHE 的周长是__________厘米。
【例题2】【题干】如右图所示,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和L 形区域乙和丙。
甲的边长为4厘米,乙的边长是甲的边长的1.5倍,丙的边长是乙的边长的1.5倍,那么丙的周长为多少厘米?EF 长多少厘米?A CBF E HB A【题干】如下图所示,200米赛跑的起点和终点都在直跑道上,中间的弯道是一个半圆。
已知每条跑道宽1.22米,那么外道的起点在内道起点前面多少米?(精确到0.01米)【例题4】【题干】左下图中四个圆的半径都是5厘米,求阴影部分的面积。
四、随堂练习【基础】1.一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米(如图虚线所示),则面积增加9900平方米,问原来这块正方形苗圃的面积是多少平方米?2.在右图中(单位:厘米),两个阴影部分面积的和是多少平方厘米.【巩固】1. 算出圆内正方形的面积为. 1215206厘米EDCBA 2.,直角边长2厘米,图中阴影部分面积是多少平方厘米.【拔高】1.右图中的圆是以O 为圆心、径是10厘米的圆,求阴影部分的面积。
圆的周长与面积
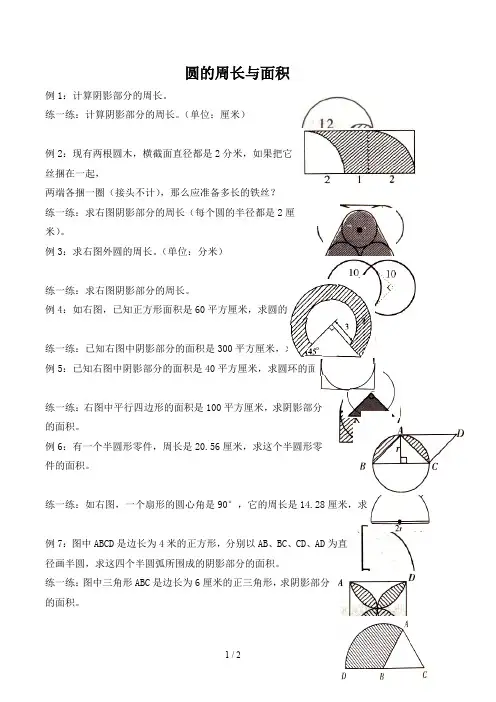
例1:计算阴影部分的周长。
练一练:计算阴影部分的周长。
(单位:厘米)
例2:现有两根圆木,横截面直径都是2分米,如果把它们用铁丝捆在一起,
两端各捆一圈(接头不计),那么应准备多长的铁丝?
练一练:求右图阴影部分的周长(每个圆的半径都是2厘
米)。
例3:求右图外圆的周长。
(单位:分米)
练一练:求右图阴影部分的周长。
例4:如右图,已知正方形面积是60平方厘米,求圆的面积。
练一练:已知右图中阴影部分的面积是300平方厘米,求圆的面积。
例5:已知右图中阴影部分的面积是40平方厘米,求圆环的面积。
练一练:右图中平行四边形的面积是100平方厘米,求阴影部分
的面积。
例6:有一个半圆形零件,周长是20.56厘米,求这个半圆形零
件的面积。
练一练:如右图,一个扇形的圆心角是90°,它的周长是14.28厘米,求它的面积。
例7:图中ABCD是边长为4米的正方形,分别以AB、BC、CD、AD为直
径画半圆,求这四个半圆弧所围成的阴影部分的面积。
练一练:图中三角形ABC是边长为6厘米的正三角形,求阴影部分
的面积。
例8:计算阴影部分的面积。
练一练:计算阴影部分的面积。
(单位:厘米)
例9:求出右图中正方形面积与圆的面积比。
练一练:右图圆的面积是942平方分米,那么正方形的面积是多少?如果正方形的面积是360平方厘米,那么圆的面积是多少?。

小学六年级奥数教材课程圆的周长和面积一条线段绕着它固定的一端在平面内旋转一周,它的另一端在平面内画出一条封闭的曲线,这条封闭的曲线就是圆。
画圆时,固定的一点叫做圆心,从圆心到圆上任意一点的线段叫做圆的半径,在同一个圆中,所有的半径都相等。
通过圆心,并且两端在圆上的线段叫做直径。
在同一个圆中,所有的直径都相等,且等于半径的2倍。
圆心决定圆的位置,半径决定圆的大小。
任意一个圆,它的周长除以直径的商总是一个固定的数,这个数叫圆周率。
如果用C 表示圆周的长度,d 表示这个圆的直径,r 表示它的半径,π表示圆周率,就有C dπ=或2C r。
π是一个无限不循环小数,π=3.14159265358979323846…。
圆的周长:C=2πr 或C=πd,圆的面积:S=πr 2。
圆的周长和面积计算的基本方法是仔细观察,发现特点,找出内在的联系,常常通过对图形的割补、旋转、平移、等积变形等方法加以解决。
需要精巧的构思和恰当的设计,把形象思维和抽象思维结合起来。
(本讲π均取 3.14)例1、上海外滩海关大钟钟面的直径是5.8米,钟面的面积是多少平方米?时针长2.7米,时针绕一圈时针尖端走过途径的长度是多少米?(得数保留一位小数)分析与解法:钟面的直径是5.8米这个条件是直接的,时针长指的是半径。
解:钟面的面积是:3.14×(5.8×2)2≈26.4(平方米)。
时针绕一圈时针尖端走过途径的长度是:2×3.14×2.7≈17.0(米)。
例2、如图所示,试比较大圆的面积与阴影部分的面积、大圆的周长与阴影部分的周长。
图图(1)分析与解法:本题有两问,一是比较阴影部分面积与大圆的面积;二是比较阴影部分周长与大圆的周长。
为了考虑问题方便,我们把图经过割补成图(1),在图(1)中更容易看出大圆与小圆阴影部分的关系。
学习目标总结重点AOB解:先比较大圆面积与阴影部分的面积。
设大圆半径为r,则小圆半径为r,大圆面积为S 1=πr 2。

小学圆的面积奥数题100道及答案(完整版)题目1一个圆的半径是3 厘米,它的面积是多少平方厘米?答案:圆的面积= π×半径×半径,即3.14×3×3 = 28.26(平方厘米)题目2圆的直径是8 分米,求面积。
答案:半径= 8÷2 = 4 分米,面积= 3.14×4×4 = 50.24(平方分米)题目3一个圆的周长是18.84 米,求其面积。
答案:周长= 2×π×半径,所以半径= 18.84÷(2×3.14)= 3 米,面积= 3.14×3×3 = 28.26(平方米)题目4圆的面积是12.56 平方厘米,求半径。
答案:3.14×半径×半径= 12.56,半径×半径= 4,半径= 2 厘米题目5直径为10 厘米的圆,面积比半径为6 厘米的圆的面积小多少?答案:直径10 厘米的圆半径为5 厘米,面积为 3.14×5×5 = 78.5 平方厘米;半径6 厘米的圆面积为3.14×6×6 = 113.04 平方厘米,小113.04 - 78.5 = 34.54 平方厘米题目6一个圆的半径扩大3 倍,面积扩大多少倍?答案:原来面积= π×半径×半径,半径扩大3 倍后,面积= π×(3×半径)×(3×半径)= 9×π×半径×半径,面积扩大9 倍题目7两个圆的半径分别是2 厘米和3 厘米,它们面积的和是多少?答案:面积分别为3.14×2×2 = 12.56 平方厘米,3.14×3×3 = 28.26 平方厘米,和为12.56 + 28.26 = 40.82 平方厘米题目8一个圆的面积是50.24 平方分米,在里面画一个最大的正方形,正方形的面积是多少?答案:圆的半径= √(50.24÷3.14)= 4 分米,正方形的对角线是圆的直径为8 分米,正方形面积= 对角线×对角线÷2 = 8×8÷2 = 32 平方分米题目9圆的半径由4 厘米增加到6 厘米,面积增加了多少平方厘米?答案:原来面积= 3.14×4×4 = 50.24 平方厘米,新面积= 3.14×6×6 = 113.04 平方厘米,增加了113.04 - 50.24 = 62.8 平方厘米题目10在一个边长为8 厘米的正方形中画一个最大的圆,圆的面积是多少?答案:圆的直径= 8 厘米,半径= 4 厘米,面积= 3.14×4×4 = 50.24 平方厘米题目11已知圆的面积是28.26 平方米,求周长。
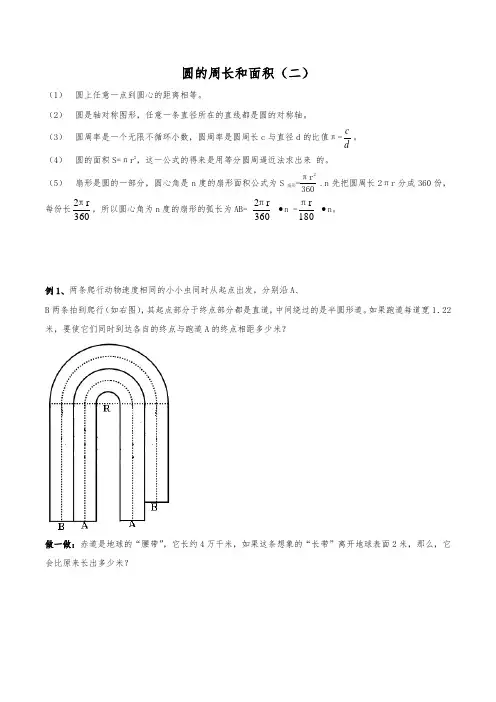
圆的周长和面积(二)(1) 圆上任意一点到圆心的距离相等。
(2) 圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴。
(3) 圆周率是一个无限不循环小数,圆周率是圆周长c 与直径d 的比值π=d c 。
(4) 圆的面积S=πr 2,这一公式的得来是用等分圆周逼近法求出来 的。
(5) 扇形是圆的一部分,圆心角是n 度的扇形面积公式为S 扇形=πr 2360.n 先把圆周长2πr 分成360份,每份长360r 2π,所以圆心角为n 度的扇形的弧长为AB= 360r 2π •n =180r π •n 。
例1、两条爬行动物速度相同的小小虫同时从起点出发,分别沿A 、B 两条拍到爬行(如右图),其起点部分于终点部分都是直道,中间绕过的是半圆形道。
如果跑道每道宽1.22米,要使它们同时到达各自的终点与跑道A 的终点相距多少米?做一做:赤道是地球的“腰带”,它长约4万千米,如果这条想象的“长带”离开地球表面2米,那么,它会比原来长出多少米?例2、如右下图,如果四个圆的半径为1厘米,求:(1)阴影部分的总面积。
(2)四个圆盖住的总面积。
做一做:求右下图中阴影部分与大圆的面积之比和周长之比。
例3、如右图,其中圆的周长等于正三角形的一条边的边长。
该圆沿着三角形外周滚动一周,问:圆自转了多少圈?做一做:桌上放置着大小一样的两枚硬币,其中一枚硬币固定不动,另外一枚硬币沿着定币的外缘做无滑动的滚动。
当动币绕着定币滚动一周之后,动币自动转了几圈?例4、如下图所示,一个圆正在五角星形的外侧,从A处开始做于正五角形的变相切(即紧靠边)的滚动。
如果BC长度等于圆周长,问:当此圆滚动回到原出发点时(包括自转)共转了几圈?做一做:如右图,若一个圆的周长等于一个正方形的边长,将此圆绕着正方形外侧滚动一周,则圆转了几圈??例5、如下图,在一个大正方形里有一个小正方形里有一个小正方形ABCD,小正方形沿大正方形的变翻转,翻转两次后,求顶点B所划过的曲线的长度,并画出这一曲线(大正方形的边长为2厘米,小正方形的边长为1 厘米)。
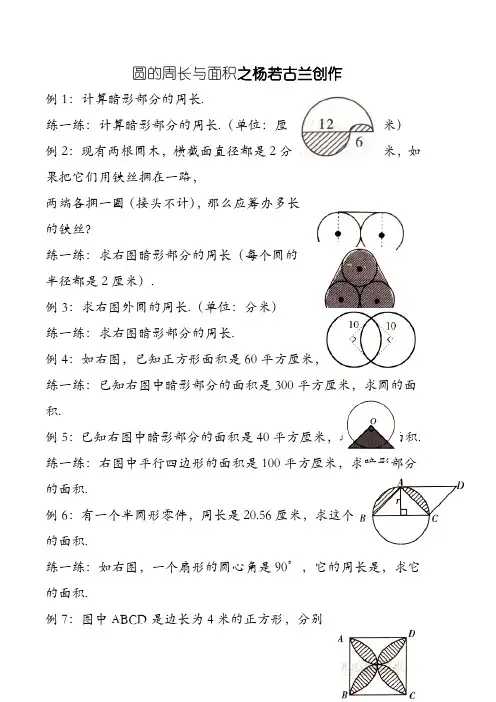
圆的周长与面积之杨若古兰创作
例1:计算暗影部分的周长.
练一练:计算暗影部分的周长.(单位:厘米)例2:现有两根圆木,横截面直径都是2分米,如果把它们用铁丝捆在一路,
两端各捆一圈(接头不计),那么应筹办多长
的铁丝?
练一练:求右图暗影部分的周长(每个圆的
半径都是2厘米).
例3:求右图外圆的周长.(单位:分米)
练一练:求右图暗影部分的周长.
例4:如右图,已知正方形面积是60平方厘米,求圆的面积.
练一练:已知右图中暗影部分的面积是300平方厘米,求圆的面积.
例5:已知右图中暗影部分的面积是40平方厘米,求圆环的面积.练一练:右图中平行四边形的面积是100平方厘米,求暗影部分的面积.
例6:有一个半圆形零件,周长是20.56厘米,求这个半圆形零件的面积.
练一练:如右图,一个扇形的圆心角是90°,它的周长是,求它的面积.
例7:图中ABCD是边长为4米的正方形,分别
以AB、BC、CD、AD为直径画半圆,求这四个半圆弧所围成的暗影部分的面积.
练一练:图中三角形ABC是边长为6厘米的正三角形,求暗影部分的面积.
例8:计算暗影部分的面积.
练一练:计算暗影部分的面积.(单位:厘米)
例9:求出右图中正方形面积与圆的面积比.
练一练:右图圆的面积是942平方分米,那么正方形的面积是多少?如果正方形的面积是360平方厘米,那么圆的
面积是多少?。
第十八章 圆的周长和面积知识要点如右图所示,当一条线段OA 绕着固定端点O 在平面内旋转一周,它的另一端点A 在平面内画出了一条封闭的曲线,这条封闭的曲线叫做圆。
围成圆的曲线叫做圆周,线段OA 叫做圆的半径,通常用r 或R 表示。
O 点是这个圆的圆心。
在同一个圆中,所有的半径都相等。
通过圆心,并且两端都在圆上的线段叫做直径。
在同一个圆内,所有直径都相等,且等于半径的2倍。
圆心决定圆的位置,半径决定圆的大小。
无论什么圆,它的周长除以直径的商是一个固定的数,这个数叫圆周率,用π表示。
如果用C 表示圆周的长度,d 表示这个圆的直径,那么,π=C d 。
π是一个无限不循环小数:π=3.14159265358979323846…圆的周长:C =2πr 或C =πd圆的面积:S =πr 2=π(2d )2=π(2C π)2=24C π 扇形是由圆心角的两条半径和圆心角所对的弧围成的图形。
如果扇形的圆心角是n ,那么当圆周长C =2πr 时,扇形的弧长计算方法:L =360n ×2πr =180n ×πr 例1 (第五届“希望杯”邀请赛试题)如图,ABCD 是边长为10厘米的正方形,且AB 是半圆的直径,则阴影部分的面积是 平方厘米。
(π取3.14)点拨 过E 点作AB 的垂线,垂足为O ,因为∠CAB=45°,所以点O 是半圆的圆心,则阴影部分的面积等于梯形OECB 的面积,减去圆O 面积的14。
解 过E 点作AB 的垂线,垂足为0。
∵∠CAB =45°,∴点0是半圆的圆心。
则S 阴影=S 梯形OECB -14S ⊙O=(5+10)×5÷2- ×52=17.875(平方厘米)例2 将半径分别是4厘米和3厘米的两个半圆,如图放置。
求阴影部分的周长。
点拨阴影部分的周长为小半圆的弧长加上大半圆的弧长,再加两条线段的长。
两个半圆的半径分别为4厘米和3厘米;两条线段分别是4厘米和3×2-4=2(厘米)。
第七章圆的周长和面积
一、典型例题
1、一个半径10米的圆形花坛,它的占地面积是多少?在它的一周围一圈篱笆,篱笆长多少米?
思路点拨:圆的面积公式:S=πr2,圆的周长公式:C=2πr,根据公式可以做出来。
解答:
S=π102C=2πr
=3.14×100 =2×3.14×10
=314(平方米) =62.8(米)
答:它的占地面积是314平方米,篱笆长62.8米。
二、知识运用
1、一根长5米的绳子系着一只羊,栓在草地中央的树桩上,羊吃草的面积最多是多少平方米?
2、一种麦田的自动旋转喷灌器的射程是10米,它能喷灌的面积多少平方米?
3、求右图阴影部分面积:(单位:厘米)
4、一元硬币的半径是1.2厘米,求它的周长和面积。
5、用一块边长6分米的正方形纸剪一个最大的圆,圆的面积是多少?
6、用26米长的篱笆围成一个圆形苗圃,篱笆接头处用去0.88米。
苗圃的面积多少?
7、在长6分米,宽4分米的长方形中画一个最大的圆,圆的周长和面积各是多少?
8、求各图的周长和面积:(单位:米)。
圆的周长与面积
例1:计算阴影部分的周长。
练一练:计算阴影部分的周长。
(单位:厘米)
例2:现有两根圆木,横截面直径都是2分米,如果把它们用铁丝捆在一起,两端各捆一圈(接头不计),那么应准备多长的铁丝?
练一练:求右图阴影部分的周长(每个圆的半径都是2厘米)。
例3:求右图外圆的周长。
(单位:分米)
练一练:求右图阴影部分的周长。
例4:如右图,已知正方形面积是60平方厘米,求圆的面积。
练一练:已知右图中阴影部分的面积是300平方厘米,求圆的面积。
例5:已知右图中阴影部分的面积是40平方厘米,求圆环的面积。
练一练:右图中平行四边形的面积是100平方厘米,求阴影部分的面积。
例6:有一个半圆形零件,周长是20.56厘米,求这个半圆形零件的面积。
练一练:如右图,一个扇形的圆心角是90°,它的周长是14.28厘米,求它的面积。
例7:图中ABCD是边长为4米的正方形,分别以AB、BC、CD、AD为直径画半圆,求这四个半圆弧所围成的阴影部分的面积。
练一练:图中三角形ABC是边长为6厘米的正三角形,求阴影部分的面积。
例8:计算阴影部分的面积。
练一练:计算阴影部分的面积。
(单位:厘米)
例9:求出右图中正方形面积与圆的面积比。
练一练:右图圆的面积是942平方分米,那么正方形的面积是多少?如果正方形的面积是360平方厘米,那么圆的面积是多少?。
奥数训练 圆的周长和面积附答案 A m 阪文 第4题 O A A 第5题 图中阴影部分 的面积等于 平方厘 米 平 16平方厘平方厘米(取 C 第8题 C 点•那么 20厘米为直径画一个半圆,阴影部分①的面积比②的面积小 厘米,其中,圆弧BD 的圆心是 6 .两个半径为2厘米的二圆如右图摆放 第2题 则阴影部分的面积是 其中四边形 OABC 是正方形,图中阴影部分的面积是 如果圆的半径为1厘米,那么,阴影部分的面积是 5 •如图,ABCD 是正方形,边长是 a 厘米 10•如图,以直角三角形的直角边长 米.BC= ___________ . B 点移动到B'点,则阴影 第3题 _____ 平方厘米 3•如图,ABCD 是边长为10厘米的正方形,且AB 是半圆的直径,则阴影部分的面积是 取 3.14 ) 4.如图是半径为6厘米的半圆,让这个半圆绕 A 点按顺时针方向旋转 30°,此时 部分的面积是 _______________________ 平方厘米. 2.如图是 第1题 个边长为 4厘米的正方形 ,吟 n =3). 7.如右图,正方形DEOF 在四分之一圆中 方厘米.(n 取3.14 .) &如图,ABC 是等腰直角三角形,D 是半圆周的中点,BC 是半圆的直径•已知 AB=BC=10厘米,那么阴影部分 的面积是 _______________ 平方厘米.(n 的值取3.14 ) 9.如图,其中AB=10厘米,C 点是半圆的中点.那么,阴影部分的面积是 平方厘米.(n 取3.14 ) 平方厘米.(n 其中 P 点是半圆的中点,点 Q 是正方形一 (取 n =3.14) (共 11小题) 10厘米的正方形和直径是 10厘米的半圆组成如图所示 则阴影部分的面积为 __________________ 平方厘米 一.填空题 1 .边长是 边的中点, A I c 第6题 B E 9 第7题第9题 第10题第11题 11 •如图,阴影部分的面积是 _ _ 平方厘米. 二•解答题(共7小题)12•如图是一个圆心为 0,半径是10厘米的圆•以C 为圆心,CA 为半径画一圆弧,求阴影部分的面积.13•求下列各图中阴影部分的周长.(1) 图1中,两个小半圆的半径均为 3厘米.(2)图2中,四边形为平行四边形圆弧形对的圆心角为 60°,半径为6厘米.(3)图3中,正方形内有一个以正方形的边长为半径的 二圆弧和两个以正方形边长为直径的 二圆弧,已知正 4 215・如图,有一只狗被缚在一建筑物的墙角上,这个建筑物是边长都等于6米的等边三角形,绳长是 8米•求绳被狗拉紧时,狗运动后所围成的总面积. 方形边长为4厘米.(4)图4中,在半径为14•下面是由一个平行四边形和一个半圆形组成的图形,已知半圆的半径是 10厘米,计算图中阴影部分的面16.左图正方形边长为2厘米.以顶点A为圆心边长AB为半径作二圆弧,再分别以ABAC为直径作半圆弧.求阴影部分面积.17•如图三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小14.88平方厘米,直径AB长8厘米,BC长多少厘米?18•如图所示,正方形ABCD等腰三角形ADE及半圆CAE若AB=2厘米,则阴影部分的面积是多少平方厘米?B A10x - 314* 2=16, x=17.3 ;答: 10x -157=16, BC 的长度是17.3厘米.故答案为: 10x=173 17.3厘米. 参考答案与试题解析一•填空题(共11小题)一 2 解:正方形和半圆的面积之和:10X 10+3.14 X ( 10*2) -2, =100+39.25=139.25 (平方厘米),三 角形PAB 的面积是:10X 15*2=75 (平方厘米),三角形PBQ 的面积是5X 5*2=12.5 (平方厘米), 则阴影部分的面积是:139.25 - 75 - 12.5=51.75 (平方厘米);答:阴影部分的面积是51.75平方厘米. 故答案为:51.75 . 此题考查了三角形、正方形和圆的面积公式的综合应用;连接 BP,找出这两个白色三角形的高,求出 空白部分的面积是解决本题的关键. 解:如图,4X 4X 1+3.14 X ( % 2*2=4X 4x2+3.14 X2 2*2=4+6.28=10.28 (平方厘米), 4 図 4 答:阴影部分的面积是 10.28平方厘米;故答案为:10.28 . 2 解:连接BE,如图:半圆面积:3.14 x ( 10*2) *2=39.25 (平方厘米), 2 三角形ABE 面积:10 *2*2=25 (平方厘米),月牙面积:(39.25 - 25)* 2=7.125 (平方厘米), 阴影面积: 25 - 7.125=17.875 (平方厘米).故答案为:17.875 . 解: S 阴影=S 扇形ABB'+S 半圆ADB'- S 半圆ADB',又S 半圆ACB=S^圆ADB', 所以S 阴影=S 扇形ABB'.扇形部分应该半径为 6X 2=12 (厘米),二X 3.14 X22-二x 2X 上x 2, =3.14 - 2=1.14 (平方厘米), 4 2 2 答:阴影部分的面积是 1.14平方厘米.故答案为:1.14 . 解:如图,正方形的面积=对角线x 对角线x 弊1U (平方厘米)四分之一圆的面积 -X 3.14 XI 2=0.785 (平方厘米)阴影部分的面积 =0.785 - -=0.285 (平方厘米)故填 0.285 . 4 2 =25 (平方厘米),SAFDB 梯形ABEF 的面积+半圆BDE 的面积, 梯形ABEF 的面积=(10* 2+10)X ( 10* 2)* 2= (平方厘米),半圆BDE 的面积=扌/哼冗 阴影部分的面积=AFDB 的面积-三角形 AFD 的面积,=(—+二n )- 25, =32.125 (平方厘米). 答:阴影部分的面积是 32.125平方厘米.故答案为:32.125 . 解: : 3.14 X 102 - 10X 」*2,=二X 3.14 X 100- 10X 5*2, =39.25 - 25, =14.25 (平方厘米) 360 2 S 答:阴影部分的面积是 14.25 (平方厘米).故答案为:14.25 . 1 九? 解: BC 的长度为 x 厘米,-X 20X x -3.14 X *2=16 2 1.解答:点评:2.解答:3.解答:4.解答:5.解答:6.解答:7.解答:8.解答:9.解答:10.解答: 即: 解: 360 1 2 5a x 3a 2+a x 卫 360 -2(吩a ) =37.68 (平方厘米).故答案为:37.68 . (平方厘米). 答: 图中阴影部分的面积等于 0.45a 平方厘米.故答案为: 2 0.45a . 解:阴影部分的面积是: 2 Xnr 解:因为 AFD=X 10x ( 10*2) 10x - 3.14 X 100* 2=16, a= 2 2 a =0.45aX 3.14 X2 2 - 2X 2-2, =3.14 - 2 , =1.14 (平方厘米);阴影部分的面积是 1.14平方厘米•故答案为:1.14 . (共 7小题)2 三角形 ABC 的面积为:所以 AC -2=ABK OO2=10X 2X 10*2=100 (平方厘米),2由上面计算可得: AC=100X 2=200,所以阴影部分的面积是:3.14 X 10X 10-2-( -X 3.14 X 200- 100) =157-( 157 - 100),4=157 - 57, =100 (平方厘米),答:阴影部分的面积是 100平方厘米.13. 解答:解:(1)大半圆的圆弧长:2X 3.14 X ( 3+3)* 2=18.84 (厘米);小半圆的圆弧长:2X 3.14 X 3-2=9.42 (厘米);阴影部分周长:18.84+9.42 X 2=37.68 (厘米).(2) 圆弧长:2X 3.14 X 6X 一=6.28 (厘米);平行四边形周长:6X 4=24 (厘米);360 阴影部分周长:6.28+24=30.28 (厘米).(3) 一个以正方形的边长为半径的丄圆弧长:2X 3.14 X 4X 二=6.28 (厘米); 4 4 两个以正方形边长为直径的丄圆弧长:3.14 X 4=12.56 (厘米);阴影部分周长:6.28+12.56=18.84 (厘米).(4) 阴影部分周长:2X 3.14 X 4=25.12 (厘米). 14. 解:如图,解答:把半圆内的阴影部分从左边割下补到左边,阴影部分即成为一个底为半圆半径的2倍,高是半圆半径-X 10X 2X 10=100(平方厘米);答:图中阴影部分的面积是 100平方厘米 215. 解:根据图可知:解答:大扇形的圆心角为:360 - 60=300 (度), 小扇形的圆心角为:180 - 60=120 (度),故总面积为: ^ . (平方米),360 360 答:狗运动后所围成的总面积为 175.84平方米.点评:此题考查如何求扇形的面积,还要注意圆心角度数的求法.11解: •解答: 答: •解答题 12.解答: 解:16. 左图正方形边长为2厘米.以顶点A为圆心边长AB为半径作一圆弧,再分别以AB AC为直径作半圆弧.求考点:组合图形的面积.专题:压轴题;平面图形的认识与计算.分析:如图所示,作出辅助线,则4个小弓形的面积相等,将①、②经过旋转、平移到③、④的位置,贝V阴影部分的面积=以正方形的边长为半径的丄乙的面积-三角形ABC的面积,代入数据即可求解.解答•丹2解答解:3.14 X2 X 2X 2-2,4=3.14 - 2,=1.14 (平方厘米);答:阴影部分的面积是1.14平方厘米.点评:此题主要考查了正方形的性质以及旋转的性质,难度适中,关键是将所求的阴影部分的面积转化为与圆和正方形的面积有关的图形的面积.17•如图三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小14.88平方厘米,直径AB长8厘米,BC长多少厘米?考占: P 八、、•组合图形的面积.专题:平面图形的认识与计算.分析:从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC的面积.又已知①的面积比②的面积小14.88平方厘米,故半圆面积比三角形ABC的面积小14.88平方厘米•求出半圆面积,再加上14.88即为三角形的面积,再根据三角形的面积公式解答即可.阴影部分面积.解答:2解:半圆面积为3.14 X(8—2)*2=25.12 (平方厘米),三角形ABC的面积为:25.12+14.88=40 (平方厘米).BC的长为:40X 2* 8=10 (厘米).答:BC长10厘米.点评:此题考查了学生三角形以及圆的面积公式及其应用,同时考查了学生观察图形的能力.18. 如图所示,正方形ABCD等腰三角形ADE及半圆CAE若AB=2厘米,贝V阴影部分的面积是多少平方厘米?考占: p 八、、•组合图形的面积.专题:平面图形的认识与计算.分析:把原图ADE以及圆弧AE移补到ADC以及圆弧AC,那么阴影部分的面积就是正方形的面积的一半,然后再进一步解答.解答:解:正方形的面积:2X 2=4 (平方厘米);阴影部分的面积:4-2=2 (平方厘米). 答:阴影部分的面积是2平方厘米.点评:分析图形,根据图形特点进行割补,寻求问题突破点.。
圆的周长与面积(二)
月 日 姓名:
【典型例题】
例1 如图,已知正方形的面积为15平方厘米,求圆的面积。
例2 如图,求阴影部分的周长和面积。
(单位:厘米)
例3 如图,求阴影部分的面积。
(单位:厘米)
例4 求图中阴影部分的面积?
例5.如图,∠BOA=90°,以AO 为直径画半圆交OD 于E ,如果图中①的面 积为1平方厘米,求阴影部分的面积。
5
4
例6.如图,O为圆心,CO垂直于AB,
为圆心,CA为半径画弧将圆分成二部分,
姓名:
1.如图所示,已知圆内正方形的面积为
2.面积都为100
144
3.求图中阴影部分的面积。
4.等腰直角三角形腰长1240
5.如图,求阴影部分面积。
(单位:厘米)
6.如图所示,∠AOB=90°,C 为AB 中点,已知阴影部分甲的面积为16
平方厘米,求阴影部分乙的面积?
课后作业
姓名: 家长签字: 成绩:
1.如图,已知正方形的面积为30平方厘米,求圆的面积。
2.有一个图案是由5个环组成,每个环内外直径分别为8和10,图中 两两相交的小曲边四边形(黑色部分)的面积相等。
已知5个环覆盖的总面 积是122.5,求每个小曲边四边形的面积。
3.如图,在边长为3的正方形内有一花瓶状的阴影部分图形,图中所 有曲线都是半径为1的圆弧,阴影部分的面积是多少?
4.求图中阴影部分是大圆面积的几分之几?阴影部分周长是大圆的几
5.如图,每个圆的直径都是6厘米,求阴影部分的面积。
【最新整理,下载后即可编辑】
圆的周长与面积
例1:计算阴影部分的周长。
练一练:计算阴影部分的周长。
(单位:厘米)
例2:现有两根圆木,横截面直径都是2分米,如果把它们用铁丝捆在一起,
两端各捆一圈(接头不计),那么应准备多长的
铁丝?
练一练:求右图阴影部分的周长(每个圆的半径都是2厘米)。
例3:求右图外圆的周长。
(单位:分米)
练一练:求右图阴影部分的周长。
例4:如右图,已知正方形面积是60平方厘米,求圆的面积。
练一练:已知右图中阴影部分的面积是300平方厘米,求圆的面积。
例5:已知右图中阴影部分的面积是40平方厘米,求圆环的面积。
练一练:右图中平行四边形的面积是100平方厘米,求阴影部分的面积。
例6:有一个半圆形零件,周长是20.56厘米,求这个半圆形零件的面积。
练一练:如右图,一个扇形的圆心角是90°,它的周长是14.28厘米,求它的面积。
例7:图中ABCD是边长为4米的正方形,分别以AB、BC、CD、AD 为直径画半圆,求这四个半圆弧所围成的阴影部分的
面积。
练一练:图中三角形ABC是边长为6厘米的正三角形,求阴影部分的面积。
例8:计算阴影部分的面积。
练一练:计算阴影部分的面积。
(单位:厘米)
例9:求出右图中正方形面积与圆的面积比。
练一练:右图圆的面积是942平方分米,那么正方形的面积是多少?如果正方形的面积是360平方厘米,那么圆的面积是
多少?。
第11讲圆的周长与面积(一)
例1:右图中大圆的周长与大圆中四个小圆周长的和相比,谁大?
思路分析:设大圆的直径为D,四个小圆的直径为d1,d2,d3,
d4,则有D= d1+d2+d3+d4。
大圆的周长=πD,四个小圆周长的和
=πd1+πd2+πd3+πd4=π(d1+d2+d3+d4),显然两周长相等。
解:两圆周长相等。
例2:求右图中阴影部分的周长。
思路分析:阴影部分周长包括三个部分:半圆的直径(扇形的
一条半径);二是半圆的弧长;三是圆心角为30°的扇形的弧长。
解:半圆的弧长:3.14×30÷2=47.1(厘米)
扇形的弧长:2×3.14×30÷12=15.7(厘米)
阴影部分周长:47.1+15.7+30=92.8(厘米)
例3:如右图,已知正方形的面积是60平方厘米,求圆的面积。
思路分析:圆的面积公式是S=πr²,但这里不能求出半径。
我们
可以将r²看作一个整体,就可以求出圆的面积。
解:3.14×(60÷4)=47.1(平方厘米)
例4:右图中,三个圆的面积都是200平方分米,求阴影部分面积。
思路分析:首先三个圆的半径相等,而阴影部分拼起来正好是
一个半圆。
(三角形内角和为180°)
解:200÷2=100(平方分米)
例5:下图中,圆的半径为6厘米,求阴影部分面积。
思路分析:将左图沿水平直径折叠,使阴影部分拼合成两个三角形,如图(a)。
再将图(a)带阴影的三角形绕长方形AB边中点O逆时针方向旋转90°,于是两个带阴影的三角形就拼合成了一个正方形,如图(b)。
解:S=6×6=36(平方厘米)
例6:求右图中阴影部分的面积。
(单位:厘米)
思路分析:连结点A与圆心O。
阴影部分的面积可用扇形
ABO的面积减去△ABO的面积求得。
阴影部分的面积还可以
用半圆的面积先减去扇形AOC的面积,再减去△ABO的面积
求得。
解法一:12÷2=6(厘米)
3.14×6²×(180-30×2)÷360-6×5.2÷2
=22.08(平方厘米)
解法二:3.14×6²÷2-3.14×6²×60÷360-6×5.2÷2=22.08(平方厘米)
例7:如图是由正方形和半圆形组成的图形。
其中P点为半圆周的中点,Q点为正方形一边的中点。
已知正方形的边长为10,那么阴影部分的面积是多少?(π取3.14)思路分析:过P做AD平行线,交AB于O点,P为半圆周的中点,所以O为AB中点。
有2ABCD DPC 101S 1010100S 12.522
ππ=⨯==⨯⨯=半圆,(). AOP OPQB 101101S 510+37.5S 105550.2222∆⎡⎤⎛⎫=⨯⨯==++⨯⨯= ⎪⎢⎥⎝
⎭⎣⎦梯形(), ABCD AOP DPC OPQB S S S S 10012.537.55012.512.551.75.ππ∆+-=+--=+≈半圆梯形- 作业:
1. 图中的等边三角形边长10厘米,求阴影部分周长。
2. 右图中有A 、B 、C 三个圆,已知C 圆的半径是1厘米,
求 A 、B 两个圆的周长相差几厘米?
3. 求图中阴影部分的周长。
(单位:厘米)
4. 如右图,在正方形ABCD 中,BD=20厘米,另外C 又在以
A 为圆心的圆周上。
求阴影部分的面积。
5. 如图,正方形面积是90平方厘米,求阴影部分面积。
6. 如下图,已知AD=BD=3厘米,求阴影部分面积。
7. 如上图半圆内有一个直角三角形ABC ,AB 长3厘米,
AC 长4厘米,求阴影部分面积。
(AB ²+AC ²=BC ²)
8. 右图中,圆O 的直径为8厘米,求阴影部分面积。
9. 如右图,圆的直径AB=6厘米,平行四边形ABCD 的面积
是7平方厘米,∠ABC=30°,求阴影部分面积。
1.
2.2*3.14*1=6.28(厘米)3.
4.114平方厘米
5.
6.
7.
8.
9.
[2×2-3.14×(2÷2)²]×2=1.72(平方厘米)。