电路—第12章问题习题解答

第12章三相电路12.1复习笔记一、对称三相电源如图12-1-1所示，由同频率、等幅值、相位互差120°的三个正弦电压源连接成的电源被称为对称三相电源。

对称三相电源有星形（Y）和三角形（△）两种。

这3个电源依次称为A相、B相和C相，它们的电压瞬时表达式及相量如表12-1-1所示。

图12-1-1表12-1-1电压时域及相量表示二、三相电路的线电压（电流）与相电压（电流）的关系三相系统中，流经输电线中的电流称为线电流；电源端或是负载端各输电线线端之间的电压都称为线电压；三相电源和三相负载中每一相的电压、电流称为相电压和相电流。

三相系统中的线电压和相电压、线电流和相电流之间的关系都与连接方式有关，如表12-1-2所示。

表12-1-2线电压（电流）与相电压（电流）的关系三、对称三相电路的分析计算计算的一般步骤：①将△形电源和负载均变成Y形；②用短路线连接所有中性点，画出一相等效电路进行计算；③根据对称性推算其他两相电压和电流。

图12-1-2（a）的一相等效电路如图（b）所示。

图12-1-2四、三相电路的功率1．三相电路的功率计算有功功率：P＝P A ＋P B ＋P C 。

无功功率：Q＝Q A ＋Q B ＋Q C 。

视在功率：22Q P S +=若负载对称，则有A P P p p 33cos 3cos l l P P U I U I ϕϕ===A P P p p33sin 3sin l l Q Q U I U I ϕϕ===223l l S U I P Q ==+式中，φp 是指每相负载的阻抗角；对称三相电路的其他计算完全可以用正弦电流电路的相量分析方法。

2．三相电路有功功率的测量三相电路有功功率测量的三表法和两表法，如图12-1-3所示。

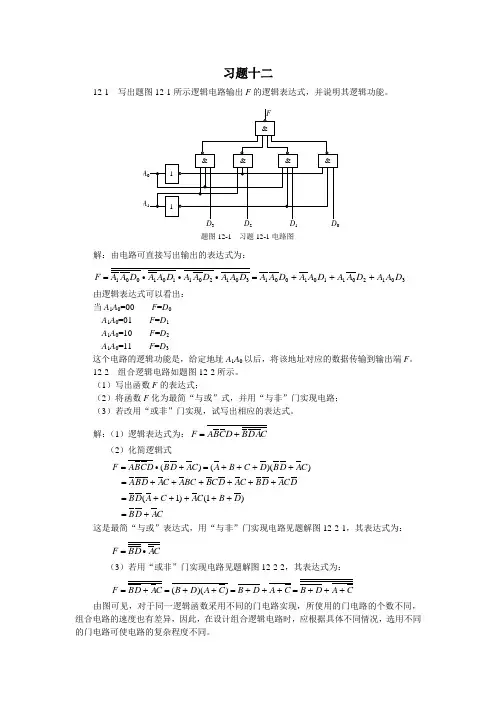
习题十二12-1 写出题图12-1所示逻辑电路输出F 的逻辑表达式，并说明其逻辑功能。

解：由电路可直接写出输出的表达式为：301201101001301201101001D A A D A A D A A D A A D A A D A A D A A D A A F +++==∙∙∙由逻辑表达式可以看出： 当A 1A 0=00 F =D 0 A 1A 0=01 F =D 1A 1A 0=10 F =D 2 A 1A 0=11 F =D 3这个电路的逻辑功能是，给定地址A 1A 0以后，将该地址对应的数据传输到输出端F 。

12-2 组合逻辑电路如题图12-2所示。

（1）写出函数F 的表达式；（2）将函数F 化为最简“与或”式，并用“与非”门实现电路； （3）若改用“或非”门实现，试写出相应的表达式。

解：（1）逻辑表达式为：C A D B D C B A F += （2）化简逻辑式CA DB D BC A C AD B D C A D B C A D C B BC A C A D B A C A D B D C B A C A D B D C B A F +=+++++=++++++=++++=+=∙)1()1())(()(这是最简“与或”表达式，用“与非”门实现电路见题解图12-2-1，其表达式为： C A D B F ∙=（3）若用“或非”门实现电路见题解图12-2-2，其表达式为： C A D B C A D B C A D B C A D B F +++=+++=++=+=))((由图可见，对于同一逻辑函数采用不同的门电路实现，所使用的门电路的个数不同，组合电路的速度也有差异，因此，在设计组合逻辑电路时，应根据具体不同情况，选用不同的门电路可使电路的复杂程度不同。

A A3210题图12-1 习题12-1电路图12-3 组合逻辑电路如题图12-3分析的结果，列成真值表的形式。

解：对于图12-3电路可以写出逻辑函数表达式为：ABCC AB C B ABC C A C B ABC C A F +=++==∙∙ =（AB ）⊙C真值表如右图所示，由真值表可以看出，该电路是实现AB 与C 的“同或”，及当AB 与C 的值相同时，电路输出为“1”，否则输出为“0”。

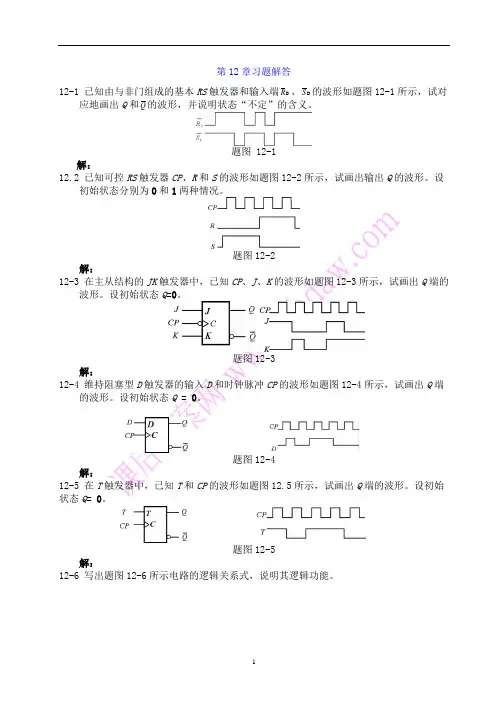
第12章习题解答12-1 已知由与非门组成的基本RS触发器和输入端D R、D S的波形如题图12-1所示，试对应地画出Q和Q的波形，并说明状态“不定”的含义。

题图 12-1解：12.2 已知可控RS触发器CP、R和S的波形如题图12-2所示，试画出输出Q的波形。

设初始状态分别为0和1两种情况。

题图12-2解：12-3 在主从结构的JK触发器中，已知CP、J、K的波形如题图12-3所示，试画出Q端的波形。

设初始状态Q=0。

题图12-3解：12-4 维持阻塞型D触发器的输入D和时钟脉冲CP的波形如题图12-4所示，试画出Q端的波形。

设初始状态Q = 0。

题图12-4解：12-5 在T触发器中，已知T和CP的波形如题图12.5所示，试画出Q端的波形。

设初始状态Q= 0。

题图12-5解：12-6 写出题图12-6所示电路的逻辑关系式，说明其逻辑功能。

题图12-6解：逻辑关系为：Q D AQ BQ==+所以其功能为JK触发器。

12-7 如题图12-7所示的电路和波形，试画出D端和Q端的波形。

设初始状态Q= 0。

题图12-7解：12-8 将主从型JK触发器转换为T'触发器有几种方案？画出外部连线图。

解：12-9 电路如题图12-9所示。

画出Q0端和Q1端在六个时钟脉冲CP作用下的波形。

设初态Q=Q0= 0。

1题图12-9解：12-10 用题图12.10(a)所给器件构成电路，并在示波器上观察到如图12.10（b）所示波形。

试问电路是如何连接的？请画出逻辑电路图。

(a) (b)题图12-10解：12-11 已知如题图12.11(a)所示电路的各输入端信号如题图12-11(b)所示。

试画出触发器输出端Q0和Q1的波形。

设触发器的初态均为0。

(a) (b)题图12-11解：12-12 已知电路和时钟脉冲CP及输入端A的波形如题图12-12所示，试画出输出端Q、1Q 的波形。

假定各触发器初态为1。

(a) (b)题图12-12解：12-13 已知题图12-13(a)所示电路中输入A及CP的波形如题图12-13(b)所示。

第十二章习题解答12－1周期性矩形脉冲如图所示，试求其傅立叶级数展开形式。

t解：02212w T πππ=== 00011()22T m mU a f t dt U dt T πππ===⎰⎰ 0002211()cos 2cos sin 0Tm k m U a f t kw tdt U ktdt ktT kππππ=⋅===⎰⎰0002()sin 12sin 2211()cos ()(cos 1)21cos 41,3,5,00,2,4,Tk m mm m mb f t kw tdtT U ktdtU U kt k k k U k k U k k k πππππππππ=⋅===⋅⋅----=⎧=⎪=⎨⎪=⎩⎰⎰ ∴14mU b π=，343m U b π=，54,5mU b π=0135()sin sin 3sin 5444sin sin 3sin 5354111(sin sin 3sin 5sin 7)357mmm m m m f t a b t b t b t U U U Ut t t U U t t t t ππππππ=++++=++++=+++++12-2已知某信号半个 周期的 波形如图所示。

试在下列各不同条件下画出整个周期的波形：（1）00a =；（2）所有0k b =;(3) 所有0k a =；（4）k a k a 和k b 只能出现在k 为奇数时。

t解：(1)00a =t（2）所有0k b =t（3）所有0k a =t(4) k a 和k b 只能出现在k 为奇数时t12－3一个RLC 串连电路，其中11R =Ω,0.015L H =,70C F μ=,外加电压()11141.4cos100035.4sin 2000V u t t t =+-，试求电路中的电流()i t 和电路消耗的功率。

RC-+()u t解：∵012()11141.4cos100035.4sin 2000V ()()u t t t u u t u t =+-=++ (1)直流分量单独作用，即011V u =单独作用∵电容具有隔直作用，∴00I = (2)1()u t 单独作用∵.21()141.4cos1000141.4sin(1000)V u t t t π==+ ∴.110090V U ︒=∠110000.01515L X wL ==⨯=Ω1611110014.29100070107C X w C --=-==-=-Ω⨯⨯ 相量模型为：-+11Ω15j Ω14.29j -Ω.1U11(1514.29)110.6911.02 3.6Z j j ︒=+-=+=∠Ω..11100909.0786.4A 11.02 3.6U I Z ︒︒︒∠===∠∠ ∴1()12.83sin(100086.4)A i t t ︒=+ (3)2()u t 单独作用∵2()35.4sin 200035.4sin(2000180)V u t t t ︒=-=+∴.218025180V U ︒︒==∠ 21221530L L X X ==⨯=Ω，127.1452C C X X ==-Ω 相量模型为-+11Ω30j Ω7.145j -Ω.2U11(307.145)1122.8525.3664.3Z j j ︒=+-=+=∠Ω..12251800.986115.7A 25.3664.3U I Z ︒︒︒∠===∠∠ 2() 1.39sin(2000115.7)A i t t ︒=+∴012()()()12.83sin(100086.4) 1.39sin(2000115.7)A i t I i t i t t t ︒︒=++=+++9.12A I =≈229.1211915.6W P I R =⋅=⨯=12-4在图示的电路中，12R =Ω,2wL =Ω,118wC=Ω, ()1030)V u t wt wt ︒=+++,求电磁式电流表，电动式电压表及电动式瓦特表的读数。

第十二章三相电路习题一、选择题。

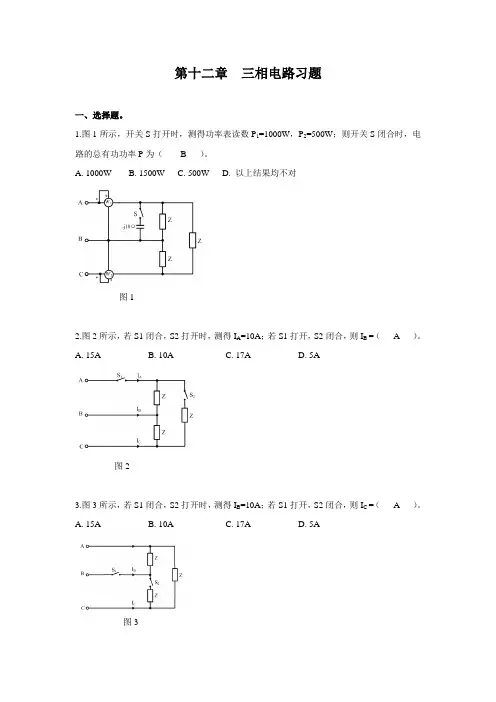
1.图1所示，开关S打开时，测得功率表读数P1=1000W，P2=500W；则开关S闭合时，电路的总有功功率P为（ B ）。

A. 1000WB. 1500WC. 500WD. 以上结果均不对图12.图2所示，若S1闭合，S2打开时，测得I A=10A；若S1打开，S2闭合，则I B =（ A ）。

A. 15AB. 10AC. 17AD. 5A图23.图3所示，若S1闭合，S2打开时，测得I B=10A；若S1打开，S2闭合，则I C =（ A ）。

A. 15AB. 10AC. 17AD. 5A图34.图4示三相三线制电路两个功率表W 1 的读数为2KW,W 2的读数为5KW ，则负载吸收的功率为 ( D )A.2KWB.5KWC.3KWD.7KW图45.三相对称Ｙ形负载的线电压ο30320UAB ∠=•V,线电流ο60-2I A ∠=•A ，则每相负载的阻抗为( B )A.ο6010-∠ΩB.ο6010∠ΩC.ο90310∠ΩD.ο30310-∠Ω6.图6所示，三相对称负载的有功功率为5KW ，负载的阻抗角ο60=ϕ，则两个功率表W 1 和W 2的读数分别为（ B ）A. 2KW ，3KWB. 5KW,0KWC. 3KW,2KWD. 0KW,5KW图67.三相电路如图7所示，已知开关S 闭合时，电流表A1读数为17.32A ；则开关S 打开后，电流表A2读数为（ A ）。

A. 17.32AB. 7.32AC. 10AD. 15AA1A2ZZZAB8.三相电路如图8所示，已知开关S 闭合时，电流表A 读数为10A ；则开关S 打开后，电流表A 读数为（ C ）。

A. 5AB. 17.32AC. 10AD. 12A图109.图9所示，开关S 闭合时A 1=17.32A ，则开关S 打开后后A 2为（ C ）。

A ．17.32A B ．3A C ．10A D ．7A图9二、计算题。

第12章 集成运算放大器 习题参考答案一、填空题：1. 理想运放同相输入端和反相输入端的“虚短”指的是 同相输入端与反相输入端两点电位相等，在没有短接的情况下出现相当于短接时的现象。

2. 将放大器 输出信号 的全部或部分通过某种方式回送到输入端，这部分信号叫做 反馈 信号。

使放大器净输入信号减小，放大倍数也减小的反馈，称为 负 反馈；使放大器净输入信号增加，放大倍数也增加的反馈，称为 正 反馈。

放大电路中常用的负反馈类型有 并联电压 负反馈、 串联电压 负反馈、 并联电流 负反馈和 串联电流 负反馈。

3. 若要集成运放工作在线性区，则必须在电路中引入 负 反馈；若要集成运放工作在非线性区，则必须在电路中引入 开环 或者 正 反馈。

集成运放工作在线性区的特点是 输入电流 等于零和 输出电阻 等于零；工作在非线性区的特点：一是输出电压只具有 高电平、低电平两种稳定 状态和净输入电流等于 零 ；在运算放大器电路中，集成运放工作在 线性 区，电压比较器集成运放工作在 非线性 区。

4. 集成运放有两个输入端，称为 同相 输入端和 反相 输入端，相应有 同相输入 、 反相输入 和 双端输入 三种输入方式。

5. 放大电路为稳定静态工作点，应该引入 直流 负反馈；为提高电路的输入电阻，应该引入 串联 负反馈；为了稳定输出电压，应该引入 电压 负反馈。

6. 理想运算放大器工作在线性区时有两个重要特点是“虚短”和 “虚断” 。

三、选择题：（每小题2分，共16分）1.集成运算放大器能处理（ C ）。

A 、直流信号；B 、交流信号；C 、交流信号和直流信号。

2. 为使电路输入电阻高、输出电阻低，应引入（ A ）。

A 、电压串联负反馈；B 、电压并联负反馈；C 、电流串联负反馈；D 电流并联负反馈。

3. 在由运放组成的电路中，运放工作在非线性状态的电路是（ D ）。

A 、反相放大器；B 、差值放大器；C 、有源滤波器；D 、电压比较器。

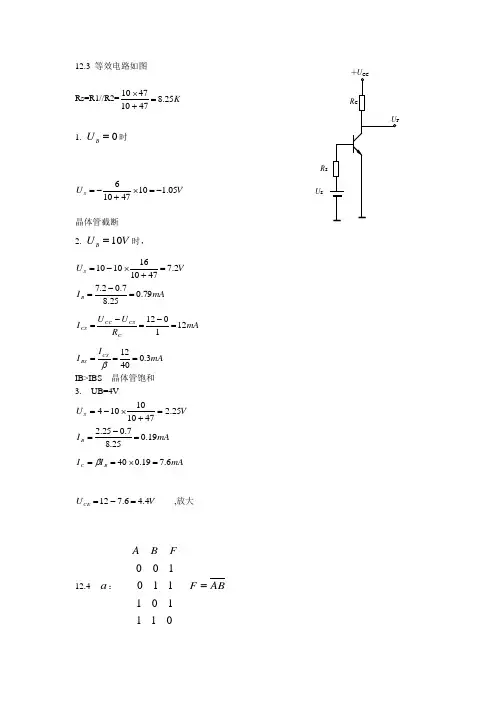
12.3 等效电路如图Rs=R1//R2=K 25.847104710=+⨯1. 0B U =时V U S 05.11047106-=⨯+-=晶体管截断 2. 10BU V =时，V U S 2.74710161010=+⨯-=mA I B 79.025.87.02.7=-=mA R U U I C CS CC CS 121012=-=-=mA I I CSBS 3.04012===βIB>IBS 晶体管饱和 3. UB=4VV U S 25.2471010104=+⨯-=mA I B 19.025.87.025.2=-=mAI I B C 6.719.040=⨯==βV U C E 4.46.712=-= ,放大12.4a ：001011101110A B FF A B=R SU Sb ：此图的12,D D 方向画反了 ：001010100110A B FF A B=+ 12.5 证明：（1）()()()()()A B A C B C A B AB A C BC C +++=++++()()A B AB C AC AB BC =++=++而 ()()A B A C AC AB BC ++=++故等式成立。

（2）()AB BD AD CDE DA AB BD D A A CDE ++++=++++();()a F AB b F AB AC BC ==++（3）()AB AB ABC AB C C AB ABC ++=+++ABC ABC AB ABC=+++()ABC AB BC A A ABC AB BC =+++=++（4）AB BC C A BA CB A C ++=∙∙=()()()A B B C C A+++=()()AB A C BC C A ABC ABC +++=+12.6对（1）式，当输入ABC 为001、010、100时11F =，其他输入时10F =。

对（2）式，当ABC 为111、000时20F =，其他输入时21F =。

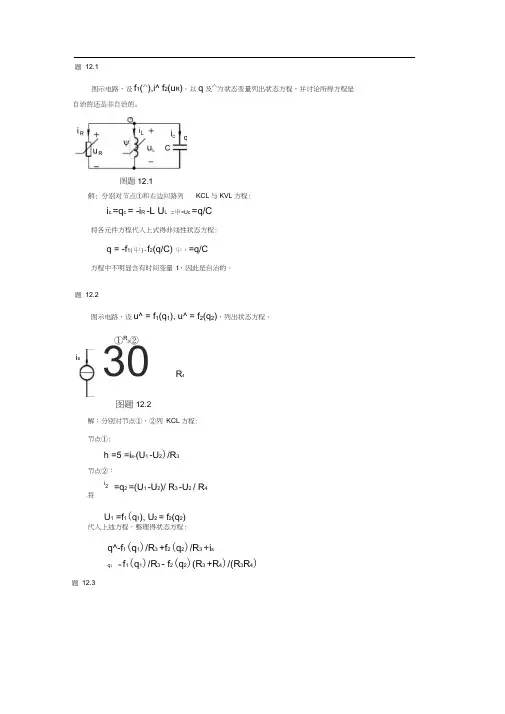
题 12.1图示电路，设f 1(^),i^ f 2(u R )。

以q 及^为状态变量列出状态方程，并讨论所得方程是i c =q c = -i R -L U L =申=Uc =q/C将各元件方程代入上式得非线性状态方程:q = -f 1(屮)-f 2(q/C) 屮・=q/C方程中不明显含有时间变量 t ，因此是自治的。

题 12.2图示电路，设u^ = f 1(q 1), u^ = f 2(q 2)，列出状态方程。

图题12.2解：分别对节点①、②列 KCL 方程:节点①: h =5 =i s-(U 1 -U 2)/R 3节点②：=q 2 =(U 1 -U 2)/ R 3 -U 2 / R 4代入上述方程，整理得状态方程:q^-f 1(q 1)/R 3 +f 2(q 2)/R 3 +i sq ； = f 1(q 1)/R 3 - f 2(q 2)(R 3 +R 4)/(R 3R 4)题 12.3①R 3②30R 4i2将U 1 =f 1(q 1), U 2 = f 2(q 2)KCL 与KVL 方程:i sU3为非状态变量，须消去。

由节点①的KCL方程得:在图示电路中电容的电荷与电压关系为比=f1（q1），电感的磁链电流关系为= f2（2）。

试列出电路的状态方程。

+ R4 i4 U s()+ #U1 q -图题12.3解：分别对节点①列KCL方程和图示回路列KVL方程得:q1 = i 2 — U3 / R3 屮；=Us —U3 (1) ⑵解得-i^i^i^-i2 +■R^ + U R U1=0R3R4 U3 将屮= (U i +R4i2)R3/(R3 中尺)=[f l(q i)+R4f2(2)]R3/(R3+R4) =f1（q1）、i2 = f2（叽）及U3代入式（1）、（2）整理得：日；Af'qJ/R 椀）卄2（巴）R s/R 示4）胆"（qJR s/R +引—f2（巴）明/（艮+农）+u sU i题12.4图示电路，设i = a勺仃,U s = P sin（«t），试分别写出用前向欧拉法、后向欧拉法和梯形法计算响应叽t）的迭代公式，步长为h。

第12章 集成逻辑门电路习题解答【12-1】填空 解：1． 开关 ， 截止 ， ， b ， 加深 ，减轻 ， 增大 ， 加速 。

2． 灌 ， ， 拉 ，160μA 。

3．3V ， ， ， ， ， ， ， ， ， 15mA ， 10 。

4． 高电平 ， 。

5． 输出与电源 。

6． 极低 ， 增加 ， 很大 ， 高 。

7． 30MHz 。

【12-2】电路如题图12-2(a)～(f)所示，试写出其逻辑函数的表达式。

解：F 1=A ，F 2=1，F 3=B A +，F 4=AB ，F 5=1，F 6=B【12-3】TTL 三态门电路如题图12-3所示。

在下图示输入波形的情况下，画出其输出端的波形。

解：当1=C 时，AB F = 当0=C 时，B A B A F +==于是，逻辑表达式 C B A C AB F )(++= F 的波形见解图12-3所示。

A B C F解图12-3【12-4】题图12-4中各电路中凡是能实现非功能的要打号，否则打×号。

图(a)为TTL门电路，图(b)为CMOS 门电路。

解：&1&&&1A 5VAAA1001M "1"A Ω=1Ω(a) TTL 门A(b) CMOS 门 解图12-4【12-5】要实现题图12-5中各TTL 门电路输出端所示的逻辑关系各门电路的接法是否正确如不正确，请予更正。

解：见解图12-5。

CB A X AXB X A +=AB=CDAB F +=解图12-5【12-6】由CMOS 传输门和反相器构成的电路如题图12-6（a ）所示，试画出在图（b ）波形作用下的输出u O 的波形（u I1=10V u I2=5V ）解：输出波形见解图12-6。

ttu解图12-6【12-7】甲乙两人用指针式万用表测量一个由TTL 门组成的电路，发现某点的电位为。

对此甲认为是由于该点的负载过重，导致灌电流或拉电流太大所致；乙则认为应先观察一下该点的波形，才能做出判断。

第12章 直流稳压电源的习题答案12。

1判断下列说法是否正确，用“√”或者“×"表示判断结果并填入空内.（1）直流电源是一种将正弦信号转换为直流信号的波形变换电路。

（ ) （2）直流电源是一种能量转换电路，它将交流能量转换为直流能量。

( ）（3）在变压器副边电压和负载电阻相同的情况下，桥式整流电路的输出电流是半波整流电路输出电流的2倍.（ )因此,它们的整流管的平均电流比值为2：1。

( ） （4)若V 2为电源变压器副边电压的有效值，则半波整流电容滤波电路和全波整流电容滤波电路在空载时的输出电压均为22V 。

（ ）(5）当输入电压V I 和负载电流I L 变化时，稳压电路的输出电压是绝对不变的。

（ ） （6）一般情况下，开关型稳压电路比线性稳压电路效率高。

( ） （7）整流电路可将正弦电压变为脉动的直流电压。

（ )（8）电容滤波电路适用于小负载电流，而电感滤波电路适用于大负载电流。

（ ）（9）在单相桥式整流电容滤波电路中，若有一只整流管断开，输出电压平均值变为原来的一半。

（ ) (10）对于理想的稳压电路，△V O /△V I ＝0,R o ＝0。

（ ）（11）线性直流电源中的调整管工作在放大状态，开关型直流电源中的调整管工作在开关状态。

( ） （12）因为串联型稳压电路中引入了深度负反馈，因此也可能产生自激振荡。

（ ） （13）在稳压管稳压电路中，稳压管的最大稳定电流必须大于最大负载电流；（ ） 而且,其最大稳定电流与最小稳定电流之差应大于负载电流的变化范围.（ ） 解:（1） × （2）√ （3）√；× （4）√ (5）× (6)√ (7）√ （8）√ （9） × （10）√ (11）√ （12） √(13)×；√ 12.2选择填空题1.在题12。

2.1图所示的桥式整流电容滤波电路中，已知变压器副边电压有效值V 2为10V ，2/3T RC (T 为电网电压的周期).测得输出直流电压V O 可能的数值为①14V ②12V ③ 9V ④ 4。

教材习题12答案部分（p341）答案12.1略 答案12.2略 答案12.3解：由非线性电阻的电压电流关系特性110.1I U =，220.05I U =得211100U I = ，222400U I = （1） 对回路列KVL 方程125V U U +=（2） 将式（1）代入式（2）22121004005I I +=由非线性电阻串联可知 12I I = 即215005I =解得10.1A I '= ，10.1A I ''=-（舍去）即 10.1A I =2111001V U I ==答案12.4解：对节点①、②列节点电压方程，其中非线性电阻电流设为未知量：121221112()n n s G G U G U G U II +-=-- (1) 21232S 2()n n G U G G U I I -++=+ (2) 为消去12I I 、，须列补充方程11111222212S 2()()(3)()()(4)n n n I fU fU I fU fU UU ==⎧⎨==--⎩将式(3)代入式(1)、(2)，整理后得1212211212S 11S 121232212S 2S ()()()()()n n n n n n n n n G G U G U f UfU U U G U G U G G U fU U UI +-++--=⎧⎨-++---=⎩答案12.5略答案12.6解：参考点及独立节点编号如图所示。

图中节点①与参考点之间为纯电压源支路，则该节点电压为S U 。

设非线性电阻电流12I I 、为未知量，对图示电路节点②、③列KCL 方程：节点②: 1222230n n I G U I G U -++-= (1) 节点③: 1122123()n n n SG U G U G G U I --++= (2) 将压控非线性电阻电流用节点电压表示，流控非线性电阻电压用节点电压来表示，即22222()()n I f U f U == (3) 12111()n n UU U f I -== (4)将式(3)代入式(1)，将1S n U U =代入式(2)，再与式(4)联立得该电路方程： 122222322123S 1S 1211()0()()n n n n n n n I G U f U G U G U G G U I G U U U f I -++-=⎧⎪-++=+⎨⎪-=⎩ 答案12.7解：对节点列KCL 方程节点①:313A 0I I -++= （1） 节点②:1240I I I -++= （2） 由图示电路可知112311n U U UI +==ΩΩ （3）2242V 2V 11n U U I --==ΩΩ （4） 将式（3）、（4）及已知条件311I U =和322U I =代入式（1）、（2）得331223311223U I I U U I ⎧--=-⎨++=⎩ 即为所求二元方程组。

电路习题第⼗⼆章第⼗⼆章三相电路习题⼀、选择题。

1.图1所⽰，开关S打开时，测得功率表读数P1=1000W，P2=500W；则开关S闭合时，电路的总有功功率P为（ B ）。

A. 1000WB. 1500WC. 500WD. 以上结果均不对图12.图2所⽰，若S1闭合，S2打开时，测得I A=10A；若S1打开，S2闭合，则I B =（ A ）。

A. 15AB. 10AC. 17AD. 5A图23.图3所⽰，若S1闭合，S2打开时，测得I B=10A；若S1打开，S2闭合，则I C =（ A ）。

A. 15AB. 10AC. 17AD. 5A图34.图4⽰三相三线制电路两个功率表W 1 的读数为2KW,W 2的读数为5KW ，则负载吸收的功率为 ( D )A.2KWB.5KWC.3KWD.7KW图45.三相对称Ｙ形负载的线电压30320U AB ∠=?V,线电流 60-2I A ∠=?A ，则每相负载的阻抗为( B )A. 6010-∠ΩB. 6010∠ΩC. 90310∠ΩD. 30310-∠Ω6.图6所⽰，三相对称负载的有功功率为5KW ，负载的阻抗⾓ 60=?，则两个功率表W 1 和W 2的读数分别为（ B ）A. 2KW ，3KWB. 5KW,0KWC. 3KW,2KWD. 0KW,5KW图67.三相电路如图7所⽰，已知开关S 闭合时，电流表A1读数为17.32A ；则开关S 打开后，电流表A2读数为（ A ）。

A. 17.32AB. 7.32AC. 10AD. 15AAB8.三相电路如图8所⽰，已知开关S 闭合时，电流表A 读数为10A ；则开关S 打开后，电流表A 读数为（ C ）。

A. 5AB. 17.32AC. 10AD. 12A图109.图9所⽰，开关S 闭合时A 1=17.32A ，则开关S 打开后后A 2为（ C ）。

A ．17.32A B ．3A C ．10A D ．7A图9⼆、计算题。

习题十二12-1图12-1所示线性单口网路中，已知Ω=1R ，H 1=L ，F 1=C ，的试求驱动点阻抗()s Z 。

答：（a ）()1122+++=s s s s Z ；（b ）()112+++=s s s s Z ；（c ）()11++=s s s Z（a ）()1111111222+++=++=++=s s s s s ss s Z（b ）()()111111112+++=++++=++=s s s s s s s ss s Y ()112+++=s s s s Z（c ）()1111111111++=+++=+++=s s s ss sss Y ()11++=s s s Z12-2就图12-2电路，试求对()s I 2的系统函数。

答：()75.0=s H解：()()s s U s I +⨯=75.0175.02()75.075.0+=s s H ——转移导纳12-3图12-3电路有一个输入端，两个输出端，试分别写出系统函数()()()s U s U s H s o 11=和()()()s Us U s H so 22=C图12-2 习题12-2题图答：()1121++=s s s H ； ()1222++=s s ss H解：()()11111111121++=++=+++=s s s s s s ss H ()()()1111111122222++=++=++++=+++=s s sss s s s s s s sss s s s ss H12-4试求图12-4()a ，()b 所示电路的系统函数()()()s I s I s H s 2=和()()()s U s U s H o 1=。

答：（a ）()12++=s s ss H ；()2710+-+=s s s H解：（a ）()11112++=++=s s s s s s H（b ） ()()()()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+--+s U s U s U s U s ss s o 2121012 ()()()()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡++--+0110212s U s U s U s s s s o()()()()()s U s s s s s s U 10101210+-+++=图12-3 习题12-3题图图12-4习题12-4题图（b ）（a ）1Ωu 1()()()()()()27101023101012102212+-+=--+++=+-+++==s s ss s s s s s s s s s U s U s H12-5 求图12-5所示电路的系统函数()()()s U s U s H 12=。

第12章非线性电阻电路习题解答电路如图题所示，已知非线性电阻的特性方程为2111.2I U =（单位：V ，A ），10U >求支路电流1I 和2I 。

24Ω图题 图(a)解：将非线性电阻以外电路用戴维南电路进行等效化简，如图(a)所示。

列KVL 方程 1125V I U Ω⨯+= (1) 将非线性电阻特性2111.2I U =代入方程(1)，得2112.450U U +-=解得 1 1.25V U '=，1 1.667V U ''=-（舍去）22111.2() 1.2 1.25 1.875A I U '=⨯=⨯= 21/4 1.25/40.3125A I U '==="图题所示电路，已知非线性电阻的特性方程为221U I =+（单位：V ，A ），求电压U 。

图题 图(a)解：将非线性电阻以外电路用戴维南电路进行等效化简，如图(a)所示。

列KVL 方程 811V I U Ω⨯+= (1) 将非线性电阻特性221U I =+代入方程(1)，得2450I I +-=解得 1A I '=，5A I ''=-22()13V U I ''=+= 22()151VU I ''''=+=图示电路，已知1I =单位：A,V) ( U 1≥0) ，2I =(单位：A,V) (U 2≥0)。

求I 1和U 1。

'52图题解：由非线性电阻的电压电流关系特性1I =2I =得211100U I = ，222400U I = （1）对回路列KVL 方程125V U U += （2）将式（1）代入式（2） 22121004005I I += 由非线性电阻串联可知 12I I =.即 215005I = 解得 10.1A I '= ，10.1A I ''=-（舍去） 即 10.1A I =2111001V U I ==设图示电路中非线性电阻均为压控的，I 1=f 1(U 1)，I 2=f 2(U 2)。