matlab曲线拟合2010a演示

Matlab中的曲线拟合方法引言在科学与工程领域，数据拟合是一个重要的技术，可用于分析实验数据、预测未知的对应关系，并量化观察到的现象。

其中，曲线拟合是一种常见的数据拟合方法，而Matlab作为一种功能强大的科学计算软件，提供了多种曲线拟合工具和函数，方便用户进行数据分析和模型建立。

本文将对Matlab中的曲线拟合方法进行详细介绍和讨论。

一、线性拟合线性拟合是最简单且常见的曲线拟合方法，其基本思想是通过一条直线拟合数据点，找到最佳拟合直线的参数。

在Matlab中，可以使用polyfit函数实现线性拟合。

该函数接受两个输入参数，第一个参数为数据点的x坐标，第二个参数为数据点的y坐标。

返回结果为一个一次多项式拟合模型的参数。

例如，我们有一组实验测量数据如下：x = [1, 2, 3, 4, 5];y = [3, 5, 7, 9, 11];通过polyfit函数进行线性拟合：coeff = polyfit(x, y, 1);其中，1表示要拟合的多项式的次数，这里我们选择了一次多项式（直线）。

coeff即为拟合得到的直线的参数，可以通过polyval函数将参数代入直线方程，得到对应x的y值。

y_fit = polyval(coeff, x);接下来，我们可以使用plot函数将原始数据点和拟合曲线都绘制在同一张图上：figure;plot(x, y, 'o', 'MarkerSize', 10); % 绘制原始数据点hold on;plot(x, y_fit); % 绘制拟合曲线xlabel('x');ylabel('y');legend('原始数据点', '拟合曲线');通过观察图像，我们可以初步判断拟合的效果如何。

如果数据点较为分散，直线拟合效果可能较差。

在此情况下，可以考虑使用更高次的多项式进行拟合。

二、多项式拟合多项式拟合是一种常见的曲线拟合方法，其基本思想是通过一个一定次数的多项式函数来拟合数据点。

matlab 拟合曲线
Matlab 拟合曲线是 Matlab 中一项常见的功能，它可以将一组数据进行拟合，并生成一条拟合曲线。

拟合曲线可以用来描述两个变量之间的关系，或者用来预测未知数据。

Matlab 拟合曲线是一个强大的工具，可以自动对输入数据进行分析处理，根据分析结果来拟合出曲线，从而得到相关的参数和结果。

在使用 Matlab 拟合曲线功能之前，首先需要准备好要拟合的数据，数据包括 x 和 y 的数值，x 表示输入数据，y 表示输出数据，这些数据可以来自实验的测量值，也可以是一些已知的模型数据。

拟合曲线的类型可以是线性，指数，多项式，伽马，指数等等，具体取决于要拟合的数据特征。

当准备好要拟合的数据之后，就可以使用 Matlab 拟合曲线功能来进行处理。

Matlab 拟合曲线功能提供了不同的函数，用户可以根据自己需要选择使用哪一个函数，然后把准备好的数据输入到 Matlab 命令行中，就可以得到拟合曲线的结果。

Matlab 拟合曲线的结果可以用来确定拟合的曲线类型，以及拟合曲线的参数；同时，拟合曲线的过程也可以作为一种分析工具，可以帮助用户更好地理解数据，并得
出一些有价值的结论。

拟合曲线还可以用来预测未知数据，比如给定 x 值，可以预测出 y 值，这样就可以帮助用户更好地分析数据及其规律。

总之，Matlab 拟合曲线功能是一个非常有用的工具，可以帮助用户更好地理解数据，找出数据之间的关系、规律，并利用这些规律来预测未知数据。

matlab 数据曲线拟合全文共四篇示例，供读者参考第一篇示例：Matlab是一款功能强大的数据分析和曲线拟合工具，广泛应用于科学研究、工程设计、金融分析等领域。

在实际工作中，我们经常需要对实验数据进行处理和分析，而曲线拟合是其中一个常见的操作。

本文将介绍在Matlab中如何进行数据曲线拟合，并通过实例详细说明其使用方法。

我们需要准备一组实验数据，这些数据通常是以表格的形式存储在Excel或文本文件中。

假设我们有一组随机产生的数据点，存储在一个文本文件中，每行包含一对(x, y)坐标。

我们可以通过Matlab的文件读取函数将这些数据导入到Matlab中，然后进行曲线拟合分析。

接下来，我们需要选择适合数据走势的拟合模型。

根据实际情况，可以选择线性函数、多项式函数、指数函数、对数函数等不同类型的拟合模型。

在Matlab中，使用`polyfit`函数可以进行多项式拟合，使用`expfit`函数可以进行指数拟合，使用`fit`函数可以进行其他自定义的拟合操作。

以多项式拟合为例，我们假设要对一组数据进行二次多项式拟合。

通过`load`函数读取数据文件，然后将数据分成两个数组`x`和`y`，分别表示x坐标和y坐标。

接下来，使用`polyfit`函数进行拟合操作，语法如下：```matlabp = polyfit(x, y, 2);````2`表示进行二次多项式拟合。

拟合结果会保存在向量`p`中，`p`的元素表示拟合多项式的系数。

完成拟合操作后，我们可以利用拟合结果绘制曲线图。

通过`polyval`函数，可以根据拟合结果生成拟合曲线的y坐标值，并与原始数据一起绘制在图上，以便进行对比和分析。

除了多项式拟合之外，Matlab还提供了许多其他灵活的拟合方法。

对于非线性数据，可以使用`fit`函数进行非线性拟合。

该函数允许用户根据实际数据特点选择不同的拟合模型，并进行参数估计和优化。

在实际应用中，曲线拟合是数据分析的重要环节之一。

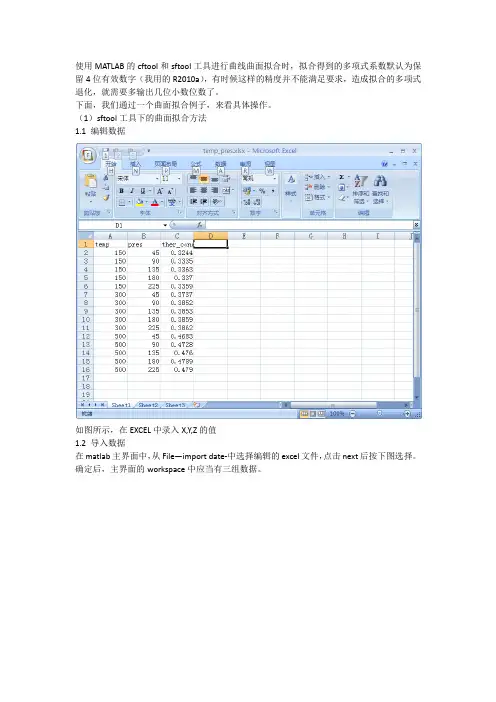
使用MATLAB的cftool和sftool工具进行曲线曲面拟合时，拟合得到的多项式系数默认为保留4位有效数字（我用的R2010a），有时候这样的精度并不能满足要求，造成拟合的多项式退化，就需要多输出几位小数位数了。

下面，我们通过一个曲面拟合例子，来看具体操作。

（1）sftool工具下的曲面拟合方法1.1 编辑数据如图所示，在EXCEL中录入X,Y,Z的值1.2 导入数据在matlab主界面中，从File—import date-中选择编辑的excel文件，点击next后按下图选择。

确定后，主界面的workspace中应当有三组数据。

1.3 基于sftool工具的曲面拟合通过Start—toolboxes—curve fitting—surface fitting tool进入曲面拟合界面。

在x，y，z的input 中选择数据，选择非线性拟合Polynomial，选好自变量的阶数，点击fit进行拟合。

（也可以选用custom equation来自定义函数拟合）此时，拟合得到的多项式，及其各项系数、相关系数都在左侧的result中给出。

在此例中，由于所得的z值很小，自变量又较大，所以得到的系数带入方程并不能计算出原来的结果，换句话说，所得系数的小数位数不够。

那么如何增加小数位数的显示呢？（2）拟合结果的小数位数显示2.1 预设置在matlab主界面中，依次点击file—preferences--command window和variable editor，在其中的format下拉框中选择long e。

（也就是科学计数法15位）2.2 拟合代码回到sftool界面，点击file—general M-file获取拟合源代码。

复制其中的拟合代码段（选中的那一段，上面的部分为说明，下面的部分为作图，均不需要）。

2.3 将该段代码粘贴到matlab主界面的command window中2.4 回车后，输入fitresult，得到如下结果可以看到，计算得到的系数仍然是4位有效数字，和在sftool工具中得到的一样。

matlab 曲线拟合函数⽤法以及例⼦⼯具/原料matlab 曲线拟合在运⾏MATLAB 编程进⾏数据的处理过程当中，我们常常⽤到matlab 曲线拟合，但是⼯具箱由于需要⼈⼯交互，得到的拟合结果，需要⼈⼯的去提取，再输⼊，所以，⼯具箱拟合结果⼗分不适合调⽤，以及继续下⾯的操作，所以我们需要⽤到matlab 曲线拟合函数,并且以最常⽤的多项式拟合函数为例作为matlab 曲线拟合例⼦，进⾏详细介绍。

MATLAB数据准备：关于MATLAB曲线拟合，我写了⼀系列的经验，为了相互统⼀，采⽤下⾯的数据：x=[0 0.3000 0.6000 0.9000 1.2000 1.5000 1.8000 2.1000 2.4000 2.7000 3.0000]y=[2.0000 2.3780 3.9440 7.3460 13.2320 22.2500 35.0480 52.2740 74.5760 102.6020 137.0000]由函数y=4*x^3+3*x^2+2 产⽣。

1函数命令拟合：MATLAB为我们提供了多项式拟合函数命令polyfit，下⾯我们就⽤这个函数命令进⾏拟合。

在MATLAB主窗⼝中输⼊y1=polyfit(x,y,3)，回车我们会看到下⾯结果：y1 =4.0000 3.0000 0.0000 2.00002函数的说明：y1=polyfit(x,y,N)，这⾥函数polyfit第⼀个参数传递的是拟合数据的⾃变量，第⼆个参数是因变量，第三个参数是拟合多项式的阶数，这个由我们给定。

如下图。

我们可以给定不同的N，运⽤不同的多项式进⾏拟合。

输出结果：在上⾯的例⼦中我们看到输出的结果是：y1 =4.0000 3.0000 0.0000 2.0000对照原始的函数y=4*x^3+3*x^2+2 ，我们可以看到，y1其实输出的是拟合函数的系数，并且由⾼次到低次由左到右输出。

3多项式阶数N的确定：这⾥有些⼈可能会有问题了，我们事先不知道要拟合的数据是⼏阶的，那么我们如何判断我们给定的拟合阶数N最终为多少呢？4matlab 曲线拟合结果调⽤及显⽰阶数确定⽅法⼀：这种⽅法是最常⽤的确定⽅法，⼀般情况下，我们拟合函数的⽬的，就是为了调⽤，所以在⽤函数拟合之前会⽤matlab曲线拟合⼯具箱进⾏拟合函数阶数的确定，由其确定拟合的阶数，然后我们⽤这个函数命令在其他地⽅进⾏⼗分⽅便地调⽤，这是最常⽤的做法。

matlab曲线拟合函数的具体步骤编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（matlab曲线拟合函数的具体步骤）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为matlab曲线拟合函数的具体步骤的全部内容。

matlab曲线拟合函数的具体步骤是什么1、在命令行输入数据：2、启动曲线拟合工具箱》cftool3、进入曲线拟合工具箱界面“Curve Fitting tool"（1）点击“Data”按钮，弹出“Data”窗口；（2)利用X data和Y data的下拉菜单读入数据x，y,可修改数据集名“Data set name”，然后点击“Create data set”按钮，退出“Data”窗口，返回工具箱界面,这时会自动画出数据集的曲线图；（3）点击“Fitting”按钮,弹出“Fitting"窗口；（4）点击“New fit”按钮，可修改拟合项目名称“Fit name”，通过“Data set"下拉菜单选择数据集，然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有：Custom Equations:用户自定义的函数类型Exponential:指数逼近,有2种类型， a＊exp(b*x）、 a*exp(b＊x) + c＊exp（d*x)Fourier：傅立叶逼近，有7种类型,基础型是 a0 + a1＊cos（x*w） + b1*sin(x＊w）Gaussian：高斯逼近,有8种类型，基础型是 a1*exp（—((x—b1）/c1)^2) Interpolant：插值逼近，有4种类型,linear、nearest neighbor、cubic spline、shape—preservingPolynomial：多形式逼近,有9种类型，linear ~、quadratic ～、cubic ~、4-9th degree ~Power:幂逼近，有2种类型，a*x^b 、a*x^b + cRational：有理数逼近，分子、分母共有的类型是linear ～、quadratic ～、cubic ~、4—5th degree ~；此外，分子还包括constant型Smoothing Spline：平滑逼近（翻译的不大恰当，不好意思）Sum of Sin Functions：正弦曲线逼近，有8种类型，基础型是 a1＊sin（b1＊x+ c1）Weibull：只有一种，a*b*x^(b-1）＊exp（—a*x^b）选择好所需的拟合曲线类型及其子类型,并进行相关设置:——如果是非自定义的类型，根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数；——如果选Custom Equations，点击“New”按钮，弹出自定义函数等式窗口。

使用MATLAB进行曲线拟合的步骤与技巧曲线拟合是一种常用的数学方法，用于生成一个与给定数据点集最匹配的曲线。

MATLAB是一种强大的数值计算软件，提供了多种工具和函数，可用于进行曲线拟合。

本文将介绍使用MATLAB进行曲线拟合的步骤与技巧，帮助读者更好地理解和使用该工具。

1. 数据准备在进行曲线拟合之前，首先需要准备好要拟合的数据。

这些数据可以是实验测量得到的，也可以是从其他来源获得的。

确保数据的质量和准确性对于得到好的拟合结果至关重要。

将数据保存在一个.txt或.csv等常见格式的文件中，以便后续导入MATLAB进行处理。

2. 导入数据将准备好的数据导入MATLAB中是进行曲线拟合的第一步。

使用MATLAB内置的导入函数，如`csvread`或`dlmread`，可以轻松地从文本文件中导入数据。

如果数据保存在Excel文件中，可以使用`xlsread`函数进行导入。

确保正确指定文件路径和文件名，以及数据在文件中的位置。

3. 数据可视化在进行曲线拟合之前，建议先对数据进行可视化，以更好地理解数据的特点和趋势。

使用MATLAB的绘图函数，如`plot`或`scatter`，可以将数据点绘制在坐标轴上。

通过观察数据的分布和走势，可以作出一些初步的判断，如选择适当的拟合函数类型。

4. 选择拟合函数选择适当的拟合函数是曲线拟合的关键步骤。

不同的数据集可能需要使用不同类型的函数进行拟合。

MATLAB提供了多种内置的拟合函数，如多项式拟合、指数拟合、幂函数拟合等。

可以使用命令窗口中的`help`命令来查找和了解这些函数的用法和参数设置。

5. 执行拟合在选择拟合函数后，可以执行拟合操作。

MATLAB提供了各种拟合函数，如`polyfit`、`fittype`和`fit`等，用于实现不同类型的拟合。

使用合适的函数，根据数据和所选的拟合函数类型，进行参数估计和模型拟合。

根据拟合结果，可以得到拟合曲线的参数和拟合曲线本身。

matlab数据拟合曲线
在Matlab中，可以通过拟合曲线方法来实现拟合数据。

拟合曲线就是根据数据构造出函数曲线，这条曲线可以描绘出数据之间的关系，从而推导出有用的信息。

Matlab的拟合曲线功能可以让用户快速拟合数据，使用简单。

首先，用户可以在Matlab中输入想要拟合的数据，然后使用拟合曲线命令，根据数据输入计算出复杂的统计模型或简单的函数模型，从而得到最佳的拟合曲线。

当拟合曲线得到时，用户可以在Matlab中绘制该曲线，把原始数据和最佳拟合曲线一起显示出来，用于比较分析和更加准确地描述数据之间的关系。

此外，用户还可以在Matlab中取得这条拟合曲线的相关信息，包括斜率、拟合误差、函数参数等。

曲线拟合方法在MATLAB中的应用本篇文章主要介绍了曲线拟合方法在MATLAB中的应用，包括曲线拟合的基本原理、MATLAB中的曲线拟合工具箱、曲线拟合的步骤以及应用实例。

通过本篇文章的学习，读者可以掌握曲线拟合方法在MATLAB中的应用，为解决实际问题提供有力支持。

曲线拟合方法在MATLAB中的应用曲线拟合是数学中常见的一种数据处理方法，通过拟合曲线可以更好地描述数据之间的关系。

在科学研究和工程实践中，曲线拟合方法的应用非常广泛。

MATLAB作为一种常用的数学软件，提供了强大的曲线拟合工具箱，使得曲线拟合变得更加方便和简单。

一、曲线拟合的基本原理曲线拟合是指通过寻找一条曲线，使得这条曲线尽可能地贴近原始数据点。

在数学上，曲线拟合可以表示为一个方程组，即要求解一个多元非线性方程组。

通过最小二乘法等方法，可以求得最优解，即拟合曲线。

二、MATLAB中的曲线拟合工具箱MATLAB中的曲线拟合工具箱提供了多种拟合方法，包括线性回归、非线性回归、多项式拟合等。

用户可以根据需要选择不同的拟合方法，并进行参数调整和优化。

通过工具箱提供的可视化工具，可以直观地观察拟合结果，并进行相应的调整。

三、曲线拟合的步骤1. 准备数据：将原始数据导入MATLAB中，并进行必要的预处理，如去除异常值、标准化等。

2. 选择拟合方法：根据数据的特点和需求选择合适的拟合方法，如线性回归、非线性回归、多项式拟合等。

3. 拟合曲线：使用所选的拟合方法进行曲线拟合，得到拟合曲线和参数。

4. 可视化结果：使用MATLAB中的可视化工具，将原始数据和拟合曲线可视化展示出来。

5. 结果分析：根据可视化结果和拟合参数进行分析，得出结论。

四、应用实例1. 股票价格预测：通过收集股票历史价格数据，使用曲线拟合方法预测未来价格趋势。

2. 气象数据分析：通过收集气象数据，使用曲线拟合方法分析气温、湿度等因素之间的关系。

3. 生物医学研究：通过曲线拟合方法分析基因序列与蛋白质结构之间的关系。

在MATLAB中批量拟合曲线可以使用多种方法，其中一种常用的方法是使用`cftool`工具箱进行操作。

以下是使用`cftool`进行批量拟合的步骤：
1. 输入`cftool`打开工具箱，只选取一组数据拟合。

2. 点击生成代码。

3. 查看代码并做修改。

另外，还可以使用多项式拟合（`polyfit`和`polyval`）方法进行批量拟合。

这种方法可以对数据进行拟合（自定义用几次多项式），返回相应的参数，然后用`polyval`生成拟合后的数据点。

例如，以下代码对抛物线`y=3x^2+6x+5`进行拟合：
```matlab
x = -5:0.1:5; % 自变量范围
y = 3*x.^2+6*x + 5 + randn(size(x)); % 因变量，添加随机噪声
p = polyfit(x,y,2); % 用二次曲线（抛物线）进行拟合
yy = polyval(p,x); % 生成拟合后的数据点
plot(x,y,'.'); % 原始数据点
hold on; % 保持当前图像
plot(x,yy,'r','LineWidth',2) % 拟合后的曲线
```
在`polyfit(x,y,2)`中，`x`表示自变量，`y`表示因变量，`2`表示用二次曲线（抛物线）进行拟合，得到的`p`其实是对应的参数估计值，`yy`为拟合数据点。

另外在实验中还加了一个随机噪声。

以上是两种常用的MATLAB批量拟合曲线的方法，根据具体需求选择适合的方法进行操作。

使用MATLAB的cftool和sftool工具进行曲线曲面拟合时，拟合得到的多项式系数默认为保留4位有效数字（我用的R2010a），有时候这样的精度并不能满足要求，造成拟合的多项式退化，就需要多输出几位小数位数了。

下面，我们通过一个曲面拟合例子，来看具体操作。

（1）sftool工具下的曲面拟合方法1.1 编辑数据如图所示，在EXCEL中录入X,Y,Z的值1.2 导入数据在matlab主界面中，从File—import date-中选择编辑的excel文件，点击next后按下图选择。

确定后，主界面的workspace中应当有三组数据。

1.3 基于sftool工具的曲面拟合通过Start—toolboxes—curve fitting—surface fitting tool进入曲面拟合界面。

在x，y，z的input 中选择数据，选择非线性拟合Polynomial，选好自变量的阶数，点击fit进行拟合。

（也可以选用custom equation来自定义函数拟合）此时，拟合得到的多项式，及其各项系数、相关系数都在左侧的result中给出。

在此例中，由于所得的z值很小，自变量又较大，所以得到的系数带入方程并不能计算出原来的结果，换句话说，所得系数的小数位数不够。

那么如何增加小数位数的显示呢？（2）拟合结果的小数位数显示2.1 预设置在matlab主界面中，依次点击file—preferences--command window和variable editor，在其中的format下拉框中选择long e。

（也就是科学计数法15位）2.2 拟合代码回到sftool界面，点击file—general M-file获取拟合源代码。

复制其中的拟合代码段（选中的那一段，上面的部分为说明，下面的部分为作图，均不需要）。

2.3 将该段代码粘贴到matlab主界面的command window中2.4 回车后，输入fitresult，得到如下结果可以看到，计算得到的系数仍然是4位有效数字，和在sftool工具中得到的一样。

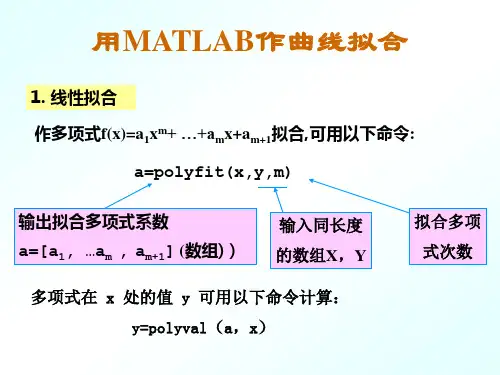
[ZZ]MATLAB曲线拟合MATLAB曲线拟合MATLAB软件提供了基本的曲线拟合函数的命令：多项式函数拟合： a = polyfit（xdata，ydata，n）其中n表⽰多项式的最⾼阶数，xdata，ydata 为要拟合的数据，它是⽤数组的⽅式输⼊。

输出参数a为拟合多项式y = a1x n + … + a n x +a n+1的系数a = [a1, …, a n, a n+1]。

多项式在x处的值y可⽤下⾯程序计算。

y = polyval (a, x)⼀般的曲线拟合： p = curvefit（‘Fun’，p0，xdata，ydata）其中Fun表⽰函数Fun (p, xdata)的M-⽂件，p0表⽰函数的初值。

curvefit命令的求解问题形式是：min{p} sum {(Fun (p, xdata)-ydata).^2}若要求解点x处的函数值可⽤程序f = Fun(p, x) 计算。

例如已知函数形式y = a e - bx + c e – dx，并且已知数据点(x i, y i), i = 1,2,…, n，要确定四个未知参数a, b, c, d。

使⽤curvefit命令，数据输⼊xdata = [x1,x2, …, x n]; ydata = [y1,y2, …, y n];初值输⼊p0 = [a0,b0,c0,d0]; 并且建⽴函数y = a e - bx + c e – dx的M-⽂件（Fun.m）。

若定义p1 = a, p2 = b, p3 = c, p4= d , 则输出p = [p1, p2, p3, p4]。

引例求解：t=[1:16]; %数据输⼊y=[4 6.4 8 8.4 9.28 9.5 9.7 9.86 10 10.2 10.32 10.42 10.5 10.55 10.58 10.6];plot(t,y,'o') %画散点图p=polyfit(t,y,2) (⼆次多项式拟合)计算结果：p = -0.0445 1.0711 4.3252 %⼆次多项式的系数从⽽得到某化合物的浓度y与时间t的拟合函数：y = 4.3252+1.0711t– 0.0445t2对函数的精度如何检测呢？仍然以图形来检测，将散点与拟合曲线画在⼀个画⾯上。

在MATLAB中，可以使用`fit`函数来拟合指数曲线。

以下是一个示例代码，演示如何拟合指数曲线：
```matlab
% 生成数据
x = linspace(0,10,100);
y = exp(2*x) + 0.1*randn(size(x));
% 拟合指数曲线
p = fit(x', y', 'exp1');
% 绘制拟合曲线和原始数据
plot(x, y, 'o');
hold on;
plot(x, p(x), '-');
hold off;
```
在这个示例中，我们首先生成了一组指数分布的数据，其中`x`是自变量，`y`是因变量。

然后，我们使用`fit`函数拟合指数曲线，其中`'exp1'`表示指数分布的公式。

最后，我们使用`plot`函数绘制原始数据和拟合曲线。

需要注意的是，拟合指数曲线时，自变量和因变量必须是数值型数据。

如果数据中包含分类变量，则需要进行相应的预处理，例如将分类变量转换为虚拟变量或哑变量。

matlab 自动拟合曲线
在MATLAB中，你可以使用`fit`函数来自动拟合曲线。

以下是一个简单的例子：
```matlab
% 创建一些数据
x = linspace(0, 10, 100);
y = 2 * x .* exp(-x / 5) + randn(size(x)) * 2; % y = 2x*exp(-x/5) + 噪声
% 使用fit函数拟合数据
f = fit(x', y', 'exp1'); % 使用指数函数进行拟合
% 显示拟合曲线和原始数据
figure;
plot(f, x, y);
```
在这个例子中，我们创建了一个线性模型`y = 2x*exp(-x/5)`，并添加了一些噪声。

然后我们使用`fit`函数和指数函数`exp1`来拟合数据。

最后，我们使用`plot`函数来显示拟合的曲线和原始数据。

注意，MATLAB提供了多种预设的函数类型，如'exp1'、'exp2'、'poly1'、'poly2'等，你也可以自定义函数来进行拟合。

你可以在MATLAB 的文档中查看更多关于`fit`函数的信息。