MATLAB数据拟合例子

标题：探索MATLAB中各类拟合曲线的代码应用在MATLAB中，拟合曲线是数据分析和模型建立中常用的技术之一。

通过拟合曲线，我们可以了解数据之间的关联性并建立预测模型，为进一步分析和应用数据奠定基础。

本文将深入探讨MATLAB中各类拟合曲线的代码应用，帮助读者更深入地理解该主题。

一、线性拟合曲线1. 使用MATLAB进行线性拟合曲线的代码示例在MATLAB中，使用polyfit函数可以进行线性拟合。

对一组数据点(x, y)进行线性拟合，代码如下：```matlabx = [1, 2, 3, 4, 5];y = [2, 3.5, 5, 7, 8.5];p = polyfit(x, y, 1);```其中，x为自变量，y为因变量，1表示进行一次线性拟合。

通过polyfit函数，可以得到线性拟合的系数p。

2. 线性拟合曲线的应用和特点线性拟合曲线适用于线性关系较为明显的数据，例如物理实验数据中的直线关系。

通过线性拟合，可以获得各项系数，对数据进行预测和建模。

二、多项式拟合曲线1. 使用MATLAB进行多项式拟合曲线的代码示例在MATLAB中，使用polyfit函数同样可以进行多项式拟合。

对一组数据点(x, y)进行二次多项式拟合，代码如下：```matlabx = [1, 2, 3, 4, 5];y = [1, 4, 9, 16, 25];p = polyfit(x, y, 2);```其中，x为自变量，y为因变量，2表示进行二次多项式拟合。

通过polyfit函数，同样可以得到多项式拟合的系数p。

2. 多项式拟合曲线的应用和特点多项式拟合曲线适用于数据中存在曲线关系的情况，通过选择合适的最高次数，可以灵活地拟合各种曲线形状。

三、非线性拟合曲线1. 使用MATLAB进行非线性拟合曲线的代码示例在MATLAB中，使用fit函数可以进行非线性拟合。

对一组数据点(x, y)进行指数函数拟合，代码如下：```matlabx = [1, 2, 3, 4, 5];y = [2.1, 7.4, 16.1, 29.3, 48.2];f = fit(x', y', 'exp1');```其中，x为自变量，y为因变量，'exp1'表示进行指数函数拟合。

以下是使用MATLAB 进行高斯拟合的示例代码：假设有一组数据，需要使用高斯函数对其进行拟合，可以按照以下步骤进行操作：1. 定义数据假设有一组数据需要拟合，可以将其保存在一个向量中，例如：```matlabdata = [1.2, 3.4, 4.5, 5.6, 6.7, 7.8, 8.9, 9.0];```2. 定义高斯函数高斯函数的一般形式为：```matlabf(x) = a * exp(-(x-b)^2/(2c^2))```其中，`a`是峰值，`b`是均值，`c`是标准差。

可以定义一个函数来计算高斯函数在给定均值和标准差下的值，例如：```matlabfunction y = gaussian(x, a, b, c)y = a * exp(-(x-b).^2/(2*c^2));end```3. 拟合数据可以使用MATLAB 中的`lsqcurvefit` 函数来拟合数据。

该函数可以找到使误差平方和最小的参数值。

例如：```matlab定义高斯函数gaussianFunction = @(p,x)(p(1)*exp(-(x-p(2)).^2/(2*p(3)^2)));初始化参数值（均值和标准差可自行设定）p0 = [1, 0, 1];拟合数据xdata = linspace(min(data), max(data), 100);[p,resnorm,~,exitflag] = lsqcurvefit(gaussianFunction, p0, xdata, data);输出拟合参数值fprintf('a = f, b = f, c = f\n', p);```在以上代码中，`p0`是初始参数值，`lsqcurvefit` 是用于拟合的函数，`xdata` 是用于拟合的自变量取值，`data` 是因变量数据。

拟合完成后，参数值保存在`p` 中，并输出到控制台中。

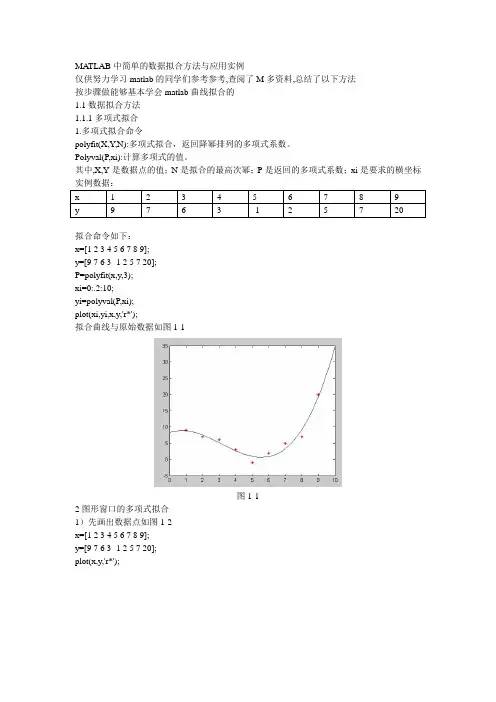
MATLAB中简单的数据拟合方法与应用实例仅供努力学习matlab的同学们参考参考,查阅了M多资料,总结了以下方法按步骤做能够基本学会matlab曲线拟合的1.1数据拟合方法1.1.1多项式拟合1.多项式拟合命令polyfit(X,Y,N):多项式拟合，返回降幂排列的多项式系数。

Polyval(P,xi):计算多项式的值。

其中,X,Y是数据点的值；N是拟合的最高次幂；P是返回的多项式系数；xi是要求的横坐标拟合命令如下：x=[1 2 3 4 5 6 7 8 9];y=[9 7 6 3 -1 2 5 7 20];P=polyfit(x,y,3);xi=0:.2:10;yi=polyval(P,xi);plot(xi,yi,x,y,'r*');拟合曲线与原始数据如图1-1图1-12图形窗口的多项式拟合1）先画出数据点如图1-2x=[1 2 3 4 5 6 7 8 9];y=[9 7 6 3 -1 2 5 7 20];plot(x,y,'r*');图1-22）在图形窗口单击Tools—Basic Fitting,如图1-3勾选.图1-3图1-3右方分别是线性、二阶、三阶对数据进行多项式拟合。

下面的柱状图显示残差，可以看出,三阶多项式的拟合效果是最好的。

1.1.2指定函数拟合已知M组数据点和对应的函数形式f t （t）=acos(kt)eXY编写M文件：syms tx=[0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];y=[1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.08;0.032;-0.015;-0.02];f=fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'});cfun=fit(x,y,f)xi=0:.1:20;yi=cfun(xi);plot(x,y,'r*',xi,yi,'b-');图1-4运行程序,在命令窗口可达到以下运行结果，图像如图1-4Warning: Start point not provided, choosing random start point.> In fit>handlewarn at 715In fit at 315In Untitled2 at 5cfun =General model:cfun(t) = a*cos(k*t)*exp(w*t)Coefficients (with 95% confidence bounds):a = 0.9987 ( 0.9835, 1.014)k = 1.001 (0.9958, 1.006)w = -0.2066 (-0.2131, -0.2002)从结果可以看出,拟合的曲线为：(0.2066) ()0.9987cos(1.001)*tf t t e-=。

matlab指数拟合程序Matlab是一种广泛应用于科学计算和工程领域的编程语言和环境。

其中，指数拟合是一种常用的数据拟合方法，可以用来拟合具有指数形式的数据。

本文将介绍如何使用Matlab进行指数拟合，并给出相应的程序示例。

指数函数的一般形式为：y = a * exp(b * x)，其中a和b为拟合参数，x和y为已知数据点的坐标。

在Matlab中，可以使用“fittype”函数定义指数拟合模型。

例如，可以使用以下代码定义一个指数模型：```matlabmodel = fittype('a * exp(b * x)');```接下来，我们需要选择一个合适的拟合算法。

常见的算法包括最小二乘法（Least Squares）和非线性最小二乘法（Nonlinear Least Squares）。

在这里，我们选择使用最小二乘法进行拟合。

```matlaboptions = fitoptions('Method','NonlinearLeastSquares');```然后，我们需要指定拟合的起始点。

这是一个重要的步骤，起始点的选择将直接影响到拟合结果的准确性。

一般来说，我们可以根据已知数据点的大致趋势来选择起始点。

在这里，我们假设a的初始值为1，b的初始值为-1。

```matlabstartPoints = [1, -1];```接下来，我们可以使用“fit”函数进行拟合。

该函数的输入参数包括已知数据点的坐标，拟合模型，拟合起始点和拟合选项。

例如，我们可以使用以下代码进行拟合：```matlab[fitresult, gof] = fit(xData, yData, model, 'StartPoint', startPoints, 'Options', options);```其中，xData和yData分别是已知数据点的x坐标和y坐标。

在MATLAB 中拟合曲线可以使用fit 函数。

fit 函数可以对给定的数据进行拟合，返回拟合参数以及拟合结果的统计信息。

下面是一个简单的例子，假设我们有一组数据点(x1, y1), (x2, y2), ..., (xn, yn)，我们想要拟合一条直线方程y = ax + b，可以按照以下步骤进行操作：
1. 将数据点存储为一个向量，例如：
x = [1 2 3 4 5];
y = [2 5 8 11 14];
2. 使用fit 函数进行拟合，例如：
p = fit(x', y', 'poly1');
其中，'poly1' 表示拟合模型为一次函数。

如果要拟合二次函数，可以使用'poly2'。

3. 查看拟合参数和结果：
f = p.a; a 是拟合系数
summary(p) 显示拟合参数和结果
summary(p) 可以显示拟合参数和结果的统计信息，例如标准误差、残差、拟合优度等。

除了一次函数和二次函数，MATLAB 还支持其他类型的拟合模型，例如三次函数、指数函数、对数函数等。

具体可以使用'polyN'、'expon'、'logistic'、'probit'、'nthf'、'spline'、'trend'、'bayes'、'gamfit' 等模型。

matlab 数据曲线拟合全文共四篇示例，供读者参考第一篇示例：Matlab是一款功能强大的数据分析和曲线拟合工具，广泛应用于科学研究、工程设计、金融分析等领域。

在实际工作中，我们经常需要对实验数据进行处理和分析，而曲线拟合是其中一个常见的操作。

本文将介绍在Matlab中如何进行数据曲线拟合，并通过实例详细说明其使用方法。

我们需要准备一组实验数据，这些数据通常是以表格的形式存储在Excel或文本文件中。

假设我们有一组随机产生的数据点，存储在一个文本文件中，每行包含一对(x, y)坐标。

我们可以通过Matlab的文件读取函数将这些数据导入到Matlab中，然后进行曲线拟合分析。

接下来，我们需要选择适合数据走势的拟合模型。

根据实际情况，可以选择线性函数、多项式函数、指数函数、对数函数等不同类型的拟合模型。

在Matlab中，使用`polyfit`函数可以进行多项式拟合，使用`expfit`函数可以进行指数拟合，使用`fit`函数可以进行其他自定义的拟合操作。

以多项式拟合为例，我们假设要对一组数据进行二次多项式拟合。

通过`load`函数读取数据文件，然后将数据分成两个数组`x`和`y`，分别表示x坐标和y坐标。

接下来，使用`polyfit`函数进行拟合操作，语法如下：```matlabp = polyfit(x, y, 2);````2`表示进行二次多项式拟合。

拟合结果会保存在向量`p`中，`p`的元素表示拟合多项式的系数。

完成拟合操作后，我们可以利用拟合结果绘制曲线图。

通过`polyval`函数，可以根据拟合结果生成拟合曲线的y坐标值，并与原始数据一起绘制在图上，以便进行对比和分析。

除了多项式拟合之外，Matlab还提供了许多其他灵活的拟合方法。

对于非线性数据，可以使用`fit`函数进行非线性拟合。

该函数允许用户根据实际数据特点选择不同的拟合模型，并进行参数估计和优化。

在实际应用中，曲线拟合是数据分析的重要环节之一。

matlab 多组数据拟合曲线在MATLAB中，可以使用多种方法对多组数据进行拟合。

其中，一种常用的方法是使用fit函数，它允许用户拟合多个数据集到一条或多条曲线。

下面是一个简单的例子来说明如何对多组数据进行拟合。

假设你有三组数据，分别存储在三个数组中：x1, y1, x2, y2, x3, y3。

% 创建数据x1 = 0:0.1:10; % x1的数据点y1 = 2*x1 + 1 + randn(size(x1)); % y1是x1的函数，加入一些随机噪声x2 = 5:0.5:20; % x2的数据点y2 = 3*x2 - 5 + randn(size(x2)); % y2是x2的函数，加入一些随机噪声x3 = 1:0.2:15; % x3的数据点y3 = 4*x3 + 3 + randn(size(x3)); % y3是x3的函数，加入一些随机噪声% 将数据组合到一起X = [x1; x2; x3]; % 所有x的数据组合到一起Y = [y1; y2; y3]; % 所有y的数据组合到一起% 使用fit函数拟合数据fitresult = fit(X,Y,'poly1'); % 使用一次多项式进行拟合% 绘制原始数据和拟合曲线figure;hold on;plot(X,Y,'o'); % 原始数据plot(fitresult); % 拟合曲线legend('Data','Fitted Polynomial');在上面的代码中，我们首先创建了三组数据，每组数据都是一些函数的值，其中包含一些随机噪声。

然后，我们将所有数据组合到一起，并使用fit函数对数据进行拟合。

在这个例子中，我们使用了一次多项式进行拟合，也就是'poly1'。

最后，我们将原始数据和拟合曲线一起绘制出来。

注意，如果你的数据适合更复杂的模型，你可以选择其他的拟合类型。

Matlab数据拟合与曲线拟合方法【引言】数据拟合与曲线拟合是在科学研究和工程应用中常见的问题之一。

随着大数据时代的到来，数据拟合与曲线拟合方法在各个领域的重要性日益凸显。

本文将介绍基于Matlab的数据拟合与曲线拟合方法，包括最小二乘法、多项式拟合、样条拟合、指数拟合等，以及在实际应用中的一些注意事项。

【数据拟合方法一：最小二乘法】最小二乘法是一种常见的数据拟合方法，它通过最小化残差平方和，寻找最优解。

在Matlab中，我们可以使用内置函数“polyfit”来实现最小二乘法拟合。

该函数可以使用一条直线或多项式进行拟合，并返回拟合参数。

对于非线性函数，可以通过线性化或迭代求解的方式进行。

【数据拟合方法二：多项式拟合】多项式拟合是一种常用的数据拟合方法，它用一个多项式函数来近似拟合数据。

在Matlab中，我们可以使用“polyfit”函数实现多项式拟合。

该函数可以拟合任意次数的多项式，并返回拟合系数。

然后，利用这些系数可以计算拟合曲线，并评估拟合的准确性。

【数据拟合方法三：样条拟合】样条拟合是一种平滑且灵活的数据拟合方法，它基于样条函数的概念，将数据划分为多个区间，并在每个区间内拟合一个多项式。

在Matlab中，我们可以使用“spline”函数来实现样条拟合。

该函数需要提供拟合的数据点和拟合阶数，并返回拟合曲线。

【数据拟合方法四：指数拟合】指数拟合是一种适用于指数增长或衰减趋势的数据拟合方法，它将数据拟合为一个指数函数。

在Matlab中，我们可以使用“fit”函数和指数模型来实现指数拟合。

该函数可以自动调整模型参数，使拟合曲线与数据最匹配。

通过评估拟合结果的可靠性指标，我们可以判断拟合是否准确。

【数据拟合实例：气象数据分析】为了更好地理解数据拟合方法的应用，我们以气象数据分析为例进行探讨。

假设我们有一组记录了气温变化的数据点，并希望找到一个拟合曲线以准确地预测未来的气温变化情况。

通过应用多项式拟合或样条拟合方法，我们可以得到一个平滑的曲线，并计算出拟合曲线与实际数据的拟合度。

在MATLAB中，你可以使用`polyfit` 和`polyval` 函数来进行三次样条曲线拟合。

以下是一个简单的样例代码：
```matlab
样本数据
x = [1, 2, 3, 4, 5]; x 数据
y = [1, 4, 9, 16, 25]; y 数据
计算差分，得到差分数据
dx = diff(x);
dy = diff(y);
拟合样条曲线，得到系数
p = polyfit(x(1:end-1), y(1:end-1), 3);
计算三次样条曲线
xx = x(1:end-1);
yy = polyval(p, xx);
画图
figure;
plot(x, y, 'o', xx, yy, '-');
legend('原始数据', '三次样条曲线');
xlabel('x');
ylabel('y');
```
在这个例子中，我们首先定义了一组x 和y 数据。

然后，我们计算了差分，得到了连续的x 和y 值。

使用`polyfit` 函数，我们得到了描述三次样条曲线的系数。

使用这些系数和`polyval` 函数，我们可以在任何x 值上计算出对应的y 值。

最后，我们画出了原始数据和三次样条曲线。

注意，这个例子假设你的数据是等间隔的。

如果你的数据不是等间隔的，你可能需要更复杂的方法来计算差分和拟合样条曲线。

在 MATLAB 中，可以使用样条函数进行数据拟合。

样条函数拟合是一种插值技术，它可以通过使用多项式段来逼近数据点，并在这些段之间实现平滑曲线。

下面是一个简单的示例，演示如何在 MATLAB 中使用样条函数进行数据拟合：
```matlab
% 创建一些示例数据
x = linspace(0, 10, 10); % 创建 x 数据点
y = sin(x); % 创建对应的 y 数据点
% 使用样条拟合数据
xx = linspace(0, 10, 100); % 创建用于绘图的更多 x 值
yy = spline(x, y, xx); % 使用样条函数拟合数据
% 绘制原始数据和拟合曲线
plot(x, y, 'o', xx, yy);
legend('原始数据', '样条拟合曲线');
xlabel('X');
ylabel('Y');
title('样条函数拟合示例');
```
在这个示例中，`linspace` 函数用于生成 x 值，`sin` 函数用于生成对应的 y 值。

然后，`spline` 函数用于拟合数据并生成平滑的曲线，最后使用 `plot` 函数将原始数据点和拟合曲线进行可视化展示。

请注意，在实际应用中，可以根据需要调整插值方法、拟合阶数或其他参数来获得更好的拟合效果。

MATLAB 还提供了其他的插值函数和拟合工具，可以根据具体需求选择合适的方法进行数据拟合。

matlab上三次样条拟合代码MATLAB是一种强大的数学软件，可以用于各种数学计算和数据分析。

在MATLAB中，三次样条拟合是一种常用的数据拟合方法，可以用于拟合非线性数据。

下面是一个简单的MATLAB代码示例，用于实现三次样条拟合。

首先，我们需要准备一组数据，这里以x和y为例。

x是自变量的取值，y是对应的因变量的取值。

我们可以使用MATLAB中的数组来表示这组数据。

```matlabx = [1, 2, 3, 4, 5];y = [2, 4, 1, 5, 3];```接下来，我们可以使用MATLAB中的`spline`函数来进行三次样条拟合。

`spline`函数的输入参数是自变量x和因变量y，输出参数是一个函数对象，表示拟合的曲线。

```matlabf = spline(x, y);```现在，我们可以使用这个函数对象来计算拟合曲线上的任意点的取值。

例如，我们可以计算自变量为2.5时的因变量的取值。

```matlaby_fit = ppval(f, 2.5);```最后，我们可以使用MATLAB中的`plot`函数来绘制原始数据和拟合曲线。

```matlabplot(x, y, 'o', 'MarkerSize', 10); % 绘制原始数据点hold on;xx = linspace(min(x), max(x), 100); % 生成用于绘制拟合曲线的自变量取值yy = ppval(f, xx); % 计算拟合曲线上的因变量取值plot(xx, yy, 'r-', 'LineWidth', 2); % 绘制拟合曲线hold off;```这样，我们就完成了三次样条拟合的代码编写。

通过运行这段代码，我们可以得到原始数据和拟合曲线的图像。

三次样条拟合是一种常用的数据拟合方法，可以用于拟合非线性数据。

MATLAB提供了方便的函数和工具，可以轻松实现三次样条拟合。

matlab数据拟合应用题数据拟合是指根据已知的数据点，寻找一个函数模型，使该模型与给定的数据点最为接近。

在Matlab中，数据拟合是一个常见的应用，可以通过多种方法实现，比如多项式拟合、线性回归、非线性最小二乘拟合等。

下面我将从应用角度介绍一些常见的数据拟合应用题。

1. 天气预测，假设我们有一系列历史气温数据，我们可以使用Matlab进行数据拟合，找到一个函数模型来预测未来的气温变化。

通过拟合历史数据，我们可以得到一个趋势模型，从而预测未来的气温变化趋势。

2. 股票价格预测，对于股票市场的数据，我们可以使用Matlab进行数据拟合，找到一个模型来预测股票价格的变化。

通过拟合历史股票价格数据，我们可以得到一个模型，从而预测未来股票价格的趋势。

3. 经济增长预测，对于经济增长数据，我们可以使用Matlab 进行数据拟合，找到一个模型来预测未来的经济增长趋势。

通过拟合历史的经济增长数据，我们可以得到一个模型，从而预测未来的经济增长趋势。

4. 化学反应动力学，在化学工程中，我们经常需要对反应动力学进行建模和预测。

通过实验数据，我们可以使用Matlab进行数据拟合，找到一个合适的动力学模型，从而预测反应的速率和趋势。

5. 生物学数据分析，在生物学研究中，我们经常需要对生物数据进行拟合和分析。

比如，对于生物体内某种物质的浓度随时间的变化，我们可以使用Matlab进行数据拟合，找到一个模型来描述这种变化趋势，从而对生物过程进行分析和预测。

总之，数据拟合在各个领域都有着广泛的应用。

在Matlab中，通过合适的数据拟合方法，我们可以找到一个合适的模型来描述数据的变化趋势，从而进行预测和分析。

希望以上的例子能够帮助你更好地理解Matlab数据拟合的应用。

在MATLAB中，可以使用 `gamfit` 函数对数据进行Gamma函数拟合。

首先，你需要确保你的数据已经导入到MATLAB中。

然后，你可以使用以下步骤进行拟合：
1. 定义Gamma函数形式。

2. 使用 `gamfit` 函数进行拟合。

以下是一个简单的示例：
```matlab
% 导入数据
data = [1 2 3 4 5 6 7 8 9 10]; % 示例数据，你可以替换为你的数据
% 定义Gamma函数形式
gamma_func = @(x, param)(param(1)./(x.^param(2)).*exp(-param(3).*x);
% 使用gamfit函数进行拟合
param = gamfit(data, gamma_func);
% 输出拟合参数
disp(param);
```
在这个例子中，`gamma_func` 是Gamma函数的定义，其中`param` 是一个向量，包含了函数的参数。

`gamfit` 函数会对输入的数据 `data` 进行拟合，并返回拟合参数 `param`。

你可以使用
`disp` 函数来查看拟合的参数值。