第6章 动力学
- 格式:ppt
- 大小:570.00 KB
- 文档页数:3

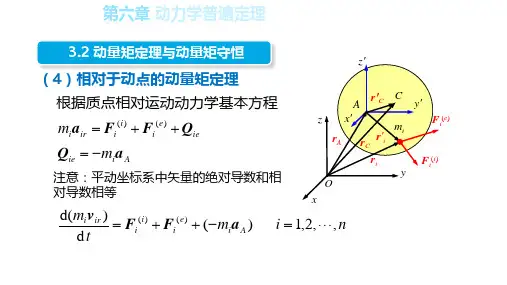
3.2 动量矩定理与动量矩守恒根据质点相对运动动力学基本方程注意:平动坐标系中矢量的绝对导数和相对导数相等(e )(4)相对于动点的动量矩定理iee ii i ir i m Q F F a ++=)()(Ai ie m a Q −=ni m tm A i e i i i ir i ,,2,1)(d )d()()( =−++=a F F v3.2 动量矩定理与动量矩守恒两边叉乘r i ′,并求和(对动点A 取矩)注意到:内力系的主矩等于零;质心计算公式;叉乘性质n i m tm A i e i i i ir i ,,2,1)(d )d()()( =−++=a F F v ()=×′=′=∑∑ir i ir Cii i ie im M m v v r r F[])(d d)(A Ce iiiri iM m ta r Fr v r −×′+×′=×′∑∑是质点系相对动点A是外力系对动点A 的主矩是牵连惯性力的合力对动点A 的力矩注意平动系惯性力合力作用点3.2 动量矩定理与动量矩守恒Ar ir i i m L v r =×′∑ )()(e Ae iiMFr =×′∑ )()(e A A CM Q M a r =−×′d t[∑r i′×m i v ir])(d )(A Ce iiM a r Fr −×′+×′=∑(e )质点系相对动点的动量矩定理=质点系相对动点的动量矩对时间的导数外力系对该点的主矩加在质心上的牵连惯性力的合力对该点之矩+3.2 动量矩定理与动量矩守恒3.2 动量矩定理与动量矩守恒①如果动点为质心C ,则动点的动量矩定理为相对质心的动量矩定理)(d d )(e A e A Ar tQ M M L +=3.2 动量矩定理与动量矩守恒②如果a A = 0,则③如果A 点的加速度方向通过质心,则)(d d )(e A e A Ar tQ M M L +=)(d d e A Ar tM L =)(d d e AAr tM L =3.2 动量矩定理与动量矩守恒④对质心的动量矩守恒定律则对质心的动量矩守恒)(d d e CCr tM L =0)(=e CM()=e Cz M cL =cr constL cz =3.2 动量矩定理与动量矩守恒【例】质量为m半径为r的均质圆盘从静止开始,沿倾角为θ的斜面无滑动的滚下。