澳洲高中数学课程

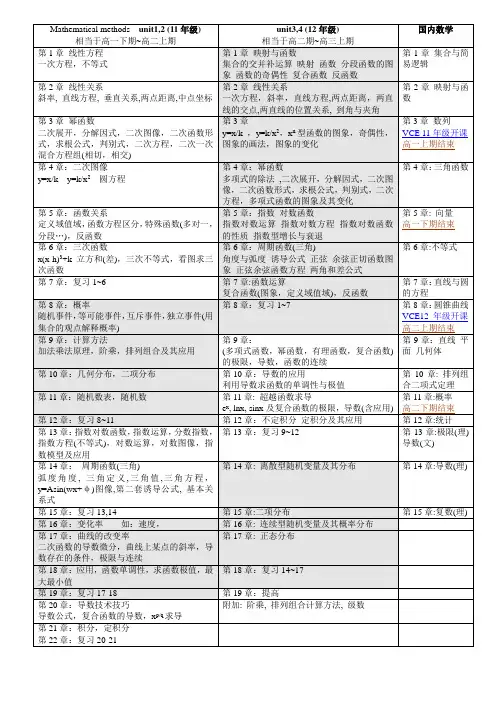
关于Further Mathematics 与Mathematics Methods注：11年级的课时计划会打乱书上章节的顺序●分析：1) Further Mathematics内容覆盖广(6年级~大一)，与现行高中数学教材接轨小，在内容上仅有不到20%相同的地方，且难度较小，但除应用性强外，对国内数学帮助不大；但国内高中数学对Math有较大帮助。

2) Mathematics Methods 内容与国内高中数学内容相近，大约有70~80%相同，尽管在要求上更重于应用，理论难度要略低于国内数学，但它与国内数学互相辅助程度较大。

然而要考虑的是：学生的英语水平及难度会对学生的VCE总分产生影响。

3) 假设只学习Mathematical Methods，根据Mathematical Methods教学安排调整中文数学的教学顺序例如：中文数学中的数列、向量内容后置，将Mathematical Methods中的概率统计前移。

●方向1)为了保证学生VCE的总分，应该保留Further Mathematic；2)而为了让学生在报考国外大学的专业时有更多的选择(尤其指理工科)或得到更高的分数，应该学习Mathematical Methods，且Methods与国内数学的关系更为紧密。

只是在学科的课时上，外教的配置上，学生的学费改变与否上考虑。

●建议：1、鉴于学生水平的参差不齐，理想状态：所有学生必修Further Mathematic，数学不错的(将来可能报国外理科专业)的同学选修Mathematical Methods。

这将会增加学生的课时。

2、学生学Further Mathematic和Mathematical Methods，多增加一门Mathematical Methods。

------- 11年级学生学习Further Mathematic的3,4单元；12年级学生学习Mathematical Methods的3,4单元，最后参加5个学科的VCE大考。

澳洲SACE（南澳大利亚州教育综合）是澳大利亚南澳大利亚州的高中证书体系。

在SACE的十二年级数学课程中，学生将学习高等数学的理论和实践，为日后进入大学或职业学校做准备。

以下是澳洲SACE 十二年级数学内容的详细介绍：一、数学方法1. 函数和图像在这一部分，学生将学习各种函数的定义和性质，包括线性函数、二次函数、指数函数、对数函数和三角函数等。

他们将学习如何绘制这些函数的图像，并理解函数的变化趋势。

2. 微积分的基本概念学生将开始接触微积分的基本概念，包括导数和积分。

他们将学习如何计算函数的导数和积分，以及如何应用这些概念来研究变化率和曲线下面积。

3. 统计学这一部分将介绍统计学的基本概念，包括数据收集、数据展示、概率和推断。

学生将学习如何分析和解释数据，并掌握统计学方法来做出推断和预测。

4. 离散数学学生将学习离散数学的基本概念，包括集合、排列组合、图论和逻辑推理。

他们将学习如何应用这些概念解决实际问题，并理解离散数学在计算机科学和信息技术中的应用。

二、专业数学1. 线性代数学生将学习线性代数的基本概念，包括向量、矩阵、线性方程组和向量空间等。

他们将学习如何解决线性代数相关的实际问题，并理解线性代数在工程、物理、经济等领域的应用。

2. 微积分的应用这一部分将深入探讨微积分的应用，包括曲线的长度、曲面的面积、体积和物理学中的应用等。

学生将学习如何应用微积分解决实际问题，并掌握微积分的工程和科学应用技巧。

3. 统计学进阶学生将深入研究统计学的高级方法，包括回归分析、方差分析、时间序列分析和统计推断的方法等。

他们将学习如何应用这些方法解决实际问题，并掌握统计学在商业、经济、金融等领域的应用技巧。

4. 计算数学这一部分将介绍计算数学的基本概念，包括差分方程、数值方法和优化算法等。

学生将学习如何应用计算数学方法解决实际问题，并掌握计算数学在科学工程和计算机科学领域的应用技巧。

三、高级数学1. 微积分的拓展学生将深入研究微积分的高级概念，包括多元函数、偏导数、重积分和曲线积分等。

澳洲中学高等数学教材数学是一门普遍被认为是具有挑战性和重要性的学科，它不仅为我们提供了解决实际问题的工具，还培养了我们的逻辑思维和解决复杂问题的能力。

在澳洲的中学阶段，学生们接触到了高等数学教材，这些教材为他们提供了深入学习和探索数学的机会。

澳洲中学的高等数学教材广泛覆盖了各个核心内容领域，包括代数、微积分、几何学和统计学等。

这些教材旨在帮助学生建立坚实的数学基础，并培养他们的问题解决和批判性思维能力。

教材的编写者们注重从真实世界问题中找到数学的应用，以激发学生的兴趣和提高他们的学习动力。

在高等数学教材中，代数是一个非常重要的领域。

教材会引导学生从简单的代数表达式开始，逐渐引入复杂的方程和不等式。

通过解决实际问题，学生可以学习到各种代数技巧和策略，比如因式分解、配方法和二次方程求解等。

这些技能不仅在数学中有用，也在其他科学领域和日常生活中有广泛的应用。

在微积分领域，教材会向学生介绍导数和积分的概念与应用。

学生将学会计算导数和积分，理解它们的几何和物理意义，并运用它们解决实际问题。

通过学习微积分，学生可以深入理解变化率、速度、加速度等概念，并将其应用于物理、经济学和工程学等领域。

几何学也是高等数学教材的一个重要组成部分。

学生将学习到平面几何和立体几何的各种概念和性质，包括图形的面积、体积、角度关系等。

教材会引导学生进行证明和推理，培养他们的逻辑思维和几何直觉。

几何学的学习不仅可以帮助学生理解几何形状和空间关系，还有助于培养他们的空间想象力和几何建模能力。

此外，统计学也是澳洲中学高等数学教材中的一项重要内容。

学生将学习到各种数据收集、整理和分析的方法，以及如何通过统计推断和概率计算得出结论。

统计学的学习将帮助学生理解和评估数据的可靠性，并培养他们的数据解释和沟通能力。

在信息时代，统计学的应用已经渗透到各个领域，学习统计学将使学生更好地理解与数据相关的问题和决策。

总之，澳洲中学高等数学教材提供了丰富的学习资源和挑战。

澳洲VCE教材中关于非线性数据的回归分析作者：***来源：《福建中学数学》2023年第11期数据分析作为数学核心素养之一，要求学生具有基于数据表达现实问题的意识和较强的数据处理能力．本文以研究澳洲VCE课程（Victoria Certifi-cate of Education）高中数学教材中关于非线性数据的回归分析为切入点，探讨数据分析与图形计算器的运用，进而在现实情境中提出探究性问题，旨在通过海外教材中有关数据处理的教学内容和特点的分析，为国内高中数学课程中相关板块的实际课堂教学提供借鉴，也为今后结合本土教育教学特色进行有效融合与创新提供思路．1 一元线性回归分析回归分析（regression analysis）是一种统计分析方法，用于确定两种或两种以上变量之间的定量关系．根据涉及的变量数量，分为一元回归和多元回归分析．根据自变量和因变量之间的关系类型，回归分析可分为线性回归分析和非线性回归分析．在高中阶段，主要学习一元回归分析．对于一元线性回归分析，基于最小二乘法原理，可以用形式为的直线来进行拟合．利用图形计算器输入已知数据，可以较容易地获得拟合直线，通过相关系数或者拟合优度判定系数的大小来判断直线拟合的程度．越接近1或者越接近1，说明拟合程度越高．计算器一般会在每次函数拟合后自动算出对应的相关系数和拟合优度判定系数．2 一元非线性回归分析在统计离散数据时，往往利用散点图（scatter-plot）呈现数据之间的关系．一些数据之间的关系并非是线性的，如果单单依靠线性拟合来表征，往往并不准确．澳洲教材在处理一元非线性数据时，利用函数变换和化归的数学思想，化曲为直来进行数据的拟合．相比于单纯使用图形计算器来解决拟合问题，这样的处理方式能够锻炼学生运用数学工具进行分析及解决问题的能力．2.1 非线性数据的变换处理澳洲教材中在处理非线性数据时，首先利用散点图呈现数据间的关系．散点图的形状不同，对应的数据关系也不同，因此需要运用合理的变换以达到“化曲为直”的效果．值得注意的是，同一种非线性的数据形态会有多种不同的变换处理方式．如图1，左上角的散点图对应的变换可以是． y2，lgx，1/x这里澳洲教材只讨论单调递增或者单调递减的非线性数据回归分析，这也与国内高中阶段对于数据统计的教学要求较一致．以教科书中的平方变换、对数变换和倒数变换为例（见表1），解释说明其变换对于非线性数据“化曲为直”的原理．2.2 图形计算器在非线性回归中的运用在解决实际应用问题时，通常需要确定变量并收集一定数量的数据，然后根据数据绘制出相应的散点图．之后根据绘制后的散点图形态选择合适的函数，建立函数关系式并进行回归分析，最终得到回归方程．对于回归方程，还需进行相关性检验．这整个过程需要大量的计算和时间，容易让学生感到繁琐和重复．作为传统教学方式的一种补充，图形计算器能够有效地实现曲线拟合与数学其它分支的多元联系，突破了曲线拟合教学的瓶颈．因此，图形计算器在教学中发挥着重要作用．表2列举了12个国家人口平均寿命（年）和国内生产总值GDP（亿美元）的数据：（1）根据表2中各组对应的数据，能否找到一种关系式，使它能够近似反映人口寿命（用表示）关于国内生产总值（用表示）的关系？试写出一个人口寿命关于国内生产总值的关系式（系数保留三位有效位数）．（2）若一个国家的国内生产总值GDP为20000亿美元，利用（1）问求得的关系式，推测其人口的平均寿命（保留一位小数位数）．（3）查询相关统计数据，分析其他影响人口寿命的因素，进一步探究其关联程度，概括总结出报告；预测近一年我国的人口平均寿命，讨论可能产生偏差的成因．在以往课堂教学活动中，对于问题（1），容易想到先画出表2数据的散点图（如图2），利用图象直观分析数据的变化规律，适当选择函数用以描述人口寿命与国内生产总值的关系．之后借助图象计算器快捷地拟合出函数解析式．最后根据拟合优度判定系数r 2，其值越接近于1拟合度越高．相比之下，澳洲教材用数据的变换角度来解决这个非线性拟合问题：首先从原始散点图直观上观察到点的分布呈现凹的递增形状，可以利用y2，lgx或x/1等非线性变换使数据线性化，即化曲为直．这里我们不妨使用变换，也就是把横坐标标度调整为对数标度lg （GDP）：，使得原本呈曲线形态的散点图变换成近似线性形态（如图3）．此时人口寿命y与国内生产总值的常用对数lgx呈近似线性形态，即y x lgx），问题化归为一元线性回归分析问题，于是基于最小二乘法原理，采用直线y = a lg（x）+b来进行拟合（如图4）．最后得到关系式：lifespan = 54.3+5.59×lg（GDP）．对于问题（2），只需令x = 20000，代入上式可得lifespan = 54.3+5.59×1g（20000）= 78.3years ，因此，当国内生产总值GDP为20000亿美元时，人口平均寿命的预测值为78.3岁.当然，也可选择其他类型的变换进行拟合，根据拟合优度判定系数，选择较优模型进行预测．问题（3）是开放型试题，可以作为一个挑战性的学习主题．学生们能够在现实情境中查找资料，获取信息，并经历数学建模的过程．这类问题有助于培养学生以数学的视角观察世界，運用数学思维思考世界，以及用数学语言表达世界．因此，这类问题对于学生的综合素养提高有着积极的促进作用．另外数据来源于真实世界，并非人为拼凑，学生在建立模型、数据分析之后所得的结果并非完美，也能够进一步促使学生思考、修正、探究数据背后的信息．这也符合数学课程跨学科融合的大趋势，值得借鉴．3 启示与思考作为上海市“试点高中国际课程”的一线数学教师，笔者致力于在不同教学模式中找到契合点，寻找有利于国内培养核心素养的元素，当然在本文关于非线性数据回归教学中也有着进一步的反思．3.1 信息技术与数学课程的深度融合数学教学应注重信息技术的运用，优化课堂教与学的方式．进一步地，教师应为学生提供理解概念所需的背景，并引导学生课后自主获取资源．教师和学生可以共同探索利用信息技术探索算法，进行大规模计算，从数据库中获取数据，实现传统教学方式难以达到的效果．因此，信息技术在数学教学中的应用有着重要的意义，可以为学生和教师提供更丰富、更高效的教学资源和方法． 3.2 在综合情境中阐释科学规律高中数学教育的目标不仅是传授数学知识，更要培养学生的综合素养和实践能力，提升他们的思维水平和创新能力．数学教学中的实际应用问题可以激发学生的兴趣和动力，帮助他们理解数学知识与现实世界的联系，开拓视野和思维．相信在“双新”背景下的教学将来更加开放与多元．参考文献[1]中华人民共和国教育部．普通高中数学课程标准（2017年版）[S]．北京：人民教育出版社，2018[2]Peter Jones，Kay Lipson，Michael Evans．General Mathematics[M]． Melbourne：Cambridge University Press，2022。

澳洲vce数学分类澳大利亚墨尔本州高中毕业考试（VCE）是一个重要的考试，涵盖了各个学科，其中数学是其中之一。

在VCE数学考试中，学生可以选择不同的数学类别，以适应他们的兴趣和能力水平。

以下是澳洲VCE数学分类的简要介绍：高级数学（Mathematical Methods）高级数学针对那些对数学具有较强基础并希望继续深入学习的学生。

课程涵盖代数、函数、微积分和统计学。

这门课程适合那些希望继续学习大学数学、物理学、工程学等学科的学生。

在VCE数学考试中，高级数学也是最受欢迎的课程之一。

专业数学（Specialist Mathematics）专业数学是高级数学的深入拓展，它主要关注更高级的代数、微积分和几何学。

这门课程适合那些对数学具有很强兴趣并希望在数学方面深入研究的学生。

学生需要在高级数学中获得优异的成绩才有资格学习专业数学。

常规数学（Further Mathematics）常规数学课程适合那些对数学感兴趣，但不想深入研究高级数学和专业数学的学生。

它涵盖了代数、函数和统计学，适合那些学生打算进入商科、社会科学和其他非数学学科的大学课程。

数学方法（Mathematical Methods CAS）数学方法是一个计算机辅助学习（CAS）的数学课程。

这门课程旨在通过计算机科技的应用，帮助学生更好地理解数学概念、解决问题和进行模拟。

数学方法适合那些对科技感兴趣的学生，例如计算机科学、数学或工程学等领域。

总而言之，澳洲VCE数学分类为学生提供了广泛的选择，以满足他们不同的兴趣和能力水平。

学生可以根据自己的职业目标和未来学习计划来选择适合自己的数学课程。

澳大利亚高中数学课程四种不同类型
1、Mathematics Standard（标准数学）。

学习数字、图像、代数、数据、
测量、空间以及几何等基础知识，难度比较基础，主要为之后的学习做铺垫。

2、Mathematics Advanced（高阶数学）。

在标准数学的基础上，拓展学习
的深度和广度，进行更高层次的数学能力提升，学习代数、坐标几何、统计学、函数和三角学等方面技能。

3、Mathematics Extension（数学延伸）。

数学延伸的课程包含所有澳洲高
考数学科目所有知识内容，并将这些概念扩展到更深的深度和专业的学术研究上。

4、Mathematics Extension 1 and 2（数学延伸1和2）。

数学延伸1和2
是数学延伸的更高阶段，在数字、代数、几何和微积分方面的分析和推算能力都需要有更高层次的要求。

中澳（VCE）数学课程的研究与实践VCE即Victoria Certificate of Education的英文缩写，是澳大利亚维多利亚州课程评估署VCAA（全称Victorian Curriculum and Assessment Authority）向完成11、12年级(相当于我国国内的高二和高三)的学习,并达到教学要求的毕业生颁发的学历证书，所得成绩将直接进入澳大利亚的大学录取系统。

我校与澳大利亚维多利亚州HAILEYBURY COLLEGE的课程合作是一个“双学籍、双文凭、双通道”的项目，其中VCE数学课程引进澳大利亚原版英文教材《Mathematic Methods》,学生通过学习，与澳大利亚本土学生同时参加全英文环境的VCE数学课程评估.一、中澳（VCE）数学课程比较中澳（VCE）双方的数学课程目标都是为了提高学生作为未来公民所必要的数学素养，以满足个人发展与社会进步的需要.1、从课程结构设置看VCE数学课程有四种教材可供学生选择,根据知识侧重点和难度的不同设有Further Mathematics，Specialist Mathematics,Mathematical Methods和Mathematical Methods CAS，学生一旦选定教材就参加相应的课程评估，我校VCE课程合作班选择的是Mathematical Methods，这套教材侧重于数理知识和数学方法，强调数学在日常生活和社会中的广泛应用。

我国的数学新课程由必修和选修两部分构成,学生通过对必修部分不同的模块和根据自己兴趣选择的选修部分的学习，参加统一形式的考试。

相比而言，VCE数学对教材的分类比较固定，相对应的考试统一度高；国内新课程模块分类细致，特别是选修部分各系列的选择灵活性强，有利于学生兴趣的培养和今后的延续学习。

2、从课程内容看（见表1)表 1：课程内容比较表3、课程的整合VCE课程的合作项目要求VCE教学在高二年级真正展开,并在高三年级第一学期的期中阶段参加课程考核。