江苏省连云港市岗埠中学中考数学《反比例函数的图象与性质》复习教案2 苏科版

9.2反比例函数的图象与性质（2）
一、设计思路
本节课是在学习上节课初步感知反比例函数的图象特点基础上，进一步探索反比例函数的性质，形成数学能力．
本节课通过学生对一次函数的图象与性质复习，教者展示上节课学生所做书中练习的6个反比例函数图象，引导学生进行分类并说明分类的依据，从而使学生在对照正比例函数的性质的基础上，总结、归纳、揭示反比例函数的性质，并了解反比例函数的图象不可能与坐标轴相交的原因．运用类比的方法，使学生感受到学习反比例函数图象和性质与学习其它函数一样，要善于形数结合，由函数关系式联想到图象的位置及其性质，由图象和性质联想到比例系数K的符号，通过探究加深对反比例函数图象及性质的理解与领悟，提高了学生分析问题、解决问题的能力．
二、目标设计
1．认识反比例函数的图象与性质，并能简单运用．
2．结合反比例函数的图象，揭示与其对应的函数关系式之间的内在联系及其几何意义．3．能根据图象分析并掌握反比例函数的性质，进一步感受形数结合的思想方法．
四、例题设计
说明：解决含有字母系数的不同函数在同一直角坐标系内的图象这一类题目的方法一般有两种：一是根据图象确定所含字母的取值范围，看字母系数的取在不同函数中是否一致；二是先假设字母系数的取值，确定不同函数的图象的位置，再看
建湖县近湖中学八年级数学备课组。

11.2 反比例函数的图像与性质（2）学习目标1．会用待定系数法确定反比例函数解析式；2．能根据图像分析并掌握反比例函数的性质，进一步感受形数结合的思想 方法．重点、难点：分析并掌握反比例函数的性质．学习过程一.【预学指导】初步感知、激发兴趣 1．反比例函数y=1m x-的图象在第二、四象限，则m 的取值范围是________． 2．已知反比例函数y=5m x -的图象在每一个象限内，y 随x 增大而增大， 则m________．3．已知反比例函数y=k x与一次函数y=2x+k 的图象的一个交点的横坐标是 -4，则k 的值是__________．二.【问题探究】问题1：在上节课我们画出了反比例函数4y x＝、4y x ＝－、6y x＝、 6y x ＝－的图像，请观察这些函数的图像，思考反比例函数k y x ＝ （k 为常数，k ≠0）的图像有什么特征？思考如下问题：（1）每个函数的图像分别在哪几个象限？（2）在每一个象限内，随着x 的增大，y 是怎样变化的？（3）反比例函数的图像与x 轴有交点吗？与y 有交点吗？为什么？ （小组讨论）总结：反比例函数k y x ＝的图像随k 值的变化情况． 反比例函数y ＝k x(k 为常数，k ≠0)的图像是_________． 当k ＞0时，双曲线的两支分别在第_________象限，在每一个象限内， y 随x 的增大而_________；当k ＜0时，双曲线的两支分别在第_________象限，在每一个象限内， y 随x 的增大而_________．问题2：已知反比例函数y ＝k x的图像经过点A （2，－4）． 个人复备O xy（1）求k的值；（2）这个函数的图像在哪几个象限？y随x的增大怎样变化？（3）画出函数的图像；（4）点B（12，－16）、C（－3，5）在这个函数的图像上吗？问题3：（1）点A（4 ，－2 ）在函数8yx＝－的图像上吗？写出点A关于原点O对称的点A′的坐标，点A′在函数8yx＝－的图像上吗？（2）在函数8yx＝－的图像上任取一点B，点B关于原点O的对称点B′在这个函数的图像上吗？总结：反比例函数的两支图像关于________对称三.【拓展提升】1．如图，是反比例函数y =2－mx的图象的一支．(1)函数图象的另一支在第几象限？(2)求常数m的取值范围。

江苏省涟水县徐集中学八年级数学 反比例函数图像与性质导学案（2） 苏科版一、预习预习P67--69在平面直角坐标系中画出下列函数图像（1）y=x 1，y=－x 1，（2）y=x 4，y=－x4，同桌两个人分别选择一题，并一起比较讨论：问题1：你能将展示的4个反比例函数图象进行分类吗？并说明这样分类的依据问题2：每个函数的图象分别在哪几个象限？问题3：在每个象限内，随着x 的增大，y 是怎样变化的？问题4：反比例函数的图象与x 轴有交点吗？与y 轴有交点吗？为什么？二、新知探究1、结合预习说说怎样判定函数图象在哪象限？在每一个象限内，随着x 的增大，y 是怎样变化的？反比例函数的图象与x 轴有交点吗？与y 有交点吗？为什么？2、如果将反比例函数的图象绕原点旋转0180，你有什么发现？三、例题讲解例1已知反比例函数y=xk 的图象经过A （2，—4）。

（1）k 的值 （2）这个函数的图象在哪几个象限？y 随x 的增大怎样变化？（3）点B （21，—16）、C （—3，5）在这个函数的图象上吗？ 例2、若反比例函数y=24212-+m x m 的图象经过第二、四象限，求函数的解析式。

四、小结 反比例函数性质是什么五、课后作业大练习册P49—50页 1--7六、课堂作业1．已知反比例函数x m y 23-=，当______m 时，其图象的两个分支在第二、四象限内；当______m 时，其图象在每个象限内y 随x 的增大而减小。

2．若反比例函数xk y 3-=的图象位于一、三象限内，正比例函数x k y )92(-=过二、四象限，则k 的整数值是________。

3．已知P （1，m 2+1）在双曲线x k y =上，则双曲线在第_________象限，在每个象限y 随x 的增大而________.4.下列函数中,当x>0时,y 随x 的增大而增大的是 ( ) A.y=2-3x B.y=2x C.y=-2x-1 D.y=-12x2.下列函数中,图象大致为如图的是( ) A.y=1x (x<0) B.y=1x (x>0) C.y=-1x (x>0) D.y=-1x (x<0)。

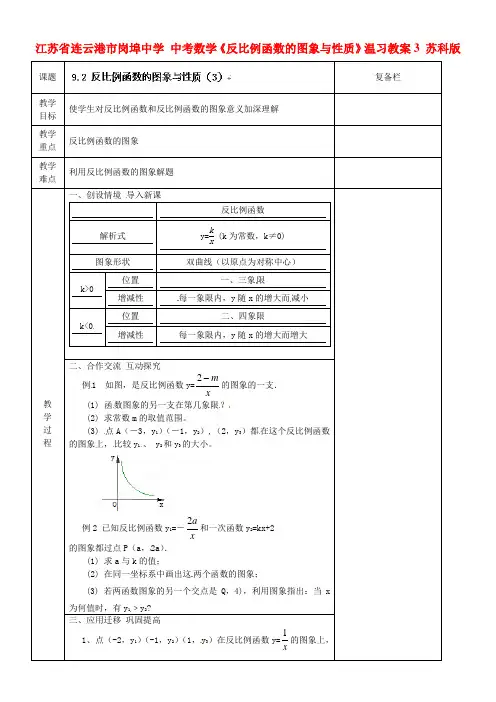
江苏省连云港市岗埠中学中考数学《反比例函数的图象与性质》温习教案3 苏科版课题复备栏教学目标使学生对反比例函数和反比例函数的图象意义加深理解教学重点反比例函数的图象教学难点利用反比例函数的图象解题教学过程一、创设情境导入新课反比例函数解析式y=kx(k为常数，k≠0)图象形状双曲线（以原点为对称中心）k>0位置一、三象限增减性每一象限内，y随x的增大而减小k<0位置二、四象限增减性每一象限内，y随x的增大而增大二、合作交流互动探究例1 如图，是反比例函数y=xm2的图象的一支．(1) 函数图象的另一支在第几象限？(2) 求常数m的取值范围。

(3) 点A（－3，y1）（－1，y2）,（2，y3）都在这个反比例函数的图象上，比较y1、、 y2和y3的大小。

例2 已知反比例函数y1=－xa2和一次函数y2=kx+2的图象都过点P（a，2a）．(1) 求a与k的值；(2) 在同一坐标系中画出这两个函数的图象；(3) 若两函数图象的另一个交点是Q，4)，利用图象指出：当x为何值时，有y1﹥y2?三、应用迁移巩固提高1、点（-2，y1）（-1，y2）（1，y3）在反比例函数y=x1的图象上，比较y1、、y2、y3的大小。

2、已知反比例函数y=xk与一次函数y=mx+b的图象交于P(－2,1)和Q（1，n）两点．(1) 求反比例函数的解析式；(2) 求n的值；(3) 求一次函数y=mx+b的解析式四、总结反思拓展升华1．填表完成反比例函数的性质．任意写出一个反比例函数k的符号图象所在象限增减性一、三象限每个分支y随x的增大而增大2. 已知一次函数y=kx+b（k≠0）的图象与x轴、y轴交于A、B两点，且与反比例函数y=xm（m≠0）的图象在第一象限交于点C，CD⊥X轴于D，且OA=OB=OD=1．（1）求点A、B、D的坐标；(2) 求一次函数和反比例函数的解析式．作业布置补充习题课后反思。

反比例函数的图像与性质教案（2）教学目标1学会用描点法作反比例函数的图象2能结合函数图象进行探索、理解并掌握反比例函数的性质3观察、分析、探究、归纳及概括能力教学重点:反比例函数图像的画法，反比例函数的性质教学难点:反比例函数的性质教学过程:：一、课前预习与导学1．下列函数图像位于第一、三象限的是_________________①②③④２．已知函数的图像位于第二、四象限，则m的取值范围是_______________3．已知正比例函数中y随x的增大而增大，则反比例函数的图像在第_____象限。

二、情境创设探究1、作反比例函数y=和y=的图象;并根据图象完成下表.思考:①、当函数为y=, y=具有与y=一样的性质吗?②、当函数为 y=, y=具有与y=一样的性质吗?③、当函数为y=（k≠0）又具有怎样的性质?归纳：反比例函数y=（k≠0）的图象，当k＞0时，在每一象限内，y的值随着x值的增大而减小；当k＜0时，在每一象限内，y的值随着x值的增大而增大二、例题讲解例1.：已知反比例函数y=的图象经过A（2，—4）。

（1）k的值.（2）这个函数的图象在哪几个象限？y随x的增大怎样变化？（3）画出函数的图象.（4）点B（，—16）、C（—3，5）在这个函数的图象上吗？例2：.已知一次函数图象与反比例函数图象交于点（-1, m )，且过点（0，-3)，求一次函数的解析式．三、课堂小结四、板书设计五、教学反思1.反比例函数的图象在（）A.第一、三象限B.第一、二象限C.第二、四象限D.第三、四象限2.若函数的图象在第一、三象限，则函数y=kx-3的图象经过( )A.第二、三、四象限B.第一、二、三象限C.第一、二、四象限D.第一、三、四象限3.下列函数中，y随x的增大而减小的有（）A.2个B.3个C.4个D.5个4.以下各图表示正比例函数y=kx与反比例函数的大致图象，其中正确的是（）5.若反比例函数的图象在第二、四象限，则 m 的取值范围是 .6.反比例函数经过（-3, 2)，则图象在象限.7.若反比例函数图像位于第一、三象限，则k .8.已知函数的图象与直线y=x-1都经过点（-2, m )，则m= ，k= .9.已知一次函数图象与反比例函数图象交于点（-1, m )，且过点（0，-3)，求一次函数的解析式．10、已知反比例函数的图象在每一个象限内函数值y随x的增大而减小，且k的值满足9-2（2k-1）≥2k-1，若k为整数，求反比例函数的解析式。

拓展练习1．已知点A（1，
1
y）、B（2，
2
y）、C（－3，
3
y）都在反比例函数
x
y
6
=的图象
上，则
1
y、
3
y、
2
y的大小关系是 .
2．在反比例函数3
k
y
x
-
=图象的每一支曲线上，y都随x的增大而减小，则k的取值范围是，若A（a1，b1），B（a2，b2）在这个函数图像上, 且
a
1
＜a2＜0，则b1与b2的大小关系是 .
3.已知A（﹣1，y1），B（2，y2）两点在双曲线y=上，且y1＞y2，则m的取
值范围是 .
4．已知反比例函数的图像经过点A（－ 6，－3）.
（1）确定这个反比例函数的表达式；
（2）这个函数的图像在哪几个象限？y随x的增大怎样变化？
（3）点B（4，
9
2），C（2，－5）在这个函数的图像上吗？
5.反比例函数y＝
m
x
的图象如图所示，以下结论：
①常数m＜－1；
②在每个象限内，y随x的增大而增大；
③若A（－1，h），B（2，k）在图象上，则h＜k；
④若P（x，y）在图象上，则P′（－x，－y）也在图象上.
其中正确的是 .
课堂小结学习收获。

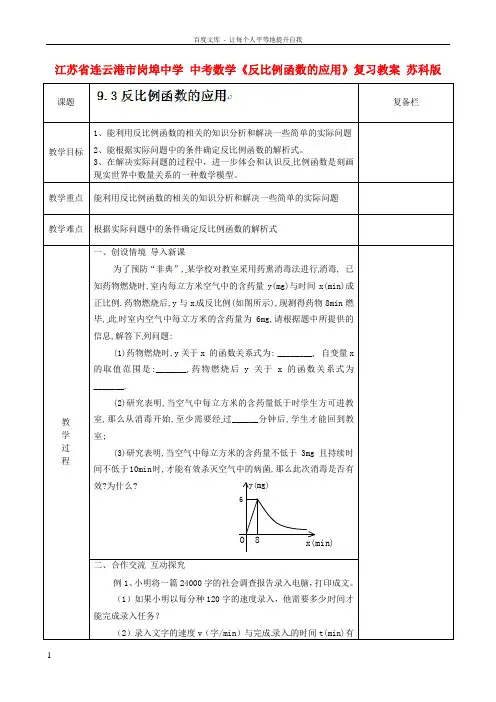
6O 8x(min)y(mg)江苏省连云港市岗埠中学 中考数学《反比例函数的应用》复习教案 苏科版课题复备栏教学目标 1、能利用反比例函数的相关的知识分析和解决一些简单的实际问题2、能根据实际问题中的条件确定反比例函数的解析式。

3、在解决实际问题的过程中，进一步体会和认识反比例函数是刻画现实世界中数量关系的一种数学模型。

教学重点 能利用反比例函数的相关的知识分析和解决一些简单的实际问题教学难点 根据实际问题中的条件确定反比例函数的解析式教学 过 程一、创设情境 导入新课为了预防“非典”,某学校对教室采用药熏消毒法进行消毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y 与x 成反比例(如图所示),现测得药物8min 燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y 关于x 的函数关系式为: ________, 自变量x 的取值范围是:_______,药物燃烧后y 关于x 的函数关系式为_______.(2)研究表明,当空气中每立方米的含药量低于时学生方可进教室,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室;(3)研究表明,当空气中每立方米的含药量不低于3mg 且持续时间不低于10min 时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?二、合作交流 互动探究例1、小明将一篇24000字的社会调查报告录入电脑，打印成文。

（1）如果小明以每分种120字的速度录入，他需要多少时间才能完成录入任务？（2）录入文字的速度v （字/min ）与完成录入的时间t(min)有怎样的函数关系？（3）小明希望能在3h 内完成录入任务，那么他每分钟至少应录入多少个字？例2某自来水公司计划新建一个容积为43410m ⨯的长方形蓄水池。

（1）蓄水池的底部S ()3m 与其深度()h m 有怎样的函数关系？（2）如果蓄水池的深度设计为5m ，那么蓄水池的底面积应为多少平方米？（3）由于绿化以及辅助用地的需要，经过实地测量，蓄水池的长与宽最多只能设计为100m 和60m ，那么蓄水池的深度至少达到多少才能满足要求？（保留两位小数） 三、应用迁移 巩固提高1、见P74练习2、一定质量的氧气,它的密度ρ (kg/m 3)是它的体积V( m 3) 的反比例函数, 当V=10m 3时,ρ=1.43kg/m 3. (1)求ρ与V 的函数关系式；(2)求当V=2m 3时求氧气的密度ρ.四、总结反思 拓展升华某地上年度电价为元/度,年用电量为1亿度.本年度计划将电价调至元至元之间.经测算,若电价调至x 元,则本年度新增用电量y(亿度)与(x －(元)成反比例,当x=时,y=.(1)求y 与x 之间的函数关系式；(2)若每度电的成本价为元,则电价调至多少元时,本年度电力部门的收益将比上年度增加20%? [收益=(实际电价－成本价)×(用电量)]4、如图,矩形ABCD 中,AB=6,AD=8,点P 在BC 边上移动(不与点B 、C 重合),设PA=x,点D 到P A 的距离DE=y.求y 与x 之间的函数关系式及自变量x 的取值范围. 作业布置补充习题课后反思。

苏科版数学八年级下册教学设计11.2 反比例函数的图象与性质（2）一. 教材分析本节课是苏科版数学八年级下册第11.2节反比例函数的图象与性质（2），教材通过实例和图形，让学生进一步理解反比例函数的图象与性质，掌握反比例函数的图象特点，以及如何运用反比例函数解决实际问题。

本节课的内容与学生的生活实际紧密相连，有利于激发学生的学习兴趣和积极性。

二. 学情分析学生在学习本节课之前，已经掌握了反比例函数的定义，比例函数的图象与性质等相关知识。

但学生对于反比例函数的图象与性质的理解和应用还有一定的困难，需要通过本节课的学习，进一步深化学生对反比例函数的认识，提高学生解决实际问题的能力。

三. 教学目标1.让学生理解反比例函数的图象与性质，进一步掌握反比例函数的图象特点。

2.培养学生运用反比例函数解决实际问题的能力。

3.提高学生对数学学习的兴趣和积极性。

四. 教学重难点1.反比例函数的图象与性质的理解和应用。

2.如何引导学生运用反比例函数解决实际问题。

五. 教学方法1.采用问题驱动法，引导学生通过观察实例和图形，发现反比例函数的图象与性质。

2.采用合作学习法，让学生在小组内讨论和分享反比例函数的图象与性质的理解，以及如何运用反比例函数解决实际问题。

3.采用案例教学法，通过具体的实例，让学生理解和掌握反比例函数的图象与性质。

六. 教学准备1.准备相关的实例和图形，用于引导学生观察和发现反比例函数的图象与性质。

2.准备一些实际问题，让学生运用反比例函数解决。

3.准备PPT，用于展示反比例函数的图象与性质的相关知识点。

七. 教学过程1.导入（5分钟）通过展示一些实际问题，让学生感受反比例函数在实际生活中的应用，激发学生的学习兴趣。

2.呈现（15分钟）通过PPT展示反比例函数的图象与性质的相关知识点，引导学生观察和发现反比例函数的图象特点。

3.操练（10分钟）让学生在小组内讨论和分享反比例函数的图象与性质的理解，以及如何运用反比例函数解决实际问题。

9.2反比例函数的图象与性质（2）知识目标：使学生理解反比例函数y=k x (k≠0)的增减性质。

培养、提高学生的空间想象能力。

教学重点：反比例函数的对称性质教学难点：反比例函数的对称性质教学程序：一、情景创设1、画出反比例函数y=2x ，y=4x ，y=6x 的图象2、画出反比例函数y=-2x ，y=-4x ，y=-6x 的图象二、新授：1、观察反比例函数y=2x ，y=4x ，y=6x 的图象，回答下列问题？（1）函数图象分别位于哪几个象限内；（2）在每一个象限内，随着x 值的增大，y 的值怎样变化的？能说明这是为什么吗？（3）反比例函数的图象可能与x 轴相交吗？可能与y 轴相交吗？为什么？答：（1）第一、三象限（2）y 的值随着x 值的增大而减小；（3）不可能与x 轴相交，也不可能与y 轴相交，因为x≠0，所以图象与y 轴不可能有交点，因为不论x 取何实数值，y 的值永不为0（因k≠0）所以图象与x 轴不可能有交点。

2、考察当k=―2，―4，―6时，反比例函数y=k x 的图象，回答（1）中的三个问题。

3、反比例函数图象的性质：反比例函数y=k x的图象，当k >0时，在第一象限内，y 的值随x 的增大而减小；当k<0时，在每一象限内，y 的值随x 的增大而增大。

4、在一个反比例函数图象上任取两点P 、Q ，过点P 分别作x 轴、y 轴的平行线，与坐标轴围成的矩形面积为S 1，过点Q 分别作x 轴，y 轴的平行线，与坐标轴围成的面积为S 2,S 1与S 2有什么关系？为什么？S1=S2= | K |5、将反比例函数的图象绕原点旋转180°后，能与原来的图象重合吗？ 反比例函数的图象是一个以原点为中心的中心对称图形；反比例函数是一个以y=±x 为对称轴的轴对称图形。

三、例题精选例1、已知反比例函数k y x =的图象经过点A （2，－4） （1）求k 的值； （2）这个函数的图象在哪几个象限？y 随x 的增大怎样变化？ （3）画出函数的图象 （4） 点1(,16)2A -、C(-3,5)在这个函数的图象上吗？ 例2、如图所示,一个反比例函数的图象在第二象限内,点 A 是图象上的任意一点,A M⊥x 轴于M,O 是原点,若S △AOM =3,求该反比例函数的解析式,并写出自变量的取值范围.四、随堂练习：P85 1、21．已知反比例函数xm y 23-=，当______m 时， 其图象的两个分支在第二、四象限内；当______m 时，其图象在每个象限内y 随x 的增大而减小。

苏科版数学八年级下册11.2《反比例函数的图象与性质》教学设计2一. 教材分析《苏科版数学八年级下册11.2《反比例函数的图象与性质》》这一节的内容是在学生已经学习了比例函数、一次函数和二次函数的基础上进行教学的。

本节课的主要内容是让学生掌握反比例函数的图象与性质，理解反比例函数的概念，能够判断一个函数是否为反比例函数，以及能够运用反比例函数解决实际问题。

二. 学情分析学生在学习这一节的内容时，已经有了一定的函数知识基础，对于比例函数、一次函数和二次函数的概念和图象都有了一定的了解。

但是，反比例函数的概念和图象与这些函数有很大的不同，学生可能会感到困惑。

因此，在教学过程中，需要引导学生通过观察、分析和归纳来理解反比例函数的图象与性质。

三. 教学目标1.让学生理解反比例函数的概念，掌握反比例函数的图象与性质。

2.培养学生观察、分析和归纳的能力，提高学生的数学思维能力。

3.培养学生运用反比例函数解决实际问题的能力。

四. 教学重难点1.反比例函数的概念的理解。

2.反比例函数的图象与性质的理解和应用。

五. 教学方法采用问题驱动的教学方法，引导学生通过观察、分析和归纳来理解反比例函数的图象与性质。

在教学过程中，注重学生的主体地位，鼓励学生积极参与，培养学生的数学思维能力。

六. 教学准备1.准备反比例函数的图象和性质的相关教学素材。

2.准备多媒体教学设备，如投影仪、计算机等。

七. 教学过程1.导入（5分钟）通过复习比例函数、一次函数和二次函数的图象与性质，引导学生思考：这些函数的图象与性质有什么共同点？有什么不同点？从而引出反比例函数的概念。

2.呈现（10分钟）利用多媒体教学设备，展示反比例函数的图象和性质，引导学生观察和分析，让学生通过自己的观察和思考，理解反比例函数的图象与性质。

3.操练（15分钟）让学生通过解决一些具体的反比例函数问题，运用所学的反比例函数的图象与性质，从而加深对反比例函数的理解。

4.巩固（10分钟）通过一些练习题，让学生巩固所学的反比例函数的图象与性质，提高学生的应用能力。

苏版数学初三下册教案：26一、教学目标1．核心素养通过学习反比例函数的图象和性质，充分表达几何直观，渗透模型思想．2．学习目标（1）进一步明白得和把握反比例函数的图象和性质．（2）灵活运用反比例函数的图象和性质解决问题．（3）领会反比例函数的解析式与图象之间的联系，表达数形结合及转化的思想方法．3．学习重点灵活运用反比例函数的图象和性质解决问题．4．学习难点与反比例函数相关的面积的运算，以及自变量和函数值大小的比较．二、教学设计（一）课前设计1．预习任务任务1阅读教材P7－P8，摸索：如何样用待定系数法求反比例函数的解析式？任务2如何样判定一个点是否在反比例函数的图象上？任务3摸索1：过反比例函数图象上任意一点作坐标轴的垂线，与坐标轴形成的矩形面积与k有什么关系？摸索2：过反比例函数图象上任意一点作某一个坐标轴的垂线，并将那个点与原点相连，形成的三角形的面积积与k有什么关系？2．预习自测1．一个反比例函数的图象通过点（2.5，-3），则那个函数的图象位于第（）象限．A ．一、三B ．二、四C ．一、四D ．二、三答案：B2．如图，点A 为反比例函数3y x=上的任一点，过点A 作AB ⊥x 轴于点B ，则AOB S ∆等于（ ）A ．3B ．32C ．1D ．无法确定答案：B3．若点（1.5，2）在反比例函数xky =的图象上，则k = ，在图象的每一支上，y 随x 的增大而 ．答案：3，减小 （二）课堂设计 1．知识回忆（1）反比例函数的图象是双曲线．（2）当k >0时，它的两个分支位于一、三象限；在每一个象限内，y 随x 的增大而减小．（3）当k <0时，它的两个分支位于二 、四象限；在每一个象限内，y 随x 的增大而增大．（4）反比例函数的图象既关于x 轴对称，还关于y 轴对称，也关于原点对称．（5）同学们预习本课，明白过双曲线上一点作坐标轴的垂线，与坐标轴围成的矩形面积等于|k |．2．问题探究问题探究一 感受“数”与“形”结合的必要性 ●活动一 回忆旧知，加深明白得问题1 下列反比例函数：①2y x=-；②1y 3x =；③107y x =-；④3y 100x=． （1）图象位于第一、三象限的是 ；（2）图象位于第二、四象限的是 ． 教师提出如下问题，学生独立摸索并写出答案． （1）上述四个答案中，k 的值分别是多少？（2）当k 0>时，反比例函数的图象分别位于第几象限？ （3）当k 0<时，反比例函数的图象分别位于第几象限？问题2 在反比例函数：①2y x=-；②1y 3x =；③107y x =-；④3y 100x=的图象上，11(x ,y )、22(x ,y )分别是图象上同一象限内的点：（1）若12x x <，则12y y <的函数是 ． （2）若12x x <，则12y y >的函数是 ．教师提出如下问题，学生独立摸索并回答，然后独立写出答案，再交流反馈．（1）反比例函数2y x=-的图象位于哪几个象限？y 随x 的变化趋势是什么？ （2）反比例函数107y x =-的图象位于哪几个象限？y 随x 的变化趋势是什么？问题探究二 探究反比例函数图象的性质 ●活动一 探究矩形面积与k 值 重点知识★例1 如图，点A 为2y x=上的任意一点，过点A 分别作x 轴和y 轴的垂线，垂足分别为点B 和点C ，求矩形ABOC 的面积．【知识点：反比例函数的性质，矩形的面积；数学思想：数形结合】 详解：设点A 的坐标为(a ，b)，则矩形的面积为ab ∵x2y =过点A （a ，b ） ∴ab=2，即矩形的面积刚好等于反比例的k 值2． ●活动二 若将反比例函数的解析式改为xky =，请仿照上述解答过程得出准确答案．详解：设点A 的坐标为(a ，b)，则矩形的面积为ab ∵xky =过点A （a ，b ） ∴ab=k ，即矩形的面积刚好等于反比例的k 值． ●活动三 探究三角形面积与k 值 重点知识★例2 如图，点A 为xky =上的任意一点，过点A 分别作x 轴的垂线，垂足为点B ，求三角形ABO 的面积．【知识点：反比例函数的性质，三角形的面积；数学思想：数形结合】详解：设点A 的坐标为(a ，b)，则三角形ABO 的面积为ab 21∵xky =过点A （a ，b ） ∴ab k =，即ab k =∴k 21S ΔABO =，即△ABO 的面积刚好等于k 的绝对值的一半．问题探究二 反比例函数图象离原点的距离与k 值的关系 在同一坐标系中，作x 1y =、x 2y =、x 3y =、x4y =的图象，如图． 能够发觉，当k>0时，随着k 的增大，反比例函数xky =的图象的位置相关于原点越来越远．在同一坐标系中，作出一系列k <0反比例函数xky =的图象． 能够发觉，当k <0时，随着k 的增大，反比例函数xky =的图象的位置相关于原点越来越近．综上所述，在同一坐标系中，作多个反比例函数xky =的图象． 能够发觉，当|k |越大时，反比例函数xky =的图象的位置相关于原点越来越远．问题探究三 反比例函数性质的应用． 重点、难点知识★▲●活动一 面积与k 的关系的应用例3 如图，正比例函数x y =与反比例函数xy 1=的图象相交于A 、B两点，BC ⊥x 轴于点C ，则△ABC 的面积为（ ）A ．1B ．2C ．23D ．25【知识点：反比例函数的性质；数学思想：数形结合】详解：设点B 的坐标为(m ，n) ∵反比例函数xy 1=过点B(m ，n) ∴ mn=1由反比例函数的对称性知：点A 与点B 关于原点O 对称，即AO=BO ∴BOC AOB S S ∆∆=2=1方法2：由反比例函数的性质知：21k 21S ΔBOC =⨯= ∴由对称性知OA=OB ，BOC AOBS S ∆∆=2=1．●活动二 反比例函数图象与性质的关系例4 已知反比例函数的图象通过点A （2，6）．（1）反比例函数的图象在第几象限？y 随x 的增大而如何变化？（2）点B （3，4），C （-212，544-），D （2，5）是否在那个反比例函数的图象上？【知识点：反比例函数的性质；数学思想：数形结合】 师生共同分析，教师引导并提出下列问题： （1）点A （2，6）在图象上的含义是什么？（2）图象的位置由哪两个量来确定？我们如何救出那个量？（3）反比例函数y 随x 的变化情形与哪个量有关？y 随x 的变化情形有没有限制条件？（4）某点不在函数图象上的含义是什么？学生解答，在小组里讨论，互相检查，小组代表展现解答过程． 详解：（1）设反比例函数的解析式为xk y = ∵它过点（2，6） ∴k xy 2612==⨯=，它的图象过一、三象限；在每一个象限内，y 随x 的增大而减小．（2）∵12y x=∴x 3=时，y 4=x =-122时，244y 455=-=-x 2=时，y 6=∴点B 和点C 在此反比例函数上，而点D （2，5）不在那个反比例函数的图象上．●活动三 拓展提高 活学活用例5 过反比例函数)01>=x xy （的图象上的任意两点A 、B 分别作x 轴的垂线，垂足分别为C 、D ，连接OA 、OB ，设AC 与OB 的交点为E ，△AOE 与梯形ECDB 的面积分别为S1、 S2，则它们的大小关系为（ ）A ．S1＞S2B ．S1＜S2C ．S1=S2D ．不能确定【知识点：反比例函数的性质；数学思想：数形结合】 详解：∵2k S S ΔBOD ΔAOC == ∴COE COE S S ∆∆-=-ΔBODΔAOC S S ，即S1=S2，故先C ．3．课堂总结 【知识梳理】(1)判定反比例函数的图象的两个分支在哪些象限，只需判定k 的正负即可． 当k 为正时，它的两个分支分别在一、三象限；当k 为负时，它的两个分支分别在二、四象限．(2)判定一个点是否在函数图象上，只需将它的横（纵）坐标代入求出纵（横）坐标，假如刚好相等，则表示那个点在在此函数图象上；若求出的值与告知的坐标不相等，则说明那个点不在函数的图象上．(3)过反比例函数的图象上任一点作坐标轴的垂线，它们与坐标轴围成的面积等于|k |．(4)过反比例函数的图象上任一点作某一坐标轴的垂线，则那个点与垂足和原点围成的三角形面积等于k 的绝对值的一半．【重难点突破】(1) 过反比例函数的图象上任一点作坐标轴的垂线，它们与坐标轴围成的面积等于k 的绝对值．利用与坐标轴围成矩形面积求k 时专门要注意，要紧是图象过二、四象限时容易显现符号错误．(2) 过反比例函数的图象上任一点作某一坐标轴的垂线，则那个点与垂足和原点围成的三角形面积等于k 的绝对值的一半．利用三角形面积求k 时专门要注意，要紧是图象过二、四象限时容易显现符号错误．(3)判定一个点是否在反比例函数图象上时，只需要将它的一个坐标代入，若另一个坐标刚好也相等，则函数必过这一点；否则函数只是那个点．4．随堂检测1．如图，点P 是反比例函数2y x=-图象上的一点，若PD ⊥x 轴于点D ，则△POD 的面积为（ ）．A ．1B ．2C ．4D ．12答案：A 解析：2．如图，点P 是反比例函数xmy =图象上第二象限内的一点，且矩形O EPF 的面积为3，则m 的值为（ ）．A ．3B ．6C ．-3D ．-1.5答案：C 解析：3．如图，点P 是反比例函数xmy =图象上的一点，若PD ⊥x 轴于点D ，△POD 的面积为2，则m 的值为（ ）A ．-2B ．-4C ．-1D ．4答案：B 解析：4． 反比例函数xa y =的图象上有一点A ，AB ∥x 轴交y 轴于点B ，△A BO 的面积为1，则反比例函数的解析式为（ ）A ．2x1y -= B ．x1y -= C ．x2y-= D ．4x1y -=答案：C 解析：5．如图，A 、B 两点在双曲线xy 4=上，分别通过A 、B 两点向坐标轴作垂线段，已知1阴影=S ，则12S S +=（ ）A ．3B ．4C ．5D ．6答案：D 解析：。

《反比例函数的图象与性质（2）》教学案学习目标1．认识反比例函数的图象与性质，并能简单运用．2．能根据图象分析并掌握反比例函数的性质，进一步感受形数结合的思想方法． 学习难点：分析并掌握反比例函数的性质教学过程：一、自主探究1．请画出下列6个反比例函数的图象：y=1x ，y=－1x ，y=4x ，y=－4x ，y=3x ，y=－3x，请大家进行分类并说明分类的依据，探索图象的特征；(1)每个函数的图象分别在哪几个象限？(2)在每一个象限内，随着x 的增大，y 是怎样变化的？(3)反比例函数的图象与x 轴有交点吗？与y 有交点吗？为什么？反比例函数y =k x(k 为常数，k ≠0)的图象是双曲线． 当k ＞0时，双曲线的两支分别在第一、三象限，在每一个象限内，y 随x 的增大而减小；当k ＜0时，双曲线的两支分别在第二、四象限，在每一个象限内，y 随x 的增大而增大．2．如果将反比例函数的图象绕原点旋转180°，你有什么发现？将反比例函数的图象绕原点旋转180°后，能与原来的图象重合，因此反比例函数图象是中心对称图形，它的对称中心是坐标系的原点．二、自主合作例1．已知反比例函数y =k x的图象经过点A （2，—4）. (1)求k 的值； (2)这个函数的图象在哪几个象限？y 随x 的增大怎样变化？ (3)画出函数的图象； (4)点B （12，—16）、C （—3，5）在这个函数的图象上吗？ 例2．已知反比例函数 y =x 5的图象上有两点P(1,a), Q(b,2.5). (1) 求a 、b 的值；(2) 过点P 作y 轴的垂线交y 轴于点M ，求△PMO 的面积； (3) 过点Q 作x 轴的垂线交x 轴于点N ，求△QNO 的面积；(4)过双曲线上任意一点A （m,n ）作x 轴(或y 轴)的垂线，垂足为B ，求△ABO 的面积；(5)你发现了什么规律？三、自主展示1.反比例函数①y =2x ；②y =13x ；③7y = —10x ；④y =3100x的图象中： (1)在第一、三象限的是 ，在第二、四象限的是(2)在其所在的每一个象限内，y 随x 的增大而增大的是2．已知反比例函数的图象经过点A （—6，—3）.(1)写出函数关系式；(2)这个函数的图象在哪几个象限？y 随x 的增大怎样变化？(3)点B （4，92），C （2，—5）在这个函数的图象上吗？四、自主拓展五、自主评价【课后作业】班级 姓名 学号1．已知反比例函数y=k x(k ≠0)与一次函数y=x 的图象有交点, 则k 的范围是______ . 2．已知反比例函数xm y 23-=，当______m 时，其图象的两个分支在第二、四象限内；当______m 时，其图象在每个象限内y 随x 的增大而减小．3．若反比例函数x k y 3-=的图象位于一、三象限内，正比例函数x k y )92(-=过二、四象限，则k 的整数值是________．4．已知P （1，m 2+1）在双曲线xk y =上，则双曲线在第_________象限，在每个象限y 随x 的增大而________. 5．若点(3,4)是反比例函数y=221m m x+- 图象上一点,则此函数图象必经过点( ) A.(2,6) B.(2,-6) C.(4,-3) D.(3,-4)6．一次函数y=kx －k 与反比例函数y=k x在同一直角坐标系内的图象大致( )7.下列函数中,当x>0时,y 随x 的增大而增大的是 ( )A.y=2-3xB.y=2xC.y=-2x-1D.y=-12x8．已知一次函数y=kx+b 的图象经过第二、三、四象限，则反比例函数kb y x =的图象在( ) A.第一、二象限 B ．第三、四象限 C ．第一、三象限 D ．第二、四象限9.下列函数中,图象大致为如图的是( ) A.y=1x (x<0) B.y=1x (x>0) C.y=-1x (x>0) D.y=-1x(x<0) 10．已知圆柱体的侧面积为80πcm 2,若圆柱底面半径为r(cm),高线长为h(cm),则h 关于r 的函数的图象大致是( )11．如图所示,一个反比例函数的图象在第二象限内,点A 是图象上的任意一点,AM⊥x 轴于M,O 是原点,若S △AOM =3,求该反比例函数的解析式,并写出自变量的取值范围.12．已知反比例函数x k y =图象与直线x y 2=和1+=x y 的图象过同一点． (1)求反比例函数；(2)当x ＞0时，这个反比例函数值y 随x 的增大如何变化？O AM xy。