第二章 拉氏变换

02第二章拉氏变换的数学方法拉氏变换是一种重要的数学工具，广泛应用于信号与系统、控制理论、电路分析、通信工程等领域。

本文将介绍拉氏变换的数学方法，包括拉氏变换的定义、性质和常见的拉氏变换对列表。

一、拉氏变换的定义拉氏变换是一种将时间域函数转换为频率域函数的数学工具。

对于一个连续时间函数f(t)，其拉氏变换F(s)定义为：F(s) = L{f(t)} = ∫[0,∞] f(t)e^(-st)dt其中s是复变量，通常为一个复平面上的点。

拉氏变换可以将一个函数从时间域表示转换为频率域表示，提供了一种更便于分析和处理的数学工具。

二、拉氏变换的性质拉氏变换具有一些重要的性质，如线性性质、平移性质、尺度性质等。

下面简要介绍几个常用的性质：1.线性性质：如果f(t)和g(t)的拉氏变换分别为F(s)和G(s)，那么对于任意常数a和b，有a*f(t)+b*g(t)的拉氏变换为a*F(s)+b*G(s)。

2. 平移性质：如果f(t)的拉氏变换为F(s)，那么e^(-at)f(t)的拉氏变换为F(s+a)。

3. 尺度性质：如果f(t)的拉氏变换为F(s)，那么f(at)的拉氏变换为(1/a)F(s/a)。

这些性质使得我们能够利用拉氏变换进行函数的变换和计算，简化了分析过程。

三、常见的拉氏变换对列表拉氏变换对列表是一些常见的函数及其在拉氏变换下的变换对。

常见的拉氏变换对列表如下：1.常数函数：L{1}=1/s2.单位阶跃函数：L{u(t)}=1/s3.单位冲激函数：L{δ(t)}=14. 指数函数：L{e^(at)} = 1/(s-a)，其中a为实数5. 正弦函数：L{sin(ωt)} = ω/(s^2 + ω^2)6. 余弦函数：L{cos(ωt)} = s/(s^2 + ω^2)7. 方波函数：L{rect(t/T)} = (T/s) * sin(Ts/2)8. 指数衰减函数：L{e^(-at)u(t)} = 1/(s+a)，其中a为正数这些变换对可以通过拉氏变换的定义进行推导得到，可以用于解决各种信号与系统的分析和计算问题。

第二章拉氏变换的数学方法拉普拉斯变换（Laplace transform）是一种积分变换方法，用于求解线性常系数微分方程组的初值问题。

它是法国数学家皮埃尔-西蒙·拉普拉斯（Pierre-Simon Laplace）于18世纪末发展起来的。

拉普拉斯变换在工程和物理学中有着广泛的应用，特别是在控制系统分析和信号处理中。

拉普拉斯变换将一个时间函数f(t)（t为实数）转换为一个复变函数F(s)（s为复数），可以表达为：F(s) = L[f(t)] = ∫[0,∞] f(t) e^(-st) dt其中，s是复平面上的一个复数，而e^(-st)为拉普拉斯变换的核函数。

拉普拉斯变换的定义域是右半平面Re(s) > 0，当Re(s)=0时，定义域为共轭虚轴Im(s)=0。

这是为了保证积分的绝对收敛性。

拉普拉斯变换有许多基本的性质和定理，其中包括线性性、平移性、尺度性、微分性等。

利用这些性质，我们可以对不同类型的函数进行拉普拉斯变换，从而求解常系数线性微分方程组的初值问题。

在应用拉普拉斯变换求解微分方程组时，首先将微分方程转化为代数方程。

假设我们要求解一个线性常系数微分方程组：a0y^(n) + a1y^(n-1) + ... + an-1y' + any = f(t)其中，a0, a1, ..., an 为常数，y^(n)表示y的n阶导数，f(t)为所给激励函数。

对微分方程两边同时进行拉普拉斯变换，根据拉普拉斯变换的性质和核函数的定义，将方程转化为代数方程：[a0s^nY(s) - a0s^(n-1)y(0) - a0s^(n-2)y'(0) - ... - a0y^(n-1)(0)] + [a1s^(n-1)Y(s) - a1s^(n-2)y(0) - a1s^(n-3)y'(0) - ... - a1y^(n-2)(0)] + ... + [an-1sY(s) - an-1y(0) - an-2y'(0) - ... - y(0)] + [anY(s) - y(0)] = F(s)其中，Y(s)为未知函数y(t)的拉普拉斯变换，y(0),y'(0),...,y^(n-1)(0)为初始值条件，F(s)为激励函数f(t)的拉普拉斯变换。

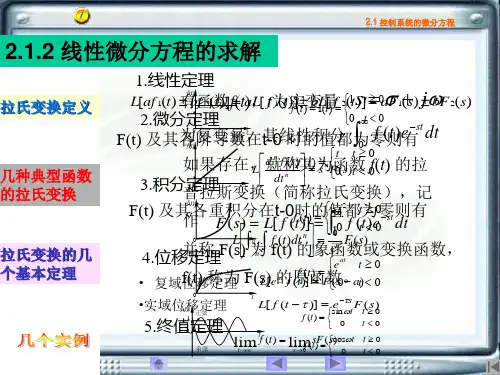
第二章拉普拉斯(Laplace) 变换第二节Laplace变换的性质1. 线性性质若α, β 是常数，且ℒ[f 1(t )]=F 1(s ),ℒ[f 2(t )]=F 2(s ),则有ℒ[αf 1(t )+ βf 2(t )]=α F 1(s )+β F 2(s )ℒ−1[α F 1(s )+β F 2(s )]=α f 1(t )+β f 2(t )此线性性质根据拉氏变换的定义就可得出.2. 微分性质若ℒ[ f (t )]=F (s ),则ℒ[ f '(t )]= sF (s ) -f (0)e ()()deststf t f t +∞+∞−−=−∫证明0[()]()ed stf t f t t +∞−′′=∫L 0e d ()stf t +∞−=∫[()](0)s f t f =−L 0(0)()e d stf s f t t+∞−=−+∫()]()(0)(Re())f t sF s f s c ′=−>推论:若L [ f (t )]=F (s ), 则L [ f ''(t )]=s L [f '(t )]-f '(0)特别, 当初值 f (0)= f '(0)=......= f (n -1)(0)=0时, 有ℒ[ f '(t )]= sF (s ),ℒ[f ''(t )]=s 2F (s ), ......,ℒ[ f (n )(t )]=s n F (s )=s {s L [ f (t )]-f (0)} –f '(0)= s 2 L [ f (t )] –s f (0) -f '(0)…...L L [ f (n )(t )]=s LL [ f (n -1)(t )]-f (n -1)(0)=s n F (s ) -s n -1f (0) -s n -2f '(0) -...... -f (n -1)(0)10).mm m t s s+=>由于f (0) = f '(0)=…...= f (m -1)(0)= 0, 而f (m )(t ) =m !例1. 利用微分性质, 求函数f (t )=t m 的拉氏变换, 其中m 是正整数.解即所以ℒ[m !]= ℒ[ [f (m )(t )]=s m ℒ[ f (t )]!!]! [1]m m m s ==L 111(Re()0).m m s ++>）(1m t m t e dt ∞−Γ+∫+0）=象函数的微分性质:若ℒ[ f (t )]=F (s ), 则F '(s )= ℒ[-t f (t )], Re(s )>c .和F (n )(s )= ℒ[(-t )n f (t )], Re(s )>c .d d ()()e d stF s f t t +∞−=∫证明0()e d ()e d d stf t t tf t t s +∞−=−∫()]tf t −()()]()()](1)()nn t F s f t Fs ′=−=−例2.求函数f (t )=t sin kt 的拉氏变换.22[sin ]kkt s k=+∵2222222222221()()s s ks k s k s k −−=+++解由象函数的微分性质知22d [sin ]k t kt k =− L 2222()kss k =+22d d s s s k=− +3. 积分性质若ℒ[ f (t )]=F (s ), 则01()d ()tf t t F s s= ∫L []11)d ()()t f t F s ss== L 证明设0()()d ,t h t f t t =∫则()(),(0)0h t f t h ′==且 [()](0) [()],s h t h s h t −=L L重复应用上式, 就可得到:)9.2()(1d )(d d }{000s F s t t f n t t n ttt=∫∫∫次L象函数的积分性质:若ℒ[ f (t )]=F (s ),则0()d ()e d d tssF f t t ττττ∞∞+∞−=∫∫∫()e d d tsf t tττ+∞∞−=∫∫e d t s t τ∞− 0()e d st f t t t +∞−=∫()f t t =L ()()d sf t F s st ∞=∫L象函数的积分性质:,()d d ()d n s s s f t s s F s st ∞∞∞= ∫∫∫一般地有L例3 求函数sin()ktf tt=的拉氏变换.()()dsf tF s st∞=∫L(其中F (s )= ℒ[ f (t )]).,d )(d )(0,)10.2(,d )(000∫∫∫∞∞++∞==s s F t tt f s t t t f 则有取式按存在如果积分2|arctan d 11,110022π==+=+=∞∞∫s s s t s 则有()()d s f t F s s t ∞ =∫L4.位移性质若ℒ[ f (t )]=F (s ),则有ℒ[e at f (t )]=F (s -a )(Re(s -a )>c ).(2.12)0[e ()]e ()e d atatstf t f t t+∞−=∫L =F (s -a )(Re(s -a )>c )证根据拉氏变换式, 有()0()ed s a tf t t+∞−−=∫22[sin ],kkt s k=+已知 由位移性得L 例4求ℒℒ[e -at sin kt ]2[esin ]atkkt k−=+L sin 3]t =23(2)9s ++sin 3]t =23(1)9s −+5. 延迟性质若ℒ[ f (t )]=F (s ), 又t <0时f (t )=0,则对于任一非负数τ ≥0, 有ℒ[ f (t −τ)]= e −s τF (s )(2.13)[()]()e d stf t f t tττ+∞−−=−∫L 证由拉氏变换的定义得)e d tτ−()ed stf t tττ+∞−−())ed s u u u τ−+,,d d u t u t u τ=+=() (R e())s s c >0e()ed s suf u uτ+∞−−=∫函数f (t −τ)与f (t )相比, f (t )从t =0开始有非零数值. 而f (t −τ)是从t =τ (τ ≧0)开始才有非零数值. 即延迟了一个时间τ. 从它的图象讲, f (t −τ) 是由f (t )沿t 轴向右平移τ 而得, 其拉氏变换也多一个因子e −s τ.tτf (t )f (t −τ)例5求函数0(),(0)1t u t t ττττ< −=>> 1[()]s u t eττ−−=L 的拉氏变换.τt1[()],u t s=已知L 根据延迟性性质小结性质小结，，设ℒ[ f (t ) ]= F (s )，ℒ[ g (t ) ]= G (s )()()()()f t g t F s G s αβαβ+↔+线性() ()(0)f t sF s f ′↔−微分()12(1)() ()(0)(0)(0)n n n n n ft s F s sf sf f−−−↔−′−−− ()()n s ()d F s s τ↔()()s t F s ds∞↔∫() ()t F s a ↔−) () (0,()00)s t s t e F f ττ−<↔<≥且性质小结性质小结，，设ℒ[ f (t ) ]= F (s )，ℒ[ g (t ) ]= G (s )相似性(书P92,2)常见函数的拉氏变换1(), (0)s f at F a a a↔>ℒ[ 1 ]=122k k+22ss k+1(1)m m s+Γ+ℒ[ ]=mt 1!m m s +ℒ[ ]=mt m 为正整数利用常见函数的拉氏变换以及拉氏变换的性质可求：利用常见函数的拉氏变换以及拉氏变换的性质可求：1、其他函数的拉氏变换2、拉氏逆变换求解微分、、积分方程3、求解微分例6.求下列函数的拉氏变换F (s ).(1)()sin ,2t f t at a=4(2)()cos 4,t f t e t −=30sin 2.t u e u du −∫(1)te −−例7.求下列函数的拉氏逆变换f (t ).41(1) (),(1)F s s =+21(2) (),(4)F s s s =+2.413s ++作业P92: 1(1, 3, 5, 7, 9); 2(4); 3(1, 4);4(4); 6(2, 4, 6)。