基本不等式

、柯西不等式等。
优化问题
02
在优化问题中，幂平均不等式可以用于寻找最优解或确定最优
解的范围。
统计学应用
03
在统计学中，幂平均不等式可以用于分析数据的分布和离散程
度。
24
06
排序原理与切比雪夫（ Chebyshev）不等式
2024/1/26
25
排序原理简介
2024/1/26
01
排序原理是一种基本的数学原理，用于比较和排列一组数的大 小。
2024/1/26
因式分解法
将一元二次不等式因式分解，然后利用不等式的性质进行求解。
14
一元二次不等式组解法
2024/1/26
分别求解法
分别求出每个不等式的解集，然 后取它们的交集作为不等式组的 解集。
图像法
在同一坐标系中画出每个不等式 的图像，然后找出满足所有不等 式的区域作为不等式组的解集。
15
17
算术平均值-几何平均值（AM-GM）不等式
对于所有非负实数 $a_1, a_2, ldots, a_n$，有
$frac{a_1 + a_2 + cdots + a_n}{n} geq sqrt[n]{a_1a_2cdots a_n}$当且仅当 $a_1 = a_2 = ldots = a_n$ 时取等号。
2024/1/26
加权平均值不等式是AM-GM不等式的推广，具有更广泛的应用范围。
19
柯西-施瓦茨（Cauchy-Schwarz）不等式
对于任意实数 $a_1, a_2, ldots, a_n$ 和 $b_1, b_2, ldots, b_n$，有
2024/1/26
$(a_1^2 + a_2^2 + cdots + a_n^2)(b_1^2 + b_2^2 + cdots + b_n^2) geq (a_1b_1 + a_2b_2 + cdots + a_nb_n)^2$当且仅当 $a_i = kb_i (i = 1, 2, ldots, n)$ 时取等号，其中 $k$ 为常数。

不等式
第三节 基本不等式
目
录
1
高考引航
2
必备知识
3
关键能力
高考引航
必备知识
知识清单
一 基本不等式 ≤
+
2
(1)基本不等式成立的条件:
a>0,b>0
(2)等号成立的条件:当且仅当ຫໍສະໝຸດ a=b..
二 几个重要的不等式
(1)a2+b2≥


(2) + ≥
(3)ab≤
(4)
2ab
2
(a,b∈R);
通道,如图.设矩形温室的室内长为 x(单位:m),三块种植植物的矩形区域的总面积为
S(单位:m2).
(1)求 S 关于 x 的函数关系式;
(2)求 S 的最大值.
解析
【解析】(1)由题设,得 S=(x-8)
900

7200
-2 =-2x-

+916,x∈(8,450).
(2)因为 8<x<450,
时,等号成立.
答案
解析
关键能力
题型归纳
题型一
利用基本不等式求最值
1
1
【例 1】(1)已知 a,b∈R,且 a-3b+6=0,则 2a+8 的最小值为 4
(2)(2020 届南昌市模拟)已知函数 y=x+

-2
的值为
4
.
(x>2)的最小值为 6,则正数 m
.
(3)(2020 届安徽天长模拟)已知正数 a、b 满足 a2+b2=6,则 b 2 + 4的最
大值为
5
.

基本不等式完整版一、知识点总结1.基本不等式原始形式：若 $a,b\in\mathbb{R}$，则 $a^2+b^2\geq 2ab$。

2.基本不等式一般形式（均值不等式）：若 $a,b\in\mathbb{R^*}$，则 $a+b\geq 2\sqrt{ab}$。

3.基本不等式的两个重要变形：1）若 $a,b\in\mathbb{R^*}$，则 $\frac{a+b}{2}\geq \sqrt{ab}$。

2）若 $a,b\in\mathbb{R^*}$，则 $ab\leq\left(\frac{a+b}{2}\right)^2$。

总结：当两个正数的积为定值时，它们的和有最小值；当两个正数的和为定值时，它们的积有最小值。

特别说明：以上不等式中，当且仅当 $a=b$ 时取“=”。

4.求最值的条件：“一正，二定，三相等”。

5.常用结论：1）若 $x>0$，则 $x+\frac{1}{x}\geq 2$（当且仅当$x=1$ 时取“=”）。

2）若 $x<0$，则 $x+\frac{1}{x}\leq -2$（当且仅当 $x=-1$ 时取“=”）。

3）若 $a,b>0$，则 $\frac{a}{b}+\frac{b}{a}\geq 2$（当且仅当 $a=b$ 时取“=”）。

4）若 $a,b>0$，则 $ab\leq \left(\frac{a+b}{2}\right)^2\leq \frac{a^2+b^2}{2}$。

5）若 $a,b\in\mathbb{R^*}$，则 $\frac{1}{a+b}\leq\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}\right)\leq\frac{1}{2}\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}$。

特别说明：以上不等式中，当且仅当 $a=b$ 时取“=”。

6.柯西不等式：1）若 $a,b,c,d\in\mathbb{R}$，则$(a^2+b^2)(c^2+d^2)\geq (ac+bd)^2$。

基本不等式知识点基本不等式是数学中的重要概念，它可以帮助我们判断数值大小关系，是各种不等式的基础。

在本文中，我们将介绍基本不等式的相关知识点，包括基本不等式的定义、证明方法、应用以及一些例题分析等方面。

1. 基本不等式的定义基本不等式也称为“平均数不等式”，它是数学中一个基本但又重要的不等式。

对于任意的正数 a1、a2、…、an，有以下不等式成立：(a1 + a2 + … + an) / n ≥ (a1 * a2 * … * an)1/n其中n表示正整数。

基本不等式描述了一组数的算术平均数和它们的几何平均数之间的关系。

可以看出，算术平均数大于等于几何平均数，且当且仅当所有数相等时等号成立。

2. 基本不等式的证明方法基本不等式的证明方法有很多种，下面列举一种简单易懂的证明方法。

首先，对于所有正数x，y，由均值不等式可得：(x + y) / 2 ≥ √(xy)⇒ x + y ≥ 2√(xy)接着，考虑一个序列a1，a2，……，an，它们的乘积为p。

对于每一对(aj，ak)，有：aj + ak ≥ 2√(ajak)即：a1 + a2 ≥ 2√(a1a2)a1 + a2 + a3 ≥ 3√(a1a2a3)a1 + a2 + … + an ≥ n√(a1a2…an)我们可以将上述不等式相乘，得到：(a1 + a2) * (a3 + a4) * … * (an-1 + an) ≥ 2n/2* √(a1a2) * 2n/2 * √(a3a4) * … * 2n/2 * √(an-1an) 即：(a1 + a2 + … + an) / n ≥ (a1 * a2 * … * an)1/n故基本不等式得证。

3. 基本不等式的应用基本不等式在数学中应用广泛，以下列举几个经典的例子。

（1）一种常见的问题是，给定一个定值的周长，什么形状的图形可以使面积最大。

答案是正方形，因为在所有形状中，正方形的面积和周长之比最大，这个比值为4π。

对数函数单调性，注意底数的取值范围
6
指数不等式
ax≥ay（a>0,a =1）
指数函数单调性，注意底数的取值范围
7
一次不等式
ax+b≥c
一次函数，斜率决定单调性
8
二次不等式
ax2+bx+c≥0
二次函数，根据判别式判断解集
9பைடு நூலகம்
均值不等式
2a+b ≥ab （a>0,b>0）
均值不小于几何均值
10
柯西不等式
(∑i=1n ai2 )(∑i=1n bi2 )≥(∑i=1n ai bi )2
多元变量的不等式关系
11
切比雪夫不等式
n1 ∑i=1n ai bi ≥(n1 ∑i=1n ai )(n1 ∑i=1n bi )（ai ,bi 同号）
适用于序列的加权平均与算术平均比较
12
伯努利不等式
(1+x)n≥1+nx（n≥1,x>−1）
幂函数与线性函数的比较
13
排序不等式
乱序和 ≤ 反序和 ≤ 同序和
17种基本不等式
序号
不等式名称
表达式
备注
1
绝对值不等式
$
a
2
平方不等式
a2≥b2
平方后非负，常用于消去根号或处理二次项
3
平方根不等式
a ≥b （a≥0,b≥0）
平方根函数单调递增
4
分数不等式
ba ≥dc （b>0,d>0）
分数比较时，注意分母的正负
5
对数不等式
loga x≥loga y（a>0,a =1）
适用于已排序的序列

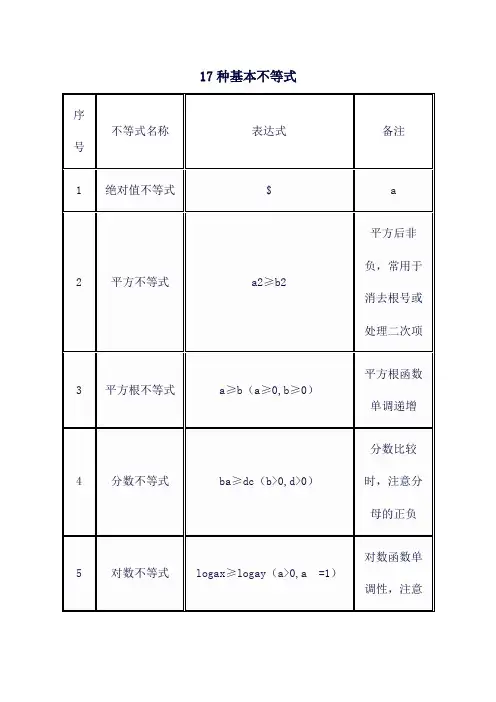
基本不等式基本不等式是数学中一个重要的概念。

其中，重要不等式指的是a²＋b²≥2ab，当且仅当a=b时等号成立。

而基本不等式则是指a＋b≥2√(ab)，当且仅当a=b时等号成立。

此外，还有一条基本不等式是任意两个正数的算术平均数不小于它们的几何平均数。

在利用基本不等式求函数的最大值、最小值时，需要注意函数式中各项必须都是正数，含变数的各项的积或者必须是常数，等号成立条件必须存在。

举例来说，如果0<a<b且a＋b＝1，则a²＋b²＞2ab，a＋b≥2√(ab)，2ab＜2(1/2-a)²，a²＋b²＞(1/2-a)²＋(1/2-b)²，因此b 最大。

又如，如果a、b、c都是正数，则(a＋b+c)(1/a+1/b+1/c)≥9，即a/b+b/a+b/c+c/b+c/a+a/c≥6，证明过程中利用了基本不等式。

例3、已知$a,b,c$为不等正实数，且$abc=1$。

求证：$a+b+c<\sqrt{a}+\sqrt{b}+\sqrt{c}$。

证明：根据柯西不等式，$(1+1+1)(a+b+c)\geq(\sqrt{a}+\sqrt{b}+\sqrt{c})^2$，即$3(a+b+c)\geq(a+b+c+2\sqrt{ab}+2\sqrt{bc}+2\sqrt{ca})$。

因为$abc=1$，所以$2\sqrt{ab}+2\sqrt{bc}+2\sqrt{ca}=2\sqrt{abc}(1/\sqrt{a}+1/\sqrt {b}+1/\sqrt{c})\leq3\sqrt[3]{abc}\cdot3=9$。

所以$3(a+b+c)\geq(a+b+c+9)$，即$2(a+b+c)\geq9$，即$a+b+c\geq\frac{9}{2}$。

又因为$a,b,c$不全相等，所以$a+b+c>\frac{9}{2}$。

4个基本不等式不等式是数学中的一种重要概念，用于描述数值之间的相对大小关系。

在数学中，我们常常会遇到各种各样的不等式，其中最基本的有四个，被称为”四个基本不等式”。

这四个基本不等式分别是：加法不等式、减法不等式、乘法不等式和除法不等式。

在本文中，我们将详细介绍这四个基本不等式及其应用。

1. 加法不等式加法不等式是最简单也是最容易理解的一种不等式。

它用于描述两个数相加后与另一个数的大小关系。

加法不等式的性质：•如果 a > b，则 a + c > b + c （对任意实数 c 成立）•如果 a > b 且 c > d，则 a + c > b + d加法不等式的应用：加法不等式常常被用于解决实际问题。

例如，假设小明去商场购买商品，他手上有100 元钱，并且他想要买一件价格为 x 元的商品。

如果 x 小于或者等于 100 元，则小明能够购买这件商品；反之，如果 x 大于 100 元，则小明将无法购买该商品。

2. 减法不等式减法不等式是加法不等式的一种推广，它用于描述两个数相减后与另一个数的大小关系。

减法不等式的性质：•如果 a > b，则 a - c > b - c （对任意实数 c 成立）•如果 a > b 且 c > d，则 a - c > b - d减法不等式的应用：减法不等式同样常常被用于解决实际问题。

例如，假设小明和小红参加了一次数学竞赛，他们分别得到了 x 分和 y 分。

如果小明得分比小红多 10 分以上，则可以说小明在这次竞赛中获胜；反之，如果小明得分比小红少于或者等于 10 分，则可以说小红在这次竞赛中获胜。

3. 乘法不等式乘法不等式是描述两个数相乘后与另一个数的大小关系的一种不等式。

乘法不等式的性质：•如果 a > b 且 c > 0，则 ac > bc•如果 a > b 且 c < 0，则 ac < bc （注意：当乘以一个负数时，不等号方向会发生改变）乘法不等式的应用：乘法不等式同样经常被应用于解决实际问题。

基本不等式6个公式
基本不等式是初中数学中常见的一类不等式，包括以下6个公式：
1. 两个非负实数的平均数大于等于它们的几何平均数：(a+b)/2≥√ab
这个公式表明，对于两个非负实数a和b，它们的平均数不会小于它们的几何平均数。

2. 两个非负实数的平方和大于等于它们的算术平均数的平方：a²+b²≥(a+b)²/4
这个公式表明，对于两个非负实数a和b，它们的平方和不会小于它们的算术平均数的平方。

3. 两个正实数的积大于等于它们的几何平均数的平方：ab≥(a+b)²/4
这个公式表明，对于两个正实数a和b，它们的积不会小于它们的几何平均数的平方。

4. 两个正实数的积大于等于它们的调和平均数的平方：ab≥4/(1/a+1/b)²
这个公式表明，对于两个正实数a和b，它们的积不会小于它们的调和平均数的
平方。

5. n个正实数的算术平均数大于等于它们的几何平均数：(a1+a2+...+an)/n≥√(a1a2...an)
这个公式表明，对于n个正实数a1、a2、...、an，它们的算术平均数不会小于它们的几何平均数。

6. n个正实数的调和平均数大于等于它们的算术平均数：n/(1/a1+1/a2+...+1/an)≥(a1+a2+...+an)/n
这个公式表明，对于n个正实数a1、a2、...、an，它们的调和平均数不会小于它们的算术平均数。

基本不等式常用公式四个
嘿，朋友！今天咱来唠唠基本不等式常用的四个公式哈。

第一个公式就是“a+b≥2√(ab)”（a>0，b>0）。

比如说，咱想围一个长方形的篱笆，长是 3 米，宽是 2 米，那这个长方形的周长最小是不是就是2×(3+2)=10 米呀，这就和这个公式有关系呢！
第二个公式是“(a+b)²≥4ab”（a，b 为实数）。

就好像你要盖房子，你得保证材料足够多才能盖得牢固呀，这个公式就像是保证房子牢固的一个条件一样！
第三个公式是“a²+b²≥2ab”。

这就好比两个人比赛跑步，要想跑得快，那自身的实力得过硬呀，这就是一种实力的保障呢！比如说，一个数是5，另一个数是 3，那5²+3² 肯定是大于等于2×5×3 的呀！
第四个公式是“ab≤(a²+b²)/2”。

可以想象成你有一堆糖果要分给小伙伴们，怎么分才能更公平呢，这个公式就能帮助你来衡量！像有两个数字4 和 6，那4×6 肯定是小于等于(4²+6²)/2 嘛！
怎么样，这四个公式是不是挺有意思的呀！好好去琢磨琢磨吧！。

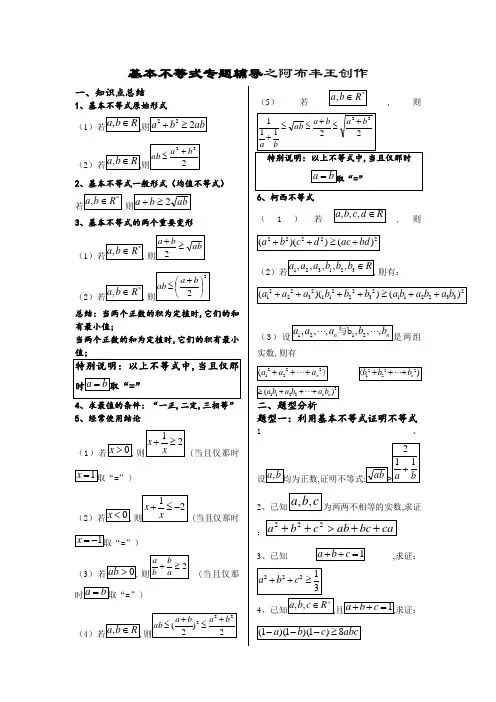
基本不等式专题辅导之阿布丰王创作一、知识点总结1、基本不等式原始形式（1（22、基本不等式一般形式（均值不等式）3、基本不等式的两个重要变形（1（2总结：当两个正数的积为定植时,它们的和有最小值；当两个正数的和为定植时,它们的积有最小4、求最值的条件：“一正,二定,三相等”5、经常使用结论（1当且仅那时=”）（2当且仅那时=”）（3当且仅那=”）（4（5）若,则6、柯西不等式 （1）若,则（2则有：（3两组实数,则有题型一：利用基本不等式证明不等式1、,2,求证3、已知,求证：45、已知,,a b c R +∈,且1a b c ++=,求证：1111118a b c ⎛⎫⎛⎫⎛⎫---≥ ⎪⎪⎪⎝⎭⎝⎭⎝⎭6、（2013年新课标Ⅱ卷数学（理）选修4—5：不等式选讲设,,a b c 均为正数,且1a b c ++=,证明: (Ⅰ)13ab bc ca ++≤; (Ⅱ)2221a b c b c a++≥.7、（2013年江苏卷（数学）选修4—5：不等式选讲 已知>≥b a ,求证:b a ab b a 223322-≥-题型二：利用不等式求函数值域1、求下列函数的值域（1）22213x x y +=（2）)4(x x y -= （3）)0(1>+=x x x y（4）)0(1<+=x x x y题型三：利用不等式求最值 （一）（凑项）1、已知2>x ,求函数42442-+-=x x y 的最小值；变式1：已知2>x ,求函数4242-+=x x y 的最小值；变式2：已知2<x ,求函数4242-+=x x y 的最年夜值；练习：1、已知54x >,求函数14245y x x =-+-的最小值；2、已知54x <,求函数14245y x x =-+-的最年夜值；题型四：利用不等式求最值 （二）（凑系数）1、那时,求(82)y x x =-的最年夜值；变式14(82)y x x =-的最年夜值；变式2：设230<<x ,求函数)23(4x x y -=的最年夜值.202<<x ,y x x =-()63的最年夜值；变式40<<x ,)28(x x y -=的最年夜值；3、求函数)2521(2512<<-+-=x x x y 的最年夜值；（提示：平方,利用基本不等式） 数)41143(41134<<-+-=x x x y 的最年夜值；题型五：巧用“1”的代换求最值问题1最小值；法一： 法二：变式1：已知,求变式2最小值；变式3：已求.变式4：值；变式5： （1）值；（2）若且,求变式6：使得题型六：分离换元法求最值（了解）1、求函数的值域；变式：2、示：换元法）变式：题型七：基本不等式的综合应用1小值2、（2009天津）已知,求变式1：（2010求关值；变式2：（2012湖北武汉诊断）已知,那时像恒过定点,若点在直线,3、已知,,求变式1：变式2：（2010山东）已知值；（提示：通分或三角换元）变式3：（2011浙江）已知年夜值；4、（2013年山东（理））取得最年夜值时值为（）（）A（提示：代入换元,利用基本不等式以及函数求最值）变式：设是正数,满足题型八：利用基本不等式求参数范围1、（2012且,最小值；2、已知且,4）（提示：分离参数,换元法）变式：已若,题型九：利用柯西不等式求最值1、二维柯西不等式若,则2、二维形式的柯西不等式的变式3、二维形式的柯西不等式的向量形式4、三维柯西不等式则有：5,。

基本不等式四个公式不等式是一个有效的数学方法，用来描述两个量的差异，它的限制两个数的大小范围，有利于我们理解数字之间的关系，应用也很广泛。

基本不等式四个公式是不等式的基础，是推理计算的基础，一般在有限的条件下，由四个不等式构成，分别为：大于等于、小于等于、小于、大于式。

第一个不等式公式是大于等于式，又称为“不小于等于式”，表示两个数之间的不等式关系，它可以用来表示一个数不小于另外一个数，表达形式为：A≥B，其中A代表被比较数，B代表比较数，表示A不小于B。

例如：4≥2，表明4不小于2。

第二个不等式公式是小于等于式，又称为“不大于等于式”，表示两个数之间的不等式关系，它可以用来表示一个数不大于另外一个数，表达形式为：A≤B，其中A代表被比较数，B代表比较数，表示A不大于B。

例如：4≤5，表明4不大于5。

第三个不等式公式是小于式，又称为“不大于式”，表示两个数之间的不等式关系，它可以用来表示一个数小于另外一个数，表达形式为：A<B，其中A代表被比较数，B代表比较数，表示A小于B。

例如：3<4，表明3小于4。

第四个不等式公式是大于式，又称为“不小于式”，表示两个数之间的不等式关系，它可以用来表示一个数大于另外一个数，表达形式为：A>B，其中A代表被比较数，B代表比较数，表示A大于B。

例如：5>2，表明5大于2。

在工作中使用不等式是非常常见的，可以用于判断某人的年龄是否已满18岁、是否满足报考条件等。

在教学中，不等式也起着重要作用，有助于学生全面地掌握数学知识，更好地推理计算。

基本不等式四个公式的范围很广，可以用于科学研究、实践中的不等式推理，可以用来判断两个数之间的大小关系，也可以用来判断函数的单调性，恒等式和变换形式，对高中生、大学生和学习数学有很大帮助。

综上所述，基本不等式四个公式是不等式的基础，是推理计算的基础，它有助于学习者全面掌握数学知识，并帮助学习者正确判断数字之间的关系，从而更好地推理计算，在科学研究和实践中也具有重要的作用。

解代数不等式
基本不等式是解代数不等 式的重要工具，通过比较 不同项的大小，可以得出 不等式的解集。
代数运算的优化
在解决一些代数问题时， 使用基本不等式可以优化 计算过程，提高解题效率。
几何应用
几何图形的性质
基本不等式可以用来推导 几何图形的性质，例如三 角形的边长关系、平行四 边形的对角线性质等。
等。
代数证明方法通常需要一定的代 数技巧和推理能力，是数学竞赛 和数学研究中的常见证明方法。
几何证明
几何证明是通过几何图形和几 何性质来证明基本不等式的方 法。ቤተ መጻሕፍቲ ባይዱ
常用的几何性质包括三角形不 等式、平行四边形不等式、圆 的不等式等。
几何证明方法直观易懂，能够 帮助学生更好地理解基本不等 式的几何意义和应用。
几何不等式的证明
基本不等式是证明几何不 等式的重要手段，例如 Cauchy-Schwarz不等式、 Minkowski不等式等。
几何问题的求解
在解决一些几何问题时， 如求最值、面积等，基本 不等式可以提供有效的解 题思路。
函数应用
函数的单调性
基本不等式可以用来判断函数的 单调性，例如一元函数的导数与
应用
切比雪夫不等式在概率论、统计学等领域有广泛的应用，它可以用来估计概率 分布的性质和参数，也可以用来解决一些数学问题。
05 基本不等式的实际应用案 例
金融领域
投资组合优化
基本不等式可以用于确定投资组 合的最优配置，以实现风险和收
益之间的平衡。
保险精算
在保险精算中，基本不等式可用 于评估风险和制定合理的保费策
它通常表示为两个数 的和、差、积或比的 不等式。
性质
基本不等式具有传递性

高中数学中常见的基本不等式公式包括以下几个：
1. 算术平均值大于等于几何平均值：设n为正整数，x1, x2, ..., xn为实数，则有：
(x1 + x2 + ... + xn)/n >= √(x1 * x2 * ... * xn)
这就是著名的算术平均值与几何平均值之间的不等式。

2. 调和平均值大于等于几何平均值：设x1, x2, ..., xn为实数，则有：
(nx1/2 + nx2/2 + ... + nxn/2) >= √(x1 * x2 * ... * xn)
这就是著名的调和平均值与几何平均值之间的不等式。

3. 三角不等式：设x和y为非零实数向量，则有：
|x·y| <= |x|·|y|
其中，x·y表示向量x和y的点积，|x|和|y|分别表示向量x和y的模长。

4. 柯西-施瓦茨不等式：设x1, x2, ..., xn和y1, y2, ..., yn为实数向量，则有：
(x1*y1 + x2*y2 + ... + xn*yn) <= sqrt((x1^2 + x2^2 + ... + xn^2) * (y1^2 + y2^2 + ... + yn^2))这就是著名的柯西-施瓦茨不等式，用于衡量向量的相关性。

以上这些基本不等式在高中数学中非常常见，并且在解决许多数学问题时都非常有用。

基本不等式(很全面)基本不等式基本不等式原始形式：对于任意实数a和b，有a+b≥2ab/(a^2+b^2)。

基本不等式一般形式（均值不等式）：对于任意实数a和b，有a+b≥2ab/2.基本不等式的两个重要变形：1）对于任意实数a和b，有(a+b)/2≥√(ab)。

2）对于任意实数a和b，有ab≤(a^2+b^2)/2.求最值的条件：“一正，二定，三相等”。

常用结论：1）对于任意正实数x，有x+1/x≥2（当且仅当x=1时取“=”）。

2）对于任意负实数x，有x+1/x≤-2（当且仅当x=-1时取“=”）。

3）对于任意正实数a和b，有(a/b+b/a)≥2（当且仅当a=b 时取“=”）。

4）对于任意实数a和b，有ab≤(a^2+b^2)/2≤(a+b)^2/4.5）对于任意实数a和b，有1/(a+b)≤1/2√(ab)≤(1/a+1/b)/(a+b/2)。

特别说明：以上不等式中，当且仅当a=b时取“=”。

柯西不等式：1）对于任意实数a、b、c和d，有(a+b)(c+d)≥(ac+bd)^2.2）对于任意实数a1、a2、a3、b1、b2和b3，有(a1^2+a2^2+a3^2)(b1^2+b2^2+b3^2)≥(a1b1+a2b2+a3b3)^2.3）对于任意实数a1、a2、…、an和b1、b2、…、bn，有(a1^2+a2^2+…+an^2)(b1^2+b2^2+…+bn^2)≥(a1b1+a2b2+…+an bn)^2.题型归纳：题型一：利用基本不等式证明不等式。

题目1：设a、b均为正数，证明不等式ab≥2/(1/a+1/b)。

题目2：已知a、b、c为两两不相等的实数，求证：a/(b-c)^2+b/(c-a)^2+c/(a-b)^2≥2/(a-b+b-c+c-a)。

题目3：已知a+b+c=1，求证：a^2+b^2+c^2+9abc≥2(ab+bc+ca)。

题目4：已知a、b、c为正实数，且abc=1，求证：a/b+b/c+c/a≥a+b+c。

基本不等式专题辅导一、知识点总结1、基本不等式原始形式（1）若R b a ∈,，则ab b a 222≥+（2）若R b a ∈,，则222b a ab +≤2、基本不等式一般形式（均值不等式）若*,R b a ∈，则ab b a 2≥+3、基本不等式的两个重要变形 （1）若*,R b a ∈，则ab ba ≥+2（2）若*,R b a ∈，则22⎪⎭⎫ ⎝⎛+≤b a ab总结：当两个正数的积为定植时，它们的和有最小值； 当两个正数的和为定植时，它们的积有最小值；特别说明：以上不等式中，当且仅当b a =时取“=”4、求最值的条件：“一正，二定，三相等”5、常用结论 （1）若0x >，则12x x+≥ (当且仅当1x =时取“=”） （2）若0x <，则12x x+≤- (当且仅当1x =-时取“=”） （3）若0>ab ，则2≥+ab b a (当且仅当b a =时取“=”）（4）若R b a ∈,，则2)2(222b a b a ab +≤+≤ （5）若*,R b a ∈，则2211122b a b a ab b a +≤+≤≤+ 特别说明：以上不等式中，当且仅当b a =时取“=” 6、柯西不等式（1）若,,,abc d R ∈，则22222()()()a b c d a c b d ++≥+（2）若123123,,,,,a a a b b b R ∈，则有：22222221231123112233()()()a a a b b b a b a b a b ++++≥++（3）设1212,,,,,,n n a a a b b ⋅⋅⋅⋅⋅⋅与b 是两组实数，则有 222(a a a ++⋅⋅⋅+)222)b b b ++⋅⋅⋅+(2()a b a b a b ≥++⋅⋅⋅+二、题型分析题型一：利用基本不等式证明不等式1、设b a ,均为正数，证明不等式:ab ≥ba 112+2、已知cb a ,,为两两不相等的实数，求证：ca bc ab c b a ++>++2223、已知1a b c ++=，求证：22213a b c ++≥4、已知,,a b c R+∈，且1a b c ++=，求证：a b cc b a 8)1)(1)(1(≥---5、已知,,a b c R+∈，且1a b c ++=，求证：1111118a bc ⎛⎫⎛⎫⎛⎫---≥ ⎪⎪⎪⎝⎭⎝⎭⎝⎭6、（2013年新课标Ⅱ卷数学（理）选修4—5：不等式选讲 设,,a b c 均为正数,且1a b c ++=,证明:(Ⅰ)13ab bc ca ++≤; (Ⅱ)2221a b c b c a++≥.7、（2013年江苏卷（数学）选修4—5：不等式选讲 已知0>≥b a ，求证:b a ab b a 223322-≥- 题型二：利用不等式求函数值域1、求下列函数的值域 （1）22213x x y += （2）)4(x x y -=（3）)0(1>+=x x x y （4）)0(1<+=x xx y题型三：利用不等式求最值 （一）（凑项）1、已知2>x ，求函数42442-+-=x x y 的最小值；变式1：已知2>x ，求函数4242-+=x x y 的最小值；变式2：已知2<x ，求函数4242-+=x x y 的最大值；练习：1、已知54x >，求函数14245y x x =-+-的最小值；2、已知54x <，求函数14245y x x =-+-的最大值；题型四：利用不等式求最值 （二）（凑系数）1、当时，求(82)y x x =-的最大值；变式1：当时，求4(82)y x x =-的最大值；变式2：设230<<x ，求函数)23(4x x y -=的最大值。

考研七个基本不等式公式
1.平均数不等式：对于任意正整数n和正实数a1、a2、...、an，有(a1+a2+...+an)/n≥(a1×a2×...×an)^(1/n)。

2. 均方根不等式：对于任意正整数n和正实数a1、a2、...、an，有[(a1^2+a2^2+...+an^2)/n]^(1/2) ≥ (a1+a2+...+an)/n。

3. 柯西-施瓦茨不等式：对于任意正整数n和实数a1、b1、a2、b2、...、an、bn，有(a1b1+a2b2+...+anbn)^2 ≤
(a1^2+a2^2+...+an^2)(b1^2+b2^2+...+bn^2)。

4. 什么不等式：对于任意正实数a、b、c，有(a+b+c)^2 ≥
3(ab+bc+ca)。

5. 三角形不等式：对于任意三角形的三条边a、b、c，有a+b>c、b+c>a、c+a>b。

6. 柯西不等式：对于任意两个n维向量a和b，有|a·b|≤|a|·|b|。

7. 线性规划基本定理：对于任意一个线性规划问题，其最优解
一定在可行域的一条顶点上取得。

注意：以上七个基本不等式公式只是考研数学中的部分内容，考生在备考过程中需要全面了解数学知识点。

- 1 -。

基本不等式：ab ≤a ＋b 21．基本不等式设a ，b ∈R ，则①a 2≥0；②a 2＋b 2≥2ab ，a ，b ∈R ，要认识到a 和b 代表的实数既可以是具体数字，也可以是比较复杂的变量式，应用广泛．2．均值不等式设a ，b ∈(0，＋∞)，则a ＋b 2≥ab ，当且仅当a ＝b 时，不等式取等号．它的证明要能从基本不等式中得出，既是对基本不等式中a ，b 的灵活变式，又具有自身特点，a ，b ∈(0，＋∞)．对勾函数()k f x x x =+，扩展：3a b c ++≥ 3．灵活变式（2112a b a b +≥≥≥+）①a 2＋b 2≥(a ＋b )22；②ab ≤a 2＋b 22；③ab ≤(a ＋b 2)2；④(a ＋b 2)2≤a 2＋b 22；⑤(a ＋b )2≥4ab . 当且仅当a ＝b 时，各式中等号成立．四个平均数4．利用均值不等式求最大、最小值问题（一正，二定，三相等，用了二次，条件要统一）(1)如果x ，y ∈(0，＋∞)，且xy ＝p (定值)，那么当x ＝y 时，x ＋y 有最小值2p .(2)如果x ，y ∈(0，＋∞)，且x ＋y ＝s (定值)，那么当x ＝y 时，xy 有最大值s 24.一 利用基本不等式证明不等式1．利用基本不等式证明不等式是综合法证明不等式的一种情况，其实质就是从已知的不等式入手，借助不等式性质和基本不等式，经过逐步的逻辑推理，最后推得所证问题，其特征是“由因导果”．2．证明不等式时要注意灵活变形，多次利用基本不等式时，注意每次等号是否都成立．同时也要注意应用基本不等式的变形形式．[例1] 设a ，b 均为正实数，求证：1a 2＋1b 2＋ab ≥2 2训练 已知x >0，y >0，z >0.求证：(y x ＋z x )(x y ＋z y )(x z ＋y z )≥8二 利用基本不等式求最值1．在利用均值不等式求最值时要注意三点：一是各项为正；二是寻求定值，求和式最小值时应使积为定值，求积式最大值时应使和为定值(恰当变形，合理发现拆分项或配凑因式、分离常数法是常用的解题技巧)；三是考虑等号成立的条件．如果用了二个或二个以上，条件一定要统一2．在应用基本不等式求最值时，分以下三步进行：(1)首先，看式子能否出现和(或积)的定值，若不具备，需对式子变形，凑出需要的定值；(2)其次，看所用的两项是否同正，若不满足，通过分类解决，同负时，可提取(－1)变为同正；(3)利用已知条件对取等号的情况进行验证．若满足，则可取最值，若不满足，则可通过函数单调性或导数解决．[例2] (1)设0<x <2，求函数y ＝3x (8－3x )的最大值；(2)求3a －4＋a 的取值范围； (3)已知x >0，y >0，且x ＋y ＝1，求8x ＋2y 的最小值．训练 (1)设x >0，则函数y ＝x －1＋22x ＋1的最小值等于________． （2）a ，b >0，a +b ＝1 求1()f x ab ab=+的值域。