高一数学基本不等式1

高一数学基本不等式1的代换基本不等式是高中数学中的重要概念，它在解决各类数学问题时起到了关键作用。

本文将通过讲解基本不等式1的代换，来帮助同学们更好地理解和应用这一概念。

基本不等式1的代换是指，在给定的不等式中，通过对不等式两边进行代换或变形，得到一个新的不等式，从而方便求解问题。

在这个过程中，我们要注意保持不等式的方向性和有效性。

我们来看一个简单的例子：已知不等式 a > b，现在我们要将其代换为另一个不等式。

我们可以令x = a - b，这样原不等式可以变形为x > 0。

通过这个代换，我们将原来的不等式转化为了一个更简单的形式，从而更方便地进行分析和推导。

接下来，我们来看一个稍微复杂一些的例子：已知不等式2x - 3 > 5，现在我们要将其代换为另一个不等式。

我们可以令y = 2x - 8，这样原不等式可以变形为y > 0。

通过这个代换，我们将原来的不等式转化为了一个更简单的形式，从而更方便地进行分析和推导。

除了代换外，我们还可以通过变形的方式来改写不等式。

例如，对于不等式3x + 2 > 7，我们可以通过将其两边同时减去2，得到3x > 5。

这样，我们就将原不等式转化为了一个更简单的形式，从而更方便地进行分析和推导。

基本不等式1的代换在解决实际问题中起到了重要作用。

例如，当我们需要求解一个含有多个变量的不等式时，可以通过代换的方式将其转化为只含有一个变量的不等式，从而更方便地进行求解。

另外，基本不等式1的代换也可以帮助我们简化不等式的形式，从而更容易观察和发现不等式的特点。

在应用基本不等式1的代换时，我们需要注意以下几点：首先，代换应该是合理的，即代换后的不等式与原不等式的关系应该一致。

其次，代换应该能够简化不等式的形式，从而更便于进行分析和推导。

最后，代换后的不等式应该保持原不等式的方向性和有效性，即代换不应该改变不等式的结论。

基本不等式1的代换是解决数学问题中常用的方法之一。

高一数学基本不等式1的代换高一数学基本不等式1的代换基本不等式是高中数学中的重要概念之一，它在解决数学问题和证明数学定理时起到了关键作用。

而基本不等式1的代换则是在解决一些复杂的不等式问题中的常用技巧之一。

本文将通过几个具体的例子，来介绍基本不等式1的代换方法及其应用。

我们先回顾一下基本不等式1的表达式。

基本不等式1是指对于任意的正实数a、b和正整数n，都有(a+b)^n≥C(n,0) * a^n * b^0 + C(n,1) * a^(n-1) * b^1 + C(n,2) * a^(n-2) * b^2 + ... + C(n,n) * a^0 * b^n。

其中，C(n,m)表示从n个元素中选取m个元素的组合数。

下面，我们将通过实例来介绍基本不等式1的代换方法。

例1：证明当x>0时，有x^2 + 1/x^2 ≥ 2。

解：由于不等式中含有平方项，我们可以尝试将其转化为基本不等式1的形式。

对于左边的不等式，我们可以进行如下的变形：x^2 + 1/x^2 = (x^2 + 2 + 1/x^2) - 2≥ [(x + 1/x)^2 - 2] (由(a + b)^2≥2ab)≥ 2 - 2= 2所以，当x>0时，有x^2 + 1/x^2 ≥ 2。

例2：证明当a、b、c均为正实数时，有(a+b+c)(1/a+1/b+1/c) ≥ 9。

解：同样地，我们可以利用基本不等式1的代换方法来解决这个不等式。

对于左边的不等式，我们可以进行如下的变形：(a+b+c)(1/a+1/b+1/c) = (a+b+c)(ab+bc+ca)/(abc)= [(a+b+c)/3][(ab+bc+ca)/3]/(abc)≥ [(√(abc))/3][(√(abc))/3](abc) (由基本不等式1)= abc/9由于a、b、c均为正实数，所以abc>0，所以abc/9>0。

所以，当a、b、c均为正实数时，有(a+b+c)(1/a+1/b+1/c) ≥ 9。

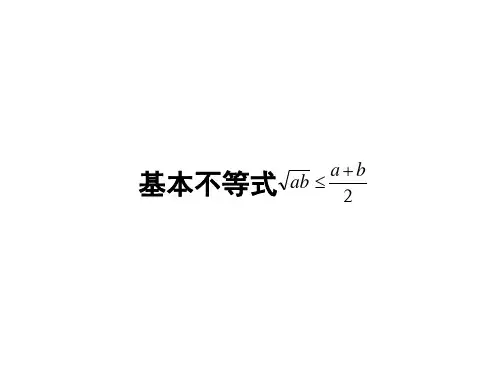
高一数学 基本不等式及其应用1．基本不等式1 对任意实数a 和b ，有222a b ab +≥，当且仅当a b =时等号成立．基本不等式2 对任意正实数a 和b ，有2a b +≥a b =时等号成立．说明：对于基本不等式2，有两个重要变形○1若,a b ∈+R ，则a b +≥○2若,a b ∈+R ，则2)2(b a ab +≤，它们的主要作用是求代数式的最小值和最大值．2．设0x >，求142x x ++的最小值并指出最小值取得时x 的值．3．已知0, 0a b >>且4ab =，求下列各式最小值及此时,a b 的值．（1）2a b +； （2）11a b +．4．设1x >，求1251x x ++-的最小值并指出最小值取得时x 的值．5．设2x >，求2332x x x -+-的最小值并指出最小值取得时x 的值．62的最小值．7．已知0, 0a b >>且4a b +=，求下列各式最大值及此时,a b 的值．（1）4ab ； （2）22a b ； （3）(1)(2)a b ++．8．已知302x <<，求()532x x -的最大值并指出最小值取得时x 的值．9．已知22, 02a b a b >+=且，求12y =10．已知,0a b >且3ab a b =++，求a b +的最小值11．（1）已知正数x y 、满足21x y +=，求11x y +的最小值． （2）190,0,2x y x y>>+=设且，求x y +的最小值．12．已知集合{}25M y y x ==-+，4,11N y y x x x ⎧⎫==+>⎨⎬-⎩⎭，则M P = ______ 13. 若703x <<，则()73x x -的最大值为 ________ 14．已知x ∈R 2的最小值是_____________________．15．若0,0,231a b a b >>+=，则ab 的最大值是____________________．16．建造一个容积为8立方米、深为2米的长方体无盖水池．如果池底和池壁的造价每 平方米分别为120元和80元，那么水池的最低造价是多少元？17．若直角三角形面积为24cm ，求此三角形周长的最小值．18．如图，某小区要在一块矩形的绿化地块（图中的阴影部分）四周筑路，使上、下路面 的宽为1米，左右路面的宽为2米 ．为了保证绿化面积为72平方米，并且使路面与绿 化地块的占地总面积最小，那么绿化地块的长和宽应该分别为多少米？19．求下列不等式的解集．（1）131x x +≥- ； （2）|||1|a x x ->-．20．若不等式 2||<+b ax 的解集为)6,2(，求实数b a ,的值．21．关于x 的不等式()211ax a x -<-的解集非空，则a 的取值范围是______________．22．设x R ∈，用[]x 表示不大于x 的最大整数，如：[]3π=，[ 1.4]2-=-，[5]5=．（1） 若[]2x =，则x 的范围为________________________；(2 ) 若[|1|]3x -=，则x 的范围为_____________________．23．已知集合102x A x x +⎧⎫=<⎨⎬-⎩⎭，{}40B x px =+<，若B A ⊆，求实数p 的范围．。

高一数学基本不等式有哪几个?
高中数学基本不等式常用的有六个，在以后学习的过程中还要积累一些常见的不等式。

1.基本不等式a^2+b^2≧2ab
对于任意的实数a,b都成立，当且仅当a=b时，等号成立。

证明的过程：因为（a-b）^2≧0，展开的a^2+b^2-2ab≧0，将2ab右移就得到了公式a^2+b^2≧2ab。

它的几何意义就是一个正方形的面积大于等于这个正方形内四个全等的直角三角形的面积和。

2.基本不等式√ab≦(a+b)/2
这个不等式需要a，b均大于0，等式才成立，当且仅当a=b时等号成立。

证明过程：要证(a+b)/2≧√ab，只需要证a+b≧2√ab，只需证（√a-√b）^2≧0，显然（√a-√b）^ 2≧0是成立的。

它的几何意义是圆内的直径大于被弦截后得到直径的两部分的乘积的二倍。

3.b/a+a/b≧2
这个不等式的要求ab＞0，当且仅当a=b时等号成立，也就是说a，b可以同时为正数，也可以同时为负数。

证明的过程：b/a+a/b=(a^2+b^2)/ab≧2，只需证a^2+b^2≧2ab即可。

4.基本不等式的拓展公式：a^3+b^3+c^3≧3abc，a，b，c均为正数。

5.（a+b+c）/3≧³√abc，a，b，c均为正数，当且仅当a=b=c时等号成立。

6.柯西不等式。

第一节从简到繁：基本不等式的核心概念基本不等式在高一数学必修一中是一个非常基础且重要的概念，它为我们理解和解决各类不等式问题奠定了基础。

在本节中，我们将从简到繁，逐步深入探讨基本不等式的定义、特点和应用。

1.1 基本不等式的定义基本不等式是指形如a≥b或a≤b的不等式，其中a和b是两个数。

当a≥b时，我们称a大于等于b；当a≤b时，我们称a小于等于b。

在这里，我们需要深入理解等号的含义：等号在不等式中表示两个数相等或等价。

基本不等式并不仅仅局限于大于或小于的关系，更包括了等于的情况。

1.2 基本不等式的特点基本不等式有许多特点，其中最重要的是传递性和对称性。

传递性指的是如果a≥b且b≥c，则a≥c；如果a≤b且b≤c，则a≤c。

对称性则表示如果a≥b，则-b≥-a；如果a≤b，则-b≤-a。

这些特点使得基本不等式在推导和转化过程中能够起到重要作用，也为后续的应用奠定了基础。

1.3 基本不等式的应用基本不等式在实际问题中有着广泛的应用，例如在代数、几何和概率等领域。

特别是在二元一次不等式的求解中，基本不等式的运用尤为重要。

通过将不等式转化为标准形式，我们可以利用基本不等式的特点进行简化和求解，从而解决各类实际问题。

第二节深入探讨：基本不等式的转化和应用2.1 基本不等式的转化在实际问题中，我们经常会遇到需要将不等式进行转化或简化的情况。

在这里，我们可以运用基本不等式的传递性和对称性进行变形，并通过加减乘除等运算来实现不等式的转化。

通过加减同一个数或式子，我们可以将不等式的左右两边进行平移或合并；通过乘除正数或负数，我们可以改变不等式的方向或大小。

这些转化方法为我们解决实际问题提供了有力的工具。

2.2 基本不等式在二元一次不等式中的应用二元一次不等式是指形如ax+by≤c的不等式，其中a、b和c为已知数，x和y为未知数。

在实际问题中，通过运用基本不等式的转化和特点，我们可以将二元一次不等式转化为标准形式，并利用基本不等式进行求解。

高一数学必修一基本不等式高一数学必修一中的基本不等式是指在数学中常见且重要的一类不等式，它们在解决实际问题和证明数学定理时起着重要的作用。

本文将对高一数学必修一中的基本不等式进行介绍和解析，帮助读者更好地理解和掌握这一内容。

我们来讨论一元一次不等式。

一元一次不等式是指只含有一个未知数的一次函数不等式。

对于一元一次不等式的解法，我们可以使用逆向思维，将不等式转化为等式，再根据等式的性质进行分析。

例如，对于不等式2x + 3 > 7，我们可以将其转化为2x + 3 = 7，然后解得x = 2。

由于不等式的解集包括等号的解和不包括等号的解，因此不等式的解集为x > 2。

接下来，我们来讨论一元二次不等式。

一元二次不等式是指只含有一个未知数的二次函数不等式。

对于一元二次不等式的解法，我们可以使用图像法、配方法、因式分解法等多种方法。

其中，图像法是最直观和易于理解的方法。

我们可以将二次函数的图像绘制出来，通过观察图像的形状和位置来确定不等式的解集。

例如，对于不等式x^2 - 4x + 3 > 0，我们可以将其对应的二次函数y = x^2 - 4x + 3的图像绘制出来，然后观察图像在哪些区间上大于0，从而确定不等式的解集为x < 1或x > 3。

除了一元一次不等式和一元二次不等式，高一数学必修一中还有其他类型的不等式，如绝对值不等式、分式不等式等。

对于绝对值不等式，我们需要根据绝对值的定义和性质进行分析。

例如，对于不等式|2x - 3| ≤ 5，我们可以将其分为两种情况进行讨论，即2x - 3 ≥ 0和2x - 3 < 0。

对于分式不等式，我们需要注意分母不等于0的条件，并根据分式的性质进行分析。

例如，对于不等式(2x - 1)/(x + 2) > 0，我们需要考虑x + 2 ≠ 0的条件，并根据分式的正负性进行讨论。

除了以上介绍的基本不等式，高一数学必修一中还包括一些常见的不等式定理和不等式性质。

教学设计课程基本信息学科数学年级高一学期春季课题基本不等式（1）教科书书名：普通高中教科书数学（必修第一册）教材出版社：江苏凤凰教育出版社教学目标1.学会推导并掌握基本不等式定理；2.数学能够应用定理证明不等式并解决一些简单的证明和求最值问题.教学内容教学重点：1. 基本不等式的定义、证明方法和几何解释；2. 用基本不等式解决简单的证明和最值问题。

教学难点：1. 基本不等式的几何解释；2.在解题中灵活使用基本不等式；教学过程一、情景引入将物体放在天平的一个盘子上，在另一个盘子上放砝码使天平平衡，称得物体的质量为a.如果天平制造得不精确，天平的两臂长略有不同（其他因素不计），那么a并非物体的实际质量.不过，我们可作第二次测量：把物体调换到天平的另一个盘子上，此时称得物体的质量为b.思考：如何合理地表示物体的质量呢？表示物体的质量. 做法1：把两次称得物体的质量“平均”一下，以A=a+b2问题1：这样的做法合理吗？做法2：设天平的两臂长分别为l1,l2,物体实际质量为M，根据力学原理有l1M=l2a, l2M=l1b.将上述两个等式的两边分别相乘，得l1l2M2=l1l2ab,所以M=√ab. 由此可知，物体的实际质量为√ab.对于正数，我们把a+b2称为a,b的算术平均数，√ab称为a,b的几何平均数.二、探索新知问题2：两个正数a,b的算术平均数和几何平均数之间具有怎样的大小关系呢？如图，AB是圆⊙O的直径，点C是AB上一点,AC=a,BC=b，过点C作CD⊥AB 垂直交半圆于点D，连接AD，BD.思考：你能在图中找到长度为a+b2、√ab的线段吗？OD =a+b2表示圆的半径.图中三角形均为直角三角形，可证△ACD∼△DCB，因而CD2=AC∙BC(射影定理), 得CD =√ab表示圆的半弦长.问题3： OD与 CD大小关系如何呢？CD ≤OD√ab≤a+b2，当且仅当点C与圆心重合，即当a=b时，等号成立.得到一个猜想：∀a>0,b>0,√ab≤a+b2，当且仅当a=b时等号成立.三、探究—基本不等式的证明问题4：在前面学习不等式性质中，我们已经解决过一些不等式的证明，有哪些常用方法呢？作差法、分析法、利用不等式性质法等. 请同学们尝试用以上方法证明基本不等式.思考:“√ab≤a+b2”还有哪些等价形式？ab≤(a+b2)2思考: 两个数的“平方和与积”的不等关系呢？用a2替换a，b2替换b，得ab≤a 2+b2 2ab≤(a+b2)2当且仅当a=b时等号成立.ab≤a2+b22,当且仅当a=b时等号成立.问：请问上述a、b的范围是多少？四、学以致用例1 设a,b为正数，证明下列不等式成立.（1）ba+ab≥2 ; （2）a+b+1a+1b≥4(1)分析：观察ba 、ab的结构，发现积为定值ba∙ab=1.基本不等式揭示了两个非负数的和与积的不等关系，即它们的几何平均数不大于它们的算术平均数.(2) 分析：观察a、b、1a 、1b的结构，发现a∙1a=1，b∙1b=1.分别使用基本不等式.例2 已知函数y =x +16x+2(x >−2)求此函数的最小值.分析：观察x 、16x+2的结构，发现二者积不为定值，并且从x >−2，有x +2>0，但x 可能为负数，不能直接使用基本不等式.思考：能不能凑成积为定值，且均为正数呢？四、课堂小结最后我们回顾一下这节课的内容，请同学们思考以下问题：（1）什么是基本不等式？∀ a >0,b >0,√ab ≤ a+b2，当且仅当a =b 时等号成立.文字语言：两个非负数的几何平均数不大于它们的算术平均数.几何解释：在圆中，半弦长小于或等于半径长.（2）还收获了哪些不等式呢？∀a , b ∈R ，ab ≤(a +b 2)2,当且仅当a =b 时等号成立. ∀a , b ∈R ，ab ≤a 2+b 22,当且仅当a =b 时等号成立. （3）利用不等式解决问题时，需要注意什么？首先用整体思想，看能否转化为两个正数的和或者积的形式，再观察和或积是否为一个定值，最后计算检验不等式中的等号能否取到，简言之就是“一正、二定、三相等”.备注：教学设计应至少含教学目标、教学内容、教学过程等三个部分，如有其它内容，可自行补充增加。