特殊三角形存在性(等腰直角三角形存在性一)(人教版)(含答案)

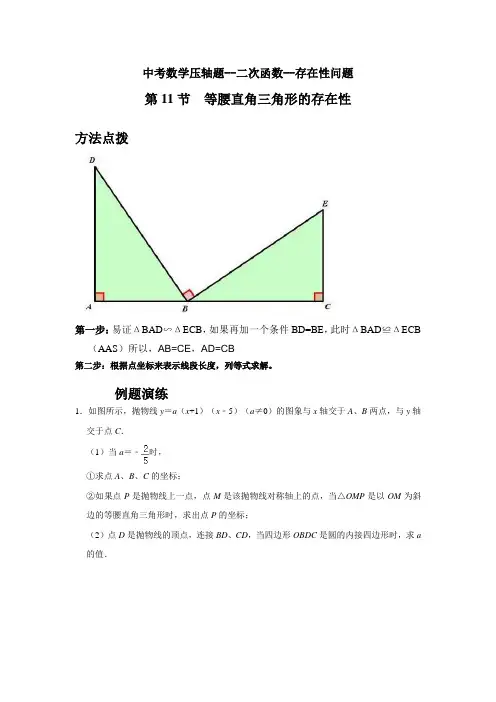
中考数学压轴题--二次函数--存在性问题第11节等腰直角三角形的存在性方法点拨第一步：易证ΔBAD∽ΔECB，如果再加一个条件BD=BE，此时ΔBAD≌ΔECB （AAS）所以，AB=CE，AD=CB第二步：根据点坐标来表示线段长度，列等式求解。

例题演练1．如图所示，抛物线y＝a（x+1）（x﹣5）（a≠0）的图象与x轴交于A、B两点，与y轴交于点C．（1）当a＝﹣时，①求点A、B、C的坐标；②如果点P是抛物线上一点，点M是该抛物线对称轴上的点，当△OMP是以OM为斜边的等腰直角三角形时，求出点P的坐标；（2）点D是抛物线的顶点，连接BD、CD，当四边形OBDC是圆的内接四边形时，求a 的值．【解答】解：对于y＝a（x+1）（x﹣5）（a≠0），令y＝a（x+1）（x﹣5）＝0，解得x ＝5或﹣1，令x＝0，则y＝﹣5a，故点A、B、C的坐标分别为（5，1）、（﹣1，0）、（0，﹣5a），当x＝2时，y＝a（x+1）（x﹣5）＝﹣9a，顶点的坐标为（2，﹣9a）．（1）①当a＝﹣时，函数的表达式为y＝﹣（x+1）（x﹣5），则点A、B、C的坐标分别为（5，1）、（﹣1，0）、（0，2）；②过点P作y轴的平行线交过点M与x轴的平行线于点F，交x轴于点E，设点P的坐标为（x，﹣（x+1）（x﹣5）），∵∠MPO＝90°，∴∠MPF+∠OPE＝90°，∵∠OPE+∠POE＝90°，∴∠POE＝∠MPF，∵∠PFM＝∠OEP＝90°，PM＝PO，∴△PFM≌△OEP（AAS），∴PE＝MF，则﹣（x+1）（x﹣5）＝x﹣2，解得x＝﹣或4，故点P的坐标为（﹣，﹣）或（4，2）；（2）点B、C的坐标分别为（﹣1，0）、（0，﹣5a），顶点D的坐标为（2，﹣9a）．当四边形OBDC是圆的内接四边形时，则BC的中点为该圆的圆心，设BC的中点为点Q，由中点坐标公式得，点Q（，﹣a），则OQ＝DQ，即（）2+（﹣）2＝（2﹣）2+（﹣9a+a）2，解得a＝±．2．如图，已知抛物线y＝ax2+4x+c与直线AB相交于点A（0，1）和点B（3，4）．（1）求该抛物线的解析式；（2）设C为直线AB上方的抛物线上一点，当△ABC的面积最大时，求点C的坐标；（3）将该抛物线向左平移2个单位长度得到抛物线y＝a1x2+b1x+c1（a1≠0），平移后的抛物线与原抛物线相交于点D，是否存在点E使得△ADE是以AD为腰的等腰直角三角形？若存在，直接写出点E的坐标；若不存在，请说明理由．【解答】解：（1）将A、B两点代入到解析式中，得，，解得，∴抛物线的解析式为：y＝﹣x2+4x+1；（2）设直线AB为：y＝k1x+1，代入点B，得，3k1+1＝4，解得k1＝1，∴直线AB为：y＝x+1，设C（m，﹣m2+4m+1），过C作CM∥y轴交AB于M，如图1，则M（m，m+1），∴CM＝﹣m2+4m+1﹣m﹣1＝﹣m2+3m，∴S△ABC＝S△ACM+S△BCM＝＝，∵C为直线AB上方抛物线上一点，∴0＜m＜3，∴时，△ABC的面积最大值为，此时C（）；（3）∵抛物线y＝﹣（x﹣2）2+5，∴将抛物线向右平移2个单位后得到的抛物线为：y＝﹣x2+5，联立，解得，∴D（1，4），①如图2，当DA＝DE，∠EDA＝90°，E在AD右侧时，过D作x轴平行线交y轴于N，过E作y轴平行线，两线交于F点∵∠DAN+∠NDA＝∠NDA+∠EDF＝90°∴∠DAN＝∠EDF，又∠DNA＝∠EFD＝90°，DA＝DE，∴△DNA≌△EFD（AAS），∴DN＝EF＝1，AN＝DF＝3，∴E（4，3），②当DA＝DE，∠EDA＝90°，E在AD左侧，同理可得，E（﹣2，5），③当AD＝AE，∠DAE＝90°，E在AD左侧时，同理可得，E（﹣3，2），④当AD＝AE，∠DAE＝90°，E在AD右侧时，同理可得，E（3，0），综上所述，E（4，3）或（﹣2，5）或（﹣3，2）或（3，0）．3．如图，已知抛物线y＝﹣x2+bx+c与x轴交于A，B两点，与y轴交于点C，其中A（﹣1，0），C（0，3）．（1）求该抛物线的函数表达式；（2）抛物线与直线y＝﹣x﹣1交于A、E两点，P是x轴上点B左侧一动点，当以P、B、C为顶点的三角形与△ABE相似时，求点P的坐标；（3）若F是直线BC上一动点，在抛物线上是否存在动点M，使△MBF为等腰直角三角形，若存在，请直接写出点M的坐标；否则说明理由．【解答】解：（1）把A（﹣1，0），C（0，3）代入y＝﹣x2+bx+c，得：，解得：，∴抛物线的函数表达式为y＝﹣x2+2x+3；（2）联立直线AE和抛物线的函数关系式成方程组，得：，解得：，，∴点E的坐标为（4，﹣5），∴AE＝＝5，在y＝﹣x2+2x+3中，令y＝0，得：﹣x2+2x+3＝0，解得：x1＝3，x2＝﹣1，∴点B的坐标为（3，0），∵C（0，3），∴OB＝OC＝3，∵∠BOC＝90°，∴∠CBO＝45°，BC＝3，∵直线AE的函数表达式为y＝﹣x﹣1，∴∠BAE＝45°＝∠CBO．设点P的坐标为（m，0），则PB＝3﹣m，∵以P、B、C为顶点的三角形与△ABE相似，∴＝或＝，∴＝或＝，解得：m＝或m＝﹣，∴点P的坐标为（，0）或（﹣，0）；（3）∵∠CBO＝45°，∴存在两种情况（如图2）．①取点M1与点A重合，过点M1作M1F1∥y轴，交直线BC于点F1，∵∠CBM1＝45°，∠BM1F1＝90°，∴此时△BM1F1为等腰直角三角形，∴点M1的坐标为（﹣1，0）；②取点C′（0，﹣3），连接BC′，延长BC′交抛物线于点M2，过点M2作M2F2∥y 轴，交直线BC于点F2，∵点C、C′关于x轴对称，∠OBC＝45°，∴∠CBC′＝90°，BC＝BC′，∴△CBC′为等腰直角三角形，∵M2F2∥y轴，∴△M2BF2为等腰直角三角形．∵点B（3，0），点C′（0，﹣3），∴直线BC′的函数关系式为y＝x﹣3，联立直线BC′和抛物线的函数关系式成方程组，得：，解得：，，∴点M2的坐标为（﹣2，﹣5），综上所述：点M的坐标为（﹣1，0）或（﹣2，﹣5）．4．如图，抛物线y＝ax2+bx﹣3（a＞0）与x轴交于A、B两点，交y轴于点C，OB＝3，抛物线经过点（2，5）．（1）求该抛物线解析式；（2）如图1，该抛物线顶点D，连接BD、BC，点P是线段BD下方抛物线上一点，过点P作PE∥y轴，分别交线段BD、BC于点F、E，过点P作PG⊥BD于点G，求2PG+EF 的最大值，及此时点P的坐标；（3）如图2，在y轴左侧抛物线上有一动点M，在y轴上有一动点N，是否存在以AN 为直角边的等腰直角三角形AMN？若存在，请直接写出点M的坐标．【解答】解：（1）∵OB＝3，∴B（﹣3，0）把C（﹣3，0）和点（2，5），代入抛物线y＝ax2+bx﹣3，得，解得，∴抛物线解析式为y＝x2+2x﹣3；（2）延长PE与x轴交于点M，FM⊥x轴，PG⊥BD，如图所示，∠FMB＝90°，∠PGF＝90°，∵∠BFM＝∠PFG，∴∠MBF＝∠GPF，∴B（﹣3，0），D（﹣1，﹣4），B、D两点的横坐标距离为2，纵坐标距离为4，由勾股定理得BD＝＝2，∴cos∠MBF＝cos∠GPF＝，∴2PG+EF＝EF+2FP，∴C（0，﹣3），设直线BC解析式为l BC：y＝kx+b（b≠0），把B（﹣3，0）和C（0，﹣3）代入得，，解得，∴l BC：y＝﹣x﹣3，同理，直线BD得解析式为：y＝﹣2x﹣6，设E（m，﹣m﹣3），P（m，m2+2m﹣3），F（m，﹣2m﹣6），∴EF+2FP＝[﹣m﹣3﹣（﹣2m﹣6）]+2[（﹣2m﹣6）﹣（m2+2m﹣3）]＝﹣2（m+）2+，∴当m＝﹣时，EF+2FP有最大值，∵2PG+EF＝EF+2FP，∴此时，P点坐标为P（﹣，﹣）；（3）存在，设N（0，y1），M（x2，+2x2﹣3），当y＝0时，代入抛物线y＝x2+2x+3中，解得两根为﹣3和1，A在y轴右侧，∴A（1，0），∴AN2＝OA2+ON2＝1+y12，AM2＝（x2﹣1）2+（+2x2﹣3）2，MN2＝+（+2x2﹣3﹣y1）2，①当AN⊥MN时，此时由AN＝MN，等腰直角三角形各边比为1：1：，∴M点横坐标为﹣﹣1或﹣3﹣1，将M的横坐标为﹣﹣1或﹣3﹣1，代入y＝x2+2x﹣3中得，∴M点坐标为（﹣﹣1，﹣2）或（﹣3﹣1，14），②由AN⊥MA得：M点横坐标为﹣2﹣2或﹣2﹣2，将M点横坐标为﹣2﹣2或﹣2﹣2代入y＝x2+2x+3中，得M点坐标为（﹣2﹣2，17+8﹣4﹣4）或（﹣2﹣2，33+8﹣4﹣4），综上所述，M点坐标为（﹣﹣1，﹣2）或（﹣3﹣1，14），（﹣2﹣2，17+8﹣4﹣4）或（﹣2﹣2，33+8﹣4﹣4），5．如图，抛物线C1：y＝x2+bx+c经过原点，与x轴的另一个交点为（2，0），将抛物线C1向右平移m（m＞0）个单位得到物度C2，C2交x轴于A、B两点（点A在点B的左边），交y轴于点C．（1）求抛物线C1的解析式及顶点坐标；（2）以AC为斜边向上作等腰直角三角形ACD，当点D落在抛物线C2的对称轴上时，求抛物线C2的解析式及D点坐标．【解答】解：（1）∵抛物线C1经过原点，与x轴的另一个交点为（2，0），∴，解得，∴抛物线C1的解析式为y＝x2﹣2x，∴抛物线C1的顶点坐标（1，﹣1）．（2）如图，∵抛物线C1的向右平衡m（m＞0）个单位得到抛物线C2，∴C2的解析式为y＝（x﹣m﹣1）2﹣1，∴A（m，0），B（m+2，0），C（0，m2+2m），过点C作CH⊥对称轴DE，垂足为H，∵△ACD为等腰直角三角形，∴AD＝CD，∠ADC＝90°，∴∠CDH+∠ADE＝90°，∴△HCD＝△ADE，∵∠DEA＝90°，∴△CHD≌△DEA，∴AE＝HD＝1，CH＝DE＝m+1，∴EH＝HD+DE＝1+m+1＝m+2，由OC＝EH得m2+2m＝m+2，解得m1＝1，m2＝﹣2（舍去），∴抛物线C2的解析式为：y＝（x﹣2）2﹣1，∴D点坐标（2，2）．6．已知：如图，抛物线y＝ax2+bx+6与x轴交于点B（6，0），C（﹣2，0），与y轴交于点A，点P是线段AB上方抛物线上的一个动点．（1）如图，连接P A、PB．设△P AB的面积为S，点P的横坐标为m．请说明当点P运动到什么位置时，△P AB的面积有最大值？（2）过点P作x轴的垂线，交线段AB于点D，再过点P作PE∥x轴交抛物线于点E，连接DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+bx+6与x轴交于点B（6，0），C（﹣2，0），∴可设抛物线的表达式为：y＝a（x+2）（x﹣6），∴﹣12a＝6，解得a＝﹣，∴抛物线的表达式为：y＝﹣x2+2x+6，∴A（0，6）∴直线AB的表达式为：y＝﹣x+6，点P的横坐标为m，则P（m，﹣m2+2m+6），过点P作x轴的垂线，交线段AB于点D，则D（m，﹣m+6），∴S＝×OB×PD＝×6×（﹣m2+2m+6+m﹣6）＝＝﹣（m﹣3）2+，∴当m＝3时，S的值取最大，此时P（3，）；（2）存在，理由如下：由题意可知，PD⊥PE，若△PDE是等腰直角三角形，则PE＝PD，由（1）可得，PD＝﹣m2+2m+6+m﹣6＝﹣m2+3m，∵PE∥x轴，∴E（4﹣m，﹣m2+2m+6），∴PE＝|2m﹣4|，∴|2m﹣4|＝﹣m2+3m，解得m1＝﹣2（舍），m2＝4，m3＝5+（舍），m4＝5﹣，∴当△PDE是等腰直角三角形时，点P的坐标为（4，6），（5﹣，3﹣5）．7．如图1．二次函数y＝﹣x2+6与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．（1）求出点A，B，C的坐标；（2）连接AC，求直线AC的表达式；（3）如图2，点D为线段AC上的一个动点，连接BD，以点D为直角顶点，BD为直角边，在x轴的上方作等腰直角三角形BDE，若点E在y轴上时，求点D的坐标；（4）若点D在线段AC上，点D由A到C运动的过程中，以点D为直角顶点，BD为直角边作等腰直角三角形BDE，当抛物线的顶点C在等腰直角三角形BDE的边上（包括三角形的顶点）时，请直接写出顶点E的坐标．【解答】解：（1）当x＝0时，y＝6．∴C点坐标为（0，6）．当y＝0时，．解得x1＝﹣4，x2＝4．∵A点在B点左侧，∴点A坐标为（﹣4，0），点B坐标为（4，0）．（2）设直线AC的表达式为：y＝kx+b．∵点A坐标为（﹣4，0），点C坐标为（6，0）．∴．解得．∴直线AC的表达式为．（3）如答图1，过点D分别作DF⊥x轴于点F，DG⊥y轴于G. ∴四边形DGOF为矩形，∠FDG＝90°．∵△BDE为等腰直角三角形，BD为直角边．∴BD＝ED，∠EDB＝90°．∴∠EDB﹣∠GDB＝∠FDG﹣∠GDB．即∠EDG＝∠BDF．在△BDF和△EDG中，．∴△BDF≌△EDG（AAS）．∴DF＝DG．设点D的坐标为（m，）．∴．解得m＝，∴点D的坐标为（）．（4）由（2）可得直线AC的表达式为．∵点D在直线AC上，∴设点D坐标为（）．设直线BC的解析式为：y＝kx+b．将B（4，0），C（0，6）代入得．解得．∴直线BC的解析式为．①当C位于斜边BE上时，∵点E在直线BC上，∴设点E坐标为（b，）．如答图2所示.作EM⊥x轴于点M，DQ⊥x轴于点Q，DN⊥EM于点N．易知四边形DQMN为矩形．∴∠QDN＝90°．∵△BDE为等腰直角三角形，BD为直角边．∴BD＝ED，∠EDB＝90°．∴∠EDB﹣∠NDB＝∠QDN﹣∠NDB．即∠EDN＝∠BDQ．在△BDQ和△EDN中，．∴△BDQ≌△EDN（AAS）．∴DN＝DQ，EN＝BQ．∵E坐标为（b，），D坐标为（）．∴DN＝b﹣a，EN＝．DQ＝，BQ＝4﹣a．∴．解得．∴＝．∴点E的坐标是（）．②当点D在直角边DE上时，BD交y轴于点F，如答图3所示．∵∠CDF＝∠BOF＝90°，∠CFD＝∠BFO．∴∠DCF＝∠OBF．∴tan∠DCF＝tan∠OBF．即．亦即．∴OF＝．∴点F坐标为（0，）．设直线BF解析式为y＝kx+b．将B（4，0），F（0，）代入得．解得．∴直线BF解析式为y＝．∵B、F、D三点共线，亦即直线BD解析式为y＝．联立直线AC解析式得解得．故点D坐标为（）．∵BD⊥AC，BD＝DE，∴BD2＝DE2．∴．解得b＝．∴＝．∴点E的坐标为（）．③当点D与点C重合时，即点C为直角顶点时．如答图4所示.作EG⊥y轴于点G．∵∠BCE＝90°．∴∠ECG+∠BCO＝90°．又∵∠ECG+∠GEC＝90°∴∠BCO＝∠GEC．在△GEC和△OCB中，．∴△GEC≌△OCB（AAS）．∴GE＝OC＝6，GC＝OB＝4．∴点E的坐标为（6，10）．由图知点E关于点C对称的点E'亦满足题意．则由中点坐标公式可得点E'的横坐标为2×0﹣6＝﹣6，纵坐标为2×6﹣10＝2．故点E'坐标为（﹣6，2）．综上所述，点E的坐标为（）或（）或（6，10）或（﹣6，2）．8．如图，抛物线y＝ax2+bx+5交x轴于A（﹣1，0）、B（5，0）两点，交y轴于点C．（1）求抛物线的解析式；（2）点P是对称轴上一点，当P A+PC达到最小值时，求点P的坐标；（3）M、N为线段BC上两点（N在M的右侧，且M、N不与B、C重合），MN＝2，在第一象限的抛物线上是否存在这样的点R，使△MNR为等腰直角三角形？若存在，求出点R的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+bx+5交x轴于A（﹣1，0），B（5，0），∴，解得：，∴抛物线的解析式为：y＝﹣x2+4x+5；（2）当x＝0时，y＝5，∴C（0，5），∵A与B关于抛物线的对称轴对称，∴直线BC与对称轴的交点就是点P，此时P A+PC达到最小值，∵y＝﹣x2+4x+5＝﹣（x﹣2）2+9，∴抛物线对称轴为直线x＝2，设直线BC的解析式为：y＝kx+b（k≠0），∵点B坐标为（5，0），则，解得：，∴直线BC的解析式为y＝﹣x+5，与对称轴的交点为（2，3），∴点P的坐标（2，3）；（3）分三种情况：①以点M为直角顶点，如图1，∵MN＝2，∴RN＝MN＝4，∵C（0，5），B（5，0），∴OC＝OB＝5，∴∠OCB＝∠OBC＝45°，∵∠RNM＝45°＝∠BCO，∴RN∥OC，由（2）知：直线BC的解析式为y＝﹣x+5，设R（m，﹣m2+4m+5），则N（m，﹣m+5），则RN＝（﹣m2+4m+5）﹣（﹣m+5）＝4，解得m1＝4，m2＝1，∵点N在点M右侧，∴m＝4，∴R（4，5）；②以点R为直角顶点，如图2，∵MN＝2，∴RN＝MN＝2，设R（m，﹣m2+4m+5），则Q（m，﹣m+5），∴RN＝（﹣m2+4m+5）﹣（﹣m+5）＝2，解得m1＝，m2＝，∵点N在点M右侧，∴m＝，∴R（，）；③以点N为直角顶点，如图3，∵MN＝2，∴RM＝MN＝4，∵∠RMN＝∠OBC＝45°，∴MR∥OB，设R（m，﹣m2+4m+5），则M（m﹣4，﹣m2+4m+5），把M（m﹣4，﹣m2+4m+5）代入y＝﹣x+5，得﹣（m﹣4）+5＝﹣m2+4m+5，解得m1＝4，m2＝1，此时点M（0，5），因为点M在线段BC上运动，且不与B、C重合，所以不存在以N为直角顶点的情况；综上所述：当R（4，5）或（，）时，△MNR为等腰直角三角形．9．抛物线y＝ax2﹣6ax+4（a≠0）交y轴正半轴于点C，交x轴负半轴于点A，交x轴正半轴于点B，且AB＝10．（1）如图（1），求抛物线的解析式；（2）如图（2），连接BC，点P为第一象限抛物线上一点，设点P横坐标为t，△PBC 的面积为S，求S与t之间的函数关系式（不用写出自变量t的取值范围）；（3）如图（3），在（2）的条件下，连接P A交y轴于点D，过点P作x轴的垂线，交x轴于点E，交BC于点F，连接DF，当∠APE+∠CFD＝90°时，在抛物线上是否存在点Q，使得点Q、PE的中点N、点C、是构成以CN为斜边的等腰直角三角形？若存在，请求出点Q的坐标，若不存在，请说明理由．【解答】解：（1）如图1中，设A（m，0），B（n，0），由题意：，解得，∴A（﹣2，0），B（8，0），把A（﹣2，0）代入y＝ax2﹣6ax+4，得到a＝﹣，∴抛物线的解析式为y＝﹣x2+x+4．（2）如图2中，连接OP．设P（t，﹣t2+t+4），∵B（8，0），C（0，4），∴OB＝8，OC＝4，∴S＝S△POC+S△POB﹣S△OBC＝×4×t+×8×（﹣t2+t+4）﹣×4×8＝﹣t2+8t（0＜t＜8）．（3）存在．理由：如图3中，设P（t，﹣t2+t+4），∵A（﹣2，0），B（8，0），C（0，4），∴直线P A的解析式为y＝﹣（t﹣8）x﹣t+4，直线BC的解析式为y＝﹣x+4，∵PE⊥x轴，∴F（t，﹣t+4），∵D（0，﹣t+4），∴FD∥AB，∴∠CFD＝∠CBA，∵∠APF+∠CFD＝90°，∠APF+∠P AE＝90°，∴∠P AB＝∠CFD＝∠CBO，∴tan∠CBO＝tan∠P AB＝＝，∴＝，∵OA＝2，∴OD＝1，∴﹣t+4＝1，∴t＝6，∴P（6，4），E（6，0），∵PN＝NE，∴N（6，2），∵C（0，4），△CNQ是等腰直角三角形，CN是斜边，当点Q在CN的上方时，如图3，过点Q作x轴的平行线交y轴于点G，交EP的延长线于点H，设点Q（s，k），易证△QGC≌△NHQ（AAS），则GC＝QH，GQ＝HN，即s＝k﹣2，k﹣4＝6﹣s，解得，∴点Q的坐标为（4，6），∵当x＝4时，y＝﹣×42+×4+4＝6，∴点Q在抛物线y＝﹣x2+x+4上，∴满足条件的点Q的坐标为（4，6）．10．如图，抛物线y＝ax2+bx过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．（1）求抛物线的表达式；（2）直接写出点C的坐标和△ABC的面积．（3）点P是抛物线对称轴上一点，且使得P A﹣PC最大，求点P的坐标．（4）若点M在直线BH上运动，点N在x轴上运动，当以点C、M、N为顶点的三角形为等腰直角三角形时，请直接写出此时△CMN的面积．【解答】解：（1）∵抛物线y＝ax2+bx过A（4，0），B（1，3）两点，∴，解得，∴抛物线的解析式为y＝﹣x2+4x．（2）如图1中，∵y＝﹣x2+4x＝﹣（x﹣2）2+4，∴对称轴x＝2，∵B，C关于对称轴对称，B（1，3），∴C（3，3），∴S△ABC＝×2×3＝3．（3）如图1中，∵A（4，0），C（3，3），∴直线AC的解析式为y＝﹣3x+12，∵P A﹣PC≤AC，∴当点P在直线AC上时，P A﹣PC的值最大，此时P（2，6）．（4）如图4﹣1中，如图，当∠CNM＝90°，NC＝NM时，可知N（4，0），M（1，﹣1），CN＝NM＝，∴S△MNC＝×CN×MN＝5．如图4﹣2中，当∠CMN＝90°，MN＝MC时，M（1，﹣2），N（﹣4，0），可知MN ＝MC＝＝，∴S△MNC＝．如图4﹣3中，当∠CMN＝90°，MC＝MN时，可知M（1，2），N（2，0），MN＝CM ＝＝，∴S△MNC＝××＝，如图4﹣4中，当∠CNM＝90°，CN＝MN时，N（﹣2，0），M（1，﹣5），可得S△MNC ＝17．综上所述，满足条件的△MNC的面积为5或或或17．。

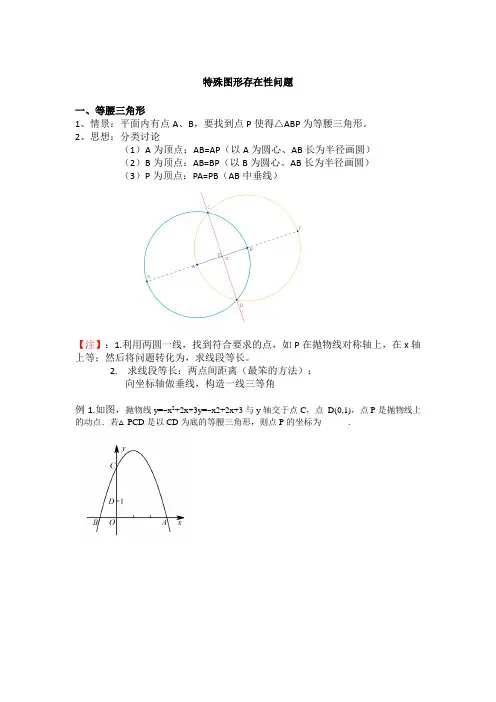
特殊图形存在性问题一、等腰三角形1、情景：平面内有点A、B，要找到点P使得△ABP为等腰三角形。

2、思想：分类讨论（1）A为顶点：AB=AP（以A为圆心、AB长为半径画圆）（2）B为顶点：AB=BP（以B为圆心、AB长为半径画圆）（3）P为顶点：PA=PB（AB中垂线）【注】：1.利用两圆一线，找到符合要求的点，如P在抛物线对称轴上，在x轴上等；然后将问题转化为，求线段等长。

2.求线段等长：两点间距离（最笨的方法）；向坐标轴做垂线，构造一线三等角例1.如图，抛物线y=−x2+2x+3y=−x2+2x+3与y轴交于点C，点D(0,1)，点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为______．练习1.如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A,B 两点，A点在原点的左侧，B点的坐标为(3,0)，与y轴交于C(0,−3)点，点P是直线BC下方的抛物线上一动点．(1)求这个二次函数的表达式；(2)在直线BC找一点Q，使得△QOC为等腰三角形，写出Q点坐标．练习2、已知抛物线y=ax2+bx+c经过A（﹣1，0）、B（3，0）、C（0，3）三点，直线l 是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；（3）在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．练习3.如图，抛物线y=ax2+bx﹣3（a≠0）的顶点为E，该抛物线与x轴交于A、B两点，与y轴交于点C，且BO=OC=3AO，直线y=﹣x+1与y轴交于点D．（1）求抛物线的解析式；（2）证明：△DBO∽△EBC；（3）在抛物线的对称轴上是否存在点P，使△PBC是等腰三角形？若存在，请直接写出符合条件的P点坐标，若不存在，请说明理由．练习4.如图，在平面直角坐标系中，已知抛物线y=ax2+bx+c(a≠0)与x轴交A(−1,0),B(−3,0)两点，与y轴交于点C(0,−3)，其顶点为D．(1)求该抛物线的解析式，并用配方法把解析式化为y=a(x−h)2+k的形式；(2)动点M从点D出发，沿抛物线对称轴方向向上以每秒1个单位的速度运动，运动时间为t，连接OM,BM，当t为何值时，△OMB为等腰三角形？练习5.如图，在平面直角坐标系中，点A的坐标为（m，m），点B的坐标为（n，﹣n），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点C．已知实数m、n （m＜n）分别是方程x2﹣2x﹣3=0的两根．（1）求抛物线的解析式；（2）若点P为线段OB上的一个动点（不与点O、B重合），直线PC与抛物线交于D、E 两点（点D在y轴右侧），连接OD、BD．①当△OPC为等腰三角形时，求点P的坐标；②求△BOD 面积的最大值，并写出此时点D的坐标．25．（10分）如图，在平面直角坐标系中，抛物线y＝x2+bx+c经过原点O，与x轴交于点A（5，0），第一象限的点C（m，4）在抛物线上，y轴上有一点B（0，10）．（Ⅰ）求抛物线的解析式及它的对称轴；（Ⅱ）点P（0，n）在线段OB上，点Q在线段BC上，若OP＝2BQ，且P A＝QA．求n 的值；（Ⅲ）在抛物线的对称轴上，是否存在点M，使以A，B，M为顶点的三角形是等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．19-红桥一模25．（10分）如图，抛物线y＝x2+bx+c与y轴交于点C（0，﹣4），与x轴交于点A，B，且B点的坐标为（2，0）．（1）求该抛物线的解析式．（2）若点P是AB上的一动点，过点P作PE∥AC，交BC于E，连接CP，求△PCE面积的最大值．（3）若点D为OA的中点，点M是线段AC上一点，且△OMD为等腰三角形，求M点的坐标．(17河北一模)25(10分）如图，己知抛物线y=x2+bx+c图象经过点A（﹣1，0），B（0，﹣3），抛物线与x轴的另一个交点为C．（1）求这个抛物线的解析式：（2）若抛物线的对称轴上有一动点D，且△BCD为等腰三角形（CB≠CD），试求点D的坐标；二、直角三角形1.情景：平面内有点A、B，要找到点P使得△ABP为直角三角形2.思想：分类讨论（1）A为顶点：∠A（过A做垂线）（2）B为顶点：∠B（过B做垂线）（3）P为顶点：∠C（AB为直径的圆）【注】1.等腰直角三角形，只需在两直线上上下找与AB等长以及过O做AB垂线与圆交点即可例1.如图，在平面直角坐标系中，二次函数y=ax2+bx+c的图象经过矩形OABC的顶点A，B与x 轴交于点E，F且B，E两点的坐标分别为B(2，32)E(−1，0)(1)求二次函数的解析式；(2)在抛物线上是否存在点Q，使△QBF为直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．练习1.如图，抛物线y=x2+bx+3顶点为P，且分别与x轴、y轴交于A、B两点，点A在点P的右侧，tan∠ABO=13(1)求抛物线的对称轴和PP的坐标．(2)在抛物线的对称轴上是否存在这样的点D，使△ABD为直角三角形？如果存在，求点D 的坐标；如果不存在，请说明理由．例2.如图，抛物线y=−x2+bx+c与x轴相交于AB两点，与y 轴相交与点C，且点B与点CC 的坐标分别为(3,0)，C(0,3)，点M是抛物线的顶点．(1)求二次函数的关系式(2)在MB上是否存在点P，过点P作PD⊥x轴于点D,OD=m,使△PCD为直角三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由练习2.如图，在平面直角坐标系中，直线y=−13x+2交x轴点P，交y轴于点A．抛物线y=x2+bx+c的图象过点E(−1,0)，并与直线相交于A、B两点．(1)求抛物线的解析式（关系式）；(2)过点A作AC⊥AB交x轴于点C，求点C的坐标；(3)除点C外，在坐标轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M 的坐标；若不存在，请说明理由．练习3.如图，抛物线y=x2+bx+c与直线y=x﹣3交于A、B两点，其中点A在y轴上，点B坐标为（﹣4，﹣5），点P为y轴左侧的抛物线上一动点，过点P作PC⊥x轴于点C，交AB于点D．（1）求抛物线的解析式；（2）以O，A，P，D为顶点的平行四边形是否存在？如存在，求点P的坐标；若不存在，说明理由．（3）当点P运动到直线AB下方某一处时，过点P作PM⊥AB，垂足为M，连接PA使△PAM为等腰直角三角形，请直接写出此时点P的坐标．（18东丽-一模）25.如图，在平面直角坐标系中，点A、B的坐标分别为（1，1）、（1，2），过点A、B分别作y轴的垂线，垂足为D、C，得到正方形ABCD，抛物线y=x2+bx+c经过A、C两点，点P为第一象限内抛物线上一点（不与点A重合），过点P分别作x轴y轴的垂线，垂足为E、F，设点P的横坐标为m，矩形PFOE与正方形ABCD重叠部分图形的周长为l．（1）直接写出抛物线所对应的函数表达式．（2）当矩形PFOE的面积被抛物线的对称轴平分时，求m的值．（3）当m＜2时，求L与m之间的函数关系式．（4）设线段BD与矩形PFOE的边交于点Q，当△FDQ为等腰直角三角形时，直接写出m的取值范围．三、平行四边形存在性问题类型一：1.情景：一直平面内三点A、B、C，求一点P使四边形ABCP为平行四边形2.思想：分类讨论（1）以AC为对角线：ABCP1（2）以AB为对角线：ACBP3（3）以BC为对角线：ACP2B【注】找到P点后，用平行四边形的判定定理，求等长线段，或利用等角度、平行线求坐标即可。

等腰直角三角形存在性（通用版）试卷简介:考查在动态框架和函数框架下等腰直角三角形存在性的处理原则，调用存在性问题的处理手段，分析定点、动点，从直角入手，确定分类，借助等腰三角形自身的性质或构造弦图模型解决问题。

一、单选题(共5道，每道20分)1.如图，抛物线交x轴于A，C两点（点A在点C的右侧），交y轴于点B．点D的坐标为（-1，0），若在直线AB上存在点P，使得以A，D，P为顶点的三角形是等腰直角三角形，则点P的坐标为( )A. B.（-1，3）或（1，2）C.（-1，4）或（1，2）D.（-1，4），（1，2）或（5，-2）答案：C解题思路：1．解题要点①观察题目特征，确定为等腰直角三角形存在性问题．②分析定点、动点、不变特征．从直角入手，分类讨论．③画图，表达线段长，借助等腰直角三角形性质建等式．2．解题过程由题意得，A（3，0），B（0，3），AO=BO=3．在△ADP中，A，D为定点，P为直线AB上的动点．①当点A是直角顶点时，在直线AB上不存在点P，使△ADP为等腰直角三角形．②如图，当点D为直角顶点时，过点D作⊥DA，交直线AB于点．由∠1=45°可得，为等腰直角三角形，点满足题意．此时，点的坐标为（-1，4）．③如图，当点P为直角顶点时，过点D作⊥AB于点．易知为等腰直角三角形，点满足题意．过点作轴于点M．易得，OM=1，∴点的坐标为（1，2）．综上得，点P的坐标为（-1，4）或（1，2）．试题难度：三颗星知识点：等腰直角三角形存在性2.如图，抛物线与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．P是线段AC上的一个动点（不与点A，C重合），过点P作平行于x轴的直线，交BC于点Q，若在x轴上存在点R，使得△PQR是等腰直角三角形，则点R的坐标为( )A. B.C. D.答案：C解题思路：1．解题要点①观察题目特征，确定为等腰直角三角形存在性问题．②分析定点、动点、不变特征．从直角入手，分类讨论．③画图，表达线段长，借助等腰直角三角形性质建等式．2．解题过程由题意，得A（-1，0），B（3，0），C（0，2），则，．设，则，PQ=-2m+4．①如图，当点Q为直角顶点时，PQ=RQ．，，由-2m+4=m，得，∴．②如图，当点P为直角顶点时，PQ=PR．，，由-2m+4=m，得，∴．③如图，当点R为直角顶点时，RP=RQ．过点R作RD⊥于点D，则，由，得m=1，∴．综上得，点R的坐标为．试题难度：三颗星知识点：等腰直角三角形存在性3.如图，二次函数的图象与x轴交于A，B两点（点A在点B的左侧），以AB为边在x轴上方作正方形ABCD，P是x轴上的一动点（不与点A重合），连接DP，过点P作PE⊥DP交y轴于点E．当△PED是等腰直角三角形时，点P的横坐标为( )A.-4B.-3C.-3或-4D.-4或4答案：D解题思路：∵，∴A（-3，0），B（1，0）．∵四边形ABCD是正方形，∴D（-3，4）．∵∠DPE=90°，要使得△PED是等腰直角三角形，只能是DP=PE．设点P的横坐标为．①如图，当时，∵∠DAP=∠DPE=90°，∴∠ADP+∠DPA=∠OPE+∠DPA，∴∠ADP =∠OPE．又∵∠DAP=∠POE=90°，DP=PE，∴△ADP≌△OPE，∴OP=AD=4，∴．②如图，当时，易证△DAP≌△POE，∴OP=AD=4，∴（不合题意，舍去）．③如图，当时，易证△DAP≌△POE，∴OP=AD=4，∴．综上得，当△PED是等腰直角三角形时，点P的横坐标为-4或4．试题难度：三颗星知识点：等腰直角三角形存在性4.如图，已知直线经过A（0，1），B（1，0）两点，P是x轴正半轴上的一动点，且OP的垂直平分线交直线于点Q，交x轴于点M，直线经过点A且与x轴平行．若在直线上存在点C，使得△CPQ是以Q为直角顶点的等腰直角三角形，则点C的坐标为( )A.（1，1）B.（1，1）或（2，1）C.（2，1）D.（1，1）或（0，1）答案：A解题思路：1．解题要点①观察题目特征，确定为等腰直角三角形存在性问题．②分析定点、动点、不变特征．③从已知出发，借助等腰直角三角形的性质（直角和两腰相等）和坐标系处理斜放置直角的原则，构造弦图模型解决问题．2．解题过程由题意得，OA=OB=1，△AOB为等腰直角三角形，点C的纵坐标为1．①如图，当点Q在x轴上方时，延长MQ交直线于点E，则ME⊥．易证△CEQ≌△QMP，△QMB为等腰直角三角形，四边形AOME为矩形，∴CE=QM=MB，AE=OM，∴AC=AE+CE=OM+MB=OB=1，∴点C的坐标为（1，1）．②如图，当点Q在x轴下方时，延长QM交直线于点F．同理，得CF=QM=MB，AF=OM，∴AC=AF-CF=OM-MB=OB=1，∴点C的坐标为（1，1）．综上得，点C的坐标为（1，1）．试题难度：三颗星知识点：等腰直角三角形存在性5.如图，在平面直角坐标系xOy中，直线y=x+4与x轴、y轴分别交于点A，B，D为线段AB 上一动点，过点D作x轴的垂线，垂足为点C，CD的延长线交抛物线于点E，连接BE．若△DBE为等腰直角三角形，则点D的坐标为( )A.（-2，2）B.（-2，6）C.（-3，4）或（-2，6）D.（-3，1）或（-2，2）答案：D解题思路：由题意得，A（-4，0），B（0，4），∴OA=OB．又∵∠AOB=90°，∴∠BAO=45°．∵CD⊥x轴，∴∠ADC=45°，∴EDB=45°．在△DBE中，B是定点，D，E均为动点，要使得△DBE为等腰直角三角形，需从直角出发进行分类讨论．①如图，当点E为直角顶点时，BE∥AO．此时点E的纵坐标为4，代入二次函数表达式可得点E的坐标为（-3，4），∴，∴．②如图，当点B为直角顶点时，BE⊥AB．由直线AB的斜率为1可知直线BE的斜率为-1，结合点B的坐标（0，4），可求得直线BE的表达式为y=-x+4．由得，，∴点E的坐标为（-2，6），∴，∴．综上得，点D的坐标为（-3，1）或（-2，2）．试题难度：三颗星知识点：等腰直角三角形存在性。

等腰直角三角形存在性问题一、复习回顾二次函数存在性问题中等腰三角形的存在性、直角三角形存在性问题，等腰三角形的存在性问题有两种思路：①两圆一线确定点的位置，结合图形特点解决问题；②不考虑点的位置，利用两点间距离公式表示线段长构建方程求解；直角三角形的存在性问题有两种思路：①两线一圆构图，“改斜归正”转化横平竖直线段长，②不考虑点的位置，利用两点间距离公式表示线段长构建方程求解。

二、特殊三角形之等腰直角三角形存在性问题如图，抛物线y=x2-2x-3与x轴交于A、B两点，（点A在点B的左侧），与y轴交于点C，点P是抛物线上一动点，点Q在直线x=-3上，是否存在以点P为顶点的等腰直角三角形△PBQ，若存在，求出点P的横坐标，若不存在说明理由。

解法分析：通过读题，不难求得A、B、C三点坐标，点P、Q是两个动点，位置不确定，如何确定它们的位置是解决问题的一个难点。

此时不妨通过草图分析，大体分两种情况：①直角顶点在BQ下方，②直角点P在BQ上方，结合上辑课讲到的直角三角形存在性问题的处理思路，容易考虑使用“改斜归正”的处理办法结合等腰直角三角形的特点构造一线三等角全等模型，从而顺利转化线段长建立等量。

三、练习1.(本小题25分)如图，抛物线y=x2-4x+3交x轴于A，C两点（点A在点C的右侧），交y 轴于点B．点D的坐标为(-1，0)，若在直线AB上存在点P，使得以A，D，P为顶点的三角形是等腰直角三角形，则点P的坐标为()A.(-1,4) 或(1/2,5/2)B. (-1，3)或(1，2)C. (-1，4)或(1，2)D. (-1，4)，(1，2)或(5，-2)2.如图，抛物线与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．P是线段AC上的一个动点（不与点A，C重合），过点P作平行于x轴的直线l，交BC于点Q，若在x轴上存在点R，使得△PQR是等腰直角三角形，则点R的坐标为() A.(1,4/3)或(3/2,1) B.(-1/3,4/3)或(-1/2,1) C.(1,0)或(-1/3,0)或(1/2,0) D.(1,0)或(-1/3,0)或(4/3,0)3.如图，二次函数的图象与x轴交于A，B两点（点A在点B的左侧），以AB为边在x轴上方作正方形ABCD，P是x轴上的一动点（不与点A重合），连接DP，过点P作PE⊥DP交y轴于点E．当△PED是等腰直角三角形时，点P的横坐标为()A. -4B. -3C. -3或-4D. -4或44.如图，在平面直角坐标系xOy中，直线y=x+4与x轴、y轴分别交于点A，B，D为线段AB上一动点，过点D作x轴的垂线，垂足为点C，CD的延长线交抛物线y=-x2-3x+4于点E，连接BE．若△DBE为等腰直角三角形，则点D的坐标为()A. (-2，2)B. (-2，6)C. (-3，4)或(-2，6)D. (-3，1)或(-2，2)5.如图，抛物线y=-x2+4x经过A（4，0），B（1，3）两点，点C与点B关于抛物线的对称轴对称，过点B作直线BH△x轴于点H，点M在直线BH上运动，点N在x轴上运动，是否存在以点C、M、N为顶点的三角形为等腰直角三角形时，若存在，求出点M坐标，若不存在说明理由。

一次函数之等腰直角三角形存在性（人教版）（专
题）
一、单选题(共4道，每道25分)
1.如图，直线y=2x+2与x轴、y轴分别交于点A，点B，点P是平面内一点且在直线AB下方，若使△ABP为等腰直角三角形，则点P的坐标为( )
A.（-3，1），（-2，3）或
B.（1，-1），（2，1）或
C.（1，-1），（2，1），（-3，1）或（-2，3）
D.（1，-1），（2，1）（-3，1），（-2，3），或
答案：B
解题思路：
试题难度：三颗星知识点：略
2.如图，直线与x轴、y轴分别交于点A、点B，点D是线段OA的中点，点P 是第一象限内一点，且使△BDP是等腰直角三角形，则点P的坐标为( )
A. B.
C.（2，8），（8，2），（4，4）
D.（2，5），（5，3），（4，4）
答案：B
解题思路：
试题难度：三颗星知识点：略
3.如图，直线与x轴、y轴分别交于点A、点B，其中点．点P 是平面内一点，若△ABP是以点A为直角顶点的等腰直角三角形，则点P的坐标为( )
A.
B.
C.
D.
答案：A
解题思路：
试题难度：三颗星知识点：略
4.如图，直线y=2x-4与x轴、y轴分别交于点A，点B，点P是平面内一点，若△ABP是以线段AB为直角边的等腰直角三角形，则点P的坐标为( )
A.(6，-2)或(4，-6)
B.(-2，2)，(4，-6)或（3，-3）
C.(-2，2)，(6，-2)，(-4，-2)或(4，-6)
D.(-2，2)，(6，-2)，(-4，-2)，(4，-6)，（3，-3）或（1，-1）
答案：C
解题思路：
试题难度：三颗星知识点：略。

2020中考专题17——存在性问题之特殊三角形姓名____________ . 【方法解读】特殊二和形存化件问题L婪足指寻找符介条件的点使之构成等腰二角形、江用三角形、全第一;角形等特殊二用形.解决此类问题的美犍在于恰当地分类4M避免M籽.【例题分析】例L如图，直线产3x-3交x轴例点A,交y轴J点B,过A, B两点的他物线交x例J另一点C(3, 0).(1)求点A,B的坐标.(2)求旭物线对应的函数表认式.(3)在附物线的对称轴上是否存在点Q,使△ABQ皓笔腰三角形?若存在，求出符合条件的点Q的坐标: 若不存在.请说明毋山.例2.如凰tl知直线.kx 6与抛物线y』x'b乂，c相交十A, 3两点，口点A(l,⑷为抛物段的顶点, 点B 在x轴上.⑴求旭利线对应的函数及辽揖⑵任⑴中：次函数的第.拿限的图象上是否存在•点P,便△FOB与APOC全等?若存在，求出点P 的％标:若不存在,请说明理由.(3)若点Q是y轴上…点,HAABQ为直角三角形,求点Q的坐标.D.【巩固训练】1.（2019•止宾〉已刈抛物纹y = x'-l，j轴文于点A.。

宜纹/=代内为任总实数）出文于S , C两点.则下列结论不正确的是（）A.存在实数使得448C为等腰三角形民存在实数A ,使得&46C的内角中仃两角分别为3伊和60）C.任意实数A,伐得部为血角三角形D.存在实数4,使得M8c为等边三处形2. M图.在平行四边形ABCD中,AB 7 cm, BC 4 c0 NA-30' .点P从点A出发沿着AB边向燃B运劭, 速度为I cm/.连结印，若以运动时间为则当〔二 w时,AADP为等小」角形.3.（2019 •泰安）已知次函数】七公十）的图象。

反比例函数y =巴的图象大丁点T,与x他交丁x 点用 5.U）.若 08 二4 8, H.S^=y .（1）求反比例函数与一次函数的表达式，<2）苦点P为x粕上一点,是等股三角形.求点「的坐乐.1. （2D18・ F州）如图，池物线y = a/+bx-4经过,4（-3.0）.£（5.-4）两点, I j•地文于点C ,性接力&•4C. RC.（1）求抛物线的表达式，（2）求证，.48平分NO6（3）抛物线的对称轴卜.是否存在点M,使得M8W是以48为宜用边的汽角H角形，若存在，求山点M的坐标：苍不存在，请说刚理由.5.(2019•的卅)如图I.在平面直用坐标系中•点。

等腰三角形存在性问题（两圆一线）类型一、格点中的等腰三角形1、在如图所示的5×5方格中，每个小方格都是边长为1的正方形，△ABC是格点三角形（即顶点恰好是正方形的顶点），则与△ABC有一条公共边且全等的所有格点三角形的个数是（）2、.如图，在正方形网格的格点（即最小正方形的顶点）中找一点C，使得△ABC是等腰三角形，且AB为其中一腰．这样的C点有( )个．3、如图，A、B是网格中的两个格点，点C也是网格中的一个格点，连接AB、BC、AC，当△ABC为等腰三角形时，格点C的不同位置有处，设网格中的每个小正方形的边长为1，则所有满足题意的等腰三角形ABC的面积之和等于．4、如图，在图中能画出与△ABC全等的格点三角形有几个？类型二、定边几何法讨论：两圆一线5、以线段AB为一边的等腰直角三角形有个，请在下列图中画出来6、（1）如图所示，线段OD的一个端点O在直线AB上，以OD为一边的等腰三角形ODP，并且使点P也在AB 上，这样的等腰三角形能画个（在图中作出点P）（2）若△DOB=60°，其它条件不变，则这样的等腰三角形能画个，（只写出结果）（3）若改变（2）中△DOB的度数，其他条件不变，则等腰三角形ODP的个数和（2）中的结果相同，则改变后△DOB=．7、如图，南北向的公路上有一点A，东西向的公路上有一点B，若要在南北向的公路上确定点P，使得△PAB是等腰三角形，则这样的点P最多能确定（）个．8、线段AB和直线l在同一平面上．则下列判断可能成立的有个直线l上恰好只有个1点P，使△ABP为等腰三角形直线l上恰好只有个2点P，使△ABP为等腰三角形直线l上恰好只有个3点P，使△ABP为等腰三角形直线l上恰好只有个4点P，使△ABP为等腰三角形直线l上恰好只有个5点P，使△ABP为等腰三角形直线l 上恰好只有个6点P ，使△ABP 为等腰三角形．9、如图AOB ∠,当ο30为AOB ∠，ο60，ο120时，请在射线OA 上找点P ，使POB ∆为等腰三角形，并分析出当AOB ∠发生变化时，点P 个数的情况；类型三、三角形、长方形和正方形中的等腰三角形10、如图，在长方形ABCD 中，AB=4，AD=10，点Q 是BC 的中点，点P 在AD 边上运动，若△BPQ 是腰长为5的等腰三角形，则满足题意的点P 有( )个11、如图所示，在长方形ABCD的对称轴上找一点P，使得△PAB，△PBC均为等腰三角形，则满足条件的点P有( )个12、如图，边长为6的正方形ABCD内部有一点P，BP=4，△PBC=60°，点Q为正方形边上一动点，且△PBQ是等腰三角形，则符合条件的Q点有____个．13、在等边△ABC所在的平面内求一点P，使△PAB，△PBC，△PAC都是等腰三角形，请画出所有满足条件的点；等腰三角形存在性问题（两圆一线）答案类型一、格点中的等腰三角形1、在如图所示的5×5方格中，每个小方格都是边长为1的正方形，△ABC是格点三角形（即顶点恰好是正方形的顶点），则与△ABC有一条公共边且全等的所有格点三角形的个数是（4）2、.如图，在正方形网格的格点（即最小正方形的顶点）中找一点C，使得△ABC是等腰三角形，且AB为其中一腰．这样的C点有( B )个．A.8B.9C.10D.113、如图，A、B是网格中的两个格点，点C也是网格中的一个格点，连接AB、BC、AC，当△ABC为等腰三角形时，格点C的不同位置有3处，设网格中的每个小正方形的边长为1，则所有满足题意的等腰三角形ABC的面积之和等于15．【解答】解：格点C的不同位置分别是：C、C′、C″，∵网格中的每个小正方形的边长为1，∴S△ABC=×4×3=6，S△ABC′=20﹣2×3﹣=6.5，S△ABC″=2.5，∴S△ABC+S△ABC′+S△ABC″=6+6.5+2.5=15．故答案分别为：3；15．4、如图，在图中能画出与△ABC全等的格点三角形有几个？类型二、定边几何法讨论：两圆一线5、以线段AB为一边的等腰直角三角形有个，请在下列图中画出来6、（1）如图所示，线段OD的一个端点O在直线AB上，以OD为一边的等腰三角形ODP，并且使点P也在AB 上，这样的等腰三角形能画4个（在图中作出点P）（2）若△DOB=60°，其它条件不变，则这样的等腰三角形能画2个，（只写出结果）（3）若改变（2）中△DOB的度数，其他条件不变，则等腰三角形ODP的个数和（2）中的结果相同，则改变后△DOB= 90°．7、如图，南北向的公路上有一点A，东西向的公路上有一点B，若要在南北向的公路上确定点P，使得△PAB是等腰三角形，则这样的点P最多能确定（）个．8、线段AB和直线l在同一平面上．则下列判断可能成立的有5个直线l上恰好只有个1点P，使△ABP为等腰三角形直线l上恰好只有个2点P，使△ABP为等腰三角形直线l上恰好只有个3点P，使△ABP为等腰三角形直线l上恰好只有个4点P，使△ABP为等腰三角形直线l上恰好只有个5点P，使△ABP为等腰三角形直线l 上恰好只有个6点P ，使△ABP 为等腰三角形．9、如图AOB ∠,当ο30为AOB ∠，ο60，ο120时，请在射线OA 上找点P ，使POB ∆为等腰三角形，并分析出当AOB ∠发生变化时，点P 个数的情况；【结论】当AOB ∠为锐角，AOB ∠ο60≠，有三个点，当AOB ∠=ο60，只有一个点；当AOB ∠为钝角或直角，只有一个点；类型三、三角形、长方形和正方形中的等腰三角形10、如图，在长方形ABCD中，AB=4，AD=10，点Q是BC的中点，点P在AD边上运动，若△BPQ是腰长为5的等腰三角形，则满足题意的点P有( B )A.2个B.3个C.4个D.5个11、如图所示，在长方形ABCD的对称轴上找一点P，使得△PAB，△PBC均为等腰三角形，则满足条件的点P有( C )A.1个B.3个C.5个D.无数多个12、如图，边长为6的正方形ABCD内部有一点P，BP=4，△PBC=60°，点Q为正方形边上一动点，且△PBQ是等腰三角形，则符合条件的Q点有____个．13、在等边△ABC所在的平面内求一点P，使△PAB，△PBC，△PAC都是等腰三角形，请画出所有满足条件的点；。

学生做题前请先回答以下问题问题1:问题2：30。

角所对的直角边是直角三角形斜边上的中线等于BC = -AB问题3：已知：如图，在RtA ABC中，ZC=90°, ZA=30°.求证：2.你是怎么思、考的？特殊三角形（直角三角形）人教版一、单选题（共9道，每道□分）2.如图,在RtA ABC中，ZACB=90°, AB=4, CD是AB边上的中线,则CD的长为（A.lB.2C.3D.8答案:B解题思路：在Rt△九BC中，Z.4C5=90°, CD是九8边上的中线, 可知CD = ^AB f '：AB=4, ；・CD=2・故选B.试题难度：三颗星知识点：直角三角形2.如图是屋架设计图的一部分，其中ZA=30°,点D 是斜梁AB 的中点，BC, DE 垂直于横梁 AC, AB=16m,则 DE 的长为（ ）答案:B解题思路：•：BC, QE 垂直于横梁川C,・•・乙DEA=/BCA=9y,・・・D 为斜梁九8的中点，九8=16,・•・ ZD = ±13=1x16 = 8, 2 2在 Rt △且DE 中，Z.4=30°, AD=8・•・ Z)£=l.W=-x8 = 4(m)・ 2 2故选B.3.如图，在RtA ABC 中，ZACB=90°, D 是AB 的中点，过点C 作EF 〃AB, 若ZBCF=35°,则ZACD 的度数是（）A.65°C.45°D.35°难度：三颗星知识点：直角三角形A.2mB.4mC.6mD.8mB.55°答案：B解题思路：\'EFl)AB f・•・乙B=ZBCFT 乙BCF=3T・・・Z5=35°在RtAACB中，仞是斜边•站上的中线/. CD=BD•I ZBCD=/B=35。

•・• Z-4C5=90°・•・ZACD=ZACB-ZBCD=55O故选B・试题难度：三颗星知识点：直角三角形4.如图，在△ABC44, ZA=60°, BE±AC,垂足为E, CF丄AB,垂足为F, BE, CF交于点M.若CM=4, FM=5,则BE 等于（）A.14B.13C.12D.9答案：C解题思路：如图,答案:C 解题思路:\'BE1AC, CF1AB, ・・・ZQFW90。

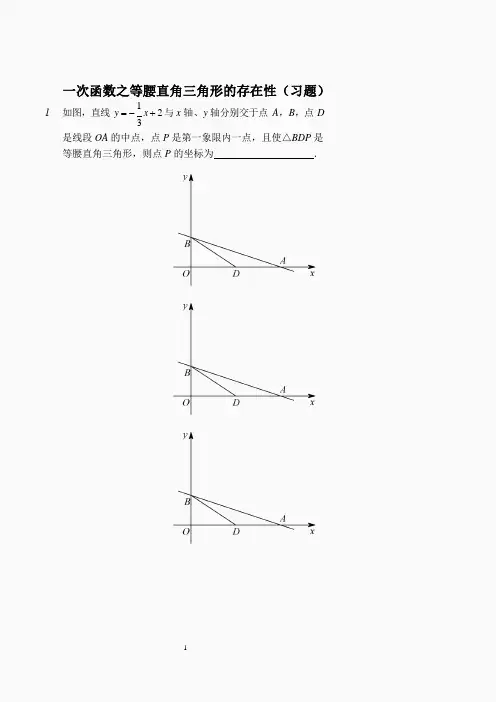
一次函数之等腰直角三角形的存在性（习题）
1.如图，直线y =-1
x + 2 与x 轴、y 轴分别交于点A，B，点D 3
是线段OA 的中点，点P 是第一象限内一点，且使△BDP 是等腰直角三角形，则点P 的坐标为．
2.如图，直线AB：y=-x+b 交y 轴于点A(0，4)，交x 轴于点B，
直线l 垂直平分OB 交AB 于点D，交x 轴于点E，点P 是直线l 上一点，且在点D 的上方，PD=4．
（1）求点P 的坐标；
（2）以PB 为直角边作等腰直角△PBQ，直接写出所有符合条件的点Q 的坐标．
3.如图，直线y=-2x+4 与x 轴、y 轴分别交于点A，B，点P 是
直线x=5 上的一个动点，点Q 是射线AB 上的一个动点，若△APQ 为等腰直角三角形，则点Q 的坐标为．
4.如图，直线l1：y=-x+10 与y 轴交于点A，与直线l2：y 1 x 2
交于点B，点C 是线段AB 上的一动点，过点C 作y 轴的平行线交直线l2 于点D，点P 是y 轴上一动点，且满足△CDP 是等腰直角三角形，则点P 的坐标为．
【参考答案】
1. (2，5)，(5，3)，( 5
，
5
)．
2 2
2. （1）点P 的坐标为(2，6)；
（2）点Q 的坐标为(-4，4)，(8，8)，(-2，-2) 或(10，2)．
3. ( 1
，3)，(-4，12)，(-1，6)；
2
4. (0，6)，(0，2)，(0，30
)．7。

( 带答等腰三角形存在性问题等腰三角形存在性问题（两圆一线）类型一、格点中的等腰三角形1、在如图所示的5×5方格中，每个小方格都是边长为 1 的正方形，△ ABC 是格点三角形（即顶点恰好是正方形的顶点），则与△ ABC 有一条公共边且全等的所有格点三角形的个数是（）2、. 如图，在正方形网格的格点（即最小正方形的顶点）中找一点C，使得△ ABC是等腰三角形，且AB为其中一腰．这样的C 点有（）个．3、如图，A、B 是网格中的两个格点，点C也是网格中的一个格点，连接AB、BC、AC，当△ ABC为等腰三角形时，格点 C 的不同位置有处，设网格中的每个小正方形的边长为1，则所有满足题意的等腰三角形ABC的面积之和等于．4、如图，在图中能画出与△ ABC全等的格点三角形有几个？类型二、定边几何法讨论：两圆一线5、以线段AB为一边的等腰直角三角形有个，请在下列图中画出来6、（1）如图所示，线段OD的一个端点O在直线AB 上，以OD为一边的等腰三角形ODP，并且使点P 也在AB上，这样的等腰三角形能画个（在图中作出点P）2）若∠ DOB=6°0 ，其它条件不变，则这样的等腰三角形能画个，（只写出结果）（3）若改变（2）中∠ DOB的度数，其他条件不变，则等腰三角形ODP的个数和（2）中的结果相同，则改变后∠DOB= ．7、如图，南北向的公路上有一点A，东西向的公路上有一点B，若要在南北向的公路上确定点P，使得△ PAB是等腰三角形，则这样的点P 最多能确定（）个．8、线段AB和直线l 在同一平面上．则下列判断可能成立的有个直线l 上恰好只有个 1 点P，使△ ABP为等腰三角形直线l 上恰好只有个 2 点P，使△ ABP为等腰三角形直线l 上恰好只有个 3 点P，使△ ABP为等腰三角形直线l 上恰好只有个 4 点P，使△ ABP为等腰三角形直线l 上恰好只有个 5 点P，使△ ABP为等腰三角形直线l 上恰好只有个 6 点P，使△ ABP为等腰三角形．9、如图AOB, 当AOB为30 ，60 ，120 时，请在射线OA上找点P，使POB为等腰三角形，并分析出当AOB发生变化时，点P 个数的情况；类型三、三角形、长方形和正方形中的等腰三角形10、如图，在长方形ABCD中，AB=4，AD=10，点Q是BC的中点，点P在AD边上运动，若△ BPQ是腰长为 5 的等腰三角形，则满足题意的点P有( )个11、如图所示，在长方形ABCD的对称轴上找一点P，使得△PAB，△PBC均为等腰三角形，则满足条件的点P有( ) 个12、如图，边长为 6 的正方形ABCD内部有一点P，BP=4，∠PBC=60°，点Q为正方形边上一动点，且△ PBQ是等腰三角形，则符合条件的Q点有个．13、在等边△ ABC所在的平面内求一点P，使△ PAB，△PBC，△PAC都是等腰三角形，请画出所有满足条件的点；等腰三角形存在性问题（两圆一线）答案类型一、格点中的等腰三角形1、在如图所示的5×5方格中，每个小方格都是边长为 1 的正方形，△ ABC 是格点三角形（即顶点恰好是正方形的顶点），则与△ ABC 有一条公共边且全等的所有格点三角形的个数是（ 4 ）2、. 如图，在正方形网格的格点（即最小正方形的顶点）中找一点C，使得△ ABC是等腰三角形，且AB为其中一腰．这样的 C 点3、如图， A 、B 是网格中的两个格点，点 C 也是网格中的一个格点，连接 AB 、BC 、AC ，当△ ABC 为等腰三角形时，格点 C 的不同位置有 3 处，设网格中的每个小正方形的边长 为 1，则所有满足题意的等腰三角形 ABC 的面积之和等于 15 ．∵网格中的每个小正方形的边长为 1， ∴ S △ABC= ×4×3=6，S△ABC ′=20﹣2×3﹣ =6.5 ，故答案分别为： 3；15．格点 C 的不同位置分别是： C 、C ′、C ″，S△A BC ″=2.54、如图，在图中能画出与△ ABC全等的格点三角形有几个？类型二、定边几何法讨论：两圆一线5、以线段AB为一边的等腰直角三角形有个，请在下列图中画出来6、（1）如图所示，线段OD的一个端点O在直线AB上，以OD为一边的等腰三角形ODP，并且使点P 也在AB 上，这样的等腰三角形能画 4 个（在图中作出点P）（2）若∠ DOB=6°0 ，其它条件不变，则这样的等腰三角形能画 2 个，（只写出结果）（3）若改变（2）中∠ DOB的度数，其他条件不变，则等腰三角形ODP的个数和（2）中的结果相同，则改变后∠ DOB= 907、如图，南北向的公路上有一点A，东西向的公路上有一点B，若要在南北向的公路上确定点P，使得△ PAB是等腰三角形，则这样的点P 最多能确定（）个．8、线段AB和直线l 在同一平面上．则下列判断可能成立的有5 个直线l 上恰好只有个1点P，使△ ABP为等腰三角形直线l 上恰好只有个2点P，使△ ABP为等腰三角形直线l 上恰好只有个3点P，使△ ABP为等腰三角形直线l 上恰好只有个4点P，使△ ABP为等腰三角形直线l 上恰好只有个5点P，使△ ABP为等腰三角形直线l 上恰好只有个6点P，使△ ABP为等腰三角形．9、如图AOB, 当AOB为30 ，60 ，120 时，请在射线OA上找点P，使POB为等腰三角形，并分析出当AOB发生变化时，点P 个数的情况；结论】当AOB为锐角，AOB 60 ，有三个点，当AOB= 60 ，只有一个点；当AOB 为钝角或直角，只有一个点；类型三、三角形、长方形和正方形中的等腰三角形10、如图，在长方形ABCD中，AB=4，AD=10，点Q是BC的中点，点P在AD边上运动，若△ BPQ是腰长为 5 的等腰三角形，则满足题意的点P有( B )A.2 个B.3 个C.4 个D.5 个11、如图所示，在长方形ABCD的对称轴上找一点P，使得△PAB，△PBC均为等腰三角形，则满足条件的点P 有( C ) A.1 个 B.3 个 C.5 个 D. 无数多个12、如图，边长为 6 的正方形ABCD内部有一点P，BP=4，∠PBC=60°，点Q为正方形边上一动点，且△ PBQ是等腰三角形，则符合条件的Q点有个．13、在等边△ ABC所在的平面内求一点P，使△ PAB，△PBC，△PAC都是等腰三角形，请画出所有满足条件的点；。

专题02反比例函数与特殊三角形存在性问题类型一、等腰三角形存在性问题(1)求双曲线的解析式；(2)求点E B F ，，的坐标：(3)若点P 为x 轴上一动点，使得标【答案】(1)()20=>y x x∴(,0)A a ，(0,)C b ，OA =∵F E 、分别是AB BC 、边中点，∴11,22AF b CE a ==，F ⎛ ⎝∴1124AOF S AF OA ab == △∵(1,2)E ，5OE =，∴点G 的横坐标为10122+=在Rt ,Rt OGM OCE △△中，∵GOM COE ∠=∠，OGM ∠∴OGM OCE △∽△，OG OC∴(2,1)E ，11,2G ⎛⎫ ⎪⎝⎭，OE 在Rt ,Rt OGM OCE △△中，∵GOM COE ∠=∠，OGM ∠∴OGM OCE △∽△，∴OG OC OM OE =，1OC =，OE(1)试说明反比例函数ky x=的图象也经过点B ；(2)如图2，正方形ABCD 向下平移得到正方形MNPQ ，边MN 在x 轴上，反比例函数图象分别交正方形MNPQ 的边PQ 、PN 于点E 、F ．①求MEF 的面积；②在x 轴上是否存在一点G ，使得GEF △是等腰三角形，若存在，直接写出点G②点F 、E 的坐标分别为：()3,1、3,22⎛⎫⎪⎝⎭，设点(),0G m ，则222313(3)(21)24EF =-+-=，2(FG m =当EF EG =时，即213(3)14m =-+，解得：92m =或32，当9m =时，点E 、F 、G 三点共线，故舍去，3m ∴=(1)求k 的值．(2)将正方形OABC 分别沿直线AB BC ，翻折，得到正方形【点睛】本题考查正方形的性质，轴对称的性质，待定系数法求解析式，等腰三角形性质，两点距离求解；坐标系内灵活运用轴对称性质求解点坐标是解题的关键．【变式训练3】．如图，一次函数y ax b =+的图象与反比例函数点，与x 轴交于点C ，与y 轴交于点D ，已知点A 坐标为(1)求反比例函数的解析式和一次函数的解析式；(2)连接OA 、OB ，求AOB 的面积；(3)观察图象直接写出kax b x+>时x 的取值范围是；(4)直接写出：P 为x 轴上一动点，当三角形OAP 为等腰三角形时点【答案】(1)3y x=，1122y x =-；(2)54AOB S =(1,0)C ∴，111122AOB AOC BOC S S S ∴=+=⨯⨯+ （3）解：由图象得：kax b x+>（4）解：当AOP ∆是等腰三角形时，存在以下三种情况：①当OA OP =时，如图2，(3,1)A ，10OA ∴=，1(10P ∴-②当OA AP =时，如图3，(6,0)P ∴；③当OP AP =时，如图4，过A 作AE 设OP x =，则AP x =，3PE x =-，AP ∴2221(3)x x ∴+-=，53x =，5(3P ∴，0)综上，P 的坐标为()10,0或()10,0-，【点睛】本题考查了反比例函数与一次函数的综合问题，数与一次函数的解析式，等腰三角形的判定，三角形面积公式，本题难度适中，并运用了分类讨论的思想解决问题．类型二、直角三角形存在性问题(1)求m和k的值；(2)x轴上是否存在一点请说明理由．m=，【答案】(1)2(2)存在，()50，或(5(1)求反比例函数的解析式；(2)连接EF、OE、OF，求OEF的面积；(3)是否存在x轴上的一点P，使得EFP△是不以点P为直角顶点的直角三角形？若存在，请求出符合题意的点P的坐标；若不存在，请说明理由．【答案】(1)12yx=；(2)452(3)155,0 8P⎛⎫⎪，25,0 2P⎛⎫- ⎪8OA =Q ，8x ∴=时，32y =，38,2F ⎛⎫∴ ⎪⎝⎭，即，32AF =，39622BF =-=，设所求点P 坐标为(,0)a ，38,2F ⎛⎫⎪⎝⎭，(2,6)E ，()222322582624EF ⎛⎫∴-+- ⎪⎝⎭==()()22222064EP a a a -+--==(1)若4BC=，求点E的坐标；(2)连接AE，OE．①若AOE△的面积为24，求k的值；②是否存在某一位置使得AE OA⊥【答案】(1)4 6,3 E⎛⎫ ⎪⎝⎭(2)①18；②不存在，理由见解析(1)求a ，b 的值及反比例函数的解析式；(2)若1OD =，求点C 的坐标，判断四边形ABCD 的形状并说明理由；(3)若点M 是反比例函数(0)k y x x=>图象上的一个动点，当（3）①当90MAD ∠=︒∴56n =，则 1.2n =，()5,1.2M ∴，②当90AMD ∠= 时，由图得()3,M n n +∴()(36n n +=，解得：12333333,22n n -+--==(舍去)(M ∴3332+，3332-+)333333设点3,2Q a a ⎛⎫- ⎪⎝⎭，则2PQ a =+∵45PAQ ∠=︒∴AQ 平分PAO ∠．∴322a a +=-，解得45a =-3346a ⎛⎫-=-⨯-=∵AQ 平分PAO ∠，∴322a a -=+，∴45a =-∴33462255a ⎛⎫-=-⨯-=⎪⎝⎭∴361222PA a ⎛⎫=⨯-=⨯=⎪∴2AQ AP ==，∴2PA =，∴()2,2P -，综上所述，存在点P 使得APQ △【点睛】本题主要考查了待定系数法求反比例函数的解析式，的性质，解题的关键是分三种情况求出点(1)求反比例函数ky x=的表达式及E 点坐标；(2)如图2，连接DE ，AC ，试判断DE 与AC 的数量和位置关系，并说明理由；(3)如图3，连接AE ，在反比例函数ky x=的图象上是否存在点F ，使得AEF ∠=在，请求出点F 的坐标；若不存在，说明理由．【答案】(1)反比例函数的表达式为12y x=，点E 坐标为()6,2作AG AE ⊥，且使AG AE =点E 作EN y ⊥轴于点N ，易得∴6AM NE AB ===，MG ∴点G 坐标为()1,9将()6,2E 和()1,9G 代入直线7k ⎧=-(1)=a，b=；设点()0N m ，（其中0m >），则90MCN ∠=︒Q ，90MCF NCE ∴∠+∠=︒．NE l ⊥ 于点E ，90CMN ∠=︒ ，90CME NMG ∴∠+∠=︒ME l ⊥ 于点E ，。

《二次函数专题提优》：特殊三角形存在性问题（一）、直角三角形存在性问题：1、在平面直角坐标系x O y 中，抛物线y =ax 2+bx +2过点A （-2，0），B （2，2），与y 轴交于点C ． （1）、求抛物线y =ax 2+bx +2的函数表达式；（2）、若点D 在抛物线y =ax 2+bx +2的对称轴上，求△ACD 的周长的最小值；（3）、在抛物线y =ax 2+bx +2的对称轴上是否存在点P ，使△ACP 是直角三角形？若存在直接写出点P 的坐标，若不存在，请说明理由．2、如图，在矩形OABC 中，点O 为原点，点A 的坐标为（0，8），点C 的坐标为（6，0）．抛物线y ＝﹣94x 2+bx +c 经过点A 、C ，与AB 交于点D ． （1）、求抛物线的函数解析式；（2）、点P 为线段BC 上一个动点（不与点C 重合），点Q 为线段AC 上一个动点，AQ ＝CP ，连接PQ ，设CP ＝m ，△CPQ 的面积为S ．①、求S 关于m 的函数表达式； ②、当S 最大时，在抛物线y ＝﹣94x 2+bx +c 的对称轴l 上，若存在点F ，使△DFQ 为直角三角形， 请直接写出所有符合条件的点F 的坐标；若不存在，请说明理由．3、如图所示，直线y=x+2与抛物线y=ax 2+bx+6（a ≠0）相交于A （21，25）和B （4，m ），点P 是线段AB 上异于A 、B 的动点，过点P 作PC ⊥x 轴于点D ，交抛物线于点C ． （1）、求抛物线的解析式；（2）、是否存在这样的P 点，使线段PC 的长有最大值？若存在，求出这个最大值；若不存在，请说明理由； （3）、求△PAC 为直角三角形时点P 的坐标．4、如图，已知一条直线过点（0，4），且与抛物线2x 41y 交于A ，B 两点，其中点A 的横坐标是﹣2． （1）、求这条直线的函数关系式及点B 的坐标；（2）、在x 轴上是否存在点C ，使得△ABC 是直角三角形？若存在，求出点C 的坐标，若不存在，请说明理由； （3）、过线段AB 上一点P ，作PM ∥x 轴，交抛物线于点M ，点M 在第一象限，点N （0，1），当点M 的横坐标为何值时，MN +3MP 的长度最大？最大值是多少？（二）、等腰三角形存在性问题：5、如图所示，已知抛物线y=ax2+bx+c与x轴的一个交点为A（3，0），与y轴的交点为B（0，3），其顶点为C，对称轴为x=1．（1）、求抛物线的解析式；（2）、已知点M为y轴上的一个动点，当△ABM为等腰三角形时，求点M的坐标；（3）、将△AOB沿x轴向右平移m个单位长度（0＜m＜3）得到另一个三角形，将所得的三角形与△ABC重叠部分的面积记为S，用m的代数式表示S．6、如图所示，在平面直角坐标系中，已知点C（0，4），点A、B在x轴上，并且OA＝OC＝4OB，动点P在过A、B、C三点的抛物线上．（1）、求抛物线的函数表达式；（2）、在直线AC上方的抛物线上，是否存在点P，使得△PAC的面积最大？若存在，求出P点坐标及△PAC面积的最大值；若不存在，请说明理由．（3）、在x轴上是否存在点Q，使得△ACQ是等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．7、如图，在平面直角坐标系中，已知点C（0，4），点A、B在x轴上，并且OA＝OC＝4OB，动点P在过A、B、C三点的抛物线上．（1）、求抛物线的函数表达式；（2）、在直线AC上方的抛物线上，是否存在点P，使得△PAC的面积最大？若存在，求出P点坐标及△PAC面积的最大值；若不存在，请说明理由．（3）、在x轴上是否存在点Q，使得△ACQ是等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．8、已知抛物线y=ax²+bx+c经过A（-1，0）、B（3，0）、C（0，3）三点，直线l是抛物线的对称轴．（1）、求抛物线的函数关系式；（2）、设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；（3）、在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．9、如图1，抛物线与4x 31x 31-y 2++=与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ， 连接AC 、BC ，点D 是线段AB 上一点，且AD ＝CA ，连接CD ．（1）、如图2，点P 是直线BC 上方抛物线上的一动点，在线段BC 上有一动点Q ，连接PC 、PD 、PQ ，当△PCD 面积最大时，求PQ +1010CQ 的最小值； （2）、将过点D 的直线绕点D 旋转，设旋转中的直线l 分别与直线AC 、直线CO 交于点M 、N ，当△CMN 为等腰三角形时，直接写出CM 的长．10、如图，在平面直角坐标系中，抛物线y =√33x 2-2√33x -√3与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，对称轴与x 轴交于点D ，点E （4，n ）在抛物线上． （1）求直线AE 的解析式；（2）点P 为直线CE 下方抛物线上的一点，连接PC ，PE ．当△PCE 的面积最大时，连接CD ，CB ，点K 是线段CB 的中点，点M 是CP 上的一点，点N 是CD 上的一点，求KM+MN+NK 的最小值； （3）点G 是线段CE 的中点，将抛物线y =√33x 2-2√33x -√3沿x 轴正方向平移得到新抛物线y ′，y ′经过点D ，y ′的顶点为点F ．在新抛物线y ′的对称轴上，是否存在一点Q ，使得△FGQ 为等腰三角形？若存在，直接写出点Q 的坐标；若不存在，请说明理由．10、如图，已知二次函数y＝ax2﹣6ax﹣16a（a＜0）的图象与y轴交于点A，与x轴交于B、C两点，其对称轴与x轴交于点D，连接AC．（1）、①线段BC的长为；②点A的坐标为（用a的代数式表示）．（2）、设M是抛物线的对称轴上的一点，以点A、C、M为顶点的三角形能否成为以AC为斜边且有一个锐角是30°的直角三角形？若能，求出a的值；若不能，请说明理由．（3）、若a＝﹣，点P为x轴上方的抛物线上的一个动点，连接PA、PC，若所得△PAC的面积为S，则S取何值时，相应的点P有且只有2个？（三）、等腰直角三角形的存在性问题：11、如图,抛物线bxaxy+=2经过A(4,0),B(1,3)两点，点B. C关于抛物线的对称轴l对称，过点B作直线BH⊥x轴，交x轴于点H.(1)、求抛物线的解析式；(2)、若点M在直线BH上运动，点N在x轴上运动，是否存在这样的点M、N，使得以点M为直角顶点的△CNM是等腰直角三角形?若存在，请求出点M、N的坐标；若不存在，请说明理由。

等腰三角形的存在性问题【考题研究】近几年各地的中考数学试题中，探索等腰三角形的存在性问题频频出现，这类试题的知识覆盖面较广，综合性较强，题意构思精巧，要求学生要有较高的分析问题的能力和解决问题的能力，这类问题符合课标对学生能力提高的要求。

【解题攻略】在讨论等腰三角形的存在性问题时，一般都要先分类．如果△ABC是等腰三角形，那么存在①AB＝AC，②BA＝BC，③CA＝CB三种情况．解等腰三角形的存在性问题，有几何法和代数法，把几何法和代数法相结合，可以使得解题又好又快．几何法一般分三步：分类、画图、计算．哪些题目适合用几何法呢？如果△ABC的∠A（的余弦值）是确定的，夹∠A的两边AB和AC可以用含x的式子表示出来，那么就用几何法．①如图1，如果AB＝AC，直接列方程；②如图2，如果BA＝BC，那么；③如图3，如果CA＝CB，那么．代数法一般也分三步：罗列三边长，分类列方程，解方程并检验．如果三角形的三个角都是不确定的，而三个顶点的坐标可以用含x的式子表示出来，那么根据两点间的距离公式，三边长（的平方）就可以罗列出来．【解题类型及其思路】解题类型：动态类型：1.一动点类型问题；2.双动点或多动点类型问题背景类型：1.几何图形背景；2.平面直角坐标系和几何图形背景解题思路：几何法一般分三步：分类、画图、计算；代数法一般也分三步：罗列三边长，分类列方程，解方程并检验．如果△ABC是等腰三角形，那么存在①AB＝AC，②BA＝BC，③CA＝CB三种情况．已知腰长画等腰三角形用圆规画圆，已知底边画等腰三角形用刻度尺画垂直平分线．解等腰三角形的存在性问题，有几何法和代数法，把几何法和代数法相结合，可以使得解题又好又快．【典例指引】类型一【二次函数综合题中根据条件判定三角形的形状】典例指引1．抛物线2y x bx c =++与x 轴交于点A ，点B （1，0），与y 轴交于点C （0，﹣3），点M 是其顶点． （1）求抛物线解析式；（2）第一象限抛物线上有一点D,满足∠DAB=45°,求点D 的坐标；（3）直线x t = (﹣3＜t ＜﹣1)与x 轴相交于点H ．与线段AC ，AM 和抛物线分别相交于点E ，F ，P ．证明线段HE ，EF ，FP 总能组成等腰三角形.【举一反三】（2020·江西初三期中）如图①，已知抛物线y=ax 2+bx+3（a≠0）与x 轴交于点A （1，0）和点B （-3，0），与y 轴交于点C ．（1）求抛物线的解析式；（2）设抛物线的对称轴与x 轴交于点M ，问在对称轴上是否存在点P ，使△CMP 为等腰三角形？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由；（3）如图②，若点E 为第二象限抛物线上一动点，连接BE 、CE ，求四边形BOCE 面积的最大值，并求此时E 点的坐标．类型二【利用二次函数的性质与等腰三角形的性质确定点的坐标】典例指引2．（2019·山东初三期末）如图1，已知抛物线2()30y ax bx a =++≠与x 轴交于点(1,0)A 和点(3,0)B -，与y 轴交于点C .（l ）求抛物线的表达式；（2）如图l ，若点E 为第二象限抛物线上一动点，连接,BE CE ，求四边形BOCE 面积的最大值，并求此时E 点的坐标；（3）如图2，在x 轴上是否存在一点D 使得ACD ∆为等腰三角形？若存在，请求出所有符合条件的点D 的坐标；若不存在，请说明理由.【举一反三】（2019·广东省中山市中山纪念中学三鑫双语学校初三期中）如图，已知抛物线y ＝ax 2+bx +c 的图象与x 轴交于A （2，0），B （﹣8，0）两点，与y 轴交于点C （0，﹣8）．（1）求抛物线的解析式；（2）点F是直线BC下方抛物线上的一点，当△BCF的面积最大时，求出点F的坐标；（3）在（2）的条件下，是否存在这样的点Q（0，m），使得△BFQ为等腰三角形？如果有，请直接写出点Q的坐标；如果没有，请说明理由．类型三【确定满足等腰三角形的动点的运动时间】典例指引3．（2018济南中考）如图1，抛物线平移后过点A（8，,0）和原点，顶点为B，对称轴与轴相交于点C，与原抛物线相交于点D．（1）求平移后抛物线的解析式并直接写出阴影部分的面积；（2）如图2，直线AB与轴相交于点P，点M为线段OA上一动点，为直角，边MN与AP相交于点N，设，试探求：①为何值时为等腰三角形；②为何值时线段PN的长度最小，最小长度是多少．【举一反三】如图所示，抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0）、B（3，0）、C（0，3）三点．点D从C出发，沿线段CO以1个单位/秒的速度向终点O运动，过点D作OC的垂线交BC于点E，作EF∥OC，交抛物线于点F．（1）求此抛物线的解析式；（2）小明在探究点D运动时发现，①当点D与点C重合时，EF长度可看作O；②当点D与点O重合时，EF长度也可以看作O，于是他猜想：设点D运动到OC中点位置时，当线段EF最长，你认为他猜想是否正确，为什么？（3）连接CF、DF，请直接写出△CDF为等腰三角形时所有t的值．【新题训练】1．（2020·江西初三）如图，在平面直角坐标系中，已知点A(﹣2，﹣4)，直线x=﹣2与x轴相交于点B，连接OA，抛物线y=﹣x2从点O沿OA方向平移，与直线x=﹣2交于点P，顶点M到点A时停止移动．（1）线段OA 所在直线的函数解析式是 ；（2）设平移后抛物线的顶点M 的横坐标为m ，问：当m 为何值时，线段PA 最长？并求出此时PA 的长． （3）若平移后抛物线交y 轴于点Q ，是否存在点Q 使得△OMQ 为等腰三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由．2．（2018·山东中考真题）如图，在平面直角坐标系中，二次函数2y ax bx c =++交x 轴于点()4,0A -、()2,0B ，交y 轴于点()0,6C ，在y 轴上有一点()0,2E -，连接AE .（1）求二次函数的表达式；（2）若点D 为抛物线在x 轴负半轴上方的一个动点，求ADE ∆面积的最大值；（3）抛物线对称轴上是否存在点P ，使AEP ∆为等腰三角形，若存在，请直接写出所有P 点的坐标，若不存在请说明理由.3．（2016·广西中考真题）在平面直角坐标系中，抛物线223y x x =--+与x 轴交于A ，B 两点（A 在B的左侧），与y 轴交于点C ，顶点为D ． （1）请直接写出点A ，C ，D 的坐标；（2）如图（1），在x 轴上找一点E ，使得△CDE 的周长最小，求点E 的坐标；（3）如图（2），F 为直线AC 上的动点，在抛物线上是否存在点P ，使得△AFP 为等腰直角三角形？若存在，求出点P的坐标，若不存在，请说明理由．4．（2019·广东广州市第二中学初三）如图（1），在平面直角坐标系中，矩形ABCO，B点坐标为（4，3），抛物线y＝12-x2＋bx＋c经过矩形ABCO的顶点B、C，D为BC的中点，直线AD与y轴交于E点，与抛物线y＝12-x2＋bx＋c交于第四象限的F点．（1）求该抛物线解析式与F点坐标；（2）如图，动点P从点C出发，沿线段CB以每秒1个单位长度的速度向终点B运动；同时，动点M从点A出发，沿线段AE 13个单位长度的速度向终点E运动．过点P作PH⊥OA，垂足为H，连接MP，MH．设点P的运动时间为t秒．①问EP＋PH＋HF是否有最小值，如果有，求出t的值；如果没有，请说明理由．②若△PMH是等腰三角形，求出此时t的值．5．（2019·湖南中考模拟）如图，关于x的二次函数y=x2+bx+c的图象与x轴交于点A（1，0）和点B与y 轴交于点C（0，3），抛物线的对称轴与x轴交于点D．（1）求二次函数的表达式；（2）在y轴上是否存在一点P，使△PBC为等腰三角形？若存在．请求出点P的坐标；（3）有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N从点D与点M 同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积．6．（2018·山东中考模拟）如图，抛物线y=﹣x2+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．（1）求抛物线的表达式；（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；（3）点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．7．（2019·山东中考模拟）已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C （﹣2，0），点P是线段AB上方抛物线上的一个动点．（1）求抛物线的解析式；（2）当点P运动到什么位置时，△PAB的面积有最大值？（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P 使△PDE 为等腰直角三角形？若存在，求出点P 的坐标；若不存在，说明理由．8．（2018·广东中考模拟）如图，在平面直角坐标系xOy 中，二次函数24y ax bx =+-（0a ≠）的图象与x 轴交于A （﹣2，0）、B （8，0）两点，与y 轴交于点B ，其对称轴与x 轴交于点D ．（1）求该二次函数的解析式；（2）如图1，连结BC ，在线段BC 上是否存在点E ，使得△CDE 为等腰三角形？若存在，求出所有符合条件的点E 的坐标；若不存在，请说明理由；（3）如图2，若点P （m ，n ）是该二次函数图象上的一个动点（其中m ＞0，n ＜0），连结PB ，PD ，BD ，求△BDP 面积的最大值及此时点P 的坐标．9．（2019·四川中考模拟）如图，已知二次函数y ＝﹣x 2+bx+c （c ＞0）的图象与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，且OB ＝OC ＝3，顶点为M ．（1）求二次函数的解析式；（2）点P 为线段BM 上的一个动点，过点P 作x 轴的垂线PQ ，垂足为Q ，若OQ ＝m ，四边形ACPQ 的面积为S ，求S 关于m 的函数解析式，并写出m 的取值范围；（3）探索：线段BM 上是否存在点N ，使△NMC 为等腰三角形？如果存在，求出点N 的坐标；如果不存在，请说明理由．10．（2019·甘肃中考模拟）如图，已知二次函数y=ax 2+bx+c 的图象与x 轴相交于A （﹣1，0），B （3，0）两点，与y 轴相交于点C （0，﹣3）． （1）求这个二次函数的表达式；（2）若P 是第四象限内这个二次函数的图象上任意一点，PH ⊥x 轴于点H ，与BC 交于点M ，连接PC ． ①求线段PM 的最大值；②当△PCM 是以PM 为一腰的等腰三角形时，求点P 的坐标．11．（2019·安徽中考模拟）如图，已知直线1y x =+与抛物线2y ax 2x c =++相交于点()1,0A -和点()2,B m 两点.（1）求抛物线的函数表达式；（2）若点P 是位于直线AB 上方抛物线上的一动点，当PAB ∆的面积S 最大时，求此时PAB ∆的面积S 及点P 的坐标；（3）在x 轴上是否存在点Q ，使QAB ∆是等腰三角形？若存在，直接写出Q 点的坐标（不用说理）；若不存在，请说明理由.12．（2018·江苏中考模拟）（2017南宁，第26题，10分）如图，已知抛物线2239y ax ax a =--与坐标轴交于A ，B ，C 三点，其中C （0，3），∠BAC 的平分线AE 交y 轴于点D ，交BC 于点E ，过点D 的直线l 与射线AC ，AB 分别交于点M ，N ．（1）直接写出a的值、点A的坐标及抛物线的对称轴；（2）点P为抛物线的对称轴上一动点，若△PAD为等腰三角形，求出点P的坐标；（3）证明：当直线l绕点D旋转时，11AM AN均为定值，并求出该定值．13．（2019·重庆中考模拟）如图，在平面直角坐标系中，一抛物线的对称轴为直线，与y轴负半轴交于C点，与x轴交于A、B两点，其中B点的坐标为（3，0），且OB＝OC．（1）求此抛物线的解析式；（2）若点G（2，y）是该抛物线上一点，点P是直线AG下方的抛物线上一动点，当点P运动到什么位置时，△APG的面积最大？求出此时P点的坐标和△APG的最大面积.（3）若平行于x轴的直线与该抛物线交于M、N两点（其中点M在点N的右侧），在x轴上是否存在点Q，使△MNQ为等腰直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．14．（2019·辽宁中考模拟）抛物线y＝ax2+bx﹣3（a≠0）与直线y＝kx+c（k≠0）相交于A（﹣1，0）、B（2，﹣3）两点，且抛物线与y轴交于点C．（1）求抛物线的解析式；（2）求出C、D两点的坐标（3）在第四象限抛物线上有一点P，若△PCD是以CD为底边的等腰三角形，求出点P的坐标．15．（2020·浙江初三期末）如图，抛物线y＝﹣12x2+2x+6交x轴于A，B两点（点A在点B的右侧），交y轴于点C，顶点为D，对称轴分別交x轴、线段AC于点E、F．（1）求抛物线的对称轴及点A的坐标；（2）连结AD，CD，求△ACD的面积；（3）设动点P从点D出发，沿线段DE匀速向终点E运动，取△ACD一边的两端点和点P，若以这三点为顶点的三角形是等腰三角形，且P为顶角顶点，求所有满足条件的点P的坐标．16．（2020·湖北初三期末）如图，已知二次函数的图象经过点A（4，4），B（5，0）和原点O，P为二次函数图象上的一个动点，过点P作x轴的垂线，垂足为D（m，0），并与直线OA相较于点C．（1）求出二次函数的解析式；（2）当点P在直线OA的上方时，求线段PC的最大值；（3）当点P在直线OA的上方时，是否存在一点P，使射线OP平分∠AOy，若存在，请求出P点坐标；若不存在．请说明理由；（4）当m＞0时，探索是否存在点P，使得△PCO为等腰三角形，若存在，求出P点的坐标；若不存在，请说明理由．17．（2019·吉林初三）如图1，抛物线与y ＝﹣211433x x ++与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，连接AC 、BC ，点D 是线段AB 上一点，且AD ＝CA ，连接CD ．（1）如图2，点P 是直线BC 上方抛物线上的一动点，在线段BC 上有一动点Q ，连接PC 、PD 、PQ ，当△PCD 面积最大时，求PQ +10CQ 的最小值； （2）将过点D 的直线绕点D 旋转，设旋转中的直线l 分别与直线AC 、直线CO 交于点M 、N ，当△CMN 为等腰三角形时，直接写出CM 的长．18．（2020·江苏初三期末）在平面直角坐标系xOy 中，抛物线2y x mx n =-++与x 轴交于点A,B ( A 在B的左侧)(1)如图1，若抛物线的对称轴为直线3,4x AB =-= .①点A 的坐标为( ， )，点B 的坐标为( ， ); ②求抛物线的函数表达式;(2)如图2，将(1)中的抛物线向右平移若干个单位，再向下平移若干个单位，使平移后的抛物线经过点O ，且与x 正半轴交于点C ，记平移后的抛物线顶点为P ，若OCP ∆是等腰直角三角形，求点P 的坐标.等腰三角形的存在性问题【考题研究】近几年各地的中考数学试题中，探索等腰三角形的存在性问题频频出现，这类试题的知识覆盖面较广，综合性较强，题意构思精巧，要求学生要有较高的分析问题的能力和解决问题的能力，这类问题符合课标对学生能力提高的要求。

专题2.6二次函数与特殊三角形存在性综合问题（三大题型）【题型1等腰三角形的存在性问题】【题型2直角三角形的存在性问题】【题型3等腰直角三角形存在性问题】等腰三角形的存在性问题【方法1几何法】“两圆一线”（1）以点A 为圆心，AB 为半径作圆，与x 轴的交点即为满足条件的点C，有AB=AC；（2）以点B 为圆心，AB 为半径作圆，与x 轴的交点即为满足条件的点C，有BA=BC；（3）作AB 的垂直平分线，与x 轴的交点即为满足条件的点C，有CA=CB．注意：若有重合的情况，则需排除．以点C 1为例，具体求点坐标：过点A 作AH⊥x 轴交x 轴于点H，则AH=1，又32121131311==-=∴=HC AC ，()03211，坐标为故点-C 类似可求点C 2、C 3、C 4．关于点C 5考虑另一种方法．【方法2代数法】点-线-方程表示点：设点C 5坐标为(m ,0)，又A （1,1）、B （4,3），表示线段：11-m 225+=）（AC 94-m 225+=）（BC 联立方程：914-m 1-m 22+=+）（）（，623m =解得：，），坐标为（故点06232C 直角三角形的存在性【方法1几何法】“两线一圆”（1）若∠A 为直角，过点A 作AB 的垂线，与x 轴的交点即为所求点C ；（2）若∠B 为直角，过点B 作AB 的垂线，与x 轴的交点即为所求点C ；（3）若∠C 为直角，以AB 为直径作圆，与x 轴的交点即为所求点C ．（直径所对的圆周角为直角）如何求得点坐标？以C2为例：构造三垂直．），坐标为（故代入得：坐标得、由易证0213232222C C C BN AM B A N MB BN AM BN AMB ===∆≈∆()），坐标为（，，坐标为故或故又即代入得：，设，坐标得、由易证求法相同，如下：、040231a ,4a ,3ab ,3a b 1N a,31,4333333343C C C C C C C CCC b bM BN AM B A NB M N AM NB AM ==+=======∆≈∆【方法2代数法】点-线-方程23m 20352235110,m 135-m 1-m 35-m 11-m 22222122111=+=+=+=+==，解得：）代入得方程（，，，）表示线段：（）；，（）、，（），又坐标为（）表示点：设（：不妨来求下）（）（）（）（BC C C C A AB B A 【题型1等腰三角形的存在性问题】【典例1】（2023•兴庆区校级模拟）如图，已经抛物线经过点O （0，0），A （5，5），且它的对称轴为x ＝2．（1）求此抛物线的解析式；（2）若点B 是x 轴上的一点，且△OAB 为等腰三角形，请直接写出B 点坐标．【变式1-1】（2023•青海）如图，二次函数y＝﹣x2+bx+c的图象与x轴相交于点A和点C（1，0），交y轴于点B（0，3）．（1）求此二次函数的解析式；（2）设二次函数图象的顶点为P，对称轴与x轴交于点Q，求四边形AOBP 的面积（请在图1中探索）；（3）二次函数图象的对称轴上是否存在点M，使得△AMB是以AB为底边的等腰三角形？若存在，请求出满足条件的点M的坐标；若不存在，请说明理由（请在图2中探索）．【变式1-2】（2022秋•亳州期末）如图，关于x的二次函数y＝x2+bx+c的图象与x轴交于点A（1，0）和点B，与y轴交于点C（0，3），抛物线的对称轴与x轴交于点D．（1）求二次函数的表达式；（2）在y轴上是否存在一点P，使△PBC为等腰三角形？若存在．请求出点P的坐标；【变式1-3】（2023春•中山市期中）已知二次函数y＝ax2+bx﹣3a经过点A（﹣1，0）、C（0，3），与x轴交于另一点B，抛物线的顶点为D．（1）求此二次函数解析式；（2）连接DC、BC、DB，求证：△BCD是直角三角形；（3）在对称轴右侧的抛物线上是否存在点P，使得△PDC为等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由．【变式1-4】（2022秋•怀远县期末）如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（﹣1，0），B（4，0），C（0，﹣4）三点，点P是直线BC下方抛物线上一动点．（1）求这个二次函数的解析式；（2）是否存在点P，使△POC是以OC为底边的等腰三角形？若存在，求出P点坐标；若不存在，请说明理由；【变式1-5】（2023•兴宁区校级模拟）如图，抛物线y＝﹣x2+bx+c过点A（﹣1，0），B（3，0），与y轴交于点C．（1）求抛物线的解析式；（2）点P为抛物线对称轴上一动点，当△PCB是以BC为底边的等腰三角形时，求点P的坐标；【变式1-6】（2023•隆昌市校级三模）如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，点P的横坐标为m，过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．（1）求此抛物线的表达式：（2）过点P作PN⊥BC，垂足为点N，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？（3）试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由．【变式1-7】（2023春•沙坪坝区校级月考）如图，在平面直角坐标系中，二次函数y＝x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．（1）求这个二次函数的表达式；（2）求出四边形ABPC的面积最大时的P点坐标和四边形ABPC的最大面积；（3）在直线BC找一点Q，使得△QOC为等腰三角形，写出Q点坐标．【变式1-8】（2022秋•朔州期末）如图，已知抛物线y＝﹣+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（﹣2，0）．（1）求抛物线的解析式及它的对称轴方程；（2）求点C的坐标，连接AC、BC并求线段BC所在直线的解析式；（3）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．【变式1-9】（2022秋•港南区期末）如图，抛物线y＝ax2+3x+c（a≠0）与x轴交于点A（﹣2，0）和点B，与y轴交于点C（0，8），点P为直线BC上方抛物线上的动点，连接CP，PB，直线BC与抛物线的对称轴l交于点E．（1）求抛物线的解析式；（2）求△BCP的面积最大值；（3）点M是抛物线的对称轴l上一动点．是否存在点M，使得△BEM为等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．【题型2直角三角形的存在性问题】【典例2】（2022秋•云阳县期末）如图，抛物线y＝ax2+bx+c经过点A（﹣3，0），B（1，0），C（0，﹣3）．（1）求抛物线得解析式；（2）若点P为第三象限内抛物线上的一点，设△P AC的面积为S，求S的最大值并求此时点P的坐标．（3）设抛物线的顶点为D，DE⊥x轴于点E，在y轴上确定一点M，使得△ADM是直角三角形，写出所有符合条件的点M的坐标，并任选其中一个点的坐标，写出求解过程．【变式2-1】（2023春•兴宁区校级月考）如图1，在平面直角坐标系中，直线l1：y＝x+1与直线l2：x＝﹣2相交于点D，点A是直线l2上的动点，过点A 作AB⊥l1于点B，点C的坐标为（0，3），连接AC，BC．设点A的纵坐标为t，△ABC的面积为s．（1）当点B的坐标为时，直接写出t的值；（2）s关于t的函数解析式为，其图象如图2所示，结合图1、2的信息，求出a与b的值；（3）在l2上是否存在点A，使得△ABC是直角三角形？若存在，请求出此时点A的坐标和△ABC的面积；若不存在，请说明理由．【变式2-2】（2023•庄浪县三模）如图：已知二次函数y＝ax2+x+c的图象与x 轴交于A，B点，与y轴交于点C，其中B（2，0），C（0，4）．（1）求该抛物线的解析式；（2）P是第一象限抛物线的一个动点，当P点运动到何处时，由点P，B，C 构成的三角形的面积最大，求出此时P点的坐标；（3）若M是抛物线上的一个动点，当M运动到何处时，△MBC是以BC为直角边的直角三角形，求出此时点M的坐标．【变式2-3】（2023•喀喇沁旗一模）如图①，已知抛物线y＝﹣x2+bx+c与x轴交于点A、B（3，0），与y轴交于点C（0，3），直线l经过B、C两点．抛物线的顶点为D．（1）求抛物线和直线l的解析式；（2）判断△BCD的形状并说明理由．（3）如图②，若点E是线段BC上方的抛物线上的一个动点，过E点作EF ⊥x轴于点F，EF交线段BC于点G，当△ECG是直角三角形时，求点E的坐标．【变式2-4】（2023•铁岭模拟）如图，一次函数的图象与x轴交于点A，与y轴交于点B，二次函数y＝的图象与一次函数y＝﹣的图象交于B、C两点，与x轴交于D、E两点，且点D坐标为（﹣1，0）．（1）求二次函数的解析式；（2）求四边形BDEC的面积S；（3）在x轴上是否存在点P，使得△PBC是直角三角形？若存在，请直接写出所有满足条件的点P的坐标，若不存在，请说明理由．【变式2-5】（2023•怀化二模）如图，在平面直角坐标系中，一次函数的图象分别交x轴、y轴于点A、B，抛物线y＝x2+bx+c经过点A、B，E是线段OA的中点．（1）求抛物线的解析式；（2）点F是抛物线上的动点，当∠OEF＝∠BAE时，求点F的横坐标；（3）在抛物线上是否存在点P，使得△ABP是以点A为直角顶点的直角三角形，若存在，请求出P点坐标，若不存在，请说明理由；【变式2-6】（2023•金湾区一模）如题22图，抛物线y＝ax2+bx+3的对称轴为直线x＝2，并且经过点A（﹣2，0），交x轴于另一点B，交y轴于点C．（1）求抛物线的解析式；（2）在直线BC上方的抛物线上有一点P，求点P到直线BC距离的最大值及此时点P的坐标；（3）在直线BC下方的抛物线上是否存在点Q，使得△QBC为直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．【题型3等腰直角三角形存在性问题】【典例3】（2023•增城区校级一模）如图，在平面直角坐标系中，抛物线y＝ax2+bx ﹣3（a＞0）与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）点P为直线BC下方抛物线上的一动点，PM⊥BC于点M，PN∥y轴交BC于点N．求线段PM的最大值和此时点P的坐标；（3）点E为x轴上一动点，点Q为抛物线上一动点，是否存在以CQ为斜边的等腰直角三角形CEQ？若存在，请直接写出点E的坐标；若不存在，请说明理由．【变式3-1】（2023•抚远市二模）如图，抛物线y＝x2+bx+c与x轴相交于点A （﹣1，0）和点B（2，0）．（1）求抛物线的解析式；（2）在抛物线上有一点P，过点P作x轴的垂线交x轴于点Q，若△APQ是等腰直角三角形，求点P的坐标．【变式3-2】（2023•富锦市校级一模）如图，是抛物线y＝x2+bx+c与x轴相交于点A（﹣1，0）和点B（2，0）．（1）求抛物线的解析式；（2）在抛物线上有一点P，过点P作x轴的垂线交x轴于点Q，若△APQ是等腰直角三角形，求点P的坐标．【变式3-3】（2023•碑林区校级模拟）如图，已知抛物线y＝ax2+bx+3（a≠0）与x轴交于点A（﹣1，0）和点B（3，0），与y轴交于点C．（1）求该抛物线的解析式；（2）点M为该抛物线的对称轴l上一点，点P为该抛物线上的点且在l左侧，当△AMP是以M为直角顶点的等腰直角三角形时，求符合条件的点M的坐标．【变式3-4】（2023•西安一模）如图，在平面直角坐标系中，抛物线y＝ax2+bx ﹣1的顶点A的坐标为，与y轴交于点B．（1）求抛物线的函数表达式；（2）点P是抛物线上的动点，过点P作PM⊥x轴于点M，以PM为斜边作等腰直角三角形PMN，当点N恰好落在y轴上时，求点P的坐标．【变式3-5】（2023•惠民县自主招生）已知：如图，抛物线y＝ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．（1）求抛物线的解析式；（2）当点P运动到什么位置时，△P AB的面积有最大值？（3）过点P作x轴的垂线，交线段AB于点D，再过点P作PE∥x轴交抛物线于点E，连接DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．。

等腰三角形的性质与判定（人教版）试卷简介:本套试卷主要考查等腰三角形的判定及性质，等边对等角、等角对等边；三线合一等，以此为载体考查同学们几何学习的有序操作能力.一、单选题(共10道，每道10分)1.已知等腰三角形的一个内角为70°,则另两个内角的度数是( )A.55°,55°B.70°,40°C.55°,55°或70°,40°D.以上都不对答案：C解题思路：此题仅告诉我们等腰三角形的一个内角为70°，并没有确定是顶角还是底角，所以需分两种情况考虑.①当70°为顶角时，另外两个角是底角，度数相等，为（180°-70°）÷2=55°，②当70°为底角时，另外一个底角也是70°，顶角是180°-140°=40°．综上，另两个内角度数为55°，55°或70°，40°.故选C．试题难度：三颗星知识点：等腰三角形的性质2.一个等腰三角形的两边长分别为2和5,则它的周长为( )A.7B.9C.12D.9或12答案：C解题思路：求等腰三角形的周长，即是确定等腰三角形的腰与底的长，题目给出等腰三角形有两条边长为2和5，而没有明确腰、底分别是多少，所以要进行讨论，还需应用三角形的三边关系验证能否组成三角形．①若2为腰长，5为底边长，由于2+2<5，则三角形不存在；②若5为腰长，2为底边长，则符合三角形的两边之和大于第三边．所以这个三角形的周长为5+5+2=12．故选C试题难度：三颗星知识点：三角形的三边关系3.如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别是∠ABC,∠BCD的角平分线,则图中的等腰三角形有( )A.5个B.4个C.3个D.2个答案：A解题思路：∵AB=AC，∴△ABC是等腰三角形.∵AB=AC，∠A=36°，∴∠ABC=∠ACB=72°.∵BD，CE分别是∠ABC，∠BCD的角平分线，∴，，∴∠DBC=∠BCE，∠CED=∠DBC+∠BCE=36°+36°=72°，∠A=∠ABD，∠BDC=180°-∠DBC-∠BCD=180°-72°-36°=72°，∴△EBC，△ABD是等腰三角形；∵∠BDC=∠BCD，∠CED=∠CDE，∴△BCD，△CDE是等腰三角形，∴图中的等腰三角形有5个．故选A试题难度：三颗星知识点：等腰三角形的判定及性质4.如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,则下列五个结论:①AD上任意一点到AB,AC两边的距离相等;②AD上任意一点到B,C两点的距离相等;③AD⊥BC,且BD=CD;④∠BDE=∠CDF;⑤AE=AF.其中正确的有( )A.2个B.3个C.4个D.5个答案：D解题思路：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合（三线合一）；故AD所在直线可以看成△ABC的对称轴，再根据角平分线的性质、垂直平分线的性质可得①②③④⑤都正确.故选D试题难度：三颗星知识点：全等三角形的判定与性质5.如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③;④△ABD一定是正三角形.请写出正确结论的序号是( )A.①②B.①③C.②④D.①②③答案：B解题思路：①∵AB=AC=AD，AC平分∠DAB∴AC垂直平分BD，①正确；②由①可知DC=CB，DE=BE，∠DEC=90°，∴DC＞DE∴BC＞DE，②错误；③在Rt△BCE中，∠DBC=90°-∠ACB，在等腰△ABC中，∠BAC=180°-2∠ACB，即∠DAC=180°-2∠ACB，∴，③正确；④△ABD是等腰三角形，但不一定是等边三角形，而且根据题中条件也推导不出△ABD是等边三角形，④错误.正确的为①③，故选B试题难度：三颗星知识点：等腰三角形的判定与性质6.如图,在△ABC中,BC=9cm,BP,CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是( )A.6cmB.9cmC.10cmD.12cm答案：B解题思路：∵BP，CP分别是∠ABC和∠ACB的角平分线，∴∠ABP=∠PBD，∠ACP=∠PCE.∵PD∥AB，PE∥AC，∴∠ABP=∠BPD，∠ACP=∠CPE，∴∠PBD=∠BPD，∠PCE=∠CPE，∴BD=PD，CE=PE，∴PD+DE+PE=BD+DE+EC=BC=9，即△PDE的周长为9cm.故选B试题难度：三颗星知识点：等腰三角形的判定及性质7.如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠AOC=125°,则∠ABC的度数为( )A.60°B.65°C.70°D.75°答案：C解题思路：∵AD⊥BC，∠AOC=125°，∴∠C=∠AOC-∠ADC=125°-90°=35°，∵D为BC的中点，AD⊥BC，∴OB=OC，∴∠OBC=∠C=35°，∵BO平分∠ABC，∴∠ABC=2∠OBC=2×35°=70°．故选C试题难度：三颗星知识点：等腰三角形的性质8.如图,在等腰三角形ABC中,AB=AC=8,,点D为底边BC上一动点(不与点B,C重合),DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF的长为( )A.2B.3C.4D.5答案：C解题思路：连接AD，∵AB=AC=8，∴DE+DF=4.故选C试题难度：三颗星知识点：等腰三角形的性质9.如图,在3×3的网格中,每个网格线的交点称为格点.已知图中A,B两个格点,请在图中再寻找另一个格点C,使△ABC成为等腰三角形,则满足条件的点C有( )A.4个B.6个C.8个D.10个答案：C解题思路：已知A，B两个定点，再寻找点C使得△ABC为等腰三角形，可知需要利用“两圆一线”解题，即：分别以A，B为圆心，以AB的长为半径画圆；作线段AB的垂直平分线.再来判断点C 的个数.如图所示，图中的10个格点均在圆或垂直平分线上，但是点M，N与A，B在同一直线上，构不成等腰三角形，故舍去，所以有8个点.故选C试题难度：三颗星知识点：等腰三角形的存在性10.如图,在平面直角坐标系中,O为原点,已知A(2,-1),P是x轴上的一个动点,如果以点P,O,A为顶点的三角形是等腰三角形,那么符合条件的动点P的个数为( )A.2B.3C.4D.5答案：C解题思路：已知O，A两个定点，再寻找点P使得△OAP为等腰三角形，可知需要利用“两圆一线”解题，即：分别以O，A为圆心，以OA的长为半径画圆；作线段OA的垂直平分线，与x轴的交点即为所求.如图所示，图中，，，即为所求．故选C．试题难度：三颗星知识点：等腰三角形的存在性。

2015年上海中考数学专题-等腰相似直角三角形存在性问题试题一和参考答案研究创造才智，知识成就未来。

以下是上海市初中数学考试的几道题目。

题目一：等腰相似直角三角形存在性问题给定顶点为P(4,-4)的二次函数图像，经过原点，并且点A在该图像上。

连接OA与对称轴l的交点为M，点M和N 关于点P对称，连接AN和ON。

1) 求该二次函数的关系式。

2) 若点A的坐标是(6,-3)，求△ANO的面积。

3) 当点A在对称轴l右侧的二次函数图像上运动时，请回答以下问题：①证明：∠ANM=∠XXX。

②△ANO能否为直角三角形？如果能，请求出所有符合条件的点A的坐标，如果不能，请说明理由。

题目二：等腰三角形的存在性问题在△ABC中，已知AB=AC=5，BC=6，且△ABC≌△DEF，将△XXX与△XXX重合在一起，△XXX不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE、始终经过点A，EF与AC交于M点。

1) 求证：△ABE∽△ECM。

2) 探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，请求出BE的长；若不能，请说明理由。

3) 当线段AM最短时，求重叠部分的面积。

题目三：抛物线问题已知抛物线y=3/2x^2+bx+63经过A(2,0)。

设顶点为点P，与x轴的另一交点为点B。

1) 求b的值，求出点P、点B的坐标。

2) 如图，在直线y=3x上是否存在点D，使四边形OPBD 为平行四边形？若存在，求出点D的坐标；若不存在，请说明理由。

3) 在x轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在，请举例验证你的猜想；如果不存在，请说明理由。

题目四：三角形问题在△ABC中，∠ABC=45°，tan∠ACB=1.把△XXX的一边BC放置在x轴上，有OB=14，OC=AC与y轴交于点E。

1) 求AC所在直线的函数解析式。

2) 过点O作OG⊥AC，垂足为G，求△OEG的面积。

专题：二次函数中等腰三角形存在性问题类型一、等腰三角形存在性问题以(,)A A A x y 、(,)B B B x y 为三角形的边，在x 轴上找一点P 使得△PAB 为等腰三角形（二定一动）一.找法：画圆和作垂直平分线①以A 为圆心，线段AB 为半径画圆，与x 轴交点即为1P 、2P 点；（AB=AP ）②以B 为圆心，线段AB 为半径画圆，与x 轴交点即为3P 、4P 点；（AB=BP ）③作线段AB 的垂直平分线，与x 轴交点即为5P 点；（AP=BP ）二、算法：利用两点距离公式进行计算 公式：22()()A B A B AB x x y y =-+- ，设(,)p p P x y ，分三种情况：①AB=AP 时 2222()()()()A B A B A P A P x x y y x x y y -+-=-+-可得1P 、2P ，（特殊情况可能是一个点，例如2P 与B 重合）②AB=BP 时2222()()()()A B A B B P B P x x y y x x y y -+-=-+-可得3P 、4P ，（特殊情况可能是一个点，例如3P 与A 重合）③AP=BP 时2222()()()()A P A P B P B P x x y y x x y y -+-=-+-可得5P 、例题1、如图，已知二次函数2y x bx c =++的图像与x 轴交于点A 、B 两点，其中A 点坐标为（-3,0），与y 轴交于点C ，点D （-2，-3）在抛物线上.（1）求抛物线的表达式；（2）抛物线的对称轴上是否存在动点Q ，使得△BCQ 为等腰三角形？若存在，求出点Q 的坐标；若不存在，说明理由.1、（2021·云南九年级一模）如图所示，抛物线()240y ax bx a =++≠经过点()1,0A -，点()4,0B ，与y 轴交于点C ，连接AC ，BC ．点M 是线段OB 上不与点O 、B 重合的点，过点M 作DM x ⊥轴，交抛物线于点D ，交BC 于点E ．（1）求抛物线的表达式；（2）过点D 作DF BC ⊥，垂足为点F ．设M 点的坐标为(),0M m ，请用含m 的代数式表示线段DF 的长，并求出当m 为何值时DF 有最大值，最大值是多少？（3）试探究是否存在这样的点E ，使得以A ，C ，E 为顶点的三角形是等腰三角形．若存在，请求出此时点E 的坐标；若不存在，请说明理由．2、（八中2020级初三第三次月考）如图在平面直角坐标系中，已知抛物线2(0)y ax bx c a =++≠交x 轴于A （-4,0），B （1,0），交y 轴于C （0,3）（1）求此抛物线解析式；（2）如图1，点P 为直线AC 上方抛物线上一点，过点P 作PQ ⊥x 轴于点Q ，再过点Q 作QR//AC 交y 轴于点R ，求PQ+QR 的最大值及此时点P 的坐标；（3）如图2，点E 在抛物线上，横坐标为-3，连接AE ，将线段AE 沿直线AC 平移，得到线段''A E ，连接'CE ，当△''A E C 为等腰三角形时，只写写出点'A 的坐标。

等腰三角形存在性问题技巧讲义等腰三角形是一种有两条边相等的三角形，其中也包括一种特殊情况，即等边三角形，即三条边均相等的三角形。

存在性问题指的是给定一些条件，判断是否存在符合条件的等腰三角形。

下面将介绍一些解决等腰三角形存在性问题的技巧。

1.通过边长关系判断：等腰三角形的存在性与边长的关系密切相关。

设三角形的三个边长分别为a、b和c，如果a=b，则存在等腰三角形；如果a=c，则存在等腰三角形；如果b=c，则存在等腰三角形。

因此，可以通过比较三个边长的大小关系，来判断是否存在等腰三角形。

2.使用三角形内角和定理：三角形的内角和为180度。

对于等腰三角形而言，设其两个等边的边长为a，非等边的边长为b，那么根据三角形的内角和定理可得2a+b=180。

通过这个方程，可以求得非等边的边长b的值，如果b大于0，则存在等腰三角形。

3.使用三角形的高和底边关系：等腰三角形的高是从等腰边的顶点到底边的垂直距离。

如果一条边是等腰边，那么从该边对应的顶点到底边的垂直距离一定是这条边的高。

因此，可以通过计算等腰边顶点到底边的垂直距离，与底边的关系来判断是否存在等腰三角形。

4.利用等腰三角形的旋转对称性：等腰三角形具有旋转对称性，即一个等腰三角形可以绕其顶点旋转一定角度后得到另一个等腰三角形。

因此，当给定一个等腰三角形的一些条件时，可以通过旋转该等腰三角形来判断是否存在满足条件的等腰三角形。

5.利用等腰三角形的镜像对称性：等腰三角形也具有镜像对称性，即通过等腰边作为对称轴，可以得到两个镜像对称的等腰三角形。

因此，当给定一个等腰三角形的一些条件时，可以通过对称该等腰三角形来判断是否存在满足条件的等腰三角形。

以上是一些解决等腰三角形存在性问题的技巧。

通过比较边长关系、使用三角形内角和定理、考虑高和底边关系、利用等腰三角形的旋转对称性和镜像对称性等方法，我们可以有效地判断等腰三角形是否存在。

实际应用中，可以结合以上方法，根据具体条件进行判断。