沪教版九年级数学上册相似三角形常用辅助线
- 格式:ppt
- 大小:1.55 MB
- 文档页数:42


相似三角形之常用辅助线在与相似有关得几何证明、计算得过程中,常常需要通过相似三角形,研究两条线段之间得比例关系,或者转移线段或角。
而有些时候,这样得相似三角形在问题中,并不就是十分明显、因此,我们需要通过添加辅助线,构造相似三角形,进而证明所需得结论。
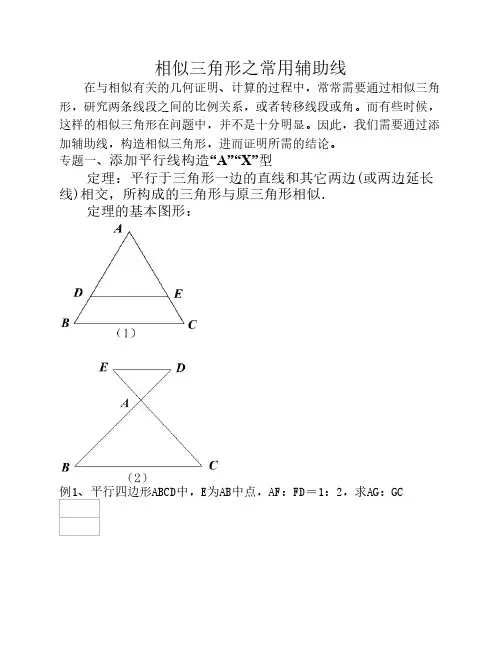
专题一、添加平行线构造“A"“X”型定理:平行于三角形一边得直线与其它两边(或两边延长线)相交,所构成得三角形与原三角形相似。
定理得基本图形:例1、平行四边形ABCD中,E为AB中点,AF:FD=1:2,求AG:GC变式练习:已知在△ABC中,AD就是∠BAC得平分线.求证:、(本题有多种解法,多想想)例2、如图,直线交△ABC得BC,AB两边于D,E,与CA延长线交于F,若==2,求BE:EA得比值、变式练习:如图,直线交△ABC得BC,AB两边于D,E,与CA延长线交于F,若错误!= 错误!=2,求BE:E A得比值。
例3、BE=AD,求证:EF·BC=AC·DF变式1、如图,△ABC中,AB<AC,在AB、AC上分别截取BD=CE,DE,BC得延长线相交于点F,证明:AB·DF=AC·EF。
例4、已知:如图,在△ABC中,AD为中线,E在AB上,AE=AC,CE交AD于F,EF∶FC=3∶5,EB=8cm,求AB、AC得长、变式:如图,,求。
(试用多种方法解)说明:此题充分展示了添加辅助线,构造相似形得方法与技巧.在解题中方法要灵活,思路要开阔.总结:(1)遇燕尾,作平行,构造字一般行。
(2)引平行线应注意以下几点:1)选点:一般选已知(或求证)中线段得比得前项或后项,在同一直线得线段得端点作为引平行线得EF EF EFEF点。
2)引平行线时尽量使较多已知线段、求证线段成比例。
专题二、作垂线构造相似直角三角形 一、基本图形例1、,,那么吗?试说明AC BD AC BC CA CD ⊥=⋅22理由?(用多种解法)v变式练习:平行四边形ABC D中,CE ⊥A E,CF ⊥AF,求证:A B·AE+AD ·AF=AC 2例2、如图,RtA BC 中,CD 为斜边AB 上得高,E 为CD 得中点,AE 得延长线交B C于F,FG AB 于G,求证:FG =CFBF【练习】1.如图,一直线与△ABC 得边AB,AC 及BC 得延长线分别交于D,E,F 。


中考相似三角形之常用辅助线Revised on November 25, 2020相似三角形之常用辅助线在与相似有关的几何证明、计算的过程中,常常需要通过相似三角形,研究两条线段之间的比例关系,或者转移线段或角。
而有些时候,这样的相似三角形在问题中,并不是十分明显。
因此,我们需要通过添加辅助线,构造相似三角形,进而证明所需的结论。
专题一、添加平行线构造“A ”“X ”型定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似.定理的基本图形: 例1、平行四边形ABCD 中,E 为AB 中点,AF :FD =1:2,求AG :GC变式练习:已知在△ABC 中,AD 是∠BAC 的平分线.求证:. (本题有多种解法,多想想)例2、如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若DCBD =FA FC=2,求BE:EA 的比值.变式练习:如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若BD DC = FEED =2,求BE:EA 的比值.例3、BE =AD ,求证:EF ·BC =AC ·DF变式1、如图,△ABC 中,AB<AC ,在AB 、AC 上分别截取BD=CE ,DE ,BC 的延长线相交于点F ,证明:AB·DF=AC·EF 。
例4、已知:如图,在△ABC 中,AD 为中线,E 在AB 上,AE=AC ,CE 交AD 于F ,EF ∶FC=3∶5,EB=8cm,求AB 、AC 的长.变式:如图,21==DE AE CD BD ,求BFAF。
(试用多种方法解)CDBDAC AB =A B CEF A B C EF A BCEF A BC EF说明:此题充分展示了添加辅助线,构造相似形的方法和技巧.在解题中方法要灵活,思路要开阔. 总结:(1)遇燕尾,作平行,构造 字一般行。

相似三角形中的辅助线在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或得出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。
主要的辅助线有以下几种:一、作平行线例1. 如图,∆ABC的AB边和AC边上各取一点D和E,且使AD=AE,DE延长线与BC延长线相交于F,求证:BFCFBDCE=BDA CFE证明:过点C作CG//FD交AB于GF小结:本题关键在于AD=AE这个条件怎样使用。
由这道题还可以增加一种证明线段相等的方法:相似、成比例。
例2. 如图,△ABC中,AB<AC,在AB、AC上分别截取BD=CE,DE,BC的延长线相交于点F,证明:AB·DF=AC·EF。
分析:证明等积式问题常常化为比例式,再通过相似三角形对应边成比例来证明。
欲证,需证,而这四条线段所在的两个三角形显然AB DF AC EFABACEFDF⋅=⋅=不相似,因而要通过两组三角形相似,运用中间比代换得到,为构造相似三角形,需添加平行线。
方法一:过E 作EM//AB ,交BC 于点M ,则△EMC ∽△ABC (两角对应相等,两三角形相似)。
∴=⋅=⋅EM AB EC AC EM AC AB EC 即,∴=AB AC EMEC同理可得∆∆EMF DBF ~ ∴=EF DF EMBD,又, BD EC EM EC EM BD =∴=(为中间比),EMBD∴=AB AC EF DF, ∴⋅=⋅AB DF AC EF方法二:如图,过D 作DN//EC 交BC 于N则有,,∆∆BDN BAC ~∴=⋅=⋅BD AB DNAC BD AC AB DN ,即(比例的基本性质) ∴=AB AC BD DN同理,∆∆ECF DNF ~∴==EC DN EFDF BD EC ,而(已知) ∴=BD DN EC DN ECDN (为中间比), ∴=∴⋅=⋅AB AC EFDFAB DF AC EF ,又 BCM ADN ∆≅∆ ∴ AN=CM∴ 2)(AC CM AM AC AF AD AE AB =+=⋅+⋅三、作延长线例5. 如图,在梯形ABCD 中,AD ∥BC ,若∠BCD 的平分线CH ⊥AB 于点H ,BH=3AH ,且四边形AHCD 的面积为21,求△HBC 的面积。

中考相似三角形之常用辅助线Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998相似三角形之常用辅助线在与相似有关的几何证明、计算的过程中,常常需要通过相似三角形,研究两条线段之间的比例关系,或者转移线段或角。
而有些时候,这样的相似三角形在问题中,并不是十分明显。
因此,我们需要通过添加辅助线,构造相似三角形,进而证明所需的结论。
专题一、添加平行线构造“A”“X”型定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似.定理的基本图形:例1、平行四边形ABCD中,E为AB中点,AF:FD=1:2,求AG:GC变式练习:已知在△ABC中,AD是∠BAC的平分线.求证:.(本题有多种解法,多想想)GFED CBAGFED CBACDBDACAB例2、如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若DCBD =FA FC=2,求BE:EA 的比值.变式练习:如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若BD DC = FEED =2,求BE:EA 的比值.例3、BE =AD ,求证:EF ·BC =AC ·DF变式1、如图,△ABC 中,AB<AC ,在AB 、AC 上分别截取BD=CE ,DE ,BC 的延长线相交于点F ,证明:AB·DF=AC·EF 。
ACFEB D ACFEB D EDCBA例4、已知:如图,在△ABC 中,AD 为中线,E 在AB 上,AE=AC ,CE 交AD 于F ,EF ∶FC=3∶5,EB=8cm,求AB 、AC 的长.变式:如图,21==DE AE CD BD ,求BFAF。
(试用多种方法解)A B CD EF A B C D EF A BCDEF A BC D EF说明:此题充分展示了添加辅助线,构造相似形的方法和技巧.在解题中方法要灵活,思路要开阔. 总结:(1)遇燕尾,作平行,构造 字一般行。

版权归作者全部,仅供学习参照之用,更多学习资料,请关注民众号上海数学教课!相像三角形之常用协助线在与相像相关的几何证明、计算的过程中,经常需要经过相像三角形,研究两条线段之间的比率关系,或许转移线段或角。
而有些时候,这样的相像三角形在问题中,其实不是十分显然。
所以,我们需要经过增添协助线,结构相像三角形,从而证明所需的结论。
专题一、增添平行线结构“A”“X”型定理:平行于三角形一边的直线和其余两边原三角形相像.定理的基本图形:(或两边延伸线)订交,所组成的三角形与例1、平行四边形ABCD中,E为AB中点,AF:FD=1:2,求AG:GCD C D CF FGGA AB BE E变式练习:AB BD已知在△ABC中,AD是∠BAC的均分线.求证:.(本题有多种解法,多想一想)AC CD版权归作者全部,仅供学习参照之用,更多学习资料,请关注民众号上海数学教课!例2、如图,直线交△ABC的BC,AB两边于D,E,与 CA 延伸线交于F,BD= FC =2,求BE:EA的比值.若DCFAF A EB D C变式练习:如图,直线交△ABC 的BC,AB 两边于B DF E D,E,与CA 延伸线交于F,=若DCE D=2, 求BE:EA 的比 值. F A EB D C例3、BE =AD ,求证:EF·BC=AC·DFADECB变式1、如图,△ABC中,AB<AC,在AB、AC上分别截取BD=CE,DE,BC的延伸线订交于点F,证明:AB·DF=AC·EF。
版权归作者全部,供仅学习参照之用,更多学习资料,关请注民众号上海数学教课!例4、已知:如图,在△ABC中,AD中为,线E在AB上,AE=AC,CE交AD于F,EF∶FC=3∶5,EB=8cm, 求AB、AC的长.变式:如图,AF E BD AE1,求AF。
(用试多种方法解)CD DE 2 BFA A AF E F E F EB DC BD C B D C B D C说明:本题充足展现了增添协助,线结构相像形的方法和技巧.在解题中方法要灵巧,思路要宽阔.总结:(1)遇燕尾,作平行,结构字一般行。

相似三角形添加辅助线的方法举例1.垂直角辅助线:当三角形中存在垂直角时,我们可以通过添加一条垂直角辅助线来将问题简化。
例如,在一个直角三角形中,我们可以通过从直角顶点到斜边的任意一点画一条垂直辅助线,这样可以将原问题转化为两个相似的直角三角形的求解。
2.中位线辅助线:在一个任意三角形中,我们可以通过连接每个顶点与对边中点的线段来得到三条中位线。
这些中位线的交点被称为三角形的重心。
通过画三角形重心与其他顶点的连线,可以将原问题转化为多个相似的三角形的求解。
3.等角辅助线:当我们需要证明两个三角形相似时,可以通过添加等角辅助线来帮助我们得到一些相等的角度。
例如,在两个直角三角形中,如果我们能找到一个等角辅助线使得两个直角形成的角相等,那么我们可以推断这两个三角形相似。
4.比例辅助线:当我们需要求解相似三角形的长边与短边的比例时,可以利用比例辅助线。
例如,在两个相似三角形中,我们可以通过添加比例辅助线,将两个相似三角形分割成若干个相似的小三角形,并且利用小三角形的边长比例来求解长边与短边的比例关系。
5.平行辅助线:当我们需要证明两个三角形相似时,可以通过添加平行辅助线来帮助我们得到一些对应边平行的关系。
例如,在两个直角三角形中,如果我们能找到一条边使得它与另一个直角三角形的对边平行,那么我们可以推断这两个三角形相似。
以上是一些常见的相似三角形添加辅助线的方法,它们可以帮助我们更好地理解问题、简化问题以及找到解决问题的方法。
在实际解题过程中,根据问题的不同,我们可以选择适合的辅助线方法来解决问题。

(完整)中考相似三角形之常用辅助线编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)中考相似三角形之常用辅助线)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)中考相似三角形之常用辅助线的全部内容。
相似三角形之常用辅助线在与相似有关的几何证明、计算的过程中,常常需要通过相似三角形,研究两条线段之间的比例关系,或者转移线段或角。
而有些时候,这样的相似三角形在问题中,并不是十分明显。
因此,我们需要通过添加辅助线,构造相似三角形,进而证明所需的结论。
专题一、添加平行线构造“A”“X”型定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似.定理的基本图形:例1、平行四边形ABCD中,E为AB中点,AF:FD=1:2,求AG:GC变式练习:已知在△ABC中,AD是∠BAC的平分线.求证:.(本题有多种解法,多想想)GFEDCBAGFED CBACDBDACAB例2、如图,直线交△ABC 的BC ,AB 两边于D ,E,与CA 延长线交于F,若DCBD =FA FC=2,求BE:EA 的比值.变式练习:如图,直线交△ABC 的BC,AB 两边于D,E ,与CA 延长线交于F ,若BDDC = 错误!=2,求BE:EA 的比值。
例3、BE =AD,求证:EF ·BC =AC ·DF变式1、如图,△ABC 中,AB<AC ,在AB 、AC 上分别截取BD=CE ,DE,BC 的延长线相交于点F,证明:AB·DF=AC·EF。
ACFEB D ACFEB D EDCBA例4、已知:如图,在△ABC 中,AD 为中线,E 在AB 上,AE=AC ,CE 交AD 于F ,EF ∶FC=3∶5,EB=8cm,求AB 、AC 的长.变式:如图,21==DE AE CD BD ,求BFAF。
相似三角形之常用辅助线在与相似有关的几何证明、计算的过程中,常常需要通过相似三角形,研究两条线段之间的比例关系,或者转移线段或角。
而有些时候,这样的相似三角形在问题中,并不是十分明显。
因此,我们需要通过添加辅助线,构造相似三角形,进而证明所需的结论。
专题一、添加平行线构造“A”“X”型定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似.定理的基本图形:例1、平行四边形ABCD中,E为AB中点,AF:FD=1:2,求AG:GC变式练习:已知在△ABC中,AD是∠BAC的平分线.求证:.(本题有多种解法,多想想)例2、如图,直线交△ABC的BC,AB两边于D,E,与CA延长线交于F,若==2,求BE:EA的比值.变式练习:如图,直线交△ABC的BC,AB两边于D,E,与CA延长线交于F,若= =2,求BE:EA的比值.例3、BE=AD,求证:EF·BC=AC·DF变式1、如图,△ABC中,AB<AC,在AB、AC上分别截取BD=CE,DE,BC的延长线相交于点F,证明:AB·DF=AC·EF。
例4、已知:如图,在△ABC中,AD为中线,E在AB上,AE=AC,CE交AD于F,EF∶FC=3∶5,EB=8cm,求AB、AC的长.变式:如图,,求。
(试用多种方法解)ABCDEFABCDEFABCDEFABCDEF说明:此题充分展示了添加辅助线,构造相似形的方法和技巧.在解题中方法要灵活,思路要开阔.总结:(1)遇燕尾,作平行,构造 字一般行。
(2)引平行线应注意以下几点:1)选点:一般选已知(或求证)中线段的比的前项或后项,在同一直线的线段的端点作为引平行线的点。
2)引平行线时尽量使较多已知线段、求证线段成比例。
专题二、作垂线构造相似直角三角形一、基本图形ABDEFC例1、理由?(用多种解法)v变式练习:平行四边形ABCD中,CE⊥AE,CF⊥AF,求证:AB·AE+AD·AF=AC2例2、如图,RtABC中,CD为斜边AB上的高,E为CD的中点,AE的延长线交BC于F,FGAB于G,求证:FG=CFBF【练习】1.如图,一直线与△ABC的边AB,AC及BC的延长线分别交于D,E,F。