实验三戴维南定理

实验三戴维南定理报告
戴维南定理是一个关于信号还原能力的重要定理，它是由对分析信号及信号处理相关
领域杰出贡献的美国学者戴维南（David Alan Wallece）在1973年所提出的定理，因此
又称为“戴维南定理”。

这个定理可以用来解释实际的信号滤波器的最低信号恢复阈值。

简单来说，戴维南定
理指出，信号恢复的最低值由三个因素决定：滤波器的抗干扰能力、输入信号的质量及信
号的质量的输出。

它可以帮助我们深入了解信号恢复的限制，并有助于信号恢复技术的改
进和发展。

戴维南定理可以利用信号处理系统中的滤波器来描述，假设T是信号恢复系统的输入
信号，R是信号恢复系统的输出信号，那么戴维南定理可以表示为：“当输入信号的性能
达到一定水平，信号恢复系统的输出信号与输入信号的差异越小，滤波器的抗干扰能力越强，信号恢复能力越强。

”
戴维南定理在信号处理系统中有重要的意义，它可以帮助我们深入了解信号恢复的特性。

戴维南定理可以明确地表示信号恢复能力受到滤波器能力和信号质量的影响，并且在
使用滤波器时，可以利用它来提高信号恢复的效果。

在信号处理系统中，戴维南定理的应用非常普遍，它可以用来估算和优化滤波器的抗
干扰能力，使其满足较高的信号恢复质量要求。

当确定滤波器的抗干扰能力时，可以根据
戴维南定理来规定达到最低恢复标准所需的滤波器能力，并进一步验证所选滤波器的功效。

总结起来，戴维南定理真是一个重要且实用的定理，它不仅成功地解释了信号恢复系
统中的相关特性，而且还可以帮助我们有效地完成对信号恢复系统性能的测试和评价，从
而改善和优化信号处理技术。

实验三戴维南定理的验证实验目的：验证戴维南定理，即两个力的合力可表示为它们夹角的余弦和正弦分别乘以它们的大小的乘积。

实验器材：万能传感器、数据采集器、几何夹具、两个力传感器、悬挂支架、并联弹簧、砝码组、指南针。

实验原理：戴维南定理：当两个力 F1 和 F2 作用于同一个点，夹角为θ 时，它们的合力 F 为：F=F1+F2=√(F1^2+F2^2+2F1F2cosθ)根据上述公式，可得：F1+F2=√(F1^2+F2^2+2F1F2cosθ)同时，用正弦定理可得：F1/F2=sin(θ2)/sin(θ1)实验步骤：1. 将悬挂支架固定在水平桌面上。

2. 将两个力传感器分别固定在悬挂支架上，并将它们的读数清零。

3. 将几何夹具固定在力传感器上，并调整两个夹具，使得它们之间夹角为θ。

4. 在夹具的正中央挂上并联弹簧和砝码组，记录下此时的读数F1。

5. 更改夹具的位置，调整夹角至相反方向，重复步骤 4，记录下此时的读数 F2。

6. 将 F1 和 F2 的读数输入数据采集器，计算出 F 和θ2/θ1。

7. 使用指南针测量出夹角θ 的实际值。

8. 根据实际值和计算值进行比较，验证戴维南定理的正确性。

注意事项：1. 实验中夹具的位置应固定且夹角应准确测量。

2. 实验过程中力传感器的不少于两组读数应记录。

3. 实验结果应与理论值相符合。

实验结果与分析：将实验得到的数据代入戴维南定理的公式中计算，得到 F 和θ2/θ1 的值。

并使用指南针测量夹角θ 的实际值，将计算值和实际值进行比较。

根据实验数据计算得到 F 的值为 3.10 N，θ2/θ1 的值为 0.911。

测量得到夹角θ 的实际值为 40°。

将具体数值代入公式中，计算出此时的 F1 和 F2。

F1=2.01 N，F2=2.24 N，F1+F2=4.25 N。

可见，计算值与实际值的误差较小。

综上所述，实验结果验证了戴维南定理的正确性。

第1篇一、实验目的1. 深入理解并掌握戴维南定理的基本原理。

2. 通过实验验证戴维南定理的正确性。

3. 学习并掌握测量线性有源一端口网络等效电路参数的方法。

4. 提高使用Multisim软件进行电路仿真和分析的能力。

二、实验原理戴维南定理指出：任何一个线性有源一端口网络，对于外电路而言，都可以用一个理想电压源和电阻的串联形式来等效代替。

理想电压源的电压等于原一端口网络的开路电压Uoc，其电阻（又称等效内阻）等于网络中所有独立源置零时的入端等效电阻Req。

三、实验仪器与材料1. Multisim软件2. 电路仿真实验板3. 直流稳压电源4. 电压表5. 电流表6. 可调电阻7. 连接线四、实验步骤1. 搭建实验电路根据实验原理，搭建如图1所示的实验电路。

电路包括一个线性有源一端口网络、电压表、电流表和可调电阻。

图1 实验电路图2. 测量开路电压Uoc断开可调电阻，用电压表测量一端口网络的开路电压Uoc。

3. 测量等效内阻Req将可调电阻接入电路，调节其阻值，记录不同阻值下的电压和电流值。

根据公式Req = Uoc / I，计算等效内阻Req。

4. 搭建等效电路根据戴维南定理，搭建等效电路，如图2所示。

其中，理想电压源的电压等于Uoc，等效内阻为Req。

图2 等效电路图5. 测量等效电路的外特性在等效电路中，接入电压表和电流表，调节可调电阻的阻值，记录不同阻值下的电压和电流值。

6. 比较实验结果比较原电路和等效电路的实验结果，验证戴维南定理的正确性。

五、实验结果与分析1. 测量数据表1 实验数据| 阻值RΩ | 电压V | 电流A | ReqΩ || ------ | ----- | ----- | ---- || 10 | 2.5 | 0.25 | 10 || 20 | 1.25 | 0.125 | 10 || 30 | 0.833 | 0.083 | 10 |2. 分析从实验数据可以看出，随着负载电阻的增大，原电路和等效电路的电压和电流值逐渐接近。

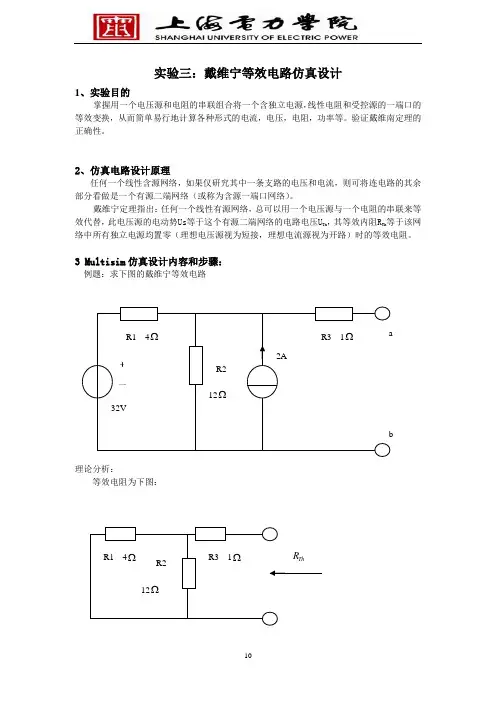
实验三：戴维宁等效电路仿真设计1、实验目的掌握用一个电压源和电阻的串联组合将一个含独立电源，线性电阻和受控源的一端口的等效变换，从而简单易行地计算各种形式的电流，电压，电阻，功率等。

验证戴维南定理的正确性。

2、仿真电路设计原理任何一个线性含源网络，如果仅研究其中一条支路的电压和电流，则可将连电路的其余部分看做是一个有源二端网络（或称为含源一端口网络）。

戴维宁定理指出：任何一个线性有源网络，总可以用一个电压源与一个电阻的串联来等效代替，此电压源的电动势Us等于这个有源二端网络的电路电压U Th，其等效内阻R Th等于该网络中所有独立电源均置零（理想电压源视为短接，理想电流源视为开路）时的等效电阻。

3 Multisim仿真设计内容和步骤：例题：求下图的戴维宁等效电路理论分析：等效电阻为下图：R Th =Ω=+⨯=+4116124112||4 等效电压如下图：我们设定两个回路电流i 1,i 2, 则根据回路法可得：0)(12432211=-++-II IA I 22-=A I 5.01=所以戴维宁等效电压为：V I I V Th 30)0.25.0(12)(1221=+=-=V所以戴维宁等效电路为：3、建立电路仿真图电路图：等效电压测试电路图：等效电阻测试电路图为：测试结果与计算值完全一致。

4、结果与误差分析戴维南等效电路无法一下子就求的，通过电路转换如测试等效电阻时，需将电源略去等，从而有效计算测量所需数值，通过计算等效电阻和等效电压，从而得到等效电路，由此证明了一个含独立电源、线性电阻和受控源的一端口，对外电路来说，可以用一个电压源和电阻的串联组合等效变换。

2、理论计算结果与仿真测量结果没有误差。

5．设计总结1、在本实验中我遇到的第一个问题是在连接好原件进行测量时无法测量，原因是未接地，经过接地后这个问题得以解决，它让我了解了在这个仿真系统中还是很多地方与实际连接中有很大的差异，接地原件就很好的表现了这一点。

实验三戴维南定理和诺顿定理的验证一、实验目的1、理解戴维南定理和诺顿定理的内涵与应用。

2、初步掌握使用直流电桥、电流表、电压表等测量仪器的能力。

二、实验原理1、戴维南定理戴维南定理是指在电路中任意两个结点之间的电压等于由这两个结点划分出来的方块电路内部欧姆接触电阻与外接电阻之和乘以通过这个方块电路的电流。

戴维南定理的实际应用与布朗—博利定理类似，也是希望通过这个定理来简化电路分析和设计过程中繁琐的计算。

学习戴维南定理主要是为了在电路分析和设计中寻找我们需要的信息。

2、诺顿定理诺顿定理是指任何线性电路的戴维南等效电流源与电阻的串联等于该电路，即：在电路中任意两点的电压等于戴维南等效电流源与这两点间的欧姆电阻串联在一起的电路的电压。

诺顿定理与戴维南定理是等价的，因此学习它们两个定理的任一一个都可以很好地理解和应用它们两个。

三、实验器材和器件示波器万用表直流电源初始化电阻电箱直流电桥四、实验步骤（1）连接和调节实验电路：按照实验电路图连接电路。

（2）找寻电路中的方块电路：将电路按照结点手法分成方块，再将方块内的欧姆电阻与外接电阻相加，求出它们的和R。

（3）测量电路电流：在电路中加入电流表I01、I02，分别测量出I01、I02，作为通过方块电路的电流Ip。

（5）计算电路方块的电压：将U01 - U02的值除以Ip，求出方块电路的电压Up。

（6）实验验证：实验中得到的Up和实际测量值的误差小于5％，表明戴维南定理的应用正确。

（2）求出诺顿等效电流源的电流：通过电路中的电阻电箱，依次取出100Ω、1kΩ、10kΩ、100kΩ等不同阻值的电阻，将它们依次串联在电路中，通过万用表测量电阻电箱电阻值并各自记下，然后将测量出的电流值与电阻值计算出来，可以得到诺顿等效电流源的电流。

（3）在电路中加入一电阻：通过电路中的电阻电箱，在电路中加入一电阻表现为RL。

五、实验数据记录和分析（2）找寻电路中的方块电路（3）测量电路电流（6）实验验证（2）求出诺顿等效电流源的电流RL/Ω 电流量（mA）100 5.0001k 0.82410k 0.100100k 0.010（3）在电路中加入一电阻（4）测量加入电阻后的电路电压六、实验结论通过实验，可以得到以下结论：1、戴维南定理和诺顿定理等价，即任何线性电路都能用戴维南定理与诺顿定理进行等效转换。

实验三、四 戴维南定理的验证及最大功率传输定理的验证一、实验目的1. 验证戴维南定理的正确性，加深对该定理的理解。

2. 掌握测量有源二端网络等效参数的一般方法。

3. 掌握测量开路电压与等效内阻的方法。

4. 掌握最大功率传输定理。

二、实验原理1. 戴维南定理任何一个线性有源网络，如果仅研究其中一条支路的电压和电流，则可将电路的其余部分看作是一个有源二端网络（或称为有源一端口网络）。

戴维南定理指出：任何一个线性有源网络，总可以用一个电压源与一个电阻的串联来等效代替，此电压源的电动势U S 等于这个有源二端网络的开路电压U OC ，其等效内阻R 0等于该网络中所有独立源均置零（理想电压源视为短接，理想电流源视为开路）时的等效电阻。

U OC （U S ）和R 0称为有源二端网络的等效参数。

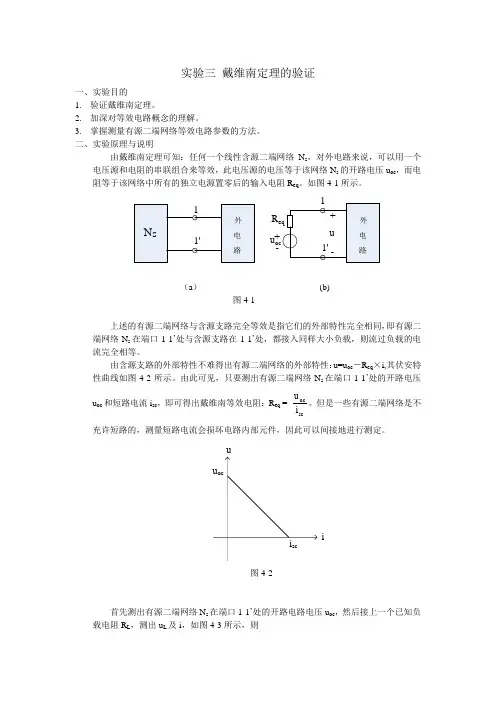
2. 有源二端网络等效电阻的测量方法 （1）开路电压、短路电流法测R 0在有源二端网络输出端开路时，用电压表直接测其输出端的开路电压U OC ，然后再将其输出端短路，用电流表测其短路电流I SC ，则等效内阻为：SCOC0I U R =如果二端网络的内阻很小，若将其输出端口短路则易损坏其内部元件，因此不宜用此法。

（2）伏安法测R 0用电压表、电流表测出有源二端网络的外特性曲线，如图5-1所示。

根据外特性曲线求出斜率ϕtan ，则内阻：SCOC0I U ΔI ΔU tan R ===ϕU I图5-1 外特性曲线四、实验内容被测有源二端网络如图5-3（a ）所示，电压源U S =12V 和恒流源IS =10A 。

Ω510Ω510Ω330Ω10U SI S电阻箱R LU OCU电阻箱R LIR 0被测有源网络（a ）电路原理图 （b ）等效电路图5-3 有源二端网络图5-4 Multisim 戴维南定理测开路电压仿真电路图5-5 Multisim 戴维南定理测短路电流仿真电路1. 用开路电压、短路电流法测量戴维南等效电路的U OC、R0。

实验三 戴维南定理的验证一、实验目的1. 验证戴维南定理。

2. 加深对等效电路概念的理解。

3. 掌握测量有源二端网络等效电路参数的方法。

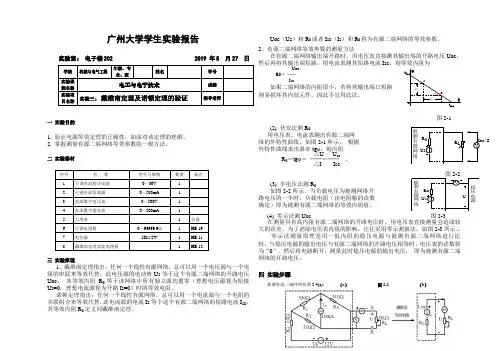
二、实验原理与说明由戴维南定理可知：任何一个线性含源二端网络N s ，对外电路来说，可以用一个电压源和电阻的串联组合来等效，此电压源的电压等于该网络N s 的开路电压u oc ，而电阻等于该网络中所有的独立电源置零后的输入电阻R eq 。

如图4-1所示。

Ru +- （a ） (b) 图4-1上述的有源二端网络与含源支路完全等效是指它们的外部特性完全相同，即有源二端网络N s 在端口1-1’处与含源支路在1-1’处，都接入同样大小负载，则流过负载的电流完全相等。

由含源支路的外部特性不难得出有源二端网络的外部特性：u=u oc －R eq ×i,其伏安特性曲线如图4-2所示。

由此可见，只要测出有源二端网络N s 在端口1-1’处的开路电压u oc 和短路电流i sc ，即可得出戴维南等效电阻：R eq =ocscu i 。

但是一些有源二端网络是不充许短路的，测量短路电流会损坏电路内部元件，因此可以间接地进行测定。

u ocu ii sc图4-2首先测出有源二端网络N s 在端口1-1’处的开路电路电压u oc ，然后接上一个已知负载电阻R L ，测出u L 及i ，如图4-3所示，则L L oc LL L oc L oc R u uR u u u i u u q ⨯-=-=-=)1(ReR u +-L图4-3求戴维南等效电阻还可以用下面的方法。

首先把有源二端网络N s 变成无源二端网络N o ，即将有源二端网络中的独立电源去掉（电压源用短路线代替，电流源开路）。

然后在无源二端网络N o 端口1-1’处施加已知电压u 并测出电流i ，如图4-4所示。

oc -+图4-4三、实验内容与方法1. 按图4-5联接电路，u s 接直流稳压电源。

经实验指导教师检查后，接通电源。

广州大学学生实验报告实验室：电子楼202 2019 年5 月27 日学院机械与电气工程年级、专业、班姓名学号实验课程名称电工与电子技术成绩实验项目名称实验三:戴维南定理及诺顿定理的验证指导老师一实验目的1. 验证电源等效定理的正确性，加深对该定理的理解。

2. 掌握测量有源二端网络等效参数的一般方法。

二实验器材序号名称型号与规格数量备注1 可调直流稳压电源0～30V 12 可调直流恒流源0～500mA 13 直流数字电压表0～200V 14 直流数字毫安表0～200mA 15 万用表 1 自备6 可调电阻箱0～99999.9Ω 1 HE-197 电位器1KΩ/2W 1 HE-118 戴维南定理实验电路板 1 HE-12三实验原理1、戴维南定理指出：任何一个线性有源网络，总可以用一个电压源与一个电阻的串联来等效代替，此电压源的电动势Us等于这个有源二端网络的开路电压Uoc，其等效内阻R0等于该网络中所有独立源均置零（理想电压源视为短接Us=0，理想电流源视为开路Is=0）时的等效电阻。

诺顿定理指出：任何一个线性有源网络，总可以用一个电流源与一个电阻的并联组合来等效代替，此电流源的电流Is等于这个有源二端网络的短路电流I SC，其等效内阻R0定义同戴维南定理。

Uoc（Us）和R0或者I SC（I S）和R0称为有源二端网络的等效参数。

2、有源二端网络等效参数的测量方法在有源二端网络输出端开路时，用电压表直接测其输出端的开路电压Uoc，然后再将其输出端短路，用电流表测其短路电流Isc，则等效内阻为UocR0＝──Isc如果二端网络的内阻很小，若将其输出端口短路则易损坏其内部元件，因此不宜用此法。

图2-1(2) 伏安法测R0用电压表、电流表测出有源二端网络的外特性曲线，如图2-1所示。

根据外特性曲线求出斜率tgφ，则内阻△U U ocR0＝tgφ＝──＝──。

△I Isc图2-2(3) 半电压法测R0如图2-2所示，当负载电压为被测网络开路电压的一半时，负载电阻（由电阻箱的读数确定）即为被测有源二端网络的等效内阻值。

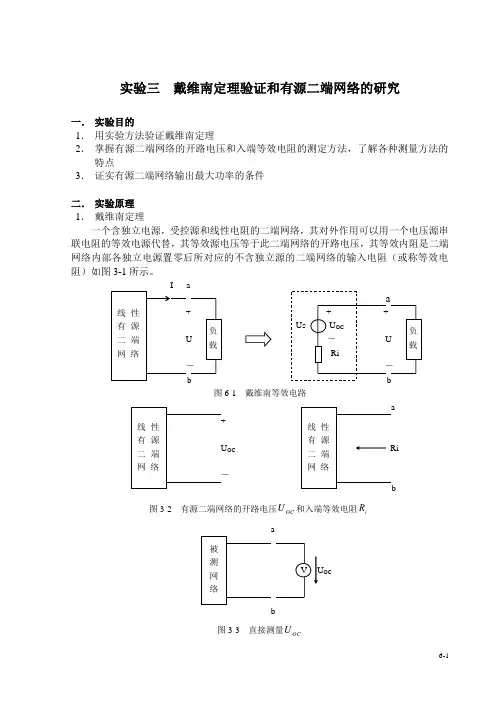
实验三 戴维南定理验证和有源二端网络的研究一． 实验目的1． 用实验方法验证戴维南定理2． 掌握有源二端网络的开路电压和入端等效电阻的测定方法，了解各种测量方法的特点3． 证实有源二端网络输出最大功率的条件二． 实验原理 1． 戴维南定理一个含独立电源，受控源和线性电阻的二端网络，其对外作用可以用一个电压源串联电阻的等效电源代替，其等效源电压等于此二端网络的开路电压，其等效内阻是二端网络内部各独立电源置零后所对应的不含独立源的二端网络的输入电阻（或称等效电阻）如图3-1所示。

图6-1 戴维南等效电路OC图3-2 有源二端网络的开路电压OC U 和入端等效电阻i RU OCb图3-3 直接测量OC U2． 开路电压的测定方法 （1） 直接测量法当有源二端网络的入端等效电阻i R 与万用表电压档的内阻V R 相比可以忽略不计时，可以用电压表直接测量该网络的开路电压OC U 。

如图3-3所示。

（2） 补偿法当有源二端网络的入端电阻i R 较大时，用电压表直接测量开路电压的误差较大，这时采用补偿法测量开路电压则较为准确。

图3-4中虚线框内为补偿电路，'S U 为另一个直流电压源，可变电阻器P R 接成分压器使用，G 为检流计。

当需要测量网络A 、B 两端的开路电压时，将补偿电路'A 、'B 端分别与A 、B 两端短接，调节分压器的输出电压，使检流计的指示为零，被测网络即相当于开路，此时电压表所测得的电压就是该网络的开路电压OC U 。

由于这时被测网络不输出电流，网络内部无电压降测得的开路电压数值较前一种方法准确。

图3-4 补偿法测量开路电压3． 入端等效电阻i R 的测定方法（1） 外加电源法将有源二端网络内部的独立电压源Us 处短接，独立电流源Is 处开路，被测网络成为无独立源的二端网络，然后在端口上加一给定的电源电压"S U ，测量流入网络的电流I ，如图3-5所示。

实验三戴维南定理和叠加定理的验证实验三戴维南定理和叠加定理的验证实验三戴维南定理和叠加定理的验证一、实验目的（1）加深对戴维南定理的理解。

(2)学习戴维南等效参数的各种测量方法。

(3)理解等效置换的概念。

（4）通过实验加深对叠加定理的理解。

（5）研究了叠加定理的适用范围和条件。

(6)学习直流稳压电源、万用表、直流电流表和电压表的正确使用方法。

二、实验原理及说明1.戴维南定理是指具有独立电源、线性电阻和受控源的端口。

对于外部电路，可以用电压源和电阻的串联组合来代替。

该电压源的电压等于端口的开路电压UOC，该电阻等于端口的所有独立电源设置为零后的输入电阻，如图2.3-1所示。

这种电压源和电阻的串联组合称为戴维南等效电路。

等效电路中的电阻称为戴维南等效电阻。

所谓等效是指用戴维南等效电路把有源一端口网络置换后，对有源端口（1-1’）以外的电路的求解是没有任何影响的，也就是说对端口1-1’以外的电路而言，电流和电压仍然等于置换前的值。

外电路可以是不同的。

2.诺顿定理是戴维南定理的对偶形式。

指出对于外部电路，包含独立电源、线性电阻和受控源的端口可以被电流源和电导的并联组合所取代。

电流源的电流等于端口的短路电流ISC，该端口的所有独立电源设置为零后，电导等于输入电导GEQ=L/req，如图2.3-1所示。

3、戴维南一诺顿定理的等效电路是对外部特性而言的，也就是说不管是时变的还是定常的，只要含源网络内部除独立的电源外都是线性元件，上述等值电路都是正确的。

4.戴维南等效电路参数的测量方法。

开路电压UOC的测量相对简单，可直接用电压表或补偿法测量；对于戴维南等效电阻req的获取，可采用以下方法：当网络包含电源时，应使用开路电压和短路电流法，但这种方法不能用于不允许外部电路直接短路的网络（例如，当网络的内部元件可能因短路电流过大而损坏时）；当网络不含电源时，采用伏安法、半电流法、半电压法、直接测量法等。

5、叠加定理（1）叠加定理是线性电路的一个重要定理，是分析线性电路的基础。

戴维南定理和诺顿定理实验_模板(优选)word资料实验三戴维南定理和诺顿定理实验姓名学号专业实验台号实验时间一、实验目的1．通过实验验证戴维南定理和诺顿定理，加深理解等效电路的概念2．学习用补偿法测量开路电压二、原理1．戴维南定理：一个含独立电源、线性电阻和受控源的一端口，对外电路来说，可以用一个电压源和电阻的串联组合等效置换。

诺顿定理：一个含独立电源、线性电阻和受控源的一端口，对外电路来说，可以用一个电流源和电导的并联组合等效电路。

以上等效变换的电路如图3-1所示。

(a) 线性含源一端口电路(b) 基于戴维南定理的替代电路(c) 基于诺顿定理的替代电路图3-1 等效变换图2．含源一端口网络开路电压的测量方法（1）直接测量法：当电压表内阻R v相比可以忽略不计时，可以直接用电压表测量器开路电压U oc。

（2）补偿法：当电压表内阻R v相比不可忽略时，补偿法可以消除或减小电压表内阻在测量中产生的误差。

图3-23．测量一端口网络输入端等效电阻R i（1）测量含源一端口网络的开路电压U oc和短路电流I sc，则oci scU R I =（2）将含源一端口网络除源，化为无源网络P ，然后按图接线，测量U s 和I ，则si U R I=图3-3三、实验仪器和器材1． 0-30V 可调直流稳压电源 2． +15直流稳压电源 3． 0~200mA 可调恒流源 4． 电阻 5． 电阻箱6． 交直流电压电流表/电流表 7． 实验电路板 8． 短接桥 9． 导线四、实验内容及步骤1． 测量含源一端口网络的外部伏安特性测量含源一端口网络的外部伏安特性：用电阻箱作为一端口网络的外接电阻R L ，如图3-4所示，测量结果在表3-1中。

()L R ω0 500 1k 1.5k 2k 2.5k 开路 I(mA) U(V)图3-42． 验证戴维南定理电压源用直流稳压电源代替，调节电源输出电压，使之等于U OC ，R i 用电阻箱代替，在CD 端接入负载电阻R L ，改变电阻值，侧去电流和电压。

实验三戴维南定理戴维南定理是几何学中的一条重要定理，又称作“派斯卡定理”。

它描述了一个圆内外每条六边形相对的三对对边的交点共线。

在平面几何中，如果我们有一个圆和一个六边形，该圆可以在六边形内或外，在六边形内时，它的直径必定至少有一对顶点在六边形的对边上，同时其它至少两条相对的直径必然相交于六边形内的一点，此时相交点恰是六边形对角线的交点。

类似地，当圆在六边形的外部时，也会出现相同的道理，并且这个交点也是六边形两对对边的交点。

“戴维南定理”的形式路线还可以进一步拓展，将六边形变换成任意多边形，并将区域从平面扩展到球面、欧几里得空间、非欧几里得空间等。

在这些更复杂的情形中，定理的证明更为棘手，但都保留了基本的“相对对边相交点共线”的结构。

例如，在球面上，圆的概念被广义为“连通的极小闭弧”（即一个不包含两点的最短路径，其两端点不计顺序）。

此时，戴维南定理仍然成立，并且仍然保留陈述“任意六边形的交点共线”的形式。

但是，这个共线点在球面上的实际位于极圈（两个极点间的大圆）上，而不是平面中的一条直线。

在非欧几里得几何中，球面上的概念被推广到了超几何学中的“球面”，从而得到了“戴维南定理”的非欧几里得版本。

在这个版本中，六边形的对边必须满足另外的要求，而不仅仅是相对。

例如，如果我们考虑有双曲几何空间（用模型模拟），并将六边形的对边约束为跨越相反的点对称的线，则戴维南定理仍然适用。

在这个情况下，定理告诉我们跨越相邻角的三对交点共线。

总之，戴维南定理是几何学中最基本、最有用的定理之一，它涵盖了平面、球面和非欧几里得空间中相当广泛的几何形体。

定理是建立在一些简单的假设之上，但它的实际应用极其复杂和广泛。

无论是在数学还是其他领域，这个定理都是一个重要而有用的工具。