1113三角形的稳定性1

1．如图，盖房子时，在窗框未安装好之前，木工师傅常常先在窗框上斜钉一根木条，为什么要这样做呢？(防止窗框变形)2．动手操作探究三角形的稳定性．(1)三根木条用钉子钉成一个三角形木架，然后扭动它，它的形状会改变吗？(不会)(2)四根木条用钉子钉成一个四边形木架，然后扭动它，它的形状会改变吗？(会)(3)在四边形的木架上再钉一根木条，将它的一对顶点连接起来，然后扭动它，它的形状会改变吗？(不会)从上面的实验过程中你能得出什么结论？与同学交流．解：三角形木架形状不会改变，四边形木架形状会改变，这就是说，三角形具有稳定性，四边形没有稳定性．第一个三角形不变形，第二个四边形变形，当在四边形的木架上再钉一根木条，然后扭动它，不变形．通过对比得出三角形具有稳定性的结论．还有什么发现？解：还可以发现，斜钉一根木条的四边形木架的形状不会改变．原因是斜钉一根木条后，四边形变成两个三角形，由于三角形有稳定性，所以斜钉一根木条的四边形木架的形状不会改变．现在你知道为什么窗框未安装好之前，要先在窗框上斜钉一根木条了吧．其实就是利用了三角形的稳定性．3．四边形的不稳定性的应用四边形的不稳定性是我们常常需要克服的，那么四边形的不稳定性在生活中有没有应用价值呢？如果有，你能举出实例吗？活动2跟踪训练1．下列图形中哪些具有稳定性？判断一个图形是否稳定，关键是看图形中是否都是三角形．2．如图，桥梁的斜拉钢索是三角形的结构，主要是为了()A．节省材料，节约成本B．保持对称C．利用三角形的稳定性D．美观漂亮3．如图，工人师傅砌门时，常用木条EF和EG固定门框ABCD，使其不变形，这种做法的根据是()A．两点之间线段最短B．矩形的对称性C．矩形的四个角都是直角D．三角形的稳定性活动3课堂小结运用三角形的稳定性和四边形的不稳定性解释其在生活中的应用．【预习导学】知识探究具有没有自学反馈1．C 2.三角形的稳定性 3.A【合作探究】活动2跟踪训练1．图(1)，(4)，(6)具有稳定性． 2.C 3.D。

11.1.3 三角形的稳定性教学目标一，知识与能力通过观察，操作实践，想象推理，交流等活动，让学生理解三角形的稳定性，培养学生的实践能力，推理能力和表达能力。

二，过程与方法探究质疑，总结结果。

和学生共同探究三角形稳定性的实列，解决前面的疑惑。

三，情感，态度与价值观引导学生通过实验探究三角形的稳定性，培养其独立思考的想象习惯和动手能力教学重点会画三角形的稳定性，中线与角平分线。

教学难点理解“首尾顺次相连”等关键语句，熟练掌握和判断构成三角形的三条边的关系，钝角三角形和直角三角形的高。

教学过程一，复习回顾，导入新课教师和学生共同回顾前面两节课内容（第一节课，三角形的定义，三要素，三遍的关系：第二节课：三角形的高，中线和角平分线各有三条，三角形有关高，中线和角平分线的简单计算）。

教师可以在复习的同时，一边说，一边在黑板上画一个三角形，演示与三角形的有关咯线段。

教师进一步启发学生，我们学过了前面不少与三角形有关的线段的知识，而且在第一节开始我们还讲了三角形在现实生活中有非常广泛的应用。

那么这一节课我们就来做实验看看三角形是不是真的那么有用，如果没有三角形会怎么样？教师同时在黑板上写出本节课的题目-——三角形的稳定性。

二，实物演示1. 教师先在黑板上向学生展示下面三个不同的木架，然后把准备好的多组木架给学生，让他们亲自动手实验。

2. 给学生5分钟时间思考，然后提问学生：第一个木架和第二个木架有什么不同？(第一个木架不易变形，第二个木架很容易变形)。

第三个木架呢？为什么？(第三个木架很稳定，因为第三个木架中间那根木条将木架分成了两个不易变形的三角形)3. 拓展探索(1) 教师启发学生，再试着举出周围生活中有关三角形应用的例子。

(如桥梁起重机)最后给学校生演示生活中最常见的一个例子。

(2) 顺便给学生讲一讲四边形不稳定性的应用。

（衣服挂架，放缩尺等）通过实验，一方面让学生知道，学习就在生活中，这要用心就能在生活中有所发现，学习到很多学习到很多数学知识，解释很多现象，另一方面又可以提高学生学习数学知识的兴趣。

人教版数学八年级上册《11.1.3三角形的稳定性》教案一. 教材分析《11.1.3三角形的稳定性》是人教版数学八年级上册的一章，主要介绍三角形的稳定性原理。

本节内容是在学生已经掌握了三角形的基本概念和性质的基础上进行教学的，旨在让学生通过观察和操作，理解三角形的稳定性，并能运用这一原理解决实际问题。

二. 学情分析八年级的学生已经具备了一定的几何知识，对三角形有一定的了解。

但是，他们可能对抽象的稳定性概念难以理解，需要通过具体的操作和实践来加深理解。

同时，学生可能对实际问题的解决能力有待提高，需要教师通过实例进行引导和培养。

三. 教学目标1.理解三角形的稳定性原理。

2.能够运用三角形的稳定性原理解决实际问题。

3.培养学生的观察能力、操作能力和解决实际问题的能力。

四. 教学重难点1.重点：三角形的稳定性原理。

2.难点：如何运用三角形的稳定性原理解决实际问题。

五. 教学方法采用问题驱动法、操作实践法和实例教学法，引导学生通过观察、操作和思考，理解三角形的稳定性原理，并能运用到实际问题中。

六. 教学准备1.教具：三角板、直尺、圆规。

2.课件：相关的图片和实例。

七. 教学过程1.导入（5分钟）通过提问方式引导学生回顾三角形的基本概念和性质，为新课的学习做好铺垫。

2.呈现（10分钟）讲解三角形的稳定性原理，让学生通过观察和思考，理解三角形的稳定性。

3.操练（10分钟）让学生分组进行操作实践，用三角板、直尺和圆规画出不同形状的三角形，并观察它们的稳定性。

4.巩固（10分钟）让学生通过解决实际问题，运用三角形的稳定性原理。

如：为什么三角形的结构更稳定？在实际生活中有哪些应用？5.拓展（10分钟）引导学生思考：除了三角形，还有哪些形状具有稳定性？它们在实际生活中有哪些应用？6.小结（5分钟）对本节课的主要内容进行总结，强调三角形的稳定性原理及其在实际问题中的应用。

7.家庭作业（5分钟）布置一道关于三角形稳定性原理的应用题，让学生课后思考和解答。

11.1.3三角形的稳定性1113 三角形的稳定性在我们的日常生活和数学世界中，三角形是一个非常常见且重要的几何图形。

而三角形的稳定性这一特性，更是在众多领域发挥着关键作用。

让我们先来思考一下什么是稳定性。

简单来说，稳定性就是指一个物体或者结构在受到外力作用时，能够保持其原有形状和结构不发生变形或倒塌的能力。

那么，为什么说三角形具有稳定性呢？想象一下，我们用三根木棍钉成一个三角形。

无论我们怎么用力去推拉这个三角形，它的形状都很难发生改变。

这是因为三角形的三条边相互牵制，形成了一种内在的稳固结构。

从数学角度来看，三角形的稳定性是由其边和角的关系所决定的。

三角形的三条边长度一旦确定，其三个角的大小也就随之确定，而且这个三角形的形状和大小就完全固定下来了。

这种稳定性在建筑领域有着广泛的应用。

比如，在建造房屋的框架时，常常会使用三角形的结构来增加稳定性。

屋顶的三角架结构能够承受较大的重量和风力，使房屋更加坚固耐用。

桥梁的建设中也离不开三角形的稳定性。

许多大型桥梁的支撑结构都采用了三角形的设计，以确保桥梁在车辆通行和自然环境的影响下能够保持稳定。

在机械制造方面，三角形的稳定性同样不可或缺。

例如，一些机械零件的设计采用了三角形的结构，以提高其强度和稳定性，从而保证机器的正常运转。

日常生活中，我们也能随处发现三角形稳定性的应用。

自行车的车架通常是三角形的，这样在骑行过程中能够更好地承受各种力量，保证骑行的安全和稳定。

再比如晾衣架，它的结构往往也是三角形的，这样即使挂上很多衣物，也不容易变形。

甚至在一些运动器材中，三角形的稳定性也发挥着作用。

比如健身器材中的某些支撑部件，采用三角形结构可以增加器材的稳定性和安全性。

与三角形的稳定性形成对比的是四边形。

四边形的不稳定性在某些情况下也是有用的，但在大多数需要稳定结构的场景中，三角形显然更具优势。

如果我们用四根木棍钉成一个四边形，轻轻一推，它的形状就很容易发生改变。

这是因为四边形的边长和角度之间没有像三角形那样固定的关系，所以它的形状容易变动。

11.1.3三角形的稳定性1113 三角形的稳定性在我们日常生活和数学的学习中，三角形是一个非常常见且重要的几何图形。

而三角形的稳定性更是其独特而又关键的性质之一。

那什么是三角形的稳定性呢？简单来说，就是三角形的形状一旦确定，它的边长和角度就不会轻易改变，能够保持相对的固定。

我们先来想象一下，如果用三根木棍钉成一个三角形，无论怎么用力去推拉它，这个三角形的形状都很难发生改变。

但是如果换成四根木棍钉成一个四边形，轻轻一推，它的形状就很容易发生变化。

这就是三角形稳定性的一个直观体现。

三角形稳定性的原理其实与三角形的内角和以及三边的关系密切相关。

三角形的内角和总是 180 度，这就决定了三角形三个角的大小是固定的。

而且三角形任意两边之和大于第三边，任意两边之差小于第三边，这样的边的关系使得三角形的形状具有很强的稳定性。

在实际生活中，三角形稳定性的应用无处不在。

比如建筑领域，许多大型的桥梁结构中都会用到三角形。

像著名的埃菲尔铁塔，它的塔身就包含了大量的三角形结构，这使得铁塔能够在风雨中屹立不倒，承受巨大的重量和外力。

再看我们常见的自行车车架，它也是由许多三角形组成的。

这不仅保证了自行车在骑行过程中的稳定性，还能使车架更加坚固耐用。

在家具制造中，三角形稳定性同样发挥着重要作用。

一些椅子和桌子的支撑结构常常采用三角形，这样可以避免家具在使用过程中出现摇晃或者变形的情况。

甚至在一些简单的工具中，比如衣架，其挂钩部分通常也是三角形的设计，这样能够更好地挂住衣物，不容易变形。

三角形稳定性在机械制造方面也有着广泛的应用。

比如一些起重机的起重臂、挖掘机的铲斗支撑结构等，都采用了三角形的设计，以确保在工作时能够承受巨大的压力和重量，保持结构的稳定和安全。

从物理学的角度来看，三角形稳定性可以理解为一种力学上的平衡。

当外力作用于三角形结构时，三角形的三边和三个角能够共同分担和抵抗外力，从而使整个结构保持稳定。

与三角形的稳定性相对的是四边形等其他多边形的不稳定性。

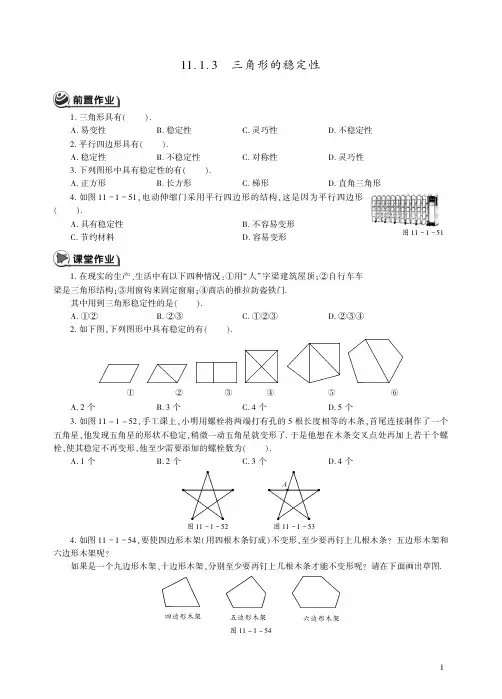
㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀１１.１.３㊀三角形的稳定性１.三角形具有(㊀㊀).Ａ.易变性Ｂ.稳定性Ｃ.灵巧性Ｄ.不稳定性２.平行四边形具有(㊀㊀).Ａ.稳定性Ｂ.不稳定性Ｃ.对称性Ｄ.灵巧性３.下列图形中具有稳定性的有(㊀㊀).Ａ.正方形Ｂ.长方形Ｃ.梯形Ｄ.直角三角形图１１－１－５１４.如图１１－１－５１ꎬ电动伸缩门采用平行四边形的结构ꎬ这是因为平行四边形(㊀㊀).Ａ.具有稳定性Ｂ.不容易变形Ｃ.节约材料Ｄ.容易变形１.在现实的生产㊁生活中有以下四种情况:①用 人 字梁建筑屋顶ꎻ②自行车车梁是三角形结构ꎻ③用窗钩来固定窗扇ꎻ④商店的推拉防盗铁门.其中用到三角形稳定性的是(㊀㊀).Ａ.①②Ｂ.②③Ｃ.①②③Ｄ.②③④２.如下图ꎬ下列图形中具有稳定的有(㊀㊀).①㊀②㊀③㊀④㊀⑤㊀⑥Ａ.２个Ｂ.３个Ｃ.４个Ｄ.５个３.如图１１－１－５２ꎬ手工课上ꎬ小明用螺栓将两端打有孔的５根长度相等的木条ꎬ首尾连接制作了一个五角星ꎬ他发现五角星的形状不稳定ꎬ稍微一动五角星就变形了.于是他想在木条交叉点处再加上若干个螺栓ꎬ使其稳定不再变形ꎬ他至少需要添加的螺栓数为(㊀㊀).Ａ.１个Ｂ.２个Ｃ.３个Ｄ.４个图１１－１－５２㊀㊀㊀㊀图１１－１－５３４.如图１１－１－５４ꎬ要使四边形木架(用四根木条钉成)不变形ꎬ至少要再钉上几根木条?五边形木架和六边形木架呢?如果是一个九边形木架㊁十边形木架ꎬ分别至少要再钉上几根木条才能不变形呢?请在下面画出草图.㊀四边形木架㊀㊀㊀五边形木架㊀㊀㊀六边形木架图１１－１－５４１基础训练１.下列图形具有稳定性的是(㊀㊀).Ａ.正五边形Ｂ.正方形Ｃ.梯形Ｄ.等腰三角形２.下列不是利用三角形稳定性的是(㊀㊀).Ａ.伸缩晾衣架Ｂ.三角形房架Ｃ.自行车的三角形车架Ｄ.矩形门框的斜拉条３.下列关于三角形稳定性和四边形不稳定性的说法正确的是(㊀㊀).Ａ.稳定性总是有益的ꎬ而不稳定性总是有害的Ｂ.稳定性有利用价值ꎬ而不稳定性没有利用价值Ｃ.稳定性和不稳定性均有利用价值Ｄ.以上说法都不对图１１－１－５６４.如图１１－１－５６ꎬ一扇窗户打开后用窗钩ＡＢ可将其固定ꎬ这里所运用的几何原理是(㊀㊀).Ａ.三角形的稳定性Ｂ.两点确定一条直线Ｃ.两点之间线段最短Ｄ.垂线段最短５.判断题(正确的画 ɿ ꎬ错误的画 ˑ ).(１)三角形具有稳定性.(㊀㊀)(２)四边形不具有稳定性.(㊀㊀)(３)三角形的稳定性在生产㊁生活中有广泛的应用ꎬ而四边形的不稳定性在生产㊁生活中没有应用.(㊀㊀)(４)只要在四边形的对角线上加钉一根木条ꎬ这个四边形就可以固定了.(㊀㊀)拓展提高６.下列图形具有稳定性的有(㊀㊀).①㊀②㊀③㊀④㊀⑤Ａ.①②Ｂ.②③⑤Ｃ.③⑤Ｄ.①②③④⑤７.一个六边形钢架ＡＢＣＤＥＦꎬ如图１１－１－５７所示ꎬ它由６条钢管绞接而成.在生活中ꎬ要保持该钢架稳定且形状不变ꎬ必须在接点处增加一些钢管绞接.通过实践至少再用三根钢管.请同学们想一想ꎬ下面固定方法中ꎬ如图１１－１－５８所示ꎬ能保持该六边形钢架稳定且形状不变的有㊀㊀㊀㊀.(只填序号)图１１－１－５７㊀㊀㊀图１１－１－５８８.多边形木架具有不稳定性ꎬ但加钉一些木条可以使其保持形状不变.多边形４５６７至少要加钉木条根数１２３４㊀㊀根据上面规律ꎬ要使一个２ｎ(ｎȡ２)边形的木架形状不变ꎬ至少要钉㊀㊀㊀㊀根木条.２发散思维９.如图１１－１－５９都是由若干木条钉成的多边形木框ꎬ要想把它们固定住ꎬ那么至少要用多少根木条才能保持木框的稳定性ꎬ设多边形的边数为ｎꎬ所用的木条数为ｍꎬ请填空:㊀㊀(１)㊀㊀㊀㊀㊀(２)㊀㊀㊀㊀㊀(３)㊀㊀㊀㊀㊀㊀(４)㊀㊀㊀㊀㊀㊀㊀㊀(５)图１１－１－５９当ｎ＝３时ꎬｍ＝㊀㊀㊀㊀ꎻ当ｎ＝４时ꎬｍ＝㊀㊀㊀㊀ꎻ当ｎ＝５时ꎬｍ＝㊀㊀㊀㊀ꎻ写出多边形木框的木条数ｎ与ｍ的关系式为㊀㊀㊀㊀.１０.六边形钢架ＡＢＣＤＥＦꎬ由６条钢管铰接而成ꎬ如图１１－１－６０所示ꎬ为使这一钢架稳固ꎬ试用三条钢管连接使之不能活动ꎬ方法很多ꎬ请至少画出三种方法.(只需画图ꎬ不必写出作法)㊀㊀图１１－１－６０３。