2010届山东莘县实验高中高三第一次月考数学(理)

山东省聊城实验高中高三第一次月考数学试题：高三同学的复习整在全国各高中火热上演，第一次月考也随着总复习的进行陆续展开，精品的小编邀请大家在课后参考练习山东省聊城实验高中高三第一次月考数学试题，帮助您提高成绩!一、问答题：(本题共10个小题，每小题5分，共50分)2.已知(，，)，(，，0)，则向量与的夹角为3. 已知，，则的最小值是4. 若，则等于5. 函数在点处的导数是6. 在棱长为的正四面体中，若、分别是棱、的中点，则=7. 某校共有7个车位，现要停放3辆不同的汽车，若要求4个空位必须都相邻，则不同[来源:ZXXK]的停放方法共有8. 若幂函数的图象经过点，则它在点处的切线方程为9. 若函数的图象的顶点在第四象限，则函数的图象可能是10. 设是定义在R上的奇函数，,当时，有恒成立，则不等式的解集是二、填空题：(本题共4个小题，每小题4分，共16分)[来源:Zxxk]11. 若，其中、，是虚数单位，则_________。

[来源:]12. 函数的单调增区间为_________________。

13. 定积分的值等于_________________。

14. 若内一点满足，则。

类比以上推理过程可得如下命题：若四面体内一点满足，则 .[来源:学.科.网Z.X.X.K]三、解答题：(本题共5个小题，共54分)15.(本题共10分)已知函数。

(Ⅰ)若曲线在处的切线与直线垂直，求的值;(Ⅱ)若函数在区间(，)内是增函数，求的取值范围。

16. (本题共10分)[来源:]已知函数，当时，有极大值。

(Ⅰ)求的值; (Ⅱ)求函数的极小值。

17.(本题共10分)将两块三角板按图甲方式拼好，其中，，，，现将三角板沿折起，使在平面上的射影恰好在上，如图乙. (Ⅰ)求证：平面;w.w.w.zxxk.c.o.m(Ⅱ)求二面角的余弦值;18.(本题共12分)据统计某种汽车的最高车速为120千米∕时，在匀速行驶时每小时的耗油量(升)与行驶速度(千米∕时)之间有如下函数关系：。

Unit 4 Food Grammar (1) Speak up Say something about your diets and lifestyles. Listen and answer What does he/ she have for breakfast/ lunch/ supper/breakfast? How often does he/ she have them? Listen and answer What sports does he/she do after school? How often does he/she do it? Practice Complete Part A. Work in pairs and talk about your diets and lifestyles using the adverbs of frequency. How often do you…? I never/ seldom/ sometimes/ often/ usually/ always… My daily activities I always walk to school. I never drive. I sometimes eat lunch in a restaurant. I often eat fruit and salad at lunchtime. Write down your diets and liftestyles I have… I play… Asking and answering Ask and answer about the diets and lifestyles Ss write. How often do you…? Sandy’s activities Mon day Tues day Wednes-day Tues-day Friday Satur-day Sun-day Dance Music Dance Basket-ball Music Dance Dance Film Dance Music Dance Film Compu-ter Music Music Compu-ter Comp-ter Film Dance Music Film Sandydances. Sandy listens to music. Sandy goes basketball. Sandyplays computer games Sandy watches a film. 太阳总是从东方升起,西方落下. The sun ____ _ rises in the east and sets in the west. 他通常１０点钟睡觉． He ______ goes to bed at ten o’clock.他上学经常迟到． He is _____ late for school. always usually often 有时他晚饭后去图书馆. He__________ goes to the library after supper. 莉莉不常读报． Lily ________reads newspaper. 我上学从来不迟到． I am _____late for school. never seldom sometimes countable uncountable … … apple orange cup plate egg dish pot salt beef bread cake hamburger cheese Coke vinegar bowl juice meat milk rice tomato cake Can you help them find the right family? Fill in the blanks: 1.This is ____ Tom. He is ___American boy. 2.-Where are _____flowers? -They are on ___ desk. 3.-What can you see in ____picture? - I can see ___girl and ____apple. - Who is ____ girl? - She is ____my sister. / an the the a the the an / 1.Class Two have____map. ____map is on ____wall of their classroom. It’s _____map of _____China. 2.-Is it _____ “U”? -Yes, it is. a the The an the / * *。

2021——2021学年度第一学期第一次月考高三数学试题〔理〕第一卷一、选择题：本大题共12小题，每题5分，总分值60分.在每题给出的四个选项中，只有一项为哪一项符合题目要求的.1．假设集合{}1,A x x x R =≤∈，{}2,B y y x x R ==∈，那么AB =A ．{}11x x -≤≤ B ．{}0x x ≥ C ．{}01x x ≤≤ D ．∅ 2．以下命题中的假命题是A ．∀x R ∈,120x -> B. ∀*x N ∈,2(1)0x ->C ．∃x R ∈,lg 1x < D. ∃x R ∈,tan 2x = 3．幂函数的图象过点〔2，41〕，那么它的单调递增区间是A.()∞+，0B. [)∞+，0C. ()0，∞-D. ()∞+∞-，4. 函数221)(x x x f x--=5．设0abc >，二次函数()2f x ax bx c =++的图象可能是A 、B 、C 、D 、6．假设372log πlog 6log 0.8a b c ===，，，那么A ．a b c >>B ．b a c >>C ．c a b >>D ．b c a >>7. )(x f y =是定义在R 上的奇函数，当0≥x 时，x x x f 2)(2-=，那么在R 上)(x f 的表达式是A.)2(--x xB.)2(-x xC.)2(-x xD.)2(-x x8.函数2()24(03),f x ax ax a =++<<假设1212,1,x x x x a <+=-那么 A ．12()()f x f x >B ．12()()f x f x <C ．12()()f x f x =D ．1()f x 与2()f x 的大小不9．函数()21xf x =-，假设a b c <<且()()()f a f c f b >>，那么以下式子成立的是A.0,0,0a b c <<<B. 0,0,0a b c <≥>C. 22ac -< D. 222a c +<10. “14m <〞是“一元二次方程20x x m ++=〞有实数解的11．设函数()x f =x x sin ，假设⎥⎦⎤⎢⎣⎡-∈2,2,21ππx x ，且()()21x f x f >，那么以下不等式必定成立的是A.2221x x >B.21x x <C.21x x >D.021>+x x12．用{}min ,a b 表示a ，b 两数中的最小值。

山东省莘县实验高中2010届高三第一次月考物理试题（时间：100分钟总分：100分）一．选择题：（每题3分，部分对2分，共36分）1．甲、乙两个质点同时、同地向同一方向做直线运动，它们的速度一时间图象如右图所示，则由图象可知（）A．甲质点比乙质点运动得快，故乙追不上甲B．在2s末时乙追上甲C．在2s末时甲、乙的位移相同D．甲做匀速直线运动，乙做初速度为零的匀加速直线运动2．从某一高度相隔1s释放两个相同的小球甲和乙，不计空气阻力，它们在空中任一时刻（）A．甲、乙两球距离越来越大，甲、乙两球速度之差越来越大B．甲、乙两球距离始终保持不变，甲、乙两球速度之差保持不变C．甲、乙两球距离越来越大，但甲、乙两球速度之差保持不变D．甲、乙两球距离越来越小，甲、乙两球速度之差越来越小3．如图A、B两物体叠放在一起，用手托住，让它们静靠在竖直墙边，然后释放，它们同时沿墙面向下滑，已知m A＞m B,则物体B ( )A．只受一个重力B．受到重力和一个摩擦力C．受到重力、一个弹力和一个摩擦力D．受到重力、一个摩擦力和两个弹力4．一质点沿直线Ox方向做变速运动，它离开O点的距离x随时间变化的关系，它的速度随时间t变化的关系为v=6t2（m/s），该质点在t=0到t=2s间的平均速度和t=2s到t=3s间的平均速度的大小分别为（）A．12m/s，39m/s B．8m/s，38m/sC．12m/s，19.5m/s D．8m/s，13m/s5.如右图所示，A.B两物体重力分别是3N和4N，A用细绳悬挂在天花板上，B放在水平地面上，连接A.B间的轻弹簧的弹力F=2N，则绳中张力T及B对地面的压力N的可能值分别是（）A．7N和2N B．5N和2NC．1N和6N D．2N和5N6．如右图所示，一个质量为m=2.0kg的物体，放在倾角为θ=300的面上静止不动，若用竖直向上的大小为F=5.0N的力提物体，物体仍静止（g取10m/s2），下列结论正确的是（）A．物体受到合外力减少5.0NB．物体受到摩擦力减少5.0NC．斜面受到压力减少5.0ND．物体对斜面的作用力减少5.0N7．如图所示，质量均为m的钩码A和B，用绳连接后挂在两个高度相同的光滑的滑轮上，处于平衡状态，在两滑轮中点再挂一个质量为m的钩码C，设竖直绳足够长，放手后，则（）A．C仍保持静止在原来的位置B．C一直加速下落，直到A碰到滑轮为止C．C下落的加速度方向不变D．C下落的过程是先加速再减速8．在升降机里，一个小球系于弹簧下端，如图所示，升降机静止时，弹簧伸长4cm，升降机运动时，弹簧伸长2cm，则升降机运动情况可能是（）A．以1m/s2的加速度加速下降 B．以4.9m/s2的加速度减速上升C．以1m/s2的加速度加速上升 D．以4.9m/s2的加速度加速下降9．如图所示，一个重为5N的大砝码，用细线悬挂在O点，现在用力F拉法码，使悬线偏离竖直方向30°时处于静止状态，此时所用拉力F的最小值为（）A．5.0N B．2.5NC．8.65N D．4.3N10.完全相同的直角三角形滑块AB按如右图所示叠放，设AB接触的斜面光滑，A与桌面的动摩擦因数为，现在B上作用一水平推力F，恰好使AB一起在桌面上匀速运动，且AB保持相对静止，则A与桌面的动摩擦因数与斜面倾角的关系为（）A． B．C． D．11、如图所示，一人坐在小车的水平台面上，用水平力拉绕过定滑轮的细绳，使人和车以相同的加速度向右运动，水平地面光滑（）A．若人的质量大于车的质量，则车对人的摩擦力方向向右B．若人的质量小于车的质量，则车对人的摩擦力方向向右C．若人的质量等于车的质量，则车对人的摩擦力为零D．不管人、车的质量关系如何，则车对人的摩擦力都为零12．如图所示，一个木块A放在长木板B上，长木板B放在水平地面上．在恒力F作用下，长木板B以速度v匀速运动，水平弹簧秤的示数为T．下列关于摩擦力的说法正确的是( )A．木块A受到的滑动摩擦力的大小等于TB．木块A受到的静摩擦力的大小等于TC．若长木板B以2，的速度匀速运动时，木块A受到的摩擦力大小等于2TD．若用2F的力作用在长木板上，木块A受到的摩擦力大于T二．实验题：（13题4分，14题6分，共10分）13．在验证力的平行四边形定则的实验中，橡皮绳的一端固定在木板上，用两个测力计把橡皮绳另一端拉到一个确定的点O。

莘县实验高中高二年级阶段性检测高二数学试题（理科）一、 选择题：（本题共12个小题，每小题4分，共48分，每题所给的四个选项中只有一个正确的）1. 函数()y f x =在0x x =处的导数定义中，自变量x 在0x 处的增量x ∆ （ ）A 、大于0B 、小于0C 、等于0D 、不等于0 2. 已知)1(2)(/2xf x x f += ，则)0(/f = （ ）A 、0B 、-4C 、-2D 、23. 函数13)(23+-=x x x f 是减函数的区间是 （ ）)2,0(.)0,(.)2,(.),2(.D C B A -∞-∞+∞ 4.考函数），在（∞+∞-=-cos 2)(x x x f 上 （ ）A.是增函数B.是减函数C.有最大值D.有最小值5. 以下四个关于复合函数如何复合而成的结论中，不正确的结论是 ( )A.y=sin4(1+31x )是由y=u4 u=sinv v=1+31x 复合而成B.y=(3+4xm)n 是由y=un,u=3+4xm 复合而成C.y=log2(2x+1-1)是由y=log2u u=2v v=x+1复合而成D.y=Asin(ωx+φ)是由y=Asinu u=ωx+φ复合而成6．函数y=xxsin 的导数为 ( ) A.y ′=2sin cos x x x x + B.y ′=2sin cos x xx x - C.y ′=2cos sin x x x x - D.y ′=2cos sin xxx x + 7. 函数y=xa x 22+(a>0)的导数为0，那么x 等于 ( )A.aB.±aC.-aD.2a8. 若函数f(x)＝3)1()1(2131/2/3+-+x f x f x ，则f(x)在点(0，f(0))处切线的倾斜角为( )A.π4B.π3C.2π3D.3π49．物体A 以速度v ＝3t2＋1(m/s)在一直线l 上运动，物体B 在直线l 上，且在物体A 的正前方5 m 处，同时以v ＝10t(m/s)的速度与A 同向运动，出发后物体A 追上物体B 所用的时间t(s)为 ( ) A.3 B.4 C.5 D.610．函数c bx ax x x f +++=23)(，其中c b a ,,为实数，当032<-b a 时，)(x f （）A.增函数B.减函数C.常数D.既不是增函数也不是减函数11．如图，直线l 和圆C ，当l 从0l 开始在平面上绕点P 按逆时针方向匀速转动（转动角度不超过900）时，它扫过的圆内阴影部分的面积S 是时间t 的函数， 这个函数的图象大致是 ( )12.函数 )(x f =223x a bx ax +--在1=x 时有极值10，则b a ,的值为 （ ） A .11,43,3=-=-==b a b a 或 B.1,4=-=b a 11,1-==b a 或 C.11,4==b a D.以上都不对二、填空题（本题共4个小题，每小题4分，共16分）13. .___________2)1()1(lim ,1 1)(0=-+=→xf x f x x f x 则处的导数为在已知函数14.=⎰dx 211-x -1_________.15. 如图，函数)(x f y =的图象在点P 处的切线是l ，则=+)2()2(/f f ___ ______.4.5y l P16. 将正数a 分成两部分，使其平方和为最小，这两部分应分成_____ 和_____ ．三．解答题：（共56分，解答应写出必要的文字说明、证明过程或演算步骤.）17. （本题满分10分）已知函数193)(23+++-=x x x x f .（Ⅰ）求)(x f 的单调递减区间；（Ⅱ）求)(x f 在区间[]2,2-上的最大值和最小值18. （本题满分10分）计算由直线,4-=x y 曲线x y 2=以及x 轴所围成的面积.19. （本题满分12分） 已知函数x a x x f ln 21)(2-=(R x ∈) （1）若函数)(x f 的图象在2x =处的切线方程为b x y +=，求b a ,的值； （2）若函数)(x f 在(1,∞)上是增函数，求a 的取值范围.20. （本题满分12分）某个体户计划经销A 、B 两种商品，据调查统计，当投资额为x （0≥x ）万元时，在经销A 、B 商品中所获得的收益分别为)(x f 万元与)(x g 万元， 其中2)1()(+-=x a x f ，)ln(6)(b x x g +=（0,0>>b a ），已知投资额为零时，收益为零． （Ⅰ）试求出a 、b 的值；（Ⅱ）如果该个体户准备投入5万元经营这两种商品，请你帮他制定一个资金投入方案，使他能获得最大收益，并求出其收入的最大值．（精确到0.1，参考数据：10.13ln ≈）21．（本题满分12分） 已知函数f(x)=x 321-x 2+bx+c.(1)若f(x)在（-∞，+∞）上是增函数，求b 的取值范围;(2)若f(x)在x=1处取得极值，且x ∈［-1,2］时，f(x)<c2恒成立， 求c 的取值范围.莘县实验高中高二年级阶段性检测高二数学试题（理科）参考答案一、选择题：1. D2. B3. D4. A5. C（C中函数y=log2(2x+1-1)是由y=log2u u=2v-1 v=x+1复合而成的.）9. C 因为物体A 在t 秒内行驶的路程为∫t 0(3t2＋1)dt ，物体B 在t 秒内行驶的路程为∫t 010tdt ，所以∫t 0(3t2＋1－10t)dt ＝ (t3＋t －5t2)|t 0＝t3＋t －5t2＝5 ⇒(t －5)(t2＋1)＝0，即t ＝5. 10. A 11. D 12. C二、填空题：13、 12 14、2π 15、98 16、;22a a三、解答题：17.解：（Ⅰ）'2()369f x x x =-++令'2()03690f x x x <-++<即(,1)(3,)x ∴∈-∞-+∞解得x>3或x<-1 和单调递减（Ⅱ）令()0f x =解得x=-1或x=3(舍）f(2)=-8+12+18+1=23f(-2)=8+12-18+1=3f(-1)=1+3-9+1=-4f(x)的最大值为23，最小值为-4.18解：340（见课本57P 例2）19.解：（1）()21ln ()(0)2af x x a x f x x x x '=-⇒=->由题意得：(2)12212(2)22ln 22ln 22a f a f b b a b ⎧'==-=⎧⎧⎪⇔⇔⎨⎨⎨=+=-⎩⎩⎪-=+⎩（2）函数()f x 在1x >上是增函数()0af x x x '⇔=-≥在1x >上恒成立2a x ⇔≤在1x >上恒成立1a ⇔≤21.解：（1）)(x f ' =3x2-x+b,因f(x)在（-∞，+∞）上是增函数， 则)(x f '≥0.即3x2-x+b ≥0,∴b ≥x-3x2在（-∞，+∞）恒成立.设g(x)=x-3x2. 当x=61时，g(x)max=121,∴b ≥121.(2)由题意知)1('f =0，即3-1+b=0，∴b=-2.x ∈［-1,2］时，f(x)<c2恒成立，只需f(x)在［-1，2］上的最大值小于c2即可.因)(x f '=3x2-x-2,令)(x f '=0,得x=1或x=-32.∵f(1)=-23+c,f(-,21)1(,2722)32c f c +=-+=f(2)=2+c.∴f(x)max=f(2)=2+c,∴2+c<c2.解得c>2或c<-1，所以c 的取值范围为 （-∞，-1）∪（2，+∞）.。

山东省聊城市莘县实验高级中学高三数学理联考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 偶函数与奇函数的定义域均为，在，在上的图象如图，则不等式的解集为（）A. B.C. D.参考答案：B略2. 若存在，，使得成立，则实数的取值范围是( )A. B. C. D.参考答案：D3. 已知m，n是两条不同的直线，是两个不同的平面，则下列命题中的真命题是（）A．若 B．若C．若 D．若则参考答案：D略4.已知，，则等于（）A. B. C. D. 7参考答案：答案: A5. 过抛物线：的焦点的直线与抛物线C交于，两点，与其准线交于点，且，则A．B．C．D．1参考答案：B6. 椭圆的离心率为（）Ａ．Ｂ．Ｃ．Ｄ．参考答案：B7. 是内的一点，，则的面积与的面积之比为A． B． C． D．参考答案：A8. 如图，网格纸上小正方形的为长为1，粗实线面出的是某几何体的三视图，该几何体的各个面中有若干个是梯形，这些梯形的面积之和为（）A. 6B. 9C.D.参考答案：A【分析】画出几何体的直观图，利用三视图的数据求解即可．【详解】由三视图可知该几何体的各个面分别为，两个梯形PQCD和PQBA，一个矩形ABCD，两个三角形PDA和三角形QCB，所以两个梯形的面积相等，和为．故选：A．【点睛】本题考查三视图与直观图的关系，解题的关键是几何体的直观图的形状，考查空间想象能力以及计算能力．9. 若，则的值为（）Ａ．Ｂ．Ｃ．Ｄ．参考答案：C略10.过椭圆的右焦点作轴的垂线交椭圆于A,B两点，已知双曲线的焦点在轴上，对称中心在坐标原点且两条渐近线分别过A,B两点，则双曲线的离心率为 ( )A B C D 2参考答案：答案:B二、填空题:本大题共7小题,每小题4分,共28分11. 椭圆一个长轴的一个顶点为，以为直角顶点做一个内接于椭圆的等腰直角三角形，则此直角三角形的面积等于__________．参考答案：设内切于椭圆的等腰直角三角形为，则，，直线，可求得，，．12. 函数的图象与函数的图象的公共点个数是_________个.参考答案：2个略13. 若α∈，且sinα＝，则sin＋cos＝．参考答案：【知识点】两角和与差的余弦函数；同角三角函数间的基本关系；两角和与差的正弦函数.C2,C5【答案解析】解析：解：∵，且，∴cosα=﹣,又=cosα∴=×（﹣）=故答案为【思路点拨】由题设条件知本题是一个三角化简求值题，可先由同角三角函数的基本关系求出角α的余弦，再由正弦的和角公式，余弦的和角公式将展开成用角α的余弦，正弦表示，代入值即可求得答案14. 从圆外一点作这个圆的切线，设两条切线之间所夹的角为，则．参考答案：15. 在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若其面积S=（b 2+c2﹣a 2），则∠A=．参考答案：考点：余弦定理．专题：计算题．分析：根据三角形的面积公式S=bcsinA，而已知S=（b2+c2﹣a2），两者相等得到一个关系式，利用此关系式表示出sinA，根据余弦定理表示出cosA，发现两关系式相等，得到sinA等于cosA，即tanA等于1，根据A的范围利用特殊角的三角函数值即可得到A的度数．解答：解：由已知得：S=bcsinA=（b2+c2﹣a2）变形为：=sinA，由余弦定理可得：cosA=，所以cosA=sinA即tanA=1，又A∈（0，π），则A=．故答案为：。

高三年级第一次月考 数学试题（理）（满分150分，考试时刻120分）一、选择题(5×12＝60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项用2B 铅笔涂黑答题纸上对应题目的答案标号)1．分析人的身高与体重的关系，能够用 A ．残差分析 B ．回归分析 C ．等高条形图D ．独立性检验2．甲、乙、丙3位同窗选修课程，从4门课程中，甲选修2门，乙、丙各选修3门，则不同的选修方案共有A ．36B ．48种C ．96种D ．192种3．已知f (x )＝⎩⎪⎨⎪⎧x －6x ≥6f x ＋2 x <6，则f (3)为A ．1B ．2C ．4D ．54．设随机变量X 服从二项散布X ～B (n ，p )，则D X2E X2等于A ．p 2B ．(1－p )2C ．1－pD ．以上都不对5．张、王两家夫妇各带1个小孩一路到动物园游玩，购票后排队依次入园．为安全起见，首尾必然要排两位爸爸，另外，两个小孩必然要排在一路，则这6人的入园顺序排法种数共有A ．12种B ．24种C ．36种D ．48种6．若f (x )是R 上周期为5的奇函数，且知足f (1)＝1，f (2)＝2，则f (3)－f (4)＝A ．1 B ． 1 C ．2 D ．-27．已知函数y ＝1－x ＋x ＋3的最大值为M ，最小值为m ，则mM的值为 A.32 B. 22 C. 12 D. 148．1sin10º－3sin80º等于 .2 C D.149．已知0<a<1，则方程a |x|=|log a x|的实根的个数是A ．1B ．2C ．3D ．1或2或310．函数f (x )＝12e x (sin x ＋cos x )在区间⎣⎢⎡⎦⎥⎤0，π2上的值域为A ．211,e 22π⎡⎤⎢⎥⎣⎦B ．211,e 22π⎛⎫ ⎪⎝⎭C ．[1，2e π] D ．(1，2e π)11．设m 为正整数，(x ＋y )2m展开式的二项式系数的最大值为a ，(x ＋y )2m ＋1展开式的二项式系数的最大值为b .若13a ＝7b ，则m 等于( )A ．8B ．7C ．6D ．5 12．在(x 2＋3x ＋2)5的展开式中x 的系数为A ．800B ．360C ．240D ．160二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题纸的相应位置上) 13．若关于任意的实数x ，有x 3＝a 0＋a 1(x －2)＋a 2(x －2)2＋a 3(x －2)3.则a 2的值为______． 14．已知tan 2α=-，()1tan 7αβ+=，则tan β的值为_______. 15．若“0,,tan 4x x m π⎡⎤∀∈≤⎢⎥⎣⎦”是真命题，则实数m 的最小值为 . 16．设32,,(),.x x a f x x x a ⎧<⎪=⎨≥⎪⎩若存在实数b ，使得函数()()g x f x b =-有两个零点，则a 的取值范围是 .三、解答题(本大题6小题,共70分,解许诺写出文字说明、证明进程或演算步骤，并把解答写在答卷纸的相应位置上)17．(本题满分12分）1{24}32x A x-=≤≤，{}012322<--+-=m m mx x x B . （1）当N x ∈错误！未找到引用源。

2009——2010学年度第一学期第一次诊断性测试高三数学试题（文）第Ⅰ卷一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设全集U 是实数集R ，}034|{},22|{2<+-=>-<=x x x N x x x M 或，则图中阴影部分所表示的集合是( ) A ．}12|{<≤-x x B ．}22|{≤≤-x xC ．}21|{≤<x xD ．}2|{<x x 2．函数)1(log 12)(2---=x x x f 的定义域是( )A.[),3+∞B. )1,31(-C. )3,31(- D. )3,(--∞ 3．函数xx f 1)(=（x>1）的值域是（ ） A.()()∞+∞-，，00 B. R C. ),1(+∞ D. )1,0( 4.下列函数中，在其定义域内是减函数的是( )A.1)(2++-=x x x f B. xx f 1)(=C. ||)31()(x x f = D. )2ln()(x x f -=5．设)(x f 是定义在R 上的函数，其图像关于原点对称，且当x >0时，32)(-=xx f ，则=-)2(f ( )A ．1B ．-1C ．41D ．411-6．已知a<b<0，奇函数f(x)的定义域为[a,-a]，在区间[-b,-a]上单调递减且f(x)>0，则在区间[a,b]上( )A ．f (x)>0且| f (x)|单调递减B ．f (x)>0且| f (x)|单调递增C ．f (x)<0且| f (x)|单调递减D ．f (x)<0且| f (x)|单调递增 7. 函数)1(log )(++=x a x f a x在区间]1,0[上的最大值与最小值之和为a ，则a =( ) A ．41 B ．21C ．2D ．4 8. 设函数⎪⎩⎪⎨⎧>≤++=0,20,)(2x x c bx x x f ，若2)2(),0()4(-=-=-f f f ，则关于x 的方程x x f =)(的解的个数是( )A ．1B ．2C ．3D ．49．已知实数b a ,满足等式ba 32=，下列五个关系式：①;0ab <<②;0<<b a ③;0b a << ④;0<<a b ⑤.b a =其中可能成立的关系式有( ) A ．①②③B ．①②⑤C ．①③⑤D ．③④⑤10.函数()x x f 3log =在区间[]b a ,上的值域为[]1,0，则a b -的最小值为 （ ）A ．2B ．1C ．31 D ．3211．函数()f x 满足()()213f x f x ⋅+=，若()20=f ，则)2010(f = （ ） A. 13 B. 2 C. 132 D. 21312．若1x 满足272=+xx ，2x 满足27log 2=+x x ，则21x x +等于（ ）A ．25 B ．3 C ．27D ． 4 第II 卷二、填空题：本大题共4小题，每小题4分，满分16分.13.当0<x<1时，2212)(,)(,)(-===x x h x x g x x f 的大小关系是 _________. 14. 设()f x 是定义在R 上的以3为周期的奇函数，若23(1)1,(2)1a f f a ->=+，则a 的取值范围是_________.15. 已知f(x)是R 上的偶函数，且在(－∞,0)上是减函数，则不等式f(x)≤f(3)的解集是_________.16. 若函数)1,0()(≠>--=a a a x a x f x且有两个零点，则实数a 的取值范围_________.三、解答题：本大题共6小题，满分70分.解答须写出文字说明，证明过程和演算步骤. 17．（本题满分12分）已知集合}.02|{},,116|{2<--=∈≥+=m x x x B R x x x A （1）当m =3时，求)(B C A R ；（2）若}41|{<<-=x x B A ，求实数m 的值.18. （本小题满分12分）设命题p :函数()⎪⎭⎫⎝⎛+-=a x ax x f 161lg 2的定义域为R; 命题q :不等式a x x <-93对一切正实数均成立（1）如果p 是真命题，求实数a 的取值范围；（2）如果命题“p 或q ”为真命题且“p 且q ”为假命题，求实数a 的取值范围.19．（本小题满分12分）某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元，已知总收入满足函数：⎪⎩⎪⎨⎧>≤≤-=)400(,80000)4000(,21400)(2x x x x x g ，其中x 是仪器的月产量。

2010年普通高等学校招生全国统一考试（山东卷）理科综合能力全真模拟测试本试卷分第I卷（选择题）和第n卷（非选择题）两部分，满分240分，考生用时150分钟。

考试结束后，答题卡和答题纸一并交回。

答卷前，考生务必将自己的姓名、准考证号、考试科目填答题卡规定的地方。

第I卷（必做题，共88 分）注意事项：1•每小题选出答案后，用2B铅笔把答题卡上对应的答案标号涂黑，如需改动，用橡皮擦干净以后，再涂写其他答案标号。

不涂答题卡，只答在试卷上不得分。

2•第I卷共22小题，每小题4分，共88分。

相对原子质量：H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27K 39 Ca 40 Mn 55 Fe 56 Cu 64 Br 80 Ag 108 I 127 性一•选择题（本题包括15小题。

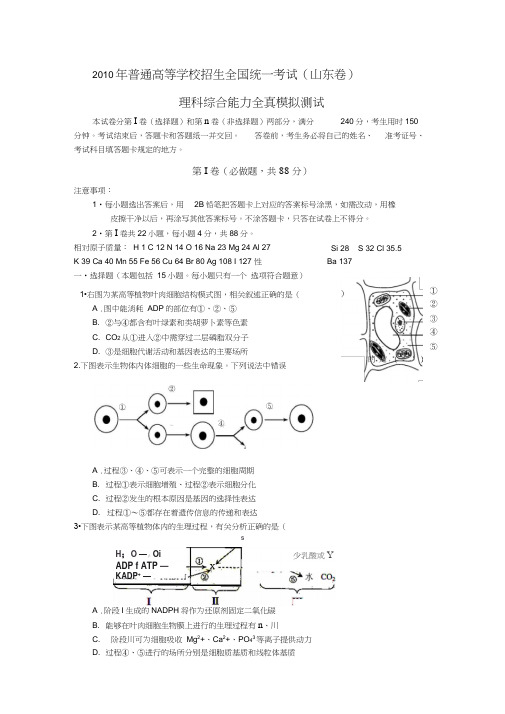
每小题只有一个选项符合题意）1•右图为某高等植物叶肉细胞结构模式图，相关叙述正确的是（A .图中能消耗ADP的部位有①、②、⑤B. ②与④都含有叶绿素和类胡萝卜素等色素C. CO2从①进入②中需穿过二层磷脂双分子D. ③是细胞代谢活动和基因表达的主要场所2.下图表示生物体内体细胞的一些生命现象。

下列说法中错误A .过程③、④、⑤可表示一个完整的细胞周期B. 过程①表示细胞增殖、过程②表示细胞分化C. 过程②发生的根本原因是基因的选择性表达D. 过程①〜⑤都存在着遗传信息的传递和表达3•下图表示某高等植物体内的生理过程，有关分析正确的是（A .阶段I生成的NADPH将作为还原剂固定二氧化碳B. 能够在叶肉细胞生物膜上进行的生理过程有n、川C. 阶段川可为细胞吸收Mg2+、Ca2+、PO43等离子提供动力D. 过程④、⑤进行的场所分别是细胞质基质和线粒体基质S 32 Cl 35.5Si 28Ba 137①②③④⑤①⑤④H；O —卜Oi ADP f ATP —KADP+—少乳酸或Y S4•下图表示人体体液免疫的过程。